A Mixed Integer (linear) Programming problem. More...
Inherits parma_polyhedra_library.PPL_Object.
Public Member Functions | |
Functions that Do Not Modify the MIP_Problem | |
| native long | max_space_dimension () |
| Returns the maximum space dimension an MIP_Problem can handle. | |
| native long | space_dimension () |
| Returns the space dimension of the MIP problem. | |
| native Variables_Set | integer_space_dimensions () |
| Returns a set containing all the variables' indexes constrained to be integral. | |
| native Constraint_System | constraints () |
| Returns the constraints . | |
| native Linear_Expression | objective_function () |
| Returns the objective function. | |
| native Optimization_Mode | optimization_mode () |
| Returns the optimization mode. | |
| native String | ascii_dump () |
Returns an ascii formatted internal representation of this. | |
| native String | toString () |
Returns a string representation of this. | |
| native long | total_memory_in_bytes () |
| Returns the total size in bytes of the memory occupied by the underlying C++ object. | |
| native boolean | OK () |
| Checks if all the invariants are satisfied. | |
Functions that May Modify the MIP_Problem | |
| native void | clear () |
Resets this to be equal to the trivial MIP problem. More... | |
| native void | add_space_dimensions_and_embed (long m) |
Adds m new space dimensions and embeds the old MIP problem in the new vector space. More... | |
| native void | add_to_integer_space_dimensions (Variables_Set i_vars) |
Sets the variables whose indexes are in set i_vars to be integer space dimensions. More... | |
| native void | add_constraint (Constraint c) |
Adds a copy of constraint c to the MIP problem. More... | |
| native void | add_constraints (Constraint_System cs) |
Adds a copy of the constraints in cs to the MIP problem. More... | |
| native void | set_objective_function (Linear_Expression obj) |
Sets the objective function to obj. More... | |
| native void | set_optimization_mode (Optimization_Mode mode) |
Sets the optimization mode to mode. | |
Computing the Solution of the MIP_Problem | |
| native boolean | is_satisfiable () |
Checks satisfiability of this. More... | |
| native MIP_Problem_Status | solve () |
| Optimizes the MIP problem. More... | |
| native void | evaluate_objective_function (Generator evaluating_point, Coefficient num, Coefficient den) |
Sets num and den so that 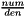 is the result of evaluating the objective function on is the result of evaluating the objective function on evaluating_point. More... | |
| native Generator | feasible_point () |
Returns a feasible point for this, if it exists. More... | |
| native Generator | optimizing_point () |
Returns an optimal point for this, if it exists. More... | |
| native void | optimal_value (Coefficient num, Coefficient den) |
Sets num and den so that 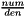 is the solution of the optimization problem. More... is the solution of the optimization problem. More... | |
Querying/Setting Control Parameters | |
| native Control_Parameter_Value | get_control_parameter (Control_Parameter_Name name) |
Returns the value of control parameter name. | |
| native void | set_control_parameter (Control_Parameter_Value value) |
Sets control parameter value. | |
Constructors and Destructor | |
| MIP_Problem (long dim) | |
| Builds a trivial MIP problem. More... | |
| MIP_Problem (long dim, Constraint_System cs, Linear_Expression obj, Optimization_Mode mode) | |
Builds an MIP problem having space dimension dim from the constraint system cs, the objective function obj and optimization mode mode. More... | |
| MIP_Problem (MIP_Problem y) | |
Builds a copy of y. | |
| native void | free () |
Releases all resources managed by this, also resetting it to a null reference. | |
| native void | finalize () |
Releases all resources managed by this. | |
Detailed Description
A Mixed Integer (linear) Programming problem.
An object of this class encodes a mixed integer (linear) programming problem. The MIP problem is specified by providing:
- the dimension of the vector space;
- the feasible region, by means of a finite set of linear equality and non-strict inequality constraints;
- the subset of the unknown variables that range over the integers (the other variables implicitly ranging over the reals);
- the objective function, described by a Linear_Expression;
- the optimization mode (either maximization or minimization).
The class provides support for the (incremental) solution of the MIP problem based on variations of the revised simplex method and on branch-and-bound techniques. The result of the resolution process is expressed in terms of an enumeration, encoding the feasibility and the unboundedness of the optimization problem. The class supports simple feasibility tests (i.e., no optimization), as well as the extraction of an optimal (resp., feasible) point, provided the MIP_Problem is optimizable (resp., feasible).
By exploiting the incremental nature of the solver, it is possible to reuse part of the computational work already done when solving variants of a given MIP_Problem: currently, incremental resolution supports the addition of space dimensions, the addition of constraints, the change of objective function and the change of optimization mode.
Constructor & Destructor Documentation
|
inline |
Builds a trivial MIP problem.
A trivial MIP problem requires to maximize the objective function 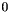 on a vector space under no constraints at all: the origin of the vector space is an optimal solution.
on a vector space under no constraints at all: the origin of the vector space is an optimal solution.
- Parameters
-
dim The dimension of the vector space enclosing this.
- Exceptions
-
Length_Error_Exception Thrown if dimexceedsmax_space_dimension().
|
inline |
Builds an MIP problem having space dimension dim from the constraint system cs, the objective function obj and optimization mode mode.
- Parameters
-
dim The dimension of the vector space enclosing this.cs The constraint system defining the feasible region. obj The objective function. mode The optimization mode.
- Exceptions
-
Length_Error_Exception Thrown if dimexceedsmax_space_dimension().Invalid_Argument_Exception Thrown if the constraint system contains any strict inequality or if the space dimension of the constraint system (resp., the objective function) is strictly greater than dim.
Member Function Documentation
| native void parma_polyhedra_library.MIP_Problem.clear | ( | ) |
Resets this to be equal to the trivial MIP problem.
The space dimension is reset to 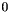 .
.
| native void parma_polyhedra_library.MIP_Problem.add_space_dimensions_and_embed | ( | long | m | ) |
Adds m new space dimensions and embeds the old MIP problem in the new vector space.
- Parameters
-
m The number of dimensions to add.
- Exceptions
-
Length_Error_Exception Thrown if adding mnew space dimensions would cause the vector space to exceed dimensionmax_space_dimension().
The new space dimensions will be those having the highest indexes in the new MIP problem; they are initially unconstrained.
| native void parma_polyhedra_library.MIP_Problem.add_to_integer_space_dimensions | ( | Variables_Set | i_vars | ) |
Sets the variables whose indexes are in set i_vars to be integer space dimensions.
- Exceptions
-
Invalid_Argument_Exception Thrown if some index in i_varsdoes not correspond to a space dimension inthis.
| native void parma_polyhedra_library.MIP_Problem.add_constraint | ( | Constraint | c | ) |
Adds a copy of constraint c to the MIP problem.
- Exceptions
-
Invalid_Argument_Exception Thrown if the constraint cis a strict inequality or if its space dimension is strictly greater than the space dimension ofthis.
| native void parma_polyhedra_library.MIP_Problem.add_constraints | ( | Constraint_System | cs | ) |
Adds a copy of the constraints in cs to the MIP problem.
- Exceptions
-
Invalid_Argument_Exception Thrown if the constraint system cscontains any strict inequality or if its space dimension is strictly greater than the space dimension ofthis.
| native void parma_polyhedra_library.MIP_Problem.set_objective_function | ( | Linear_Expression | obj | ) |
Sets the objective function to obj.
- Exceptions
-
Invalid_Argument_Exception Thrown if the space dimension of objis strictly greater than the space dimension ofthis.
| native boolean parma_polyhedra_library.MIP_Problem.is_satisfiable | ( | ) |
Checks satisfiability of this.
- Returns
trueif and only if the MIP problem is satisfiable.
| native MIP_Problem_Status parma_polyhedra_library.MIP_Problem.solve | ( | ) |
Optimizes the MIP problem.
- Returns
- An MIP_Problem_Status flag indicating the outcome of the optimization attempt (unfeasible, unbounded or optimized problem).
| native void parma_polyhedra_library.MIP_Problem.evaluate_objective_function | ( | Generator | evaluating_point, |
| Coefficient | num, | ||
| Coefficient | den | ||
| ) |
Sets num and den so that 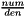 is the result of evaluating the objective function on
is the result of evaluating the objective function on evaluating_point.
- Parameters
-
evaluating_point The point on which the objective function will be evaluated. num On exit will contain the numerator of the evaluated value. den On exit will contain the denominator of the evaluated value.
- Exceptions
-
Invalid_Argument_Exception Thrown if thisandevaluating_pointare dimension-incompatible or if the generatorevaluating_pointis not a point.
| native Generator parma_polyhedra_library.MIP_Problem.feasible_point | ( | ) |
Returns a feasible point for this, if it exists.
- Exceptions
-
Domain_Error_Exception Thrown if the MIP problem is not satisfiable.
| native Generator parma_polyhedra_library.MIP_Problem.optimizing_point | ( | ) |
Returns an optimal point for this, if it exists.
- Exceptions
-
Domain_Error_Exception Thrown if thisdoesn't not have an optimizing point, i.e., if the MIP problem is unbounded or not satisfiable.
| native void parma_polyhedra_library.MIP_Problem.optimal_value | ( | Coefficient | num, |
| Coefficient | den | ||
| ) |
Sets num and den so that 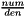 is the solution of the optimization problem.
is the solution of the optimization problem.
- Exceptions
-
Domain_Error_Exception Thrown if thisdoesn't not have an optimizing point, i.e., if the MIP problem is unbounded or not satisfiable.
The documentation for this class was generated from the following file:
- MIP_Problem.java
