parma_polyhedra_library.PIP_Problem Class Reference

A Parametric Integer Programming problem. More...

Inherits parma_polyhedra_library.PPL_Object.

Public Member Functions
	PIP_Problem (long dim)
	Builds a trivial PIP problem. More...
	PIP_Problem (long dim, Constraint_System cs, Variables_Set params)
	Builds a PIP problem from a sequence of constraints. More...
	PIP_Problem (PIP_Problem y)
	Builds a copy of y.
native void	free ()
	Releases all resources managed by this, also resetting it to a null reference.
Functions that Do Not Modify the PIP_Problem
native long	max_space_dimension ()
	Returns the maximum space dimension an PIP_Problem can handle.
native long	space_dimension ()
	Returns the space dimension of the PIP problem.
native long	number_of_parameter_space_dimensions ()
	Returns the number of parameter space dimensions of the PIP problem.
native Variables_Set	parameter_space_dimensions ()
	Returns all the parameter space dimensions of problem pip.
native long	get_big_parameter_dimension ()
	Returns the big parameter dimension of PIP problem pip.
native long	number_of_constraints ()
	Returns the number of constraints defining the feasible region of pip.
native Constraint	constraint_at_index (long dim)
	Returns the i-th constraint defining the feasible region of the PIP problem pip.
native Constraint_System	constraints ()
	Returns the constraints .
native String	ascii_dump ()
	Returns an ascii formatted internal representation of this.
native String	toString ()
	Returns a string representation of this.
native long	total_memory_in_bytes ()
	Returns the size in bytes of the memory occupied by the underlying C++ object.
native long	external_memory_in_bytes ()
	Returns the size in bytes of the memory managed by the underlying C++ object.
native boolean	OK ()
	Returns true if the pip problem is well formed, i.e., if it satisfies all its implementation invariants; returns 0 and perhaps makes some noise if broken. Useful for debugging purposes.
Functions that May Modify the PIP_Problem
native void	clear ()
	Resets this to be equal to the trivial PIP problem. More...
native void	add_space_dimensions_and_embed (long pip_vars, long pip_params)
	Adds pip_vars + pip_params new space dimensions and embeds the PIP problem in the new vector space. More...
native void	add_to_parameter_space_dimensions (Variables_Set vars)
	Sets the space dimensions in vars to be parameter dimensions of the PIP problem.
native void	set_big_parameter_dimension (long d)
	Sets the big parameter dimension of PIP problem to d.
native void	add_constraint (Constraint c)
	Adds a copy of constraint c to the PIP problem. More...
native void	add_constraints (Constraint_System cs)
	Adds a copy of the constraints in cs to the PIP problem. More...
Computing the Solution of the PIP_Problem
native boolean	is_satisfiable ()
	Checks satisfiability of this. More...
native PIP_Problem_Status	solve ()
	Optimizes the PIP problem. More...
native PIP_Tree_Node	solution ()
	Returns a solution for the PIP problem, if it exists.
native PIP_Tree_Node	optimizing_solution ()
	Returns an optimizing solution for the PIP problem, if it exists.
Querying/Setting Control Parameters
native PIP_Problem_Control_Parameter_Value	get_pip_problem_control_parameter (PIP_Problem_Control_Parameter_Name name)
	Returns the value of control parameter name.
native void	set_pip_problem_control_parameter (PIP_Problem_Control_Parameter_Value value)
	Sets control parameter value.

Protected Member Functions
native void	finalize ()
	Releases all resources managed by this.

Detailed Description

A Parametric Integer Programming problem.

An object of this class encodes a parametric integer (linear) programming problem. The PIP problem is specified by providing:

• the dimension of the vector space;
• the subset of those dimensions of the vector space that are interpreted as integer parameters (the other space dimensions are interpreted as non-parameter integer variables);
• a finite set of linear equality and (strict or non-strict) inequality constraints involving variables and/or parameters; these constraints are used to define:
  • the feasible region, if they involve one or more problem variable (and maybe some parameters);
  • the initial context, if they only involve the parameters;
• optionally, the so-called big parameter, i.e., a problem parameter to be considered arbitrarily big.

Note that all problem variables and problem parameters are assumed to take non-negative integer values, so that there is no need to specify non-negativity constraints.

The class provides support for the (incremental) solution of the PIP problem based on variations of the revised simplex method and on Gomory cut generation techniques.

The solution for a PIP problem is the lexicographic minimum of the integer points of the feasible region, expressed in terms of the parameters. As the problem to be solved only involves non-negative variables and parameters, the problem will always be either unfeasible or optimizable.

As the feasibility and the solution value of a PIP problem depend on the values of the parameters, the solution is a binary decision tree, dividing the context parameter set into subsets. The tree nodes are of two kinds:

• Decision nodes. These are internal tree nodes encoding one or more linear tests on the parameters; if all the tests are satisfied, then the solution is the node's true child; otherwise, the solution is the node's false child;
• Solution nodes. These are leaf nodes in the tree, encoding the solution of the problem in the current context subset, where each variable is defined in terms of a linear expression of the parameters. Solution nodes also optionally embed a set of parameter constraints: if all these constraints are satisfied, the solution is described by the node, otherwise the problem has no solution.

It may happen that a decision node has no false child. This means that there is no solution if at least one of the corresponding constraints is not satisfied. Decision nodes having two or more linear tests on the parameters cannot have a false child. Decision nodes always have a true child.

Both kinds of tree nodes may also contain the definition of extra parameters which are artificially introduced by the solver to enforce an integral solution. Such artificial parameters are defined by the integer division of a linear expression on the parameters by an integer coefficient.

By exploiting the incremental nature of the solver, it is possible to reuse part of the computational work already done when solving variants of a given PIP_Problem: currently, incremental resolution supports the addition of space dimensions, the addition of parameters and the addition of constraints.

Constructor & Destructor Documentation

parma_polyhedra_library.PIP_Problem.PIP_Problem ( long  dim )

inline

Builds a trivial PIP problem.

A trivial PIP problem requires to compute the lexicographic minimum on a vector space under no constraints and with no parameters: due to the implicit non-negativity constraints, the origin of the vector space is an optimal solution.

Parameters

dim	The dimension of the vector space enclosing this (optional argument with default value ).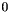

Exceptions

Length_Error_Exception

Thrown if dim exceeds max_space_dimension().

parma_polyhedra_library.PIP_Problem.PIP_Problem ( long  dim, Constraint_System  cs, Variables_Set  params  )

inline

Builds a PIP problem from a sequence of constraints.

Builds a PIP problem having space dimension dim from the constraint system cs; the dimensions vars are interpreted as parameters.

Member Function Documentation

native void parma_polyhedra_library.PIP_Problem.clear

(

)

Resets this to be equal to the trivial PIP problem.

The space dimension is reset to .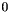

native void parma_polyhedra_library.PIP_Problem.add_space_dimensions_and_embed	(	long	pip_vars,
		long	pip_params
	)

Adds pip_vars + pip_params new space dimensions and embeds the PIP problem in the new vector space.

Parameters

pip_vars	The number of space dimensions to add that are interpreted as PIP problem variables (i.e., non parameters). These are added before adding the pip_params parameters.
pip_params	The number of space dimensions to add that are interpreted as PIP problem parameters. These are added after having added the pip_vars problem variables.

The new space dimensions will be those having the highest indexes in the new PIP problem; they are initially unconstrained.

native void parma_polyhedra_library.PIP_Problem.add_constraint

(

Constraint

c

)

Adds a copy of constraint c to the PIP problem.

Exceptions

Invalid_Argument_Exception

Thrown if the constraint c is a strict inequality or if its space dimension is strictly greater than the space dimension of this.

native void parma_polyhedra_library.PIP_Problem.add_constraints

(

Constraint_System

cs

)

Adds a copy of the constraints in cs to the PIP problem.

Exceptions

Invalid_Argument_Exception

Thrown if the constraint system cs contains any strict inequality or if its space dimension is strictly greater than the space dimension of this.

native boolean parma_polyhedra_library.PIP_Problem.is_satisfiable

(

)

Checks satisfiability of this.

Returns

true if and only if the PIP problem is satisfiable.

native PIP_Problem_Status parma_polyhedra_library.PIP_Problem.solve

(

)

Optimizes the PIP problem.

Solves the PIP problem, returning an exit status.

Returns

UNFEASIBLE_PIP_PROBLEM if the PIP problem is not satisfiable; OPTIMIZED_PIP_PROBLEM if the PIP problem admits an optimal solution.

---

The documentation for this class was generated from the following file:

• PIP_Problem.java