A class collecting library-level functions. More...
Static Public Member Functions | |
Library initialization and finalization | |
| static native void | initialize_library () |
| Initializes the Parma Polyhedra Library. More... | |
| static native void | finalize_library () |
| Finalizes the Parma Polyhedra Library. More... | |
Version Checking | |
| static native int | version_major () |
| Returns the major number of the PPL version. | |
| static native int | version_minor () |
| Returns the minor number of the PPL version. | |
| static native int | version_revision () |
| Returns the revision number of the PPL version. | |
| static native int | version_beta () |
| Returns the beta number of the PPL version. | |
| static native String | version () |
| Returns a string containing the PPL version. | |
| static native String | banner () |
| Returns a string containing the PPL banner. More... | |
Floating-point rounding and precision settings. | |
| static native void | set_rounding_for_PPL () |
| Sets the FPU rounding mode so that the PPL abstractions based on floating point numbers work correctly. More... | |
| static native void | restore_pre_PPL_rounding () |
| Sets the FPU rounding mode as it was before initialization of the PPL. More... | |
| static native int | irrational_precision () |
| Returns the precision parameter for irrational calculations. | |
| static native void | set_irrational_precision (int p) |
| Sets the precision parameter used for irrational calculations. More... | |
Timeout handling | |
| static native void | set_timeout (int csecs) |
| Sets the timeout for computations whose completion could require an exponential amount of time. More... | |
| static native void | reset_timeout () |
| Resets the timeout time so that the computation is not interrupted. | |
| static native void | set_deterministic_timeout (int unscaled_weight, int scale) |
| Sets a threshold for computations whose completion could require an exponential amount of time. More... | |
| static native void | reset_deterministic_timeout () |
| Resets the deterministic timeout so that the computation is not interrupted. | |
Detailed Description
A class collecting library-level functions.
Member Function Documentation
|
static |
Initializes the Parma Polyhedra Library.
This method must be called after loading the library and before calling any other method from any other PPL package class.
|
static |
Finalizes the Parma Polyhedra Library.
This method must be called when work with the library is done. After finalization, no other library method can be called (except those in class Parma_Polyhedra_Library), unless the library is re-initialized by calling initialize_library().
|
static |
Returns a string containing the PPL banner.
The banner provides information about the PPL version, the licensing, the lack of any warranty whatsoever, the C++ compiler used to build the library, where to report bugs and where to look for further information.
|
static |
Sets the FPU rounding mode so that the PPL abstractions based on floating point numbers work correctly.
This is performed automatically at initialization-time. Calling this function is needed only if restore_pre_PPL_rounding() has been previously called.
|
static |
Sets the FPU rounding mode as it was before initialization of the PPL.
After calling this function it is absolutely necessary to call set_rounding_for_PPL() before using any PPL abstractions based on floating point numbers. This is performed automatically at finalization-time.
|
static |
Sets the precision parameter used for irrational calculations.
If p is less than or equal to INT_MAX, sets the precision parameter used for irrational calculations to p. Then, in the irrational calculations returning an unbounded rational, (e.g., when computing a square root), the lesser between numerator and denominator will be limited to 2**p.
|
static |
Sets the timeout for computations whose completion could require an exponential amount of time.
- Parameters
-
csecs The number of centiseconds sometimes after which a timeout will occur; it must be strictly greater than zero.
Computations taking exponential time will be interrupted some time after csecs centiseconds have elapsed since the call to the timeout setting function, by throwing a Timeout_Exception object. Otherwise, if the computation completes without being interrupted, then the timeout should be reset by calling reset_timeout().
|
static |
Sets a threshold for computations whose completion could require an exponential amount of time.
If unscaled_weight has value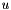 
and scale has value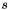 
, then the (scaled) weight threshold is computed as 
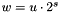. Computations taking exponential time will be interrupted some time after reaching the complexity threshold 
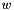, by throwing a Timeout_Exception object. Otherwise, if the computation completes without being interrupted, then the deterministic timeout should be reset by calling reset_deterministic_timeout().
- Parameters
-
unscaled_weight The unscaled maximum computational weight; it has to be strictly greater than zero. scale The scaling factor to be applied to unscaled_weight; it has to be non-negative.
- Exceptions
-
Invalid_Argument_Exception Thrown if the computation of the weight threshold exceeds the maximum allowed value.
- Note
- This "timeout" checking functionality is said to be deterministic because it is not based on actual elapsed time. Its behavior will only depend on (some of the) computations performed in the PPL library and it will be otherwise independent from the computation environment (CPU, operating system, compiler, etc.).
- Warning
- The weight mechanism is under beta testing. In particular, there is still no clear relation between the weight threshold and the actual computational complexity. As a consequence, client applications should be ready to reconsider the tuning of these weight thresholds when upgrading to newer version of the PPL.
The documentation for this class was generated from the following file:
- Parma_Polyhedra_Library.java
