The structure of this section is as follows:

Predicates for the Int8_Box Domain

Here we provide a short description for each of the predicates available for the domain of int8 boxes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for int8 boxes

The constructor predicates build a int8 box from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Int8_Box_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new int8 box $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Int8_Box_from_space_dimension(3, universe, X).

creates the int8 box defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Int8_Box_from_constraints(+Constraint_System, -Handle)
Builds a new int8 box P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Int8_Box_from_congruences(+Congruence_System, -Handle)
Builds a new int8 box P from Congruence_System. Handle is unified with the handle for P.

ppl_new_Int8_Box_from_generators(+Generator_System, -Handle)
Builds a new int8 box P from Generator_System. Handle is unified with the handle for P.

Predicates that build new int8 boxes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Int8_Box_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Z_Box(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Grid(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Float_Box(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Double_Box(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new int8 box P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int8_Box_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int8 box P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Int8_Box domain.

ppl_delete_Int8_Box(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the int8 box

Test Predicates

These predicates test the int8 box for different properties and succeed or fail depending on the outcome.

ppl_Int8_Box_is_empty(+Handle)
Succeeds if and only if the int8 box referenced by Handle is empty.

ppl_Int8_Box_is_universe(+Handle)
Succeeds if and only if the int8 box referenced by Handle is the universe.

ppl_Int8_Box_is_bounded(+Handle)
Succeeds if and only if the int8 box referenced by Handle is bounded.

ppl_Int8_Box_contains_integer_point(+Handle)
Succeeds if and only if the int8 box referenced by Handle contains an integer point.

ppl_Int8_Box_is_topologically_closed(+Handle)
Succeeds if and only if the int8 box referenced by Handle is topologically closed.

ppl_Int8_Box_is_discrete(+Handle)
Succeeds if and only if the int8 box referenced by Handle is discrete.

ppl_Int8_Box_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the int8 box referenced by Handle.

ppl_Int8_Box_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the int8 box referenced by Handle.

ppl_Int8_Box_contains_Int8_Box(+Handle_1, +Handle_2)
Succeeds if and only if the int8 box referenced by Handle_2 is included in or equal to the int8 box referenced by Handle_1.

ppl_Int8_Box_strictly_contains_Int8_Box(+Handle_1, +Handle_2)
Succeeds if and only if the int8 box referenced by Handle_2 is included in but not equal to the int8 box referenced by Handle_1.

ppl_Int8_Box_is_disjoint_from_Int8_Box(+Handle_1, +Handle_2)
Succeeds if and only if the int8 box referenced by Handle_2 is disjoint from the int8 box referenced by Handle_1.

ppl_Int8_Box_equals_Int8_Box(+Handle_1, +Handle_2)
Succeeds if and only if the int8 box referenced by Handle_1 is equal to the int8 box referenced by Handle_2.

ppl_Int8_Box_OK(+Handle)
Succeeds only if the int8 box referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Int8_Box_constrains(+Handle, +PPL_Var)
Succeeds if and only if the int8 box referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the int8 box

These predicates will obtain more detailed information about the int8 box unifying some of their arguments with the results.

ppl_Int8_Box_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the int8 box referenced by Handle.

ppl_Int8_Box_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the int8 box referenced by Handle.

ppl_Int8_Box_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the int8 box referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Int8_Box_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the int8 box referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Int8_Box_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the int8 box referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Int8_Box_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the int8 box referenced by Handle.

ppl_Int8_Box_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the int8 box referenced by Handle.

ppl_Int8_Box_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the int8 box referenced by Handle.

ppl_Int8_Box_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the int8 box referenced by Handle.

ppl_Int8_Box_has_upper_bound(+Handle, +Var, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if Var is upper bounded in int8 box P referenced by Handle. It is assumed that P is not empty and its space dimension is greater than or equal to that of Var, otherwise the behavior is undefined.

Coeff_1 is unified with the numerator of the upper bound and Coeff_2 with the denominator of the upper bound. If the upper is included in P, then Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Int8_Box_has_lower_bound(+Handle, +Var, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if Var is lower bounded in int8 box P referenced by Handle. It is assumed that P is not empty and its space dimension is greater than or equal to that of Var, otherwise the behavior is undefined.

Coeff_1 is unified with the numerator of the lower bound and Coeff_2 with the denominator of the lower bound. If the lower is included in P, then Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Int8_Box_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if int8 box P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Int8_Box_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if int8 box P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Int8_Box_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if int8 box P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Int8_Box_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if int8 box P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Int8_Box_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the int8 box referenced by Handle.

ppl_Int8_Box_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the int8 box referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Int8_Box_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the int8 box referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the int8 box

These predicates may modify the int8 box referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the int8 box by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Int8_Box_add_constraint(+Handle, +Constraint)
Updates the int8 box referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Int8_Box_add_congruence(+Handle, +Congruence)
Updates the int8 box referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Int8_Box_add_constraints( +Handle, +Constraint_System)
Updates the int8 box referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Int8_Box_add_congruences( +Handle, +Congruence_System)
Updates the int8 box referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Int8_Box_refine_with_constraint( +Handle, +Constraint)
Updates the int8 box referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Int8_Box_refine_with_congruence( +Handle, +Congruence)
Updates the int8 box referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Int8_Box_refine_with_constraints( +Handle, +Constraint_System)
Updates the int8 box referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Int8_Box_refine_with_congruences( +Handle, +Congruence_System)
Updates the int8 box referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the int8 box

These predicates enable transformations such as taking the topological closure (which for the domain of int8 box is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Int8_Box_topological_closure_assign(+Handle)
Assigns to the int8 box referenced by Handle its topological closure.

ppl_Int8_Box_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the int8 box P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Int8_Box_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the int8 box P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Int8_Box_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the int8 box referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Int8_Box_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the int8 box referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Int8_Box_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to int8 box P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Int8_Box_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to int8 box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Int8_Box_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to int8 box P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Int8_Box_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to int8 box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Int8_Box_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to int8 box P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Int8_Box_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to int8 box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Int8_Box_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the int8 box P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one int8 box

These predicates include the binary operators which will assign to the int8 box referred to by the first argument its combination with the int8 box referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Int8_Box_intersection_assign(+Handle_1, +Handle_2)
Assigns to the int8 box P referenced by Handle_1 the intersection of P and the int8 box referenced by Handle_2.

ppl_Int8_Box_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the int8 box P referenced by Handle_1 the upper bound of P and the int8 box referenced by Handle_2.

ppl_Int8_Box_difference_assign(+Handle_1, +Handle_2)
Assigns to the int8 box P referenced by Handle_1 the difference of P and the int8 box referenced by Handle_2.

ppl_Int8_Box_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the int8 box P referenced by Handle_1 the time elapse of P and the int8 box referenced by Handle_2.

ppl_Int8_Box_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the int8 box P_1 referenced by Handle_1 with the int8 box referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Int8_Box_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of int8 box P_1 referenced by Handle_1 and the int8 box P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_Int8_Box_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the Int8_Box domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the int8 box referred to by the second argument has to be contained in (or equal to) the int8 box referred to by the first argument.

ppl_Int8_Box_CC76_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the int8 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the int8 box referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Int8_Box_CC76_widening_assign(+Handle_1, +Handle_2)
Assigns to the int8 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the int8 box referenced by Handle_2.

ppl_Int8_Box_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_Int8_Box_CC76_widening_assign_with_tokens/4

ppl_Int8_Box_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_Int8_Box_CC76_widening_assign/2

ppl_Int8_Box_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the int8 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the int8 box referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Int8_Box_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the int8 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the int8 box referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Int8_Box_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the int8 box P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the int8 box referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the int8 box referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Int8_Box_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the int8 box P referenced by Handle_1 the concatenation of P and the int8 box referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the int8 box referred to in the first argument. These predicates enable the modification of the vector space of the int8 box referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Int8_Box_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the int8 box P referenced by Handle and and_embeds P in this space.

ppl_Int8_Box_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the int8 box P referenced by Handle and and_projects P in this space.

ppl_Int8_Box_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the int8 box P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Int8_Box_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the int8 box P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Int8_Box_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the int8 box referenced by Handle to Dimension_Type new space dimensions.

ppl_Int8_Box_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the int8 box referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Int8_Box_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Int16_Box Domain

Here we provide a short description for each of the predicates available for the domain of int16 boxes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for int16 boxes

The constructor predicates build a int16 box from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Int16_Box_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new int16 box $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Int16_Box_from_space_dimension(3, universe, X).

creates the int16 box defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Int16_Box_from_constraints(+Constraint_System, -Handle)
Builds a new int16 box P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Int16_Box_from_congruences(+Congruence_System, -Handle)
Builds a new int16 box P from Congruence_System. Handle is unified with the handle for P.

ppl_new_Int16_Box_from_generators(+Generator_System, -Handle)
Builds a new int16 box P from Generator_System. Handle is unified with the handle for P.

Predicates that build new int16 boxes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Int16_Box_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Z_Box(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Grid(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Float_Box(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Double_Box(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new int16 box P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int16_Box_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int16 box P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Int16_Box domain.

ppl_delete_Int16_Box(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the int16 box

Test Predicates

These predicates test the int16 box for different properties and succeed or fail depending on the outcome.

ppl_Int16_Box_is_empty(+Handle)
Succeeds if and only if the int16 box referenced by Handle is empty.

ppl_Int16_Box_is_universe(+Handle)
Succeeds if and only if the int16 box referenced by Handle is the universe.

ppl_Int16_Box_is_bounded(+Handle)
Succeeds if and only if the int16 box referenced by Handle is bounded.

ppl_Int16_Box_contains_integer_point(+Handle)
Succeeds if and only if the int16 box referenced by Handle contains an integer point.

ppl_Int16_Box_is_topologically_closed(+Handle)
Succeeds if and only if the int16 box referenced by Handle is topologically closed.

ppl_Int16_Box_is_discrete(+Handle)
Succeeds if and only if the int16 box referenced by Handle is discrete.

ppl_Int16_Box_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the int16 box referenced by Handle.

ppl_Int16_Box_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the int16 box referenced by Handle.

ppl_Int16_Box_contains_Int16_Box(+Handle_1, +Handle_2)
Succeeds if and only if the int16 box referenced by Handle_2 is included in or equal to the int16 box referenced by Handle_1.

ppl_Int16_Box_strictly_contains_Int16_Box(+Handle_1, +Handle_2)
Succeeds if and only if the int16 box referenced by Handle_2 is included in but not equal to the int16 box referenced by Handle_1.

ppl_Int16_Box_is_disjoint_from_Int16_Box(+Handle_1, +Handle_2)
Succeeds if and only if the int16 box referenced by Handle_2 is disjoint from the int16 box referenced by Handle_1.

ppl_Int16_Box_equals_Int16_Box(+Handle_1, +Handle_2)
Succeeds if and only if the int16 box referenced by Handle_1 is equal to the int16 box referenced by Handle_2.

ppl_Int16_Box_OK(+Handle)
Succeeds only if the int16 box referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Int16_Box_constrains(+Handle, +PPL_Var)
Succeeds if and only if the int16 box referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the int16 box

These predicates will obtain more detailed information about the int16 box unifying some of their arguments with the results.

ppl_Int16_Box_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the int16 box referenced by Handle.

ppl_Int16_Box_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the int16 box referenced by Handle.

ppl_Int16_Box_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the int16 box referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Int16_Box_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the int16 box referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Int16_Box_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the int16 box referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Int16_Box_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the int16 box referenced by Handle.

ppl_Int16_Box_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the int16 box referenced by Handle.

ppl_Int16_Box_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the int16 box referenced by Handle.

ppl_Int16_Box_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the int16 box referenced by Handle.

ppl_Int16_Box_has_upper_bound(+Handle, +Var, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if Var is upper bounded in int16 box P referenced by Handle. It is assumed that P is not empty and its space dimension is greater than or equal to that of Var, otherwise the behavior is undefined.

Coeff_1 is unified with the numerator of the upper bound and Coeff_2 with the denominator of the upper bound. If the upper is included in P, then Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Int16_Box_has_lower_bound(+Handle, +Var, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if Var is lower bounded in int16 box P referenced by Handle. It is assumed that P is not empty and its space dimension is greater than or equal to that of Var, otherwise the behavior is undefined.

Coeff_1 is unified with the numerator of the lower bound and Coeff_2 with the denominator of the lower bound. If the lower is included in P, then Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Int16_Box_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if int16 box P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Int16_Box_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if int16 box P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Int16_Box_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if int16 box P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Int16_Box_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if int16 box P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Int16_Box_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the int16 box referenced by Handle.

ppl_Int16_Box_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the int16 box referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Int16_Box_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the int16 box referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the int16 box

These predicates may modify the int16 box referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the int16 box by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Int16_Box_add_constraint(+Handle, +Constraint)
Updates the int16 box referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Int16_Box_add_congruence(+Handle, +Congruence)
Updates the int16 box referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Int16_Box_add_constraints( +Handle, +Constraint_System)
Updates the int16 box referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Int16_Box_add_congruences( +Handle, +Congruence_System)
Updates the int16 box referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Int16_Box_refine_with_constraint( +Handle, +Constraint)
Updates the int16 box referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Int16_Box_refine_with_congruence( +Handle, +Congruence)
Updates the int16 box referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Int16_Box_refine_with_constraints( +Handle, +Constraint_System)
Updates the int16 box referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Int16_Box_refine_with_congruences( +Handle, +Congruence_System)
Updates the int16 box referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the int16 box

These predicates enable transformations such as taking the topological closure (which for the domain of int16 box is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Int16_Box_topological_closure_assign(+Handle)
Assigns to the int16 box referenced by Handle its topological closure.

ppl_Int16_Box_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the int16 box P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Int16_Box_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the int16 box P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Int16_Box_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the int16 box referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Int16_Box_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the int16 box referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Int16_Box_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to int16 box P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Int16_Box_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to int16 box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Int16_Box_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to int16 box P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Int16_Box_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to int16 box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Int16_Box_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to int16 box P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Int16_Box_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to int16 box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Int16_Box_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the int16 box P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one int16 box

These predicates include the binary operators which will assign to the int16 box referred to by the first argument its combination with the int16 box referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Int16_Box_intersection_assign(+Handle_1, +Handle_2)
Assigns to the int16 box P referenced by Handle_1 the intersection of P and the int16 box referenced by Handle_2.

ppl_Int16_Box_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the int16 box P referenced by Handle_1 the upper bound of P and the int16 box referenced by Handle_2.

ppl_Int16_Box_difference_assign(+Handle_1, +Handle_2)
Assigns to the int16 box P referenced by Handle_1 the difference of P and the int16 box referenced by Handle_2.

ppl_Int16_Box_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the int16 box P referenced by Handle_1 the time elapse of P and the int16 box referenced by Handle_2.

ppl_Int16_Box_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the int16 box P_1 referenced by Handle_1 with the int16 box referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Int16_Box_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of int16 box P_1 referenced by Handle_1 and the int16 box P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_Int16_Box_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the Int16_Box domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the int16 box referred to by the second argument has to be contained in (or equal to) the int16 box referred to by the first argument.

ppl_Int16_Box_CC76_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the int16 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the int16 box referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Int16_Box_CC76_widening_assign(+Handle_1, +Handle_2)
Assigns to the int16 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the int16 box referenced by Handle_2.

ppl_Int16_Box_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_Int16_Box_CC76_widening_assign_with_tokens/4

ppl_Int16_Box_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_Int16_Box_CC76_widening_assign/2

ppl_Int16_Box_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the int16 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the int16 box referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Int16_Box_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the int16 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the int16 box referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Int16_Box_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the int16 box P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the int16 box referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the int16 box referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Int16_Box_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the int16 box P referenced by Handle_1 the concatenation of P and the int16 box referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the int16 box referred to in the first argument. These predicates enable the modification of the vector space of the int16 box referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Int16_Box_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the int16 box P referenced by Handle and and_embeds P in this space.

ppl_Int16_Box_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the int16 box P referenced by Handle and and_projects P in this space.

ppl_Int16_Box_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the int16 box P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Int16_Box_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the int16 box P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Int16_Box_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the int16 box referenced by Handle to Dimension_Type new space dimensions.

ppl_Int16_Box_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the int16 box referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Int16_Box_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Int32_Box Domain

Here we provide a short description for each of the predicates available for the domain of int32 boxes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for int32 boxes

The constructor predicates build a int32 box from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Int32_Box_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new int32 box $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Int32_Box_from_space_dimension(3, universe, X).

creates the int32 box defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Int32_Box_from_constraints(+Constraint_System, -Handle)
Builds a new int32 box P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Int32_Box_from_congruences(+Congruence_System, -Handle)
Builds a new int32 box P from Congruence_System. Handle is unified with the handle for P.

ppl_new_Int32_Box_from_generators(+Generator_System, -Handle)
Builds a new int32 box P from Generator_System. Handle is unified with the handle for P.

Predicates that build new int32 boxes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Int32_Box_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Z_Box(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Grid(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Float_Box(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Double_Box(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new int32 box P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int32_Box_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int32 box P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Int32_Box domain.

ppl_delete_Int32_Box(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the int32 box

Test Predicates

These predicates test the int32 box for different properties and succeed or fail depending on the outcome.

ppl_Int32_Box_is_empty(+Handle)
Succeeds if and only if the int32 box referenced by Handle is empty.

ppl_Int32_Box_is_universe(+Handle)
Succeeds if and only if the int32 box referenced by Handle is the universe.

ppl_Int32_Box_is_bounded(+Handle)
Succeeds if and only if the int32 box referenced by Handle is bounded.

ppl_Int32_Box_contains_integer_point(+Handle)
Succeeds if and only if the int32 box referenced by Handle contains an integer point.

ppl_Int32_Box_is_topologically_closed(+Handle)
Succeeds if and only if the int32 box referenced by Handle is topologically closed.

ppl_Int32_Box_is_discrete(+Handle)
Succeeds if and only if the int32 box referenced by Handle is discrete.

ppl_Int32_Box_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the int32 box referenced by Handle.

ppl_Int32_Box_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the int32 box referenced by Handle.

ppl_Int32_Box_contains_Int32_Box(+Handle_1, +Handle_2)
Succeeds if and only if the int32 box referenced by Handle_2 is included in or equal to the int32 box referenced by Handle_1.

ppl_Int32_Box_strictly_contains_Int32_Box(+Handle_1, +Handle_2)
Succeeds if and only if the int32 box referenced by Handle_2 is included in but not equal to the int32 box referenced by Handle_1.

ppl_Int32_Box_is_disjoint_from_Int32_Box(+Handle_1, +Handle_2)
Succeeds if and only if the int32 box referenced by Handle_2 is disjoint from the int32 box referenced by Handle_1.

ppl_Int32_Box_equals_Int32_Box(+Handle_1, +Handle_2)
Succeeds if and only if the int32 box referenced by Handle_1 is equal to the int32 box referenced by Handle_2.

ppl_Int32_Box_OK(+Handle)
Succeeds only if the int32 box referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Int32_Box_constrains(+Handle, +PPL_Var)
Succeeds if and only if the int32 box referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the int32 box

These predicates will obtain more detailed information about the int32 box unifying some of their arguments with the results.

ppl_Int32_Box_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the int32 box referenced by Handle.

ppl_Int32_Box_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the int32 box referenced by Handle.

ppl_Int32_Box_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the int32 box referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Int32_Box_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the int32 box referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Int32_Box_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the int32 box referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Int32_Box_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the int32 box referenced by Handle.

ppl_Int32_Box_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the int32 box referenced by Handle.

ppl_Int32_Box_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the int32 box referenced by Handle.

ppl_Int32_Box_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the int32 box referenced by Handle.

ppl_Int32_Box_has_upper_bound(+Handle, +Var, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if Var is upper bounded in int32 box P referenced by Handle. It is assumed that P is not empty and its space dimension is greater than or equal to that of Var, otherwise the behavior is undefined.

Coeff_1 is unified with the numerator of the upper bound and Coeff_2 with the denominator of the upper bound. If the upper is included in P, then Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Int32_Box_has_lower_bound(+Handle, +Var, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if Var is lower bounded in int32 box P referenced by Handle. It is assumed that P is not empty and its space dimension is greater than or equal to that of Var, otherwise the behavior is undefined.

Coeff_1 is unified with the numerator of the lower bound and Coeff_2 with the denominator of the lower bound. If the lower is included in P, then Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Int32_Box_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if int32 box P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Int32_Box_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if int32 box P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Int32_Box_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if int32 box P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Int32_Box_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if int32 box P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Int32_Box_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the int32 box referenced by Handle.

ppl_Int32_Box_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the int32 box referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Int32_Box_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the int32 box referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the int32 box

These predicates may modify the int32 box referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the int32 box by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Int32_Box_add_constraint(+Handle, +Constraint)
Updates the int32 box referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Int32_Box_add_congruence(+Handle, +Congruence)
Updates the int32 box referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Int32_Box_add_constraints( +Handle, +Constraint_System)
Updates the int32 box referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Int32_Box_add_congruences( +Handle, +Congruence_System)
Updates the int32 box referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Int32_Box_refine_with_constraint( +Handle, +Constraint)
Updates the int32 box referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Int32_Box_refine_with_congruence( +Handle, +Congruence)
Updates the int32 box referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Int32_Box_refine_with_constraints( +Handle, +Constraint_System)
Updates the int32 box referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Int32_Box_refine_with_congruences( +Handle, +Congruence_System)
Updates the int32 box referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the int32 box

These predicates enable transformations such as taking the topological closure (which for the domain of int32 box is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Int32_Box_topological_closure_assign(+Handle)
Assigns to the int32 box referenced by Handle its topological closure.

ppl_Int32_Box_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the int32 box P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Int32_Box_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the int32 box P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Int32_Box_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the int32 box referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Int32_Box_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the int32 box referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Int32_Box_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to int32 box P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Int32_Box_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to int32 box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Int32_Box_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to int32 box P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Int32_Box_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to int32 box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Int32_Box_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to int32 box P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Int32_Box_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to int32 box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Int32_Box_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the int32 box P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one int32 box

These predicates include the binary operators which will assign to the int32 box referred to by the first argument its combination with the int32 box referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Int32_Box_intersection_assign(+Handle_1, +Handle_2)
Assigns to the int32 box P referenced by Handle_1 the intersection of P and the int32 box referenced by Handle_2.

ppl_Int32_Box_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the int32 box P referenced by Handle_1 the upper bound of P and the int32 box referenced by Handle_2.

ppl_Int32_Box_difference_assign(+Handle_1, +Handle_2)
Assigns to the int32 box P referenced by Handle_1 the difference of P and the int32 box referenced by Handle_2.

ppl_Int32_Box_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the int32 box P referenced by Handle_1 the time elapse of P and the int32 box referenced by Handle_2.

ppl_Int32_Box_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the int32 box P_1 referenced by Handle_1 with the int32 box referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Int32_Box_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of int32 box P_1 referenced by Handle_1 and the int32 box P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_Int32_Box_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the Int32_Box domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the int32 box referred to by the second argument has to be contained in (or equal to) the int32 box referred to by the first argument.

ppl_Int32_Box_CC76_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the int32 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the int32 box referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Int32_Box_CC76_widening_assign(+Handle_1, +Handle_2)
Assigns to the int32 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the int32 box referenced by Handle_2.

ppl_Int32_Box_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_Int32_Box_CC76_widening_assign_with_tokens/4

ppl_Int32_Box_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_Int32_Box_CC76_widening_assign/2

ppl_Int32_Box_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the int32 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the int32 box referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Int32_Box_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the int32 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the int32 box referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Int32_Box_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the int32 box P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the int32 box referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the int32 box referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Int32_Box_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the int32 box P referenced by Handle_1 the concatenation of P and the int32 box referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the int32 box referred to in the first argument. These predicates enable the modification of the vector space of the int32 box referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Int32_Box_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the int32 box P referenced by Handle and and_embeds P in this space.

ppl_Int32_Box_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the int32 box P referenced by Handle and and_projects P in this space.

ppl_Int32_Box_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the int32 box P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Int32_Box_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the int32 box P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Int32_Box_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the int32 box referenced by Handle to Dimension_Type new space dimensions.

ppl_Int32_Box_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the int32 box referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Int32_Box_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Int64_Box Domain

Here we provide a short description for each of the predicates available for the domain of int64 boxes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for int64 boxes

The constructor predicates build a int64 box from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Int64_Box_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new int64 box $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Int64_Box_from_space_dimension(3, universe, X).

creates the int64 box defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Int64_Box_from_constraints(+Constraint_System, -Handle)
Builds a new int64 box P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Int64_Box_from_congruences(+Congruence_System, -Handle)
Builds a new int64 box P from Congruence_System. Handle is unified with the handle for P.

ppl_new_Int64_Box_from_generators(+Generator_System, -Handle)
Builds a new int64 box P from Generator_System. Handle is unified with the handle for P.

Predicates that build new int64 boxes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Int64_Box_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Z_Box(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Grid(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Float_Box(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Double_Box(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new int64 box P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Int64_Box_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new int64 box P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Int64_Box domain.

ppl_delete_Int64_Box(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the int64 box

Test Predicates

These predicates test the int64 box for different properties and succeed or fail depending on the outcome.

ppl_Int64_Box_is_empty(+Handle)
Succeeds if and only if the int64 box referenced by Handle is empty.

ppl_Int64_Box_is_universe(+Handle)
Succeeds if and only if the int64 box referenced by Handle is the universe.

ppl_Int64_Box_is_bounded(+Handle)
Succeeds if and only if the int64 box referenced by Handle is bounded.

ppl_Int64_Box_contains_integer_point(+Handle)
Succeeds if and only if the int64 box referenced by Handle contains an integer point.

ppl_Int64_Box_is_topologically_closed(+Handle)
Succeeds if and only if the int64 box referenced by Handle is topologically closed.

ppl_Int64_Box_is_discrete(+Handle)
Succeeds if and only if the int64 box referenced by Handle is discrete.

ppl_Int64_Box_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the int64 box referenced by Handle.

ppl_Int64_Box_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the int64 box referenced by Handle.

ppl_Int64_Box_contains_Int64_Box(+Handle_1, +Handle_2)
Succeeds if and only if the int64 box referenced by Handle_2 is included in or equal to the int64 box referenced by Handle_1.

ppl_Int64_Box_strictly_contains_Int64_Box(+Handle_1, +Handle_2)
Succeeds if and only if the int64 box referenced by Handle_2 is included in but not equal to the int64 box referenced by Handle_1.

ppl_Int64_Box_is_disjoint_from_Int64_Box(+Handle_1, +Handle_2)
Succeeds if and only if the int64 box referenced by Handle_2 is disjoint from the int64 box referenced by Handle_1.

ppl_Int64_Box_equals_Int64_Box(+Handle_1, +Handle_2)
Succeeds if and only if the int64 box referenced by Handle_1 is equal to the int64 box referenced by Handle_2.

ppl_Int64_Box_OK(+Handle)
Succeeds only if the int64 box referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Int64_Box_constrains(+Handle, +PPL_Var)
Succeeds if and only if the int64 box referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the int64 box

These predicates will obtain more detailed information about the int64 box unifying some of their arguments with the results.

ppl_Int64_Box_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the int64 box referenced by Handle.

ppl_Int64_Box_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the int64 box referenced by Handle.

ppl_Int64_Box_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the int64 box referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Int64_Box_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the int64 box referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Int64_Box_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the int64 box referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Int64_Box_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the int64 box referenced by Handle.

ppl_Int64_Box_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the int64 box referenced by Handle.

ppl_Int64_Box_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the int64 box referenced by Handle.

ppl_Int64_Box_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the int64 box referenced by Handle.

ppl_Int64_Box_has_upper_bound(+Handle, +Var, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if Var is upper bounded in int64 box P referenced by Handle. It is assumed that P is not empty and its space dimension is greater than or equal to that of Var, otherwise the behavior is undefined.

Coeff_1 is unified with the numerator of the upper bound and Coeff_2 with the denominator of the upper bound. If the upper is included in P, then Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Int64_Box_has_lower_bound(+Handle, +Var, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if Var is lower bounded in int64 box P referenced by Handle. It is assumed that P is not empty and its space dimension is greater than or equal to that of Var, otherwise the behavior is undefined.

Coeff_1 is unified with the numerator of the lower bound and Coeff_2 with the denominator of the lower bound. If the lower is included in P, then Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Int64_Box_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if int64 box P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Int64_Box_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if int64 box P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Int64_Box_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if int64 box P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Int64_Box_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if int64 box P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Int64_Box_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the int64 box referenced by Handle.

ppl_Int64_Box_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the int64 box referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Int64_Box_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the int64 box referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the int64 box

These predicates may modify the int64 box referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the int64 box by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Int64_Box_add_constraint(+Handle, +Constraint)
Updates the int64 box referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Int64_Box_add_congruence(+Handle, +Congruence)
Updates the int64 box referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Int64_Box_add_constraints( +Handle, +Constraint_System)
Updates the int64 box referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Int64_Box_add_congruences( +Handle, +Congruence_System)
Updates the int64 box referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Int64_Box_refine_with_constraint( +Handle, +Constraint)
Updates the int64 box referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Int64_Box_refine_with_congruence( +Handle, +Congruence)
Updates the int64 box referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Int64_Box_refine_with_constraints( +Handle, +Constraint_System)
Updates the int64 box referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Int64_Box_refine_with_congruences( +Handle, +Congruence_System)
Updates the int64 box referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the int64 box

These predicates enable transformations such as taking the topological closure (which for the domain of int64 box is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Int64_Box_topological_closure_assign(+Handle)
Assigns to the int64 box referenced by Handle its topological closure.

ppl_Int64_Box_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the int64 box P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Int64_Box_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the int64 box P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Int64_Box_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the int64 box referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Int64_Box_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the int64 box referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Int64_Box_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to int64 box P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Int64_Box_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to int64 box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Int64_Box_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to int64 box P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Int64_Box_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to int64 box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Int64_Box_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to int64 box P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Int64_Box_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to int64 box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Int64_Box_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the int64 box P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one int64 box

These predicates include the binary operators which will assign to the int64 box referred to by the first argument its combination with the int64 box referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Int64_Box_intersection_assign(+Handle_1, +Handle_2)
Assigns to the int64 box P referenced by Handle_1 the intersection of P and the int64 box referenced by Handle_2.

ppl_Int64_Box_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the int64 box P referenced by Handle_1 the upper bound of P and the int64 box referenced by Handle_2.

ppl_Int64_Box_difference_assign(+Handle_1, +Handle_2)
Assigns to the int64 box P referenced by Handle_1 the difference of P and the int64 box referenced by Handle_2.

ppl_Int64_Box_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the int64 box P referenced by Handle_1 the time elapse of P and the int64 box referenced by Handle_2.

ppl_Int64_Box_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the int64 box P_1 referenced by Handle_1 with the int64 box referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Int64_Box_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of int64 box P_1 referenced by Handle_1 and the int64 box P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_Int64_Box_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the Int64_Box domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the int64 box referred to by the second argument has to be contained in (or equal to) the int64 box referred to by the first argument.

ppl_Int64_Box_CC76_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the int64 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the int64 box referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Int64_Box_CC76_widening_assign(+Handle_1, +Handle_2)
Assigns to the int64 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the int64 box referenced by Handle_2.

ppl_Int64_Box_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_Int64_Box_CC76_widening_assign_with_tokens/4

ppl_Int64_Box_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_Int64_Box_CC76_widening_assign/2

ppl_Int64_Box_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the int64 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the int64 box referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Int64_Box_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the int64 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the int64 box referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Int64_Box_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the int64 box P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the int64 box referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the int64 box referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Int64_Box_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the int64 box P referenced by Handle_1 the concatenation of P and the int64 box referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the int64 box referred to in the first argument. These predicates enable the modification of the vector space of the int64 box referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Int64_Box_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the int64 box P referenced by Handle and and_embeds P in this space.

ppl_Int64_Box_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the int64 box P referenced by Handle and and_projects P in this space.

ppl_Int64_Box_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the int64 box P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Int64_Box_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the int64 box P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Int64_Box_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the int64 box referenced by Handle to Dimension_Type new space dimensions.

ppl_Int64_Box_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the int64 box referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Int64_Box_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Uint8_Box Domain

Here we provide a short description for each of the predicates available for the domain of uint8 boxes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for uint8 boxes

The constructor predicates build a uint8 box from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Uint8_Box_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new uint8 box $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Uint8_Box_from_space_dimension(3, universe, X).

creates the uint8 box defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Uint8_Box_from_constraints(+Constraint_System, -Handle)
Builds a new uint8 box P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Uint8_Box_from_congruences(+Congruence_System, -Handle)
Builds a new uint8 box P from Congruence_System. Handle is unified with the handle for P.

ppl_new_Uint8_Box_from_generators(+Generator_System, -Handle)
Builds a new uint8 box P from Generator_System. Handle is unified with the handle for P.

Predicates that build new uint8 boxes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Uint8_Box_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Z_Box(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Grid(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Float_Box(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Double_Box(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new uint8 box P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint8_Box_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint8 box P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Uint8_Box domain.

ppl_delete_Uint8_Box(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the uint8 box

Test Predicates

These predicates test the uint8 box for different properties and succeed or fail depending on the outcome.

ppl_Uint8_Box_is_empty(+Handle)
Succeeds if and only if the uint8 box referenced by Handle is empty.

ppl_Uint8_Box_is_universe(+Handle)
Succeeds if and only if the uint8 box referenced by Handle is the universe.

ppl_Uint8_Box_is_bounded(+Handle)
Succeeds if and only if the uint8 box referenced by Handle is bounded.

ppl_Uint8_Box_contains_integer_point(+Handle)
Succeeds if and only if the uint8 box referenced by Handle contains an integer point.

ppl_Uint8_Box_is_topologically_closed(+Handle)
Succeeds if and only if the uint8 box referenced by Handle is topologically closed.

ppl_Uint8_Box_is_discrete(+Handle)
Succeeds if and only if the uint8 box referenced by Handle is discrete.

ppl_Uint8_Box_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the uint8 box referenced by Handle.

ppl_Uint8_Box_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the uint8 box referenced by Handle.

ppl_Uint8_Box_contains_Uint8_Box(+Handle_1, +Handle_2)
Succeeds if and only if the uint8 box referenced by Handle_2 is included in or equal to the uint8 box referenced by Handle_1.

ppl_Uint8_Box_strictly_contains_Uint8_Box(+Handle_1, +Handle_2)
Succeeds if and only if the uint8 box referenced by Handle_2 is included in but not equal to the uint8 box referenced by Handle_1.

ppl_Uint8_Box_is_disjoint_from_Uint8_Box(+Handle_1, +Handle_2)
Succeeds if and only if the uint8 box referenced by Handle_2 is disjoint from the uint8 box referenced by Handle_1.

ppl_Uint8_Box_equals_Uint8_Box(+Handle_1, +Handle_2)
Succeeds if and only if the uint8 box referenced by Handle_1 is equal to the uint8 box referenced by Handle_2.

ppl_Uint8_Box_OK(+Handle)
Succeeds only if the uint8 box referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Uint8_Box_constrains(+Handle, +PPL_Var)
Succeeds if and only if the uint8 box referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the uint8 box

These predicates will obtain more detailed information about the uint8 box unifying some of their arguments with the results.

ppl_Uint8_Box_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the uint8 box referenced by Handle.

ppl_Uint8_Box_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the uint8 box referenced by Handle.

ppl_Uint8_Box_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the uint8 box referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Uint8_Box_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the uint8 box referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Uint8_Box_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the uint8 box referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Uint8_Box_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the uint8 box referenced by Handle.

ppl_Uint8_Box_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the uint8 box referenced by Handle.

ppl_Uint8_Box_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the uint8 box referenced by Handle.

ppl_Uint8_Box_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the uint8 box referenced by Handle.

ppl_Uint8_Box_has_upper_bound(+Handle, +Var, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if Var is upper bounded in uint8 box P referenced by Handle. It is assumed that P is not empty and its space dimension is greater than or equal to that of Var, otherwise the behavior is undefined.

Coeff_1 is unified with the numerator of the upper bound and Coeff_2 with the denominator of the upper bound. If the upper is included in P, then Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Uint8_Box_has_lower_bound(+Handle, +Var, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if Var is lower bounded in uint8 box P referenced by Handle. It is assumed that P is not empty and its space dimension is greater than or equal to that of Var, otherwise the behavior is undefined.

Coeff_1 is unified with the numerator of the lower bound and Coeff_2 with the denominator of the lower bound. If the lower is included in P, then Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Uint8_Box_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if uint8 box P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Uint8_Box_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if uint8 box P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Uint8_Box_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if uint8 box P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Uint8_Box_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if uint8 box P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Uint8_Box_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the uint8 box referenced by Handle.

ppl_Uint8_Box_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the uint8 box referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Uint8_Box_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the uint8 box referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the uint8 box

These predicates may modify the uint8 box referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the uint8 box by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Uint8_Box_add_constraint(+Handle, +Constraint)
Updates the uint8 box referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Uint8_Box_add_congruence(+Handle, +Congruence)
Updates the uint8 box referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Uint8_Box_add_constraints( +Handle, +Constraint_System)
Updates the uint8 box referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Uint8_Box_add_congruences( +Handle, +Congruence_System)
Updates the uint8 box referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Uint8_Box_refine_with_constraint( +Handle, +Constraint)
Updates the uint8 box referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Uint8_Box_refine_with_congruence( +Handle, +Congruence)
Updates the uint8 box referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Uint8_Box_refine_with_constraints( +Handle, +Constraint_System)
Updates the uint8 box referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Uint8_Box_refine_with_congruences( +Handle, +Congruence_System)
Updates the uint8 box referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the uint8 box

These predicates enable transformations such as taking the topological closure (which for the domain of uint8 box is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Uint8_Box_topological_closure_assign(+Handle)
Assigns to the uint8 box referenced by Handle its topological closure.

ppl_Uint8_Box_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the uint8 box P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Uint8_Box_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the uint8 box P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Uint8_Box_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the uint8 box referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Uint8_Box_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the uint8 box referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Uint8_Box_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to uint8 box P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Uint8_Box_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to uint8 box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Uint8_Box_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to uint8 box P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Uint8_Box_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to uint8 box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Uint8_Box_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to uint8 box P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Uint8_Box_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to uint8 box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Uint8_Box_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the uint8 box P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one uint8 box

These predicates include the binary operators which will assign to the uint8 box referred to by the first argument its combination with the uint8 box referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Uint8_Box_intersection_assign(+Handle_1, +Handle_2)
Assigns to the uint8 box P referenced by Handle_1 the intersection of P and the uint8 box referenced by Handle_2.

ppl_Uint8_Box_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the uint8 box P referenced by Handle_1 the upper bound of P and the uint8 box referenced by Handle_2.

ppl_Uint8_Box_difference_assign(+Handle_1, +Handle_2)
Assigns to the uint8 box P referenced by Handle_1 the difference of P and the uint8 box referenced by Handle_2.

ppl_Uint8_Box_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the uint8 box P referenced by Handle_1 the time elapse of P and the uint8 box referenced by Handle_2.

ppl_Uint8_Box_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the uint8 box P_1 referenced by Handle_1 with the uint8 box referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Uint8_Box_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of uint8 box P_1 referenced by Handle_1 and the uint8 box P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_Uint8_Box_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the Uint8_Box domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the uint8 box referred to by the second argument has to be contained in (or equal to) the uint8 box referred to by the first argument.

ppl_Uint8_Box_CC76_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the uint8 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the uint8 box referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Uint8_Box_CC76_widening_assign(+Handle_1, +Handle_2)
Assigns to the uint8 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the uint8 box referenced by Handle_2.

ppl_Uint8_Box_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_Uint8_Box_CC76_widening_assign_with_tokens/4

ppl_Uint8_Box_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_Uint8_Box_CC76_widening_assign/2

ppl_Uint8_Box_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the uint8 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the uint8 box referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Uint8_Box_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the uint8 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the uint8 box referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Uint8_Box_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the uint8 box P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the uint8 box referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the uint8 box referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Uint8_Box_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the uint8 box P referenced by Handle_1 the concatenation of P and the uint8 box referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the uint8 box referred to in the first argument. These predicates enable the modification of the vector space of the uint8 box referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Uint8_Box_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the uint8 box P referenced by Handle and and_embeds P in this space.

ppl_Uint8_Box_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the uint8 box P referenced by Handle and and_projects P in this space.

ppl_Uint8_Box_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the uint8 box P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Uint8_Box_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the uint8 box P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Uint8_Box_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the uint8 box referenced by Handle to Dimension_Type new space dimensions.

ppl_Uint8_Box_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the uint8 box referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Uint8_Box_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Uint16_Box Domain

Here we provide a short description for each of the predicates available for the domain of uint16 boxes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for uint16 boxes

The constructor predicates build a uint16 box from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Uint16_Box_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new uint16 box $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Uint16_Box_from_space_dimension(3, universe, X).

creates the uint16 box defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Uint16_Box_from_constraints(+Constraint_System, -Handle)
Builds a new uint16 box P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Uint16_Box_from_congruences(+Congruence_System, -Handle)
Builds a new uint16 box P from Congruence_System. Handle is unified with the handle for P.

ppl_new_Uint16_Box_from_generators(+Generator_System, -Handle)
Builds a new uint16 box P from Generator_System. Handle is unified with the handle for P.

Predicates that build new uint16 boxes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Uint16_Box_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Z_Box(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Grid(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Float_Box(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Double_Box(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new uint16 box P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint16_Box_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint16 box P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Uint16_Box domain.

ppl_delete_Uint16_Box(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the uint16 box

Test Predicates

These predicates test the uint16 box for different properties and succeed or fail depending on the outcome.

ppl_Uint16_Box_is_empty(+Handle)
Succeeds if and only if the uint16 box referenced by Handle is empty.

ppl_Uint16_Box_is_universe(+Handle)
Succeeds if and only if the uint16 box referenced by Handle is the universe.

ppl_Uint16_Box_is_bounded(+Handle)
Succeeds if and only if the uint16 box referenced by Handle is bounded.

ppl_Uint16_Box_contains_integer_point(+Handle)
Succeeds if and only if the uint16 box referenced by Handle contains an integer point.

ppl_Uint16_Box_is_topologically_closed(+Handle)
Succeeds if and only if the uint16 box referenced by Handle is topologically closed.

ppl_Uint16_Box_is_discrete(+Handle)
Succeeds if and only if the uint16 box referenced by Handle is discrete.

ppl_Uint16_Box_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the uint16 box referenced by Handle.

ppl_Uint16_Box_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the uint16 box referenced by Handle.

ppl_Uint16_Box_contains_Uint16_Box(+Handle_1, +Handle_2)
Succeeds if and only if the uint16 box referenced by Handle_2 is included in or equal to the uint16 box referenced by Handle_1.

ppl_Uint16_Box_strictly_contains_Uint16_Box(+Handle_1, +Handle_2)
Succeeds if and only if the uint16 box referenced by Handle_2 is included in but not equal to the uint16 box referenced by Handle_1.

ppl_Uint16_Box_is_disjoint_from_Uint16_Box(+Handle_1, +Handle_2)
Succeeds if and only if the uint16 box referenced by Handle_2 is disjoint from the uint16 box referenced by Handle_1.

ppl_Uint16_Box_equals_Uint16_Box(+Handle_1, +Handle_2)
Succeeds if and only if the uint16 box referenced by Handle_1 is equal to the uint16 box referenced by Handle_2.

ppl_Uint16_Box_OK(+Handle)
Succeeds only if the uint16 box referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Uint16_Box_constrains(+Handle, +PPL_Var)
Succeeds if and only if the uint16 box referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the uint16 box

These predicates will obtain more detailed information about the uint16 box unifying some of their arguments with the results.

ppl_Uint16_Box_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the uint16 box referenced by Handle.

ppl_Uint16_Box_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the uint16 box referenced by Handle.

ppl_Uint16_Box_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the uint16 box referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Uint16_Box_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the uint16 box referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Uint16_Box_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the uint16 box referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Uint16_Box_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the uint16 box referenced by Handle.

ppl_Uint16_Box_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the uint16 box referenced by Handle.

ppl_Uint16_Box_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the uint16 box referenced by Handle.

ppl_Uint16_Box_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the uint16 box referenced by Handle.

ppl_Uint16_Box_has_upper_bound(+Handle, +Var, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if Var is upper bounded in uint16 box P referenced by Handle. It is assumed that P is not empty and its space dimension is greater than or equal to that of Var, otherwise the behavior is undefined.

Coeff_1 is unified with the numerator of the upper bound and Coeff_2 with the denominator of the upper bound. If the upper is included in P, then Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Uint16_Box_has_lower_bound(+Handle, +Var, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if Var is lower bounded in uint16 box P referenced by Handle. It is assumed that P is not empty and its space dimension is greater than or equal to that of Var, otherwise the behavior is undefined.

Coeff_1 is unified with the numerator of the lower bound and Coeff_2 with the denominator of the lower bound. If the lower is included in P, then Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Uint16_Box_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if uint16 box P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Uint16_Box_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if uint16 box P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Uint16_Box_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if uint16 box P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Uint16_Box_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if uint16 box P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Uint16_Box_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the uint16 box referenced by Handle.

ppl_Uint16_Box_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the uint16 box referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Uint16_Box_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the uint16 box referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the uint16 box

These predicates may modify the uint16 box referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the uint16 box by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Uint16_Box_add_constraint(+Handle, +Constraint)
Updates the uint16 box referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Uint16_Box_add_congruence(+Handle, +Congruence)
Updates the uint16 box referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Uint16_Box_add_constraints( +Handle, +Constraint_System)
Updates the uint16 box referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Uint16_Box_add_congruences( +Handle, +Congruence_System)
Updates the uint16 box referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Uint16_Box_refine_with_constraint( +Handle, +Constraint)
Updates the uint16 box referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Uint16_Box_refine_with_congruence( +Handle, +Congruence)
Updates the uint16 box referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Uint16_Box_refine_with_constraints( +Handle, +Constraint_System)
Updates the uint16 box referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Uint16_Box_refine_with_congruences( +Handle, +Congruence_System)
Updates the uint16 box referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the uint16 box

These predicates enable transformations such as taking the topological closure (which for the domain of uint16 box is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Uint16_Box_topological_closure_assign(+Handle)
Assigns to the uint16 box referenced by Handle its topological closure.

ppl_Uint16_Box_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the uint16 box P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Uint16_Box_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the uint16 box P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Uint16_Box_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the uint16 box referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Uint16_Box_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the uint16 box referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Uint16_Box_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to uint16 box P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Uint16_Box_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to uint16 box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Uint16_Box_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to uint16 box P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Uint16_Box_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to uint16 box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Uint16_Box_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to uint16 box P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Uint16_Box_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to uint16 box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Uint16_Box_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the uint16 box P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one uint16 box

These predicates include the binary operators which will assign to the uint16 box referred to by the first argument its combination with the uint16 box referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Uint16_Box_intersection_assign(+Handle_1, +Handle_2)
Assigns to the uint16 box P referenced by Handle_1 the intersection of P and the uint16 box referenced by Handle_2.

ppl_Uint16_Box_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the uint16 box P referenced by Handle_1 the upper bound of P and the uint16 box referenced by Handle_2.

ppl_Uint16_Box_difference_assign(+Handle_1, +Handle_2)
Assigns to the uint16 box P referenced by Handle_1 the difference of P and the uint16 box referenced by Handle_2.

ppl_Uint16_Box_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the uint16 box P referenced by Handle_1 the time elapse of P and the uint16 box referenced by Handle_2.

ppl_Uint16_Box_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the uint16 box P_1 referenced by Handle_1 with the uint16 box referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Uint16_Box_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of uint16 box P_1 referenced by Handle_1 and the uint16 box P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_Uint16_Box_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the Uint16_Box domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the uint16 box referred to by the second argument has to be contained in (or equal to) the uint16 box referred to by the first argument.

ppl_Uint16_Box_CC76_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the uint16 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the uint16 box referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Uint16_Box_CC76_widening_assign(+Handle_1, +Handle_2)
Assigns to the uint16 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the uint16 box referenced by Handle_2.

ppl_Uint16_Box_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_Uint16_Box_CC76_widening_assign_with_tokens/4

ppl_Uint16_Box_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_Uint16_Box_CC76_widening_assign/2

ppl_Uint16_Box_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the uint16 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the uint16 box referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Uint16_Box_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the uint16 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the uint16 box referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Uint16_Box_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the uint16 box P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the uint16 box referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the uint16 box referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Uint16_Box_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the uint16 box P referenced by Handle_1 the concatenation of P and the uint16 box referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the uint16 box referred to in the first argument. These predicates enable the modification of the vector space of the uint16 box referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Uint16_Box_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the uint16 box P referenced by Handle and and_embeds P in this space.

ppl_Uint16_Box_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the uint16 box P referenced by Handle and and_projects P in this space.

ppl_Uint16_Box_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the uint16 box P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Uint16_Box_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the uint16 box P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Uint16_Box_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the uint16 box referenced by Handle to Dimension_Type new space dimensions.

ppl_Uint16_Box_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the uint16 box referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Uint16_Box_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Uint32_Box Domain

Here we provide a short description for each of the predicates available for the domain of uint32 boxes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for uint32 boxes

The constructor predicates build a uint32 box from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Uint32_Box_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new uint32 box $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Uint32_Box_from_space_dimension(3, universe, X).

creates the uint32 box defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Uint32_Box_from_constraints(+Constraint_System, -Handle)
Builds a new uint32 box P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Uint32_Box_from_congruences(+Congruence_System, -Handle)
Builds a new uint32 box P from Congruence_System. Handle is unified with the handle for P.

ppl_new_Uint32_Box_from_generators(+Generator_System, -Handle)
Builds a new uint32 box P from Generator_System. Handle is unified with the handle for P.

Predicates that build new uint32 boxes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Uint32_Box_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Z_Box(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Grid(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Float_Box(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Double_Box(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new uint32 box P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint32_Box_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint32 box P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Uint32_Box domain.

ppl_delete_Uint32_Box(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the uint32 box

Test Predicates

These predicates test the uint32 box for different properties and succeed or fail depending on the outcome.

ppl_Uint32_Box_is_empty(+Handle)
Succeeds if and only if the uint32 box referenced by Handle is empty.

ppl_Uint32_Box_is_universe(+Handle)
Succeeds if and only if the uint32 box referenced by Handle is the universe.

ppl_Uint32_Box_is_bounded(+Handle)
Succeeds if and only if the uint32 box referenced by Handle is bounded.

ppl_Uint32_Box_contains_integer_point(+Handle)
Succeeds if and only if the uint32 box referenced by Handle contains an integer point.

ppl_Uint32_Box_is_topologically_closed(+Handle)
Succeeds if and only if the uint32 box referenced by Handle is topologically closed.

ppl_Uint32_Box_is_discrete(+Handle)
Succeeds if and only if the uint32 box referenced by Handle is discrete.

ppl_Uint32_Box_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the uint32 box referenced by Handle.

ppl_Uint32_Box_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the uint32 box referenced by Handle.

ppl_Uint32_Box_contains_Uint32_Box(+Handle_1, +Handle_2)
Succeeds if and only if the uint32 box referenced by Handle_2 is included in or equal to the uint32 box referenced by Handle_1.

ppl_Uint32_Box_strictly_contains_Uint32_Box(+Handle_1, +Handle_2)
Succeeds if and only if the uint32 box referenced by Handle_2 is included in but not equal to the uint32 box referenced by Handle_1.

ppl_Uint32_Box_is_disjoint_from_Uint32_Box(+Handle_1, +Handle_2)
Succeeds if and only if the uint32 box referenced by Handle_2 is disjoint from the uint32 box referenced by Handle_1.

ppl_Uint32_Box_equals_Uint32_Box(+Handle_1, +Handle_2)
Succeeds if and only if the uint32 box referenced by Handle_1 is equal to the uint32 box referenced by Handle_2.

ppl_Uint32_Box_OK(+Handle)
Succeeds only if the uint32 box referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Uint32_Box_constrains(+Handle, +PPL_Var)
Succeeds if and only if the uint32 box referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the uint32 box

These predicates will obtain more detailed information about the uint32 box unifying some of their arguments with the results.

ppl_Uint32_Box_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the uint32 box referenced by Handle.

ppl_Uint32_Box_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the uint32 box referenced by Handle.

ppl_Uint32_Box_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the uint32 box referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Uint32_Box_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the uint32 box referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Uint32_Box_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the uint32 box referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Uint32_Box_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the uint32 box referenced by Handle.

ppl_Uint32_Box_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the uint32 box referenced by Handle.

ppl_Uint32_Box_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the uint32 box referenced by Handle.

ppl_Uint32_Box_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the uint32 box referenced by Handle.

ppl_Uint32_Box_has_upper_bound(+Handle, +Var, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if Var is upper bounded in uint32 box P referenced by Handle. It is assumed that P is not empty and its space dimension is greater than or equal to that of Var, otherwise the behavior is undefined.

Coeff_1 is unified with the numerator of the upper bound and Coeff_2 with the denominator of the upper bound. If the upper is included in P, then Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Uint32_Box_has_lower_bound(+Handle, +Var, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if Var is lower bounded in uint32 box P referenced by Handle. It is assumed that P is not empty and its space dimension is greater than or equal to that of Var, otherwise the behavior is undefined.

Coeff_1 is unified with the numerator of the lower bound and Coeff_2 with the denominator of the lower bound. If the lower is included in P, then Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Uint32_Box_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if uint32 box P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Uint32_Box_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if uint32 box P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Uint32_Box_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if uint32 box P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Uint32_Box_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if uint32 box P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Uint32_Box_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the uint32 box referenced by Handle.

ppl_Uint32_Box_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the uint32 box referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Uint32_Box_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the uint32 box referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the uint32 box

These predicates may modify the uint32 box referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the uint32 box by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Uint32_Box_add_constraint(+Handle, +Constraint)
Updates the uint32 box referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Uint32_Box_add_congruence(+Handle, +Congruence)
Updates the uint32 box referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Uint32_Box_add_constraints( +Handle, +Constraint_System)
Updates the uint32 box referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Uint32_Box_add_congruences( +Handle, +Congruence_System)
Updates the uint32 box referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Uint32_Box_refine_with_constraint( +Handle, +Constraint)
Updates the uint32 box referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Uint32_Box_refine_with_congruence( +Handle, +Congruence)
Updates the uint32 box referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Uint32_Box_refine_with_constraints( +Handle, +Constraint_System)
Updates the uint32 box referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Uint32_Box_refine_with_congruences( +Handle, +Congruence_System)
Updates the uint32 box referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the uint32 box

These predicates enable transformations such as taking the topological closure (which for the domain of uint32 box is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Uint32_Box_topological_closure_assign(+Handle)
Assigns to the uint32 box referenced by Handle its topological closure.

ppl_Uint32_Box_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the uint32 box P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Uint32_Box_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the uint32 box P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Uint32_Box_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the uint32 box referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Uint32_Box_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the uint32 box referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Uint32_Box_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to uint32 box P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Uint32_Box_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to uint32 box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Uint32_Box_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to uint32 box P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Uint32_Box_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to uint32 box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Uint32_Box_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to uint32 box P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Uint32_Box_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to uint32 box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Uint32_Box_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the uint32 box P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one uint32 box

These predicates include the binary operators which will assign to the uint32 box referred to by the first argument its combination with the uint32 box referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Uint32_Box_intersection_assign(+Handle_1, +Handle_2)
Assigns to the uint32 box P referenced by Handle_1 the intersection of P and the uint32 box referenced by Handle_2.

ppl_Uint32_Box_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the uint32 box P referenced by Handle_1 the upper bound of P and the uint32 box referenced by Handle_2.

ppl_Uint32_Box_difference_assign(+Handle_1, +Handle_2)
Assigns to the uint32 box P referenced by Handle_1 the difference of P and the uint32 box referenced by Handle_2.

ppl_Uint32_Box_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the uint32 box P referenced by Handle_1 the time elapse of P and the uint32 box referenced by Handle_2.

ppl_Uint32_Box_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the uint32 box P_1 referenced by Handle_1 with the uint32 box referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Uint32_Box_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of uint32 box P_1 referenced by Handle_1 and the uint32 box P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_Uint32_Box_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the Uint32_Box domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the uint32 box referred to by the second argument has to be contained in (or equal to) the uint32 box referred to by the first argument.

ppl_Uint32_Box_CC76_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the uint32 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the uint32 box referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Uint32_Box_CC76_widening_assign(+Handle_1, +Handle_2)
Assigns to the uint32 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the uint32 box referenced by Handle_2.

ppl_Uint32_Box_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_Uint32_Box_CC76_widening_assign_with_tokens/4

ppl_Uint32_Box_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_Uint32_Box_CC76_widening_assign/2

ppl_Uint32_Box_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the uint32 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the uint32 box referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Uint32_Box_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the uint32 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the uint32 box referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Uint32_Box_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the uint32 box P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the uint32 box referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the uint32 box referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Uint32_Box_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the uint32 box P referenced by Handle_1 the concatenation of P and the uint32 box referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the uint32 box referred to in the first argument. These predicates enable the modification of the vector space of the uint32 box referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Uint32_Box_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the uint32 box P referenced by Handle and and_embeds P in this space.

ppl_Uint32_Box_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the uint32 box P referenced by Handle and and_projects P in this space.

ppl_Uint32_Box_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the uint32 box P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Uint32_Box_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the uint32 box P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Uint32_Box_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the uint32 box referenced by Handle to Dimension_Type new space dimensions.

ppl_Uint32_Box_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the uint32 box referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Uint32_Box_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Uint64_Box Domain

Here we provide a short description for each of the predicates available for the domain of uint64 boxes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for uint64 boxes

The constructor predicates build a uint64 box from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Uint64_Box_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new uint64 box $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Uint64_Box_from_space_dimension(3, universe, X).

creates the uint64 box defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Uint64_Box_from_constraints(+Constraint_System, -Handle)
Builds a new uint64 box P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Uint64_Box_from_congruences(+Congruence_System, -Handle)
Builds a new uint64 box P from Congruence_System. Handle is unified with the handle for P.

ppl_new_Uint64_Box_from_generators(+Generator_System, -Handle)
Builds a new uint64 box P from Generator_System. Handle is unified with the handle for P.

Predicates that build new uint64 boxes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Uint64_Box_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Z_Box(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Grid(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Float_Box(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Double_Box(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new uint64 box P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Uint64_Box_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new uint64 box P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Uint64_Box domain.

ppl_delete_Uint64_Box(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the uint64 box

Test Predicates

These predicates test the uint64 box for different properties and succeed or fail depending on the outcome.

ppl_Uint64_Box_is_empty(+Handle)
Succeeds if and only if the uint64 box referenced by Handle is empty.

ppl_Uint64_Box_is_universe(+Handle)
Succeeds if and only if the uint64 box referenced by Handle is the universe.

ppl_Uint64_Box_is_bounded(+Handle)
Succeeds if and only if the uint64 box referenced by Handle is bounded.

ppl_Uint64_Box_contains_integer_point(+Handle)
Succeeds if and only if the uint64 box referenced by Handle contains an integer point.

ppl_Uint64_Box_is_topologically_closed(+Handle)
Succeeds if and only if the uint64 box referenced by Handle is topologically closed.

ppl_Uint64_Box_is_discrete(+Handle)
Succeeds if and only if the uint64 box referenced by Handle is discrete.

ppl_Uint64_Box_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the uint64 box referenced by Handle.

ppl_Uint64_Box_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the uint64 box referenced by Handle.

ppl_Uint64_Box_contains_Uint64_Box(+Handle_1, +Handle_2)
Succeeds if and only if the uint64 box referenced by Handle_2 is included in or equal to the uint64 box referenced by Handle_1.

ppl_Uint64_Box_strictly_contains_Uint64_Box(+Handle_1, +Handle_2)
Succeeds if and only if the uint64 box referenced by Handle_2 is included in but not equal to the uint64 box referenced by Handle_1.

ppl_Uint64_Box_is_disjoint_from_Uint64_Box(+Handle_1, +Handle_2)
Succeeds if and only if the uint64 box referenced by Handle_2 is disjoint from the uint64 box referenced by Handle_1.

ppl_Uint64_Box_equals_Uint64_Box(+Handle_1, +Handle_2)
Succeeds if and only if the uint64 box referenced by Handle_1 is equal to the uint64 box referenced by Handle_2.

ppl_Uint64_Box_OK(+Handle)
Succeeds only if the uint64 box referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Uint64_Box_constrains(+Handle, +PPL_Var)
Succeeds if and only if the uint64 box referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the uint64 box

These predicates will obtain more detailed information about the uint64 box unifying some of their arguments with the results.

ppl_Uint64_Box_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the uint64 box referenced by Handle.

ppl_Uint64_Box_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the uint64 box referenced by Handle.

ppl_Uint64_Box_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the uint64 box referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Uint64_Box_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the uint64 box referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Uint64_Box_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the uint64 box referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Uint64_Box_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the uint64 box referenced by Handle.

ppl_Uint64_Box_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the uint64 box referenced by Handle.

ppl_Uint64_Box_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the uint64 box referenced by Handle.

ppl_Uint64_Box_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the uint64 box referenced by Handle.

ppl_Uint64_Box_has_upper_bound(+Handle, +Var, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if Var is upper bounded in uint64 box P referenced by Handle. It is assumed that P is not empty and its space dimension is greater than or equal to that of Var, otherwise the behavior is undefined.

Coeff_1 is unified with the numerator of the upper bound and Coeff_2 with the denominator of the upper bound. If the upper is included in P, then Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Uint64_Box_has_lower_bound(+Handle, +Var, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if Var is lower bounded in uint64 box P referenced by Handle. It is assumed that P is not empty and its space dimension is greater than or equal to that of Var, otherwise the behavior is undefined.

Coeff_1 is unified with the numerator of the lower bound and Coeff_2 with the denominator of the lower bound. If the lower is included in P, then Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Uint64_Box_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if uint64 box P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Uint64_Box_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if uint64 box P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Uint64_Box_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if uint64 box P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Uint64_Box_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if uint64 box P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Uint64_Box_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the uint64 box referenced by Handle.

ppl_Uint64_Box_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the uint64 box referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Uint64_Box_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the uint64 box referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the uint64 box

These predicates may modify the uint64 box referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the uint64 box by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Uint64_Box_add_constraint(+Handle, +Constraint)
Updates the uint64 box referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Uint64_Box_add_congruence(+Handle, +Congruence)
Updates the uint64 box referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Uint64_Box_add_constraints( +Handle, +Constraint_System)
Updates the uint64 box referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Uint64_Box_add_congruences( +Handle, +Congruence_System)
Updates the uint64 box referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Uint64_Box_refine_with_constraint( +Handle, +Constraint)
Updates the uint64 box referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Uint64_Box_refine_with_congruence( +Handle, +Congruence)
Updates the uint64 box referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Uint64_Box_refine_with_constraints( +Handle, +Constraint_System)
Updates the uint64 box referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Uint64_Box_refine_with_congruences( +Handle, +Congruence_System)
Updates the uint64 box referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the uint64 box

These predicates enable transformations such as taking the topological closure (which for the domain of uint64 box is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Uint64_Box_topological_closure_assign(+Handle)
Assigns to the uint64 box referenced by Handle its topological closure.

ppl_Uint64_Box_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the uint64 box P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Uint64_Box_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the uint64 box P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Uint64_Box_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the uint64 box referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Uint64_Box_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the uint64 box referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Uint64_Box_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to uint64 box P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Uint64_Box_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to uint64 box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Uint64_Box_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to uint64 box P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Uint64_Box_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to uint64 box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Uint64_Box_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to uint64 box P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Uint64_Box_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to uint64 box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Uint64_Box_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the uint64 box P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one uint64 box

These predicates include the binary operators which will assign to the uint64 box referred to by the first argument its combination with the uint64 box referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Uint64_Box_intersection_assign(+Handle_1, +Handle_2)
Assigns to the uint64 box P referenced by Handle_1 the intersection of P and the uint64 box referenced by Handle_2.

ppl_Uint64_Box_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the uint64 box P referenced by Handle_1 the upper bound of P and the uint64 box referenced by Handle_2.

ppl_Uint64_Box_difference_assign(+Handle_1, +Handle_2)
Assigns to the uint64 box P referenced by Handle_1 the difference of P and the uint64 box referenced by Handle_2.

ppl_Uint64_Box_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the uint64 box P referenced by Handle_1 the time elapse of P and the uint64 box referenced by Handle_2.

ppl_Uint64_Box_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the uint64 box P_1 referenced by Handle_1 with the uint64 box referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Uint64_Box_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of uint64 box P_1 referenced by Handle_1 and the uint64 box P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_Uint64_Box_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the Uint64_Box domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the uint64 box referred to by the second argument has to be contained in (or equal to) the uint64 box referred to by the first argument.

ppl_Uint64_Box_CC76_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the uint64 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the uint64 box referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Uint64_Box_CC76_widening_assign(+Handle_1, +Handle_2)
Assigns to the uint64 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the uint64 box referenced by Handle_2.

ppl_Uint64_Box_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_Uint64_Box_CC76_widening_assign_with_tokens/4

ppl_Uint64_Box_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_Uint64_Box_CC76_widening_assign/2

ppl_Uint64_Box_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the uint64 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the uint64 box referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Uint64_Box_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the uint64 box P_1 referenced by Handle_1 the CC76-widening of P_1 with the uint64 box referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Uint64_Box_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the uint64 box P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the uint64 box referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the uint64 box referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Uint64_Box_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the uint64 box P referenced by Handle_1 the concatenation of P and the uint64 box referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the uint64 box referred to in the first argument. These predicates enable the modification of the vector space of the uint64 box referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Uint64_Box_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the uint64 box P referenced by Handle and and_embeds P in this space.

ppl_Uint64_Box_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the uint64 box P referenced by Handle and and_projects P in this space.

ppl_Uint64_Box_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the uint64 box P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Uint64_Box_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the uint64 box P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Uint64_Box_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the uint64 box referenced by Handle to Dimension_Type new space dimensions.

ppl_Uint64_Box_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the uint64 box referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Uint64_Box_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Z_Box Domain

Here we provide a short description for each of the predicates available for the domain of z boxes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for z boxes

The constructor predicates build a z box from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Z_Box_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new z box $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Z_Box_from_space_dimension(3, universe, X).

creates the z box defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Z_Box_from_constraints(+Constraint_System, -Handle)
Builds a new z box P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Z_Box_from_congruences(+Congruence_System, -Handle)
Builds a new z box P from Congruence_System. Handle is unified with the handle for P.

ppl_new_Z_Box_from_generators(+Generator_System, -Handle)
Builds a new z box P from Generator_System. Handle is unified with the handle for P.

Predicates that build new z boxes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Z_Box_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new z box P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new z box P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new z box P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new z box P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new z box P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new z box P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new z box P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new z box P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Z_Box(+Handle_1, -Handle_2)
Builds a new z box P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new z box P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new z box P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new z box P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new z box P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new z box P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new z box P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new z box P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new z box P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new z box P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new z box P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new z box P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new z box P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new z box P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new z box P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new z box P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Grid(+Handle_1, -Handle_2)
Builds a new z box P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Float_Box(+Handle_1, -Handle_2)
Builds a new z box P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new z box P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new z box P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Double_Box(+Handle_1, -Handle_2)
Builds a new z box P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new z box P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new z box P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new z box P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new z box P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new z box P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Z_Box_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new z box P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Z_Box domain.

ppl_delete_Z_Box(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the z box

Test Predicates

These predicates test the z box for different properties and succeed or fail depending on the outcome.

ppl_Z_Box_is_empty(+Handle)
Succeeds if and only if the z box referenced by Handle is empty.

ppl_Z_Box_is_universe(+Handle)
Succeeds if and only if the z box referenced by Handle is the universe.

ppl_Z_Box_is_bounded(+Handle)
Succeeds if and only if the z box referenced by Handle is bounded.

ppl_Z_Box_contains_integer_point(+Handle)
Succeeds if and only if the z box referenced by Handle contains an integer point.

ppl_Z_Box_is_topologically_closed(+Handle)
Succeeds if and only if the z box referenced by Handle is topologically closed.

ppl_Z_Box_is_discrete(+Handle)
Succeeds if and only if the z box referenced by Handle is discrete.

ppl_Z_Box_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the z box referenced by Handle.

ppl_Z_Box_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the z box referenced by Handle.

ppl_Z_Box_contains_Z_Box(+Handle_1, +Handle_2)
Succeeds if and only if the z box referenced by Handle_2 is included in or equal to the z box referenced by Handle_1.

ppl_Z_Box_strictly_contains_Z_Box(+Handle_1, +Handle_2)
Succeeds if and only if the z box referenced by Handle_2 is included in but not equal to the z box referenced by Handle_1.

ppl_Z_Box_is_disjoint_from_Z_Box(+Handle_1, +Handle_2)
Succeeds if and only if the z box referenced by Handle_2 is disjoint from the z box referenced by Handle_1.

ppl_Z_Box_equals_Z_Box(+Handle_1, +Handle_2)
Succeeds if and only if the z box referenced by Handle_1 is equal to the z box referenced by Handle_2.

ppl_Z_Box_OK(+Handle)
Succeeds only if the z box referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Z_Box_constrains(+Handle, +PPL_Var)
Succeeds if and only if the z box referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the z box

These predicates will obtain more detailed information about the z box unifying some of their arguments with the results.

ppl_Z_Box_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the z box referenced by Handle.

ppl_Z_Box_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the z box referenced by Handle.

ppl_Z_Box_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the z box referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Z_Box_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the z box referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Z_Box_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the z box referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Z_Box_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the z box referenced by Handle.

ppl_Z_Box_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the z box referenced by Handle.

ppl_Z_Box_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the z box referenced by Handle.

ppl_Z_Box_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the z box referenced by Handle.

ppl_Z_Box_has_upper_bound(+Handle, +Var, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if Var is upper bounded in z box P referenced by Handle. It is assumed that P is not empty and its space dimension is greater than or equal to that of Var, otherwise the behavior is undefined.

Coeff_1 is unified with the numerator of the upper bound and Coeff_2 with the denominator of the upper bound. If the upper is included in P, then Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Z_Box_has_lower_bound(+Handle, +Var, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if Var is lower bounded in z box P referenced by Handle. It is assumed that P is not empty and its space dimension is greater than or equal to that of Var, otherwise the behavior is undefined.

Coeff_1 is unified with the numerator of the lower bound and Coeff_2 with the denominator of the lower bound. If the lower is included in P, then Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Z_Box_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if z box P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Z_Box_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if z box P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Z_Box_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if z box P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Z_Box_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if z box P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Z_Box_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the z box referenced by Handle.

ppl_Z_Box_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the z box referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Z_Box_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the z box referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the z box

These predicates may modify the z box referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the z box by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Z_Box_add_constraint(+Handle, +Constraint)
Updates the z box referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Z_Box_add_congruence(+Handle, +Congruence)
Updates the z box referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Z_Box_add_constraints( +Handle, +Constraint_System)
Updates the z box referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Z_Box_add_congruences( +Handle, +Congruence_System)
Updates the z box referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Z_Box_refine_with_constraint( +Handle, +Constraint)
Updates the z box referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Z_Box_refine_with_congruence( +Handle, +Congruence)
Updates the z box referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Z_Box_refine_with_constraints( +Handle, +Constraint_System)
Updates the z box referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Z_Box_refine_with_congruences( +Handle, +Congruence_System)
Updates the z box referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the z box

These predicates enable transformations such as taking the topological closure (which for the domain of z box is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Z_Box_topological_closure_assign(+Handle)
Assigns to the z box referenced by Handle its topological closure.

ppl_Z_Box_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the z box P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Z_Box_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the z box P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Z_Box_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the z box referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Z_Box_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the z box referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Z_Box_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to z box P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Z_Box_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to z box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Z_Box_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to z box P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Z_Box_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to z box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Z_Box_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to z box P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Z_Box_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to z box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Z_Box_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the z box P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one z box

These predicates include the binary operators which will assign to the z box referred to by the first argument its combination with the z box referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Z_Box_intersection_assign(+Handle_1, +Handle_2)
Assigns to the z box P referenced by Handle_1 the intersection of P and the z box referenced by Handle_2.

ppl_Z_Box_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the z box P referenced by Handle_1 the upper bound of P and the z box referenced by Handle_2.

ppl_Z_Box_difference_assign(+Handle_1, +Handle_2)
Assigns to the z box P referenced by Handle_1 the difference of P and the z box referenced by Handle_2.

ppl_Z_Box_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the z box P referenced by Handle_1 the time elapse of P and the z box referenced by Handle_2.

ppl_Z_Box_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the z box P_1 referenced by Handle_1 with the z box referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Z_Box_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of z box P_1 referenced by Handle_1 and the z box P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_Z_Box_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the Z_Box domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the z box referred to by the second argument has to be contained in (or equal to) the z box referred to by the first argument.

ppl_Z_Box_CC76_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the z box P_1 referenced by Handle_1 the CC76-widening of P_1 with the z box referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Z_Box_CC76_widening_assign(+Handle_1, +Handle_2)
Assigns to the z box P_1 referenced by Handle_1 the CC76-widening of P_1 with the z box referenced by Handle_2.

ppl_Z_Box_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_Z_Box_CC76_widening_assign_with_tokens/4

ppl_Z_Box_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_Z_Box_CC76_widening_assign/2

ppl_Z_Box_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the z box P_1 referenced by Handle_1 the CC76-widening of P_1 with the z box referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Z_Box_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the z box P_1 referenced by Handle_1 the CC76-widening of P_1 with the z box referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Z_Box_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the z box P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the z box referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the z box referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Z_Box_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the z box P referenced by Handle_1 the concatenation of P and the z box referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the z box referred to in the first argument. These predicates enable the modification of the vector space of the z box referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Z_Box_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the z box P referenced by Handle and and_embeds P in this space.

ppl_Z_Box_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the z box P referenced by Handle and and_projects P in this space.

ppl_Z_Box_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the z box P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Z_Box_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the z box P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Z_Box_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the z box referenced by Handle to Dimension_Type new space dimensions.

ppl_Z_Box_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the z box referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Z_Box_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Rational_Box Domain

Here we provide a short description for each of the predicates available for the domain of rational boxes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for rational boxes

The constructor predicates build a rational box from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Rational_Box_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new rational box $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Rational_Box_from_space_dimension(3, universe, X).

creates the rational box defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Rational_Box_from_constraints(+Constraint_System, -Handle)
Builds a new rational box P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Rational_Box_from_congruences(+Congruence_System, -Handle)
Builds a new rational box P from Congruence_System. Handle is unified with the handle for P.

ppl_new_Rational_Box_from_generators(+Generator_System, -Handle)
Builds a new rational box P from Generator_System. Handle is unified with the handle for P.

Predicates that build new rational boxes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Rational_Box_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Z_Box(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Grid(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Float_Box(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Double_Box(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new rational box P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Rational_Box_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new rational box P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Rational_Box domain.

ppl_delete_Rational_Box(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the rational box

Test Predicates

These predicates test the rational box for different properties and succeed or fail depending on the outcome.

ppl_Rational_Box_is_empty(+Handle)
Succeeds if and only if the rational box referenced by Handle is empty.

ppl_Rational_Box_is_universe(+Handle)
Succeeds if and only if the rational box referenced by Handle is the universe.

ppl_Rational_Box_is_bounded(+Handle)
Succeeds if and only if the rational box referenced by Handle is bounded.

ppl_Rational_Box_contains_integer_point(+Handle)
Succeeds if and only if the rational box referenced by Handle contains an integer point.

ppl_Rational_Box_is_topologically_closed(+Handle)
Succeeds if and only if the rational box referenced by Handle is topologically closed.

ppl_Rational_Box_is_discrete(+Handle)
Succeeds if and only if the rational box referenced by Handle is discrete.

ppl_Rational_Box_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the rational box referenced by Handle.

ppl_Rational_Box_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the rational box referenced by Handle.

ppl_Rational_Box_contains_Rational_Box(+Handle_1, +Handle_2)
Succeeds if and only if the rational box referenced by Handle_2 is included in or equal to the rational box referenced by Handle_1.

ppl_Rational_Box_strictly_contains_Rational_Box(+Handle_1, +Handle_2)
Succeeds if and only if the rational box referenced by Handle_2 is included in but not equal to the rational box referenced by Handle_1.

ppl_Rational_Box_is_disjoint_from_Rational_Box(+Handle_1, +Handle_2)
Succeeds if and only if the rational box referenced by Handle_2 is disjoint from the rational box referenced by Handle_1.

ppl_Rational_Box_equals_Rational_Box(+Handle_1, +Handle_2)
Succeeds if and only if the rational box referenced by Handle_1 is equal to the rational box referenced by Handle_2.

ppl_Rational_Box_OK(+Handle)
Succeeds only if the rational box referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Rational_Box_constrains(+Handle, +PPL_Var)
Succeeds if and only if the rational box referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the rational box

These predicates will obtain more detailed information about the rational box unifying some of their arguments with the results.

ppl_Rational_Box_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the rational box referenced by Handle.

ppl_Rational_Box_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the rational box referenced by Handle.

ppl_Rational_Box_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the rational box referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Rational_Box_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the rational box referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Rational_Box_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the rational box referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Rational_Box_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the rational box referenced by Handle.

ppl_Rational_Box_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the rational box referenced by Handle.

ppl_Rational_Box_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the rational box referenced by Handle.

ppl_Rational_Box_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the rational box referenced by Handle.

ppl_Rational_Box_has_upper_bound(+Handle, +Var, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if Var is upper bounded in rational box P referenced by Handle. It is assumed that P is not empty and its space dimension is greater than or equal to that of Var, otherwise the behavior is undefined.

Coeff_1 is unified with the numerator of the upper bound and Coeff_2 with the denominator of the upper bound. If the upper is included in P, then Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Rational_Box_has_lower_bound(+Handle, +Var, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if Var is lower bounded in rational box P referenced by Handle. It is assumed that P is not empty and its space dimension is greater than or equal to that of Var, otherwise the behavior is undefined.

Coeff_1 is unified with the numerator of the lower bound and Coeff_2 with the denominator of the lower bound. If the lower is included in P, then Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Rational_Box_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if rational box P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Rational_Box_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if rational box P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Rational_Box_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if rational box P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Rational_Box_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if rational box P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Rational_Box_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the rational box referenced by Handle.

ppl_Rational_Box_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the rational box referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Rational_Box_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the rational box referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the rational box

These predicates may modify the rational box referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the rational box by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Rational_Box_add_constraint(+Handle, +Constraint)
Updates the rational box referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Rational_Box_add_congruence(+Handle, +Congruence)
Updates the rational box referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Rational_Box_add_constraints( +Handle, +Constraint_System)
Updates the rational box referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Rational_Box_add_congruences( +Handle, +Congruence_System)
Updates the rational box referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Rational_Box_refine_with_constraint( +Handle, +Constraint)
Updates the rational box referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Rational_Box_refine_with_congruence( +Handle, +Congruence)
Updates the rational box referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Rational_Box_refine_with_constraints( +Handle, +Constraint_System)
Updates the rational box referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Rational_Box_refine_with_congruences( +Handle, +Congruence_System)
Updates the rational box referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the rational box

These predicates enable transformations such as taking the topological closure (which for the domain of rational box is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Rational_Box_topological_closure_assign(+Handle)
Assigns to the rational box referenced by Handle its topological closure.

ppl_Rational_Box_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the rational box P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Rational_Box_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the rational box P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Rational_Box_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the rational box referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Rational_Box_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the rational box referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Rational_Box_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to rational box P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Rational_Box_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to rational box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Rational_Box_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to rational box P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Rational_Box_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to rational box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Rational_Box_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to rational box P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Rational_Box_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to rational box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Rational_Box_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the rational box P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one rational box

These predicates include the binary operators which will assign to the rational box referred to by the first argument its combination with the rational box referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Rational_Box_intersection_assign(+Handle_1, +Handle_2)
Assigns to the rational box P referenced by Handle_1 the intersection of P and the rational box referenced by Handle_2.

ppl_Rational_Box_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the rational box P referenced by Handle_1 the upper bound of P and the rational box referenced by Handle_2.

ppl_Rational_Box_difference_assign(+Handle_1, +Handle_2)
Assigns to the rational box P referenced by Handle_1 the difference of P and the rational box referenced by Handle_2.

ppl_Rational_Box_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the rational box P referenced by Handle_1 the time elapse of P and the rational box referenced by Handle_2.

ppl_Rational_Box_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the rational box P_1 referenced by Handle_1 with the rational box referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Rational_Box_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of rational box P_1 referenced by Handle_1 and the rational box P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_Rational_Box_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the Rational_Box domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the rational box referred to by the second argument has to be contained in (or equal to) the rational box referred to by the first argument.

ppl_Rational_Box_CC76_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the rational box P_1 referenced by Handle_1 the CC76-widening of P_1 with the rational box referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Rational_Box_CC76_widening_assign(+Handle_1, +Handle_2)
Assigns to the rational box P_1 referenced by Handle_1 the CC76-widening of P_1 with the rational box referenced by Handle_2.

ppl_Rational_Box_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_Rational_Box_CC76_widening_assign_with_tokens/4

ppl_Rational_Box_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_Rational_Box_CC76_widening_assign/2

ppl_Rational_Box_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the rational box P_1 referenced by Handle_1 the CC76-widening of P_1 with the rational box referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Rational_Box_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the rational box P_1 referenced by Handle_1 the CC76-widening of P_1 with the rational box referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Rational_Box_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the rational box P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the rational box referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the rational box referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Rational_Box_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the rational box P referenced by Handle_1 the concatenation of P and the rational box referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the rational box referred to in the first argument. These predicates enable the modification of the vector space of the rational box referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Rational_Box_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the rational box P referenced by Handle and and_embeds P in this space.

ppl_Rational_Box_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the rational box P referenced by Handle and and_projects P in this space.

ppl_Rational_Box_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the rational box P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Rational_Box_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the rational box P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Rational_Box_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the rational box referenced by Handle to Dimension_Type new space dimensions.

ppl_Rational_Box_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the rational box referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Rational_Box_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the BD_Shape_int8_t Domain

Here we provide a short description for each of the predicates available for the domain of bd shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for bd shapes

The constructor predicates build a bd shape from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_BD_Shape_int8_t_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new bd shape $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_BD_Shape_int8_t_from_space_dimension(3, universe, X).

creates the bd shape defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_BD_Shape_int8_t_from_constraints(+Constraint_System, -Handle)
Builds a new bd shape P from Constraint_System. Handle is unified with the handle for P.

ppl_new_BD_Shape_int8_t_from_congruences(+Congruence_System, -Handle)
Builds a new bd shape P from Congruence_System. Handle is unified with the handle for P.

ppl_new_BD_Shape_int8_t_from_generators(+Generator_System, -Handle)
Builds a new bd shape P from Generator_System. Handle is unified with the handle for P.

Predicates that build new bd shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_BD_Shape_int8_t_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Z_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Grid(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Float_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Double_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int8_t_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the BD_Shape_int8_t domain.

ppl_delete_BD_Shape_int8_t(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the bd shape

Test Predicates

These predicates test the bd shape for different properties and succeed or fail depending on the outcome.

ppl_BD_Shape_int8_t_is_empty(+Handle)
Succeeds if and only if the bd shape referenced by Handle is empty.

ppl_BD_Shape_int8_t_is_universe(+Handle)
Succeeds if and only if the bd shape referenced by Handle is the universe.

ppl_BD_Shape_int8_t_is_bounded(+Handle)
Succeeds if and only if the bd shape referenced by Handle is bounded.

ppl_BD_Shape_int8_t_contains_integer_point(+Handle)
Succeeds if and only if the bd shape referenced by Handle contains an integer point.

ppl_BD_Shape_int8_t_is_topologically_closed(+Handle)
Succeeds if and only if the bd shape referenced by Handle is topologically closed.

ppl_BD_Shape_int8_t_is_discrete(+Handle)
Succeeds if and only if the bd shape referenced by Handle is discrete.

ppl_BD_Shape_int8_t_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the bd shape referenced by Handle.

ppl_BD_Shape_int8_t_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the bd shape referenced by Handle.

ppl_BD_Shape_int8_t_contains_BD_Shape_int8_t(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is included in or equal to the bd shape referenced by Handle_1.

ppl_BD_Shape_int8_t_strictly_contains_BD_Shape_int8_t(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is included in but not equal to the bd shape referenced by Handle_1.

ppl_BD_Shape_int8_t_is_disjoint_from_BD_Shape_int8_t(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is disjoint from the bd shape referenced by Handle_1.

ppl_BD_Shape_int8_t_equals_BD_Shape_int8_t(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_1 is equal to the bd shape referenced by Handle_2.

ppl_BD_Shape_int8_t_OK(+Handle)
Succeeds only if the bd shape referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_BD_Shape_int8_t_constrains(+Handle, +PPL_Var)
Succeeds if and only if the bd shape referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the bd shape

These predicates will obtain more detailed information about the bd shape unifying some of their arguments with the results.

ppl_BD_Shape_int8_t_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the bd shape referenced by Handle.

ppl_BD_Shape_int8_t_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the bd shape referenced by Handle.

ppl_BD_Shape_int8_t_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_int8_t_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_int8_t_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_int8_t_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_int8_t_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_int8_t_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_int8_t_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_int8_t_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_int8_t_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_int8_t_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_int8_t_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_int8_t_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the bd shape referenced by Handle.

ppl_BD_Shape_int8_t_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the bd shape referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_BD_Shape_int8_t_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the bd shape referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the bd shape

These predicates may modify the bd shape referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the bd shape by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_BD_Shape_int8_t_add_constraint(+Handle, +Constraint)
Updates the bd shape referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_BD_Shape_int8_t_add_congruence(+Handle, +Congruence)
Updates the bd shape referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_BD_Shape_int8_t_add_constraints( +Handle, +Constraint_System)
Updates the bd shape referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_BD_Shape_int8_t_add_congruences( +Handle, +Congruence_System)
Updates the bd shape referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_BD_Shape_int8_t_refine_with_constraint( +Handle, +Constraint)
Updates the bd shape referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_BD_Shape_int8_t_refine_with_congruence( +Handle, +Congruence)
Updates the bd shape referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_BD_Shape_int8_t_refine_with_constraints( +Handle, +Constraint_System)
Updates the bd shape referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_BD_Shape_int8_t_refine_with_congruences( +Handle, +Congruence_System)
Updates the bd shape referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the bd shape

These predicates enable transformations such as taking the topological closure (which for the domain of bd shape is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_BD_Shape_int8_t_topological_closure_assign(+Handle)
Assigns to the bd shape referenced by Handle its topological closure.

ppl_BD_Shape_int8_t_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the bd shape P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_BD_Shape_int8_t_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the bd shape P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_BD_Shape_int8_t_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the bd shape referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_BD_Shape_int8_t_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the bd shape referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_BD_Shape_int8_t_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_BD_Shape_int8_t_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_BD_Shape_int8_t_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_int8_t_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_int8_t_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_int8_t_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_int8_t_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the bd shape P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one bd shape

These predicates include the binary operators which will assign to the bd shape referred to by the first argument its combination with the bd shape referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_BD_Shape_int8_t_intersection_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the intersection of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_int8_t_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the upper bound of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_int8_t_difference_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the difference of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_int8_t_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the time elapse of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_int8_t_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the bd shape P_1 referenced by Handle_1 with the bd shape referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_BD_Shape_int8_t_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of bd shape P_1 referenced by Handle_1 and the bd shape P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_BD_Shape_int8_t_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the BD_Shape_int8_t domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the bd shape referred to by the second argument has to be contained in (or equal to) the bd shape referred to by the first argument.

ppl_BD_Shape_int8_t_BHMZ05_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_int8_t_H79_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_int8_t_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2.

ppl_BD_Shape_int8_t_H79_widening_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2.

ppl_BD_Shape_int8_t_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_BD_Shape_int8_t_H79_widening_assign_with_tokens/4

ppl_BD_Shape_int8_t_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_BD_Shape_int8_t_H79_widening_assign/2

ppl_BD_Shape_int8_t_limited_BHMZ05_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_int8_t_limited_H79_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_int8_t_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_int8_t_limited_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_int8_t_limited_H79_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_int8_t_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_int8_t_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the bd shape referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the bd shape referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_BD_Shape_int8_t_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the concatenation of P and the bd shape referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the bd shape referred to in the first argument. These predicates enable the modification of the vector space of the bd shape referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_BD_Shape_int8_t_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the bd shape P referenced by Handle and and_embeds P in this space.

ppl_BD_Shape_int8_t_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the bd shape P referenced by Handle and and_projects P in this space.

ppl_BD_Shape_int8_t_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the bd shape P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_BD_Shape_int8_t_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the bd shape P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_BD_Shape_int8_t_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the bd shape referenced by Handle to Dimension_Type new space dimensions.

ppl_BD_Shape_int8_t_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the bd shape referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_BD_Shape_int8_t_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the BD_Shape_int16_t Domain

Here we provide a short description for each of the predicates available for the domain of bd shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for bd shapes

The constructor predicates build a bd shape from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_BD_Shape_int16_t_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new bd shape $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_BD_Shape_int16_t_from_space_dimension(3, universe, X).

creates the bd shape defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_BD_Shape_int16_t_from_constraints(+Constraint_System, -Handle)
Builds a new bd shape P from Constraint_System. Handle is unified with the handle for P.

ppl_new_BD_Shape_int16_t_from_congruences(+Congruence_System, -Handle)
Builds a new bd shape P from Congruence_System. Handle is unified with the handle for P.

ppl_new_BD_Shape_int16_t_from_generators(+Generator_System, -Handle)
Builds a new bd shape P from Generator_System. Handle is unified with the handle for P.

Predicates that build new bd shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_BD_Shape_int16_t_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Z_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Grid(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Float_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Double_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int16_t_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the BD_Shape_int16_t domain.

ppl_delete_BD_Shape_int16_t(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the bd shape

Test Predicates

These predicates test the bd shape for different properties and succeed or fail depending on the outcome.

ppl_BD_Shape_int16_t_is_empty(+Handle)
Succeeds if and only if the bd shape referenced by Handle is empty.

ppl_BD_Shape_int16_t_is_universe(+Handle)
Succeeds if and only if the bd shape referenced by Handle is the universe.

ppl_BD_Shape_int16_t_is_bounded(+Handle)
Succeeds if and only if the bd shape referenced by Handle is bounded.

ppl_BD_Shape_int16_t_contains_integer_point(+Handle)
Succeeds if and only if the bd shape referenced by Handle contains an integer point.

ppl_BD_Shape_int16_t_is_topologically_closed(+Handle)
Succeeds if and only if the bd shape referenced by Handle is topologically closed.

ppl_BD_Shape_int16_t_is_discrete(+Handle)
Succeeds if and only if the bd shape referenced by Handle is discrete.

ppl_BD_Shape_int16_t_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the bd shape referenced by Handle.

ppl_BD_Shape_int16_t_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the bd shape referenced by Handle.

ppl_BD_Shape_int16_t_contains_BD_Shape_int16_t(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is included in or equal to the bd shape referenced by Handle_1.

ppl_BD_Shape_int16_t_strictly_contains_BD_Shape_int16_t(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is included in but not equal to the bd shape referenced by Handle_1.

ppl_BD_Shape_int16_t_is_disjoint_from_BD_Shape_int16_t(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is disjoint from the bd shape referenced by Handle_1.

ppl_BD_Shape_int16_t_equals_BD_Shape_int16_t(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_1 is equal to the bd shape referenced by Handle_2.

ppl_BD_Shape_int16_t_OK(+Handle)
Succeeds only if the bd shape referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_BD_Shape_int16_t_constrains(+Handle, +PPL_Var)
Succeeds if and only if the bd shape referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the bd shape

These predicates will obtain more detailed information about the bd shape unifying some of their arguments with the results.

ppl_BD_Shape_int16_t_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the bd shape referenced by Handle.

ppl_BD_Shape_int16_t_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the bd shape referenced by Handle.

ppl_BD_Shape_int16_t_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_int16_t_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_int16_t_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_int16_t_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_int16_t_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_int16_t_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_int16_t_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_int16_t_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_int16_t_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_int16_t_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_int16_t_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_int16_t_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the bd shape referenced by Handle.

ppl_BD_Shape_int16_t_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the bd shape referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_BD_Shape_int16_t_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the bd shape referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the bd shape

These predicates may modify the bd shape referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the bd shape by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_BD_Shape_int16_t_add_constraint(+Handle, +Constraint)
Updates the bd shape referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_BD_Shape_int16_t_add_congruence(+Handle, +Congruence)
Updates the bd shape referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_BD_Shape_int16_t_add_constraints( +Handle, +Constraint_System)
Updates the bd shape referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_BD_Shape_int16_t_add_congruences( +Handle, +Congruence_System)
Updates the bd shape referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_BD_Shape_int16_t_refine_with_constraint( +Handle, +Constraint)
Updates the bd shape referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_BD_Shape_int16_t_refine_with_congruence( +Handle, +Congruence)
Updates the bd shape referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_BD_Shape_int16_t_refine_with_constraints( +Handle, +Constraint_System)
Updates the bd shape referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_BD_Shape_int16_t_refine_with_congruences( +Handle, +Congruence_System)
Updates the bd shape referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the bd shape

These predicates enable transformations such as taking the topological closure (which for the domain of bd shape is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_BD_Shape_int16_t_topological_closure_assign(+Handle)
Assigns to the bd shape referenced by Handle its topological closure.

ppl_BD_Shape_int16_t_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the bd shape P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_BD_Shape_int16_t_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the bd shape P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_BD_Shape_int16_t_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the bd shape referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_BD_Shape_int16_t_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the bd shape referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_BD_Shape_int16_t_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_BD_Shape_int16_t_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_BD_Shape_int16_t_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_int16_t_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_int16_t_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_int16_t_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_int16_t_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the bd shape P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one bd shape

These predicates include the binary operators which will assign to the bd shape referred to by the first argument its combination with the bd shape referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_BD_Shape_int16_t_intersection_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the intersection of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_int16_t_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the upper bound of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_int16_t_difference_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the difference of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_int16_t_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the time elapse of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_int16_t_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the bd shape P_1 referenced by Handle_1 with the bd shape referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_BD_Shape_int16_t_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of bd shape P_1 referenced by Handle_1 and the bd shape P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_BD_Shape_int16_t_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the BD_Shape_int16_t domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the bd shape referred to by the second argument has to be contained in (or equal to) the bd shape referred to by the first argument.

ppl_BD_Shape_int16_t_BHMZ05_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_int16_t_H79_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_int16_t_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2.

ppl_BD_Shape_int16_t_H79_widening_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2.

ppl_BD_Shape_int16_t_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_BD_Shape_int16_t_H79_widening_assign_with_tokens/4

ppl_BD_Shape_int16_t_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_BD_Shape_int16_t_H79_widening_assign/2

ppl_BD_Shape_int16_t_limited_BHMZ05_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_int16_t_limited_H79_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_int16_t_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_int16_t_limited_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_int16_t_limited_H79_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_int16_t_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_int16_t_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the bd shape referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the bd shape referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_BD_Shape_int16_t_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the concatenation of P and the bd shape referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the bd shape referred to in the first argument. These predicates enable the modification of the vector space of the bd shape referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_BD_Shape_int16_t_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the bd shape P referenced by Handle and and_embeds P in this space.

ppl_BD_Shape_int16_t_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the bd shape P referenced by Handle and and_projects P in this space.

ppl_BD_Shape_int16_t_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the bd shape P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_BD_Shape_int16_t_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the bd shape P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_BD_Shape_int16_t_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the bd shape referenced by Handle to Dimension_Type new space dimensions.

ppl_BD_Shape_int16_t_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the bd shape referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_BD_Shape_int16_t_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the BD_Shape_int32_t Domain

Here we provide a short description for each of the predicates available for the domain of bd shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for bd shapes

The constructor predicates build a bd shape from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_BD_Shape_int32_t_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new bd shape $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_BD_Shape_int32_t_from_space_dimension(3, universe, X).

creates the bd shape defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_BD_Shape_int32_t_from_constraints(+Constraint_System, -Handle)
Builds a new bd shape P from Constraint_System. Handle is unified with the handle for P.

ppl_new_BD_Shape_int32_t_from_congruences(+Congruence_System, -Handle)
Builds a new bd shape P from Congruence_System. Handle is unified with the handle for P.

ppl_new_BD_Shape_int32_t_from_generators(+Generator_System, -Handle)
Builds a new bd shape P from Generator_System. Handle is unified with the handle for P.

Predicates that build new bd shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_BD_Shape_int32_t_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Z_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Grid(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Float_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Double_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int32_t_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the BD_Shape_int32_t domain.

ppl_delete_BD_Shape_int32_t(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the bd shape

Test Predicates

These predicates test the bd shape for different properties and succeed or fail depending on the outcome.

ppl_BD_Shape_int32_t_is_empty(+Handle)
Succeeds if and only if the bd shape referenced by Handle is empty.

ppl_BD_Shape_int32_t_is_universe(+Handle)
Succeeds if and only if the bd shape referenced by Handle is the universe.

ppl_BD_Shape_int32_t_is_bounded(+Handle)
Succeeds if and only if the bd shape referenced by Handle is bounded.

ppl_BD_Shape_int32_t_contains_integer_point(+Handle)
Succeeds if and only if the bd shape referenced by Handle contains an integer point.

ppl_BD_Shape_int32_t_is_topologically_closed(+Handle)
Succeeds if and only if the bd shape referenced by Handle is topologically closed.

ppl_BD_Shape_int32_t_is_discrete(+Handle)
Succeeds if and only if the bd shape referenced by Handle is discrete.

ppl_BD_Shape_int32_t_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the bd shape referenced by Handle.

ppl_BD_Shape_int32_t_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the bd shape referenced by Handle.

ppl_BD_Shape_int32_t_contains_BD_Shape_int32_t(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is included in or equal to the bd shape referenced by Handle_1.

ppl_BD_Shape_int32_t_strictly_contains_BD_Shape_int32_t(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is included in but not equal to the bd shape referenced by Handle_1.

ppl_BD_Shape_int32_t_is_disjoint_from_BD_Shape_int32_t(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is disjoint from the bd shape referenced by Handle_1.

ppl_BD_Shape_int32_t_equals_BD_Shape_int32_t(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_1 is equal to the bd shape referenced by Handle_2.

ppl_BD_Shape_int32_t_OK(+Handle)
Succeeds only if the bd shape referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_BD_Shape_int32_t_constrains(+Handle, +PPL_Var)
Succeeds if and only if the bd shape referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the bd shape

These predicates will obtain more detailed information about the bd shape unifying some of their arguments with the results.

ppl_BD_Shape_int32_t_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the bd shape referenced by Handle.

ppl_BD_Shape_int32_t_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the bd shape referenced by Handle.

ppl_BD_Shape_int32_t_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_int32_t_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_int32_t_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_int32_t_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_int32_t_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_int32_t_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_int32_t_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_int32_t_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_int32_t_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_int32_t_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_int32_t_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_int32_t_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the bd shape referenced by Handle.

ppl_BD_Shape_int32_t_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the bd shape referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_BD_Shape_int32_t_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the bd shape referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the bd shape

These predicates may modify the bd shape referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the bd shape by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_BD_Shape_int32_t_add_constraint(+Handle, +Constraint)
Updates the bd shape referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_BD_Shape_int32_t_add_congruence(+Handle, +Congruence)
Updates the bd shape referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_BD_Shape_int32_t_add_constraints( +Handle, +Constraint_System)
Updates the bd shape referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_BD_Shape_int32_t_add_congruences( +Handle, +Congruence_System)
Updates the bd shape referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_BD_Shape_int32_t_refine_with_constraint( +Handle, +Constraint)
Updates the bd shape referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_BD_Shape_int32_t_refine_with_congruence( +Handle, +Congruence)
Updates the bd shape referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_BD_Shape_int32_t_refine_with_constraints( +Handle, +Constraint_System)
Updates the bd shape referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_BD_Shape_int32_t_refine_with_congruences( +Handle, +Congruence_System)
Updates the bd shape referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the bd shape

These predicates enable transformations such as taking the topological closure (which for the domain of bd shape is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_BD_Shape_int32_t_topological_closure_assign(+Handle)
Assigns to the bd shape referenced by Handle its topological closure.

ppl_BD_Shape_int32_t_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the bd shape P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_BD_Shape_int32_t_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the bd shape P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_BD_Shape_int32_t_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the bd shape referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_BD_Shape_int32_t_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the bd shape referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_BD_Shape_int32_t_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_BD_Shape_int32_t_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_BD_Shape_int32_t_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_int32_t_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_int32_t_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_int32_t_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_int32_t_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the bd shape P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one bd shape

These predicates include the binary operators which will assign to the bd shape referred to by the first argument its combination with the bd shape referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_BD_Shape_int32_t_intersection_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the intersection of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_int32_t_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the upper bound of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_int32_t_difference_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the difference of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_int32_t_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the time elapse of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_int32_t_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the bd shape P_1 referenced by Handle_1 with the bd shape referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_BD_Shape_int32_t_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of bd shape P_1 referenced by Handle_1 and the bd shape P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_BD_Shape_int32_t_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the BD_Shape_int32_t domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the bd shape referred to by the second argument has to be contained in (or equal to) the bd shape referred to by the first argument.

ppl_BD_Shape_int32_t_BHMZ05_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_int32_t_H79_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_int32_t_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2.

ppl_BD_Shape_int32_t_H79_widening_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2.

ppl_BD_Shape_int32_t_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_BD_Shape_int32_t_H79_widening_assign_with_tokens/4

ppl_BD_Shape_int32_t_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_BD_Shape_int32_t_H79_widening_assign/2

ppl_BD_Shape_int32_t_limited_BHMZ05_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_int32_t_limited_H79_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_int32_t_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_int32_t_limited_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_int32_t_limited_H79_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_int32_t_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_int32_t_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the bd shape referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the bd shape referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_BD_Shape_int32_t_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the concatenation of P and the bd shape referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the bd shape referred to in the first argument. These predicates enable the modification of the vector space of the bd shape referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_BD_Shape_int32_t_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the bd shape P referenced by Handle and and_embeds P in this space.

ppl_BD_Shape_int32_t_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the bd shape P referenced by Handle and and_projects P in this space.

ppl_BD_Shape_int32_t_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the bd shape P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_BD_Shape_int32_t_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the bd shape P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_BD_Shape_int32_t_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the bd shape referenced by Handle to Dimension_Type new space dimensions.

ppl_BD_Shape_int32_t_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the bd shape referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_BD_Shape_int32_t_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the BD_Shape_int64_t Domain

Here we provide a short description for each of the predicates available for the domain of bd shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for bd shapes

The constructor predicates build a bd shape from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_BD_Shape_int64_t_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new bd shape $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_BD_Shape_int64_t_from_space_dimension(3, universe, X).

creates the bd shape defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_BD_Shape_int64_t_from_constraints(+Constraint_System, -Handle)
Builds a new bd shape P from Constraint_System. Handle is unified with the handle for P.

ppl_new_BD_Shape_int64_t_from_congruences(+Congruence_System, -Handle)
Builds a new bd shape P from Congruence_System. Handle is unified with the handle for P.

ppl_new_BD_Shape_int64_t_from_generators(+Generator_System, -Handle)
Builds a new bd shape P from Generator_System. Handle is unified with the handle for P.

Predicates that build new bd shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_BD_Shape_int64_t_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Z_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Grid(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Float_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Double_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_int64_t_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the BD_Shape_int64_t domain.

ppl_delete_BD_Shape_int64_t(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the bd shape

Test Predicates

These predicates test the bd shape for different properties and succeed or fail depending on the outcome.

ppl_BD_Shape_int64_t_is_empty(+Handle)
Succeeds if and only if the bd shape referenced by Handle is empty.

ppl_BD_Shape_int64_t_is_universe(+Handle)
Succeeds if and only if the bd shape referenced by Handle is the universe.

ppl_BD_Shape_int64_t_is_bounded(+Handle)
Succeeds if and only if the bd shape referenced by Handle is bounded.

ppl_BD_Shape_int64_t_contains_integer_point(+Handle)
Succeeds if and only if the bd shape referenced by Handle contains an integer point.

ppl_BD_Shape_int64_t_is_topologically_closed(+Handle)
Succeeds if and only if the bd shape referenced by Handle is topologically closed.

ppl_BD_Shape_int64_t_is_discrete(+Handle)
Succeeds if and only if the bd shape referenced by Handle is discrete.

ppl_BD_Shape_int64_t_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the bd shape referenced by Handle.

ppl_BD_Shape_int64_t_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the bd shape referenced by Handle.

ppl_BD_Shape_int64_t_contains_BD_Shape_int64_t(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is included in or equal to the bd shape referenced by Handle_1.

ppl_BD_Shape_int64_t_strictly_contains_BD_Shape_int64_t(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is included in but not equal to the bd shape referenced by Handle_1.

ppl_BD_Shape_int64_t_is_disjoint_from_BD_Shape_int64_t(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is disjoint from the bd shape referenced by Handle_1.

ppl_BD_Shape_int64_t_equals_BD_Shape_int64_t(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_1 is equal to the bd shape referenced by Handle_2.

ppl_BD_Shape_int64_t_OK(+Handle)
Succeeds only if the bd shape referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_BD_Shape_int64_t_constrains(+Handle, +PPL_Var)
Succeeds if and only if the bd shape referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the bd shape

These predicates will obtain more detailed information about the bd shape unifying some of their arguments with the results.

ppl_BD_Shape_int64_t_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the bd shape referenced by Handle.

ppl_BD_Shape_int64_t_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the bd shape referenced by Handle.

ppl_BD_Shape_int64_t_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_int64_t_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_int64_t_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_int64_t_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_int64_t_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_int64_t_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_int64_t_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_int64_t_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_int64_t_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_int64_t_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_int64_t_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_int64_t_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the bd shape referenced by Handle.

ppl_BD_Shape_int64_t_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the bd shape referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_BD_Shape_int64_t_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the bd shape referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the bd shape

These predicates may modify the bd shape referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the bd shape by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_BD_Shape_int64_t_add_constraint(+Handle, +Constraint)
Updates the bd shape referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_BD_Shape_int64_t_add_congruence(+Handle, +Congruence)
Updates the bd shape referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_BD_Shape_int64_t_add_constraints( +Handle, +Constraint_System)
Updates the bd shape referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_BD_Shape_int64_t_add_congruences( +Handle, +Congruence_System)
Updates the bd shape referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_BD_Shape_int64_t_refine_with_constraint( +Handle, +Constraint)
Updates the bd shape referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_BD_Shape_int64_t_refine_with_congruence( +Handle, +Congruence)
Updates the bd shape referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_BD_Shape_int64_t_refine_with_constraints( +Handle, +Constraint_System)
Updates the bd shape referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_BD_Shape_int64_t_refine_with_congruences( +Handle, +Congruence_System)
Updates the bd shape referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the bd shape

These predicates enable transformations such as taking the topological closure (which for the domain of bd shape is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_BD_Shape_int64_t_topological_closure_assign(+Handle)
Assigns to the bd shape referenced by Handle its topological closure.

ppl_BD_Shape_int64_t_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the bd shape P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_BD_Shape_int64_t_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the bd shape P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_BD_Shape_int64_t_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the bd shape referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_BD_Shape_int64_t_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the bd shape referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_BD_Shape_int64_t_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_BD_Shape_int64_t_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_BD_Shape_int64_t_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_int64_t_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_int64_t_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_int64_t_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_int64_t_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the bd shape P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one bd shape

These predicates include the binary operators which will assign to the bd shape referred to by the first argument its combination with the bd shape referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_BD_Shape_int64_t_intersection_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the intersection of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_int64_t_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the upper bound of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_int64_t_difference_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the difference of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_int64_t_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the time elapse of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_int64_t_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the bd shape P_1 referenced by Handle_1 with the bd shape referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_BD_Shape_int64_t_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of bd shape P_1 referenced by Handle_1 and the bd shape P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_BD_Shape_int64_t_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the BD_Shape_int64_t domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the bd shape referred to by the second argument has to be contained in (or equal to) the bd shape referred to by the first argument.

ppl_BD_Shape_int64_t_BHMZ05_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_int64_t_H79_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_int64_t_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2.

ppl_BD_Shape_int64_t_H79_widening_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2.

ppl_BD_Shape_int64_t_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_BD_Shape_int64_t_H79_widening_assign_with_tokens/4

ppl_BD_Shape_int64_t_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_BD_Shape_int64_t_H79_widening_assign/2

ppl_BD_Shape_int64_t_limited_BHMZ05_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_int64_t_limited_H79_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_int64_t_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_int64_t_limited_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_int64_t_limited_H79_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_int64_t_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_int64_t_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the bd shape referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the bd shape referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_BD_Shape_int64_t_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the concatenation of P and the bd shape referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the bd shape referred to in the first argument. These predicates enable the modification of the vector space of the bd shape referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_BD_Shape_int64_t_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the bd shape P referenced by Handle and and_embeds P in this space.

ppl_BD_Shape_int64_t_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the bd shape P referenced by Handle and and_projects P in this space.

ppl_BD_Shape_int64_t_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the bd shape P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_BD_Shape_int64_t_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the bd shape P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_BD_Shape_int64_t_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the bd shape referenced by Handle to Dimension_Type new space dimensions.

ppl_BD_Shape_int64_t_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the bd shape referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_BD_Shape_int64_t_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the BD_Shape_mpz_class Domain

Here we provide a short description for each of the predicates available for the domain of bd shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for bd shapes

The constructor predicates build a bd shape from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_BD_Shape_mpz_class_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new bd shape $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_BD_Shape_mpz_class_from_space_dimension(3, universe, X).

creates the bd shape defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_BD_Shape_mpz_class_from_constraints(+Constraint_System, -Handle)
Builds a new bd shape P from Constraint_System. Handle is unified with the handle for P.

ppl_new_BD_Shape_mpz_class_from_congruences(+Congruence_System, -Handle)
Builds a new bd shape P from Congruence_System. Handle is unified with the handle for P.

ppl_new_BD_Shape_mpz_class_from_generators(+Generator_System, -Handle)
Builds a new bd shape P from Generator_System. Handle is unified with the handle for P.

Predicates that build new bd shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_BD_Shape_mpz_class_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Z_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Grid(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Float_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Double_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpz_class_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the BD_Shape_mpz_class domain.

ppl_delete_BD_Shape_mpz_class(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the bd shape

Test Predicates

These predicates test the bd shape for different properties and succeed or fail depending on the outcome.

ppl_BD_Shape_mpz_class_is_empty(+Handle)
Succeeds if and only if the bd shape referenced by Handle is empty.

ppl_BD_Shape_mpz_class_is_universe(+Handle)
Succeeds if and only if the bd shape referenced by Handle is the universe.

ppl_BD_Shape_mpz_class_is_bounded(+Handle)
Succeeds if and only if the bd shape referenced by Handle is bounded.

ppl_BD_Shape_mpz_class_contains_integer_point(+Handle)
Succeeds if and only if the bd shape referenced by Handle contains an integer point.

ppl_BD_Shape_mpz_class_is_topologically_closed(+Handle)
Succeeds if and only if the bd shape referenced by Handle is topologically closed.

ppl_BD_Shape_mpz_class_is_discrete(+Handle)
Succeeds if and only if the bd shape referenced by Handle is discrete.

ppl_BD_Shape_mpz_class_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the bd shape referenced by Handle.

ppl_BD_Shape_mpz_class_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the bd shape referenced by Handle.

ppl_BD_Shape_mpz_class_contains_BD_Shape_mpz_class(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is included in or equal to the bd shape referenced by Handle_1.

ppl_BD_Shape_mpz_class_strictly_contains_BD_Shape_mpz_class(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is included in but not equal to the bd shape referenced by Handle_1.

ppl_BD_Shape_mpz_class_is_disjoint_from_BD_Shape_mpz_class(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is disjoint from the bd shape referenced by Handle_1.

ppl_BD_Shape_mpz_class_equals_BD_Shape_mpz_class(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_1 is equal to the bd shape referenced by Handle_2.

ppl_BD_Shape_mpz_class_OK(+Handle)
Succeeds only if the bd shape referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_BD_Shape_mpz_class_constrains(+Handle, +PPL_Var)
Succeeds if and only if the bd shape referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the bd shape

These predicates will obtain more detailed information about the bd shape unifying some of their arguments with the results.

ppl_BD_Shape_mpz_class_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the bd shape referenced by Handle.

ppl_BD_Shape_mpz_class_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the bd shape referenced by Handle.

ppl_BD_Shape_mpz_class_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_mpz_class_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_mpz_class_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_mpz_class_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_mpz_class_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_mpz_class_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_mpz_class_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_mpz_class_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_mpz_class_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_mpz_class_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_mpz_class_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_mpz_class_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the bd shape referenced by Handle.

ppl_BD_Shape_mpz_class_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the bd shape referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_BD_Shape_mpz_class_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the bd shape referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the bd shape

These predicates may modify the bd shape referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the bd shape by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_BD_Shape_mpz_class_add_constraint(+Handle, +Constraint)
Updates the bd shape referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_BD_Shape_mpz_class_add_congruence(+Handle, +Congruence)
Updates the bd shape referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_BD_Shape_mpz_class_add_constraints( +Handle, +Constraint_System)
Updates the bd shape referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_BD_Shape_mpz_class_add_congruences( +Handle, +Congruence_System)
Updates the bd shape referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_BD_Shape_mpz_class_refine_with_constraint( +Handle, +Constraint)
Updates the bd shape referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_BD_Shape_mpz_class_refine_with_congruence( +Handle, +Congruence)
Updates the bd shape referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_BD_Shape_mpz_class_refine_with_constraints( +Handle, +Constraint_System)
Updates the bd shape referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_BD_Shape_mpz_class_refine_with_congruences( +Handle, +Congruence_System)
Updates the bd shape referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the bd shape

These predicates enable transformations such as taking the topological closure (which for the domain of bd shape is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_BD_Shape_mpz_class_topological_closure_assign(+Handle)
Assigns to the bd shape referenced by Handle its topological closure.

ppl_BD_Shape_mpz_class_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the bd shape P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_BD_Shape_mpz_class_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the bd shape P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_BD_Shape_mpz_class_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the bd shape referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_BD_Shape_mpz_class_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the bd shape referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_BD_Shape_mpz_class_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_BD_Shape_mpz_class_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_BD_Shape_mpz_class_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_mpz_class_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_mpz_class_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_mpz_class_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_mpz_class_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the bd shape P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one bd shape

These predicates include the binary operators which will assign to the bd shape referred to by the first argument its combination with the bd shape referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_BD_Shape_mpz_class_intersection_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the intersection of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_mpz_class_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the upper bound of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_mpz_class_difference_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the difference of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_mpz_class_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the time elapse of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_mpz_class_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the bd shape P_1 referenced by Handle_1 with the bd shape referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_BD_Shape_mpz_class_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of bd shape P_1 referenced by Handle_1 and the bd shape P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_BD_Shape_mpz_class_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the BD_Shape_mpz_class domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the bd shape referred to by the second argument has to be contained in (or equal to) the bd shape referred to by the first argument.

ppl_BD_Shape_mpz_class_BHMZ05_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_mpz_class_H79_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_mpz_class_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2.

ppl_BD_Shape_mpz_class_H79_widening_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2.

ppl_BD_Shape_mpz_class_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_BD_Shape_mpz_class_H79_widening_assign_with_tokens/4

ppl_BD_Shape_mpz_class_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_BD_Shape_mpz_class_H79_widening_assign/2

ppl_BD_Shape_mpz_class_limited_BHMZ05_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_mpz_class_limited_H79_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_mpz_class_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_mpz_class_limited_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_mpz_class_limited_H79_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_mpz_class_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_mpz_class_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the bd shape referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the bd shape referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_BD_Shape_mpz_class_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the concatenation of P and the bd shape referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the bd shape referred to in the first argument. These predicates enable the modification of the vector space of the bd shape referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_BD_Shape_mpz_class_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the bd shape P referenced by Handle and and_embeds P in this space.

ppl_BD_Shape_mpz_class_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the bd shape P referenced by Handle and and_projects P in this space.

ppl_BD_Shape_mpz_class_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the bd shape P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_BD_Shape_mpz_class_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the bd shape P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_BD_Shape_mpz_class_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the bd shape referenced by Handle to Dimension_Type new space dimensions.

ppl_BD_Shape_mpz_class_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the bd shape referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_BD_Shape_mpz_class_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the BD_Shape_mpq_class Domain

Here we provide a short description for each of the predicates available for the domain of bd shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for bd shapes

The constructor predicates build a bd shape from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_BD_Shape_mpq_class_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new bd shape $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_BD_Shape_mpq_class_from_space_dimension(3, universe, X).

creates the bd shape defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_BD_Shape_mpq_class_from_constraints(+Constraint_System, -Handle)
Builds a new bd shape P from Constraint_System. Handle is unified with the handle for P.

ppl_new_BD_Shape_mpq_class_from_congruences(+Congruence_System, -Handle)
Builds a new bd shape P from Congruence_System. Handle is unified with the handle for P.

ppl_new_BD_Shape_mpq_class_from_generators(+Generator_System, -Handle)
Builds a new bd shape P from Generator_System. Handle is unified with the handle for P.

Predicates that build new bd shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_BD_Shape_mpq_class_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Z_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Grid(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Float_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Double_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_mpq_class_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the BD_Shape_mpq_class domain.

ppl_delete_BD_Shape_mpq_class(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the bd shape

Test Predicates

These predicates test the bd shape for different properties and succeed or fail depending on the outcome.

ppl_BD_Shape_mpq_class_is_empty(+Handle)
Succeeds if and only if the bd shape referenced by Handle is empty.

ppl_BD_Shape_mpq_class_is_universe(+Handle)
Succeeds if and only if the bd shape referenced by Handle is the universe.

ppl_BD_Shape_mpq_class_is_bounded(+Handle)
Succeeds if and only if the bd shape referenced by Handle is bounded.

ppl_BD_Shape_mpq_class_contains_integer_point(+Handle)
Succeeds if and only if the bd shape referenced by Handle contains an integer point.

ppl_BD_Shape_mpq_class_is_topologically_closed(+Handle)
Succeeds if and only if the bd shape referenced by Handle is topologically closed.

ppl_BD_Shape_mpq_class_is_discrete(+Handle)
Succeeds if and only if the bd shape referenced by Handle is discrete.

ppl_BD_Shape_mpq_class_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the bd shape referenced by Handle.

ppl_BD_Shape_mpq_class_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the bd shape referenced by Handle.

ppl_BD_Shape_mpq_class_contains_BD_Shape_mpq_class(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is included in or equal to the bd shape referenced by Handle_1.

ppl_BD_Shape_mpq_class_strictly_contains_BD_Shape_mpq_class(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is included in but not equal to the bd shape referenced by Handle_1.

ppl_BD_Shape_mpq_class_is_disjoint_from_BD_Shape_mpq_class(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is disjoint from the bd shape referenced by Handle_1.

ppl_BD_Shape_mpq_class_equals_BD_Shape_mpq_class(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_1 is equal to the bd shape referenced by Handle_2.

ppl_BD_Shape_mpq_class_OK(+Handle)
Succeeds only if the bd shape referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_BD_Shape_mpq_class_constrains(+Handle, +PPL_Var)
Succeeds if and only if the bd shape referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the bd shape

These predicates will obtain more detailed information about the bd shape unifying some of their arguments with the results.

ppl_BD_Shape_mpq_class_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the bd shape referenced by Handle.

ppl_BD_Shape_mpq_class_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the bd shape referenced by Handle.

ppl_BD_Shape_mpq_class_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_mpq_class_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_mpq_class_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_mpq_class_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_mpq_class_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_mpq_class_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_mpq_class_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_mpq_class_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_mpq_class_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_mpq_class_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_mpq_class_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_mpq_class_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the bd shape referenced by Handle.

ppl_BD_Shape_mpq_class_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the bd shape referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_BD_Shape_mpq_class_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the bd shape referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the bd shape

These predicates may modify the bd shape referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the bd shape by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_BD_Shape_mpq_class_add_constraint(+Handle, +Constraint)
Updates the bd shape referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_BD_Shape_mpq_class_add_congruence(+Handle, +Congruence)
Updates the bd shape referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_BD_Shape_mpq_class_add_constraints( +Handle, +Constraint_System)
Updates the bd shape referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_BD_Shape_mpq_class_add_congruences( +Handle, +Congruence_System)
Updates the bd shape referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_BD_Shape_mpq_class_refine_with_constraint( +Handle, +Constraint)
Updates the bd shape referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_BD_Shape_mpq_class_refine_with_congruence( +Handle, +Congruence)
Updates the bd shape referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_BD_Shape_mpq_class_refine_with_constraints( +Handle, +Constraint_System)
Updates the bd shape referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_BD_Shape_mpq_class_refine_with_congruences( +Handle, +Congruence_System)
Updates the bd shape referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the bd shape

These predicates enable transformations such as taking the topological closure (which for the domain of bd shape is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_BD_Shape_mpq_class_topological_closure_assign(+Handle)
Assigns to the bd shape referenced by Handle its topological closure.

ppl_BD_Shape_mpq_class_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the bd shape P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_BD_Shape_mpq_class_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the bd shape P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_BD_Shape_mpq_class_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the bd shape referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_BD_Shape_mpq_class_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the bd shape referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_BD_Shape_mpq_class_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_BD_Shape_mpq_class_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_BD_Shape_mpq_class_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_mpq_class_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_mpq_class_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_mpq_class_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_mpq_class_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the bd shape P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one bd shape

These predicates include the binary operators which will assign to the bd shape referred to by the first argument its combination with the bd shape referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_BD_Shape_mpq_class_intersection_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the intersection of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_mpq_class_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the upper bound of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_mpq_class_difference_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the difference of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_mpq_class_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the time elapse of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_mpq_class_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the bd shape P_1 referenced by Handle_1 with the bd shape referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_BD_Shape_mpq_class_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of bd shape P_1 referenced by Handle_1 and the bd shape P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_BD_Shape_mpq_class_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the BD_Shape_mpq_class domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the bd shape referred to by the second argument has to be contained in (or equal to) the bd shape referred to by the first argument.

ppl_BD_Shape_mpq_class_BHMZ05_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_mpq_class_H79_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_mpq_class_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2.

ppl_BD_Shape_mpq_class_H79_widening_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2.

ppl_BD_Shape_mpq_class_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_BD_Shape_mpq_class_H79_widening_assign_with_tokens/4

ppl_BD_Shape_mpq_class_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_BD_Shape_mpq_class_H79_widening_assign/2

ppl_BD_Shape_mpq_class_limited_BHMZ05_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_mpq_class_limited_H79_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_mpq_class_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_mpq_class_limited_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_mpq_class_limited_H79_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_mpq_class_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_mpq_class_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the bd shape referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the bd shape referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_BD_Shape_mpq_class_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the concatenation of P and the bd shape referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the bd shape referred to in the first argument. These predicates enable the modification of the vector space of the bd shape referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_BD_Shape_mpq_class_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the bd shape P referenced by Handle and and_embeds P in this space.

ppl_BD_Shape_mpq_class_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the bd shape P referenced by Handle and and_projects P in this space.

ppl_BD_Shape_mpq_class_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the bd shape P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_BD_Shape_mpq_class_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the bd shape P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_BD_Shape_mpq_class_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the bd shape referenced by Handle to Dimension_Type new space dimensions.

ppl_BD_Shape_mpq_class_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the bd shape referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_BD_Shape_mpq_class_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Octagonal_Shape_int8_t Domain

Here we provide a short description for each of the predicates available for the domain of octagonal shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for octagonal shapes

The constructor predicates build a octagonal shape from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Octagonal_Shape_int8_t_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new octagonal shape $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Octagonal_Shape_int8_t_from_space_dimension(3, universe, X).

creates the octagonal shape defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Octagonal_Shape_int8_t_from_constraints(+Constraint_System, -Handle)
Builds a new octagonal shape P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Octagonal_Shape_int8_t_from_congruences(+Congruence_System, -Handle)
Builds a new octagonal shape P from Congruence_System. Handle is unified with the handle for P.

ppl_new_Octagonal_Shape_int8_t_from_generators(+Generator_System, -Handle)
Builds a new octagonal shape P from Generator_System. Handle is unified with the handle for P.

Predicates that build new octagonal shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Octagonal_Shape_int8_t_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Z_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Grid(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Float_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Double_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int8_t_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Octagonal_Shape_int8_t domain.

ppl_delete_Octagonal_Shape_int8_t(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the octagonal shape

Test Predicates

These predicates test the octagonal shape for different properties and succeed or fail depending on the outcome.

ppl_Octagonal_Shape_int8_t_is_empty(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is empty.

ppl_Octagonal_Shape_int8_t_is_universe(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is the universe.

ppl_Octagonal_Shape_int8_t_is_bounded(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is bounded.

ppl_Octagonal_Shape_int8_t_contains_integer_point(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle contains an integer point.

ppl_Octagonal_Shape_int8_t_is_topologically_closed(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is topologically closed.

ppl_Octagonal_Shape_int8_t_is_discrete(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is discrete.

ppl_Octagonal_Shape_int8_t_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int8_t_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int8_t_contains_Octagonal_Shape_int8_t(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is included in or equal to the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_int8_t_strictly_contains_Octagonal_Shape_int8_t(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is included in but not equal to the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_int8_t_is_disjoint_from_Octagonal_Shape_int8_t(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is disjoint from the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_int8_t_equals_Octagonal_Shape_int8_t(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_1 is equal to the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_int8_t_OK(+Handle)
Succeeds only if the octagonal shape referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Octagonal_Shape_int8_t_constrains(+Handle, +PPL_Var)
Succeeds if and only if the octagonal shape referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the octagonal shape

These predicates will obtain more detailed information about the octagonal shape unifying some of their arguments with the results.

ppl_Octagonal_Shape_int8_t_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int8_t_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int8_t_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_int8_t_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_int8_t_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_int8_t_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int8_t_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int8_t_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int8_t_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int8_t_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_int8_t_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_int8_t_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_int8_t_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_int8_t_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int8_t_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the octagonal shape referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Octagonal_Shape_int8_t_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the octagonal shape referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the octagonal shape

These predicates may modify the octagonal shape referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the octagonal shape by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Octagonal_Shape_int8_t_add_constraint(+Handle, +Constraint)
Updates the octagonal shape referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Octagonal_Shape_int8_t_add_congruence(+Handle, +Congruence)
Updates the octagonal shape referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Octagonal_Shape_int8_t_add_constraints( +Handle, +Constraint_System)
Updates the octagonal shape referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Octagonal_Shape_int8_t_add_congruences( +Handle, +Congruence_System)
Updates the octagonal shape referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Octagonal_Shape_int8_t_refine_with_constraint( +Handle, +Constraint)
Updates the octagonal shape referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Octagonal_Shape_int8_t_refine_with_congruence( +Handle, +Congruence)
Updates the octagonal shape referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Octagonal_Shape_int8_t_refine_with_constraints( +Handle, +Constraint_System)
Updates the octagonal shape referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Octagonal_Shape_int8_t_refine_with_congruences( +Handle, +Congruence_System)
Updates the octagonal shape referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the octagonal shape

These predicates enable transformations such as taking the topological closure (which for the domain of octagonal shape is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Octagonal_Shape_int8_t_topological_closure_assign(+Handle)
Assigns to the octagonal shape referenced by Handle its topological closure.

ppl_Octagonal_Shape_int8_t_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the octagonal shape P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Octagonal_Shape_int8_t_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the octagonal shape P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Octagonal_Shape_int8_t_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the octagonal shape referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Octagonal_Shape_int8_t_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the octagonal shape referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Octagonal_Shape_int8_t_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Octagonal_Shape_int8_t_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Octagonal_Shape_int8_t_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_int8_t_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_int8_t_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_int8_t_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_int8_t_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the octagonal shape P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one octagonal shape

These predicates include the binary operators which will assign to the octagonal shape referred to by the first argument its combination with the octagonal shape referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Octagonal_Shape_int8_t_intersection_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the intersection of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_int8_t_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the upper bound of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_int8_t_difference_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the difference of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_int8_t_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the time elapse of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_int8_t_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the octagonal shape P_1 referenced by Handle_1 with the octagonal shape referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Octagonal_Shape_int8_t_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of octagonal shape P_1 referenced by Handle_1 and the octagonal shape P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_Octagonal_Shape_int8_t_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the Octagonal_Shape_int8_t domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the octagonal shape referred to by the second argument has to be contained in (or equal to) the octagonal shape referred to by the first argument.

ppl_Octagonal_Shape_int8_t_BHMZ05_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_int8_t_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_int8_t_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_Octagonal_Shape_int8_t_H79_widening_assign_with_tokens/4

ppl_Octagonal_Shape_int8_t_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_Octagonal_Shape_int8_t_H79_widening_assign/2

ppl_Octagonal_Shape_int8_t_limited_BHMZ05_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_int8_t_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_int8_t_limited_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Octagonal_Shape_int8_t_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Octagonal_Shape_int8_t_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the octagonal shape referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Octagonal_Shape_int8_t_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the concatenation of P and the octagonal shape referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument. These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Octagonal_Shape_int8_t_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the octagonal shape P referenced by Handle and and_embeds P in this space.

ppl_Octagonal_Shape_int8_t_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the octagonal shape P referenced by Handle and and_projects P in this space.

ppl_Octagonal_Shape_int8_t_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the octagonal shape P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Octagonal_Shape_int8_t_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the octagonal shape P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Octagonal_Shape_int8_t_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the octagonal shape referenced by Handle to Dimension_Type new space dimensions.

ppl_Octagonal_Shape_int8_t_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the octagonal shape referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Octagonal_Shape_int8_t_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Octagonal_Shape_int16_t Domain

Here we provide a short description for each of the predicates available for the domain of octagonal shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for octagonal shapes

The constructor predicates build a octagonal shape from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Octagonal_Shape_int16_t_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new octagonal shape $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Octagonal_Shape_int16_t_from_space_dimension(3, universe, X).

creates the octagonal shape defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Octagonal_Shape_int16_t_from_constraints(+Constraint_System, -Handle)
Builds a new octagonal shape P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Octagonal_Shape_int16_t_from_congruences(+Congruence_System, -Handle)
Builds a new octagonal shape P from Congruence_System. Handle is unified with the handle for P.

ppl_new_Octagonal_Shape_int16_t_from_generators(+Generator_System, -Handle)
Builds a new octagonal shape P from Generator_System. Handle is unified with the handle for P.

Predicates that build new octagonal shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Octagonal_Shape_int16_t_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Z_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Grid(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Float_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Double_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int16_t_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Octagonal_Shape_int16_t domain.

ppl_delete_Octagonal_Shape_int16_t(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the octagonal shape

Test Predicates

These predicates test the octagonal shape for different properties and succeed or fail depending on the outcome.

ppl_Octagonal_Shape_int16_t_is_empty(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is empty.

ppl_Octagonal_Shape_int16_t_is_universe(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is the universe.

ppl_Octagonal_Shape_int16_t_is_bounded(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is bounded.

ppl_Octagonal_Shape_int16_t_contains_integer_point(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle contains an integer point.

ppl_Octagonal_Shape_int16_t_is_topologically_closed(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is topologically closed.

ppl_Octagonal_Shape_int16_t_is_discrete(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is discrete.

ppl_Octagonal_Shape_int16_t_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int16_t_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int16_t_contains_Octagonal_Shape_int16_t(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is included in or equal to the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_int16_t_strictly_contains_Octagonal_Shape_int16_t(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is included in but not equal to the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_int16_t_is_disjoint_from_Octagonal_Shape_int16_t(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is disjoint from the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_int16_t_equals_Octagonal_Shape_int16_t(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_1 is equal to the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_int16_t_OK(+Handle)
Succeeds only if the octagonal shape referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Octagonal_Shape_int16_t_constrains(+Handle, +PPL_Var)
Succeeds if and only if the octagonal shape referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the octagonal shape

These predicates will obtain more detailed information about the octagonal shape unifying some of their arguments with the results.

ppl_Octagonal_Shape_int16_t_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int16_t_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int16_t_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_int16_t_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_int16_t_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_int16_t_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int16_t_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int16_t_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int16_t_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int16_t_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_int16_t_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_int16_t_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_int16_t_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_int16_t_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int16_t_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the octagonal shape referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Octagonal_Shape_int16_t_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the octagonal shape referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the octagonal shape

These predicates may modify the octagonal shape referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the octagonal shape by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Octagonal_Shape_int16_t_add_constraint(+Handle, +Constraint)
Updates the octagonal shape referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Octagonal_Shape_int16_t_add_congruence(+Handle, +Congruence)
Updates the octagonal shape referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Octagonal_Shape_int16_t_add_constraints( +Handle, +Constraint_System)
Updates the octagonal shape referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Octagonal_Shape_int16_t_add_congruences( +Handle, +Congruence_System)
Updates the octagonal shape referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Octagonal_Shape_int16_t_refine_with_constraint( +Handle, +Constraint)
Updates the octagonal shape referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Octagonal_Shape_int16_t_refine_with_congruence( +Handle, +Congruence)
Updates the octagonal shape referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Octagonal_Shape_int16_t_refine_with_constraints( +Handle, +Constraint_System)
Updates the octagonal shape referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Octagonal_Shape_int16_t_refine_with_congruences( +Handle, +Congruence_System)
Updates the octagonal shape referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the octagonal shape

These predicates enable transformations such as taking the topological closure (which for the domain of octagonal shape is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Octagonal_Shape_int16_t_topological_closure_assign(+Handle)
Assigns to the octagonal shape referenced by Handle its topological closure.

ppl_Octagonal_Shape_int16_t_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the octagonal shape P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Octagonal_Shape_int16_t_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the octagonal shape P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Octagonal_Shape_int16_t_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the octagonal shape referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Octagonal_Shape_int16_t_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the octagonal shape referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Octagonal_Shape_int16_t_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Octagonal_Shape_int16_t_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Octagonal_Shape_int16_t_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_int16_t_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_int16_t_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_int16_t_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_int16_t_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the octagonal shape P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one octagonal shape

These predicates include the binary operators which will assign to the octagonal shape referred to by the first argument its combination with the octagonal shape referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Octagonal_Shape_int16_t_intersection_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the intersection of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_int16_t_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the upper bound of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_int16_t_difference_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the difference of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_int16_t_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the time elapse of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_int16_t_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the octagonal shape P_1 referenced by Handle_1 with the octagonal shape referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Octagonal_Shape_int16_t_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of octagonal shape P_1 referenced by Handle_1 and the octagonal shape P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_Octagonal_Shape_int16_t_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the Octagonal_Shape_int16_t domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the octagonal shape referred to by the second argument has to be contained in (or equal to) the octagonal shape referred to by the first argument.

ppl_Octagonal_Shape_int16_t_BHMZ05_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_int16_t_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_int16_t_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_Octagonal_Shape_int16_t_H79_widening_assign_with_tokens/4

ppl_Octagonal_Shape_int16_t_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_Octagonal_Shape_int16_t_H79_widening_assign/2

ppl_Octagonal_Shape_int16_t_limited_BHMZ05_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_int16_t_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_int16_t_limited_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Octagonal_Shape_int16_t_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Octagonal_Shape_int16_t_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the octagonal shape referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Octagonal_Shape_int16_t_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the concatenation of P and the octagonal shape referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument. These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Octagonal_Shape_int16_t_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the octagonal shape P referenced by Handle and and_embeds P in this space.

ppl_Octagonal_Shape_int16_t_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the octagonal shape P referenced by Handle and and_projects P in this space.

ppl_Octagonal_Shape_int16_t_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the octagonal shape P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Octagonal_Shape_int16_t_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the octagonal shape P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Octagonal_Shape_int16_t_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the octagonal shape referenced by Handle to Dimension_Type new space dimensions.

ppl_Octagonal_Shape_int16_t_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the octagonal shape referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Octagonal_Shape_int16_t_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Octagonal_Shape_int32_t Domain

Here we provide a short description for each of the predicates available for the domain of octagonal shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for octagonal shapes

The constructor predicates build a octagonal shape from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Octagonal_Shape_int32_t_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new octagonal shape $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Octagonal_Shape_int32_t_from_space_dimension(3, universe, X).

creates the octagonal shape defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Octagonal_Shape_int32_t_from_constraints(+Constraint_System, -Handle)
Builds a new octagonal shape P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Octagonal_Shape_int32_t_from_congruences(+Congruence_System, -Handle)
Builds a new octagonal shape P from Congruence_System. Handle is unified with the handle for P.

ppl_new_Octagonal_Shape_int32_t_from_generators(+Generator_System, -Handle)
Builds a new octagonal shape P from Generator_System. Handle is unified with the handle for P.

Predicates that build new octagonal shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Octagonal_Shape_int32_t_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Z_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Grid(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Float_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Double_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int32_t_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Octagonal_Shape_int32_t domain.

ppl_delete_Octagonal_Shape_int32_t(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the octagonal shape

Test Predicates

These predicates test the octagonal shape for different properties and succeed or fail depending on the outcome.

ppl_Octagonal_Shape_int32_t_is_empty(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is empty.

ppl_Octagonal_Shape_int32_t_is_universe(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is the universe.

ppl_Octagonal_Shape_int32_t_is_bounded(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is bounded.

ppl_Octagonal_Shape_int32_t_contains_integer_point(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle contains an integer point.

ppl_Octagonal_Shape_int32_t_is_topologically_closed(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is topologically closed.

ppl_Octagonal_Shape_int32_t_is_discrete(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is discrete.

ppl_Octagonal_Shape_int32_t_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int32_t_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int32_t_contains_Octagonal_Shape_int32_t(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is included in or equal to the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_int32_t_strictly_contains_Octagonal_Shape_int32_t(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is included in but not equal to the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_int32_t_is_disjoint_from_Octagonal_Shape_int32_t(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is disjoint from the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_int32_t_equals_Octagonal_Shape_int32_t(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_1 is equal to the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_int32_t_OK(+Handle)
Succeeds only if the octagonal shape referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Octagonal_Shape_int32_t_constrains(+Handle, +PPL_Var)
Succeeds if and only if the octagonal shape referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the octagonal shape

These predicates will obtain more detailed information about the octagonal shape unifying some of their arguments with the results.

ppl_Octagonal_Shape_int32_t_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int32_t_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int32_t_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_int32_t_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_int32_t_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_int32_t_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int32_t_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int32_t_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int32_t_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int32_t_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_int32_t_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_int32_t_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_int32_t_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_int32_t_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int32_t_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the octagonal shape referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Octagonal_Shape_int32_t_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the octagonal shape referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the octagonal shape

These predicates may modify the octagonal shape referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the octagonal shape by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Octagonal_Shape_int32_t_add_constraint(+Handle, +Constraint)
Updates the octagonal shape referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Octagonal_Shape_int32_t_add_congruence(+Handle, +Congruence)
Updates the octagonal shape referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Octagonal_Shape_int32_t_add_constraints( +Handle, +Constraint_System)
Updates the octagonal shape referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Octagonal_Shape_int32_t_add_congruences( +Handle, +Congruence_System)
Updates the octagonal shape referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Octagonal_Shape_int32_t_refine_with_constraint( +Handle, +Constraint)
Updates the octagonal shape referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Octagonal_Shape_int32_t_refine_with_congruence( +Handle, +Congruence)
Updates the octagonal shape referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Octagonal_Shape_int32_t_refine_with_constraints( +Handle, +Constraint_System)
Updates the octagonal shape referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Octagonal_Shape_int32_t_refine_with_congruences( +Handle, +Congruence_System)
Updates the octagonal shape referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the octagonal shape

These predicates enable transformations such as taking the topological closure (which for the domain of octagonal shape is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Octagonal_Shape_int32_t_topological_closure_assign(+Handle)
Assigns to the octagonal shape referenced by Handle its topological closure.

ppl_Octagonal_Shape_int32_t_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the octagonal shape P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Octagonal_Shape_int32_t_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the octagonal shape P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Octagonal_Shape_int32_t_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the octagonal shape referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Octagonal_Shape_int32_t_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the octagonal shape referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Octagonal_Shape_int32_t_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Octagonal_Shape_int32_t_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Octagonal_Shape_int32_t_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_int32_t_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_int32_t_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_int32_t_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_int32_t_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the octagonal shape P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one octagonal shape

These predicates include the binary operators which will assign to the octagonal shape referred to by the first argument its combination with the octagonal shape referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Octagonal_Shape_int32_t_intersection_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the intersection of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_int32_t_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the upper bound of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_int32_t_difference_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the difference of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_int32_t_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the time elapse of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_int32_t_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the octagonal shape P_1 referenced by Handle_1 with the octagonal shape referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Octagonal_Shape_int32_t_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of octagonal shape P_1 referenced by Handle_1 and the octagonal shape P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_Octagonal_Shape_int32_t_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the Octagonal_Shape_int32_t domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the octagonal shape referred to by the second argument has to be contained in (or equal to) the octagonal shape referred to by the first argument.

ppl_Octagonal_Shape_int32_t_BHMZ05_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_int32_t_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_int32_t_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_Octagonal_Shape_int32_t_H79_widening_assign_with_tokens/4

ppl_Octagonal_Shape_int32_t_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_Octagonal_Shape_int32_t_H79_widening_assign/2

ppl_Octagonal_Shape_int32_t_limited_BHMZ05_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_int32_t_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_int32_t_limited_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Octagonal_Shape_int32_t_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Octagonal_Shape_int32_t_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the octagonal shape referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Octagonal_Shape_int32_t_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the concatenation of P and the octagonal shape referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument. These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Octagonal_Shape_int32_t_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the octagonal shape P referenced by Handle and and_embeds P in this space.

ppl_Octagonal_Shape_int32_t_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the octagonal shape P referenced by Handle and and_projects P in this space.

ppl_Octagonal_Shape_int32_t_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the octagonal shape P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Octagonal_Shape_int32_t_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the octagonal shape P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Octagonal_Shape_int32_t_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the octagonal shape referenced by Handle to Dimension_Type new space dimensions.

ppl_Octagonal_Shape_int32_t_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the octagonal shape referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Octagonal_Shape_int32_t_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Octagonal_Shape_int64_t Domain

Here we provide a short description for each of the predicates available for the domain of octagonal shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for octagonal shapes

The constructor predicates build a octagonal shape from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Octagonal_Shape_int64_t_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new octagonal shape $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Octagonal_Shape_int64_t_from_space_dimension(3, universe, X).

creates the octagonal shape defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Octagonal_Shape_int64_t_from_constraints(+Constraint_System, -Handle)
Builds a new octagonal shape P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Octagonal_Shape_int64_t_from_congruences(+Congruence_System, -Handle)
Builds a new octagonal shape P from Congruence_System. Handle is unified with the handle for P.

ppl_new_Octagonal_Shape_int64_t_from_generators(+Generator_System, -Handle)
Builds a new octagonal shape P from Generator_System. Handle is unified with the handle for P.

Predicates that build new octagonal shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Octagonal_Shape_int64_t_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Z_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Grid(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Float_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Double_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_int64_t_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Octagonal_Shape_int64_t domain.

ppl_delete_Octagonal_Shape_int64_t(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the octagonal shape

Test Predicates

These predicates test the octagonal shape for different properties and succeed or fail depending on the outcome.

ppl_Octagonal_Shape_int64_t_is_empty(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is empty.

ppl_Octagonal_Shape_int64_t_is_universe(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is the universe.

ppl_Octagonal_Shape_int64_t_is_bounded(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is bounded.

ppl_Octagonal_Shape_int64_t_contains_integer_point(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle contains an integer point.

ppl_Octagonal_Shape_int64_t_is_topologically_closed(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is topologically closed.

ppl_Octagonal_Shape_int64_t_is_discrete(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is discrete.

ppl_Octagonal_Shape_int64_t_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int64_t_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int64_t_contains_Octagonal_Shape_int64_t(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is included in or equal to the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_int64_t_strictly_contains_Octagonal_Shape_int64_t(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is included in but not equal to the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_int64_t_is_disjoint_from_Octagonal_Shape_int64_t(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is disjoint from the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_int64_t_equals_Octagonal_Shape_int64_t(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_1 is equal to the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_int64_t_OK(+Handle)
Succeeds only if the octagonal shape referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Octagonal_Shape_int64_t_constrains(+Handle, +PPL_Var)
Succeeds if and only if the octagonal shape referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the octagonal shape

These predicates will obtain more detailed information about the octagonal shape unifying some of their arguments with the results.

ppl_Octagonal_Shape_int64_t_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int64_t_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int64_t_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_int64_t_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_int64_t_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_int64_t_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int64_t_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int64_t_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int64_t_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int64_t_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_int64_t_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_int64_t_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_int64_t_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_int64_t_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_int64_t_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the octagonal shape referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Octagonal_Shape_int64_t_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the octagonal shape referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the octagonal shape

These predicates may modify the octagonal shape referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the octagonal shape by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Octagonal_Shape_int64_t_add_constraint(+Handle, +Constraint)
Updates the octagonal shape referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Octagonal_Shape_int64_t_add_congruence(+Handle, +Congruence)
Updates the octagonal shape referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Octagonal_Shape_int64_t_add_constraints( +Handle, +Constraint_System)
Updates the octagonal shape referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Octagonal_Shape_int64_t_add_congruences( +Handle, +Congruence_System)
Updates the octagonal shape referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Octagonal_Shape_int64_t_refine_with_constraint( +Handle, +Constraint)
Updates the octagonal shape referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Octagonal_Shape_int64_t_refine_with_congruence( +Handle, +Congruence)
Updates the octagonal shape referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Octagonal_Shape_int64_t_refine_with_constraints( +Handle, +Constraint_System)
Updates the octagonal shape referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Octagonal_Shape_int64_t_refine_with_congruences( +Handle, +Congruence_System)
Updates the octagonal shape referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the octagonal shape

These predicates enable transformations such as taking the topological closure (which for the domain of octagonal shape is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Octagonal_Shape_int64_t_topological_closure_assign(+Handle)
Assigns to the octagonal shape referenced by Handle its topological closure.

ppl_Octagonal_Shape_int64_t_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the octagonal shape P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Octagonal_Shape_int64_t_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the octagonal shape P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Octagonal_Shape_int64_t_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the octagonal shape referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Octagonal_Shape_int64_t_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the octagonal shape referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Octagonal_Shape_int64_t_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Octagonal_Shape_int64_t_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Octagonal_Shape_int64_t_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_int64_t_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_int64_t_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_int64_t_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_int64_t_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the octagonal shape P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one octagonal shape

These predicates include the binary operators which will assign to the octagonal shape referred to by the first argument its combination with the octagonal shape referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Octagonal_Shape_int64_t_intersection_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the intersection of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_int64_t_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the upper bound of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_int64_t_difference_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the difference of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_int64_t_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the time elapse of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_int64_t_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the octagonal shape P_1 referenced by Handle_1 with the octagonal shape referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Octagonal_Shape_int64_t_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of octagonal shape P_1 referenced by Handle_1 and the octagonal shape P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_Octagonal_Shape_int64_t_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the Octagonal_Shape_int64_t domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the octagonal shape referred to by the second argument has to be contained in (or equal to) the octagonal shape referred to by the first argument.

ppl_Octagonal_Shape_int64_t_BHMZ05_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_int64_t_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_int64_t_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_Octagonal_Shape_int64_t_H79_widening_assign_with_tokens/4

ppl_Octagonal_Shape_int64_t_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_Octagonal_Shape_int64_t_H79_widening_assign/2

ppl_Octagonal_Shape_int64_t_limited_BHMZ05_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_int64_t_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_int64_t_limited_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Octagonal_Shape_int64_t_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Octagonal_Shape_int64_t_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the octagonal shape referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Octagonal_Shape_int64_t_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the concatenation of P and the octagonal shape referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument. These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Octagonal_Shape_int64_t_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the octagonal shape P referenced by Handle and and_embeds P in this space.

ppl_Octagonal_Shape_int64_t_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the octagonal shape P referenced by Handle and and_projects P in this space.

ppl_Octagonal_Shape_int64_t_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the octagonal shape P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Octagonal_Shape_int64_t_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the octagonal shape P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Octagonal_Shape_int64_t_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the octagonal shape referenced by Handle to Dimension_Type new space dimensions.

ppl_Octagonal_Shape_int64_t_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the octagonal shape referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Octagonal_Shape_int64_t_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Octagonal_Shape_mpz_class Domain

Here we provide a short description for each of the predicates available for the domain of octagonal shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for octagonal shapes

The constructor predicates build a octagonal shape from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Octagonal_Shape_mpz_class_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new octagonal shape $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Octagonal_Shape_mpz_class_from_space_dimension(3, universe, X).

creates the octagonal shape defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Octagonal_Shape_mpz_class_from_constraints(+Constraint_System, -Handle)
Builds a new octagonal shape P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Octagonal_Shape_mpz_class_from_congruences(+Congruence_System, -Handle)
Builds a new octagonal shape P from Congruence_System. Handle is unified with the handle for P.

ppl_new_Octagonal_Shape_mpz_class_from_generators(+Generator_System, -Handle)
Builds a new octagonal shape P from Generator_System. Handle is unified with the handle for P.

Predicates that build new octagonal shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Octagonal_Shape_mpz_class_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Z_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Grid(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Float_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Double_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpz_class_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Octagonal_Shape_mpz_class domain.

ppl_delete_Octagonal_Shape_mpz_class(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the octagonal shape

Test Predicates

These predicates test the octagonal shape for different properties and succeed or fail depending on the outcome.

ppl_Octagonal_Shape_mpz_class_is_empty(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is empty.

ppl_Octagonal_Shape_mpz_class_is_universe(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is the universe.

ppl_Octagonal_Shape_mpz_class_is_bounded(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is bounded.

ppl_Octagonal_Shape_mpz_class_contains_integer_point(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle contains an integer point.

ppl_Octagonal_Shape_mpz_class_is_topologically_closed(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is topologically closed.

ppl_Octagonal_Shape_mpz_class_is_discrete(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is discrete.

ppl_Octagonal_Shape_mpz_class_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_mpz_class_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_mpz_class_contains_Octagonal_Shape_mpz_class(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is included in or equal to the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_mpz_class_strictly_contains_Octagonal_Shape_mpz_class(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is included in but not equal to the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_mpz_class_is_disjoint_from_Octagonal_Shape_mpz_class(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is disjoint from the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_mpz_class_equals_Octagonal_Shape_mpz_class(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_1 is equal to the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_mpz_class_OK(+Handle)
Succeeds only if the octagonal shape referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Octagonal_Shape_mpz_class_constrains(+Handle, +PPL_Var)
Succeeds if and only if the octagonal shape referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the octagonal shape

These predicates will obtain more detailed information about the octagonal shape unifying some of their arguments with the results.

ppl_Octagonal_Shape_mpz_class_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_mpz_class_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_mpz_class_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_mpz_class_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_mpz_class_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_mpz_class_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_mpz_class_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_mpz_class_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_mpz_class_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_mpz_class_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_mpz_class_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_mpz_class_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_mpz_class_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_mpz_class_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_mpz_class_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the octagonal shape referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Octagonal_Shape_mpz_class_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the octagonal shape referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the octagonal shape

These predicates may modify the octagonal shape referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the octagonal shape by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Octagonal_Shape_mpz_class_add_constraint(+Handle, +Constraint)
Updates the octagonal shape referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Octagonal_Shape_mpz_class_add_congruence(+Handle, +Congruence)
Updates the octagonal shape referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Octagonal_Shape_mpz_class_add_constraints( +Handle, +Constraint_System)
Updates the octagonal shape referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Octagonal_Shape_mpz_class_add_congruences( +Handle, +Congruence_System)
Updates the octagonal shape referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Octagonal_Shape_mpz_class_refine_with_constraint( +Handle, +Constraint)
Updates the octagonal shape referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Octagonal_Shape_mpz_class_refine_with_congruence( +Handle, +Congruence)
Updates the octagonal shape referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Octagonal_Shape_mpz_class_refine_with_constraints( +Handle, +Constraint_System)
Updates the octagonal shape referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Octagonal_Shape_mpz_class_refine_with_congruences( +Handle, +Congruence_System)
Updates the octagonal shape referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the octagonal shape

These predicates enable transformations such as taking the topological closure (which for the domain of octagonal shape is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Octagonal_Shape_mpz_class_topological_closure_assign(+Handle)
Assigns to the octagonal shape referenced by Handle its topological closure.

ppl_Octagonal_Shape_mpz_class_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the octagonal shape P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Octagonal_Shape_mpz_class_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the octagonal shape P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Octagonal_Shape_mpz_class_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the octagonal shape referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Octagonal_Shape_mpz_class_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the octagonal shape referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Octagonal_Shape_mpz_class_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Octagonal_Shape_mpz_class_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Octagonal_Shape_mpz_class_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_mpz_class_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_mpz_class_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_mpz_class_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_mpz_class_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the octagonal shape P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one octagonal shape

These predicates include the binary operators which will assign to the octagonal shape referred to by the first argument its combination with the octagonal shape referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Octagonal_Shape_mpz_class_intersection_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the intersection of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_mpz_class_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the upper bound of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_mpz_class_difference_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the difference of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_mpz_class_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the time elapse of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_mpz_class_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the octagonal shape P_1 referenced by Handle_1 with the octagonal shape referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Octagonal_Shape_mpz_class_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of octagonal shape P_1 referenced by Handle_1 and the octagonal shape P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_Octagonal_Shape_mpz_class_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the Octagonal_Shape_mpz_class domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the octagonal shape referred to by the second argument has to be contained in (or equal to) the octagonal shape referred to by the first argument.

ppl_Octagonal_Shape_mpz_class_BHMZ05_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_mpz_class_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_mpz_class_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_Octagonal_Shape_mpz_class_H79_widening_assign_with_tokens/4

ppl_Octagonal_Shape_mpz_class_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_Octagonal_Shape_mpz_class_H79_widening_assign/2

ppl_Octagonal_Shape_mpz_class_limited_BHMZ05_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_mpz_class_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_mpz_class_limited_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Octagonal_Shape_mpz_class_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Octagonal_Shape_mpz_class_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the octagonal shape referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Octagonal_Shape_mpz_class_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the concatenation of P and the octagonal shape referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument. These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Octagonal_Shape_mpz_class_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the octagonal shape P referenced by Handle and and_embeds P in this space.

ppl_Octagonal_Shape_mpz_class_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the octagonal shape P referenced by Handle and and_projects P in this space.

ppl_Octagonal_Shape_mpz_class_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the octagonal shape P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Octagonal_Shape_mpz_class_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the octagonal shape P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Octagonal_Shape_mpz_class_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the octagonal shape referenced by Handle to Dimension_Type new space dimensions.

ppl_Octagonal_Shape_mpz_class_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the octagonal shape referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Octagonal_Shape_mpz_class_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Octagonal_Shape_mpq_class Domain

Here we provide a short description for each of the predicates available for the domain of octagonal shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for octagonal shapes

The constructor predicates build a octagonal shape from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Octagonal_Shape_mpq_class_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new octagonal shape $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Octagonal_Shape_mpq_class_from_space_dimension(3, universe, X).

creates the octagonal shape defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Octagonal_Shape_mpq_class_from_constraints(+Constraint_System, -Handle)
Builds a new octagonal shape P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Octagonal_Shape_mpq_class_from_congruences(+Congruence_System, -Handle)
Builds a new octagonal shape P from Congruence_System. Handle is unified with the handle for P.

ppl_new_Octagonal_Shape_mpq_class_from_generators(+Generator_System, -Handle)
Builds a new octagonal shape P from Generator_System. Handle is unified with the handle for P.

Predicates that build new octagonal shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Octagonal_Shape_mpq_class_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Z_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Grid(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Float_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Double_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_mpq_class_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Octagonal_Shape_mpq_class domain.

ppl_delete_Octagonal_Shape_mpq_class(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the octagonal shape

Test Predicates

These predicates test the octagonal shape for different properties and succeed or fail depending on the outcome.

ppl_Octagonal_Shape_mpq_class_is_empty(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is empty.

ppl_Octagonal_Shape_mpq_class_is_universe(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is the universe.

ppl_Octagonal_Shape_mpq_class_is_bounded(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is bounded.

ppl_Octagonal_Shape_mpq_class_contains_integer_point(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle contains an integer point.

ppl_Octagonal_Shape_mpq_class_is_topologically_closed(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is topologically closed.

ppl_Octagonal_Shape_mpq_class_is_discrete(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is discrete.

ppl_Octagonal_Shape_mpq_class_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_mpq_class_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_mpq_class_contains_Octagonal_Shape_mpq_class(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is included in or equal to the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_mpq_class_strictly_contains_Octagonal_Shape_mpq_class(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is included in but not equal to the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_mpq_class_is_disjoint_from_Octagonal_Shape_mpq_class(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is disjoint from the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_mpq_class_equals_Octagonal_Shape_mpq_class(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_1 is equal to the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_mpq_class_OK(+Handle)
Succeeds only if the octagonal shape referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Octagonal_Shape_mpq_class_constrains(+Handle, +PPL_Var)
Succeeds if and only if the octagonal shape referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the octagonal shape

These predicates will obtain more detailed information about the octagonal shape unifying some of their arguments with the results.

ppl_Octagonal_Shape_mpq_class_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_mpq_class_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_mpq_class_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_mpq_class_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_mpq_class_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_mpq_class_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_mpq_class_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_mpq_class_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_mpq_class_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_mpq_class_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_mpq_class_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_mpq_class_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_mpq_class_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_mpq_class_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_mpq_class_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the octagonal shape referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Octagonal_Shape_mpq_class_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the octagonal shape referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the octagonal shape

These predicates may modify the octagonal shape referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the octagonal shape by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Octagonal_Shape_mpq_class_add_constraint(+Handle, +Constraint)
Updates the octagonal shape referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Octagonal_Shape_mpq_class_add_congruence(+Handle, +Congruence)
Updates the octagonal shape referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Octagonal_Shape_mpq_class_add_constraints( +Handle, +Constraint_System)
Updates the octagonal shape referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Octagonal_Shape_mpq_class_add_congruences( +Handle, +Congruence_System)
Updates the octagonal shape referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Octagonal_Shape_mpq_class_refine_with_constraint( +Handle, +Constraint)
Updates the octagonal shape referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Octagonal_Shape_mpq_class_refine_with_congruence( +Handle, +Congruence)
Updates the octagonal shape referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Octagonal_Shape_mpq_class_refine_with_constraints( +Handle, +Constraint_System)
Updates the octagonal shape referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Octagonal_Shape_mpq_class_refine_with_congruences( +Handle, +Congruence_System)
Updates the octagonal shape referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the octagonal shape

These predicates enable transformations such as taking the topological closure (which for the domain of octagonal shape is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Octagonal_Shape_mpq_class_topological_closure_assign(+Handle)
Assigns to the octagonal shape referenced by Handle its topological closure.

ppl_Octagonal_Shape_mpq_class_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the octagonal shape P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Octagonal_Shape_mpq_class_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the octagonal shape P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Octagonal_Shape_mpq_class_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the octagonal shape referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Octagonal_Shape_mpq_class_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the octagonal shape referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Octagonal_Shape_mpq_class_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Octagonal_Shape_mpq_class_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Octagonal_Shape_mpq_class_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_mpq_class_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_mpq_class_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_mpq_class_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_mpq_class_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the octagonal shape P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one octagonal shape

These predicates include the binary operators which will assign to the octagonal shape referred to by the first argument its combination with the octagonal shape referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Octagonal_Shape_mpq_class_intersection_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the intersection of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_mpq_class_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the upper bound of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_mpq_class_difference_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the difference of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_mpq_class_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the time elapse of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_mpq_class_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the octagonal shape P_1 referenced by Handle_1 with the octagonal shape referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Octagonal_Shape_mpq_class_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of octagonal shape P_1 referenced by Handle_1 and the octagonal shape P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_Octagonal_Shape_mpq_class_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the Octagonal_Shape_mpq_class domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the octagonal shape referred to by the second argument has to be contained in (or equal to) the octagonal shape referred to by the first argument.

ppl_Octagonal_Shape_mpq_class_BHMZ05_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_mpq_class_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_mpq_class_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_Octagonal_Shape_mpq_class_H79_widening_assign_with_tokens/4

ppl_Octagonal_Shape_mpq_class_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_Octagonal_Shape_mpq_class_H79_widening_assign/2

ppl_Octagonal_Shape_mpq_class_limited_BHMZ05_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_mpq_class_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_mpq_class_limited_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Octagonal_Shape_mpq_class_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Octagonal_Shape_mpq_class_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the octagonal shape referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Octagonal_Shape_mpq_class_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the concatenation of P and the octagonal shape referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument. These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Octagonal_Shape_mpq_class_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the octagonal shape P referenced by Handle and and_embeds P in this space.

ppl_Octagonal_Shape_mpq_class_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the octagonal shape P referenced by Handle and and_projects P in this space.

ppl_Octagonal_Shape_mpq_class_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the octagonal shape P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Octagonal_Shape_mpq_class_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the octagonal shape P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Octagonal_Shape_mpq_class_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the octagonal shape referenced by Handle to Dimension_Type new space dimensions.

ppl_Octagonal_Shape_mpq_class_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the octagonal shape referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Octagonal_Shape_mpq_class_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Polyhedron Domain

Here we provide a short description for each of the predicates available for the domain of polyhedra.

Constructor, copy, conversion and destructor predicates

Constructor predicates for polyhedra

The constructor predicates build a polyhedron from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs. For example, a C Polyhedron can be built from a list of non-strict inequality or equality constraints or a list of equality congruences or a list of generators that contains no closure points.

ppl_new_C_Polyhedron_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new C polyhedron $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_C_Polyhedron_from_space_dimension(3, universe, X).

creates the C polyhedron defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_NNC_Polyhedron_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new NNC polyhedron $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_NNC_Polyhedron_from_space_dimension(3, universe, X).

creates the NNC polyhedron defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_C_Polyhedron_from_constraints(+Constraint_System, -Handle)
Builds a new C polyhedron P from Constraint_System. Handle is unified with the handle for P.

ppl_new_NNC_Polyhedron_from_constraints(+Constraint_System, -Handle)
Builds a new NNC polyhedron P from Constraint_System. Handle is unified with the handle for P.

ppl_new_C_Polyhedron_from_congruences(+Congruence_System, -Handle)
Builds a new C polyhedron P from Congruence_System. Handle is unified with the handle for P.

ppl_new_NNC_Polyhedron_from_congruences(+Congruence_System, -Handle)
Builds a new NNC polyhedron P from Congruence_System. Handle is unified with the handle for P.

ppl_new_C_Polyhedron_from_generators(+Generator_System, -Handle)
Builds a new C polyhedron P from Generator_System. Handle is unified with the handle for P.

ppl_new_NNC_Polyhedron_from_generators(+Generator_System, -Handle)
Builds a new NNC polyhedron P from Generator_System. Handle is unified with the handle for P.

Predicates that build new polyhedra by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class (e.g., ppl_new_Grid_from_C_Polyhedron, ppl_new_C_Polyhedron_from_BD_Shape_mpq_class, etc.).

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_C_Polyhedron_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Z_Box(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Z_Box(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Grid(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Grid(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Float_Box(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Float_Box(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Double_Box(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Double_Box(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new C polyhedron P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new NNC polyhedron P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_C_Polyhedron_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new C polyhedron P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_NNC_Polyhedron_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new NNC polyhedron P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Polyhedron domain.

ppl_delete_Polyhedron(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the polyhedron

Test Predicates

These predicates test the polyhedron for different properties and succeed or fail depending on the outcome.

ppl_Polyhedron_is_empty(+Handle)
Succeeds if and only if the polyhedron referenced by Handle is empty.

ppl_Polyhedron_is_universe(+Handle)
Succeeds if and only if the polyhedron referenced by Handle is the universe.

ppl_Polyhedron_is_bounded(+Handle)
Succeeds if and only if the polyhedron referenced by Handle is bounded.

ppl_Polyhedron_contains_integer_point(+Handle)
Succeeds if and only if the polyhedron referenced by Handle contains an integer point.

ppl_Polyhedron_is_topologically_closed(+Handle)
Succeeds if and only if the polyhedron referenced by Handle is topologically closed.

ppl_Polyhedron_is_discrete(+Handle)
Succeeds if and only if the polyhedron referenced by Handle is discrete.

ppl_Polyhedron_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the polyhedron referenced by Handle.

ppl_Polyhedron_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the polyhedron referenced by Handle.

ppl_Polyhedron_contains_Polyhedron(+Handle_1, +Handle_2)
Succeeds if and only if the polyhedron referenced by Handle_2 is included in or equal to the polyhedron referenced by Handle_1.

ppl_Polyhedron_strictly_contains_Polyhedron(+Handle_1, +Handle_2)
Succeeds if and only if the polyhedron referenced by Handle_2 is included in but not equal to the polyhedron referenced by Handle_1.

ppl_Polyhedron_is_disjoint_from_Polyhedron(+Handle_1, +Handle_2)
Succeeds if and only if the polyhedron referenced by Handle_2 is disjoint from the polyhedron referenced by Handle_1.

ppl_Polyhedron_equals_Polyhedron(+Handle_1, +Handle_2)
Succeeds if and only if the polyhedron referenced by Handle_1 is equal to the polyhedron referenced by Handle_2.

ppl_Polyhedron_OK(+Handle)
Succeeds only if the polyhedron referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Polyhedron_constrains(+Handle, +PPL_Var)
Succeeds if and only if the polyhedron referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the polyhedron

These predicates will obtain more detailed information about the polyhedron unifying some of their arguments with the results.

ppl_Polyhedron_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the polyhedron referenced by Handle.

ppl_Polyhedron_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the polyhedron referenced by Handle.

ppl_Polyhedron_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the polyhedron referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Polyhedron_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the polyhedron referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Polyhedron_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the polyhedron referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Polyhedron_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the polyhedron referenced by Handle.

ppl_Polyhedron_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the polyhedron referenced by Handle.

ppl_Polyhedron_get_generators(+Handle, ?Generator_System)
Unifies Generator_System with the generators (in the form of a list) in the generator system for the polyhedron referenced by Handle.

ppl_Polyhedron_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the polyhedron referenced by Handle.

ppl_Polyhedron_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system for the polyhedron referenced by Handle.

ppl_Polyhedron_get_minimized_generators(+Handle, ?Generator_System)
Unifies Generator_System with the generators (in the form of a list) in the minimized generator system satisfied by the polyhedron referenced by Handle.

ppl_Polyhedron_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if polyhedron P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Polyhedron_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if polyhedron P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Polyhedron_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if polyhedron P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Polyhedron_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if polyhedron P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Polyhedron_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the polyhedron referenced by Handle.

ppl_Polyhedron_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the polyhedron referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Polyhedron_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the polyhedron referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the polyhedron

These predicates may modify the polyhedron referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the polyhedron by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Polyhedron_add_constraint(+Handle, +Constraint)
Updates the polyhedron referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Polyhedron_add_congruence(+Handle, +Congruence)
Updates the polyhedron referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Polyhedron_add_generator(+Handle, +Generator)
Updates the polyhedron referenced by Handle to one obtained by adding Generator to its generator system. For a C polyhedron, Generator must be a line, ray or point.

ppl_Polyhedron_add_constraints( +Handle, +Constraint_System)
Updates the polyhedron referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Polyhedron_add_congruences( +Handle, +Congruence_System)
Updates the polyhedron referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Polyhedron_add_generators( +Handle, +Generator_System)
Updates the polyhedron referenced by Handle to one obtained by adding to its generator system the generators in Generator_System. For a C polyhedron, Generators must be a list of lines, rays and points.

ppl_Polyhedron_refine_with_constraint( +Handle, +Constraint)
Updates the polyhedron referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Polyhedron_refine_with_congruence( +Handle, +Congruence)
Updates the polyhedron referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Polyhedron_refine_with_constraints( +Handle, +Constraint_System)
Updates the polyhedron referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Polyhedron_refine_with_congruences( +Handle, +Congruence_System)
Updates the polyhedron referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the polyhedron

These predicates enable transformations such as taking the topological closure (which for the domain of polyhedron is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Polyhedron_topological_closure_assign(+Handle)
Assigns to the polyhedron referenced by Handle its topological closure.

ppl_Polyhedron_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the polyhedron P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Polyhedron_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the polyhedron P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Polyhedron_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the polyhedron referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Polyhedron_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the polyhedron referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Polyhedron_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to polyhedron P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Polyhedron_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to polyhedron P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Polyhedron_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to polyhedron P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Polyhedron_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to polyhedron P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Polyhedron_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to polyhedron P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Polyhedron_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to polyhedron P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Polyhedron_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the polyhedron P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one polyhedron

These predicates include the binary operators which will assign to the polyhedron referred to by the first argument its combination with the polyhedron referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Polyhedron_intersection_assign(+Handle_1, +Handle_2)
Assigns to the polyhedron P referenced by Handle_1 the intersection of P and the polyhedron referenced by Handle_2.

ppl_Polyhedron_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the polyhedron P referenced by Handle_1 the upper bound of P and the polyhedron referenced by Handle_2.

ppl_Polyhedron_difference_assign(+Handle_1, +Handle_2)
Assigns to the polyhedron P referenced by Handle_1 the difference of P and the polyhedron referenced by Handle_2.

ppl_Polyhedron_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the polyhedron P referenced by Handle_1 the time elapse of P and the polyhedron referenced by Handle_2.

ppl_Polyhedron_poly_hull(+Handle_1, +Handle_2)
Assigns to the polyhedron P referenced by Handle_1 the poly-hull of P and the polyhedron referenced by Handle_2.

ppl_Polyhedron_poly_difference(+Handle_1, +Handle_2)
Assigns to the polyhedron P referenced by Handle_1 the poly-difference of P and the polyhedron referenced by Handle_2.

ppl_Polyhedron_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the polyhedron P_1 referenced by Handle_1 with the polyhedron referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Polyhedron_poly_hull_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the polyhedron P_1 referenced by Handle_1 with the polyhedron referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Polyhedron_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of polyhedron P_1 referenced by Handle_1 and the polyhedron P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_Polyhedron_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the Polyhedron domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the polyhedron referred to by the second argument has to be contained in (or equal to) the polyhedron referred to by the first argument.

ppl_Polyhedron_BHRZ03_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the polyhedron P_1 referenced by Handle_1 the BHRZ03-widening of P_1 with the polyhedron referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Polyhedron_H79_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the polyhedron P_1 referenced by Handle_1 the H79-widening of P_1 with the polyhedron referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Polyhedron_BHRZ03_widening_assign(+Handle_1, +Handle_2)
Assigns to the polyhedron P_1 referenced by Handle_1 the BHRZ03-widening of P_1 with the polyhedron referenced by Handle_2.

ppl_Polyhedron_H79_widening_assign(+Handle_1, +Handle_2)
Assigns to the polyhedron P_1 referenced by Handle_1 the H79-widening of P_1 with the polyhedron referenced by Handle_2.

ppl_Polyhedron_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_Polyhedron_H79_widening_assign_with_tokens/4

ppl_Polyhedron_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_Polyhedron_H79_widening_assign/2

ppl_Polyhedron_limited_BHRZ03_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the polyhedron P_1 referenced by Handle_1 the BHRZ03-widening of P_1 with the polyhedron referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Polyhedron_bounded_BHRZ03_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the polyhedron P_1 referenced by Handle_1 the BHRZ03-widening of P_1 with the polyhedron referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1, further intersected with the smallest box containing P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Polyhedron_limited_H79_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the polyhedron P_1 referenced by Handle_1 the H79-widening of P_1 with the polyhedron referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Polyhedron_bounded_H79_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the polyhedron P_1 referenced by Handle_1 the H79-widening of P_1 with the polyhedron referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1, further intersected with the smallest box containing P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Polyhedron_limited_BHRZ03_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the polyhedron P_1 referenced by Handle_1 the BHRZ03-widening of P_1 with the polyhedron referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Polyhedron_bounded_BHRZ03_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the polyhedron P_1 referenced by Handle_1 the BHRZ03-widening of P_1 with the polyhedron referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1, further intersected with the smallest box containing P_1.

ppl_Polyhedron_limited_H79_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the polyhedron P_1 referenced by Handle_1 the H79-widening of P_1 with the polyhedron referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Polyhedron_bounded_H79_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the polyhedron P_1 referenced by Handle_1 the H79-widening of P_1 with the polyhedron referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1, further intersected with the smallest box containing P_1.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the polyhedron referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Polyhedron_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the polyhedron P referenced by Handle_1 the concatenation of P and the polyhedron referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the polyhedron referred to in the first argument. These predicates enable the modification of the vector space of the polyhedron referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Polyhedron_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the polyhedron P referenced by Handle and and_embeds P in this space.

ppl_Polyhedron_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the polyhedron P referenced by Handle and and_projects P in this space.

ppl_Polyhedron_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the polyhedron P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Polyhedron_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the polyhedron P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Polyhedron_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the polyhedron referenced by Handle to Dimension_Type new space dimensions.

ppl_Polyhedron_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the polyhedron referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Polyhedron_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Grid Domain

Here we provide a short description for each of the predicates available for the domain of grids.

Constructor, copy, conversion and destructor predicates

Constructor predicates for grids

The constructor predicates build a grid from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Grid_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new grid $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Grid_from_space_dimension(3, universe, X).

creates the grid defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Grid_from_constraints(+Constraint_System, -Handle)
Builds a new grid P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Grid_from_congruences(+Congruence_System, -Handle)
Builds a new grid P from Congruence_System. Handle is unified with the handle for P.

ppl_new_Grid_from_grid_generators(+Grid_Generator_System, -Handle)
Builds a new grid P from Grid_Generator_System. Handle is unified with the handle for P.

Predicates that build new grids by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Grid_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new grid P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new grid P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new grid P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new grid P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new grid P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new grid P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new grid P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new grid P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Z_Box(+Handle_1, -Handle_2)
Builds a new grid P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new grid P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new grid P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new grid P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new grid P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new grid P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new grid P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new grid P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new grid P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new grid P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new grid P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new grid P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new grid P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new grid P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new grid P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new grid P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Grid(+Handle_1, -Handle_2)
Builds a new grid P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Float_Box(+Handle_1, -Handle_2)
Builds a new grid P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new grid P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new grid P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Double_Box(+Handle_1, -Handle_2)
Builds a new grid P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new grid P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new grid P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new grid P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new grid P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new grid P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Grid_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new grid P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Grid domain.

ppl_delete_Grid(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the grid

Test Predicates

These predicates test the grid for different properties and succeed or fail depending on the outcome.

ppl_Grid_is_empty(+Handle)
Succeeds if and only if the grid referenced by Handle is empty.

ppl_Grid_is_universe(+Handle)
Succeeds if and only if the grid referenced by Handle is the universe.

ppl_Grid_is_bounded(+Handle)
Succeeds if and only if the grid referenced by Handle is bounded.

ppl_Grid_contains_integer_point(+Handle)
Succeeds if and only if the grid referenced by Handle contains an integer point.

ppl_Grid_is_topologically_closed(+Handle)
Succeeds if and only if the grid referenced by Handle is topologically closed.

ppl_Grid_is_discrete(+Handle)
Succeeds if and only if the grid referenced by Handle is discrete.

ppl_Grid_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the grid referenced by Handle.

ppl_Grid_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the grid referenced by Handle.

ppl_Grid_contains_Grid(+Handle_1, +Handle_2)
Succeeds if and only if the grid referenced by Handle_2 is included in or equal to the grid referenced by Handle_1.

ppl_Grid_strictly_contains_Grid(+Handle_1, +Handle_2)
Succeeds if and only if the grid referenced by Handle_2 is included in but not equal to the grid referenced by Handle_1.

ppl_Grid_is_disjoint_from_Grid(+Handle_1, +Handle_2)
Succeeds if and only if the grid referenced by Handle_2 is disjoint from the grid referenced by Handle_1.

ppl_Grid_equals_Grid(+Handle_1, +Handle_2)
Succeeds if and only if the grid referenced by Handle_1 is equal to the grid referenced by Handle_2.

ppl_Grid_OK(+Handle)
Succeeds only if the grid referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Grid_constrains(+Handle, +PPL_Var)
Succeeds if and only if the grid referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the grid

These predicates will obtain more detailed information about the grid unifying some of their arguments with the results.

ppl_Grid_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the grid referenced by Handle.

ppl_Grid_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the grid referenced by Handle.

ppl_Grid_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the grid referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Grid_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the grid referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Grid_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the grid referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Grid_relation_with_grid_generator(+Handle, +Grid_Generator, ?Relation_List)
Unifies Relation_List with the list of relations the grid referenced by Handle has with Grid_Generator. The possible relations are listed in the grammar rules above.

ppl_Grid_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the grid referenced by Handle.

ppl_Grid_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the grid referenced by Handle.

ppl_Grid_get_grid_generators(+Handle, ?Grid_Generator_System)
Unifies Grid_Generator_System with the grid_generators (in the form of a list) in the grid_generator system for the grid referenced by Handle.

ppl_Grid_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the grid referenced by Handle.

ppl_Grid_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the grid referenced by Handle.

ppl_Grid_get_minimized_grid_generators(+Handle, ?Grid_Generator_System)
Unifies Grid_Generator_System with the grid_generators (in the form of a list) in the minimized grid_generator system for the grid referenced by Handle.

ppl_Grid_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if grid P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Grid_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if grid P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Grid_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if grid P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Grid_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if grid P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Grid_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the grid referenced by Handle.

ppl_Grid_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the grid referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Grid_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the grid referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the grid

These predicates may modify the grid referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the grid by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Grid_add_constraint(+Handle, +Constraint)
Updates the grid referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Grid_add_congruence(+Handle, +Congruence)
Updates the grid referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Grid_add_grid_generator(+Handle, +Grid_Generator)
Updates the grid referenced by Handle to one obtained by adding Grid_Generator to its grid_generator system. For a C polyhedron, Grid_Generator must be a line, ray or point.

ppl_Grid_add_constraints( +Handle, +Constraint_System)
Updates the grid referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Grid_add_congruences( +Handle, +Congruence_System)
Updates the grid referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Grid_add_grid_generators( +Handle, +Grid_Generator_System)
Updates the grid referenced by Handle to one obtained by adding to its grid_generator system the grid_generators in Grid_Generator_System. For a C polyhedron, Grid_Generators must be a list of lines, rays and points.

ppl_Grid_refine_with_constraint( +Handle, +Constraint)
Updates the grid referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Grid_refine_with_congruence( +Handle, +Congruence)
Updates the grid referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Grid_refine_with_constraints( +Handle, +Constraint_System)
Updates the grid referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Grid_refine_with_congruences( +Handle, +Congruence_System)
Updates the grid referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the grid

These predicates enable transformations such as taking the topological closure (which for the domain of grid is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Grid_topological_closure_assign(+Handle)
Assigns to the grid referenced by Handle its topological closure.

ppl_Grid_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the grid P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Grid_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the grid P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Grid_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the grid referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Grid_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the grid referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Grid_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to grid P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Grid_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to grid P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Grid_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to grid P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Grid_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to grid P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Grid_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to grid P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Grid_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to grid P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Grid_generalized_affine_image_with_congruence(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff_1, +Coeff_2)
Assigns to grid P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 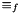$\equiv_f$ Lin_Expr_2/Coeff_1, where Coeff_2 is bound to the modulus f.

ppl_Grid_generalized_affine_preimage_with_congruence(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff_1, +Coeff_2)
Assigns to grid P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 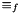$\equiv_f$ Lin_Expr_2/Coeff_1, where Coeff_2 is bound to the modulus f.

ppl_Grid_generalized_affine_image_lhs_rhs_with_congruence(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2, +Coeff)
Assigns to grid P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 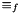$\equiv_f$ Lin_Expr_2. where Coeff is bound to the modulus f.

ppl_Grid_generalized_affine_preimage_lhs_rhs_with_congruence(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2, +Coeff)
Assigns to grid P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 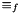$\equiv_f$ Lin_Expr_2. where Coeff is bound to the modulus f.

ppl_Grid_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the grid P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one grid

These predicates include the binary operators which will assign to the grid referred to by the first argument its combination with the grid referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Grid_intersection_assign(+Handle_1, +Handle_2)
Assigns to the grid P referenced by Handle_1 the intersection of P and the grid referenced by Handle_2.

ppl_Grid_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the grid P referenced by Handle_1 the upper bound of P and the grid referenced by Handle_2.

ppl_Grid_difference_assign(+Handle_1, +Handle_2)
Assigns to the grid P referenced by Handle_1 the difference of P and the grid referenced by Handle_2.

ppl_Grid_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the grid P referenced by Handle_1 the time elapse of P and the grid referenced by Handle_2.

ppl_Grid_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the grid P_1 referenced by Handle_1 with the grid referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Grid_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of grid P_1 referenced by Handle_1 and the grid P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_Grid_approximate_partition(+Handle_1, +Handle_2, ?Boolean, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the Grid domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of grids P_4 where:
if there is a finite linear partition of P_1 wrt P_2 Boolean is unified with the atom true and P_4 is the linear partition;
otherwise Boolean is unified with the atom false and P_4 is set to the singleton set that contains P_2.
This predicate is only provided if the class Pointset_Powerset_Grid has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the grid referred to by the second argument has to be contained in (or equal to) the grid referred to by the first argument.

ppl_Grid_congruence_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the grid P_1 referenced by Handle_1 the congruence-widening of P_1 with the grid referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Grid_generator_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the grid P_1 referenced by Handle_1 the generator-widening of P_1 with the grid referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Grid_congruence_widening_assign(+Handle_1, +Handle_2)
Assigns to the grid P_1 referenced by Handle_1 the congruence-widening of P_1 with the grid referenced by Handle_2.

ppl_Grid_generator_widening_assign(+Handle_1, +Handle_2)
Assigns to the grid P_1 referenced by Handle_1 the generator-widening of P_1 with the grid referenced by Handle_2.

ppl_Grid_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_Grid_congruence_widening_assign_with_tokens/4

ppl_Grid_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_Grid_congruence_widening_assign/2

ppl_Grid_limited_congruence_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the grid P_1 referenced by Handle_1 the congruence-widening of P_1 with the grid referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Grid_limited_generator_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the grid P_1 referenced by Handle_1 the generator-widening of P_1 with the grid referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Grid_limited_congruence_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the grid P_1 referenced by Handle_1 the congruence-widening of P_1 with the grid referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Grid_limited_generator_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the grid P_1 referenced by Handle_1 the generator-widening of P_1 with the grid referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the grid referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Grid_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the grid P referenced by Handle_1 the concatenation of P and the grid referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the grid referred to in the first argument. These predicates enable the modification of the vector space of the grid referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Grid_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the grid P referenced by Handle and and_embeds P in this space.

ppl_Grid_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the grid P referenced by Handle and and_projects P in this space.

ppl_Grid_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the grid P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Grid_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the grid P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Grid_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the grid referenced by Handle to Dimension_Type new space dimensions.

ppl_Grid_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the grid referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Grid_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Pointset_Powerset_Int8_Box Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of int8 boxes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of int8 boxes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_Int8_Box_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_Int8_Box_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_Int8_Box_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_Int8_Box_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of int8 boxes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_Int8_Box_from_Pointset_Powerset_Int8_Box(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Int8_Box_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Int8_Box_from_Pointset_Powerset_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Int8_Box_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_Int8_Box domain.

ppl_delete_Pointset_Powerset_Int8_Box(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_Int8_Box_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_Int8_Box_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_Int8_Box_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_Int8_Box_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_Int8_Box_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_Int8_Box_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_Int8_Box_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Int8_Box_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Int8_Box_contains_Pointset_Powerset_Int8_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Int8_Box_strictly_contains_Pointset_Powerset_Int8_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Int8_Box_is_disjoint_from_Pointset_Powerset_Int8_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Int8_Box_geometrically_covers_Pointset_Powerset_Int8_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Int8_Box_geometrically_equals_Pointset_Powerset_Int8_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Int8_Box_equals_Pointset_Powerset_Int8_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Int8_Box_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_Int8_Box_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_Int8_Box_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Int8_Box_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Int8_Box_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Int8_Box_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Int8_Box_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Int8_Box_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Int8_Box_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Int8_Box_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Int8_Box_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Int8_Box_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Int8_Box_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Int8_Box_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_Int8_Box_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_Int8_Box_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_Int8_Box_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_Int8_Box_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_Int8_Box_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_Int8_Box_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_Int8_Box_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_Int8_Box_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_Int8_Box_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_Int8_Box_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_Int8_Box_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_Int8_Box_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_Int8_Box_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_Int8_Box_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Int8_Box_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Int8_Box_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Int8_Box_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Int8_Box_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Int8_Box_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Int8_Box_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Int8_Box_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Int8_Box_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_Int8_Box_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Int8_Box_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Int8_Box_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Int8_Box_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Int8_Box_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_Int8_Box_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_Int8_Box_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_Int8_Box_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_Int8_Box_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_Int8_Box_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Int8_Box_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_Int8_Box_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_Int8_Box_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_Int8_Box_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_Int8_Box_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_Int8_Box_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Int8_Box_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Int8_Box_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_Int8_Box_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_Int8_Box_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_Int8_Box_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_Int8_Box_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_Int8_Box_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_Int8_Box_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_Int8_Box_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_Int16_Box Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of int16 boxes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of int16 boxes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_Int16_Box_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_Int16_Box_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_Int16_Box_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_Int16_Box_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of int16 boxes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_Int16_Box_from_Pointset_Powerset_Int16_Box(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Int16_Box_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Int16_Box_from_Pointset_Powerset_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Int16_Box_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_Int16_Box domain.

ppl_delete_Pointset_Powerset_Int16_Box(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_Int16_Box_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_Int16_Box_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_Int16_Box_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_Int16_Box_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_Int16_Box_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_Int16_Box_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_Int16_Box_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Int16_Box_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Int16_Box_contains_Pointset_Powerset_Int16_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Int16_Box_strictly_contains_Pointset_Powerset_Int16_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Int16_Box_is_disjoint_from_Pointset_Powerset_Int16_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Int16_Box_geometrically_covers_Pointset_Powerset_Int16_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Int16_Box_geometrically_equals_Pointset_Powerset_Int16_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Int16_Box_equals_Pointset_Powerset_Int16_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Int16_Box_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_Int16_Box_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_Int16_Box_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Int16_Box_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Int16_Box_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Int16_Box_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Int16_Box_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Int16_Box_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Int16_Box_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Int16_Box_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Int16_Box_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Int16_Box_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Int16_Box_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Int16_Box_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_Int16_Box_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_Int16_Box_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_Int16_Box_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_Int16_Box_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_Int16_Box_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_Int16_Box_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_Int16_Box_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_Int16_Box_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_Int16_Box_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_Int16_Box_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_Int16_Box_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_Int16_Box_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_Int16_Box_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_Int16_Box_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Int16_Box_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Int16_Box_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Int16_Box_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Int16_Box_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Int16_Box_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Int16_Box_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Int16_Box_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Int16_Box_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_Int16_Box_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Int16_Box_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Int16_Box_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Int16_Box_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Int16_Box_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_Int16_Box_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_Int16_Box_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_Int16_Box_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_Int16_Box_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_Int16_Box_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Int16_Box_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_Int16_Box_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_Int16_Box_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_Int16_Box_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_Int16_Box_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_Int16_Box_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Int16_Box_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Int16_Box_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_Int16_Box_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_Int16_Box_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_Int16_Box_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_Int16_Box_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_Int16_Box_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_Int16_Box_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_Int16_Box_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_Int32_Box Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of int32 boxes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of int32 boxes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_Int32_Box_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_Int32_Box_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_Int32_Box_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_Int32_Box_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of int32 boxes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_Int32_Box_from_Pointset_Powerset_Int32_Box(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Int32_Box_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Int32_Box_from_Pointset_Powerset_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Int32_Box_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_Int32_Box domain.

ppl_delete_Pointset_Powerset_Int32_Box(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_Int32_Box_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_Int32_Box_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_Int32_Box_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_Int32_Box_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_Int32_Box_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_Int32_Box_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_Int32_Box_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Int32_Box_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Int32_Box_contains_Pointset_Powerset_Int32_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Int32_Box_strictly_contains_Pointset_Powerset_Int32_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Int32_Box_is_disjoint_from_Pointset_Powerset_Int32_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Int32_Box_geometrically_covers_Pointset_Powerset_Int32_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Int32_Box_geometrically_equals_Pointset_Powerset_Int32_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Int32_Box_equals_Pointset_Powerset_Int32_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Int32_Box_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_Int32_Box_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_Int32_Box_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Int32_Box_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Int32_Box_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Int32_Box_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Int32_Box_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Int32_Box_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Int32_Box_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Int32_Box_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Int32_Box_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Int32_Box_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Int32_Box_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Int32_Box_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_Int32_Box_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_Int32_Box_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_Int32_Box_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_Int32_Box_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_Int32_Box_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_Int32_Box_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_Int32_Box_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_Int32_Box_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_Int32_Box_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_Int32_Box_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_Int32_Box_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_Int32_Box_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_Int32_Box_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_Int32_Box_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Int32_Box_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Int32_Box_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Int32_Box_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Int32_Box_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Int32_Box_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Int32_Box_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Int32_Box_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Int32_Box_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_Int32_Box_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Int32_Box_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Int32_Box_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Int32_Box_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Int32_Box_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_Int32_Box_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_Int32_Box_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_Int32_Box_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_Int32_Box_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_Int32_Box_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Int32_Box_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_Int32_Box_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_Int32_Box_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_Int32_Box_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_Int32_Box_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_Int32_Box_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Int32_Box_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Int32_Box_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_Int32_Box_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_Int32_Box_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_Int32_Box_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_Int32_Box_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_Int32_Box_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_Int32_Box_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_Int32_Box_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_Int64_Box Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of int64 boxes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of int64 boxes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_Int64_Box_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_Int64_Box_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_Int64_Box_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_Int64_Box_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of int64 boxes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_Int64_Box_from_Pointset_Powerset_Int64_Box(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Int64_Box_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Int64_Box_from_Pointset_Powerset_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Int64_Box_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_Int64_Box domain.

ppl_delete_Pointset_Powerset_Int64_Box(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_Int64_Box_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_Int64_Box_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_Int64_Box_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_Int64_Box_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_Int64_Box_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_Int64_Box_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_Int64_Box_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Int64_Box_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Int64_Box_contains_Pointset_Powerset_Int64_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Int64_Box_strictly_contains_Pointset_Powerset_Int64_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Int64_Box_is_disjoint_from_Pointset_Powerset_Int64_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Int64_Box_geometrically_covers_Pointset_Powerset_Int64_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Int64_Box_geometrically_equals_Pointset_Powerset_Int64_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Int64_Box_equals_Pointset_Powerset_Int64_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Int64_Box_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_Int64_Box_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_Int64_Box_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Int64_Box_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Int64_Box_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Int64_Box_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Int64_Box_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Int64_Box_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Int64_Box_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Int64_Box_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Int64_Box_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Int64_Box_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Int64_Box_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Int64_Box_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_Int64_Box_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_Int64_Box_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_Int64_Box_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_Int64_Box_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_Int64_Box_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_Int64_Box_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_Int64_Box_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_Int64_Box_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_Int64_Box_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_Int64_Box_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_Int64_Box_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_Int64_Box_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_Int64_Box_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_Int64_Box_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Int64_Box_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Int64_Box_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Int64_Box_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Int64_Box_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Int64_Box_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Int64_Box_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Int64_Box_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Int64_Box_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_Int64_Box_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Int64_Box_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Int64_Box_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Int64_Box_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Int64_Box_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_Int64_Box_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_Int64_Box_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_Int64_Box_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_Int64_Box_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_Int64_Box_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Int64_Box_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_Int64_Box_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_Int64_Box_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_Int64_Box_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_Int64_Box_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_Int64_Box_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Int64_Box_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Int64_Box_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_Int64_Box_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_Int64_Box_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_Int64_Box_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_Int64_Box_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_Int64_Box_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_Int64_Box_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_Int64_Box_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_Uint8_Box Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of uint8 boxes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of uint8 boxes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_Uint8_Box_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_Uint8_Box_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_Uint8_Box_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_Uint8_Box_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of uint8 boxes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_Uint8_Box_from_Pointset_Powerset_Uint8_Box(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Uint8_Box_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Uint8_Box_from_Pointset_Powerset_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Uint8_Box_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_Uint8_Box domain.

ppl_delete_Pointset_Powerset_Uint8_Box(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_Uint8_Box_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_Uint8_Box_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_Uint8_Box_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_Uint8_Box_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_Uint8_Box_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_Uint8_Box_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_Uint8_Box_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Uint8_Box_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Uint8_Box_contains_Pointset_Powerset_Uint8_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Uint8_Box_strictly_contains_Pointset_Powerset_Uint8_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Uint8_Box_is_disjoint_from_Pointset_Powerset_Uint8_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Uint8_Box_geometrically_covers_Pointset_Powerset_Uint8_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Uint8_Box_geometrically_equals_Pointset_Powerset_Uint8_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Uint8_Box_equals_Pointset_Powerset_Uint8_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Uint8_Box_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_Uint8_Box_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_Uint8_Box_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Uint8_Box_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Uint8_Box_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Uint8_Box_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Uint8_Box_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Uint8_Box_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Uint8_Box_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Uint8_Box_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Uint8_Box_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Uint8_Box_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Uint8_Box_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Uint8_Box_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_Uint8_Box_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_Uint8_Box_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_Uint8_Box_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_Uint8_Box_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_Uint8_Box_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_Uint8_Box_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_Uint8_Box_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_Uint8_Box_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_Uint8_Box_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_Uint8_Box_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_Uint8_Box_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_Uint8_Box_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_Uint8_Box_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_Uint8_Box_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Uint8_Box_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Uint8_Box_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Uint8_Box_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Uint8_Box_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Uint8_Box_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Uint8_Box_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Uint8_Box_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Uint8_Box_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_Uint8_Box_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Uint8_Box_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Uint8_Box_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Uint8_Box_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Uint8_Box_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_Uint8_Box_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_Uint8_Box_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_Uint8_Box_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_Uint8_Box_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_Uint8_Box_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Uint8_Box_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_Uint8_Box_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_Uint8_Box_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_Uint8_Box_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_Uint8_Box_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_Uint8_Box_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Uint8_Box_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Uint8_Box_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_Uint8_Box_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_Uint8_Box_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_Uint8_Box_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_Uint8_Box_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_Uint8_Box_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_Uint8_Box_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_Uint8_Box_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_Uint16_Box Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of uint16 boxes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of uint16 boxes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_Uint16_Box_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_Uint16_Box_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_Uint16_Box_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_Uint16_Box_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of uint16 boxes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_Uint16_Box_from_Pointset_Powerset_Uint16_Box(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Uint16_Box_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Uint16_Box_from_Pointset_Powerset_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Uint16_Box_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_Uint16_Box domain.

ppl_delete_Pointset_Powerset_Uint16_Box(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_Uint16_Box_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_Uint16_Box_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_Uint16_Box_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_Uint16_Box_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_Uint16_Box_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_Uint16_Box_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_Uint16_Box_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Uint16_Box_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Uint16_Box_contains_Pointset_Powerset_Uint16_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Uint16_Box_strictly_contains_Pointset_Powerset_Uint16_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Uint16_Box_is_disjoint_from_Pointset_Powerset_Uint16_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Uint16_Box_geometrically_covers_Pointset_Powerset_Uint16_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Uint16_Box_geometrically_equals_Pointset_Powerset_Uint16_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Uint16_Box_equals_Pointset_Powerset_Uint16_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Uint16_Box_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_Uint16_Box_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_Uint16_Box_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Uint16_Box_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Uint16_Box_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Uint16_Box_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Uint16_Box_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Uint16_Box_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Uint16_Box_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Uint16_Box_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Uint16_Box_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Uint16_Box_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Uint16_Box_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Uint16_Box_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_Uint16_Box_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_Uint16_Box_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_Uint16_Box_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_Uint16_Box_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_Uint16_Box_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_Uint16_Box_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_Uint16_Box_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_Uint16_Box_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_Uint16_Box_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_Uint16_Box_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_Uint16_Box_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_Uint16_Box_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_Uint16_Box_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_Uint16_Box_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Uint16_Box_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Uint16_Box_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Uint16_Box_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Uint16_Box_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Uint16_Box_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Uint16_Box_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Uint16_Box_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Uint16_Box_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_Uint16_Box_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Uint16_Box_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Uint16_Box_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Uint16_Box_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Uint16_Box_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_Uint16_Box_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_Uint16_Box_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_Uint16_Box_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_Uint16_Box_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_Uint16_Box_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Uint16_Box_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_Uint16_Box_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_Uint16_Box_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_Uint16_Box_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_Uint16_Box_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_Uint16_Box_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Uint16_Box_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Uint16_Box_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_Uint16_Box_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_Uint16_Box_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_Uint16_Box_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_Uint16_Box_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_Uint16_Box_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_Uint16_Box_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_Uint16_Box_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_Uint32_Box Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of uint32 boxes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of uint32 boxes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_Uint32_Box_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_Uint32_Box_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_Uint32_Box_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_Uint32_Box_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of uint32 boxes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_Uint32_Box_from_Pointset_Powerset_Uint32_Box(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Uint32_Box_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Uint32_Box_from_Pointset_Powerset_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Uint32_Box_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_Uint32_Box domain.

ppl_delete_Pointset_Powerset_Uint32_Box(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_Uint32_Box_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_Uint32_Box_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_Uint32_Box_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_Uint32_Box_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_Uint32_Box_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_Uint32_Box_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_Uint32_Box_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Uint32_Box_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Uint32_Box_contains_Pointset_Powerset_Uint32_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Uint32_Box_strictly_contains_Pointset_Powerset_Uint32_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Uint32_Box_is_disjoint_from_Pointset_Powerset_Uint32_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Uint32_Box_geometrically_covers_Pointset_Powerset_Uint32_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Uint32_Box_geometrically_equals_Pointset_Powerset_Uint32_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Uint32_Box_equals_Pointset_Powerset_Uint32_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Uint32_Box_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_Uint32_Box_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_Uint32_Box_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Uint32_Box_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Uint32_Box_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Uint32_Box_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Uint32_Box_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Uint32_Box_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Uint32_Box_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Uint32_Box_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Uint32_Box_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Uint32_Box_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Uint32_Box_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Uint32_Box_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_Uint32_Box_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_Uint32_Box_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_Uint32_Box_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_Uint32_Box_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_Uint32_Box_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_Uint32_Box_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_Uint32_Box_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_Uint32_Box_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_Uint32_Box_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_Uint32_Box_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_Uint32_Box_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_Uint32_Box_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_Uint32_Box_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_Uint32_Box_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Uint32_Box_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Uint32_Box_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Uint32_Box_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Uint32_Box_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Uint32_Box_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Uint32_Box_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Uint32_Box_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Uint32_Box_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_Uint32_Box_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Uint32_Box_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Uint32_Box_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Uint32_Box_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Uint32_Box_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_Uint32_Box_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_Uint32_Box_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_Uint32_Box_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_Uint32_Box_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_Uint32_Box_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Uint32_Box_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_Uint32_Box_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_Uint32_Box_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_Uint32_Box_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_Uint32_Box_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_Uint32_Box_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Uint32_Box_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Uint32_Box_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_Uint32_Box_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_Uint32_Box_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_Uint32_Box_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_Uint32_Box_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_Uint32_Box_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_Uint32_Box_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_Uint32_Box_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_Uint64_Box Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of uint64 boxes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of uint64 boxes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_Uint64_Box_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_Uint64_Box_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_Uint64_Box_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_Uint64_Box_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of uint64 boxes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_Uint64_Box_from_Pointset_Powerset_Uint64_Box(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Uint64_Box_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Uint64_Box_from_Pointset_Powerset_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Uint64_Box_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_Uint64_Box domain.

ppl_delete_Pointset_Powerset_Uint64_Box(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_Uint64_Box_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_Uint64_Box_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_Uint64_Box_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_Uint64_Box_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_Uint64_Box_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_Uint64_Box_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_Uint64_Box_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Uint64_Box_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Uint64_Box_contains_Pointset_Powerset_Uint64_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Uint64_Box_strictly_contains_Pointset_Powerset_Uint64_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Uint64_Box_is_disjoint_from_Pointset_Powerset_Uint64_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Uint64_Box_geometrically_covers_Pointset_Powerset_Uint64_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Uint64_Box_geometrically_equals_Pointset_Powerset_Uint64_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Uint64_Box_equals_Pointset_Powerset_Uint64_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Uint64_Box_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_Uint64_Box_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_Uint64_Box_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Uint64_Box_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Uint64_Box_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Uint64_Box_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Uint64_Box_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Uint64_Box_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Uint64_Box_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Uint64_Box_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Uint64_Box_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Uint64_Box_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Uint64_Box_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Uint64_Box_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_Uint64_Box_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_Uint64_Box_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_Uint64_Box_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_Uint64_Box_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_Uint64_Box_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_Uint64_Box_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_Uint64_Box_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_Uint64_Box_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_Uint64_Box_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_Uint64_Box_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_Uint64_Box_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_Uint64_Box_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_Uint64_Box_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_Uint64_Box_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Uint64_Box_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Uint64_Box_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Uint64_Box_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Uint64_Box_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Uint64_Box_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Uint64_Box_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Uint64_Box_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Uint64_Box_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_Uint64_Box_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Uint64_Box_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Uint64_Box_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Uint64_Box_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Uint64_Box_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_Uint64_Box_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_Uint64_Box_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_Uint64_Box_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_Uint64_Box_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_Uint64_Box_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Uint64_Box_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_Uint64_Box_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_Uint64_Box_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_Uint64_Box_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_Uint64_Box_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_Uint64_Box_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Uint64_Box_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Uint64_Box_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_Uint64_Box_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_Uint64_Box_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_Uint64_Box_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_Uint64_Box_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_Uint64_Box_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_Uint64_Box_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_Uint64_Box_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_Rational_Box Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of rational boxes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of rational boxes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_Rational_Box_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_Rational_Box_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_Rational_Box_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_Rational_Box_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of rational boxes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_Rational_Box_from_Pointset_Powerset_Rational_Box(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Rational_Box_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Rational_Box_from_Pointset_Powerset_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Rational_Box_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_Rational_Box domain.

ppl_delete_Pointset_Powerset_Rational_Box(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_Rational_Box_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_Rational_Box_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_Rational_Box_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_Rational_Box_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_Rational_Box_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_Rational_Box_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_Rational_Box_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Rational_Box_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Rational_Box_contains_Pointset_Powerset_Rational_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Rational_Box_strictly_contains_Pointset_Powerset_Rational_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Rational_Box_is_disjoint_from_Pointset_Powerset_Rational_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Rational_Box_geometrically_covers_Pointset_Powerset_Rational_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Rational_Box_geometrically_equals_Pointset_Powerset_Rational_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Rational_Box_equals_Pointset_Powerset_Rational_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Rational_Box_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_Rational_Box_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_Rational_Box_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Rational_Box_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Rational_Box_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Rational_Box_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Rational_Box_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Rational_Box_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Rational_Box_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Rational_Box_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Rational_Box_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Rational_Box_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Rational_Box_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Rational_Box_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_Rational_Box_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_Rational_Box_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_Rational_Box_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_Rational_Box_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_Rational_Box_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_Rational_Box_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_Rational_Box_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_Rational_Box_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_Rational_Box_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_Rational_Box_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_Rational_Box_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_Rational_Box_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_Rational_Box_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_Rational_Box_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Rational_Box_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Rational_Box_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Rational_Box_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Rational_Box_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Rational_Box_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Rational_Box_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Rational_Box_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Rational_Box_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_Rational_Box_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Rational_Box_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Rational_Box_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Rational_Box_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Rational_Box_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_Rational_Box_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_Rational_Box_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_Rational_Box_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_Rational_Box_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_Rational_Box_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Rational_Box_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_Rational_Box_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_Rational_Box_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_Rational_Box_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_Rational_Box_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_Rational_Box_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Rational_Box_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Rational_Box_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_Rational_Box_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_Rational_Box_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_Rational_Box_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_Rational_Box_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_Rational_Box_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_Rational_Box_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_Rational_Box_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_Z_Box Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of z boxes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of z boxes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_Z_Box_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_Z_Box_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_Z_Box_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_Z_Box_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of z boxes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_Z_Box_from_Pointset_Powerset_Z_Box(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Z_Box_from_Z_Box(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Z_Box_from_Pointset_Powerset_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Z_Box_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_Z_Box domain.

ppl_delete_Pointset_Powerset_Z_Box(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_Z_Box_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_Z_Box_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_Z_Box_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_Z_Box_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_Z_Box_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_Z_Box_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_Z_Box_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Z_Box_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Z_Box_contains_Pointset_Powerset_Z_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Z_Box_strictly_contains_Pointset_Powerset_Z_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Z_Box_is_disjoint_from_Pointset_Powerset_Z_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Z_Box_geometrically_covers_Pointset_Powerset_Z_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Z_Box_geometrically_equals_Pointset_Powerset_Z_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Z_Box_equals_Pointset_Powerset_Z_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Z_Box_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_Z_Box_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_Z_Box_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Z_Box_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Z_Box_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Z_Box_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Z_Box_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Z_Box_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Z_Box_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Z_Box_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Z_Box_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Z_Box_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Z_Box_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Z_Box_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_Z_Box_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_Z_Box_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_Z_Box_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_Z_Box_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_Z_Box_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_Z_Box_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_Z_Box_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_Z_Box_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_Z_Box_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_Z_Box_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_Z_Box_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_Z_Box_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_Z_Box_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_Z_Box_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Z_Box_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Z_Box_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Z_Box_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Z_Box_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Z_Box_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Z_Box_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Z_Box_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Z_Box_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_Z_Box_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Z_Box_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Z_Box_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Z_Box_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Z_Box_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_Z_Box_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_Z_Box_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_Z_Box_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_Z_Box_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_Z_Box_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Z_Box_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_Z_Box_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_Z_Box_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_Z_Box_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_Z_Box_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_Z_Box_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Z_Box_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Z_Box_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_Z_Box_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_Z_Box_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_Z_Box_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_Z_Box_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_Z_Box_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_Z_Box_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_Z_Box_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_BD_Shape_int8_t Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of bd shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of bd shapes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_BD_Shape_int8_t_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_BD_Shape_int8_t_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_BD_Shape_int8_t_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_BD_Shape_int8_t_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of bd shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_BD_Shape_int8_t_from_Pointset_Powerset_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_int8_t_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_int8_t_from_Pointset_Powerset_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_int8_t_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_BD_Shape_int8_t domain.

ppl_delete_Pointset_Powerset_BD_Shape_int8_t(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_BD_Shape_int8_t_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_BD_Shape_int8_t_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_BD_Shape_int8_t_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_BD_Shape_int8_t_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_BD_Shape_int8_t_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_BD_Shape_int8_t_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_BD_Shape_int8_t_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_int8_t_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_int8_t_contains_Pointset_Powerset_BD_Shape_int8_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_int8_t_strictly_contains_Pointset_Powerset_BD_Shape_int8_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_int8_t_is_disjoint_from_Pointset_Powerset_BD_Shape_int8_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_int8_t_geometrically_covers_Pointset_Powerset_BD_Shape_int8_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_int8_t_geometrically_equals_Pointset_Powerset_BD_Shape_int8_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_int8_t_equals_Pointset_Powerset_BD_Shape_int8_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_int8_t_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_BD_Shape_int8_t_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_BD_Shape_int8_t_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_int8_t_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_int8_t_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_int8_t_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_int8_t_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_int8_t_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_int8_t_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_int8_t_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_int8_t_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_int8_t_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_int8_t_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_int8_t_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_BD_Shape_int8_t_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_BD_Shape_int8_t_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_BD_Shape_int8_t_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_BD_Shape_int8_t_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_BD_Shape_int8_t_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_BD_Shape_int8_t_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_BD_Shape_int8_t_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_BD_Shape_int8_t_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_BD_Shape_int8_t_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_BD_Shape_int8_t_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_BD_Shape_int8_t_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_BD_Shape_int8_t_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_BD_Shape_int8_t_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_BD_Shape_int8_t_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_int8_t_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_BD_Shape_int8_t_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_BD_Shape_int8_t_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_BD_Shape_int8_t_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_BD_Shape_int8_t_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_int8_t_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_int8_t_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_int8_t_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_BD_Shape_int8_t_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_int8_t_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_int8_t_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_int8_t_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_int8_t_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_BD_Shape_int8_t_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

ppl_Pointset_Powerset_BD_Shape_int8_t_BHZ03_H79_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_BD_Shape_int8_t_BHZ03_H79_H79_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the H79-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_BD_Shape_int8_t_BGP99_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening and the cardinality threshold C_unsigned.

ppl_Pointset_Powerset_BD_Shape_int8_t_BGP99_H79_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the H79-widening and the cardinality threshold C_unsigned.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_BD_Shape_int8_t_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_BD_Shape_int8_t_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_BD_Shape_int8_t_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_BD_Shape_int8_t_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_int8_t_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_BD_Shape_int8_t_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_BD_Shape_int8_t_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_int8_t_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_BD_Shape_int8_t_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_BD_Shape_int8_t_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_BD_Shape_int8_t_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_BD_Shape_int8_t_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_BD_Shape_int8_t_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_BD_Shape_int8_t_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_BD_Shape_int8_t_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_BD_Shape_int8_t_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_BD_Shape_int8_t_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_BD_Shape_int8_t_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_BD_Shape_int8_t_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_BD_Shape_int16_t Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of bd shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of bd shapes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_BD_Shape_int16_t_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_BD_Shape_int16_t_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_BD_Shape_int16_t_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_BD_Shape_int16_t_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of bd shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_BD_Shape_int16_t_from_Pointset_Powerset_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_int16_t_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_int16_t_from_Pointset_Powerset_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_int16_t_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_BD_Shape_int16_t domain.

ppl_delete_Pointset_Powerset_BD_Shape_int16_t(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_BD_Shape_int16_t_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_BD_Shape_int16_t_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_BD_Shape_int16_t_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_BD_Shape_int16_t_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_BD_Shape_int16_t_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_BD_Shape_int16_t_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_BD_Shape_int16_t_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_int16_t_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_int16_t_contains_Pointset_Powerset_BD_Shape_int16_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_int16_t_strictly_contains_Pointset_Powerset_BD_Shape_int16_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_int16_t_is_disjoint_from_Pointset_Powerset_BD_Shape_int16_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_int16_t_geometrically_covers_Pointset_Powerset_BD_Shape_int16_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_int16_t_geometrically_equals_Pointset_Powerset_BD_Shape_int16_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_int16_t_equals_Pointset_Powerset_BD_Shape_int16_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_int16_t_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_BD_Shape_int16_t_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_BD_Shape_int16_t_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_int16_t_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_int16_t_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_int16_t_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_int16_t_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_int16_t_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_int16_t_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_int16_t_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_int16_t_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_int16_t_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_int16_t_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_int16_t_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_BD_Shape_int16_t_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_BD_Shape_int16_t_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_BD_Shape_int16_t_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_BD_Shape_int16_t_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_BD_Shape_int16_t_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_BD_Shape_int16_t_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_BD_Shape_int16_t_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_BD_Shape_int16_t_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_BD_Shape_int16_t_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_BD_Shape_int16_t_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_BD_Shape_int16_t_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_BD_Shape_int16_t_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_BD_Shape_int16_t_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_BD_Shape_int16_t_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_int16_t_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_BD_Shape_int16_t_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_BD_Shape_int16_t_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_BD_Shape_int16_t_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_BD_Shape_int16_t_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_int16_t_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_int16_t_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_int16_t_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_BD_Shape_int16_t_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_int16_t_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_int16_t_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_int16_t_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_int16_t_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_BD_Shape_int16_t_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

ppl_Pointset_Powerset_BD_Shape_int16_t_BHZ03_H79_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_BD_Shape_int16_t_BHZ03_H79_H79_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the H79-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_BD_Shape_int16_t_BGP99_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening and the cardinality threshold C_unsigned.

ppl_Pointset_Powerset_BD_Shape_int16_t_BGP99_H79_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the H79-widening and the cardinality threshold C_unsigned.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_BD_Shape_int16_t_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_BD_Shape_int16_t_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_BD_Shape_int16_t_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_BD_Shape_int16_t_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_int16_t_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_BD_Shape_int16_t_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_BD_Shape_int16_t_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_int16_t_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_BD_Shape_int16_t_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_BD_Shape_int16_t_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_BD_Shape_int16_t_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_BD_Shape_int16_t_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_BD_Shape_int16_t_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_BD_Shape_int16_t_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_BD_Shape_int16_t_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_BD_Shape_int16_t_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_BD_Shape_int16_t_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_BD_Shape_int16_t_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_BD_Shape_int16_t_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_BD_Shape_int32_t Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of bd shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of bd shapes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_BD_Shape_int32_t_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_BD_Shape_int32_t_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_BD_Shape_int32_t_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_BD_Shape_int32_t_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of bd shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_BD_Shape_int32_t_from_Pointset_Powerset_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_int32_t_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_int32_t_from_Pointset_Powerset_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_int32_t_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_BD_Shape_int32_t domain.

ppl_delete_Pointset_Powerset_BD_Shape_int32_t(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_BD_Shape_int32_t_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_BD_Shape_int32_t_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_BD_Shape_int32_t_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_BD_Shape_int32_t_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_BD_Shape_int32_t_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_BD_Shape_int32_t_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_BD_Shape_int32_t_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_int32_t_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_int32_t_contains_Pointset_Powerset_BD_Shape_int32_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_int32_t_strictly_contains_Pointset_Powerset_BD_Shape_int32_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_int32_t_is_disjoint_from_Pointset_Powerset_BD_Shape_int32_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_int32_t_geometrically_covers_Pointset_Powerset_BD_Shape_int32_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_int32_t_geometrically_equals_Pointset_Powerset_BD_Shape_int32_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_int32_t_equals_Pointset_Powerset_BD_Shape_int32_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_int32_t_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_BD_Shape_int32_t_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_BD_Shape_int32_t_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_int32_t_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_int32_t_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_int32_t_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_int32_t_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_int32_t_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_int32_t_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_int32_t_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_int32_t_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_int32_t_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_int32_t_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_int32_t_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_BD_Shape_int32_t_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_BD_Shape_int32_t_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_BD_Shape_int32_t_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_BD_Shape_int32_t_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_BD_Shape_int32_t_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_BD_Shape_int32_t_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_BD_Shape_int32_t_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_BD_Shape_int32_t_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_BD_Shape_int32_t_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_BD_Shape_int32_t_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_BD_Shape_int32_t_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_BD_Shape_int32_t_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_BD_Shape_int32_t_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_BD_Shape_int32_t_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_int32_t_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_BD_Shape_int32_t_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_BD_Shape_int32_t_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_BD_Shape_int32_t_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_BD_Shape_int32_t_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_int32_t_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_int32_t_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_int32_t_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_BD_Shape_int32_t_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_int32_t_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_int32_t_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_int32_t_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_int32_t_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_BD_Shape_int32_t_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

ppl_Pointset_Powerset_BD_Shape_int32_t_BHZ03_H79_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_BD_Shape_int32_t_BHZ03_H79_H79_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the H79-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_BD_Shape_int32_t_BGP99_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening and the cardinality threshold C_unsigned.

ppl_Pointset_Powerset_BD_Shape_int32_t_BGP99_H79_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the H79-widening and the cardinality threshold C_unsigned.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_BD_Shape_int32_t_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_BD_Shape_int32_t_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_BD_Shape_int32_t_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_BD_Shape_int32_t_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_int32_t_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_BD_Shape_int32_t_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_BD_Shape_int32_t_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_int32_t_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_BD_Shape_int32_t_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_BD_Shape_int32_t_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_BD_Shape_int32_t_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_BD_Shape_int32_t_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_BD_Shape_int32_t_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_BD_Shape_int32_t_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_BD_Shape_int32_t_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_BD_Shape_int32_t_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_BD_Shape_int32_t_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_BD_Shape_int32_t_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_BD_Shape_int32_t_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_BD_Shape_int64_t Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of bd shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of bd shapes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_BD_Shape_int64_t_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_BD_Shape_int64_t_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_BD_Shape_int64_t_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_BD_Shape_int64_t_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of bd shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_BD_Shape_int64_t_from_Pointset_Powerset_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_int64_t_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_int64_t_from_Pointset_Powerset_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_int64_t_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_BD_Shape_int64_t domain.

ppl_delete_Pointset_Powerset_BD_Shape_int64_t(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_BD_Shape_int64_t_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_BD_Shape_int64_t_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_BD_Shape_int64_t_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_BD_Shape_int64_t_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_BD_Shape_int64_t_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_BD_Shape_int64_t_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_BD_Shape_int64_t_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_int64_t_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_int64_t_contains_Pointset_Powerset_BD_Shape_int64_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_int64_t_strictly_contains_Pointset_Powerset_BD_Shape_int64_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_int64_t_is_disjoint_from_Pointset_Powerset_BD_Shape_int64_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_int64_t_geometrically_covers_Pointset_Powerset_BD_Shape_int64_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_int64_t_geometrically_equals_Pointset_Powerset_BD_Shape_int64_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_int64_t_equals_Pointset_Powerset_BD_Shape_int64_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_int64_t_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_BD_Shape_int64_t_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_BD_Shape_int64_t_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_int64_t_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_int64_t_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_int64_t_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_int64_t_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_int64_t_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_int64_t_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_int64_t_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_int64_t_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_int64_t_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_int64_t_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_int64_t_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_BD_Shape_int64_t_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_BD_Shape_int64_t_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_BD_Shape_int64_t_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_BD_Shape_int64_t_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_BD_Shape_int64_t_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_BD_Shape_int64_t_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_BD_Shape_int64_t_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_BD_Shape_int64_t_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_BD_Shape_int64_t_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_BD_Shape_int64_t_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_BD_Shape_int64_t_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_BD_Shape_int64_t_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_BD_Shape_int64_t_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_BD_Shape_int64_t_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_int64_t_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_BD_Shape_int64_t_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_BD_Shape_int64_t_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_BD_Shape_int64_t_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_BD_Shape_int64_t_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_int64_t_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_int64_t_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_int64_t_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_BD_Shape_int64_t_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_int64_t_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_int64_t_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_int64_t_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_int64_t_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_BD_Shape_int64_t_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

ppl_Pointset_Powerset_BD_Shape_int64_t_BHZ03_H79_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_BD_Shape_int64_t_BHZ03_H79_H79_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the H79-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_BD_Shape_int64_t_BGP99_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening and the cardinality threshold C_unsigned.

ppl_Pointset_Powerset_BD_Shape_int64_t_BGP99_H79_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the H79-widening and the cardinality threshold C_unsigned.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_BD_Shape_int64_t_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_BD_Shape_int64_t_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_BD_Shape_int64_t_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_BD_Shape_int64_t_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_int64_t_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_BD_Shape_int64_t_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_BD_Shape_int64_t_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_int64_t_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_BD_Shape_int64_t_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_BD_Shape_int64_t_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_BD_Shape_int64_t_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_BD_Shape_int64_t_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_BD_Shape_int64_t_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_BD_Shape_int64_t_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_BD_Shape_int64_t_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_BD_Shape_int64_t_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_BD_Shape_int64_t_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_BD_Shape_int64_t_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_BD_Shape_int64_t_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_BD_Shape_mpq_class Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of bd shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of bd shapes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_BD_Shape_mpq_class_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_BD_Shape_mpq_class_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_BD_Shape_mpq_class_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_BD_Shape_mpq_class_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of bd shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_BD_Shape_mpq_class_from_Pointset_Powerset_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_mpq_class_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_mpq_class_from_Pointset_Powerset_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_mpq_class_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_BD_Shape_mpq_class domain.

ppl_delete_Pointset_Powerset_BD_Shape_mpq_class(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_BD_Shape_mpq_class_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_BD_Shape_mpq_class_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_BD_Shape_mpq_class_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_BD_Shape_mpq_class_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_BD_Shape_mpq_class_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_BD_Shape_mpq_class_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_BD_Shape_mpq_class_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_mpq_class_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_mpq_class_contains_Pointset_Powerset_BD_Shape_mpq_class(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_mpq_class_strictly_contains_Pointset_Powerset_BD_Shape_mpq_class(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_mpq_class_is_disjoint_from_Pointset_Powerset_BD_Shape_mpq_class(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_mpq_class_geometrically_covers_Pointset_Powerset_BD_Shape_mpq_class(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_mpq_class_geometrically_equals_Pointset_Powerset_BD_Shape_mpq_class(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_mpq_class_equals_Pointset_Powerset_BD_Shape_mpq_class(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_mpq_class_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_BD_Shape_mpq_class_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_BD_Shape_mpq_class_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_mpq_class_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_mpq_class_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_mpq_class_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_mpq_class_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_mpq_class_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_mpq_class_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_mpq_class_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_mpq_class_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_mpq_class_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_mpq_class_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_mpq_class_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_BD_Shape_mpq_class_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_BD_Shape_mpq_class_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_BD_Shape_mpq_class_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_BD_Shape_mpq_class_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_BD_Shape_mpq_class_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_BD_Shape_mpq_class_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_BD_Shape_mpq_class_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_BD_Shape_mpq_class_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_BD_Shape_mpq_class_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_BD_Shape_mpq_class_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_BD_Shape_mpq_class_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_BD_Shape_mpq_class_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_BD_Shape_mpq_class_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_BD_Shape_mpq_class_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_mpq_class_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_BD_Shape_mpq_class_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_BD_Shape_mpq_class_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_BD_Shape_mpq_class_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_BD_Shape_mpq_class_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_mpq_class_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_mpq_class_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_mpq_class_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_BD_Shape_mpq_class_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_mpq_class_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_mpq_class_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_mpq_class_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_mpq_class_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_BD_Shape_mpq_class_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

ppl_Pointset_Powerset_BD_Shape_mpq_class_BHZ03_H79_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_BD_Shape_mpq_class_BHZ03_H79_H79_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the H79-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_BD_Shape_mpq_class_BGP99_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening and the cardinality threshold C_unsigned.

ppl_Pointset_Powerset_BD_Shape_mpq_class_BGP99_H79_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the H79-widening and the cardinality threshold C_unsigned.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_BD_Shape_mpq_class_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_BD_Shape_mpq_class_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_BD_Shape_mpq_class_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_BD_Shape_mpq_class_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_mpq_class_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_BD_Shape_mpq_class_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_BD_Shape_mpq_class_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_mpq_class_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_BD_Shape_mpq_class_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_BD_Shape_mpq_class_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_BD_Shape_mpq_class_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_BD_Shape_mpq_class_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_BD_Shape_mpq_class_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_BD_Shape_mpq_class_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_BD_Shape_mpq_class_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_BD_Shape_mpq_class_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_BD_Shape_mpq_class_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_BD_Shape_mpq_class_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_BD_Shape_mpq_class_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_BD_Shape_mpz_class Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of bd shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of bd shapes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_BD_Shape_mpz_class_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_BD_Shape_mpz_class_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_BD_Shape_mpz_class_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_BD_Shape_mpz_class_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of bd shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_BD_Shape_mpz_class_from_Pointset_Powerset_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_mpz_class_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_mpz_class_from_Pointset_Powerset_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_mpz_class_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_BD_Shape_mpz_class domain.

ppl_delete_Pointset_Powerset_BD_Shape_mpz_class(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_BD_Shape_mpz_class_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_BD_Shape_mpz_class_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_BD_Shape_mpz_class_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_BD_Shape_mpz_class_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_BD_Shape_mpz_class_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_BD_Shape_mpz_class_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_BD_Shape_mpz_class_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_mpz_class_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_mpz_class_contains_Pointset_Powerset_BD_Shape_mpz_class(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_mpz_class_strictly_contains_Pointset_Powerset_BD_Shape_mpz_class(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_mpz_class_is_disjoint_from_Pointset_Powerset_BD_Shape_mpz_class(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_mpz_class_geometrically_covers_Pointset_Powerset_BD_Shape_mpz_class(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_mpz_class_geometrically_equals_Pointset_Powerset_BD_Shape_mpz_class(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_mpz_class_equals_Pointset_Powerset_BD_Shape_mpz_class(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_mpz_class_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_BD_Shape_mpz_class_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_BD_Shape_mpz_class_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_mpz_class_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_mpz_class_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_mpz_class_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_mpz_class_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_mpz_class_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_mpz_class_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_mpz_class_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_mpz_class_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_mpz_class_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_mpz_class_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_mpz_class_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_BD_Shape_mpz_class_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_BD_Shape_mpz_class_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_BD_Shape_mpz_class_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_BD_Shape_mpz_class_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_BD_Shape_mpz_class_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_BD_Shape_mpz_class_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_BD_Shape_mpz_class_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_BD_Shape_mpz_class_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_BD_Shape_mpz_class_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_BD_Shape_mpz_class_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_BD_Shape_mpz_class_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_BD_Shape_mpz_class_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_BD_Shape_mpz_class_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_BD_Shape_mpz_class_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_mpz_class_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_BD_Shape_mpz_class_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_BD_Shape_mpz_class_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_BD_Shape_mpz_class_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_BD_Shape_mpz_class_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_mpz_class_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_mpz_class_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_mpz_class_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_BD_Shape_mpz_class_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_mpz_class_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_mpz_class_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_mpz_class_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_mpz_class_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_BD_Shape_mpz_class_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

ppl_Pointset_Powerset_BD_Shape_mpz_class_BHZ03_H79_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_BD_Shape_mpz_class_BHZ03_H79_H79_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the H79-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_BD_Shape_mpz_class_BGP99_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening and the cardinality threshold C_unsigned.

ppl_Pointset_Powerset_BD_Shape_mpz_class_BGP99_H79_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the H79-widening and the cardinality threshold C_unsigned.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_BD_Shape_mpz_class_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_BD_Shape_mpz_class_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_BD_Shape_mpz_class_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_BD_Shape_mpz_class_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_mpz_class_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_BD_Shape_mpz_class_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_BD_Shape_mpz_class_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_mpz_class_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_BD_Shape_mpz_class_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_BD_Shape_mpz_class_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_BD_Shape_mpz_class_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_BD_Shape_mpz_class_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_BD_Shape_mpz_class_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_BD_Shape_mpz_class_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_BD_Shape_mpz_class_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_BD_Shape_mpz_class_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_BD_Shape_mpz_class_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_BD_Shape_mpz_class_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_BD_Shape_mpz_class_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_Octagonal_Shape_int8_t Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of octagonal shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of octagonal shapes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_Octagonal_Shape_int8_t_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_Octagonal_Shape_int8_t_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_Octagonal_Shape_int8_t_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_Octagonal_Shape_int8_t_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of octagonal shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_Octagonal_Shape_int8_t_from_Pointset_Powerset_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_int8_t_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_int8_t_from_Pointset_Powerset_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_int8_t_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_Octagonal_Shape_int8_t domain.

ppl_delete_Pointset_Powerset_Octagonal_Shape_int8_t(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_contains_Pointset_Powerset_Octagonal_Shape_int8_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_strictly_contains_Pointset_Powerset_Octagonal_Shape_int8_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_is_disjoint_from_Pointset_Powerset_Octagonal_Shape_int8_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_geometrically_covers_Pointset_Powerset_Octagonal_Shape_int8_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_geometrically_equals_Pointset_Powerset_Octagonal_Shape_int8_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_equals_Pointset_Powerset_Octagonal_Shape_int8_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_BHZ03_H79_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_BGP99_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening and the cardinality threshold C_unsigned.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_Octagonal_Shape_int8_t_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_Octagonal_Shape_int8_t_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_int8_t_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_Octagonal_Shape_int16_t Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of octagonal shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of octagonal shapes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_Octagonal_Shape_int16_t_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_Octagonal_Shape_int16_t_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_Octagonal_Shape_int16_t_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_Octagonal_Shape_int16_t_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of octagonal shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_Octagonal_Shape_int16_t_from_Pointset_Powerset_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_int16_t_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_int16_t_from_Pointset_Powerset_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_int16_t_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_Octagonal_Shape_int16_t domain.

ppl_delete_Pointset_Powerset_Octagonal_Shape_int16_t(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_contains_Pointset_Powerset_Octagonal_Shape_int16_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_strictly_contains_Pointset_Powerset_Octagonal_Shape_int16_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_is_disjoint_from_Pointset_Powerset_Octagonal_Shape_int16_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_geometrically_covers_Pointset_Powerset_Octagonal_Shape_int16_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_geometrically_equals_Pointset_Powerset_Octagonal_Shape_int16_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_equals_Pointset_Powerset_Octagonal_Shape_int16_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_BHZ03_H79_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_BGP99_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening and the cardinality threshold C_unsigned.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_Octagonal_Shape_int16_t_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_Octagonal_Shape_int16_t_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_int16_t_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_Octagonal_Shape_int32_t Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of octagonal shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of octagonal shapes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_Octagonal_Shape_int32_t_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_Octagonal_Shape_int32_t_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_Octagonal_Shape_int32_t_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_Octagonal_Shape_int32_t_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of octagonal shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_Octagonal_Shape_int32_t_from_Pointset_Powerset_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_int32_t_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_int32_t_from_Pointset_Powerset_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_int32_t_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_Octagonal_Shape_int32_t domain.

ppl_delete_Pointset_Powerset_Octagonal_Shape_int32_t(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_contains_Pointset_Powerset_Octagonal_Shape_int32_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_strictly_contains_Pointset_Powerset_Octagonal_Shape_int32_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_is_disjoint_from_Pointset_Powerset_Octagonal_Shape_int32_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_geometrically_covers_Pointset_Powerset_Octagonal_Shape_int32_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_geometrically_equals_Pointset_Powerset_Octagonal_Shape_int32_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_equals_Pointset_Powerset_Octagonal_Shape_int32_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_BHZ03_H79_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_BGP99_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening and the cardinality threshold C_unsigned.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_Octagonal_Shape_int32_t_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_Octagonal_Shape_int32_t_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_int32_t_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_Octagonal_Shape_int64_t Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of octagonal shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of octagonal shapes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_Octagonal_Shape_int64_t_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_Octagonal_Shape_int64_t_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_Octagonal_Shape_int64_t_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_Octagonal_Shape_int64_t_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of octagonal shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_Octagonal_Shape_int64_t_from_Pointset_Powerset_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_int64_t_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_int64_t_from_Pointset_Powerset_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_int64_t_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_Octagonal_Shape_int64_t domain.

ppl_delete_Pointset_Powerset_Octagonal_Shape_int64_t(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_contains_Pointset_Powerset_Octagonal_Shape_int64_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_strictly_contains_Pointset_Powerset_Octagonal_Shape_int64_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_is_disjoint_from_Pointset_Powerset_Octagonal_Shape_int64_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_geometrically_covers_Pointset_Powerset_Octagonal_Shape_int64_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_geometrically_equals_Pointset_Powerset_Octagonal_Shape_int64_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_equals_Pointset_Powerset_Octagonal_Shape_int64_t(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_BHZ03_H79_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_BGP99_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening and the cardinality threshold C_unsigned.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_Octagonal_Shape_int64_t_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_Octagonal_Shape_int64_t_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_int64_t_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_Octagonal_Shape_mpq_class Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of octagonal shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of octagonal shapes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_Octagonal_Shape_mpq_class_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_Octagonal_Shape_mpq_class_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_Octagonal_Shape_mpq_class_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_Octagonal_Shape_mpq_class_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of octagonal shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_Octagonal_Shape_mpq_class_from_Pointset_Powerset_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_mpq_class_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_mpq_class_from_Pointset_Powerset_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_mpq_class_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_Octagonal_Shape_mpq_class domain.

ppl_delete_Pointset_Powerset_Octagonal_Shape_mpq_class(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_contains_Pointset_Powerset_Octagonal_Shape_mpq_class(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_strictly_contains_Pointset_Powerset_Octagonal_Shape_mpq_class(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_is_disjoint_from_Pointset_Powerset_Octagonal_Shape_mpq_class(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_geometrically_covers_Pointset_Powerset_Octagonal_Shape_mpq_class(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_geometrically_equals_Pointset_Powerset_Octagonal_Shape_mpq_class(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_equals_Pointset_Powerset_Octagonal_Shape_mpq_class(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_BHZ03_H79_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_BGP99_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening and the cardinality threshold C_unsigned.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_Octagonal_Shape_mpq_class_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_Octagonal_Shape_mpq_class_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_mpq_class_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_Octagonal_Shape_mpz_class Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of octagonal shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of octagonal shapes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_Octagonal_Shape_mpz_class_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_Octagonal_Shape_mpz_class_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_Octagonal_Shape_mpz_class_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_Octagonal_Shape_mpz_class_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of octagonal shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_Octagonal_Shape_mpz_class_from_Pointset_Powerset_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_mpz_class_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_mpz_class_from_Pointset_Powerset_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_mpz_class_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_Octagonal_Shape_mpz_class domain.

ppl_delete_Pointset_Powerset_Octagonal_Shape_mpz_class(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_contains_Pointset_Powerset_Octagonal_Shape_mpz_class(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_strictly_contains_Pointset_Powerset_Octagonal_Shape_mpz_class(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_is_disjoint_from_Pointset_Powerset_Octagonal_Shape_mpz_class(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_geometrically_covers_Pointset_Powerset_Octagonal_Shape_mpz_class(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_geometrically_equals_Pointset_Powerset_Octagonal_Shape_mpz_class(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_equals_Pointset_Powerset_Octagonal_Shape_mpz_class(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_BHZ03_H79_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_BGP99_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening and the cardinality threshold C_unsigned.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_Octagonal_Shape_mpz_class_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_Octagonal_Shape_mpz_class_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_mpz_class_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_C_Polyhedron Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of c polyhedra.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of c polyhedra

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_C_Polyhedron_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_C_Polyhedron_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_C_Polyhedron_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_C_Polyhedron_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of c polyhedra by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_C_Polyhedron_from_Pointset_Powerset_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_c_polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_C_Polyhedron_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_C_Polyhedron_from_Pointset_Powerset_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_c_polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_C_Polyhedron_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_C_Polyhedron domain.

ppl_delete_Pointset_Powerset_C_Polyhedron(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_C_Polyhedron_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_C_Polyhedron_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_C_Polyhedron_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_C_Polyhedron_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_C_Polyhedron_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_C_Polyhedron_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_C_Polyhedron_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_C_Polyhedron_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_C_Polyhedron_contains_Pointset_Powerset_C_Polyhedron(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_C_Polyhedron_strictly_contains_Pointset_Powerset_C_Polyhedron(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_C_Polyhedron_is_disjoint_from_Pointset_Powerset_C_Polyhedron(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_C_Polyhedron_geometrically_covers_Pointset_Powerset_C_Polyhedron(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_C_Polyhedron_geometrically_equals_Pointset_Powerset_C_Polyhedron(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_C_Polyhedron_equals_Pointset_Powerset_C_Polyhedron(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_C_Polyhedron_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_C_Polyhedron_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_C_Polyhedron_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_C_Polyhedron_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_C_Polyhedron_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_C_Polyhedron_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_C_Polyhedron_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_C_Polyhedron_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_C_Polyhedron_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_C_Polyhedron_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_C_Polyhedron_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_C_Polyhedron_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_C_Polyhedron_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_C_Polyhedron_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_C_Polyhedron_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_C_Polyhedron_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_C_Polyhedron_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_C_Polyhedron_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_C_Polyhedron_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_C_Polyhedron_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_C_Polyhedron_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_C_Polyhedron_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_C_Polyhedron_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_C_Polyhedron_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_C_Polyhedron_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_C_Polyhedron_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_C_Polyhedron_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_C_Polyhedron_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_C_Polyhedron_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_C_Polyhedron_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_C_Polyhedron_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_C_Polyhedron_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_C_Polyhedron_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_C_Polyhedron_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_C_Polyhedron_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_C_Polyhedron_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_C_Polyhedron_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_C_Polyhedron_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_C_Polyhedron_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_C_Polyhedron_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_C_Polyhedron_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_C_Polyhedron_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

ppl_Pointset_Powerset_C_Polyhedron_BHZ03_BHRZ03_BHRZ03_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the BHRZ03-widening certified by the convergence certificate for BHRZ03.

ppl_Pointset_Powerset_C_Polyhedron_BHZ03_H79_H79_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the H79-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_C_Polyhedron_BGP99_BHRZ03_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the BHRZ03-widening and the cardinality threshold C_unsigned.

ppl_Pointset_Powerset_C_Polyhedron_BGP99_H79_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the H79-widening and the cardinality threshold C_unsigned.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_C_Polyhedron_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_C_Polyhedron_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_C_Polyhedron_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_C_Polyhedron_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_C_Polyhedron_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_C_Polyhedron_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_C_Polyhedron_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_C_Polyhedron_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_C_Polyhedron_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_C_Polyhedron_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_C_Polyhedron_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_C_Polyhedron_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_C_Polyhedron_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_C_Polyhedron_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_C_Polyhedron_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_C_Polyhedron_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_C_Polyhedron_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_C_Polyhedron_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_C_Polyhedron_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_NNC_Polyhedron Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of nnc polyhedra.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of nnc polyhedra

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_NNC_Polyhedron_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_NNC_Polyhedron_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_NNC_Polyhedron_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_NNC_Polyhedron_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of nnc polyhedra by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_NNC_Polyhedron_from_Pointset_Powerset_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_nnc_polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_NNC_Polyhedron_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_NNC_Polyhedron_from_Pointset_Powerset_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_nnc_polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_NNC_Polyhedron_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_NNC_Polyhedron domain.

ppl_delete_Pointset_Powerset_NNC_Polyhedron(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_NNC_Polyhedron_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_NNC_Polyhedron_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_NNC_Polyhedron_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_NNC_Polyhedron_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_NNC_Polyhedron_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_NNC_Polyhedron_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_NNC_Polyhedron_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_NNC_Polyhedron_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_NNC_Polyhedron_contains_Pointset_Powerset_NNC_Polyhedron(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_NNC_Polyhedron_strictly_contains_Pointset_Powerset_NNC_Polyhedron(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_NNC_Polyhedron_is_disjoint_from_Pointset_Powerset_NNC_Polyhedron(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_NNC_Polyhedron_geometrically_covers_Pointset_Powerset_NNC_Polyhedron(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_NNC_Polyhedron_geometrically_equals_Pointset_Powerset_NNC_Polyhedron(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_NNC_Polyhedron_equals_Pointset_Powerset_NNC_Polyhedron(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_NNC_Polyhedron_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_NNC_Polyhedron_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_NNC_Polyhedron_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_NNC_Polyhedron_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_NNC_Polyhedron_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_NNC_Polyhedron_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_NNC_Polyhedron_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_NNC_Polyhedron_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_NNC_Polyhedron_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_NNC_Polyhedron_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_NNC_Polyhedron_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_NNC_Polyhedron_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_NNC_Polyhedron_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_NNC_Polyhedron_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_NNC_Polyhedron_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_NNC_Polyhedron_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_NNC_Polyhedron_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_NNC_Polyhedron_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_NNC_Polyhedron_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_NNC_Polyhedron_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_NNC_Polyhedron_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_NNC_Polyhedron_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_NNC_Polyhedron_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_NNC_Polyhedron_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_NNC_Polyhedron_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_NNC_Polyhedron_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_NNC_Polyhedron_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_NNC_Polyhedron_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_NNC_Polyhedron_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_NNC_Polyhedron_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_NNC_Polyhedron_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_NNC_Polyhedron_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_NNC_Polyhedron_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_NNC_Polyhedron_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_NNC_Polyhedron_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_NNC_Polyhedron_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_NNC_Polyhedron_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_NNC_Polyhedron_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_NNC_Polyhedron_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_NNC_Polyhedron_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_NNC_Polyhedron_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_NNC_Polyhedron_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

ppl_Pointset_Powerset_NNC_Polyhedron_BHZ03_BHRZ03_BHRZ03_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the BHRZ03-widening certified by the convergence certificate for BHRZ03.

ppl_Pointset_Powerset_NNC_Polyhedron_BHZ03_H79_H79_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the H79-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_NNC_Polyhedron_BGP99_BHRZ03_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the BHRZ03-widening and the cardinality threshold C_unsigned.

ppl_Pointset_Powerset_NNC_Polyhedron_BGP99_H79_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the H79-widening and the cardinality threshold C_unsigned.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_NNC_Polyhedron_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_NNC_Polyhedron_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_NNC_Polyhedron_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_NNC_Polyhedron_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_NNC_Polyhedron_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_NNC_Polyhedron_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_NNC_Polyhedron_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_NNC_Polyhedron_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_NNC_Polyhedron_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_NNC_Polyhedron_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_NNC_Polyhedron_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_NNC_Polyhedron_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_NNC_Polyhedron_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_NNC_Polyhedron_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_NNC_Polyhedron_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_NNC_Polyhedron_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_NNC_Polyhedron_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_NNC_Polyhedron_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_NNC_Polyhedron_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_Grid Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of grids.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of grids

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_Grid_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_Grid_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_Grid_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_Grid_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of grids by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_Grid_from_Pointset_Powerset_Grid(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Grid_from_Grid(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Grid_from_Pointset_Powerset_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Grid_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_Grid domain.

ppl_delete_Pointset_Powerset_Grid(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_Grid_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_Grid_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_Grid_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_Grid_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_Grid_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_Grid_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_Grid_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Grid_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Grid_contains_Pointset_Powerset_Grid(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Grid_strictly_contains_Pointset_Powerset_Grid(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Grid_is_disjoint_from_Pointset_Powerset_Grid(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Grid_geometrically_covers_Pointset_Powerset_Grid(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Grid_geometrically_equals_Pointset_Powerset_Grid(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Grid_equals_Pointset_Powerset_Grid(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Grid_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_Grid_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_Grid_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Grid_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Grid_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Grid_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Grid_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Grid_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Grid_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Grid_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Grid_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Grid_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Grid_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Grid_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_Grid_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_Grid_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_Grid_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_Grid_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_Grid_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_Grid_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_Grid_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_Grid_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_Grid_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_Grid_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_Grid_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_Grid_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_Grid_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_Grid_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Grid_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Grid_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Grid_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Grid_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Grid_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Grid_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Grid_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Grid_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_Grid_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Grid_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Grid_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Grid_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Grid_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_Grid_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

ppl_Pointset_Powerset_Grid_BHZ03_Grid_congruence_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the congruence-widening certified by the convergence certificate for Grid.

ppl_Pointset_Powerset_Grid_BHZ03_Grid_generator_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the generator-widening certified by the convergence certificate for Grid.

ppl_Pointset_Powerset_Grid_BGP99_congruence_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the congruence-widening and the cardinality threshold C_unsigned.

ppl_Pointset_Powerset_Grid_BGP99_generator_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the generator-widening and the cardinality threshold C_unsigned.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_Grid_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_Grid_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_Grid_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_Grid_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Grid_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_Grid_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_Grid_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_Grid_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_Grid_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_Grid_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Grid_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Grid_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_Grid_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_Grid_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_Grid_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_Grid_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_Grid_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_Grid_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_Grid_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Constraints_Product_C_Polyhedron_Grid Domain

Here we provide a short description for each of the predicates available for the domain of constraints products.

Constructor, copy, conversion and destructor predicates

Constructor predicates for constraints products

The constructor predicates build a constraints product from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new constraints product $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Constraints_Product_C_Polyhedron_Grid_from_space_dimension(3, universe, X).

creates the constraints product defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_constraints(+Constraint_System, -Handle)
Builds a new constraints product P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_congruences(+Congruence_System, -Handle)
Builds a new constraints product P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new constraints products by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Z_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Grid(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Float_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Double_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Constraints_Product_C_Polyhedron_Grid(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the constraints_product_c_polyhedron_grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_C_Polyhedron_Grid_from_Constraints_Product_C_Polyhedron_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the constraints_product_c_polyhedron_grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Constraints_Product_C_Polyhedron_Grid domain.

ppl_delete_Constraints_Product_C_Polyhedron_Grid(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the constraints product

Test Predicates

These predicates test the constraints product for different properties and succeed or fail depending on the outcome.

ppl_Constraints_Product_C_Polyhedron_Grid_is_empty(+Handle)
Succeeds if and only if the constraints product referenced by Handle is empty.

ppl_Constraints_Product_C_Polyhedron_Grid_is_universe(+Handle)
Succeeds if and only if the constraints product referenced by Handle is the universe.

ppl_Constraints_Product_C_Polyhedron_Grid_is_bounded(+Handle)
Succeeds if and only if the constraints product referenced by Handle is bounded.

ppl_Constraints_Product_C_Polyhedron_Grid_is_topologically_closed(+Handle)
Succeeds if and only if the constraints product referenced by Handle is topologically closed.

ppl_Constraints_Product_C_Polyhedron_Grid_is_discrete(+Handle)
Succeeds if and only if the constraints product referenced by Handle is discrete.

ppl_Constraints_Product_C_Polyhedron_Grid_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the constraints product referenced by Handle.

ppl_Constraints_Product_C_Polyhedron_Grid_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the constraints product referenced by Handle.

ppl_Constraints_Product_C_Polyhedron_Grid_contains_Constraints_Product_C_Polyhedron_Grid(+Handle_1, +Handle_2)
Succeeds if and only if the constraints product referenced by Handle_2 is included in or equal to the constraints product referenced by Handle_1.

ppl_Constraints_Product_C_Polyhedron_Grid_strictly_contains_Constraints_Product_C_Polyhedron_Grid(+Handle_1, +Handle_2)
Succeeds if and only if the constraints product referenced by Handle_2 is included in but not equal to the constraints product referenced by Handle_1.

ppl_Constraints_Product_C_Polyhedron_Grid_is_disjoint_from_Constraints_Product_C_Polyhedron_Grid(+Handle_1, +Handle_2)
Succeeds if and only if the constraints product referenced by Handle_2 is disjoint from the constraints product referenced by Handle_1.

ppl_Constraints_Product_C_Polyhedron_Grid_equals_Constraints_Product_C_Polyhedron_Grid(+Handle_1, +Handle_2)
Succeeds if and only if the constraints product referenced by Handle_1 is equal to the constraints product referenced by Handle_2.

ppl_Constraints_Product_C_Polyhedron_Grid_OK(+Handle)
Succeeds only if the constraints product referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Constraints_Product_C_Polyhedron_Grid_constrains(+Handle, +PPL_Var)
Succeeds if and only if the constraints product referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the constraints product

These predicates will obtain more detailed information about the constraints product unifying some of their arguments with the results.

ppl_Constraints_Product_C_Polyhedron_Grid_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the constraints product referenced by Handle.

ppl_Constraints_Product_C_Polyhedron_Grid_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the constraints product referenced by Handle.

ppl_Constraints_Product_C_Polyhedron_Grid_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the constraints product referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Constraints_Product_C_Polyhedron_Grid_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the constraints product referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Constraints_Product_C_Polyhedron_Grid_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the constraints product referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Constraints_Product_C_Polyhedron_Grid_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if constraints product P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Constraints_Product_C_Polyhedron_Grid_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if constraints product P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Constraints_Product_C_Polyhedron_Grid_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if constraints product P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Constraints_Product_C_Polyhedron_Grid_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if constraints product P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Constraints_Product_C_Polyhedron_Grid_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the constraints product referenced by Handle.

ppl_Constraints_Product_C_Polyhedron_Grid_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the constraints product referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Constraints_Product_C_Polyhedron_Grid_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the constraints product referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the constraints product

These predicates may modify the constraints product referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the constraints product by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Constraints_Product_C_Polyhedron_Grid_add_constraint(+Handle, +Constraint)
Updates the constraints product referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Constraints_Product_C_Polyhedron_Grid_add_congruence(+Handle, +Congruence)
Updates the constraints product referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Constraints_Product_C_Polyhedron_Grid_add_constraints( +Handle, +Constraint_System)
Updates the constraints product referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Constraints_Product_C_Polyhedron_Grid_add_congruences( +Handle, +Congruence_System)
Updates the constraints product referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Constraints_Product_C_Polyhedron_Grid_refine_with_constraint( +Handle, +Constraint)
Updates the constraints product referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Constraints_Product_C_Polyhedron_Grid_refine_with_congruence( +Handle, +Congruence)
Updates the constraints product referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Constraints_Product_C_Polyhedron_Grid_refine_with_constraints( +Handle, +Constraint_System)
Updates the constraints product referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Constraints_Product_C_Polyhedron_Grid_refine_with_congruences( +Handle, +Congruence_System)
Updates the constraints product referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the constraints product

These predicates enable transformations such as taking the topological closure (which for the domain of constraints product is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Constraints_Product_C_Polyhedron_Grid_topological_closure_assign(+Handle)
Assigns to the constraints product referenced by Handle its topological closure.

ppl_Constraints_Product_C_Polyhedron_Grid_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the constraints product P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Constraints_Product_C_Polyhedron_Grid_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the constraints product P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Constraints_Product_C_Polyhedron_Grid_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the constraints product referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Constraints_Product_C_Polyhedron_Grid_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the constraints product referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Constraints_Product_C_Polyhedron_Grid_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to constraints product P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Constraints_Product_C_Polyhedron_Grid_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to constraints product P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Constraints_Product_C_Polyhedron_Grid_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to constraints product P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Constraints_Product_C_Polyhedron_Grid_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to constraints product P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Constraints_Product_C_Polyhedron_Grid_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to constraints product P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Constraints_Product_C_Polyhedron_Grid_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to constraints product P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one constraints product

These predicates include the binary operators which will assign to the constraints product referred to by the first argument its combination with the constraints product referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Constraints_Product_C_Polyhedron_Grid_intersection_assign(+Handle_1, +Handle_2)
Assigns to the constraints product P referenced by Handle_1 the intersection of P and the constraints product referenced by Handle_2.

ppl_Constraints_Product_C_Polyhedron_Grid_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the constraints product P referenced by Handle_1 the upper bound of P and the constraints product referenced by Handle_2.

ppl_Constraints_Product_C_Polyhedron_Grid_difference_assign(+Handle_1, +Handle_2)
Assigns to the constraints product P referenced by Handle_1 the difference of P and the constraints product referenced by Handle_2.

ppl_Constraints_Product_C_Polyhedron_Grid_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the constraints product P referenced by Handle_1 the time elapse of P and the constraints product referenced by Handle_2.

ppl_Constraints_Product_C_Polyhedron_Grid_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the constraints product P_1 referenced by Handle_1 with the constraints product referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the constraints product referred to by the second argument has to be contained in (or equal to) the constraints product referred to by the first argument.

ppl_Constraints_Product_C_Polyhedron_Grid_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate

ppl_Constraints_Product_C_Polyhedron_Grid_widening_assign(+Handle_1, +Handle_2)
Same as predicate

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the constraints product referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Constraints_Product_C_Polyhedron_Grid_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the constraints product P referenced by Handle_1 the concatenation of P and the constraints product referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the constraints product referred to in the first argument. These predicates enable the modification of the vector space of the constraints product referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Constraints_Product_C_Polyhedron_Grid_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the constraints product P referenced by Handle and and_embeds P in this space.

ppl_Constraints_Product_C_Polyhedron_Grid_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the constraints product P referenced by Handle and and_projects P in this space.

ppl_Constraints_Product_C_Polyhedron_Grid_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the constraints product P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Constraints_Product_C_Polyhedron_Grid_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the constraints product P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Constraints_Product_C_Polyhedron_Grid_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the constraints product referenced by Handle to Dimension_Type new space dimensions.

ppl_Constraints_Product_C_Polyhedron_Grid_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the constraints product referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Constraints_Product_C_Polyhedron_Grid_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Constraints_Product_NNC_Polyhedron_Grid Domain

Here we provide a short description for each of the predicates available for the domain of constraints products.

Constructor, copy, conversion and destructor predicates

Constructor predicates for constraints products

The constructor predicates build a constraints product from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new constraints product $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_space_dimension(3, universe, X).

creates the constraints product defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_constraints(+Constraint_System, -Handle)
Builds a new constraints product P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_congruences(+Congruence_System, -Handle)
Builds a new constraints product P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new constraints products by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Z_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Grid(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Float_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Double_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Constraints_Product_NNC_Polyhedron_Grid(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the constraints_product_nnc_polyhedron_grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_NNC_Polyhedron_Grid_from_Constraints_Product_NNC_Polyhedron_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the constraints_product_nnc_polyhedron_grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Constraints_Product_NNC_Polyhedron_Grid domain.

ppl_delete_Constraints_Product_NNC_Polyhedron_Grid(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the constraints product

Test Predicates

These predicates test the constraints product for different properties and succeed or fail depending on the outcome.

ppl_Constraints_Product_NNC_Polyhedron_Grid_is_empty(+Handle)
Succeeds if and only if the constraints product referenced by Handle is empty.

ppl_Constraints_Product_NNC_Polyhedron_Grid_is_universe(+Handle)
Succeeds if and only if the constraints product referenced by Handle is the universe.

ppl_Constraints_Product_NNC_Polyhedron_Grid_is_bounded(+Handle)
Succeeds if and only if the constraints product referenced by Handle is bounded.

ppl_Constraints_Product_NNC_Polyhedron_Grid_is_topologically_closed(+Handle)
Succeeds if and only if the constraints product referenced by Handle is topologically closed.

ppl_Constraints_Product_NNC_Polyhedron_Grid_is_discrete(+Handle)
Succeeds if and only if the constraints product referenced by Handle is discrete.

ppl_Constraints_Product_NNC_Polyhedron_Grid_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the constraints product referenced by Handle.

ppl_Constraints_Product_NNC_Polyhedron_Grid_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the constraints product referenced by Handle.

ppl_Constraints_Product_NNC_Polyhedron_Grid_contains_Constraints_Product_NNC_Polyhedron_Grid(+Handle_1, +Handle_2)
Succeeds if and only if the constraints product referenced by Handle_2 is included in or equal to the constraints product referenced by Handle_1.

ppl_Constraints_Product_NNC_Polyhedron_Grid_strictly_contains_Constraints_Product_NNC_Polyhedron_Grid(+Handle_1, +Handle_2)
Succeeds if and only if the constraints product referenced by Handle_2 is included in but not equal to the constraints product referenced by Handle_1.

ppl_Constraints_Product_NNC_Polyhedron_Grid_is_disjoint_from_Constraints_Product_NNC_Polyhedron_Grid(+Handle_1, +Handle_2)
Succeeds if and only if the constraints product referenced by Handle_2 is disjoint from the constraints product referenced by Handle_1.

ppl_Constraints_Product_NNC_Polyhedron_Grid_equals_Constraints_Product_NNC_Polyhedron_Grid(+Handle_1, +Handle_2)
Succeeds if and only if the constraints product referenced by Handle_1 is equal to the constraints product referenced by Handle_2.

ppl_Constraints_Product_NNC_Polyhedron_Grid_OK(+Handle)
Succeeds only if the constraints product referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Constraints_Product_NNC_Polyhedron_Grid_constrains(+Handle, +PPL_Var)
Succeeds if and only if the constraints product referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the constraints product

These predicates will obtain more detailed information about the constraints product unifying some of their arguments with the results.

ppl_Constraints_Product_NNC_Polyhedron_Grid_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the constraints product referenced by Handle.

ppl_Constraints_Product_NNC_Polyhedron_Grid_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the constraints product referenced by Handle.

ppl_Constraints_Product_NNC_Polyhedron_Grid_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the constraints product referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Constraints_Product_NNC_Polyhedron_Grid_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the constraints product referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Constraints_Product_NNC_Polyhedron_Grid_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the constraints product referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Constraints_Product_NNC_Polyhedron_Grid_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if constraints product P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Constraints_Product_NNC_Polyhedron_Grid_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if constraints product P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Constraints_Product_NNC_Polyhedron_Grid_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if constraints product P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Constraints_Product_NNC_Polyhedron_Grid_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if constraints product P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Constraints_Product_NNC_Polyhedron_Grid_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the constraints product referenced by Handle.

ppl_Constraints_Product_NNC_Polyhedron_Grid_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the constraints product referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Constraints_Product_NNC_Polyhedron_Grid_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the constraints product referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the constraints product

These predicates may modify the constraints product referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the constraints product by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Constraints_Product_NNC_Polyhedron_Grid_add_constraint(+Handle, +Constraint)
Updates the constraints product referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Constraints_Product_NNC_Polyhedron_Grid_add_congruence(+Handle, +Congruence)
Updates the constraints product referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Constraints_Product_NNC_Polyhedron_Grid_add_constraints( +Handle, +Constraint_System)
Updates the constraints product referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Constraints_Product_NNC_Polyhedron_Grid_add_congruences( +Handle, +Congruence_System)
Updates the constraints product referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Constraints_Product_NNC_Polyhedron_Grid_refine_with_constraint( +Handle, +Constraint)
Updates the constraints product referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Constraints_Product_NNC_Polyhedron_Grid_refine_with_congruence( +Handle, +Congruence)
Updates the constraints product referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Constraints_Product_NNC_Polyhedron_Grid_refine_with_constraints( +Handle, +Constraint_System)
Updates the constraints product referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Constraints_Product_NNC_Polyhedron_Grid_refine_with_congruences( +Handle, +Congruence_System)
Updates the constraints product referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the constraints product

These predicates enable transformations such as taking the topological closure (which for the domain of constraints product is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Constraints_Product_NNC_Polyhedron_Grid_topological_closure_assign(+Handle)
Assigns to the constraints product referenced by Handle its topological closure.

ppl_Constraints_Product_NNC_Polyhedron_Grid_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the constraints product P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Constraints_Product_NNC_Polyhedron_Grid_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the constraints product P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Constraints_Product_NNC_Polyhedron_Grid_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the constraints product referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Constraints_Product_NNC_Polyhedron_Grid_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the constraints product referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Constraints_Product_NNC_Polyhedron_Grid_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to constraints product P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Constraints_Product_NNC_Polyhedron_Grid_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to constraints product P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Constraints_Product_NNC_Polyhedron_Grid_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to constraints product P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Constraints_Product_NNC_Polyhedron_Grid_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to constraints product P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Constraints_Product_NNC_Polyhedron_Grid_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to constraints product P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Constraints_Product_NNC_Polyhedron_Grid_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to constraints product P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one constraints product

These predicates include the binary operators which will assign to the constraints product referred to by the first argument its combination with the constraints product referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Constraints_Product_NNC_Polyhedron_Grid_intersection_assign(+Handle_1, +Handle_2)
Assigns to the constraints product P referenced by Handle_1 the intersection of P and the constraints product referenced by Handle_2.

ppl_Constraints_Product_NNC_Polyhedron_Grid_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the constraints product P referenced by Handle_1 the upper bound of P and the constraints product referenced by Handle_2.

ppl_Constraints_Product_NNC_Polyhedron_Grid_difference_assign(+Handle_1, +Handle_2)
Assigns to the constraints product P referenced by Handle_1 the difference of P and the constraints product referenced by Handle_2.

ppl_Constraints_Product_NNC_Polyhedron_Grid_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the constraints product P referenced by Handle_1 the time elapse of P and the constraints product referenced by Handle_2.

ppl_Constraints_Product_NNC_Polyhedron_Grid_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the constraints product P_1 referenced by Handle_1 with the constraints product referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the constraints product referred to by the second argument has to be contained in (or equal to) the constraints product referred to by the first argument.

ppl_Constraints_Product_NNC_Polyhedron_Grid_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate

ppl_Constraints_Product_NNC_Polyhedron_Grid_widening_assign(+Handle_1, +Handle_2)
Same as predicate

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the constraints product referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Constraints_Product_NNC_Polyhedron_Grid_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the constraints product P referenced by Handle_1 the concatenation of P and the constraints product referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the constraints product referred to in the first argument. These predicates enable the modification of the vector space of the constraints product referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Constraints_Product_NNC_Polyhedron_Grid_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the constraints product P referenced by Handle and and_embeds P in this space.

ppl_Constraints_Product_NNC_Polyhedron_Grid_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the constraints product P referenced by Handle and and_projects P in this space.

ppl_Constraints_Product_NNC_Polyhedron_Grid_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the constraints product P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Constraints_Product_NNC_Polyhedron_Grid_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the constraints product P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Constraints_Product_NNC_Polyhedron_Grid_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the constraints product referenced by Handle to Dimension_Type new space dimensions.

ppl_Constraints_Product_NNC_Polyhedron_Grid_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the constraints product referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Constraints_Product_NNC_Polyhedron_Grid_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Constraints_Product_Grid_C_Polyhedron Domain

Here we provide a short description for each of the predicates available for the domain of constraints products.

Constructor, copy, conversion and destructor predicates

Constructor predicates for constraints products

The constructor predicates build a constraints product from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new constraints product $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Constraints_Product_Grid_C_Polyhedron_from_space_dimension(3, universe, X).

creates the constraints product defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_constraints(+Constraint_System, -Handle)
Builds a new constraints product P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_congruences(+Congruence_System, -Handle)
Builds a new constraints product P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new constraints products by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Z_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Grid(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Float_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Double_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Constraints_Product_Grid_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the constraints_product_grid_c_polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_C_Polyhedron_from_Constraints_Product_Grid_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the constraints_product_grid_c_polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Constraints_Product_Grid_C_Polyhedron domain.

ppl_delete_Constraints_Product_Grid_C_Polyhedron(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the constraints product

Test Predicates

These predicates test the constraints product for different properties and succeed or fail depending on the outcome.

ppl_Constraints_Product_Grid_C_Polyhedron_is_empty(+Handle)
Succeeds if and only if the constraints product referenced by Handle is empty.

ppl_Constraints_Product_Grid_C_Polyhedron_is_universe(+Handle)
Succeeds if and only if the constraints product referenced by Handle is the universe.

ppl_Constraints_Product_Grid_C_Polyhedron_is_bounded(+Handle)
Succeeds if and only if the constraints product referenced by Handle is bounded.

ppl_Constraints_Product_Grid_C_Polyhedron_is_topologically_closed(+Handle)
Succeeds if and only if the constraints product referenced by Handle is topologically closed.

ppl_Constraints_Product_Grid_C_Polyhedron_is_discrete(+Handle)
Succeeds if and only if the constraints product referenced by Handle is discrete.

ppl_Constraints_Product_Grid_C_Polyhedron_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the constraints product referenced by Handle.

ppl_Constraints_Product_Grid_C_Polyhedron_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the constraints product referenced by Handle.

ppl_Constraints_Product_Grid_C_Polyhedron_contains_Constraints_Product_Grid_C_Polyhedron(+Handle_1, +Handle_2)
Succeeds if and only if the constraints product referenced by Handle_2 is included in or equal to the constraints product referenced by Handle_1.

ppl_Constraints_Product_Grid_C_Polyhedron_strictly_contains_Constraints_Product_Grid_C_Polyhedron(+Handle_1, +Handle_2)
Succeeds if and only if the constraints product referenced by Handle_2 is included in but not equal to the constraints product referenced by Handle_1.

ppl_Constraints_Product_Grid_C_Polyhedron_is_disjoint_from_Constraints_Product_Grid_C_Polyhedron(+Handle_1, +Handle_2)
Succeeds if and only if the constraints product referenced by Handle_2 is disjoint from the constraints product referenced by Handle_1.

ppl_Constraints_Product_Grid_C_Polyhedron_equals_Constraints_Product_Grid_C_Polyhedron(+Handle_1, +Handle_2)
Succeeds if and only if the constraints product referenced by Handle_1 is equal to the constraints product referenced by Handle_2.

ppl_Constraints_Product_Grid_C_Polyhedron_OK(+Handle)
Succeeds only if the constraints product referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Constraints_Product_Grid_C_Polyhedron_constrains(+Handle, +PPL_Var)
Succeeds if and only if the constraints product referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the constraints product

These predicates will obtain more detailed information about the constraints product unifying some of their arguments with the results.

ppl_Constraints_Product_Grid_C_Polyhedron_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the constraints product referenced by Handle.

ppl_Constraints_Product_Grid_C_Polyhedron_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the constraints product referenced by Handle.

ppl_Constraints_Product_Grid_C_Polyhedron_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the constraints product referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Constraints_Product_Grid_C_Polyhedron_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the constraints product referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Constraints_Product_Grid_C_Polyhedron_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the constraints product referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Constraints_Product_Grid_C_Polyhedron_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if constraints product P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Constraints_Product_Grid_C_Polyhedron_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if constraints product P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Constraints_Product_Grid_C_Polyhedron_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if constraints product P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Constraints_Product_Grid_C_Polyhedron_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if constraints product P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Constraints_Product_Grid_C_Polyhedron_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the constraints product referenced by Handle.

ppl_Constraints_Product_Grid_C_Polyhedron_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the constraints product referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Constraints_Product_Grid_C_Polyhedron_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the constraints product referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the constraints product

These predicates may modify the constraints product referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the constraints product by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Constraints_Product_Grid_C_Polyhedron_add_constraint(+Handle, +Constraint)
Updates the constraints product referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Constraints_Product_Grid_C_Polyhedron_add_congruence(+Handle, +Congruence)
Updates the constraints product referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Constraints_Product_Grid_C_Polyhedron_add_constraints( +Handle, +Constraint_System)
Updates the constraints product referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Constraints_Product_Grid_C_Polyhedron_add_congruences( +Handle, +Congruence_System)
Updates the constraints product referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Constraints_Product_Grid_C_Polyhedron_refine_with_constraint( +Handle, +Constraint)
Updates the constraints product referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Constraints_Product_Grid_C_Polyhedron_refine_with_congruence( +Handle, +Congruence)
Updates the constraints product referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Constraints_Product_Grid_C_Polyhedron_refine_with_constraints( +Handle, +Constraint_System)
Updates the constraints product referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Constraints_Product_Grid_C_Polyhedron_refine_with_congruences( +Handle, +Congruence_System)
Updates the constraints product referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the constraints product

These predicates enable transformations such as taking the topological closure (which for the domain of constraints product is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Constraints_Product_Grid_C_Polyhedron_topological_closure_assign(+Handle)
Assigns to the constraints product referenced by Handle its topological closure.

ppl_Constraints_Product_Grid_C_Polyhedron_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the constraints product P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Constraints_Product_Grid_C_Polyhedron_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the constraints product P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Constraints_Product_Grid_C_Polyhedron_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the constraints product referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Constraints_Product_Grid_C_Polyhedron_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the constraints product referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Constraints_Product_Grid_C_Polyhedron_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to constraints product P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Constraints_Product_Grid_C_Polyhedron_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to constraints product P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Constraints_Product_Grid_C_Polyhedron_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to constraints product P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Constraints_Product_Grid_C_Polyhedron_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to constraints product P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Constraints_Product_Grid_C_Polyhedron_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to constraints product P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Constraints_Product_Grid_C_Polyhedron_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to constraints product P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one constraints product

These predicates include the binary operators which will assign to the constraints product referred to by the first argument its combination with the constraints product referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Constraints_Product_Grid_C_Polyhedron_intersection_assign(+Handle_1, +Handle_2)
Assigns to the constraints product P referenced by Handle_1 the intersection of P and the constraints product referenced by Handle_2.

ppl_Constraints_Product_Grid_C_Polyhedron_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the constraints product P referenced by Handle_1 the upper bound of P and the constraints product referenced by Handle_2.

ppl_Constraints_Product_Grid_C_Polyhedron_difference_assign(+Handle_1, +Handle_2)
Assigns to the constraints product P referenced by Handle_1 the difference of P and the constraints product referenced by Handle_2.

ppl_Constraints_Product_Grid_C_Polyhedron_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the constraints product P referenced by Handle_1 the time elapse of P and the constraints product referenced by Handle_2.

ppl_Constraints_Product_Grid_C_Polyhedron_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the constraints product P_1 referenced by Handle_1 with the constraints product referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the constraints product referred to by the second argument has to be contained in (or equal to) the constraints product referred to by the first argument.

ppl_Constraints_Product_Grid_C_Polyhedron_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate

ppl_Constraints_Product_Grid_C_Polyhedron_widening_assign(+Handle_1, +Handle_2)
Same as predicate

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the constraints product referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Constraints_Product_Grid_C_Polyhedron_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the constraints product P referenced by Handle_1 the concatenation of P and the constraints product referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the constraints product referred to in the first argument. These predicates enable the modification of the vector space of the constraints product referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Constraints_Product_Grid_C_Polyhedron_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the constraints product P referenced by Handle and and_embeds P in this space.

ppl_Constraints_Product_Grid_C_Polyhedron_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the constraints product P referenced by Handle and and_projects P in this space.

ppl_Constraints_Product_Grid_C_Polyhedron_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the constraints product P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Constraints_Product_Grid_C_Polyhedron_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the constraints product P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Constraints_Product_Grid_C_Polyhedron_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the constraints product referenced by Handle to Dimension_Type new space dimensions.

ppl_Constraints_Product_Grid_C_Polyhedron_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the constraints product referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Constraints_Product_Grid_C_Polyhedron_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Constraints_Product_Grid_NNC_Polyhedron Domain

Here we provide a short description for each of the predicates available for the domain of constraints products.

Constructor, copy, conversion and destructor predicates

Constructor predicates for constraints products

The constructor predicates build a constraints product from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new constraints product $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_space_dimension(3, universe, X).

creates the constraints product defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_constraints(+Constraint_System, -Handle)
Builds a new constraints product P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_congruences(+Congruence_System, -Handle)
Builds a new constraints product P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new constraints products by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Z_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Grid(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Float_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Double_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Constraints_Product_Grid_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new constraints product P_1 from the constraints_product_grid_nnc_polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Constraints_Product_Grid_NNC_Polyhedron_from_Constraints_Product_Grid_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new constraints product P_1 from the constraints_product_grid_nnc_polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Constraints_Product_Grid_NNC_Polyhedron domain.

ppl_delete_Constraints_Product_Grid_NNC_Polyhedron(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the constraints product

Test Predicates

These predicates test the constraints product for different properties and succeed or fail depending on the outcome.

ppl_Constraints_Product_Grid_NNC_Polyhedron_is_empty(+Handle)
Succeeds if and only if the constraints product referenced by Handle is empty.

ppl_Constraints_Product_Grid_NNC_Polyhedron_is_universe(+Handle)
Succeeds if and only if the constraints product referenced by Handle is the universe.

ppl_Constraints_Product_Grid_NNC_Polyhedron_is_bounded(+Handle)
Succeeds if and only if the constraints product referenced by Handle is bounded.

ppl_Constraints_Product_Grid_NNC_Polyhedron_is_topologically_closed(+Handle)
Succeeds if and only if the constraints product referenced by Handle is topologically closed.

ppl_Constraints_Product_Grid_NNC_Polyhedron_is_discrete(+Handle)
Succeeds if and only if the constraints product referenced by Handle is discrete.

ppl_Constraints_Product_Grid_NNC_Polyhedron_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the constraints product referenced by Handle.

ppl_Constraints_Product_Grid_NNC_Polyhedron_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the constraints product referenced by Handle.

ppl_Constraints_Product_Grid_NNC_Polyhedron_contains_Constraints_Product_Grid_NNC_Polyhedron(+Handle_1, +Handle_2)
Succeeds if and only if the constraints product referenced by Handle_2 is included in or equal to the constraints product referenced by Handle_1.

ppl_Constraints_Product_Grid_NNC_Polyhedron_strictly_contains_Constraints_Product_Grid_NNC_Polyhedron(+Handle_1, +Handle_2)
Succeeds if and only if the constraints product referenced by Handle_2 is included in but not equal to the constraints product referenced by Handle_1.

ppl_Constraints_Product_Grid_NNC_Polyhedron_is_disjoint_from_Constraints_Product_Grid_NNC_Polyhedron(+Handle_1, +Handle_2)
Succeeds if and only if the constraints product referenced by Handle_2 is disjoint from the constraints product referenced by Handle_1.

ppl_Constraints_Product_Grid_NNC_Polyhedron_equals_Constraints_Product_Grid_NNC_Polyhedron(+Handle_1, +Handle_2)
Succeeds if and only if the constraints product referenced by Handle_1 is equal to the constraints product referenced by Handle_2.

ppl_Constraints_Product_Grid_NNC_Polyhedron_OK(+Handle)
Succeeds only if the constraints product referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Constraints_Product_Grid_NNC_Polyhedron_constrains(+Handle, +PPL_Var)
Succeeds if and only if the constraints product referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the constraints product

These predicates will obtain more detailed information about the constraints product unifying some of their arguments with the results.

ppl_Constraints_Product_Grid_NNC_Polyhedron_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the constraints product referenced by Handle.

ppl_Constraints_Product_Grid_NNC_Polyhedron_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the constraints product referenced by Handle.

ppl_Constraints_Product_Grid_NNC_Polyhedron_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the constraints product referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Constraints_Product_Grid_NNC_Polyhedron_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the constraints product referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Constraints_Product_Grid_NNC_Polyhedron_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the constraints product referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Constraints_Product_Grid_NNC_Polyhedron_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if constraints product P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Constraints_Product_Grid_NNC_Polyhedron_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if constraints product P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Constraints_Product_Grid_NNC_Polyhedron_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if constraints product P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Constraints_Product_Grid_NNC_Polyhedron_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if constraints product P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Constraints_Product_Grid_NNC_Polyhedron_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the constraints product referenced by Handle.

ppl_Constraints_Product_Grid_NNC_Polyhedron_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the constraints product referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Constraints_Product_Grid_NNC_Polyhedron_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the constraints product referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the constraints product

These predicates may modify the constraints product referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the constraints product by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Constraints_Product_Grid_NNC_Polyhedron_add_constraint(+Handle, +Constraint)
Updates the constraints product referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Constraints_Product_Grid_NNC_Polyhedron_add_congruence(+Handle, +Congruence)
Updates the constraints product referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Constraints_Product_Grid_NNC_Polyhedron_add_constraints( +Handle, +Constraint_System)
Updates the constraints product referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Constraints_Product_Grid_NNC_Polyhedron_add_congruences( +Handle, +Congruence_System)
Updates the constraints product referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Constraints_Product_Grid_NNC_Polyhedron_refine_with_constraint( +Handle, +Constraint)
Updates the constraints product referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Constraints_Product_Grid_NNC_Polyhedron_refine_with_congruence( +Handle, +Congruence)
Updates the constraints product referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Constraints_Product_Grid_NNC_Polyhedron_refine_with_constraints( +Handle, +Constraint_System)
Updates the constraints product referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Constraints_Product_Grid_NNC_Polyhedron_refine_with_congruences( +Handle, +Congruence_System)
Updates the constraints product referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the constraints product

These predicates enable transformations such as taking the topological closure (which for the domain of constraints product is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Constraints_Product_Grid_NNC_Polyhedron_topological_closure_assign(+Handle)
Assigns to the constraints product referenced by Handle its topological closure.

ppl_Constraints_Product_Grid_NNC_Polyhedron_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the constraints product P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Constraints_Product_Grid_NNC_Polyhedron_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the constraints product P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Constraints_Product_Grid_NNC_Polyhedron_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the constraints product referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Constraints_Product_Grid_NNC_Polyhedron_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the constraints product referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Constraints_Product_Grid_NNC_Polyhedron_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to constraints product P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Constraints_Product_Grid_NNC_Polyhedron_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to constraints product P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Constraints_Product_Grid_NNC_Polyhedron_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to constraints product P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Constraints_Product_Grid_NNC_Polyhedron_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to constraints product P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Constraints_Product_Grid_NNC_Polyhedron_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to constraints product P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Constraints_Product_Grid_NNC_Polyhedron_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to constraints product P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one constraints product

These predicates include the binary operators which will assign to the constraints product referred to by the first argument its combination with the constraints product referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Constraints_Product_Grid_NNC_Polyhedron_intersection_assign(+Handle_1, +Handle_2)
Assigns to the constraints product P referenced by Handle_1 the intersection of P and the constraints product referenced by Handle_2.

ppl_Constraints_Product_Grid_NNC_Polyhedron_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the constraints product P referenced by Handle_1 the upper bound of P and the constraints product referenced by Handle_2.

ppl_Constraints_Product_Grid_NNC_Polyhedron_difference_assign(+Handle_1, +Handle_2)
Assigns to the constraints product P referenced by Handle_1 the difference of P and the constraints product referenced by Handle_2.

ppl_Constraints_Product_Grid_NNC_Polyhedron_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the constraints product P referenced by Handle_1 the time elapse of P and the constraints product referenced by Handle_2.

ppl_Constraints_Product_Grid_NNC_Polyhedron_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the constraints product P_1 referenced by Handle_1 with the constraints product referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the constraints product referred to by the second argument has to be contained in (or equal to) the constraints product referred to by the first argument.

ppl_Constraints_Product_Grid_NNC_Polyhedron_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate

ppl_Constraints_Product_Grid_NNC_Polyhedron_widening_assign(+Handle_1, +Handle_2)
Same as predicate

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the constraints product referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Constraints_Product_Grid_NNC_Polyhedron_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the constraints product P referenced by Handle_1 the concatenation of P and the constraints product referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the constraints product referred to in the first argument. These predicates enable the modification of the vector space of the constraints product referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Constraints_Product_Grid_NNC_Polyhedron_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the constraints product P referenced by Handle and and_embeds P in this space.

ppl_Constraints_Product_Grid_NNC_Polyhedron_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the constraints product P referenced by Handle and and_projects P in this space.

ppl_Constraints_Product_Grid_NNC_Polyhedron_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the constraints product P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Constraints_Product_Grid_NNC_Polyhedron_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the constraints product P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Constraints_Product_Grid_NNC_Polyhedron_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the constraints product referenced by Handle to Dimension_Type new space dimensions.

ppl_Constraints_Product_Grid_NNC_Polyhedron_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the constraints product referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Constraints_Product_Grid_NNC_Polyhedron_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Float_Box Domain

Here we provide a short description for each of the predicates available for the domain of float boxes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for float boxes

The constructor predicates build a float box from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Float_Box_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new float box $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Float_Box_from_space_dimension(3, universe, X).

creates the float box defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Float_Box_from_constraints(+Constraint_System, -Handle)
Builds a new float box P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Float_Box_from_congruences(+Congruence_System, -Handle)
Builds a new float box P from Congruence_System. Handle is unified with the handle for P.

ppl_new_Float_Box_from_generators(+Generator_System, -Handle)
Builds a new float box P from Generator_System. Handle is unified with the handle for P.

Predicates that build new float boxes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Float_Box_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new float box P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new float box P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new float box P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new float box P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new float box P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new float box P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new float box P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new float box P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Z_Box(+Handle_1, -Handle_2)
Builds a new float box P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new float box P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new float box P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new float box P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new float box P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new float box P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new float box P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new float box P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new float box P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new float box P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new float box P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new float box P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new float box P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new float box P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new float box P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new float box P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Grid(+Handle_1, -Handle_2)
Builds a new float box P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Float_Box(+Handle_1, -Handle_2)
Builds a new float box P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new float box P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new float box P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Double_Box(+Handle_1, -Handle_2)
Builds a new float box P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new float box P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new float box P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new float box P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new float box P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new float box P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Float_Box_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new float box P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Float_Box domain.

ppl_delete_Float_Box(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the float box

Test Predicates

These predicates test the float box for different properties and succeed or fail depending on the outcome.

ppl_Float_Box_is_empty(+Handle)
Succeeds if and only if the float box referenced by Handle is empty.

ppl_Float_Box_is_universe(+Handle)
Succeeds if and only if the float box referenced by Handle is the universe.

ppl_Float_Box_is_bounded(+Handle)
Succeeds if and only if the float box referenced by Handle is bounded.

ppl_Float_Box_contains_integer_point(+Handle)
Succeeds if and only if the float box referenced by Handle contains an integer point.

ppl_Float_Box_is_topologically_closed(+Handle)
Succeeds if and only if the float box referenced by Handle is topologically closed.

ppl_Float_Box_is_discrete(+Handle)
Succeeds if and only if the float box referenced by Handle is discrete.

ppl_Float_Box_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the float box referenced by Handle.

ppl_Float_Box_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the float box referenced by Handle.

ppl_Float_Box_contains_Float_Box(+Handle_1, +Handle_2)
Succeeds if and only if the float box referenced by Handle_2 is included in or equal to the float box referenced by Handle_1.

ppl_Float_Box_strictly_contains_Float_Box(+Handle_1, +Handle_2)
Succeeds if and only if the float box referenced by Handle_2 is included in but not equal to the float box referenced by Handle_1.

ppl_Float_Box_is_disjoint_from_Float_Box(+Handle_1, +Handle_2)
Succeeds if and only if the float box referenced by Handle_2 is disjoint from the float box referenced by Handle_1.

ppl_Float_Box_equals_Float_Box(+Handle_1, +Handle_2)
Succeeds if and only if the float box referenced by Handle_1 is equal to the float box referenced by Handle_2.

ppl_Float_Box_OK(+Handle)
Succeeds only if the float box referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Float_Box_constrains(+Handle, +PPL_Var)
Succeeds if and only if the float box referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the float box

These predicates will obtain more detailed information about the float box unifying some of their arguments with the results.

ppl_Float_Box_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the float box referenced by Handle.

ppl_Float_Box_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the float box referenced by Handle.

ppl_Float_Box_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the float box referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Float_Box_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the float box referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Float_Box_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the float box referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Float_Box_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the float box referenced by Handle.

ppl_Float_Box_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the float box referenced by Handle.

ppl_Float_Box_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the float box referenced by Handle.

ppl_Float_Box_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the float box referenced by Handle.

ppl_Float_Box_has_upper_bound(+Handle, +Var, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if Var is upper bounded in float box P referenced by Handle. It is assumed that P is not empty and its space dimension is greater than or equal to that of Var, otherwise the behavior is undefined.

Coeff_1 is unified with the numerator of the upper bound and Coeff_2 with the denominator of the upper bound. If the upper is included in P, then Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Float_Box_has_lower_bound(+Handle, +Var, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if Var is lower bounded in float box P referenced by Handle. It is assumed that P is not empty and its space dimension is greater than or equal to that of Var, otherwise the behavior is undefined.

Coeff_1 is unified with the numerator of the lower bound and Coeff_2 with the denominator of the lower bound. If the lower is included in P, then Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Float_Box_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if float box P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Float_Box_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if float box P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Float_Box_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if float box P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Float_Box_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if float box P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Float_Box_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the float box referenced by Handle.

ppl_Float_Box_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the float box referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Float_Box_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the float box referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the float box

These predicates may modify the float box referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the float box by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Float_Box_add_constraint(+Handle, +Constraint)
Updates the float box referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Float_Box_add_congruence(+Handle, +Congruence)
Updates the float box referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Float_Box_add_constraints( +Handle, +Constraint_System)
Updates the float box referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Float_Box_add_congruences( +Handle, +Congruence_System)
Updates the float box referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Float_Box_refine_with_constraint( +Handle, +Constraint)
Updates the float box referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Float_Box_refine_with_congruence( +Handle, +Congruence)
Updates the float box referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Float_Box_refine_with_constraints( +Handle, +Constraint_System)
Updates the float box referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Float_Box_refine_with_congruences( +Handle, +Congruence_System)
Updates the float box referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the float box

These predicates enable transformations such as taking the topological closure (which for the domain of float box is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Float_Box_topological_closure_assign(+Handle)
Assigns to the float box referenced by Handle its topological closure.

ppl_Float_Box_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the float box P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Float_Box_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the float box P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Float_Box_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the float box referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Float_Box_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the float box referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Float_Box_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to float box P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Float_Box_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to float box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Float_Box_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to float box P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Float_Box_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to float box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Float_Box_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to float box P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Float_Box_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to float box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Float_Box_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the float box P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one float box

These predicates include the binary operators which will assign to the float box referred to by the first argument its combination with the float box referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Float_Box_intersection_assign(+Handle_1, +Handle_2)
Assigns to the float box P referenced by Handle_1 the intersection of P and the float box referenced by Handle_2.

ppl_Float_Box_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the float box P referenced by Handle_1 the upper bound of P and the float box referenced by Handle_2.

ppl_Float_Box_difference_assign(+Handle_1, +Handle_2)
Assigns to the float box P referenced by Handle_1 the difference of P and the float box referenced by Handle_2.

ppl_Float_Box_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the float box P referenced by Handle_1 the time elapse of P and the float box referenced by Handle_2.

ppl_Float_Box_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the float box P_1 referenced by Handle_1 with the float box referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Float_Box_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of float box P_1 referenced by Handle_1 and the float box P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_Float_Box_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the Float_Box domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the float box referred to by the second argument has to be contained in (or equal to) the float box referred to by the first argument.

ppl_Float_Box_CC76_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the float box P_1 referenced by Handle_1 the CC76-widening of P_1 with the float box referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Float_Box_CC76_widening_assign(+Handle_1, +Handle_2)
Assigns to the float box P_1 referenced by Handle_1 the CC76-widening of P_1 with the float box referenced by Handle_2.

ppl_Float_Box_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_Float_Box_CC76_widening_assign_with_tokens/4

ppl_Float_Box_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_Float_Box_CC76_widening_assign/2

ppl_Float_Box_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the float box P_1 referenced by Handle_1 the CC76-widening of P_1 with the float box referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Float_Box_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the float box P_1 referenced by Handle_1 the CC76-widening of P_1 with the float box referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Float_Box_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the float box P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the float box referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the float box referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Float_Box_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the float box P referenced by Handle_1 the concatenation of P and the float box referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the float box referred to in the first argument. These predicates enable the modification of the vector space of the float box referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Float_Box_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the float box P referenced by Handle and and_embeds P in this space.

ppl_Float_Box_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the float box P referenced by Handle and and_projects P in this space.

ppl_Float_Box_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the float box P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Float_Box_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the float box P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Float_Box_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the float box referenced by Handle to Dimension_Type new space dimensions.

ppl_Float_Box_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the float box referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Float_Box_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the BD_Shape_float Domain

Here we provide a short description for each of the predicates available for the domain of bd shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for bd shapes

The constructor predicates build a bd shape from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_BD_Shape_float_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new bd shape $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_BD_Shape_float_from_space_dimension(3, universe, X).

creates the bd shape defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_BD_Shape_float_from_constraints(+Constraint_System, -Handle)
Builds a new bd shape P from Constraint_System. Handle is unified with the handle for P.

ppl_new_BD_Shape_float_from_congruences(+Congruence_System, -Handle)
Builds a new bd shape P from Congruence_System. Handle is unified with the handle for P.

ppl_new_BD_Shape_float_from_generators(+Generator_System, -Handle)
Builds a new bd shape P from Generator_System. Handle is unified with the handle for P.

Predicates that build new bd shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_BD_Shape_float_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Z_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Grid(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Float_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Double_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_float_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the BD_Shape_float domain.

ppl_delete_BD_Shape_float(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the bd shape

Test Predicates

These predicates test the bd shape for different properties and succeed or fail depending on the outcome.

ppl_BD_Shape_float_is_empty(+Handle)
Succeeds if and only if the bd shape referenced by Handle is empty.

ppl_BD_Shape_float_is_universe(+Handle)
Succeeds if and only if the bd shape referenced by Handle is the universe.

ppl_BD_Shape_float_is_bounded(+Handle)
Succeeds if and only if the bd shape referenced by Handle is bounded.

ppl_BD_Shape_float_contains_integer_point(+Handle)
Succeeds if and only if the bd shape referenced by Handle contains an integer point.

ppl_BD_Shape_float_is_topologically_closed(+Handle)
Succeeds if and only if the bd shape referenced by Handle is topologically closed.

ppl_BD_Shape_float_is_discrete(+Handle)
Succeeds if and only if the bd shape referenced by Handle is discrete.

ppl_BD_Shape_float_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the bd shape referenced by Handle.

ppl_BD_Shape_float_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the bd shape referenced by Handle.

ppl_BD_Shape_float_contains_BD_Shape_float(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is included in or equal to the bd shape referenced by Handle_1.

ppl_BD_Shape_float_strictly_contains_BD_Shape_float(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is included in but not equal to the bd shape referenced by Handle_1.

ppl_BD_Shape_float_is_disjoint_from_BD_Shape_float(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is disjoint from the bd shape referenced by Handle_1.

ppl_BD_Shape_float_equals_BD_Shape_float(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_1 is equal to the bd shape referenced by Handle_2.

ppl_BD_Shape_float_OK(+Handle)
Succeeds only if the bd shape referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_BD_Shape_float_constrains(+Handle, +PPL_Var)
Succeeds if and only if the bd shape referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the bd shape

These predicates will obtain more detailed information about the bd shape unifying some of their arguments with the results.

ppl_BD_Shape_float_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the bd shape referenced by Handle.

ppl_BD_Shape_float_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the bd shape referenced by Handle.

ppl_BD_Shape_float_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_float_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_float_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_float_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_float_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_float_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_float_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_float_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_float_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_float_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_float_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_float_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the bd shape referenced by Handle.

ppl_BD_Shape_float_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the bd shape referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_BD_Shape_float_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the bd shape referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the bd shape

These predicates may modify the bd shape referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the bd shape by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_BD_Shape_float_add_constraint(+Handle, +Constraint)
Updates the bd shape referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_BD_Shape_float_add_congruence(+Handle, +Congruence)
Updates the bd shape referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_BD_Shape_float_add_constraints( +Handle, +Constraint_System)
Updates the bd shape referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_BD_Shape_float_add_congruences( +Handle, +Congruence_System)
Updates the bd shape referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_BD_Shape_float_refine_with_constraint( +Handle, +Constraint)
Updates the bd shape referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_BD_Shape_float_refine_with_congruence( +Handle, +Congruence)
Updates the bd shape referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_BD_Shape_float_refine_with_constraints( +Handle, +Constraint_System)
Updates the bd shape referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_BD_Shape_float_refine_with_congruences( +Handle, +Congruence_System)
Updates the bd shape referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the bd shape

These predicates enable transformations such as taking the topological closure (which for the domain of bd shape is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_BD_Shape_float_topological_closure_assign(+Handle)
Assigns to the bd shape referenced by Handle its topological closure.

ppl_BD_Shape_float_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the bd shape P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_BD_Shape_float_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the bd shape P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_BD_Shape_float_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the bd shape referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_BD_Shape_float_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the bd shape referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_BD_Shape_float_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_BD_Shape_float_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_BD_Shape_float_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_float_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_float_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_float_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_float_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the bd shape P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one bd shape

These predicates include the binary operators which will assign to the bd shape referred to by the first argument its combination with the bd shape referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_BD_Shape_float_intersection_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the intersection of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_float_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the upper bound of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_float_difference_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the difference of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_float_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the time elapse of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_float_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the bd shape P_1 referenced by Handle_1 with the bd shape referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_BD_Shape_float_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of bd shape P_1 referenced by Handle_1 and the bd shape P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_BD_Shape_float_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the BD_Shape_float domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the bd shape referred to by the second argument has to be contained in (or equal to) the bd shape referred to by the first argument.

ppl_BD_Shape_float_BHMZ05_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_float_H79_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_float_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2.

ppl_BD_Shape_float_H79_widening_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2.

ppl_BD_Shape_float_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_BD_Shape_float_H79_widening_assign_with_tokens/4

ppl_BD_Shape_float_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_BD_Shape_float_H79_widening_assign/2

ppl_BD_Shape_float_limited_BHMZ05_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_float_limited_H79_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_float_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_float_limited_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_float_limited_H79_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_float_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_float_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the bd shape referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the bd shape referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_BD_Shape_float_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the concatenation of P and the bd shape referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the bd shape referred to in the first argument. These predicates enable the modification of the vector space of the bd shape referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_BD_Shape_float_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the bd shape P referenced by Handle and and_embeds P in this space.

ppl_BD_Shape_float_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the bd shape P referenced by Handle and and_projects P in this space.

ppl_BD_Shape_float_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the bd shape P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_BD_Shape_float_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the bd shape P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_BD_Shape_float_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the bd shape referenced by Handle to Dimension_Type new space dimensions.

ppl_BD_Shape_float_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the bd shape referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_BD_Shape_float_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Octagonal_Shape_float Domain

Here we provide a short description for each of the predicates available for the domain of octagonal shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for octagonal shapes

The constructor predicates build a octagonal shape from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Octagonal_Shape_float_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new octagonal shape $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Octagonal_Shape_float_from_space_dimension(3, universe, X).

creates the octagonal shape defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Octagonal_Shape_float_from_constraints(+Constraint_System, -Handle)
Builds a new octagonal shape P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Octagonal_Shape_float_from_congruences(+Congruence_System, -Handle)
Builds a new octagonal shape P from Congruence_System. Handle is unified with the handle for P.

ppl_new_Octagonal_Shape_float_from_generators(+Generator_System, -Handle)
Builds a new octagonal shape P from Generator_System. Handle is unified with the handle for P.

Predicates that build new octagonal shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Octagonal_Shape_float_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Z_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Grid(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Float_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Double_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_float_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Octagonal_Shape_float domain.

ppl_delete_Octagonal_Shape_float(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the octagonal shape

Test Predicates

These predicates test the octagonal shape for different properties and succeed or fail depending on the outcome.

ppl_Octagonal_Shape_float_is_empty(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is empty.

ppl_Octagonal_Shape_float_is_universe(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is the universe.

ppl_Octagonal_Shape_float_is_bounded(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is bounded.

ppl_Octagonal_Shape_float_contains_integer_point(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle contains an integer point.

ppl_Octagonal_Shape_float_is_topologically_closed(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is topologically closed.

ppl_Octagonal_Shape_float_is_discrete(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is discrete.

ppl_Octagonal_Shape_float_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_float_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_float_contains_Octagonal_Shape_float(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is included in or equal to the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_float_strictly_contains_Octagonal_Shape_float(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is included in but not equal to the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_float_is_disjoint_from_Octagonal_Shape_float(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is disjoint from the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_float_equals_Octagonal_Shape_float(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_1 is equal to the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_float_OK(+Handle)
Succeeds only if the octagonal shape referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Octagonal_Shape_float_constrains(+Handle, +PPL_Var)
Succeeds if and only if the octagonal shape referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the octagonal shape

These predicates will obtain more detailed information about the octagonal shape unifying some of their arguments with the results.

ppl_Octagonal_Shape_float_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_float_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_float_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_float_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_float_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_float_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_float_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_float_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_float_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_float_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_float_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_float_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_float_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_float_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_float_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the octagonal shape referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Octagonal_Shape_float_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the octagonal shape referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the octagonal shape

These predicates may modify the octagonal shape referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the octagonal shape by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Octagonal_Shape_float_add_constraint(+Handle, +Constraint)
Updates the octagonal shape referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Octagonal_Shape_float_add_congruence(+Handle, +Congruence)
Updates the octagonal shape referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Octagonal_Shape_float_add_constraints( +Handle, +Constraint_System)
Updates the octagonal shape referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Octagonal_Shape_float_add_congruences( +Handle, +Congruence_System)
Updates the octagonal shape referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Octagonal_Shape_float_refine_with_constraint( +Handle, +Constraint)
Updates the octagonal shape referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Octagonal_Shape_float_refine_with_congruence( +Handle, +Congruence)
Updates the octagonal shape referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Octagonal_Shape_float_refine_with_constraints( +Handle, +Constraint_System)
Updates the octagonal shape referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Octagonal_Shape_float_refine_with_congruences( +Handle, +Congruence_System)
Updates the octagonal shape referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the octagonal shape

These predicates enable transformations such as taking the topological closure (which for the domain of octagonal shape is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Octagonal_Shape_float_topological_closure_assign(+Handle)
Assigns to the octagonal shape referenced by Handle its topological closure.

ppl_Octagonal_Shape_float_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the octagonal shape P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Octagonal_Shape_float_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the octagonal shape P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Octagonal_Shape_float_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the octagonal shape referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Octagonal_Shape_float_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the octagonal shape referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Octagonal_Shape_float_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Octagonal_Shape_float_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Octagonal_Shape_float_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_float_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_float_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_float_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_float_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the octagonal shape P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one octagonal shape

These predicates include the binary operators which will assign to the octagonal shape referred to by the first argument its combination with the octagonal shape referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Octagonal_Shape_float_intersection_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the intersection of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_float_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the upper bound of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_float_difference_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the difference of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_float_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the time elapse of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_float_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the octagonal shape P_1 referenced by Handle_1 with the octagonal shape referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Octagonal_Shape_float_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of octagonal shape P_1 referenced by Handle_1 and the octagonal shape P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_Octagonal_Shape_float_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the Octagonal_Shape_float domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the octagonal shape referred to by the second argument has to be contained in (or equal to) the octagonal shape referred to by the first argument.

ppl_Octagonal_Shape_float_BHMZ05_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_float_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_float_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_Octagonal_Shape_float_H79_widening_assign_with_tokens/4

ppl_Octagonal_Shape_float_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_Octagonal_Shape_float_H79_widening_assign/2

ppl_Octagonal_Shape_float_limited_BHMZ05_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_float_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_float_limited_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Octagonal_Shape_float_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Octagonal_Shape_float_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the octagonal shape referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Octagonal_Shape_float_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the concatenation of P and the octagonal shape referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument. These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Octagonal_Shape_float_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the octagonal shape P referenced by Handle and and_embeds P in this space.

ppl_Octagonal_Shape_float_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the octagonal shape P referenced by Handle and and_projects P in this space.

ppl_Octagonal_Shape_float_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the octagonal shape P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Octagonal_Shape_float_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the octagonal shape P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Octagonal_Shape_float_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the octagonal shape referenced by Handle to Dimension_Type new space dimensions.

ppl_Octagonal_Shape_float_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the octagonal shape referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Octagonal_Shape_float_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Pointset_Powerset_Float_Box Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of float boxes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of float boxes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_Float_Box_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_Float_Box_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_Float_Box_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_Float_Box_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of float boxes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_Float_Box_from_Pointset_Powerset_Float_Box(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Float_Box_from_Float_Box(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Float_Box_from_Pointset_Powerset_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Float_Box_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_Float_Box domain.

ppl_delete_Pointset_Powerset_Float_Box(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_Float_Box_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_Float_Box_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_Float_Box_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_Float_Box_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_Float_Box_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_Float_Box_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_Float_Box_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Float_Box_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Float_Box_contains_Pointset_Powerset_Float_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Float_Box_strictly_contains_Pointset_Powerset_Float_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Float_Box_is_disjoint_from_Pointset_Powerset_Float_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Float_Box_geometrically_covers_Pointset_Powerset_Float_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Float_Box_geometrically_equals_Pointset_Powerset_Float_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Float_Box_equals_Pointset_Powerset_Float_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Float_Box_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_Float_Box_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_Float_Box_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Float_Box_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Float_Box_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Float_Box_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Float_Box_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Float_Box_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Float_Box_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Float_Box_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Float_Box_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Float_Box_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Float_Box_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Float_Box_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_Float_Box_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_Float_Box_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_Float_Box_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_Float_Box_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_Float_Box_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_Float_Box_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_Float_Box_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_Float_Box_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_Float_Box_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_Float_Box_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_Float_Box_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_Float_Box_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_Float_Box_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_Float_Box_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Float_Box_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Float_Box_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Float_Box_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Float_Box_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Float_Box_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Float_Box_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Float_Box_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Float_Box_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_Float_Box_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Float_Box_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Float_Box_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Float_Box_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Float_Box_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_Float_Box_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_Float_Box_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_Float_Box_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_Float_Box_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_Float_Box_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Float_Box_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_Float_Box_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_Float_Box_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_Float_Box_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_Float_Box_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_Float_Box_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Float_Box_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Float_Box_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_Float_Box_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_Float_Box_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_Float_Box_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_Float_Box_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_Float_Box_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_Float_Box_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_Float_Box_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_BD_Shape_float Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of bd shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of bd shapes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_BD_Shape_float_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_BD_Shape_float_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_BD_Shape_float_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_BD_Shape_float_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of bd shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_BD_Shape_float_from_Pointset_Powerset_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_float_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_float_from_Pointset_Powerset_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_float_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_BD_Shape_float domain.

ppl_delete_Pointset_Powerset_BD_Shape_float(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_BD_Shape_float_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_BD_Shape_float_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_BD_Shape_float_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_BD_Shape_float_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_BD_Shape_float_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_BD_Shape_float_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_BD_Shape_float_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_float_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_float_contains_Pointset_Powerset_BD_Shape_float(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_float_strictly_contains_Pointset_Powerset_BD_Shape_float(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_float_is_disjoint_from_Pointset_Powerset_BD_Shape_float(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_float_geometrically_covers_Pointset_Powerset_BD_Shape_float(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_float_geometrically_equals_Pointset_Powerset_BD_Shape_float(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_float_equals_Pointset_Powerset_BD_Shape_float(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_float_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_BD_Shape_float_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_BD_Shape_float_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_float_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_float_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_float_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_float_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_float_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_float_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_float_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_float_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_float_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_float_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_float_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_BD_Shape_float_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_BD_Shape_float_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_BD_Shape_float_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_BD_Shape_float_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_BD_Shape_float_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_BD_Shape_float_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_BD_Shape_float_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_BD_Shape_float_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_BD_Shape_float_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_BD_Shape_float_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_BD_Shape_float_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_BD_Shape_float_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_BD_Shape_float_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_BD_Shape_float_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_float_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_BD_Shape_float_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_BD_Shape_float_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_BD_Shape_float_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_BD_Shape_float_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_float_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_float_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_float_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_BD_Shape_float_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_float_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_float_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_float_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_float_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_BD_Shape_float_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

ppl_Pointset_Powerset_BD_Shape_float_BHZ03_H79_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_BD_Shape_float_BHZ03_H79_H79_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the H79-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_BD_Shape_float_BGP99_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening and the cardinality threshold C_unsigned.

ppl_Pointset_Powerset_BD_Shape_float_BGP99_H79_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the H79-widening and the cardinality threshold C_unsigned.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_BD_Shape_float_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_BD_Shape_float_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_BD_Shape_float_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_BD_Shape_float_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_float_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_BD_Shape_float_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_BD_Shape_float_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_float_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_BD_Shape_float_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_BD_Shape_float_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_BD_Shape_float_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_BD_Shape_float_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_BD_Shape_float_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_BD_Shape_float_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_BD_Shape_float_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_BD_Shape_float_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_BD_Shape_float_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_BD_Shape_float_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_BD_Shape_float_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_Octagonal_Shape_float Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of octagonal shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of octagonal shapes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_Octagonal_Shape_float_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_Octagonal_Shape_float_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_Octagonal_Shape_float_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_Octagonal_Shape_float_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of octagonal shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_Octagonal_Shape_float_from_Pointset_Powerset_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_float_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_float_from_Pointset_Powerset_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_float_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_Octagonal_Shape_float domain.

ppl_delete_Pointset_Powerset_Octagonal_Shape_float(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_Octagonal_Shape_float_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_Octagonal_Shape_float_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_Octagonal_Shape_float_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_Octagonal_Shape_float_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_Octagonal_Shape_float_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_Octagonal_Shape_float_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_Octagonal_Shape_float_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_float_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_float_contains_Pointset_Powerset_Octagonal_Shape_float(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_float_strictly_contains_Pointset_Powerset_Octagonal_Shape_float(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_float_is_disjoint_from_Pointset_Powerset_Octagonal_Shape_float(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_float_geometrically_covers_Pointset_Powerset_Octagonal_Shape_float(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_float_geometrically_equals_Pointset_Powerset_Octagonal_Shape_float(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_float_equals_Pointset_Powerset_Octagonal_Shape_float(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_float_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_Octagonal_Shape_float_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_Octagonal_Shape_float_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_float_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_float_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_float_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_float_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_float_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_float_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_float_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_float_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_float_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_float_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_float_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_Octagonal_Shape_float_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_Octagonal_Shape_float_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_Octagonal_Shape_float_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_Octagonal_Shape_float_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_Octagonal_Shape_float_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_Octagonal_Shape_float_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_Octagonal_Shape_float_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_Octagonal_Shape_float_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_Octagonal_Shape_float_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_Octagonal_Shape_float_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_Octagonal_Shape_float_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_Octagonal_Shape_float_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_Octagonal_Shape_float_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_float_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_float_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_float_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_float_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Octagonal_Shape_float_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Octagonal_Shape_float_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_float_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_float_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_float_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_Octagonal_Shape_float_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_float_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_float_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_float_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_float_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_Octagonal_Shape_float_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

ppl_Pointset_Powerset_Octagonal_Shape_float_BHZ03_H79_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_Octagonal_Shape_float_BGP99_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening and the cardinality threshold C_unsigned.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_Octagonal_Shape_float_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_Octagonal_Shape_float_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_Octagonal_Shape_float_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_Octagonal_Shape_float_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_float_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_Octagonal_Shape_float_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_Octagonal_Shape_float_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_float_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_Octagonal_Shape_float_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_Octagonal_Shape_float_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_float_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_float_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_Octagonal_Shape_float_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_float_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_float_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_Octagonal_Shape_float_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_Octagonal_Shape_float_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_float_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_float_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Double_Box Domain

Here we provide a short description for each of the predicates available for the domain of double boxes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for double boxes

The constructor predicates build a double box from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Double_Box_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new double box $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Double_Box_from_space_dimension(3, universe, X).

creates the double box defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Double_Box_from_constraints(+Constraint_System, -Handle)
Builds a new double box P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Double_Box_from_congruences(+Congruence_System, -Handle)
Builds a new double box P from Congruence_System. Handle is unified with the handle for P.

ppl_new_Double_Box_from_generators(+Generator_System, -Handle)
Builds a new double box P from Generator_System. Handle is unified with the handle for P.

Predicates that build new double boxes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Double_Box_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new double box P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new double box P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new double box P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new double box P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new double box P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new double box P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new double box P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new double box P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Z_Box(+Handle_1, -Handle_2)
Builds a new double box P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new double box P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new double box P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new double box P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new double box P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new double box P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new double box P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new double box P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new double box P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new double box P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new double box P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new double box P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new double box P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new double box P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new double box P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new double box P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Grid(+Handle_1, -Handle_2)
Builds a new double box P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Float_Box(+Handle_1, -Handle_2)
Builds a new double box P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new double box P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new double box P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Double_Box(+Handle_1, -Handle_2)
Builds a new double box P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new double box P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new double box P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new double box P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new double box P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new double box P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Double_Box_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new double box P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Double_Box domain.

ppl_delete_Double_Box(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the double box

Test Predicates

These predicates test the double box for different properties and succeed or fail depending on the outcome.

ppl_Double_Box_is_empty(+Handle)
Succeeds if and only if the double box referenced by Handle is empty.

ppl_Double_Box_is_universe(+Handle)
Succeeds if and only if the double box referenced by Handle is the universe.

ppl_Double_Box_is_bounded(+Handle)
Succeeds if and only if the double box referenced by Handle is bounded.

ppl_Double_Box_contains_integer_point(+Handle)
Succeeds if and only if the double box referenced by Handle contains an integer point.

ppl_Double_Box_is_topologically_closed(+Handle)
Succeeds if and only if the double box referenced by Handle is topologically closed.

ppl_Double_Box_is_discrete(+Handle)
Succeeds if and only if the double box referenced by Handle is discrete.

ppl_Double_Box_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the double box referenced by Handle.

ppl_Double_Box_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the double box referenced by Handle.

ppl_Double_Box_contains_Double_Box(+Handle_1, +Handle_2)
Succeeds if and only if the double box referenced by Handle_2 is included in or equal to the double box referenced by Handle_1.

ppl_Double_Box_strictly_contains_Double_Box(+Handle_1, +Handle_2)
Succeeds if and only if the double box referenced by Handle_2 is included in but not equal to the double box referenced by Handle_1.

ppl_Double_Box_is_disjoint_from_Double_Box(+Handle_1, +Handle_2)
Succeeds if and only if the double box referenced by Handle_2 is disjoint from the double box referenced by Handle_1.

ppl_Double_Box_equals_Double_Box(+Handle_1, +Handle_2)
Succeeds if and only if the double box referenced by Handle_1 is equal to the double box referenced by Handle_2.

ppl_Double_Box_OK(+Handle)
Succeeds only if the double box referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Double_Box_constrains(+Handle, +PPL_Var)
Succeeds if and only if the double box referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the double box

These predicates will obtain more detailed information about the double box unifying some of their arguments with the results.

ppl_Double_Box_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the double box referenced by Handle.

ppl_Double_Box_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the double box referenced by Handle.

ppl_Double_Box_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the double box referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Double_Box_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the double box referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Double_Box_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the double box referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Double_Box_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the double box referenced by Handle.

ppl_Double_Box_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the double box referenced by Handle.

ppl_Double_Box_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the double box referenced by Handle.

ppl_Double_Box_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the double box referenced by Handle.

ppl_Double_Box_has_upper_bound(+Handle, +Var, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if Var is upper bounded in double box P referenced by Handle. It is assumed that P is not empty and its space dimension is greater than or equal to that of Var, otherwise the behavior is undefined.

Coeff_1 is unified with the numerator of the upper bound and Coeff_2 with the denominator of the upper bound. If the upper is included in P, then Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Double_Box_has_lower_bound(+Handle, +Var, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if Var is lower bounded in double box P referenced by Handle. It is assumed that P is not empty and its space dimension is greater than or equal to that of Var, otherwise the behavior is undefined.

Coeff_1 is unified with the numerator of the lower bound and Coeff_2 with the denominator of the lower bound. If the lower is included in P, then Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Double_Box_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if double box P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Double_Box_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if double box P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Double_Box_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if double box P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Double_Box_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if double box P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Double_Box_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the double box referenced by Handle.

ppl_Double_Box_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the double box referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Double_Box_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the double box referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the double box

These predicates may modify the double box referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the double box by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Double_Box_add_constraint(+Handle, +Constraint)
Updates the double box referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Double_Box_add_congruence(+Handle, +Congruence)
Updates the double box referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Double_Box_add_constraints( +Handle, +Constraint_System)
Updates the double box referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Double_Box_add_congruences( +Handle, +Congruence_System)
Updates the double box referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Double_Box_refine_with_constraint( +Handle, +Constraint)
Updates the double box referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Double_Box_refine_with_congruence( +Handle, +Congruence)
Updates the double box referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Double_Box_refine_with_constraints( +Handle, +Constraint_System)
Updates the double box referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Double_Box_refine_with_congruences( +Handle, +Congruence_System)
Updates the double box referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the double box

These predicates enable transformations such as taking the topological closure (which for the domain of double box is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Double_Box_topological_closure_assign(+Handle)
Assigns to the double box referenced by Handle its topological closure.

ppl_Double_Box_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the double box P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Double_Box_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the double box P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Double_Box_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the double box referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Double_Box_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the double box referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Double_Box_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to double box P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Double_Box_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to double box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Double_Box_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to double box P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Double_Box_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to double box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Double_Box_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to double box P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Double_Box_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to double box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Double_Box_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the double box P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one double box

These predicates include the binary operators which will assign to the double box referred to by the first argument its combination with the double box referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Double_Box_intersection_assign(+Handle_1, +Handle_2)
Assigns to the double box P referenced by Handle_1 the intersection of P and the double box referenced by Handle_2.

ppl_Double_Box_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the double box P referenced by Handle_1 the upper bound of P and the double box referenced by Handle_2.

ppl_Double_Box_difference_assign(+Handle_1, +Handle_2)
Assigns to the double box P referenced by Handle_1 the difference of P and the double box referenced by Handle_2.

ppl_Double_Box_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the double box P referenced by Handle_1 the time elapse of P and the double box referenced by Handle_2.

ppl_Double_Box_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the double box P_1 referenced by Handle_1 with the double box referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Double_Box_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of double box P_1 referenced by Handle_1 and the double box P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_Double_Box_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the Double_Box domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the double box referred to by the second argument has to be contained in (or equal to) the double box referred to by the first argument.

ppl_Double_Box_CC76_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the double box P_1 referenced by Handle_1 the CC76-widening of P_1 with the double box referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Double_Box_CC76_widening_assign(+Handle_1, +Handle_2)
Assigns to the double box P_1 referenced by Handle_1 the CC76-widening of P_1 with the double box referenced by Handle_2.

ppl_Double_Box_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_Double_Box_CC76_widening_assign_with_tokens/4

ppl_Double_Box_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_Double_Box_CC76_widening_assign/2

ppl_Double_Box_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the double box P_1 referenced by Handle_1 the CC76-widening of P_1 with the double box referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Double_Box_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the double box P_1 referenced by Handle_1 the CC76-widening of P_1 with the double box referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Double_Box_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the double box P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the double box referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the double box referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Double_Box_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the double box P referenced by Handle_1 the concatenation of P and the double box referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the double box referred to in the first argument. These predicates enable the modification of the vector space of the double box referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Double_Box_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the double box P referenced by Handle and and_embeds P in this space.

ppl_Double_Box_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the double box P referenced by Handle and and_projects P in this space.

ppl_Double_Box_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the double box P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Double_Box_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the double box P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Double_Box_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the double box referenced by Handle to Dimension_Type new space dimensions.

ppl_Double_Box_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the double box referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Double_Box_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the BD_Shape_double Domain

Here we provide a short description for each of the predicates available for the domain of bd shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for bd shapes

The constructor predicates build a bd shape from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_BD_Shape_double_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new bd shape $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_BD_Shape_double_from_space_dimension(3, universe, X).

creates the bd shape defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_BD_Shape_double_from_constraints(+Constraint_System, -Handle)
Builds a new bd shape P from Constraint_System. Handle is unified with the handle for P.

ppl_new_BD_Shape_double_from_congruences(+Congruence_System, -Handle)
Builds a new bd shape P from Congruence_System. Handle is unified with the handle for P.

ppl_new_BD_Shape_double_from_generators(+Generator_System, -Handle)
Builds a new bd shape P from Generator_System. Handle is unified with the handle for P.

Predicates that build new bd shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_BD_Shape_double_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Z_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Grid(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Float_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Double_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_double_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the BD_Shape_double domain.

ppl_delete_BD_Shape_double(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the bd shape

Test Predicates

These predicates test the bd shape for different properties and succeed or fail depending on the outcome.

ppl_BD_Shape_double_is_empty(+Handle)
Succeeds if and only if the bd shape referenced by Handle is empty.

ppl_BD_Shape_double_is_universe(+Handle)
Succeeds if and only if the bd shape referenced by Handle is the universe.

ppl_BD_Shape_double_is_bounded(+Handle)
Succeeds if and only if the bd shape referenced by Handle is bounded.

ppl_BD_Shape_double_contains_integer_point(+Handle)
Succeeds if and only if the bd shape referenced by Handle contains an integer point.

ppl_BD_Shape_double_is_topologically_closed(+Handle)
Succeeds if and only if the bd shape referenced by Handle is topologically closed.

ppl_BD_Shape_double_is_discrete(+Handle)
Succeeds if and only if the bd shape referenced by Handle is discrete.

ppl_BD_Shape_double_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the bd shape referenced by Handle.

ppl_BD_Shape_double_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the bd shape referenced by Handle.

ppl_BD_Shape_double_contains_BD_Shape_double(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is included in or equal to the bd shape referenced by Handle_1.

ppl_BD_Shape_double_strictly_contains_BD_Shape_double(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is included in but not equal to the bd shape referenced by Handle_1.

ppl_BD_Shape_double_is_disjoint_from_BD_Shape_double(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is disjoint from the bd shape referenced by Handle_1.

ppl_BD_Shape_double_equals_BD_Shape_double(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_1 is equal to the bd shape referenced by Handle_2.

ppl_BD_Shape_double_OK(+Handle)
Succeeds only if the bd shape referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_BD_Shape_double_constrains(+Handle, +PPL_Var)
Succeeds if and only if the bd shape referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the bd shape

These predicates will obtain more detailed information about the bd shape unifying some of their arguments with the results.

ppl_BD_Shape_double_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the bd shape referenced by Handle.

ppl_BD_Shape_double_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the bd shape referenced by Handle.

ppl_BD_Shape_double_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_double_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_double_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_double_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_double_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_double_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_double_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_double_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_double_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_double_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_double_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_double_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the bd shape referenced by Handle.

ppl_BD_Shape_double_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the bd shape referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_BD_Shape_double_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the bd shape referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the bd shape

These predicates may modify the bd shape referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the bd shape by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_BD_Shape_double_add_constraint(+Handle, +Constraint)
Updates the bd shape referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_BD_Shape_double_add_congruence(+Handle, +Congruence)
Updates the bd shape referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_BD_Shape_double_add_constraints( +Handle, +Constraint_System)
Updates the bd shape referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_BD_Shape_double_add_congruences( +Handle, +Congruence_System)
Updates the bd shape referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_BD_Shape_double_refine_with_constraint( +Handle, +Constraint)
Updates the bd shape referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_BD_Shape_double_refine_with_congruence( +Handle, +Congruence)
Updates the bd shape referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_BD_Shape_double_refine_with_constraints( +Handle, +Constraint_System)
Updates the bd shape referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_BD_Shape_double_refine_with_congruences( +Handle, +Congruence_System)
Updates the bd shape referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the bd shape

These predicates enable transformations such as taking the topological closure (which for the domain of bd shape is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_BD_Shape_double_topological_closure_assign(+Handle)
Assigns to the bd shape referenced by Handle its topological closure.

ppl_BD_Shape_double_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the bd shape P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_BD_Shape_double_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the bd shape P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_BD_Shape_double_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the bd shape referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_BD_Shape_double_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the bd shape referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_BD_Shape_double_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_BD_Shape_double_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_BD_Shape_double_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_double_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_double_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_double_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_double_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the bd shape P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one bd shape

These predicates include the binary operators which will assign to the bd shape referred to by the first argument its combination with the bd shape referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_BD_Shape_double_intersection_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the intersection of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_double_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the upper bound of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_double_difference_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the difference of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_double_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the time elapse of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_double_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the bd shape P_1 referenced by Handle_1 with the bd shape referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_BD_Shape_double_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of bd shape P_1 referenced by Handle_1 and the bd shape P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_BD_Shape_double_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the BD_Shape_double domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the bd shape referred to by the second argument has to be contained in (or equal to) the bd shape referred to by the first argument.

ppl_BD_Shape_double_BHMZ05_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_double_H79_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_double_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2.

ppl_BD_Shape_double_H79_widening_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2.

ppl_BD_Shape_double_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_BD_Shape_double_H79_widening_assign_with_tokens/4

ppl_BD_Shape_double_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_BD_Shape_double_H79_widening_assign/2

ppl_BD_Shape_double_limited_BHMZ05_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_double_limited_H79_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_double_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_double_limited_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_double_limited_H79_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_double_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_double_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the bd shape referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the bd shape referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_BD_Shape_double_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the concatenation of P and the bd shape referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the bd shape referred to in the first argument. These predicates enable the modification of the vector space of the bd shape referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_BD_Shape_double_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the bd shape P referenced by Handle and and_embeds P in this space.

ppl_BD_Shape_double_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the bd shape P referenced by Handle and and_projects P in this space.

ppl_BD_Shape_double_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the bd shape P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_BD_Shape_double_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the bd shape P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_BD_Shape_double_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the bd shape referenced by Handle to Dimension_Type new space dimensions.

ppl_BD_Shape_double_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the bd shape referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_BD_Shape_double_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Octagonal_Shape_double Domain

Here we provide a short description for each of the predicates available for the domain of octagonal shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for octagonal shapes

The constructor predicates build a octagonal shape from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Octagonal_Shape_double_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new octagonal shape $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Octagonal_Shape_double_from_space_dimension(3, universe, X).

creates the octagonal shape defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Octagonal_Shape_double_from_constraints(+Constraint_System, -Handle)
Builds a new octagonal shape P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Octagonal_Shape_double_from_congruences(+Congruence_System, -Handle)
Builds a new octagonal shape P from Congruence_System. Handle is unified with the handle for P.

ppl_new_Octagonal_Shape_double_from_generators(+Generator_System, -Handle)
Builds a new octagonal shape P from Generator_System. Handle is unified with the handle for P.

Predicates that build new octagonal shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Octagonal_Shape_double_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Z_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Grid(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Float_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Double_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_double_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Octagonal_Shape_double domain.

ppl_delete_Octagonal_Shape_double(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the octagonal shape

Test Predicates

These predicates test the octagonal shape for different properties and succeed or fail depending on the outcome.

ppl_Octagonal_Shape_double_is_empty(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is empty.

ppl_Octagonal_Shape_double_is_universe(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is the universe.

ppl_Octagonal_Shape_double_is_bounded(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is bounded.

ppl_Octagonal_Shape_double_contains_integer_point(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle contains an integer point.

ppl_Octagonal_Shape_double_is_topologically_closed(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is topologically closed.

ppl_Octagonal_Shape_double_is_discrete(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is discrete.

ppl_Octagonal_Shape_double_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_double_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_double_contains_Octagonal_Shape_double(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is included in or equal to the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_double_strictly_contains_Octagonal_Shape_double(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is included in but not equal to the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_double_is_disjoint_from_Octagonal_Shape_double(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is disjoint from the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_double_equals_Octagonal_Shape_double(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_1 is equal to the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_double_OK(+Handle)
Succeeds only if the octagonal shape referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Octagonal_Shape_double_constrains(+Handle, +PPL_Var)
Succeeds if and only if the octagonal shape referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the octagonal shape

These predicates will obtain more detailed information about the octagonal shape unifying some of their arguments with the results.

ppl_Octagonal_Shape_double_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_double_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_double_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_double_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_double_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_double_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_double_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_double_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_double_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_double_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_double_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_double_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_double_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_double_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_double_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the octagonal shape referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Octagonal_Shape_double_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the octagonal shape referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the octagonal shape

These predicates may modify the octagonal shape referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the octagonal shape by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Octagonal_Shape_double_add_constraint(+Handle, +Constraint)
Updates the octagonal shape referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Octagonal_Shape_double_add_congruence(+Handle, +Congruence)
Updates the octagonal shape referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Octagonal_Shape_double_add_constraints( +Handle, +Constraint_System)
Updates the octagonal shape referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Octagonal_Shape_double_add_congruences( +Handle, +Congruence_System)
Updates the octagonal shape referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Octagonal_Shape_double_refine_with_constraint( +Handle, +Constraint)
Updates the octagonal shape referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Octagonal_Shape_double_refine_with_congruence( +Handle, +Congruence)
Updates the octagonal shape referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Octagonal_Shape_double_refine_with_constraints( +Handle, +Constraint_System)
Updates the octagonal shape referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Octagonal_Shape_double_refine_with_congruences( +Handle, +Congruence_System)
Updates the octagonal shape referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the octagonal shape

These predicates enable transformations such as taking the topological closure (which for the domain of octagonal shape is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Octagonal_Shape_double_topological_closure_assign(+Handle)
Assigns to the octagonal shape referenced by Handle its topological closure.

ppl_Octagonal_Shape_double_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the octagonal shape P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Octagonal_Shape_double_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the octagonal shape P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Octagonal_Shape_double_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the octagonal shape referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Octagonal_Shape_double_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the octagonal shape referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Octagonal_Shape_double_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Octagonal_Shape_double_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Octagonal_Shape_double_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_double_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_double_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_double_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_double_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the octagonal shape P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one octagonal shape

These predicates include the binary operators which will assign to the octagonal shape referred to by the first argument its combination with the octagonal shape referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Octagonal_Shape_double_intersection_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the intersection of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_double_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the upper bound of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_double_difference_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the difference of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_double_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the time elapse of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_double_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the octagonal shape P_1 referenced by Handle_1 with the octagonal shape referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Octagonal_Shape_double_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of octagonal shape P_1 referenced by Handle_1 and the octagonal shape P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_Octagonal_Shape_double_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the Octagonal_Shape_double domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the octagonal shape referred to by the second argument has to be contained in (or equal to) the octagonal shape referred to by the first argument.

ppl_Octagonal_Shape_double_BHMZ05_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_double_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_double_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_Octagonal_Shape_double_H79_widening_assign_with_tokens/4

ppl_Octagonal_Shape_double_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_Octagonal_Shape_double_H79_widening_assign/2

ppl_Octagonal_Shape_double_limited_BHMZ05_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_double_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_double_limited_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Octagonal_Shape_double_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Octagonal_Shape_double_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the octagonal shape referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Octagonal_Shape_double_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the concatenation of P and the octagonal shape referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument. These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Octagonal_Shape_double_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the octagonal shape P referenced by Handle and and_embeds P in this space.

ppl_Octagonal_Shape_double_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the octagonal shape P referenced by Handle and and_projects P in this space.

ppl_Octagonal_Shape_double_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the octagonal shape P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Octagonal_Shape_double_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the octagonal shape P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Octagonal_Shape_double_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the octagonal shape referenced by Handle to Dimension_Type new space dimensions.

ppl_Octagonal_Shape_double_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the octagonal shape referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Octagonal_Shape_double_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Pointset_Powerset_Double_Box Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of double boxes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of double boxes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_Double_Box_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_Double_Box_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_Double_Box_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_Double_Box_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of double boxes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_Double_Box_from_Pointset_Powerset_Double_Box(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Double_Box_from_Double_Box(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Double_Box_from_Pointset_Powerset_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Double_Box_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_Double_Box domain.

ppl_delete_Pointset_Powerset_Double_Box(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_Double_Box_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_Double_Box_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_Double_Box_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_Double_Box_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_Double_Box_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_Double_Box_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_Double_Box_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Double_Box_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Double_Box_contains_Pointset_Powerset_Double_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Double_Box_strictly_contains_Pointset_Powerset_Double_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Double_Box_is_disjoint_from_Pointset_Powerset_Double_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Double_Box_geometrically_covers_Pointset_Powerset_Double_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Double_Box_geometrically_equals_Pointset_Powerset_Double_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Double_Box_equals_Pointset_Powerset_Double_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Double_Box_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_Double_Box_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_Double_Box_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Double_Box_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Double_Box_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Double_Box_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Double_Box_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Double_Box_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Double_Box_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Double_Box_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Double_Box_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Double_Box_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Double_Box_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Double_Box_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_Double_Box_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_Double_Box_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_Double_Box_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_Double_Box_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_Double_Box_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_Double_Box_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_Double_Box_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_Double_Box_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_Double_Box_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_Double_Box_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_Double_Box_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_Double_Box_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_Double_Box_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_Double_Box_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Double_Box_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Double_Box_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Double_Box_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Double_Box_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Double_Box_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Double_Box_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Double_Box_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Double_Box_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_Double_Box_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Double_Box_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Double_Box_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Double_Box_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Double_Box_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_Double_Box_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_Double_Box_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_Double_Box_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_Double_Box_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_Double_Box_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Double_Box_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_Double_Box_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_Double_Box_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_Double_Box_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_Double_Box_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_Double_Box_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Double_Box_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Double_Box_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_Double_Box_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_Double_Box_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_Double_Box_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_Double_Box_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_Double_Box_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_Double_Box_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_Double_Box_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_BD_Shape_double Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of bd shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of bd shapes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_BD_Shape_double_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_BD_Shape_double_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_BD_Shape_double_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_BD_Shape_double_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of bd shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_BD_Shape_double_from_Pointset_Powerset_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_double_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_double_from_Pointset_Powerset_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_double_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_BD_Shape_double domain.

ppl_delete_Pointset_Powerset_BD_Shape_double(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_BD_Shape_double_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_BD_Shape_double_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_BD_Shape_double_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_BD_Shape_double_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_BD_Shape_double_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_BD_Shape_double_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_BD_Shape_double_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_double_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_double_contains_Pointset_Powerset_BD_Shape_double(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_double_strictly_contains_Pointset_Powerset_BD_Shape_double(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_double_is_disjoint_from_Pointset_Powerset_BD_Shape_double(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_double_geometrically_covers_Pointset_Powerset_BD_Shape_double(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_double_geometrically_equals_Pointset_Powerset_BD_Shape_double(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_double_equals_Pointset_Powerset_BD_Shape_double(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_double_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_BD_Shape_double_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_BD_Shape_double_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_double_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_double_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_double_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_double_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_double_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_double_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_double_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_double_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_double_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_double_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_double_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_BD_Shape_double_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_BD_Shape_double_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_BD_Shape_double_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_BD_Shape_double_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_BD_Shape_double_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_BD_Shape_double_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_BD_Shape_double_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_BD_Shape_double_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_BD_Shape_double_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_BD_Shape_double_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_BD_Shape_double_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_BD_Shape_double_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_BD_Shape_double_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_BD_Shape_double_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_double_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_BD_Shape_double_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_BD_Shape_double_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_BD_Shape_double_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_BD_Shape_double_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_double_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_double_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_double_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_BD_Shape_double_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_double_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_double_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_double_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_double_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_BD_Shape_double_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

ppl_Pointset_Powerset_BD_Shape_double_BHZ03_H79_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_BD_Shape_double_BHZ03_H79_H79_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the H79-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_BD_Shape_double_BGP99_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening and the cardinality threshold C_unsigned.

ppl_Pointset_Powerset_BD_Shape_double_BGP99_H79_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the H79-widening and the cardinality threshold C_unsigned.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_BD_Shape_double_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_BD_Shape_double_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_BD_Shape_double_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_BD_Shape_double_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_double_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_BD_Shape_double_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_BD_Shape_double_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_double_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_BD_Shape_double_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_BD_Shape_double_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_BD_Shape_double_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_BD_Shape_double_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_BD_Shape_double_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_BD_Shape_double_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_BD_Shape_double_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_BD_Shape_double_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_BD_Shape_double_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_BD_Shape_double_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_BD_Shape_double_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_Octagonal_Shape_double Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of octagonal shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of octagonal shapes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_Octagonal_Shape_double_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_Octagonal_Shape_double_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_Octagonal_Shape_double_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_Octagonal_Shape_double_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of octagonal shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_Octagonal_Shape_double_from_Pointset_Powerset_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_double_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_double_from_Pointset_Powerset_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_double_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_Octagonal_Shape_double domain.

ppl_delete_Pointset_Powerset_Octagonal_Shape_double(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_Octagonal_Shape_double_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_Octagonal_Shape_double_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_Octagonal_Shape_double_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_Octagonal_Shape_double_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_Octagonal_Shape_double_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_Octagonal_Shape_double_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_Octagonal_Shape_double_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_double_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_double_contains_Pointset_Powerset_Octagonal_Shape_double(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_double_strictly_contains_Pointset_Powerset_Octagonal_Shape_double(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_double_is_disjoint_from_Pointset_Powerset_Octagonal_Shape_double(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_double_geometrically_covers_Pointset_Powerset_Octagonal_Shape_double(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_double_geometrically_equals_Pointset_Powerset_Octagonal_Shape_double(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_double_equals_Pointset_Powerset_Octagonal_Shape_double(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_double_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_Octagonal_Shape_double_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_Octagonal_Shape_double_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_double_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_double_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_double_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_double_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_double_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_double_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_double_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_double_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_double_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_double_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_double_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_Octagonal_Shape_double_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_Octagonal_Shape_double_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_Octagonal_Shape_double_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_Octagonal_Shape_double_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_Octagonal_Shape_double_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_Octagonal_Shape_double_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_Octagonal_Shape_double_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_Octagonal_Shape_double_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_Octagonal_Shape_double_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_Octagonal_Shape_double_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_Octagonal_Shape_double_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_Octagonal_Shape_double_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_Octagonal_Shape_double_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_double_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_double_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_double_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_double_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Octagonal_Shape_double_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Octagonal_Shape_double_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_double_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_double_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_double_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_Octagonal_Shape_double_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_double_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_double_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_double_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_double_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_Octagonal_Shape_double_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

ppl_Pointset_Powerset_Octagonal_Shape_double_BHZ03_H79_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_Octagonal_Shape_double_BGP99_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening and the cardinality threshold C_unsigned.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_Octagonal_Shape_double_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_Octagonal_Shape_double_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_Octagonal_Shape_double_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_Octagonal_Shape_double_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_double_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_Octagonal_Shape_double_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_Octagonal_Shape_double_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_double_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_Octagonal_Shape_double_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_Octagonal_Shape_double_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_double_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_double_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_Octagonal_Shape_double_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_double_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_double_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_Octagonal_Shape_double_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_Octagonal_Shape_double_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_double_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_double_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Long_Double_Box Domain

Here we provide a short description for each of the predicates available for the domain of long double boxes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for long double boxes

The constructor predicates build a long double box from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Long_Double_Box_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new long double box $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Long_Double_Box_from_space_dimension(3, universe, X).

creates the long double box defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Long_Double_Box_from_constraints(+Constraint_System, -Handle)
Builds a new long double box P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Long_Double_Box_from_congruences(+Congruence_System, -Handle)
Builds a new long double box P from Congruence_System. Handle is unified with the handle for P.

ppl_new_Long_Double_Box_from_generators(+Generator_System, -Handle)
Builds a new long double box P from Generator_System. Handle is unified with the handle for P.

Predicates that build new long double boxes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Long_Double_Box_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Z_Box(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Grid(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Float_Box(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Double_Box(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new long double box P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Long_Double_Box_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new long double box P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Long_Double_Box domain.

ppl_delete_Long_Double_Box(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the long double box

Test Predicates

These predicates test the long double box for different properties and succeed or fail depending on the outcome.

ppl_Long_Double_Box_is_empty(+Handle)
Succeeds if and only if the long double box referenced by Handle is empty.

ppl_Long_Double_Box_is_universe(+Handle)
Succeeds if and only if the long double box referenced by Handle is the universe.

ppl_Long_Double_Box_is_bounded(+Handle)
Succeeds if and only if the long double box referenced by Handle is bounded.

ppl_Long_Double_Box_contains_integer_point(+Handle)
Succeeds if and only if the long double box referenced by Handle contains an integer point.

ppl_Long_Double_Box_is_topologically_closed(+Handle)
Succeeds if and only if the long double box referenced by Handle is topologically closed.

ppl_Long_Double_Box_is_discrete(+Handle)
Succeeds if and only if the long double box referenced by Handle is discrete.

ppl_Long_Double_Box_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the long double box referenced by Handle.

ppl_Long_Double_Box_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the long double box referenced by Handle.

ppl_Long_Double_Box_contains_Long_Double_Box(+Handle_1, +Handle_2)
Succeeds if and only if the long double box referenced by Handle_2 is included in or equal to the long double box referenced by Handle_1.

ppl_Long_Double_Box_strictly_contains_Long_Double_Box(+Handle_1, +Handle_2)
Succeeds if and only if the long double box referenced by Handle_2 is included in but not equal to the long double box referenced by Handle_1.

ppl_Long_Double_Box_is_disjoint_from_Long_Double_Box(+Handle_1, +Handle_2)
Succeeds if and only if the long double box referenced by Handle_2 is disjoint from the long double box referenced by Handle_1.

ppl_Long_Double_Box_equals_Long_Double_Box(+Handle_1, +Handle_2)
Succeeds if and only if the long double box referenced by Handle_1 is equal to the long double box referenced by Handle_2.

ppl_Long_Double_Box_OK(+Handle)
Succeeds only if the long double box referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Long_Double_Box_constrains(+Handle, +PPL_Var)
Succeeds if and only if the long double box referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the long double box

These predicates will obtain more detailed information about the long double box unifying some of their arguments with the results.

ppl_Long_Double_Box_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the long double box referenced by Handle.

ppl_Long_Double_Box_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the long double box referenced by Handle.

ppl_Long_Double_Box_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the long double box referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Long_Double_Box_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the long double box referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Long_Double_Box_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the long double box referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Long_Double_Box_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the long double box referenced by Handle.

ppl_Long_Double_Box_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the long double box referenced by Handle.

ppl_Long_Double_Box_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the long double box referenced by Handle.

ppl_Long_Double_Box_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the long double box referenced by Handle.

ppl_Long_Double_Box_has_upper_bound(+Handle, +Var, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if Var is upper bounded in long double box P referenced by Handle. It is assumed that P is not empty and its space dimension is greater than or equal to that of Var, otherwise the behavior is undefined.

Coeff_1 is unified with the numerator of the upper bound and Coeff_2 with the denominator of the upper bound. If the upper is included in P, then Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Long_Double_Box_has_lower_bound(+Handle, +Var, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if Var is lower bounded in long double box P referenced by Handle. It is assumed that P is not empty and its space dimension is greater than or equal to that of Var, otherwise the behavior is undefined.

Coeff_1 is unified with the numerator of the lower bound and Coeff_2 with the denominator of the lower bound. If the lower is included in P, then Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Long_Double_Box_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if long double box P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Long_Double_Box_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if long double box P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Long_Double_Box_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if long double box P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Long_Double_Box_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if long double box P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Long_Double_Box_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the long double box referenced by Handle.

ppl_Long_Double_Box_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the long double box referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Long_Double_Box_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the long double box referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the long double box

These predicates may modify the long double box referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the long double box by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Long_Double_Box_add_constraint(+Handle, +Constraint)
Updates the long double box referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Long_Double_Box_add_congruence(+Handle, +Congruence)
Updates the long double box referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Long_Double_Box_add_constraints( +Handle, +Constraint_System)
Updates the long double box referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Long_Double_Box_add_congruences( +Handle, +Congruence_System)
Updates the long double box referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Long_Double_Box_refine_with_constraint( +Handle, +Constraint)
Updates the long double box referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Long_Double_Box_refine_with_congruence( +Handle, +Congruence)
Updates the long double box referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Long_Double_Box_refine_with_constraints( +Handle, +Constraint_System)
Updates the long double box referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Long_Double_Box_refine_with_congruences( +Handle, +Congruence_System)
Updates the long double box referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the long double box

These predicates enable transformations such as taking the topological closure (which for the domain of long double box is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Long_Double_Box_topological_closure_assign(+Handle)
Assigns to the long double box referenced by Handle its topological closure.

ppl_Long_Double_Box_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the long double box P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Long_Double_Box_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the long double box P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Long_Double_Box_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the long double box referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Long_Double_Box_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the long double box referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Long_Double_Box_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to long double box P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Long_Double_Box_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to long double box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Long_Double_Box_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to long double box P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Long_Double_Box_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to long double box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Long_Double_Box_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to long double box P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Long_Double_Box_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to long double box P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Long_Double_Box_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the long double box P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one long double box

These predicates include the binary operators which will assign to the long double box referred to by the first argument its combination with the long double box referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Long_Double_Box_intersection_assign(+Handle_1, +Handle_2)
Assigns to the long double box P referenced by Handle_1 the intersection of P and the long double box referenced by Handle_2.

ppl_Long_Double_Box_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the long double box P referenced by Handle_1 the upper bound of P and the long double box referenced by Handle_2.

ppl_Long_Double_Box_difference_assign(+Handle_1, +Handle_2)
Assigns to the long double box P referenced by Handle_1 the difference of P and the long double box referenced by Handle_2.

ppl_Long_Double_Box_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the long double box P referenced by Handle_1 the time elapse of P and the long double box referenced by Handle_2.

ppl_Long_Double_Box_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the long double box P_1 referenced by Handle_1 with the long double box referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Long_Double_Box_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of long double box P_1 referenced by Handle_1 and the long double box P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_Long_Double_Box_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the Long_Double_Box domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the long double box referred to by the second argument has to be contained in (or equal to) the long double box referred to by the first argument.

ppl_Long_Double_Box_CC76_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the long double box P_1 referenced by Handle_1 the CC76-widening of P_1 with the long double box referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Long_Double_Box_CC76_widening_assign(+Handle_1, +Handle_2)
Assigns to the long double box P_1 referenced by Handle_1 the CC76-widening of P_1 with the long double box referenced by Handle_2.

ppl_Long_Double_Box_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_Long_Double_Box_CC76_widening_assign_with_tokens/4

ppl_Long_Double_Box_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_Long_Double_Box_CC76_widening_assign/2

ppl_Long_Double_Box_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the long double box P_1 referenced by Handle_1 the CC76-widening of P_1 with the long double box referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Long_Double_Box_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the long double box P_1 referenced by Handle_1 the CC76-widening of P_1 with the long double box referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Long_Double_Box_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the long double box P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the long double box referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the long double box referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Long_Double_Box_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the long double box P referenced by Handle_1 the concatenation of P and the long double box referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the long double box referred to in the first argument. These predicates enable the modification of the vector space of the long double box referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Long_Double_Box_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the long double box P referenced by Handle and and_embeds P in this space.

ppl_Long_Double_Box_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the long double box P referenced by Handle and and_projects P in this space.

ppl_Long_Double_Box_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the long double box P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Long_Double_Box_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the long double box P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Long_Double_Box_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the long double box referenced by Handle to Dimension_Type new space dimensions.

ppl_Long_Double_Box_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the long double box referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Long_Double_Box_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the BD_Shape_long_double Domain

Here we provide a short description for each of the predicates available for the domain of bd shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for bd shapes

The constructor predicates build a bd shape from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_BD_Shape_long_double_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new bd shape $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_BD_Shape_long_double_from_space_dimension(3, universe, X).

creates the bd shape defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_BD_Shape_long_double_from_constraints(+Constraint_System, -Handle)
Builds a new bd shape P from Constraint_System. Handle is unified with the handle for P.

ppl_new_BD_Shape_long_double_from_congruences(+Congruence_System, -Handle)
Builds a new bd shape P from Congruence_System. Handle is unified with the handle for P.

ppl_new_BD_Shape_long_double_from_generators(+Generator_System, -Handle)
Builds a new bd shape P from Generator_System. Handle is unified with the handle for P.

Predicates that build new bd shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_BD_Shape_long_double_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Z_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Grid(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Float_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Double_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new bd shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_BD_Shape_long_double_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new bd shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the BD_Shape_long_double domain.

ppl_delete_BD_Shape_long_double(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the bd shape

Test Predicates

These predicates test the bd shape for different properties and succeed or fail depending on the outcome.

ppl_BD_Shape_long_double_is_empty(+Handle)
Succeeds if and only if the bd shape referenced by Handle is empty.

ppl_BD_Shape_long_double_is_universe(+Handle)
Succeeds if and only if the bd shape referenced by Handle is the universe.

ppl_BD_Shape_long_double_is_bounded(+Handle)
Succeeds if and only if the bd shape referenced by Handle is bounded.

ppl_BD_Shape_long_double_contains_integer_point(+Handle)
Succeeds if and only if the bd shape referenced by Handle contains an integer point.

ppl_BD_Shape_long_double_is_topologically_closed(+Handle)
Succeeds if and only if the bd shape referenced by Handle is topologically closed.

ppl_BD_Shape_long_double_is_discrete(+Handle)
Succeeds if and only if the bd shape referenced by Handle is discrete.

ppl_BD_Shape_long_double_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the bd shape referenced by Handle.

ppl_BD_Shape_long_double_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the bd shape referenced by Handle.

ppl_BD_Shape_long_double_contains_BD_Shape_long_double(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is included in or equal to the bd shape referenced by Handle_1.

ppl_BD_Shape_long_double_strictly_contains_BD_Shape_long_double(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is included in but not equal to the bd shape referenced by Handle_1.

ppl_BD_Shape_long_double_is_disjoint_from_BD_Shape_long_double(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_2 is disjoint from the bd shape referenced by Handle_1.

ppl_BD_Shape_long_double_equals_BD_Shape_long_double(+Handle_1, +Handle_2)
Succeeds if and only if the bd shape referenced by Handle_1 is equal to the bd shape referenced by Handle_2.

ppl_BD_Shape_long_double_OK(+Handle)
Succeeds only if the bd shape referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_BD_Shape_long_double_constrains(+Handle, +PPL_Var)
Succeeds if and only if the bd shape referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the bd shape

These predicates will obtain more detailed information about the bd shape unifying some of their arguments with the results.

ppl_BD_Shape_long_double_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the bd shape referenced by Handle.

ppl_BD_Shape_long_double_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the bd shape referenced by Handle.

ppl_BD_Shape_long_double_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_long_double_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_long_double_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the bd shape referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_BD_Shape_long_double_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_long_double_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_long_double_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_long_double_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the bd shape referenced by Handle.

ppl_BD_Shape_long_double_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_long_double_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_long_double_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_long_double_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if bd shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_BD_Shape_long_double_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the bd shape referenced by Handle.

ppl_BD_Shape_long_double_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the bd shape referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_BD_Shape_long_double_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the bd shape referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the bd shape

These predicates may modify the bd shape referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the bd shape by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_BD_Shape_long_double_add_constraint(+Handle, +Constraint)
Updates the bd shape referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_BD_Shape_long_double_add_congruence(+Handle, +Congruence)
Updates the bd shape referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_BD_Shape_long_double_add_constraints( +Handle, +Constraint_System)
Updates the bd shape referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_BD_Shape_long_double_add_congruences( +Handle, +Congruence_System)
Updates the bd shape referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_BD_Shape_long_double_refine_with_constraint( +Handle, +Constraint)
Updates the bd shape referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_BD_Shape_long_double_refine_with_congruence( +Handle, +Congruence)
Updates the bd shape referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_BD_Shape_long_double_refine_with_constraints( +Handle, +Constraint_System)
Updates the bd shape referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_BD_Shape_long_double_refine_with_congruences( +Handle, +Congruence_System)
Updates the bd shape referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the bd shape

These predicates enable transformations such as taking the topological closure (which for the domain of bd shape is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_BD_Shape_long_double_topological_closure_assign(+Handle)
Assigns to the bd shape referenced by Handle its topological closure.

ppl_BD_Shape_long_double_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the bd shape P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_BD_Shape_long_double_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the bd shape P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_BD_Shape_long_double_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the bd shape referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_BD_Shape_long_double_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the bd shape referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_BD_Shape_long_double_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_BD_Shape_long_double_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_BD_Shape_long_double_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_long_double_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_long_double_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to bd shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_long_double_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to bd shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_BD_Shape_long_double_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the bd shape P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one bd shape

These predicates include the binary operators which will assign to the bd shape referred to by the first argument its combination with the bd shape referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_BD_Shape_long_double_intersection_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the intersection of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_long_double_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the upper bound of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_long_double_difference_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the difference of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_long_double_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the time elapse of P and the bd shape referenced by Handle_2.

ppl_BD_Shape_long_double_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the bd shape P_1 referenced by Handle_1 with the bd shape referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_BD_Shape_long_double_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of bd shape P_1 referenced by Handle_1 and the bd shape P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_BD_Shape_long_double_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the BD_Shape_long_double domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the bd shape referred to by the second argument has to be contained in (or equal to) the bd shape referred to by the first argument.

ppl_BD_Shape_long_double_BHMZ05_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_long_double_H79_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_long_double_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2.

ppl_BD_Shape_long_double_H79_widening_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2.

ppl_BD_Shape_long_double_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_BD_Shape_long_double_H79_widening_assign_with_tokens/4

ppl_BD_Shape_long_double_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_BD_Shape_long_double_H79_widening_assign/2

ppl_BD_Shape_long_double_limited_BHMZ05_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_long_double_limited_H79_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_long_double_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_BD_Shape_long_double_limited_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_long_double_limited_H79_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the H79-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_long_double_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the bd shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_BD_Shape_long_double_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the bd shape referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the bd shape referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_BD_Shape_long_double_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the bd shape P referenced by Handle_1 the concatenation of P and the bd shape referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the bd shape referred to in the first argument. These predicates enable the modification of the vector space of the bd shape referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_BD_Shape_long_double_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the bd shape P referenced by Handle and and_embeds P in this space.

ppl_BD_Shape_long_double_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the bd shape P referenced by Handle and and_projects P in this space.

ppl_BD_Shape_long_double_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the bd shape P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_BD_Shape_long_double_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the bd shape P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_BD_Shape_long_double_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the bd shape referenced by Handle to Dimension_Type new space dimensions.

ppl_BD_Shape_long_double_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the bd shape referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_BD_Shape_long_double_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Octagonal_Shape_long_double Domain

Here we provide a short description for each of the predicates available for the domain of octagonal shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for octagonal shapes

The constructor predicates build a octagonal shape from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Octagonal_Shape_long_double_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new octagonal shape $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Octagonal_Shape_long_double_from_space_dimension(3, universe, X).

creates the octagonal shape defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Octagonal_Shape_long_double_from_constraints(+Constraint_System, -Handle)
Builds a new octagonal shape P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Octagonal_Shape_long_double_from_congruences(+Congruence_System, -Handle)
Builds a new octagonal shape P from Congruence_System. Handle is unified with the handle for P.

ppl_new_Octagonal_Shape_long_double_from_generators(+Generator_System, -Handle)
Builds a new octagonal shape P from Generator_System. Handle is unified with the handle for P.

Predicates that build new octagonal shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Octagonal_Shape_long_double_from_Int8_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Int16_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Int32_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Int64_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the int64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Uint8_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint8_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Uint16_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint16_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Uint32_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint32_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Uint64_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the uint64_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Z_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the z_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Rational_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the rational_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_BD_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_BD_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_BD_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_BD_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_BD_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_BD_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Octagonal_Shape_int8_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Octagonal_Shape_int16_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Octagonal_Shape_int32_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Octagonal_Shape_int64_t(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Octagonal_Shape_mpz_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Octagonal_Shape_mpq_class(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_C_Polyhedron(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_NNC_Polyhedron(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Grid(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the grid referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Float_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the float_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_BD_Shape_float(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Octagonal_Shape_float(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_float referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Double_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_BD_Shape_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Octagonal_Shape_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new octagonal shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Int8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Int16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Int32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Int64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the int64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Uint8_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint8_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Uint16_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint16_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Uint32_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint32_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Uint64_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the uint64_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Z_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the z_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Rational_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the rational_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_BD_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_BD_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_BD_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_BD_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_BD_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_BD_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Octagonal_Shape_int8_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int8_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Octagonal_Shape_int16_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int16_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Octagonal_Shape_int32_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int32_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Octagonal_Shape_int64_t_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_int64_t referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Octagonal_Shape_mpz_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_mpz_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Octagonal_Shape_mpq_class_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_mpq_class referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_C_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_NNC_Polyhedron_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the polyhedron referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Grid_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the grid referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Float_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the float_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_BD_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Octagonal_Shape_float_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_float referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_BD_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Octagonal_Shape_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Octagonal_Shape_long_double_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new octagonal shape P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Octagonal_Shape_long_double domain.

ppl_delete_Octagonal_Shape_long_double(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the octagonal shape

Test Predicates

These predicates test the octagonal shape for different properties and succeed or fail depending on the outcome.

ppl_Octagonal_Shape_long_double_is_empty(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is empty.

ppl_Octagonal_Shape_long_double_is_universe(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is the universe.

ppl_Octagonal_Shape_long_double_is_bounded(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is bounded.

ppl_Octagonal_Shape_long_double_contains_integer_point(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle contains an integer point.

ppl_Octagonal_Shape_long_double_is_topologically_closed(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is topologically closed.

ppl_Octagonal_Shape_long_double_is_discrete(+Handle)
Succeeds if and only if the octagonal shape referenced by Handle is discrete.

ppl_Octagonal_Shape_long_double_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_long_double_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_long_double_contains_Octagonal_Shape_long_double(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is included in or equal to the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_long_double_strictly_contains_Octagonal_Shape_long_double(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is included in but not equal to the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_long_double_is_disjoint_from_Octagonal_Shape_long_double(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_2 is disjoint from the octagonal shape referenced by Handle_1.

ppl_Octagonal_Shape_long_double_equals_Octagonal_Shape_long_double(+Handle_1, +Handle_2)
Succeeds if and only if the octagonal shape referenced by Handle_1 is equal to the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_long_double_OK(+Handle)
Succeeds only if the octagonal shape referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Octagonal_Shape_long_double_constrains(+Handle, +PPL_Var)
Succeeds if and only if the octagonal shape referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the octagonal shape

These predicates will obtain more detailed information about the octagonal shape unifying some of their arguments with the results.

ppl_Octagonal_Shape_long_double_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_long_double_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_long_double_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_long_double_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_long_double_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the octagonal shape referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Octagonal_Shape_long_double_get_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the constraint system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_long_double_get_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the congruence system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_long_double_get_minimized_constraints(+Handle, ?Constraint_System)
Unifies Constraint_System with the constraints (in the form of a list) in the minimized constraint system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_long_double_get_minimized_congruences(+Handle, ?Congruence_System)
Unifies Congruence_System with the congruences (in the form of a list) in the minimized congruence system satisfied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_long_double_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_long_double_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_long_double_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_long_double_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if octagonal shape P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Octagonal_Shape_long_double_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the octagonal shape referenced by Handle.

ppl_Octagonal_Shape_long_double_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the octagonal shape referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Octagonal_Shape_long_double_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the octagonal shape referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the octagonal shape

These predicates may modify the octagonal shape referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the octagonal shape by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Octagonal_Shape_long_double_add_constraint(+Handle, +Constraint)
Updates the octagonal shape referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Octagonal_Shape_long_double_add_congruence(+Handle, +Congruence)
Updates the octagonal shape referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Octagonal_Shape_long_double_add_constraints( +Handle, +Constraint_System)
Updates the octagonal shape referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Octagonal_Shape_long_double_add_congruences( +Handle, +Congruence_System)
Updates the octagonal shape referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Octagonal_Shape_long_double_refine_with_constraint( +Handle, +Constraint)
Updates the octagonal shape referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Octagonal_Shape_long_double_refine_with_congruence( +Handle, +Congruence)
Updates the octagonal shape referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Octagonal_Shape_long_double_refine_with_constraints( +Handle, +Constraint_System)
Updates the octagonal shape referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Octagonal_Shape_long_double_refine_with_congruences( +Handle, +Congruence_System)
Updates the octagonal shape referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the octagonal shape

These predicates enable transformations such as taking the topological closure (which for the domain of octagonal shape is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Octagonal_Shape_long_double_topological_closure_assign(+Handle)
Assigns to the octagonal shape referenced by Handle its topological closure.

ppl_Octagonal_Shape_long_double_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the octagonal shape P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Octagonal_Shape_long_double_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the octagonal shape P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Octagonal_Shape_long_double_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the octagonal shape referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Octagonal_Shape_long_double_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the octagonal shape referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Octagonal_Shape_long_double_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Octagonal_Shape_long_double_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Octagonal_Shape_long_double_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_long_double_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_long_double_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to octagonal shape P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_long_double_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to octagonal shape P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Octagonal_Shape_long_double_wrap_assign(+Handle, +List_of_PPL_Var, +Width, +Representation, +Overflow, +Constraint_System, +C_unsigned, +Boolean)
Transforms the octagonal shape P referenced by Handle by wrapping the dimensions given by List_of_PPL_Vars while respecting the specified Width, Representation and Overflow behavior of all these variables. The Constraint_System represents the conditional or looping construct guard with respect to which wrapping is performed. The non-negative integer C_unsigned and Boolean allow control of the complexity/precision ratio; higher values for C_unsigned will lead to possibly greater precision while a true value for Boolean indicates that the space dimensions should be wrapped individually. See Section Wrapping Operator for a more detailed description of this operator.

Predicates whose results depend on more than one octagonal shape

These predicates include the binary operators which will assign to the octagonal shape referred to by the first argument its combination with the octagonal shape referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Octagonal_Shape_long_double_intersection_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the intersection of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_long_double_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the upper bound of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_long_double_difference_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the difference of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_long_double_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the time elapse of P and the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_long_double_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the octagonal shape P_1 referenced by Handle_1 with the octagonal shape referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Octagonal_Shape_long_double_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of octagonal shape P_1 referenced by Handle_1 and the octagonal shape P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

ppl_Octagonal_Shape_long_double_linear_partition(+Handle_1, +Handle_2, -Handle_3, -Handle_4)
Handle_1 and Handle_2 are handles for elements P_1 and P_2 in the Octagonal_Shape_long_double domain. The predicate unifies handle Handle_3 to a reference to the intersection of P_1 and P_2 and Handle_4 to a reference to a pointset powerset of nnc polyhedra P_4; where P_4 is the linear partition of P_1 with respect to P_2. This predicate is only provided if the class Pointset_Powerset_NNC_Polyhedron has been enabled when configuring the library.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the octagonal shape referred to by the second argument has to be contained in (or equal to) the octagonal shape referred to by the first argument.

ppl_Octagonal_Shape_long_double_BHMZ05_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_long_double_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2.

ppl_Octagonal_Shape_long_double_widening_assign_with_tokens(+Handle_1, +Handle_2, +C_unsigned_1, ?C_unsigned_2)
Same as predicate ppl_Octagonal_Shape_long_double_H79_widening_assign_with_tokens/4

ppl_Octagonal_Shape_long_double_widening_assign(+Handle_1, +Handle_2)
Same as predicate ppl_Octagonal_Shape_long_double_H79_widening_assign/2

ppl_Octagonal_Shape_long_double_limited_BHMZ05_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_long_double_limited_CC76_extrapolation_assign_with_tokens(+Handle_1, +Handle_2, +Constraint_System, +C_unsigned_1, ?C_unsigned_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1. The widening with tokens delay technique is applied with C_unsigned_1 tokens; C_unsigned_2 is unified with the number of tokens remaining at the end of the operation.

ppl_Octagonal_Shape_long_double_limited_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the octagonal shape P_1 referenced by Handle_1 the BHMZ05-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Octagonal_Shape_long_double_limited_CC76_extrapolation_assign(+Handle_1, +Handle_2, +Constraint_System)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-widening of P_1 with the octagonal shape referenced by Handle_2 intersected with the constraints in Constraint_System that are satisfied by all the points of P_1.

ppl_Octagonal_Shape_long_double_CC76_narrowing_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P_1 referenced by Handle_1 the CC76-narrowing of P_1 and the octagonal shape referenced by Handle_2.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Octagonal_Shape_long_double_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the octagonal shape P referenced by Handle_1 the concatenation of P and the octagonal shape referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument. These predicates enable the modification of the vector space of the octagonal shape referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Octagonal_Shape_long_double_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the octagonal shape P referenced by Handle and and_embeds P in this space.

ppl_Octagonal_Shape_long_double_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the octagonal shape P referenced by Handle and and_projects P in this space.

ppl_Octagonal_Shape_long_double_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the octagonal shape P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Octagonal_Shape_long_double_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the octagonal shape P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Octagonal_Shape_long_double_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the octagonal shape referenced by Handle to Dimension_Type new space dimensions.

ppl_Octagonal_Shape_long_double_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the octagonal shape referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Octagonal_Shape_long_double_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for the Pointset_Powerset_Long_Double_Box Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of long double boxes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of long double boxes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_Long_Double_Box_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_Long_Double_Box_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_Long_Double_Box_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_Long_Double_Box_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of long double boxes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_Long_Double_Box_from_Pointset_Powerset_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Long_Double_Box_from_Long_Double_Box(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the long_double_box referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Long_Double_Box_from_Pointset_Powerset_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Long_Double_Box_from_Long_Double_Box_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the long_double_box referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_Long_Double_Box domain.

ppl_delete_Pointset_Powerset_Long_Double_Box(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_Long_Double_Box_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_Long_Double_Box_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_Long_Double_Box_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_Long_Double_Box_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_Long_Double_Box_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_Long_Double_Box_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_Long_Double_Box_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Long_Double_Box_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Long_Double_Box_contains_Pointset_Powerset_Long_Double_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Long_Double_Box_strictly_contains_Pointset_Powerset_Long_Double_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Long_Double_Box_is_disjoint_from_Pointset_Powerset_Long_Double_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Long_Double_Box_geometrically_covers_Pointset_Powerset_Long_Double_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Long_Double_Box_geometrically_equals_Pointset_Powerset_Long_Double_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Long_Double_Box_equals_Pointset_Powerset_Long_Double_Box(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Long_Double_Box_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_Long_Double_Box_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_Long_Double_Box_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Long_Double_Box_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Long_Double_Box_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Long_Double_Box_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Long_Double_Box_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Long_Double_Box_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Long_Double_Box_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Long_Double_Box_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Long_Double_Box_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Long_Double_Box_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Long_Double_Box_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Long_Double_Box_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_Long_Double_Box_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_Long_Double_Box_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_Long_Double_Box_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_Long_Double_Box_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_Long_Double_Box_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_Long_Double_Box_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_Long_Double_Box_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_Long_Double_Box_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_Long_Double_Box_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_Long_Double_Box_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_Long_Double_Box_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_Long_Double_Box_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_Long_Double_Box_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_Long_Double_Box_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Long_Double_Box_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Long_Double_Box_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Long_Double_Box_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Long_Double_Box_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Long_Double_Box_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Long_Double_Box_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Long_Double_Box_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Long_Double_Box_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_Long_Double_Box_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Long_Double_Box_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Long_Double_Box_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Long_Double_Box_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Long_Double_Box_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_Long_Double_Box_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_Long_Double_Box_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_Long_Double_Box_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_Long_Double_Box_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_Long_Double_Box_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Long_Double_Box_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_Long_Double_Box_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_Long_Double_Box_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_Long_Double_Box_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_Long_Double_Box_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_Long_Double_Box_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Long_Double_Box_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Long_Double_Box_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_Long_Double_Box_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_Long_Double_Box_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_Long_Double_Box_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_Long_Double_Box_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_Long_Double_Box_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_Long_Double_Box_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_Long_Double_Box_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_BD_Shape_long_double Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of bd shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of bd shapes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_BD_Shape_long_double_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_BD_Shape_long_double_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_BD_Shape_long_double_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_BD_Shape_long_double_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of bd shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_BD_Shape_long_double_from_Pointset_Powerset_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_long_double_from_BD_Shape_long_double(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the bd_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_long_double_from_Pointset_Powerset_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_BD_Shape_long_double_from_BD_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the bd_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_BD_Shape_long_double domain.

ppl_delete_Pointset_Powerset_BD_Shape_long_double(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_BD_Shape_long_double_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_BD_Shape_long_double_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_BD_Shape_long_double_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_BD_Shape_long_double_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_BD_Shape_long_double_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_BD_Shape_long_double_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_BD_Shape_long_double_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_long_double_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_long_double_contains_Pointset_Powerset_BD_Shape_long_double(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_long_double_strictly_contains_Pointset_Powerset_BD_Shape_long_double(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_long_double_is_disjoint_from_Pointset_Powerset_BD_Shape_long_double(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_long_double_geometrically_covers_Pointset_Powerset_BD_Shape_long_double(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_long_double_geometrically_equals_Pointset_Powerset_BD_Shape_long_double(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_BD_Shape_long_double_equals_Pointset_Powerset_BD_Shape_long_double(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_long_double_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_BD_Shape_long_double_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_BD_Shape_long_double_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_long_double_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_long_double_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_long_double_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_long_double_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_BD_Shape_long_double_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_long_double_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_long_double_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_long_double_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_BD_Shape_long_double_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_long_double_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_BD_Shape_long_double_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_BD_Shape_long_double_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_BD_Shape_long_double_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_BD_Shape_long_double_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_BD_Shape_long_double_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_BD_Shape_long_double_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_BD_Shape_long_double_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_BD_Shape_long_double_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_BD_Shape_long_double_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_BD_Shape_long_double_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_BD_Shape_long_double_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_BD_Shape_long_double_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_BD_Shape_long_double_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_BD_Shape_long_double_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_BD_Shape_long_double_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_long_double_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_BD_Shape_long_double_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_BD_Shape_long_double_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_BD_Shape_long_double_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_BD_Shape_long_double_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_long_double_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_long_double_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_BD_Shape_long_double_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_BD_Shape_long_double_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_long_double_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_long_double_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_long_double_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_BD_Shape_long_double_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_BD_Shape_long_double_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

ppl_Pointset_Powerset_BD_Shape_long_double_BHZ03_H79_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_BD_Shape_long_double_BHZ03_H79_H79_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the H79-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_BD_Shape_long_double_BGP99_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening and the cardinality threshold C_unsigned.

ppl_Pointset_Powerset_BD_Shape_long_double_BGP99_H79_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the H79-widening and the cardinality threshold C_unsigned.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_BD_Shape_long_double_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_BD_Shape_long_double_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_BD_Shape_long_double_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_BD_Shape_long_double_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_long_double_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_BD_Shape_long_double_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_BD_Shape_long_double_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_BD_Shape_long_double_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_BD_Shape_long_double_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_BD_Shape_long_double_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_BD_Shape_long_double_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_BD_Shape_long_double_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_BD_Shape_long_double_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_BD_Shape_long_double_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_BD_Shape_long_double_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_BD_Shape_long_double_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_BD_Shape_long_double_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_BD_Shape_long_double_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_BD_Shape_long_double_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).

Predicates for the Pointset_Powerset_Octagonal_Shape_long_double Domain

Here we provide a short description for each of the predicates available for the domain of pointset powersets of octagonal shapes.

Constructor, copy, conversion and destructor predicates

Constructor predicates for pointset powersets of octagonal shapes

The constructor predicates build a pointset powerset from a specification and binds the given variable to a handle for future referencing. The specification can be:

the number of space dimensions and an atom indicating if it is to be the universe or empty element.
a representation for the particular class of semantic geometric descriptors to which the element being built belongs.

ppl_new_Pointset_Powerset_Octagonal_Shape_long_double_from_space_dimension(+Dimension_Type, +Universe_or_Empty, -Handle)
Builds a new pointset powerset $\cP$ with Dimension_Type dimensions; it is empty or the universe depending on whether Atom is empty or universe, respectively. Handle is unified with the handle for $\cP$ . Thus the query

?- ppl_new_Pointset_Powerset_Octagonal_Shape_long_double_from_space_dimension(3, universe, X).

creates the pointset powerset defining the 3-dimensional vector space $\Rset^3$ with X bound to a valid handle for accessing it.

ppl_new_Pointset_Powerset_Octagonal_Shape_long_double_from_constraints(+Constraint_System, -Handle)
Builds a new pointset powerset P from Constraint_System. Handle is unified with the handle for P.

ppl_new_Pointset_Powerset_Octagonal_Shape_long_double_from_congruences(+Congruence_System, -Handle)
Builds a new pointset powerset P from Congruence_System. Handle is unified with the handle for P.

Predicates that build new pointset powersets of octagonal shapes by copying or converting from other semantic geometric descriptions

Besides the constructors listed above, the library also provides:

copy constructors that will copy an element belonging to the same class of semantic geometric descriptions
conversion operators that build a new semantic geometric description starting from a friend; that is, a semantic geometric description in different class .

The copy and conversion predicates have two versions, one with arity 2 for the source and target handles and one with an extra argument denoting the maximum complexity to be used in the conversion; this complexity argument is ignored when the the friend and the element being built are in the same class.

ppl_new_Pointset_Powerset_Octagonal_Shape_long_double_from_Pointset_Powerset_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the pointset_powerset_octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_long_double_from_Octagonal_Shape_long_double(+Handle_1, -Handle_2)
Builds a new pointset powerset P_1 from the octagonal_shape_long_double referenced by handle Handle_1. Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_long_double_from_Pointset_Powerset_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the pointset_powerset_octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

ppl_new_Pointset_Powerset_Octagonal_Shape_long_double_from_Octagonal_Shape_long_double_with_complexity(+Handle, +Complexity, -Handle)
Builds a new pointset powerset P_1 from the octagonal_shape_long_double referenced by handle Handle_1 using an algorithm whose complexity does not exceed Complexity; Handle_2 is unified with the handle for P_1.

Destructor predicate

Below is the destructor predicate for the Pointset_Powerset_Octagonal_Shape_long_double domain.

ppl_delete_Pointset_Powerset_Octagonal_Shape_long_double(+Handle)
Invalidates the handle referenced by Handle: this makes sure the corresponding resources will eventually be released.

Predicates that do not change the pointset powerset

Test Predicates

These predicates test the pointset powerset for different properties and succeed or fail depending on the outcome.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_is_empty(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is empty.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_is_universe(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is the universe.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_is_bounded(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is bounded.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_contains_integer_point(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle contains an integer point.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_is_topologically_closed(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is topologically closed.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_is_discrete(+Handle)
Succeeds if and only if the pointset powerset referenced by Handle is discrete.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_bounds_from_above(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from above in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_bounds_from_below(+Handle, +Lin_Expr)
Succeeds if and only if Lin_Expr is bounded from below in the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_contains_Pointset_Powerset_Octagonal_Shape_long_double(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in or equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_strictly_contains_Pointset_Powerset_Octagonal_Shape_long_double(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is included in but not equal to the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_is_disjoint_from_Pointset_Powerset_Octagonal_Shape_long_double(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 is disjoint from the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_geometrically_covers_Pointset_Powerset_Octagonal_Shape_long_double(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically covers the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_geometrically_equals_Pointset_Powerset_Octagonal_Shape_long_double(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_2 geometrically equals the pointset powerset referenced by Handle_1.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_equals_Pointset_Powerset_Octagonal_Shape_long_double(+Handle_1, +Handle_2)
Succeeds if and only if the pointset powerset referenced by Handle_1 is equal to the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_OK(+Handle)
Succeeds only if the pointset powerset referenced by Handle is well formed, i.e., if it satisfies all its implementation invariants. Useful for debugging purposes.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_constrains(+Handle, +PPL_Var)
Succeeds if and only if the pointset powerset referenced by Handle constrains the dimension PPL_Var.

Predicates that return information about the pointset powerset

These predicates will obtain more detailed information about the pointset powerset unifying some of their arguments with the results.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_space_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the dimension of the vector space enclosing the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_affine_dimension(+Handle, ?Dimension_Type)
Unifies Dimension_Type with the affine dimension of the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_relation_with_constraint(+Handle, +Constraint, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Constraint. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_relation_with_generator(+Handle, +Generator, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Generator. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_relation_with_congruence(+Handle, +Congruence, ?Relation_List)
Unifies Relation_List with the list of relations the pointset powerset referenced by Handle has with Congruence. The possible relations are listed in the grammar rules above.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_maximize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_minimize(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_maximize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from above in P.

Coeff_1 is unified with the numerator of the supremum value and Coeff_2 with the denominator of the supremum value and Point with a point or closure point where Lin_Expr reaches this value. If the supremum is also the maximum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_minimize_with_point(+Handle, +Lin_Expr, ?Coeff_1, ?Coeff_2, ?Boolean, ?Point)
Succeeds if and only if pointset powerset P referenced by Handle is not empty and Lin_Expr is bounded from below in P.

Coeff_1 is unified with the numerator of the infinum value and Coeff_2 with the denominator of the infinum value and Point with a point or closure point where Lin_Expr reaches this value. If the infinum is also the minimum, Boolean is unified with the atom true and, otherwise, unified with the atom false.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_external_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the total memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_total_memory_in_bytes(+Handle, ?Number)
Unifies Number with the size of the external memory in bytes occupied by the pointset powerset referenced by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_size(+Handle, ?Number)
Unifies Number with the size of the memory in bytes occupied by the pointset powerset referenced by Handle.

Ascii dump predicate

This output predicate is useful for debugging.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_ascii_dump(+Handle)
Dumps an ascii representation of the PPL internal state for the pointset powerset referenced by Handle on the standard output.

Space-dimension preserving predicates that may change the pointset powerset

These predicates may modify the pointset powerset referred to by the handle in first argument; the (dimension of the) vector space in which it is embedded is unchanged.

Predicates that may change the pointset powerset by adding to its constraint or generator descriptions

Note that there are two forms of these predicates differentiated in the names by the words "add" or "refine with"; see Section Generic Operations on Semantic Geometric Descriptors in the main PPL User Manual for the differences in the semantics and therefore, the expected behavior, between these forms.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_add_constraint(+Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by adding Constraint to its constraint system. For a C polyhedron, Constraint must be an equality or a non-strict inequality.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_add_congruence(+Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by adding Congruence to its congruence system. For a C polyhedron, Congruence must be an equality.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_add_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its constraint system the constraints in Constraint_System. For a C polyhedron, Constraints must be a list of equalities and non-strict inequalities.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_add_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by adding to its congruence system the congruences in Congruence_System. For a C polyhedron, Congruences must be a list of equalities.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_refine_with_constraint( +Handle, +Constraint)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with Constraint.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_refine_with_congruence( +Handle, +Congruence)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with Congruence.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_refine_with_constraints( +Handle, +Constraint_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its constraint system with the constraints in Constraint_System.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_refine_with_congruences( +Handle, +Congruence_System)
Updates the pointset powerset referenced by Handle to one obtained by refining its congruence system with the congruences in Congruence_System.

Predicates that transform the pointset powerset

These predicates enable transformations such as taking the topological closure (which for the domain of pointset powerset is the identity transformation), unconstraining a specified dimension as explained in the main PPL User Manual in Section Cylindrification Operator and several different image and preimage affine transfer relations; for details of the latter see Sections Images and Preimages of Affine Transfer Relations and Generalized Affine Relations

ppl_Pointset_Powerset_Octagonal_Shape_long_double_topological_closure_assign(+Handle)
Assigns to the pointset powerset referenced by Handle its topological closure.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_pairwise_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its pairwise reduction.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_omega_reduce(+Handle)
Assigns to the pointset powerset referenced by Handle its omega reduction.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_unconstrain_space_dimension(+Handle, +PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimension PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_unconstrain_space_dimensions(+Handle, +List_of_PPL_Var)
Modifies the pointset powerset P referenced by Handle by unconstraining the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_affine_image(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle assigning the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_affine_preimage(+Handle, +PPL_Var, +Lin_Expr, +Coeff)
Transforms the pointset powerset referenced by Handle substituting the affine expression for Lin_Expr/Coeff to PPL_Var.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_bounded_affine_image(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_bounded_affine_preimage(+Handle, +PPL_Var, +Lin_Expr_1, +Lin_Expr_2, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1/Coeff $\leq$ PPL_Var $\leq$ Lin_Expr_2/Coeff.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_generalized_affine_image(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_generalized_affine_preimage(+Handle, +PPL_Var, +Relation_Symbol, +Lin_Expr, +Coeff)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation PPL_Var $\bowtie$ Lin_Expr/Coeff, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_generalized_affine_image_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized image with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_generalized_affine_preimage_lhs_rhs(+Handle, +Lin_Expr_1, +Relation_Symbol, +Lin_Expr_2)
Assigns to pointset powerset P referenced by Handle the generalized preimage with respect to the generalized affine transfer relation Lin_Expr_1 $\bowtie$ Lin_Expr_2, where $\bowtie$ is the symbol represented by Relation_Symbol.

Predicates whose results depend on more than one pointset powerset

These predicates include the binary operators which will assign to the pointset powerset referred to by the first argument its combination with the pointset powerset referred to by the second argument as described in the main PPL User Manual in Sections Intersection and Convex Polyhedral Hull and Convex Polyhedral Difference; and a linear partitioning operator described below.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_intersection_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the intersection of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_upper_bound_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the upper bound of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_difference_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the difference of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_time_elapse_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the time elapse of P and the pointset powerset referenced by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_upper_bound_assign_if_exact(+Handle_1, +Handle_2)
Succeeds if the least upper bound of the pointset powerset P_1 referenced by Handle_1 with the pointset powerset referenced by Handle_2 is exact; in which case the least upper bound is assigned to P_1; fails otherwise.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_simplify_using_context_assign(+Handle_1, +Handle_2, ?Boolean)
Succeeds if and only if the intersection of pointset powerset P_1 referenced by Handle_1 and the pointset powerset P_2 referenced by Handle_2 is non-empty. Assigns to P_1 its meet-preserving simplification with respect to P_2.

Predicates for widening and extrapolation

In addition to the above binary operators, there are also a number of widening, extrapolation and narrowing operators as described in the main PPL User Manual in Sections Widening Operators, Widening with Tokens and Extrapolation Operators. Note that for all these widening and extrapolation predicates to behave as specified the pointset powerset referred to by the second argument has to be contained in (or equal to) the pointset powerset referred to by the first argument.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_BHZ03_H79_BHMZ05_widening_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P_1 referenced by Handle_1 the BHZ03-widening between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening certified by the convergence certificate for H79.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_BGP99_BHMZ05_extrapolation_assign(+Handle_1, +Handle_2, C_unsigned)
Assigns to the pointset powerset P_1 referenced by Handle_1 the result of applying the BGP99 extrapolation operator between P_1 and the pointset powerset referenced by Handle_2, using the BHMZ05-widening and the cardinality threshold C_unsigned.

Predicates that may modify the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument.

Predicate for concatenation

For more information on this operation, see Section Concatenating Polyhedra, of the main PPL User Manual.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_concatenate_assign(+Handle_1, +Handle_2)
Assigns to the pointset powerset P referenced by Handle_1 the concatenation of P and the pointset powerset referenced by Handle_2.

Predicates for mapping dimensions or changing the vector space

These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. These predicates enable the modification of the vector space of the pointset powerset referred to in the first argument. Detailed descriptions of these can be found in the main PPL User Manual in Sections Adding New Dimensions to the Vector Space, Removing Dimensions from the Vector Space, Mapping the Dimensions of the Vector Space, Expanding One Dimension of the Vector Space to Multiple Dimensions and Folding Multiple Dimensions of the Vector Space into One Dimension.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_add_space_dimensions_and_embed(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_embeds P in this space.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_add_space_dimensions_and_project(+Handle, +Dimension_Type)
Adds Dimension_Type new dimensions to the space enclosing the pointset powerset P referenced by Handle and and_projects P in this space.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_remove_space_dimensions(+Handle, +List_of_PPL_Vars)
Removes from the vector space enclosing the pointset powerset P referenced by Handle the space dimensions that are specified in List_of_PPL_Var. The presence of duplicates in List_of_PPL_Var is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_remove_higher_space_dimensions(+Handle, +Dimension_Type)
Removes the higher dimensions from the vector space enclosing the pointset powerset P referenced by Handle so that, upon successful return, the new space dimension is Dimension_Type.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_expand_space_dimension(+Handle, +PPL_Var, +Dimension_Type)
Expands the PPL_Var-th dimension of the vector space enclosing the pointset powerset referenced by Handle to Dimension_Type new space dimensions.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_fold_space_dimensions(+Handle, +List_of_PPL_Vars, +PPL_Var)
Modifies the pointset powerset referenced by Handle by folding the space dimensions contained in List_of_PPL_Vars into dimension PPL_Var. The presence of duplicates in List_of_PPL_Vars is a waste but an innocuous one.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_map_space_dimensions(+Handle, +P_Func)
Remaps the dimensions of the vector space according to a partial function. This function is specified by means of the P_Func, which has n entries. The result is undefined if P_Func does not encode a partial function.

Predicates for pointset powerset iterators and disjuncts.

Iterators allow the user to examine and change individual elements (called here disjuncts) of a pointset powerset. Detailed descriptions for adding and removing disjuncts can be found in the main PPL User Manual in Section Adding a Disjunct. The following predicates support useful operations on these iterators and disjuncts via the usual handles.

ppl_new_Pointset_Powerset_Octagonal_Shape_long_double_iterator_from_iterator(+Iterator_1, -Iterator_2)
Builds a new iterator it from the iterator referenced by Iterator_1. Iterator_2 is unified with the handle for it.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_begin_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the beginning of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_end_iterator(+Handle, -Iterator)
Unifies Iterator with a handle to an iterator "pointing" to the end of the sequence of disjuncts of the powerset referred to by Handle.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_iterator_equals_iterator(+Iterator_1, +Iterator_2)
Succeeds if and only if the iterator referenced by Iterator_1 is equal to the iterator referenced by Iterator_2.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_iterator_increment(+Iterator)
Increments the iterator referenced by Iterator so that it "points" to the next disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_iterator_decrement(+Iterator)
Decrements the iterator referenced by Iterator so that it "points" to the previous disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_iterator_get_disjunct(+Iterator, -Handle)
Unifies with Handle a reference to the disjunct referred to by Iterator_1.

ppl_delete_Pointset_Powerset_Octagonal_Shape_long_double_iterator(+Iterator)
Invalidates the handle referenced by Iterator: this makes sure the corresponding resources will eventually be released.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_add_disjunct(+Handle_1, +Handle_2)
Adds to the pointset powerset referenced by Handle_1 a disjunct referred to by Handle_2.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_drop_disjunct(+Handle, +Iterator)
If it is the iterator referred to by Iterator, drops from the pointset powerset referenced by Handle the disjunct pointed to by it and assigns to it an iterator to the next disjunct.

ppl_Pointset_Powerset_Octagonal_Shape_long_double_drop_disjuncts(+Handle, +Iterator_1, +Iterator_2)
If it_1 and it_2 are the iterators referred to by Iterator_1 and Iterator_2, respectively, drops from the pointset powerset referenced by Handle all the disjuncts from it_1 to it_2 (excluded).