PPL  1.2
Related Functions | List of all members
Parma_Polyhedra_Library::Concrete_Expression< Target > Class Template Reference

The base class of all concrete expressions. More...

#include <ppl.hh>

Related Functions

(Note that these are not member functions.)

template<typename Target , typename FP_Interval_Type >
static bool add_linearize (const Binary_Operator< Target > &bop_expr, const FP_Oracle< Target, FP_Interval_Type > &oracle, const std::map< dimension_type, Linear_Form< FP_Interval_Type > > &lf_store, Linear_Form< FP_Interval_Type > &result)
 
template<typename Target , typename FP_Interval_Type >
static bool sub_linearize (const Binary_Operator< Target > &bop_expr, const FP_Oracle< Target, FP_Interval_Type > &oracle, const std::map< dimension_type, Linear_Form< FP_Interval_Type > > &lf_store, Linear_Form< FP_Interval_Type > &result)
 
template<typename Target , typename FP_Interval_Type >
static bool mul_linearize (const Binary_Operator< Target > &bop_expr, const FP_Oracle< Target, FP_Interval_Type > &oracle, const std::map< dimension_type, Linear_Form< FP_Interval_Type > > &lf_store, Linear_Form< FP_Interval_Type > &result)
 
template<typename Target , typename FP_Interval_Type >
static bool div_linearize (const Binary_Operator< Target > &bop_expr, const FP_Oracle< Target, FP_Interval_Type > &oracle, const std::map< dimension_type, Linear_Form< FP_Interval_Type > > &lf_store, Linear_Form< FP_Interval_Type > &result)
 
template<typename Target , typename FP_Interval_Type >
static bool cast_linearize (const Cast_Operator< Target > &cast_expr, const FP_Oracle< Target, FP_Interval_Type > &oracle, const std::map< dimension_type, Linear_Form< FP_Interval_Type > > &lf_store, Linear_Form< FP_Interval_Type > &result)
 
template<typename Target , typename FP_Interval_Type >
bool linearize (const Concrete_Expression< Target > &expr, const FP_Oracle< Target, FP_Interval_Type > &oracle, const std::map< dimension_type, Linear_Form< FP_Interval_Type > > &lf_store, Linear_Form< FP_Interval_Type > &result)
 Linearizes a floating point expression. More...
 

Detailed Description

template<typename Target>
class Parma_Polyhedra_Library::Concrete_Expression< Target >

The base class of all concrete expressions.

Friends And Related Function Documentation

template<typename Target , typename FP_Interval_Type >
static bool add_linearize ( const Binary_Operator< Target > &  bop_expr,
const FP_Oracle< Target, FP_Interval_Type > &  oracle,
const std::map< dimension_type, Linear_Form< FP_Interval_Type > > &  lf_store,
Linear_Form< FP_Interval_Type > &  result 
)
related

Helper function used by linearize to linearize a sum of floating point expressions.

Makes result become the linearization of *this in the given composite abstract store.

Template Parameters
TargetA type template parameter specifying the instantiation of Concrete_Expression to be used.
FP_Interval_TypeA type template parameter for the intervals used in the abstract domain. The interval bounds should have a floating point type.
Returns
true if the linearization succeeded, false otherwise.
Parameters
bop_exprThe binary operator concrete expression to linearize. Its binary operator type must be ADD.
oracleThe FP_Oracle to be queried.
lf_storeThe linear form abstract store.
resultThe modified linear form.
Linearization of sum floating-point expressions

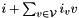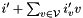Let $i + \sum_{v \in \cV}i_{v}v $ and $i' + \sum_{v \in \cV}i'_{v}v $ be two linear forms and 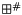$\aslf$ a sound abstract operator on linear forms such that:

\[ \left(i + \sum_{v \in \cV}i_{v}v \right) \aslf \left(i' + \sum_{v \in \cV}i'_{v}v \right) = \left(i \asifp i'\right) + \sum_{v \in \cV}\left(i_{v} \asifp i'_{v} \right)v. \]

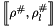Given an expression $e_{1} \oplus e_{2}$ and a composite abstract store $\left \llbracket \rho^{\#}, \rho^{\#}_l \right \rrbracket$, we construct the interval linear form 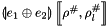$\linexprenv{e_{1} \oplus e_{2}}{\rho^{\#}}{\rho^{\#}_l}$ as follows:

\[ \linexprenv{e_{1} \oplus e_{2}}{\rho^{\#}}{\rho^{\#}_l} = \linexprenv{e_{1}}{\rho^{\#}}{\rho^{\#}_l} \aslf \linexprenv{e_{2}}{\rho^{\#}}{\rho^{\#}_l} \aslf \varepsilon_{\mathbf{f}}\left(\linexprenv{e_{1}}{\rho^{\#}}{\rho^{\#}_l} \right) \aslf \varepsilon_{\mathbf{f}}\left(\linexprenv{e_{2}}{\rho^{\#}}{\rho^{\#}_l} \right) \aslf mf_{\mathbf{f}}[-1, 1] \]

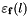where $\varepsilon_{\mathbf{f}}(l)$ is the relative error associated to 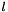$l$ (see method relative_error of class Linear_Form) and 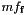$mf_{\mathbf{f}}$ is a rounding error computed by function compute_absolute_error.

template<typename Target , typename FP_Interval_Type >
static bool sub_linearize ( const Binary_Operator< Target > &  bop_expr,
const FP_Oracle< Target, FP_Interval_Type > &  oracle,
const std::map< dimension_type, Linear_Form< FP_Interval_Type > > &  lf_store,
Linear_Form< FP_Interval_Type > &  result 
)
related

Helper function used by linearize to linearize a difference of floating point expressions.

Makes result become the linearization of *this in the given composite abstract store.

Template Parameters
TargetA type template parameter specifying the instantiation of Concrete_Expression to be used.
FP_Interval_TypeA type template parameter for the intervals used in the abstract domain. The interval bounds should have a floating point type.
Returns
true if the linearization succeeded, false otherwise.
Parameters
bop_exprThe binary operator concrete expression to linearize. Its binary operator type must be SUB.
oracleThe FP_Oracle to be queried.
lf_storeThe linear form abstract store.
resultThe modified linear form.
Linearization of difference floating-point expressions

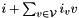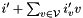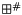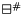Let $i + \sum_{v \in \cV}i_{v}v $ and $i' + \sum_{v \in \cV}i'_{v}v $ be two linear forms, $\aslf$ and $\adlf$ two sound abstract operators on linear form such that:

\[ \left(i + \sum_{v \in \cV}i_{v}v\right) \aslf \left(i' + \sum_{v \in \cV}i'_{v}v\right) = \left(i \asifp i'\right) + \sum_{v \in \cV}\left(i_{v} \asifp i'_{v}\right)v, \]

\[ \left(i + \sum_{v \in \cV}i_{v}v\right) \adlf \left(i' + \sum_{v \in \cV}i'_{v}v\right) = \left(i \adifp i'\right) + \sum_{v \in \cV}\left(i_{v} \adifp i'_{v}\right)v. \]

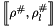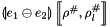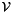Given an expression $e_{1} \ominus e_{2}$ and a composite abstract store $\left \llbracket \rho^{\#}, \rho^{\#}_l \right \rrbracket$, we construct the interval linear form $\linexprenv{e_{1} \ominus e_{2}}{\rho^{\#}}{\rho^{\#}_l}$ on $\cV$ as follows:

\[ \linexprenv{e_{1} \ominus e_{2}}{\rho^{\#}}{\rho^{\#}_l} = \linexprenv{e_{1}}{\rho^{\#}}{\rho^{\#}_l} \adlf \linexprenv{e_{2}}{\rho^{\#}}{\rho^{\#}_l} \aslf \varepsilon_{\mathbf{f}}\left(\linexprenv{e_{1}}{\rho^{\#}}{\rho^{\#}_l} \right) \aslf \varepsilon_{\mathbf{f}}\left(\linexprenv{e_{2}}{\rho^{\#}}{\rho^{\#}_l} \right) \aslf mf_{\mathbf{f}}[-1, 1] \]

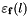where $\varepsilon_{\mathbf{f}}(l)$ is the relative error associated to 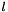$l$ (see method relative_error of class Linear_Form) and 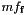$mf_{\mathbf{f}}$ is a rounding error computed by function compute_absolute_error.

template<typename Target , typename FP_Interval_Type >
static bool mul_linearize ( const Binary_Operator< Target > &  bop_expr,
const FP_Oracle< Target, FP_Interval_Type > &  oracle,
const std::map< dimension_type, Linear_Form< FP_Interval_Type > > &  lf_store,
Linear_Form< FP_Interval_Type > &  result 
)
related

Helper function used by linearize to linearize a product of floating point expressions.

Makes result become the linearization of *this in the given composite abstract store.

Template Parameters
TargetA type template parameter specifying the instantiation of Concrete_Expression to be used.
FP_Interval_TypeA type template parameter for the intervals used in the abstract domain. The interval bounds should have a floating point type.
Returns
true if the linearization succeeded, false otherwise.
Parameters
bop_exprThe binary operator concrete expression to linearize. Its binary operator type must be MUL.
oracleThe FP_Oracle to be queried.
lf_storeThe linear form abstract store.
resultThe modified linear form.
Linearization of multiplication floating-point expressions

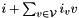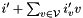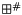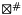Let $i + \sum_{v \in \cV}i_{v}v $ and $i' + \sum_{v \in \cV}i'_{v}v $ be two linear forms, $\aslf$ and $\amlf$ two sound abstract operators on linear forms such that:

\[ \left(i + \sum_{v \in \cV}i_{v}v\right) \aslf \left(i' + \sum_{v \in \cV}i'_{v}v\right) = \left(i \asifp i'\right) + \sum_{v \in \cV}\left(i_{v} \asifp i'_{v}\right)v, \]

\[ i \amlf \left(i' + \sum_{v \in \cV}i'_{v}v\right) = \left(i \amifp i'\right) + \sum_{v \in \cV}\left(i \amifp i'_{v}\right)v. \]

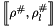Given an expression $[a, b] \otimes e_{2}$ and a composite abstract store $\left \llbracket \rho^{\#}, \rho^{\#}_l \right \rrbracket$, we construct the interval linear form $\linexprenv{[a, b] \otimes e_{2}}{\rho^{\#}}{\rho^{\#}_l}$ as follows:

\[ \linexprenv{[a, b] \otimes e_{2}}{\rho^{\#}}{\rho^{\#}_l} = \left([a, b] \amlf \linexprenv{e_{2}}{\rho^{\#}}{\rho^{\#}_l}\right) \aslf \left([a, b] \amlf \varepsilon_{\mathbf{f}}\left(\linexprenv{e_{2}}{\rho^{\#}}{\rho^{\#}_l} \right)\right) \aslf mf_{\mathbf{f}}[-1, 1]. \]

.

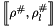Given an expression $e_{1} \otimes [a, b]$ and a composite abstract store $\left \llbracket \rho^{\#}, \rho^{\#}_l \right \rrbracket$, we construct the interval linear form $\linexprenv{e_{1} \otimes [a, b]}{\rho^{\#}}{\rho^{\#}_l}$ as follows:

\[ \linexprenv{e_{1} \otimes [a, b]}{\rho^{\#}}{\rho^{\#}_l} = \linexprenv{[a, b] \otimes e_{1}}{\rho^{\#}}{\rho^{\#}_l}. \]

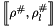Given an expression $e_{1} \otimes e_{2}$ and a composite abstract store $\left \llbracket \rho^{\#}, \rho^{\#}_l \right \rrbracket$, we construct the interval linear form 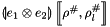$\linexprenv{e_{1} \otimes e_{2}}{\rho^{\#}}{\rho^{\#}_l}$ as follows:

\[ \linexprenv{e_{1} \otimes e_{2}}{\rho^{\#}}{\rho^{\#}_l} = \linexprenv{\iota\left(\linexprenv{e_{1}}{\rho^{\#}}{\rho^{\#}_l} \right)\rho^{\#} \otimes e_{2}}{\rho^{\#}}{\rho^{\#}_l}, \]

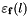where $\varepsilon_{\mathbf{f}}(l)$ is the relative error associated to 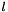$l$ (see method relative_error of class Linear_Form), 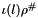$\iota(l)\rho^{\#}$ is the intervalization of 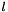$l$ (see method intervalize of class Linear_Form), and 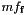$mf_{\mathbf{f}}$ is a rounding error computed by function compute_absolute_error.

Even though we intervalize the first operand in the above example, the actual implementation utilizes an heuristics for choosing which of the two operands must be intervalized in order to obtain the most precise result.

template<typename Target , typename FP_Interval_Type >
static bool div_linearize ( const Binary_Operator< Target > &  bop_expr,
const FP_Oracle< Target, FP_Interval_Type > &  oracle,
const std::map< dimension_type, Linear_Form< FP_Interval_Type > > &  lf_store,
Linear_Form< FP_Interval_Type > &  result 
)
related

Helper function used by linearize to linearize a division of floating point expressions.

Makes result become the linearization of *this in the given composite abstract store.

Template Parameters
TargetA type template parameter specifying the instantiation of Concrete_Expression to be used.
FP_Interval_TypeA type template parameter for the intervals used in the abstract domain. The interval bounds should have a floating point type.
Returns
true if the linearization succeeded, false otherwise.
Parameters
bop_exprThe binary operator concrete expression to linearize. Its binary operator type must be DIV.
oracleThe FP_Oracle to be queried.
lf_storeThe linear form abstract store.
resultThe modified linear form.
Linearization of division floating-point expressions

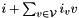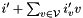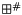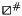Let $i + \sum_{v \in \cV}i_{v}v $ and $i' + \sum_{v \in \cV}i'_{v}v $ be two linear forms, $\aslf$ and $\adivlf$ two sound abstract operator on linear forms such that:

\[ \left(i + \sum_{v \in \cV}i_{v}v\right) \aslf \left(i' + \sum_{v \in \cV}i'_{v}v\right) = \left(i \asifp i'\right) + \sum_{v \in \cV}\left(i_{v} \asifp i'_{v}\right)v, \]

\[ \left(i + \sum_{v \in \cV}i_{v}v\right) \adivlf i' = \left(i \adivifp i'\right) + \sum_{v \in \cV}\left(i_{v} \adivifp i'\right)v. \]

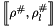Given an expression $e_{1} \oslash [a, b]$ and a composite abstract store $\left \llbracket \rho^{\#}, \rho^{\#}_l \right \rrbracket$, we construct the interval linear form $ \linexprenv{e_{1} \oslash [a, b]}{\rho^{\#}}{\rho^{\#}_l} $ as follows:

\[ \linexprenv{e_{1} \oslash [a, b]}{\rho^{\#}}{\rho^{\#}_l} = \left(\linexprenv{e_{1}}{\rho^{\#}}{\rho^{\#}_l} \adivlf [a, b]\right) \aslf \left(\varepsilon_{\mathbf{f}}\left( \linexprenv{e_{1}}{\rho^{\#}}{\rho^{\#}_l} \right) \adivlf [a, b]\right) \aslf mf_{\mathbf{f}}[-1, 1], \]

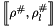given an expression $e_{1} \oslash e_{2}$ and a composite abstract store $\left \llbracket \rho^{\#}, \rho^{\#}_l \right \rrbracket$, we construct the interval linear form 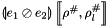$\linexprenv{e_{1} \oslash e_{2}}{\rho^{\#}}{\rho^{\#}_l}$ as follows:

\[ \linexprenv{e_{1} \oslash e_{2}}{\rho^{\#}}{\rho^{\#}_l} = \linexprenv{e_{1} \oslash \iota\left( \linexprenv{e_{2}}{\rho^{\#}}{\rho^{\#}_l} \right)\rho^{\#}}{\rho^{\#}}{\rho^{\#}_l}, \]

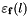where $\varepsilon_{\mathbf{f}}(l)$ is the relative error associated to 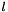$l$ (see method relative_error of class Linear_Form), 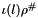$\iota(l)\rho^{\#}$ is the intervalization of 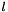$l$ (see method intervalize of class Linear_Form), and 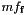$mf_{\mathbf{f}}$ is a rounding error computed by function compute_absolute_error.

template<typename Target , typename FP_Interval_Type >
static bool cast_linearize ( const Cast_Operator< Target > &  cast_expr,
const FP_Oracle< Target, FP_Interval_Type > &  oracle,
const std::map< dimension_type, Linear_Form< FP_Interval_Type > > &  lf_store,
Linear_Form< FP_Interval_Type > &  result 
)
related

Helper function used by linearize to linearize a cast floating point expression.

Makes result become the linearization of *this in the given composite abstract store.

Template Parameters
TargetA type template parameter specifying the instantiation of Concrete_Expression to be used.
FP_Interval_TypeA type template parameter for the intervals used in the abstract domain. The interval bounds should have a floating point type.
Returns
true if the linearization succeeded, false otherwise.
Parameters
cast_exprThe cast operator concrete expression to linearize.
oracleThe FP_Oracle to be queried.
lf_storeThe linear form abstract store.
resultThe modified linear form.
template<typename Target , typename FP_Interval_Type >
bool linearize ( const Concrete_Expression< Target > &  expr,
const FP_Oracle< Target, FP_Interval_Type > &  oracle,
const std::map< dimension_type, Linear_Form< FP_Interval_Type > > &  lf_store,
Linear_Form< FP_Interval_Type > &  result 
)
related

Linearizes a floating point expression.

Makes result become a linear form that correctly approximates the value of expr in the given composite abstract store.

Template Parameters
TargetA type template parameter specifying the instantiation of Concrete_Expression to be used.
FP_Interval_TypeA type template parameter for the intervals used in the abstract domain. The interval bounds should have a floating point type.
Returns
true if the linearization succeeded, false otherwise.
Parameters
exprThe concrete expression to linearize.
oracleThe FP_Oracle to be queried.
lf_storeThe linear form abstract store.
resultBecomes the linearized expression.

Formally, if expr represents the expression 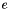$e$ and lf_store represents the linear form abstract store 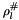$\rho^{\#}_l$, then result will become 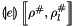$\linexprenv{e}{\rho^{\#}}{\rho^{\#}_l}$ if the linearization succeeds.

The documentation for this class was generated from the following file: