The core implementation of the Parma Polyhedra Library is written in C++. More...
Namespaces | |
| Parma_Polyhedra_Library::IO_Operators | |
| All input/output operators are confined to this namespace. | |
| std | |
| The standard C++ namespace. | |
Macros | |
| #define | PPL_VERSION_MAJOR 1 |
| The major number of the PPL version. More... | |
| #define | PPL_VERSION_MINOR 2 |
| The minor number of the PPL version. More... | |
| #define | PPL_VERSION_REVISION 0 |
| The revision number of the PPL version. More... | |
| #define | PPL_VERSION_BETA 0 |
| The beta number of the PPL version. This is zero for official releases and nonzero for development snapshots. | |
| #define | PPL_VERSION "1.2" |
| A string containing the PPL version. More... | |
Typedefs | |
| typedef size_t | Parma_Polyhedra_Library::dimension_type |
| An unsigned integral type for representing space dimensions. More... | |
| typedef size_t | Parma_Polyhedra_Library::memory_size_type |
| An unsigned integral type for representing memory size in bytes. More... | |
| typedef PPL_COEFFICIENT_TYPE | Parma_Polyhedra_Library::Coefficient |
| An alias for easily naming the type of PPL coefficients. More... | |
Variables | |
| const Throwable *volatile | Parma_Polyhedra_Library::abandon_expensive_computations |
| A pointer to an exception object. More... | |
Functions Inspecting and/or Combining Result Values | |
| Result | Parma_Polyhedra_Library::operator& (Result x, Result y) |
| Result | Parma_Polyhedra_Library::operator| (Result x, Result y) |
| Result | Parma_Polyhedra_Library::operator- (Result x, Result y) |
| Result_Class | Parma_Polyhedra_Library::result_class (Result r) |
| Result_Relation | Parma_Polyhedra_Library::result_relation (Result r) |
| Result | Parma_Polyhedra_Library::result_relation_class (Result r) |
Functions Inspecting and/or Combining Rounding_Dir Values | |
| Rounding_Dir | Parma_Polyhedra_Library::operator& (Rounding_Dir x, Rounding_Dir y) |
| Rounding_Dir | Parma_Polyhedra_Library::operator| (Rounding_Dir x, Rounding_Dir y) |
| Rounding_Dir | Parma_Polyhedra_Library::inverse (Rounding_Dir dir) |
| Rounding_Dir | Parma_Polyhedra_Library::round_dir (Rounding_Dir dir) |
| bool | Parma_Polyhedra_Library::round_down (Rounding_Dir dir) |
| bool | Parma_Polyhedra_Library::round_up (Rounding_Dir dir) |
| bool | Parma_Polyhedra_Library::round_ignore (Rounding_Dir dir) |
| bool | Parma_Polyhedra_Library::round_not_needed (Rounding_Dir dir) |
| bool | Parma_Polyhedra_Library::round_not_requested (Rounding_Dir dir) |
| bool | Parma_Polyhedra_Library::round_direct (Rounding_Dir dir) |
| bool | Parma_Polyhedra_Library::round_inverse (Rounding_Dir dir) |
| bool | Parma_Polyhedra_Library::round_strict_relation (Rounding_Dir dir) |
| fpu_rounding_direction_type | Parma_Polyhedra_Library::round_fpu_dir (Rounding_Dir dir) |
Functions for the Synthesis of Linear Rankings | |
| template<typename PSET > | |
| bool | Parma_Polyhedra_Library::termination_test_MS (const PSET &pset) |
| template<typename PSET > | |
| bool | Parma_Polyhedra_Library::termination_test_MS_2 (const PSET &pset_before, const PSET &pset_after) |
| template<typename PSET > | |
| bool | Parma_Polyhedra_Library::one_affine_ranking_function_MS (const PSET &pset, Generator &mu) |
| template<typename PSET > | |
| bool | Parma_Polyhedra_Library::one_affine_ranking_function_MS_2 (const PSET &pset_before, const PSET &pset_after, Generator &mu) |
| template<typename PSET > | |
| void | Parma_Polyhedra_Library::all_affine_ranking_functions_MS (const PSET &pset, C_Polyhedron &mu_space) |
| template<typename PSET > | |
| void | Parma_Polyhedra_Library::all_affine_ranking_functions_MS_2 (const PSET &pset_before, const PSET &pset_after, C_Polyhedron &mu_space) |
| template<typename PSET > | |
| void | Parma_Polyhedra_Library::all_affine_quasi_ranking_functions_MS (const PSET &pset, C_Polyhedron &decreasing_mu_space, C_Polyhedron &bounded_mu_space) |
| template<typename PSET > | |
| void | Parma_Polyhedra_Library::all_affine_quasi_ranking_functions_MS_2 (const PSET &pset_before, const PSET &pset_after, C_Polyhedron &decreasing_mu_space, C_Polyhedron &bounded_mu_space) |
| template<typename PSET > | |
| bool | Parma_Polyhedra_Library::termination_test_PR (const PSET &pset) |
| template<typename PSET > | |
| bool | Parma_Polyhedra_Library::termination_test_PR_2 (const PSET &pset_before, const PSET &pset_after) |
| template<typename PSET > | |
| bool | Parma_Polyhedra_Library::one_affine_ranking_function_PR (const PSET &pset, Generator &mu) |
| template<typename PSET > | |
| bool | Parma_Polyhedra_Library::one_affine_ranking_function_PR_2 (const PSET &pset_before, const PSET &pset_after, Generator &mu) |
| template<typename PSET > | |
| void | Parma_Polyhedra_Library::all_affine_ranking_functions_PR (const PSET &pset, NNC_Polyhedron &mu_space) |
| template<typename PSET > | |
| void | Parma_Polyhedra_Library::all_affine_ranking_functions_PR_2 (const PSET &pset_before, const PSET &pset_after, NNC_Polyhedron &mu_space) |
Detailed Description
The core implementation of the Parma Polyhedra Library is written in C++.
See Namespace, Hierarchical and Compound indexes for additional information about each single data type.
Macro Definition Documentation
| #define PPL_VERSION_MAJOR 1 |
The major number of the PPL version.
| #define PPL_VERSION_MINOR 2 |
The minor number of the PPL version.
| #define PPL_VERSION_REVISION 0 |
The revision number of the PPL version.
| #define PPL_VERSION "1.2" |
A string containing the PPL version.
Let M and m denote the numbers associated to PPL_VERSION_MAJOR and PPL_VERSION_MINOR, respectively. The format of PPL_VERSION is M "." m if both PPL_VERSION_REVISION (r) and PPL_VERSION_BETA (b)are zero, M "." m "pre" b if PPL_VERSION_REVISION is zero and PPL_VERSION_BETA is not zero, M "." m "." r if PPL_VERSION_REVISION is not zero and PPL_VERSION_BETA is zero, M "." m "." r "pre" b if neither PPL_VERSION_REVISION nor PPL_VERSION_BETA are zero.
Typedef Documentation
| typedef size_t Parma_Polyhedra_Library::dimension_type |
An unsigned integral type for representing space dimensions.
| typedef size_t Parma_Polyhedra_Library::memory_size_type |
An unsigned integral type for representing memory size in bytes.
| typedef PPL_COEFFICIENT_TYPE Parma_Polyhedra_Library::Coefficient |
An alias for easily naming the type of PPL coefficients.
Objects of type Coefficient are used to implement the integral valued coefficients occurring in linear expressions, constraints, generators, intervals, bounding boxes and so on. Depending on the chosen configuration options (see file README.configure), a Coefficient may actually be:
- The GMP_Integer type, which in turn is an alias for the
mpz_classtype implemented by the C++ interface of the GMP library (this is the default configuration). - An instance of the Checked_Number class template: with the policy Bounded_Integer_Coefficient_Policy, this implements overflow detection on top of a native integral type (available template instances include checked integers having 8, 16, 32 or 64 bits); with the Checked_Number_Transparent_Policy, this is a wrapper for native integral types with no overflow detection (available template instances are as above).
Enumeration Type Documentation
Possible outcomes of a checked arithmetic computation.
Rounding directions for arithmetic computations.
\ Widths of bounded integer types.
See the section on approximating bounded integers.
| Enumerator | |
|---|---|
| BITS_8 |
8 bits. |
| BITS_16 |
16 bits. |
| BITS_32 |
32 bits. |
| BITS_64 |
64 bits. |
| BITS_128 |
128 bits. |
\ Representation of bounded integer types.
See the section on approximating bounded integers.
| Enumerator | |
|---|---|
| UNSIGNED |
Unsigned binary. |
| SIGNED_2_COMPLEMENT |
Signed binary where negative values are represented by the two's complement of the absolute value. |
\ Overflow behavior of bounded integer types.
See the section on approximating bounded integers.
\ Possible representations of coefficient sequences (i.e. linear expressions and more complex objects containing linear expressions, e.g. Constraints, Generators, etc.).
\ Floating point formats known to the library.
The parameters of each format are defined by a specific struct in file Float_defs.hh. See the section on Analysis of floating point computations for more information.
Possible outcomes of the PIP_Problem solver.
| Enumerator | |
|---|---|
| UNFEASIBLE_PIP_PROBLEM |
The problem is unfeasible. |
| OPTIMIZED_PIP_PROBLEM |
The problem has an optimal solution. |
Possible outcomes of the MIP_Problem solver.
| Enumerator | |
|---|---|
| UNFEASIBLE_MIP_PROBLEM |
The problem is unfeasible. |
| UNBOUNDED_MIP_PROBLEM |
The problem is unbounded. |
| OPTIMIZED_MIP_PROBLEM |
The problem has an optimal solution. |
Possible names for PIP_Problem control parameters.
| Enumerator | |
|---|---|
| CUTTING_STRATEGY |
Cutting strategy. |
| PIVOT_ROW_STRATEGY |
Pivot row strategy. |
Possible values for PIP_Problem control parameters.
Function Documentation
|
inline |
\ Extracts the value class part of r (representable number, unrepresentable minus/plus infinity or nan).
|
inline |
\ Extracts the relation part of r.
|
inline |
|
inline |
|
inline |
|
inline |
\ Returns the inverse rounding mode of dir, ROUND_IGNORE being the inverse of itself.
|
inline |
|
inline |
|
inline |
|
inline |
|
inline |
|
inline |
|
inline |
|
inline |
|
inline |
|
inline |
| bool Parma_Polyhedra_Library::termination_test_MS | ( | const PSET & | pset | ) |
\ Termination test using an improvement of the method by Mesnard and Serebrenik [BMPZ10].
- Template Parameters
-
PSET Any pointset supported by the PPL that provides the minimized_constraints()method.
- Parameters
-
pset A pointset approximating the behavior of a loop whose termination is being analyzed. The variables indices are allocated as follows:  go onto space dimensions
go onto space dimensions 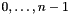 ,
, go onto space dimensions
go onto space dimensions 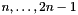 ,
,
- Returns
trueif any loop approximated bypsetdefinitely terminates;falseif the test is inconclusive. However, ifpsetprecisely characterizes the effect of the loop body onto the loop-relevant program variables, thentrueis returned if and only if the loop terminates.
| bool Parma_Polyhedra_Library::termination_test_MS_2 | ( | const PSET & | pset_before, |
| const PSET & | pset_after | ||
| ) |
\ Termination test using an improvement of the method by Mesnard and Serebrenik [BMPZ10].
- Template Parameters
-
PSET Any pointset supported by the PPL that provides the minimized_constraints()method.
- Parameters
-
pset_before A pointset approximating the values of loop-relevant variables before the update performed in the loop body that is being analyzed. The variables indices are allocated as follows:  go onto space dimensions
go onto space dimensions 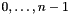 .
.
pset_after A pointset approximating the values of loop-relevant variables after the update performed in the loop body that is being analyzed. The variables indices are allocated as follows:  go onto space dimensions
go onto space dimensions 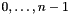 ,
, go onto space dimensions
go onto space dimensions 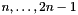 ,
,
Note that unprimed variables represent the values of the loop-relevant program variables before the update performed in the loop body, and primed variables represent the values of those program variables after the update. Note also that unprimed variables are assigned to different space dimensions in pset_before and pset_after.
- Returns
trueif any loop approximated bypsetdefinitely terminates;falseif the test is inconclusive. However, ifpset_beforeandpset_afterprecisely characterize the effect of the loop body onto the loop-relevant program variables, thentrueis returned if and only if the loop terminates.
| bool Parma_Polyhedra_Library::one_affine_ranking_function_MS | ( | const PSET & | pset, |
| Generator & | mu | ||
| ) |
\ Termination test with witness ranking function using an improvement of the method by Mesnard and Serebrenik [BMPZ10].
- Template Parameters
-
PSET Any pointset supported by the PPL that provides the minimized_constraints()method.
- Parameters
-
pset A pointset approximating the behavior of a loop whose termination is being analyzed. The variables indices are allocated as follows:  go onto space dimensions
go onto space dimensions 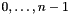 ,
, go onto space dimensions
go onto space dimensions 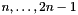 ,
,
mu When trueis returned, this is assigned a point of space dimension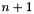 encoding one (not further specified) affine ranking function for the loop being analyzed. The ranking function is of the form
encoding one (not further specified) affine ranking function for the loop being analyzed. The ranking function is of the form 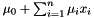 where
where 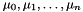 are the coefficients of
are the coefficients of mucorresponding to the space dimensions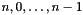 , respectively.
, respectively.
- Returns
trueif any loop approximated bypsetdefinitely terminates;falseif the test is inconclusive. However, ifpsetprecisely characterizes the effect of the loop body onto the loop-relevant program variables, thentrueis returned if and only if the loop terminates.
| bool Parma_Polyhedra_Library::one_affine_ranking_function_MS_2 | ( | const PSET & | pset_before, |
| const PSET & | pset_after, | ||
| Generator & | mu | ||
| ) |
\ Termination test with witness ranking function using an improvement of the method by Mesnard and Serebrenik [BMPZ10].
- Template Parameters
-
PSET Any pointset supported by the PPL that provides the minimized_constraints()method.
- Parameters
-
pset_before A pointset approximating the values of loop-relevant variables before the update performed in the loop body that is being analyzed. The variables indices are allocated as follows:  go onto space dimensions
go onto space dimensions 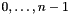 .
.
pset_after A pointset approximating the values of loop-relevant variables after the update performed in the loop body that is being analyzed. The variables indices are allocated as follows:  go onto space dimensions
go onto space dimensions 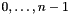 ,
, go onto space dimensions
go onto space dimensions 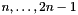 ,
,
Note that unprimed variables represent the values of the loop-relevant program variables before the update performed in the loop body, and primed variables represent the values of those program variables after the update. Note also that unprimed variables are assigned to different space dimensions in pset_before and pset_after.
- Parameters
-
mu When trueis returned, this is assigned a point of space dimension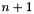 encoding one (not further specified) affine ranking function for the loop being analyzed. The ranking function is of the form
encoding one (not further specified) affine ranking function for the loop being analyzed. The ranking function is of the form 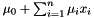 where
where 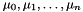 are the coefficients of
are the coefficients of mucorresponding to the space dimensions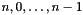 , respectively.
, respectively.
- Returns
trueif any loop approximated bypsetdefinitely terminates;falseif the test is inconclusive. However, ifpset_beforeandpset_afterprecisely characterize the effect of the loop body onto the loop-relevant program variables, thentrueis returned if and only if the loop terminates.
| void Parma_Polyhedra_Library::all_affine_ranking_functions_MS | ( | const PSET & | pset, |
| C_Polyhedron & | mu_space | ||
| ) |
\ Termination test with ranking function space using an improvement of the method by Mesnard and Serebrenik [BMPZ10].
- Template Parameters
-
PSET Any pointset supported by the PPL that provides the minimized_constraints()method.
- Parameters
-
pset A pointset approximating the behavior of a loop whose termination is being analyzed. The variables indices are allocated as follows:  go onto space dimensions
go onto space dimensions 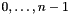 ,
, go onto space dimensions
go onto space dimensions 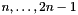 ,
,
mu_space This is assigned a closed polyhedron of space dimension 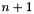 representing the space of all the affine ranking functions for the loops that are precisely characterized by
representing the space of all the affine ranking functions for the loops that are precisely characterized by pset. These ranking functions are of the form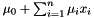 where
where 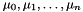 identify any point of the
identify any point of the mu_spacepolyhedron. The variables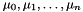 correspond to the space dimensions of
correspond to the space dimensions of mu_space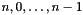 , respectively. When
, respectively. When mu_spaceis empty, it means that the test is inconclusive. However, ifpsetprecisely characterizes the effect of the loop body onto the loop-relevant program variables, thenmu_spaceis empty if and only if the loop does not terminate.
| void Parma_Polyhedra_Library::all_affine_ranking_functions_MS_2 | ( | const PSET & | pset_before, |
| const PSET & | pset_after, | ||
| C_Polyhedron & | mu_space | ||
| ) |
\ Termination test with ranking function space using an improvement of the method by Mesnard and Serebrenik [BMPZ10].
- Template Parameters
-
PSET Any pointset supported by the PPL that provides the minimized_constraints()method.
- Parameters
-
pset_before A pointset approximating the values of loop-relevant variables before the update performed in the loop body that is being analyzed. The variables indices are allocated as follows:  go onto space dimensions
go onto space dimensions 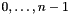 .
.
pset_after A pointset approximating the values of loop-relevant variables after the update performed in the loop body that is being analyzed. The variables indices are allocated as follows:  go onto space dimensions
go onto space dimensions 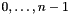 ,
, go onto space dimensions
go onto space dimensions 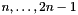 ,
,
Note that unprimed variables represent the values of the loop-relevant program variables before the update performed in the loop body, and primed variables represent the values of those program variables after the update. Note also that unprimed variables are assigned to different space dimensions in pset_before and pset_after.
- Parameters
-
mu_space This is assigned a closed polyhedron of space dimension 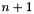 representing the space of all the affine ranking functions for the loops that are precisely characterized by
representing the space of all the affine ranking functions for the loops that are precisely characterized by pset. These ranking functions are of the form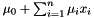 where
where 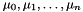 identify any point of the
identify any point of the mu_spacepolyhedron. The variables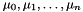 correspond to the space dimensions of
correspond to the space dimensions of mu_space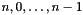 , respectively. When
, respectively. When mu_spaceis empty, it means that the test is inconclusive. However, ifpset_beforeandpset_afterprecisely characterize the effect of the loop body onto the loop-relevant program variables, thenmu_spaceis empty if and only if the loop does not terminate.
| void Parma_Polyhedra_Library::all_affine_quasi_ranking_functions_MS | ( | const PSET & | pset, |
| C_Polyhedron & | decreasing_mu_space, | ||
| C_Polyhedron & | bounded_mu_space | ||
| ) |
\ Computes the spaces of affine quasi ranking functions using an improvement of the method by Mesnard and Serebrenik [BMPZ10].
- Template Parameters
-
PSET Any pointset supported by the PPL that provides the minimized_constraints()method.
- Parameters
-
pset A pointset approximating the behavior of a loop whose termination is being analyzed. The variables indices are allocated as follows:  go onto space dimensions
go onto space dimensions 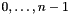 ,
, go onto space dimensions
go onto space dimensions 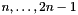 ,
,
decreasing_mu_space This is assigned a closed polyhedron of space dimension 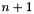 representing the space of all the decreasing affine functions for the loops that are precisely characterized by
representing the space of all the decreasing affine functions for the loops that are precisely characterized by pset.bounded_mu_space This is assigned a closed polyhedron of space dimension 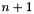 representing the space of all the lower bounded affine functions for the loops that are precisely characterized by
representing the space of all the lower bounded affine functions for the loops that are precisely characterized by pset.
These quasi-ranking functions are of the form 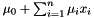 where
where 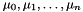 identify any point of the
identify any point of the decreasing_mu_space and bounded_mu_space polyhedrons. The variables 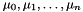 correspond to the space dimensions
correspond to the space dimensions 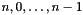 , respectively. When
, respectively. When decreasing_mu_space (resp., bounded_mu_space) is empty, it means that the test is inconclusive. However, if pset precisely characterizes the effect of the loop body onto the loop-relevant program variables, then decreasing_mu_space (resp., bounded_mu_space) will be empty if and only if there is no decreasing (resp., lower bounded) affine function, so that the loop does not terminate.
| void Parma_Polyhedra_Library::all_affine_quasi_ranking_functions_MS_2 | ( | const PSET & | pset_before, |
| const PSET & | pset_after, | ||
| C_Polyhedron & | decreasing_mu_space, | ||
| C_Polyhedron & | bounded_mu_space | ||
| ) |
\ Computes the spaces of affine quasi ranking functions using an improvement of the method by Mesnard and Serebrenik [BMPZ10].
- Template Parameters
-
PSET Any pointset supported by the PPL that provides the minimized_constraints()method.
- Parameters
-
pset_before A pointset approximating the values of loop-relevant variables before the update performed in the loop body that is being analyzed. The variables indices are allocated as follows:  go onto space dimensions
go onto space dimensions 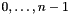 .
.
pset_after A pointset approximating the values of loop-relevant variables after the update performed in the loop body that is being analyzed. The variables indices are allocated as follows:  go onto space dimensions
go onto space dimensions 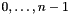 ,
, go onto space dimensions
go onto space dimensions 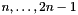 ,
,
Note that unprimed variables represent the values of the loop-relevant program variables before the update performed in the loop body, and primed variables represent the values of those program variables after the update. Note also that unprimed variables are assigned to different space dimensions in pset_before and pset_after.
- Parameters
-
decreasing_mu_space This is assigned a closed polyhedron of space dimension 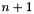 representing the space of all the decreasing affine functions for the loops that are precisely characterized by
representing the space of all the decreasing affine functions for the loops that are precisely characterized by pset.bounded_mu_space This is assigned a closed polyhedron of space dimension 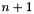 representing the space of all the lower bounded affine functions for the loops that are precisely characterized by
representing the space of all the lower bounded affine functions for the loops that are precisely characterized by pset.
These ranking functions are of the form 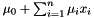 where
where 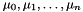 identify any point of the
identify any point of the decreasing_mu_space and bounded_mu_space polyhedrons. The variables 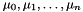 correspond to the space dimensions
correspond to the space dimensions 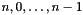 , respectively. When
, respectively. When decreasing_mu_space (resp., bounded_mu_space) is empty, it means that the test is inconclusive. However, if pset_before and pset_after precisely characterize the effect of the loop body onto the loop-relevant program variables, then decreasing_mu_space (resp., bounded_mu_space) will be empty if and only if there is no decreasing (resp., lower bounded) affine function, so that the loop does not terminate.
| bool Parma_Polyhedra_Library::termination_test_PR | ( | const PSET & | pset | ) |
\ Like termination_test_MS() but using the method by Podelski and Rybalchenko [BMPZ10].
| bool Parma_Polyhedra_Library::termination_test_PR_2 | ( | const PSET & | pset_before, |
| const PSET & | pset_after | ||
| ) |
\ Like termination_test_MS_2() but using an alternative formalization of the method by Podelski and Rybalchenko [BMPZ10].
| bool Parma_Polyhedra_Library::one_affine_ranking_function_PR | ( | const PSET & | pset, |
| Generator & | mu | ||
| ) |
\ Like one_affine_ranking_function_MS() but using the method by Podelski and Rybalchenko [BMPZ10].
| bool Parma_Polyhedra_Library::one_affine_ranking_function_PR_2 | ( | const PSET & | pset_before, |
| const PSET & | pset_after, | ||
| Generator & | mu | ||
| ) |
\ Like one_affine_ranking_function_MS_2() but using an alternative formalization of the method by Podelski and Rybalchenko [BMPZ10].
| void Parma_Polyhedra_Library::all_affine_ranking_functions_PR | ( | const PSET & | pset, |
| NNC_Polyhedron & | mu_space | ||
| ) |
\ Like all_affine_ranking_functions_MS() but using the method by Podelski and Rybalchenko [BMPZ10].
| void Parma_Polyhedra_Library::all_affine_ranking_functions_PR_2 | ( | const PSET & | pset_before, |
| const PSET & | pset_after, | ||
| NNC_Polyhedron & | mu_space | ||
| ) |
\ Like all_affine_ranking_functions_MS_2() but using an alternative formalization of the method by Podelski and Rybalchenko [BMPZ10].
Variable Documentation
| const Throwable* volatile Parma_Polyhedra_Library::abandon_expensive_computations |
A pointer to an exception object.
This pointer, which is initialized to zero, is repeatedly checked along any super-linear (i.e., computationally expensive) computation path in the library. When it is found nonzero the exception it points to is thrown. In other words, making this pointer point to an exception (and leaving it in this state) ensures that the library will return control to the client application, possibly by throwing the given exception, within a time that is a linear function of the size of the representation of the biggest object (powerset of polyhedra, polyhedron, system of constraints or generators) on which the library is operating upon.
- Note
- The only sensible way to assign to this pointer is from within a signal handler or from a parallel thread. For this reason, the library, apart from ensuring that the pointer is initially set to zero, never assigns to it. In particular, it does not zero it again when the exception is thrown: it is the client's responsibility to do so.
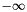 .
. 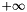 .
. 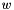 -bit bounded integer, the computation happens modulo
-bit bounded integer, the computation happens modulo 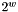 .
. 