A system of generators. More...

#include <ppl.hh>

Public Member Functions
	Generator_System (Representation r=default_representation)
	Default constructor: builds an empty system of generators.

	Generator_System (const Generator &g, Representation r=default_representation)
	Builds the singleton system containing only generator `g`.

	Generator_System (const Generator_System &gs)

	Generator_System (const Generator_System &gs, Representation r)
	Copy constructor with specified representation.

	~Generator_System ()
	Destructor.

Generator_System &	operator= (const Generator_System &y)
	Assignment operator.

Representation	representation () const
	Returns the current representation of *this.

void	set_representation (Representation r)
	Converts *this to the specified representation.

dimension_type	space_dimension () const
	Returns the dimension of the vector space enclosing `*this`.

void	set_space_dimension (dimension_type space_dim)
	Sets the space dimension of the rows in the system to `space_dim` .

void	clear ()
	Removes all the generators from the generator system and sets its space dimension to 0.

void	insert (const Generator &g)
	Inserts in `*this` a copy of the generator `g`, increasing the number of space dimensions if needed.

void	insert (Generator &g, Recycle_Input)
	Inserts in `*this` the generator `g`, stealing its contents and increasing the number of space dimensions if needed.

bool	empty () const
	Returns `true` if and only if `*this` has no generators.

const_iterator	begin () const
	Returns the const_iterator pointing to the first generator, if `*this` is not empty; otherwise, returns the past-the-end const_iterator.

const_iterator	end () const
	Returns the past-the-end const_iterator.

bool	OK () const
	Checks if all the invariants are satisfied.

void	ascii_dump () const
	Writes to `std::cerr` an ASCII representation of `*this`.

void	ascii_dump (std::ostream &s) const
	Writes to `s` an ASCII representation of `*this`.

void	print () const
	Prints `*this` to `std::cerr` using `operator<<`.

bool	ascii_load (std::istream &s)
	Loads from `s` an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets `*this` accordingly. Returns `true` if successful, `false` otherwise. More...

memory_size_type	total_memory_in_bytes () const
	Returns the total size in bytes of the memory occupied by `*this`.

memory_size_type	external_memory_in_bytes () const
	Returns the size in bytes of the memory managed by `*this`.

void	m_swap (Generator_System &y)
	Swaps `*this` with `y`.

Static Public Member Functions
static dimension_type	max_space_dimension ()
	Returns the maximum space dimension a Generator_System can handle.

static void	initialize ()
	Initializes the class.

static void	finalize ()
	Finalizes the class.

static const Generator_System &	zero_dim_univ ()
	Returns the singleton system containing only Generator::zero_dim_point().

Related Functions
(Note that these are not member functions.)
std::ostream &	operator<< (std::ostream &s, const Generator_System &gs)
	Output operator. More...

void	swap (Generator_System &x, Generator_System &y)

void	swap (Generator_System &x, Generator_System &y)

Detailed Description

A system of generators.

An object of the class Generator_System is a system of generators, i.e., a multiset of objects of the class Generator (lines, rays, points and closure points). When inserting generators in a system, space dimensions are automatically adjusted so that all the generators in the system are defined on the same vector space. A system of generators which is meant to define a non-empty polyhedron must include at least one point: the reason is that lines, rays and closure points need a supporting point (lines and rays only specify directions while closure points only specify points in the topological closure of the NNC polyhedron).

: In all the examples it is assumed that variables x and y are defined as follows:
Variable x(0);

Variable y(1);

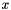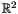Example 1: The following code defines the line having the same direction as the axis (i.e., the first Cartesian axis) in $\Rset^2$ :
Generator_System gs;

gs.insert(line(x + 0*y));

As said above, this system of generators corresponds to an empty polyhedron, because the line has no supporting point. To define a system of generators that does correspond to the 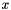axis, we can add the following code which inserts the origin of the space as a point:
gs.insert(point(0*x + 0*y));

Since space dimensions are automatically adjusted, the following code obtains the same effect:
gs.insert(point(0*x));

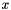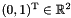In contrast, if we had added the following code, we would have defined a line parallel to the axis through the point $(0, 1)^\transpose \in \Rset^2$ .
gs.insert(point(0*x + 1*y));

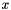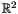Example 2: The following code builds a ray having the same direction as the positive part of the axis in $\Rset^2$ :
Generator_System gs;

gs.insert(ray(x + 0*y));

To define a system of generators indeed corresponding to the set
$\bigl\{\, (x, 0)^\transpose \in \Rset^2 \bigm| x \geq 0 \,\bigr\},$
one just has to add the origin:
gs.insert(point(0*x + 0*y));

Example 3: The following code builds a system of generators having four points and corresponding to a square in 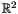$\Rset^2$ (the same as Example 1 for the system of constraints):
Generator_System gs;

gs.insert(point(0*x + 0*y));

gs.insert(point(0*x + 3*y));

gs.insert(point(3*x + 0*y));

gs.insert(point(3*x + 3*y));

Example 4: By using closure points, we can define the kernel (i.e., the largest open set included in a given set) of the square defined in the previous example. Note that a supporting point is needed and, for that purpose, any inner point could be considered.
Generator_System gs;

gs.insert(point(x + y));

gs.insert(closure_point(0*x + 0*y));

gs.insert(closure_point(0*x + 3*y));

gs.insert(closure_point(3*x + 0*y));

gs.insert(closure_point(3*x + 3*y));

Example 5: The following code builds a system of generators having two points and a ray, corresponding to a half-strip in 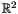$\Rset^2$ (the same as Example 2 for the system of constraints):
Generator_System gs;

gs.insert(point(0*x + 0*y));

gs.insert(point(0*x + 1*y));

gs.insert(ray(x - y));

Note: After inserting a multiset of generators in a generator system, there are no guarantees that an exact copy of them can be retrieved: in general, only an equivalent generator system will be available, where original generators may have been reordered, removed (if they are duplicate or redundant), etc.

Constructor & Destructor Documentation

Parma_Polyhedra_Library::Generator_System::Generator_System ( const Generator_System & gs )

inline

Ordinary copy constructor. The new Generator_System will have the same representation as `gs'.

Member Function Documentation

bool Parma_Polyhedra_Library::Generator_System::ascii_load ( std::istream & s )

Loads from s an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets *this accordingly. Returns true if successful, false otherwise.

Resizes the matrix of generators using the numbers of rows and columns read from s, then initializes the coordinates of each generator and its type reading the contents from s.

Friends And Related Function Documentation

std::ostream & operator<<	(	std::ostream &	s,
		const Generator_System &	gs
	)

Writes false if gs is empty. Otherwise, writes on s the generators of gs, all in one row and separated by ", ".

void swap	(	Generator_System &	x,
		Generator_System &	y
	)

void swap	(	Generator_System &	x,
		Generator_System &	y
	)

ppl.hh

Public Member Functions

Static Public Member Functions

Related Functions

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation

Friends And Related Function Documentation