A line, ray, point or closure point. More...
#include <ppl.hh>
Public Types | |
| enum | Type { LINE, RAY, POINT, CLOSURE_POINT } |
| The generator type. More... | |
| typedef Expression_Hide_Last< Expression_Hide_Inhomo< Linear_Expression > > | expr_type |
| The type of the (adapted) internal expression. | |
Public Member Functions | |
| Generator (Representation r=default_representation) | |
| Constructs the point at the origin. | |
| Generator (const Generator &g) | |
| Generator (const Generator &g, Representation r) | |
| Copy constructor with given representation. | |
| Generator (const Generator &g, dimension_type space_dim) | |
| Generator (const Generator &g, dimension_type space_dim, Representation r) | |
| Copy constructor with given representation and space dimension. | |
| ~Generator () | |
| Destructor. | |
| Generator & | operator= (const Generator &g) |
| Assignment operator. | |
| Representation | representation () const |
| Returns the current representation of *this. | |
| void | set_representation (Representation r) |
| Converts *this to the specified representation. | |
| dimension_type | space_dimension () const |
Returns the dimension of the vector space enclosing *this. | |
| void | set_space_dimension (dimension_type space_dim) |
| void | swap_space_dimensions (Variable v1, Variable v2) |
Swaps the coefficients of the variables v1 and v2 . | |
| bool | remove_space_dimensions (const Variables_Set &vars) |
| Removes all the specified dimensions from the generator. More... | |
| void | permute_space_dimensions (const std::vector< Variable > &cycle) |
| Permutes the space dimensions of the generator. More... | |
| void | shift_space_dimensions (Variable v, dimension_type n) |
| Type | type () const |
Returns the generator type of *this. | |
| bool | is_line () const |
Returns true if and only if *this is a line. | |
| bool | is_ray () const |
Returns true if and only if *this is a ray. | |
| bool | is_point () const |
Returns true if and only if *this is a point. | |
| bool | is_closure_point () const |
Returns true if and only if *this is a closure point. | |
| Coefficient_traits::const_reference | coefficient (Variable v) const |
Returns the coefficient of v in *this. More... | |
| Coefficient_traits::const_reference | divisor () const |
If *this is either a point or a closure point, returns its divisor. More... | |
| memory_size_type | total_memory_in_bytes () const |
Returns a lower bound to the total size in bytes of the memory occupied by *this. | |
| memory_size_type | external_memory_in_bytes () const |
Returns the size in bytes of the memory managed by *this. | |
| bool | is_equivalent_to (const Generator &y) const |
Returns true if and only if *this and y are equivalent generators. More... | |
| bool | is_equal_to (const Generator &y) const |
Returns true if *this is identical to y. More... | |
| bool | OK () const |
| Checks if all the invariants are satisfied. | |
| void | ascii_dump () const |
Writes to std::cerr an ASCII representation of *this. | |
| void | ascii_dump (std::ostream &s) const |
Writes to s an ASCII representation of *this. | |
| void | print () const |
Prints *this to std::cerr using operator<<. | |
| bool | ascii_load (std::istream &s) |
Loads from s an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets *this accordingly. Returns true if successful, false otherwise. | |
| void | m_swap (Generator &y) |
Swaps *this with y. | |
| expr_type | expression () const |
| Partial read access to the (adapted) internal expression. | |
Static Public Member Functions | |
| static Generator | line (const Linear_Expression &e, Representation r=default_representation) |
Returns the line of direction e. More... | |
| static Generator | ray (const Linear_Expression &e, Representation r=default_representation) |
Returns the ray of direction e. More... | |
| static Generator | point (const Linear_Expression &e=Linear_Expression::zero(), Coefficient_traits::const_reference d=Coefficient_one(), Representation r=default_representation) |
Returns the point at e / d. More... | |
| static Generator | point (Representation r) |
| Returns the origin. | |
| static Generator | point (const Linear_Expression &e, Representation r) |
Returns the point at e. | |
| static Generator | closure_point (const Linear_Expression &e=Linear_Expression::zero(), Coefficient_traits::const_reference d=Coefficient_one(), Representation r=default_representation) |
Returns the closure point at e / d. More... | |
| static Generator | closure_point (Representation r) |
| Returns the closure point at the origin. | |
| static Generator | closure_point (const Linear_Expression &e, Representation r) |
Returns the closure point at e. | |
| static dimension_type | max_space_dimension () |
| Returns the maximum space dimension a Generator can handle. | |
| static void | initialize () |
| Initializes the class. | |
| static void | finalize () |
| Finalizes the class. | |
| static const Generator & | zero_dim_point () |
Returns the origin of the zero-dimensional space 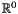 . . | |
| static const Generator & | zero_dim_closure_point () |
Returns, as a closure point, the origin of the zero-dimensional space 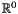 . . | |
Static Public Attributes | |
| static const Representation | default_representation = SPARSE |
| The representation used for new Generators. More... | |
Related Functions | |
(Note that these are not member functions.) | |
| std::ostream & | operator<< (std::ostream &s, const Generator &g) |
| Output operator. More... | |
| void | swap (Generator &x, Generator &y) |
Swaps x with y. More... | |
| Generator | line (const Linear_Expression &e, Representation r=Generator::default_representation) |
| Shorthand for Generator::line(const Linear_Expression& e, Representation r). More... | |
| Generator | ray (const Linear_Expression &e, Representation r=Generator::default_representation) |
| Shorthand for Generator::ray(const Linear_Expression& e, Representation r). More... | |
| Generator | point (const Linear_Expression &e=Linear_Expression::zero(), Coefficient_traits::const_reference d=Coefficient_one(), Representation r=Generator::default_representation) |
| Shorthand for Generator::point(const Linear_Expression& e, Coefficient_traits::const_reference d, Representation r). | |
| Generator | point (Representation r) |
| Shorthand for Generator::point(Representation r). More... | |
| Generator | point (const Linear_Expression &e, Representation r) |
| Shorthand for Generator::point(const Linear_Expression& e, Representation r). | |
| Generator | closure_point (const Linear_Expression &e=Linear_Expression::zero(), Coefficient_traits::const_reference d=Coefficient_one(), Representation r=Generator::default_representation) |
| Shorthand for Generator::closure_point(const Linear_Expression& e, Coefficient_traits::const_reference d, Representation r). | |
| Generator | closure_point (Representation r) |
| Shorthand for Generator::closure_point(Representation r). More... | |
| Generator | closure_point (const Linear_Expression &e, Representation r) |
| Shorthand for Generator::closure_point(const Linear_Expression& e, Representation r). | |
| bool | operator== (const Generator &x, const Generator &y) |
Returns true if and only if x is equivalent to y. More... | |
| bool | operator!= (const Generator &x, const Generator &y) |
Returns true if and only if x is not equivalent to y. More... | |
| template<typename To > | |
| bool | rectilinear_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, Rounding_Dir dir) |
Computes the rectilinear (or Manhattan) distance between x and y. More... | |
| template<typename Temp , typename To > | |
| bool | rectilinear_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, Rounding_Dir dir) |
Computes the rectilinear (or Manhattan) distance between x and y. More... | |
| template<typename Temp , typename To > | |
| bool | rectilinear_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, Rounding_Dir dir, Temp &tmp0, Temp &tmp1, Temp &tmp2) |
Computes the rectilinear (or Manhattan) distance between x and y. More... | |
| template<typename To > | |
| bool | euclidean_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, Rounding_Dir dir) |
Computes the euclidean distance between x and y. More... | |
| template<typename Temp , typename To > | |
| bool | rectilinear_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, Rounding_Dir dir) |
Computes the euclidean distance between x and y. More... | |
| template<typename Temp , typename To > | |
| bool | euclidean_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, Rounding_Dir dir, Temp &tmp0, Temp &tmp1, Temp &tmp2) |
Computes the euclidean distance between x and y. More... | |
| template<typename To > | |
| bool | l_infinity_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, Rounding_Dir dir) |
Computes the 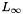 distance between distance between x and y. More... | |
| template<typename Temp , typename To > | |
| bool | l_infinity_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, Rounding_Dir dir) |
Computes the 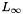 distance between distance between x and y. More... | |
| template<typename Temp , typename To > | |
| bool | l_infinity_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, Rounding_Dir dir, Temp &tmp0, Temp &tmp1, Temp &tmp2) |
Computes the 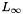 distance between distance between x and y. More... | |
| std::ostream & | operator<< (std::ostream &s, const Generator::Type &t) |
| Output operator. More... | |
| Generator | line (const Linear_Expression &e, Representation r) |
| Generator | ray (const Linear_Expression &e, Representation r) |
| Generator | point (const Linear_Expression &e, Coefficient_traits::const_reference d, Representation r) |
| Generator | point (Representation r) |
| Generator | point (const Linear_Expression &e, Representation r) |
| Generator | closure_point (const Linear_Expression &e, Coefficient_traits::const_reference d, Representation r) |
| Generator | closure_point (Representation r) |
| Generator | closure_point (const Linear_Expression &e, Representation r) |
| bool | operator== (const Generator &x, const Generator &y) |
| bool | operator!= (const Generator &x, const Generator &y) |
| template<typename Temp , typename To > | |
| bool | rectilinear_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, const Rounding_Dir dir, Temp &tmp0, Temp &tmp1, Temp &tmp2) |
| template<typename Temp , typename To > | |
| bool | rectilinear_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, const Rounding_Dir dir) |
| template<typename To > | |
| bool | rectilinear_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, const Rounding_Dir dir) |
| template<typename Temp , typename To > | |
| bool | euclidean_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, const Rounding_Dir dir, Temp &tmp0, Temp &tmp1, Temp &tmp2) |
| template<typename Temp , typename To > | |
| bool | euclidean_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, const Rounding_Dir dir) |
| template<typename To > | |
| bool | euclidean_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, const Rounding_Dir dir) |
| template<typename Temp , typename To > | |
| bool | l_infinity_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, const Rounding_Dir dir, Temp &tmp0, Temp &tmp1, Temp &tmp2) |
| template<typename Temp , typename To > | |
| bool | l_infinity_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, const Rounding_Dir dir) |
| template<typename To > | |
| bool | l_infinity_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, const Rounding_Dir dir) |
| void | swap (Generator &x, Generator &y) |
Detailed Description
A line, ray, point or closure point.
An object of the class Generator is one of the following:
- a line
 ;
; - a ray
 ;
; - a point
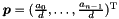 ;
; - a closure point
 ;
;
where 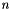 is the dimension of the space and, for points and closure points,
is the dimension of the space and, for points and closure points, 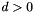 is the divisor.
is the divisor.
- A note on terminology.
- As observed in Section Representations of Convex Polyhedra, there are cases when, in order to represent a polyhedron
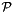 using the generator system
using the generator system 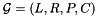 , we need to include in the finite set
, we need to include in the finite set 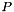 even points of
even points of 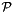 that are not vertices of
that are not vertices of 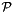 . This situation is even more frequent when working with NNC polyhedra and it is the reason why we prefer to use the word `point' where other libraries use the word `vertex'.
. This situation is even more frequent when working with NNC polyhedra and it is the reason why we prefer to use the word `point' where other libraries use the word `vertex'.
- How to build a generator.
- Each type of generator is built by applying the corresponding function (
line,ray,pointorclosure_point) to a linear expression, representing a direction in the space; the space dimension of the generator is defined as the space dimension of the corresponding linear expression. Linear expressions used to define a generator should be homogeneous (any constant term will be simply ignored). When defining points and closure points, an optional Coefficient argument can be used as a common divisor for all the coefficients occurring in the provided linear expression; the default value for this argument is 1.
- In all the following examples it is assumed that variables
x,yandzare defined as follows:Variable x(0);Variable y(1);Variable z(2);
- Example 1
- The following code builds a line with direction
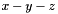 and having space dimension
and having space dimension 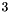 : As mentioned above, the constant term of the linear expression is not relevant. Thus, the following code has the same effect: By definition, the origin of the space is not a line, so that the following code throws an exception:
: As mentioned above, the constant term of the linear expression is not relevant. Thus, the following code has the same effect: By definition, the origin of the space is not a line, so that the following code throws an exception:
- Example 2
- The following code builds a ray with the same direction as the line in Example 1: As is the case for lines, when specifying a ray the constant term of the linear expression is not relevant; also, an exception is thrown when trying to build a ray from the origin of the space.
- Example 3
- The following code builds the point
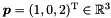 : The same effect can be obtained by using the following code: Similarly, the origin
: The same effect can be obtained by using the following code: Similarly, the origin  can be defined using either one of the following lines of code: Note however that the following code would have defined a different point, namely
can be defined using either one of the following lines of code: Note however that the following code would have defined a different point, namely  : The following two lines of code both define the only point having space dimension zero, namely
: The following two lines of code both define the only point having space dimension zero, namely  . In the second case we exploit the fact that the first argument of the function
. In the second case we exploit the fact that the first argument of the function pointis optional.Generator origin0 = Generator::zero_dim_point();
- Example 4
- The point
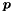 specified in Example 3 above can also be obtained with the following code, where we provide a non-default value for the second argument of the function
specified in Example 3 above can also be obtained with the following code, where we provide a non-default value for the second argument of the function point(the divisor): Obviously, the divisor can be usefully exploited to specify points having some non-integer (but rational) coordinates. For instance, the point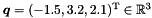 can be specified by the following code: If a zero divisor is provided, an exception is thrown.
can be specified by the following code: If a zero divisor is provided, an exception is thrown.
- Example 5
- Closure points are specified in the same way we defined points, but invoking their specific constructor function. For instance, the closure point
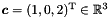 is defined by For the particular case of the (only) closure point having space dimension zero, we can use any of the following:Generator c = closure_point(1*x + 0*y + 2*z);Generator closure_origin0 = Generator::zero_dim_closure_point();Generator closure_origin0_alt = closure_point();
is defined by For the particular case of the (only) closure point having space dimension zero, we can use any of the following:Generator c = closure_point(1*x + 0*y + 2*z);Generator closure_origin0 = Generator::zero_dim_closure_point();Generator closure_origin0_alt = closure_point();
- How to inspect a generator
- Several methods are provided to examine a generator and extract all the encoded information: its space dimension, its type and the value of its integer coefficients.
- Example 6
- The following code shows how it is possible to access each single coefficient of a generator. If
g1is a point having coordinates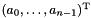 , we construct the closure point
, we construct the closure point g2having coordinates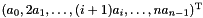 . Therefore, for the point we would obtain the following output:if (g1.is_point()) {cout << "Point g1: " << g1 << endl;Linear_Expression e;for (dimension_type i = g1.space_dimension(); i-- > 0; )e += (i + 1) * g1.coefficient(Variable(i)) * Variable(i);Generator g2 = closure_point(e, g1.divisor());cout << "Closure point g2: " << g2 << endl;}elsecout << "Generator g1 is not a point." << endl;When working with (closure) points, be careful not to confuse the notion of coefficient with the notion of coordinate: these are equivalent only when the divisor of the (closure) point is 1.Point g1: p((2*A - B + 3*C)/2)Closure point g2: cp((2*A - 2*B + 9*C)/2)
. Therefore, for the point we would obtain the following output:if (g1.is_point()) {cout << "Point g1: " << g1 << endl;Linear_Expression e;for (dimension_type i = g1.space_dimension(); i-- > 0; )e += (i + 1) * g1.coefficient(Variable(i)) * Variable(i);Generator g2 = closure_point(e, g1.divisor());cout << "Closure point g2: " << g2 << endl;}elsecout << "Generator g1 is not a point." << endl;When working with (closure) points, be careful not to confuse the notion of coefficient with the notion of coordinate: these are equivalent only when the divisor of the (closure) point is 1.Point g1: p((2*A - B + 3*C)/2)Closure point g2: cp((2*A - 2*B + 9*C)/2)
Constructor & Destructor Documentation
|
inline |
Ordinary copy constructor. The representation of the new Generator will be the same as g.
|
inline |
Copy constructor with given space dimension. The representation of the new Generator will be the same as g.
Member Function Documentation
|
static |
Returns the line of direction e.
- Exceptions
-
std::invalid_argument Thrown if the homogeneous part of erepresents the origin of the vector space.
|
static |
Returns the ray of direction e.
- Exceptions
-
std::invalid_argument Thrown if the homogeneous part of erepresents the origin of the vector space.
|
static |
Returns the point at e / d.
Both e and d are optional arguments, with default values Linear_Expression::zero() and Coefficient_one(), respectively.
- Exceptions
-
std::invalid_argument Thrown if dis zero.
|
static |
Returns the closure point at e / d.
Both e and d are optional arguments, with default values Linear_Expression::zero() and Coefficient_one(), respectively.
- Exceptions
-
std::invalid_argument Thrown if dis zero.
|
inline |
Sets the dimension of the vector space enclosing *this to space_dim .
| bool Parma_Polyhedra_Library::Generator::remove_space_dimensions | ( | const Variables_Set & | vars | ) |
Removes all the specified dimensions from the generator.
The space dimension of the variable with the highest space dimension in vars must be at most the space dimension of this.
If all dimensions with nonzero coefficients are removed from a ray or a line, it is changed into a point and this method returns false . Otherwise, it returns true .
| void Parma_Polyhedra_Library::Generator::permute_space_dimensions | ( | const std::vector< Variable > & | cycle | ) |
Permutes the space dimensions of the generator.
- Parameters
-
cycle A vector representing a cycle of the permutation according to which the space dimensions must be rearranged.
The cycle vector represents a cycle of a permutation of space dimensions. For example, the permutation 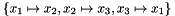 can be represented by the vector containing
can be represented by the vector containing 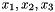 .
.
|
inline |
Shift by n positions the coefficients of variables, starting from the coefficient of v. This increases the space dimension by n.
|
inline |
Returns the coefficient of v in *this.
- Exceptions
-
std::invalid_argument Thrown if the index of vis greater than or equal to the space dimension of*this.
|
inline |
If *this is either a point or a closure point, returns its divisor.
- Exceptions
-
std::invalid_argument Thrown if *thisis neither a point nor a closure point.
| bool Parma_Polyhedra_Library::Generator::is_equivalent_to | ( | const Generator & | y | ) | const |
Returns true if and only if *this and y are equivalent generators.
Generators having different space dimensions are not equivalent.
| bool Parma_Polyhedra_Library::Generator::is_equal_to | ( | const Generator & | y | ) | const |
Returns true if *this is identical to y.
This is faster than is_equivalent_to(), but it may return `false' even for equivalent generators.
Friends And Related Function Documentation
|
related |
Output operator.
|
related |
|
related |
Shorthand for Generator::ray(const Linear_Expression& e, Representation r).
|
related |
Shorthand for Generator::point(Representation r).
|
related |
Shorthand for Generator::closure_point(Representation r).
Returns true if and only if x is equivalent to y.
Returns true if and only if x is not equivalent to y.
|
related |
Computes the rectilinear (or Manhattan) distance between x and y.
If the rectilinear distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.
The direction of the approximation is specified by dir.
All computations are performed using variables of type Checked_Number<To, Extended_Number_Policy>.
- Note
- Distances are only defined between generators that are points and/or closure points; for rays or lines,
falseis returned.
|
related |
Computes the rectilinear (or Manhattan) distance between x and y.
If the rectilinear distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.
The direction of the approximation is specified by dir.
All computations are performed using variables of type Checked_Number<Temp, Extended_Number_Policy>.
- Note
- Distances are only defined between generators that are points and/or closure points; for rays or lines,
falseis returned.
|
related |
Computes the rectilinear (or Manhattan) distance between x and y.
If the rectilinear distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.
The direction of the approximation is specified by dir.
All computations are performed using the temporary variables tmp0, tmp1 and tmp2.
- Note
- Distances are only defined between generators that are points and/or closure points; for rays or lines,
falseis returned.
|
related |
Computes the euclidean distance between x and y.
If the euclidean distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.
The direction of the approximation is specified by dir.
All computations are performed using variables of type Checked_Number<To, Extended_Number_Policy>.
- Note
- Distances are only defined between generators that are points and/or closure points; for rays or lines,
falseis returned.
|
related |
Computes the euclidean distance between x and y.
If the euclidean distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.
The direction of the approximation is specified by dir.
All computations are performed using variables of type Checked_Number<Temp, Extended_Number_Policy>.
- Note
- Distances are only defined between generators that are points and/or closure points; for rays or lines,
falseis returned.
|
related |
Computes the euclidean distance between x and y.
If the euclidean distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.
The direction of the approximation is specified by dir.
All computations are performed using the temporary variables tmp0, tmp1 and tmp2.
- Note
- Distances are only defined between generators that are points and/or closure points; for rays or lines,
falseis returned.
|
related |
Computes the 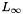 distance between
distance between x and y.
If the 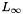 distance between
distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.
The direction of the approximation is specified by dir.
All computations are performed using variables of type Checked_Number<To, Extended_Number_Policy>.
- Note
- Distances are only defined between generators that are points and/or closure points; for rays or lines,
falseis returned.
|
related |
Computes the 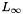 distance between
distance between x and y.
If the 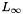 distance between
distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.
The direction of the approximation is specified by dir.
All computations are performed using variables of type Checked_Number<Temp, Extended_Number_Policy>.
- Note
- Distances are only defined between generators that are points and/or closure points; for rays or lines,
falseis returned.
|
related |
Computes the 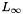 distance between
distance between x and y.
If the 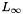 distance between
distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.
The direction of the approximation is specified by dir.
All computations are performed using the temporary variables tmp0, tmp1 and tmp2.
- Note
- Distances are only defined between generators that are points and/or closure points; for rays or lines,
falseis returned.
|
related |
Output operator.
|
related |
|
related |
|
related |
|
related |
|
related |
|
related |
|
related |
|
related |
|
related |
|
related |
|
related |
|
related |
|
related |
|
related |
|
related |
|
related |
|
related |
Member Data Documentation
|
static |
The representation used for new Generators.
- Note
- The copy constructor and the copy constructor with specified size use the representation of the original object, so that it is indistinguishable from the original object.
The documentation for this class was generated from the following file:
- ppl.hh
