The base class for convex polyhedra. More...

#include <ppl.hh>

Inheritance diagram for Parma_Polyhedra_Library::Polyhedron:

Public Types
typedef Coefficient	coefficient_type
	The numeric type of coefficients.

Public Member Functions
Member Functions that Do Not Modify the Polyhedron
dimension_type	space_dimension () const
	Returns the dimension of the vector space enclosing `*this`.

dimension_type	affine_dimension () const
	Returns 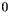, if `this` is empty; otherwise, returns the affine dimension of `this`.

const Constraint_System &	constraints () const
	Returns the system of constraints.

const Constraint_System &	minimized_constraints () const
	Returns the system of constraints, with no redundant constraint.

const Generator_System &	generators () const
	Returns the system of generators.

const Generator_System &	minimized_generators () const
	Returns the system of generators, with no redundant generator.

Congruence_System	congruences () const
	Returns a system of (equality) congruences satisfied by `*this`.

Congruence_System	minimized_congruences () const
	Returns a system of (equality) congruences satisfied by `this`, with no redundant congruences and having the same affine dimension as `this`.

Poly_Con_Relation	relation_with (const Constraint &c) const
	Returns the relations holding between the polyhedron `*this` and the constraint `c`. More...

Poly_Gen_Relation	relation_with (const Generator &g) const
	Returns the relations holding between the polyhedron `*this` and the generator `g`. More...

Poly_Con_Relation	relation_with (const Congruence &cg) const
	Returns the relations holding between the polyhedron `*this` and the congruence `c`. More...

bool	is_empty () const
	Returns `true` if and only if `*this` is an empty polyhedron.

bool	is_universe () const
	Returns `true` if and only if `*this` is a universe polyhedron.

bool	is_topologically_closed () const
	Returns `true` if and only if `*this` is a topologically closed subset of the vector space.

bool	is_disjoint_from (const Polyhedron &y) const
	Returns `true` if and only if `*this` and `y` are disjoint. More...

bool	is_discrete () const
	Returns `true` if and only if `*this` is discrete.

bool	is_bounded () const
	Returns `true` if and only if `*this` is a bounded polyhedron.

bool	contains_integer_point () const
	Returns `true` if and only if `*this` contains at least one integer point.

bool	constrains (Variable var) const
	Returns `true` if and only if `var` is constrained in `*this`. More...

bool	bounds_from_above (const Linear_Expression &expr) const
	Returns `true` if and only if `expr` is bounded from above in `*this`. More...

bool	bounds_from_below (const Linear_Expression &expr) const
	Returns `true` if and only if `expr` is bounded from below in `*this`. More...

bool	maximize (const Linear_Expression &expr, Coefficient &sup_n, Coefficient &sup_d, bool &maximum) const
	Returns `true` if and only if `this` is not empty and `expr` is bounded from above in `this`, in which case the supremum value is computed. More...

bool	maximize (const Linear_Expression &expr, Coefficient &sup_n, Coefficient &sup_d, bool &maximum, Generator &g) const
	Returns `true` if and only if `this` is not empty and `expr` is bounded from above in `this`, in which case the supremum value and a point where `expr` reaches it are computed. More...

bool	minimize (const Linear_Expression &expr, Coefficient &inf_n, Coefficient &inf_d, bool &minimum) const
	Returns `true` if and only if `this` is not empty and `expr` is bounded from below in `this`, in which case the infimum value is computed. More...

bool	minimize (const Linear_Expression &expr, Coefficient &inf_n, Coefficient &inf_d, bool &minimum, Generator &g) const
	Returns `true` if and only if `this` is not empty and `expr` is bounded from below in `this`, in which case the infimum value and a point where `expr` reaches it are computed. More...

bool	frequency (const Linear_Expression &expr, Coefficient &freq_n, Coefficient &freq_d, Coefficient &val_n, Coefficient &val_d) const
	Returns `true` if and only if there exist a unique value `val` such that `*this` saturates the equality `expr = val`. More...

bool	contains (const Polyhedron &y) const
	Returns `true` if and only if `*this` contains `y`. More...

bool	strictly_contains (const Polyhedron &y) const
	Returns `true` if and only if `*this` strictly contains `y`. More...

bool	OK (bool check_not_empty=false) const
	Checks if all the invariants are satisfied. More...

Space Dimension Preserving Member Functions that May Modify the Polyhedron
void	add_constraint (const Constraint &c)
	Adds a copy of constraint `c` to the system of constraints of `*this` (without minimizing the result). More...

void	add_generator (const Generator &g)
	Adds a copy of generator `g` to the system of generators of `*this` (without minimizing the result). More...

void	add_congruence (const Congruence &cg)
	Adds a copy of congruence `cg` to `*this`, if `cg` can be exactly represented by a polyhedron. More...

void	add_constraints (const Constraint_System &cs)
	Adds a copy of the constraints in `cs` to the system of constraints of `*this` (without minimizing the result). More...

void	add_recycled_constraints (Constraint_System &cs)
	Adds the constraints in `cs` to the system of constraints of `*this` (without minimizing the result). More...

void	add_generators (const Generator_System &gs)
	Adds a copy of the generators in `gs` to the system of generators of `*this` (without minimizing the result). More...

void	add_recycled_generators (Generator_System &gs)
	Adds the generators in `gs` to the system of generators of `*this` (without minimizing the result). More...

void	add_congruences (const Congruence_System &cgs)
	Adds a copy of the congruences in `cgs` to `*this`, if all the congruences can be exactly represented by a polyhedron. More...

void	add_recycled_congruences (Congruence_System &cgs)
	Adds the congruences in `cgs` to `*this`, if all the congruences can be exactly represented by a polyhedron. More...

void	refine_with_constraint (const Constraint &c)
	Uses a copy of constraint `c` to refine `*this`. More...

void	refine_with_congruence (const Congruence &cg)
	Uses a copy of congruence `cg` to refine `*this`. More...

void	refine_with_constraints (const Constraint_System &cs)
	Uses a copy of the constraints in `cs` to refine `*this`. More...

void	refine_with_congruences (const Congruence_System &cgs)
	Uses a copy of the congruences in `cgs` to refine `*this`. More...

template<typename FP_Format , typename Interval_Info >
void	refine_with_linear_form_inequality (const Linear_Form< Interval< FP_Format, Interval_Info > > &left, const Linear_Form< Interval< FP_Format, Interval_Info > > &right, bool is_strict=false)
	Refines `*this` with the constraint expressed by `left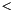` `right` if `is_strict` is set, with the constraint `left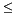` $\leq$ `right` otherwise. More...

template<typename FP_Format , typename Interval_Info >
void	generalized_refine_with_linear_form_inequality (const Linear_Form< Interval< FP_Format, Interval_Info > > &left, const Linear_Form< Interval< FP_Format, Interval_Info > > &right, Relation_Symbol relsym)
	Refines `*this` with the constraint expressed by `left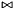` $\relsym$ `right`, where 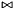$\relsym$ is the relation symbol specified by `relsym`.. More...

template<typename FP_Format , typename Interval_Info >
void	refine_fp_interval_abstract_store (Box< Interval< FP_Format, Interval_Info > > &store) const
	Refines `store` with the constraints defining `*this`. More...

void	unconstrain (Variable var)
	Computes the cylindrification of `this` with respect to space dimension `var`, assigning the result to `this`. More...

void	unconstrain (const Variables_Set &vars)
	Computes the cylindrification of `this` with respect to the set of space dimensions `vars`, assigning the result to `this`. More...

void	intersection_assign (const Polyhedron &y)
	Assigns to `this` the intersection of `this` and `y`. More...

void	poly_hull_assign (const Polyhedron &y)
	Assigns to `this` the poly-hull of `this` and `y`. More...

void	upper_bound_assign (const Polyhedron &y)
	Same as poly_hull_assign(y).

void	poly_difference_assign (const Polyhedron &y)
	Assigns to `this` the poly-difference of `this` and `y`. More...

void	difference_assign (const Polyhedron &y)
	Same as poly_difference_assign(y).

bool	simplify_using_context_assign (const Polyhedron &y)
	Assigns to `this` a meet-preserving simplification of `this` with respect to `y`. If `false` is returned, then the intersection is empty. More...

void	affine_image (Variable var, const Linear_Expression &expr, Coefficient_traits::const_reference denominator=Coefficient_one())
	Assigns to `this` the affine image of `this` under the function mapping variable `var` to the affine expression specified by `expr` and `denominator`. More...

template<typename FP_Format , typename Interval_Info >
void	affine_form_image (Variable var, const Linear_Form< Interval< FP_Format, Interval_Info > > &lf)

void	affine_preimage (Variable var, const Linear_Expression &expr, Coefficient_traits::const_reference denominator=Coefficient_one())
	Assigns to `this` the affine preimage of `this` under the function mapping variable `var` to the affine expression specified by `expr` and `denominator`. More...

void	generalized_affine_image (Variable var, Relation_Symbol relsym, const Linear_Expression &expr, Coefficient_traits::const_reference denominator=Coefficient_one())
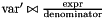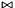	Assigns to `this` the image of `this` with respect to the generalized affine relation $\mathrm{var}' \relsym \frac{\mathrm{expr}}{\mathrm{denominator}}$ , where $\mathord{\relsym}$ is the relation symbol encoded by `relsym`. More...

void	generalized_affine_preimage (Variable var, Relation_Symbol relsym, const Linear_Expression &expr, Coefficient_traits::const_reference denominator=Coefficient_one())
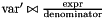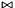	Assigns to `this` the preimage of `this` with respect to the generalized affine relation $\mathrm{var}' \relsym \frac{\mathrm{expr}}{\mathrm{denominator}}$ , where $\mathord{\relsym}$ is the relation symbol encoded by `relsym`. More...

void	generalized_affine_image (const Linear_Expression &lhs, Relation_Symbol relsym, const Linear_Expression &rhs)
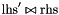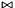	Assigns to `this` the image of `this` with respect to the generalized affine relation $\mathrm{lhs}' \relsym \mathrm{rhs}$ , where $\mathord{\relsym}$ is the relation symbol encoded by `relsym`. More...

void	generalized_affine_preimage (const Linear_Expression &lhs, Relation_Symbol relsym, const Linear_Expression &rhs)
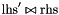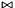	Assigns to `this` the preimage of `this` with respect to the generalized affine relation $\mathrm{lhs}' \relsym \mathrm{rhs}$ , where $\mathord{\relsym}$ is the relation symbol encoded by `relsym`. More...

void	bounded_affine_image (Variable var, const Linear_Expression &lb_expr, const Linear_Expression &ub_expr, Coefficient_traits::const_reference denominator=Coefficient_one())
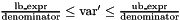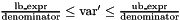	Assigns to `this` the image of `this` with respect to the bounded affine relation $\frac{\mathrm{lb\_expr}}{\mathrm{denominator}} \leq \mathrm{var}' \leq \frac{\mathrm{ub\_expr}}{\mathrm{denominator}}$ . More...

void	bounded_affine_preimage (Variable var, const Linear_Expression &lb_expr, const Linear_Expression &ub_expr, Coefficient_traits::const_reference denominator=Coefficient_one())
	Assigns to `this` the preimage of `this` with respect to the bounded affine relation $\frac{\mathrm{lb\_expr}}{\mathrm{denominator}} \leq \mathrm{var}' \leq \frac{\mathrm{ub\_expr}}{\mathrm{denominator}}$ . More...

void	time_elapse_assign (const Polyhedron &y)
	Assigns to `this` the result of computing the time-elapse between `this` and `y`. More...

void	positive_time_elapse_assign (const Polyhedron &y)
	Assigns to `this` (the best approximation of) the result of computing the positive time-elapse between `this` and `y`. More...

void	wrap_assign (const Variables_Set &vars, Bounded_Integer_Type_Width w, Bounded_Integer_Type_Representation r, Bounded_Integer_Type_Overflow o, const Constraint_System *cs_p=0, unsigned complexity_threshold=16, bool wrap_individually=true)
	Wraps the specified dimensions of the vector space. More...

void	drop_some_non_integer_points (Complexity_Class complexity=ANY_COMPLEXITY)
	Possibly tightens `*this` by dropping some points with non-integer coordinates. More...

void	drop_some_non_integer_points (const Variables_Set &vars, Complexity_Class complexity=ANY_COMPLEXITY)
	Possibly tightens `*this` by dropping some points with non-integer coordinates for the space dimensions corresponding to `vars`. More...

void	topological_closure_assign ()
	Assigns to `*this` its topological closure.

void	BHRZ03_widening_assign (const Polyhedron &y, unsigned *tp=0)
	Assigns to `this` the result of computing the BHRZ03-widening between `this` and `y`. More...

void	limited_BHRZ03_extrapolation_assign (const Polyhedron &y, const Constraint_System &cs, unsigned *tp=0)
	Assigns to `this` the result of computing the limited extrapolation between `this` and `y` using the BHRZ03-widening operator. More...

void	bounded_BHRZ03_extrapolation_assign (const Polyhedron &y, const Constraint_System &cs, unsigned *tp=0)
	Assigns to `this` the result of computing the bounded extrapolation between `this` and `y` using the BHRZ03-widening operator. More...

void	H79_widening_assign (const Polyhedron &y, unsigned *tp=0)
	Assigns to `this` the result of computing the H79_widening between `this` and `y`. More...

void	widening_assign (const Polyhedron &y, unsigned *tp=0)
	Same as H79_widening_assign(y, tp).

void	limited_H79_extrapolation_assign (const Polyhedron &y, const Constraint_System &cs, unsigned *tp=0)
	Assigns to `this` the result of computing the limited extrapolation between `this` and `y` using the H79-widening operator. More...

void	bounded_H79_extrapolation_assign (const Polyhedron &y, const Constraint_System &cs, unsigned *tp=0)
	Assigns to `this` the result of computing the bounded extrapolation between `this` and `y` using the H79-widening operator. More...

Member Functions that May Modify the Dimension of the Vector Space
void	add_space_dimensions_and_embed (dimension_type m)
	Adds `m` new space dimensions and embeds the old polyhedron in the new vector space. More...

void	add_space_dimensions_and_project (dimension_type m)
	Adds `m` new space dimensions to the polyhedron and does not embed it in the new vector space. More...

void	concatenate_assign (const Polyhedron &y)
	Assigns to `this` the concatenation of `this` and `y`, taken in this order. More...

void	remove_space_dimensions (const Variables_Set &vars)
	Removes all the specified dimensions from the vector space. More...

void	remove_higher_space_dimensions (dimension_type new_dimension)
	Removes the higher dimensions of the vector space so that the resulting space will have dimension `new_dimension`. More...

template<typename Partial_Function >
void	map_space_dimensions (const Partial_Function &pfunc)
	Remaps the dimensions of the vector space according to a partial function. More...

void	expand_space_dimension (Variable var, dimension_type m)
	Creates `m` copies of the space dimension corresponding to `var`. More...

void	fold_space_dimensions (const Variables_Set &vars, Variable dest)
	Folds the space dimensions in `vars` into `dest`. More...

Miscellaneous Member Functions
	~Polyhedron ()
	Destructor.

void	m_swap (Polyhedron &y)
	Swaps `this` with polyhedron `y`. (`this` and `y` can be dimension-incompatible.) More...

void	ascii_dump () const
	Writes to `std::cerr` an ASCII representation of `*this`.

void	ascii_dump (std::ostream &s) const
	Writes to `s` an ASCII representation of `*this`.

void	print () const
	Prints `*this` to `std::cerr` using `operator<<`.

bool	ascii_load (std::istream &s)
	Loads from `s` an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets `*this` accordingly. Returns `true` if successful, `false` otherwise.

memory_size_type	total_memory_in_bytes () const
	Returns the total size in bytes of the memory occupied by `*this`.

memory_size_type	external_memory_in_bytes () const
	Returns the size in bytes of the memory managed by `*this`.

int32_t	hash_code () const
	Returns a 32-bit hash code for `*this`. More...

Static Public Member Functions
static dimension_type	max_space_dimension ()
	Returns the maximum space dimension all kinds of Polyhedron can handle.

static bool	can_recycle_constraint_systems ()
	Returns `true` indicating that this domain has methods that can recycle constraints.

static void	initialize ()
	Initializes the class.

static void	finalize ()
	Finalizes the class.

static bool	can_recycle_congruence_systems ()
	Returns `false` indicating that this domain cannot recycle congruences.

Protected Member Functions
	Polyhedron (Topology topol, dimension_type num_dimensions, Degenerate_Element kind)
	Builds a polyhedron having the specified properties. More...

	Polyhedron (const Polyhedron &y, Complexity_Class complexity=ANY_COMPLEXITY)
	Ordinary copy constructor. More...

	Polyhedron (Topology topol, const Constraint_System &cs)
	Builds a polyhedron from a system of constraints. More...

	Polyhedron (Topology topol, Constraint_System &cs, Recycle_Input dummy)
	Builds a polyhedron recycling a system of constraints. More...

	Polyhedron (Topology topol, const Generator_System &gs)
	Builds a polyhedron from a system of generators. More...

	Polyhedron (Topology topol, Generator_System &gs, Recycle_Input dummy)
	Builds a polyhedron recycling a system of generators. More...

template<typename Interval >
	Polyhedron (Topology topol, const Box< Interval > &box, Complexity_Class complexity=ANY_COMPLEXITY)
	Builds a polyhedron from a box. More...

Polyhedron &	operator= (const Polyhedron &y)
	The assignment operator. (`*this` and `y` can be dimension-incompatible.)

void	drop_some_non_integer_points (const Variables_Set *vars_p, Complexity_Class complexity)
	Possibly tightens `this` by dropping some points with non-integer coordinates for the space dimensions corresponding to `vars_p`. More...

template<typename FP_Format , typename Interval_Info >
void	overapproximate_linear_form (const Linear_Form< Interval< FP_Format, Interval_Info > > &lf, const dimension_type lf_dimension, Linear_Form< Interval< FP_Format, Interval_Info > > &result)
	Helper function that overapproximates an interval linear form. More...

void	positive_time_elapse_assign_impl (const Polyhedron &y)
	Assuming `this` is NNC, assigns to `this` the result of the "positive time-elapse" between `*this` and `y`. More...

Static Protected Member Functions
template<typename FP_Format , typename Interval_Info >
static void	convert_to_integer_expression (const Linear_Form< Interval< FP_Format, Interval_Info > > &lf, const dimension_type lf_dimension, Linear_Expression &result)
	Helper function that makes `result` become a Linear_Expression obtained by normalizing the denominators in `lf`. More...

template<typename FP_Format , typename Interval_Info >
static void	convert_to_integer_expressions (const Linear_Form< Interval< FP_Format, Interval_Info > > &lf, const dimension_type lf_dimension, Linear_Expression &res, Coefficient &res_low_coeff, Coefficient &res_hi_coeff, Coefficient &denominator)
	Normalization helper function. More...

Related Functions
(Note that these are not member functions.)
std::ostream &	operator<< (std::ostream &s, const Polyhedron &ph)
	Output operator. More...

void	swap (Polyhedron &x, Polyhedron &y)
	Swaps `x` with `y`. More...

bool	operator== (const Polyhedron &x, const Polyhedron &y)
	Returns `true` if and only if `x` and `y` are the same polyhedron. More...

bool	operator!= (const Polyhedron &x, const Polyhedron &y)
	Returns `true` if and only if `x` and `y` are different polyhedra. More...

void	swap (Polyhedron &x, Polyhedron &y)

bool	operator!= (const Polyhedron &x, const Polyhedron &y)

Detailed Description

The base class for convex polyhedra.

An object of the class Polyhedron represents a convex polyhedron in the vector space 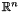$\Rset^n$ .

A polyhedron can be specified as either a finite system of constraints or a finite system of generators (see Section Representations of Convex Polyhedra) and it is always possible to obtain either representation. That is, if we know the system of constraints, we can obtain from this the system of generators that define the same polyhedron and vice versa. These systems can contain redundant members: in this case we say that they are not in the minimal form.

Two key attributes of any polyhedron are its topological kind (recording whether it is a C_Polyhedron or an NNC_Polyhedron object) and its space dimension (the dimension 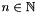$n \in \Nset$ of the enclosing vector space):

all polyhedra, the empty ones included, are endowed with a specific topology and space dimension;
most operations working on a polyhedron and another object (i.e., another polyhedron, a constraint or generator, a set of variables, etc.) will throw an exception if the polyhedron and the object are not both topology-compatible and dimension-compatible (see Section Representations of Convex Polyhedra);
the topology of a polyhedron cannot be changed; rather, there are constructors for each of the two derived classes that will build a new polyhedron with the topology of that class from another polyhedron from either class and any topology;
the only ways in which the space dimension of a polyhedron can be changed are:
- explicit calls to operators provided for that purpose;
- standard copy, assignment and swap operators.

Note that four different polyhedra can be defined on the zero-dimension space: the empty polyhedron, either closed or NNC, and the universe polyhedron 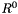$R^0$ , again either closed or NNC.

: In all the examples it is assumed that variables x and y are defined (where they are used) as follows:
Variable x(0);

Variable y(1);

Example 1: The following code builds a polyhedron corresponding to a square in 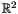$\Rset^2$ , given as a system of constraints:
Constraint_System cs;

cs.insert(x >= 0);

cs.insert(x <= 3);

cs.insert(y >= 0);

cs.insert(y <= 3);

C_Polyhedron ph(cs);

The following code builds the same polyhedron as above, but starting from a system of generators specifying the four vertices of the square:
Generator_System gs;

gs.insert(point(0*x + 0*y));

gs.insert(point(0*x + 3*y));

gs.insert(point(3*x + 0*y));

gs.insert(point(3*x + 3*y));

C_Polyhedron ph(gs);

Example 2: The following code builds an unbounded polyhedron corresponding to a half-strip in 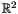$\Rset^2$ , given as a system of constraints:
Constraint_System cs;

cs.insert(x >= 0);

cs.insert(x - y <= 0);

cs.insert(x - y + 1 >= 0);

C_Polyhedron ph(cs);

The following code builds the same polyhedron as above, but starting from the system of generators specifying the two vertices of the polyhedron and one ray:
Generator_System gs;

gs.insert(point(0*x + 0*y));

gs.insert(point(0*x + y));

gs.insert(ray(x - y));

C_Polyhedron ph(gs);

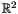Example 3: The following code builds the polyhedron corresponding to a half-plane by adding a single constraint to the universe polyhedron in $\Rset^2$ :
C_Polyhedron ph(2);

ph.add_constraint(y >= 0);

The following code builds the same polyhedron as above, but starting from the empty polyhedron in the space 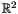$\Rset^2$ and inserting the appropriate generators (a point, a ray and a line).
C_Polyhedron ph(2, EMPTY);

ph.add_generator(point(0*x + 0*y));

ph.add_generator(ray(y));

ph.add_generator(line(x));

Note that, although the above polyhedron has no vertices, we must add one point, because otherwise the result of the Minkowski's sum would be an empty polyhedron. To avoid subtle errors related to the minimization process, it is required that the first generator inserted in an empty polyhedron is a point (otherwise, an exception is thrown).

Example 4: The following code shows the use of the function add_space_dimensions_and_embed:
C_Polyhedron ph(1);

ph.add_constraint(x == 2);

ph.add_space_dimensions_and_embed(1);

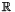We build the universe polyhedron in the 1-dimension space $\Rset$ . Then we add a single equality constraint, thus obtaining the polyhedron corresponding to the singleton set 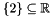$\{ 2 \} \sseq \Rset$ . After the last line of code, the resulting polyhedron is
$\bigl\{\, (2, y)^\transpose \in \Rset^2 \bigm| y \in \Rset \,\bigr\}.$

Example 5: The following code shows the use of the function add_space_dimensions_and_project:
C_Polyhedron ph(1);

ph.add_constraint(x == 2);

ph.add_space_dimensions_and_project(1);

The first two lines of code are the same as in Example 4 for add_space_dimensions_and_embed. After the last line of code, the resulting polyhedron is the singleton set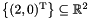 $\bigl\{ (2, 0)^\transpose \bigr\} \sseq \Rset^2$ .

Example 6: The following code shows the use of the function affine_image:
C_Polyhedron ph(2, EMPTY);

ph.add_generator(point(0*x + 0*y));

ph.add_generator(point(0*x + 3*y));

ph.add_generator(point(3*x + 0*y));

ph.add_generator(point(3*x + 3*y));

Linear_Expression expr = x + 4;

ph.affine_image(x, expr);

In this example the starting polyhedron is a square in $\Rset^2$ , the considered variable is and the affine expression is 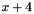. The resulting polyhedron is the same square translated to the right. Moreover, if the affine transformation for the same variable x is :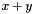
Linear_Expression expr = x + y;

the resulting polyhedron is a parallelogram with the height equal to the side of the square and the oblique sides parallel to the line . Instead, if we do not use an invertible transformation for the same variable; for example, the affine expression :
Linear_Expression expr = y;

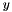the resulting polyhedron is a diagonal of the square.

Example 7: The following code shows the use of the function affine_preimage:
C_Polyhedron ph(2);

ph.add_constraint(x >= 0);

ph.add_constraint(x <= 3);

ph.add_constraint(y >= 0);

ph.add_constraint(y <= 3);

Linear_Expression expr = x + 4;

ph.affine_preimage(x, expr);

In this example the starting polyhedron, var and the affine expression and the denominator are the same as in Example 6, while the resulting polyhedron is again the same square, but translated to the left. Moreover, if the affine transformation for x is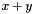
Linear_Expression expr = x + y;

the resulting polyhedron is a parallelogram with the height equal to the side of the square and the oblique sides parallel to the line 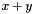. Instead, if we do not use an invertible transformation for the same variable x, for example, the affine expression :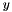
Linear_Expression expr = y;

the resulting polyhedron is a line that corresponds to the 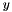axis.

Example 8: For this example we use also the variables:
Variable z(2);

Variable w(3);

The following code shows the use of the function remove_space_dimensions:
Generator_System gs;

gs.insert(point(3*x + y + 0*z + 2*w));

C_Polyhedron ph(gs);

Variables_Set vars;

vars.insert(y);

vars.insert(z);

ph.remove_space_dimensions(vars);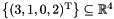

The starting polyhedron is the singleton set $\bigl\{ (3, 1, 0, 2)^\transpose \bigr\} \sseq \Rset^4$ , while the resulting polyhedron is 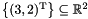$\bigl\{ (3, 2)^\transpose \bigr\} \sseq \Rset^2$ . Be careful when removing space dimensions incrementally: since dimensions are automatically renamed after each application of the remove_space_dimensions operator, unexpected results can be obtained. For instance, by using the following code we would obtain a different result:
set<Variable> vars1;

vars1.insert(y);

ph.remove_space_dimensions(vars1);

set<Variable> vars2;

vars2.insert(z);

ph.remove_space_dimensions(vars2);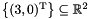

In this case, the result is the polyhedron $\bigl\{(3, 0)^\transpose \bigr\} \sseq \Rset^2$ : when removing the set of dimensions vars2 we are actually removing variable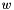 of the original polyhedron. For the same reason, the operator remove_space_dimensions is not idempotent: removing twice the same non-empty set of dimensions is never the same as removing them just once.

Constructor & Destructor Documentation

Parma_Polyhedra_Library::Polyhedron::Polyhedron	(	Topology	topol,
		dimension_type	num_dimensions,
		Degenerate_Element	kind
	)

protected

Builds a polyhedron having the specified properties.

Parameters

topol	The topology of the polyhedron;
num_dimensions	The number of dimensions of the vector space enclosing the polyhedron;
kind	Specifies whether the universe or the empty polyhedron has to be built.

Parma_Polyhedra_Library::Polyhedron::Polyhedron	(	const Polyhedron &	y,
		Complexity_Class	complexity = `ANY_COMPLEXITY`
	)

protected

Ordinary copy constructor.

The complexity argument is ignored.

Parma_Polyhedra_Library::Polyhedron::Polyhedron	(	Topology	topol,
		const Constraint_System &	cs
	)

protected

Builds a polyhedron from a system of constraints.

The polyhedron inherits the space dimension of the constraint system.

Parameters

topol	The topology of the polyhedron;
cs	The system of constraints defining the polyhedron.

Exceptions

std::invalid_argument Thrown if the topology of cs is incompatible with topol.

Parma_Polyhedra_Library::Polyhedron::Polyhedron	(	Topology	topol,
		Constraint_System &	cs,
		Recycle_Input	dummy
	)

protected

Builds a polyhedron recycling a system of constraints.

The polyhedron inherits the space dimension of the constraint system.

Parameters

topol	The topology of the polyhedron;
cs	The system of constraints defining the polyhedron. It is not declared `const` because its data-structures may be recycled to build the polyhedron.
dummy	A dummy tag to syntactically differentiate this one from the other constructors.

Exceptions

std::invalid_argument Thrown if the topology of cs is incompatible with topol.

Parma_Polyhedra_Library::Polyhedron::Polyhedron	(	Topology	topol,
		const Generator_System &	gs
	)

protected

Builds a polyhedron from a system of generators.

The polyhedron inherits the space dimension of the generator system.

Parameters

topol	The topology of the polyhedron;
gs	The system of generators defining the polyhedron.

Exceptions

std::invalid_argument Thrown if the topology of gs is incompatible with topol, or if the system of generators is not empty but has no points.

Parma_Polyhedra_Library::Polyhedron::Polyhedron	(	Topology	topol,
		Generator_System &	gs,
		Recycle_Input	dummy
	)

protected

Builds a polyhedron recycling a system of generators.

The polyhedron inherits the space dimension of the generator system.

Parameters

topol	The topology of the polyhedron;
gs	The system of generators defining the polyhedron. It is not declared `const` because its data-structures may be recycled to build the polyhedron.
dummy	A dummy tag to syntactically differentiate this one from the other constructors.

Exceptions

std::invalid_argument Thrown if the topology of gs is incompatible with topol, or if the system of generators is not empty but has no points.

template<typename Interval >

Parma_Polyhedra_Library::Polyhedron::Polyhedron	(	Topology	topol,
		const Box< Interval > &	box,
		Complexity_Class	complexity = `ANY_COMPLEXITY`
	)

protected

Builds a polyhedron from a box.

This will use an algorithm whose complexity is polynomial and build the smallest polyhedron with topology topol containing box.

Parameters

topol	The topology of the polyhedron;
box	The box representing the polyhedron to be built;
complexity	This argument is ignored.

Member Function Documentation

Poly_Con_Relation Parma_Polyhedra_Library::Polyhedron::relation_with ( const Constraint & c ) const

Returns the relations holding between the polyhedron *this and the constraint c.

Exceptions

std::invalid_argument Thrown if *this and constraint c are dimension-incompatible.

Poly_Gen_Relation Parma_Polyhedra_Library::Polyhedron::relation_with ( const Generator & g ) const

Returns the relations holding between the polyhedron *this and the generator g.

Exceptions

std::invalid_argument Thrown if *this and generator g are dimension-incompatible.

Poly_Con_Relation Parma_Polyhedra_Library::Polyhedron::relation_with ( const Congruence & cg ) const

Returns the relations holding between the polyhedron *this and the congruence c.

Exceptions

std::invalid_argument Thrown if *this and congruence c are dimension-incompatible.

bool Parma_Polyhedra_Library::Polyhedron::is_disjoint_from ( const Polyhedron & y ) const

Returns true if and only if *this and y are disjoint.

Exceptions

std::invalid_argument Thrown if x and y are topology-incompatible or dimension-incompatible.

bool Parma_Polyhedra_Library::Polyhedron::constrains ( Variable var ) const

Returns true if and only if var is constrained in *this.

Exceptions

std::invalid_argument Thrown if var is not a space dimension of *this.

bool Parma_Polyhedra_Library::Polyhedron::bounds_from_above ( const Linear_Expression & expr ) const

inline

Returns true if and only if expr is bounded from above in *this.

Exceptions

std::invalid_argument Thrown if expr and *this are dimension-incompatible.

bool Parma_Polyhedra_Library::Polyhedron::bounds_from_below ( const Linear_Expression & expr ) const

inline

Returns true if and only if expr is bounded from below in *this.

Exceptions

std::invalid_argument Thrown if expr and *this are dimension-incompatible.

bool Parma_Polyhedra_Library::Polyhedron::maximize	(	const Linear_Expression &	expr,
		Coefficient &	sup_n,
		Coefficient &	sup_d,
		bool &	maximum
	)		const

inline

Returns true if and only if *this is not empty and expr is bounded from above in *this, in which case the supremum value is computed.

Parameters

expr	The linear expression to be maximized subject to `*this`;
sup_n	The numerator of the supremum value;
sup_d	The denominator of the supremum value;
maximum	`true` if and only if the supremum is also the maximum value.

Exceptions

std::invalid_argument Thrown if expr and *this are dimension-incompatible.

If *this is empty or expr is not bounded from above, false is returned and sup_n, sup_d and maximum are left untouched.

bool Parma_Polyhedra_Library::Polyhedron::maximize	(	const Linear_Expression &	expr,
		Coefficient &	sup_n,
		Coefficient &	sup_d,
		bool &	maximum,
		Generator &	g
	)		const

inline

Returns true if and only if *this is not empty and expr is bounded from above in *this, in which case the supremum value and a point where expr reaches it are computed.

Parameters

expr	The linear expression to be maximized subject to `*this`;
sup_n	The numerator of the supremum value;
sup_d	The denominator of the supremum value;
maximum	`true` if and only if the supremum is also the maximum value;
g	When maximization succeeds, will be assigned the point or closure point where `expr` reaches its supremum value.

Exceptions

std::invalid_argument Thrown if expr and *this are dimension-incompatible.

If *this is empty or expr is not bounded from above, false is returned and sup_n, sup_d, maximum and g are left untouched.

bool Parma_Polyhedra_Library::Polyhedron::minimize	(	const Linear_Expression &	expr,
		Coefficient &	inf_n,
		Coefficient &	inf_d,
		bool &	minimum
	)		const

inline

Returns true if and only if *this is not empty and expr is bounded from below in *this, in which case the infimum value is computed.

Parameters

expr	The linear expression to be minimized subject to `*this`;
inf_n	The numerator of the infimum value;
inf_d	The denominator of the infimum value;
minimum	`true` if and only if the infimum is also the minimum value.

Exceptions

std::invalid_argument Thrown if expr and *this are dimension-incompatible.

If *this is empty or expr is not bounded from below, false is returned and inf_n, inf_d and minimum are left untouched.

bool Parma_Polyhedra_Library::Polyhedron::minimize	(	const Linear_Expression &	expr,
		Coefficient &	inf_n,
		Coefficient &	inf_d,
		bool &	minimum,
		Generator &	g
	)		const

inline

Returns true if and only if *this is not empty and expr is bounded from below in *this, in which case the infimum value and a point where expr reaches it are computed.

Parameters

expr	The linear expression to be minimized subject to `*this`;
inf_n	The numerator of the infimum value;
inf_d	The denominator of the infimum value;
minimum	`true` if and only if the infimum is also the minimum value;
g	When minimization succeeds, will be assigned a point or closure point where `expr` reaches its infimum value.

Exceptions

std::invalid_argument Thrown if expr and *this are dimension-incompatible.

If *this is empty or expr is not bounded from below, false is returned and inf_n, inf_d, minimum and g are left untouched.

bool Parma_Polyhedra_Library::Polyhedron::frequency	(	const Linear_Expression &	expr,
		Coefficient &	freq_n,
		Coefficient &	freq_d,
		Coefficient &	val_n,
		Coefficient &	val_d
	)		const

Returns true if and only if there exist a unique value val such that *this saturates the equality expr = val.

Parameters

expr	The linear expression for which the frequency is needed;
freq_n	If `true` is returned, the value is set to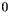 ; Present for interface compatibility with class Grid, where the frequency can have a non-zero value;
freq_d	If `true` is returned, the value is set to ;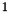
val_n	The numerator of `val`;
val_d	The denominator of `val`;

Exceptions

std::invalid_argument Thrown if expr and *this are dimension-incompatible.

If false is returned, then freq_n, freq_d, val_n and val_d are left untouched.

bool Parma_Polyhedra_Library::Polyhedron::contains ( const Polyhedron & y ) const

Returns true if and only if *this contains y.

Exceptions

std::invalid_argument Thrown if *this and y are topology-incompatible or dimension-incompatible.

bool Parma_Polyhedra_Library::Polyhedron::strictly_contains ( const Polyhedron & y ) const

inline

Returns true if and only if *this strictly contains y.

Exceptions

std::invalid_argument Thrown if *this and y are topology-incompatible or dimension-incompatible.

bool Parma_Polyhedra_Library::Polyhedron::OK ( bool check_not_empty = false ) const

Checks if all the invariants are satisfied.

Returns: true if and only if *this satisfies all the invariants and either check_not_empty is false or *this is not empty.

Parameters

check_not_empty true if and only if, in addition to checking the invariants, *this must be checked to be not empty.

The check is performed so as to intrude as little as possible. If the library has been compiled with run-time assertions enabled, error messages are written on std::cerr in case invariants are violated. This is useful for the purpose of debugging the library.

void Parma_Polyhedra_Library::Polyhedron::add_constraint ( const Constraint & c )

Adds a copy of constraint c to the system of constraints of *this (without minimizing the result).

Parameters

c	The constraint that will be added to the system of constraints of `*this`.

Exceptions

std::invalid_argument Thrown if *this and constraint c are topology-incompatible or dimension-incompatible.

void Parma_Polyhedra_Library::Polyhedron::add_generator ( const Generator & g )

Adds a copy of generator g to the system of generators of *this (without minimizing the result).

Exceptions

std::invalid_argument Thrown if *this and generator g are topology-incompatible or dimension-incompatible, or if *this is an empty polyhedron and g is not a point.

void Parma_Polyhedra_Library::Polyhedron::add_congruence ( const Congruence & cg )

Adds a copy of congruence cg to *this, if cg can be exactly represented by a polyhedron.

Exceptions

std::invalid_argument Thrown if *this and congruence cg are dimension-incompatible, of if cg is a proper congruence which is neither a tautology, nor a contradiction.

void Parma_Polyhedra_Library::Polyhedron::add_constraints ( const Constraint_System & cs )

Adds a copy of the constraints in cs to the system of constraints of *this (without minimizing the result).

Parameters

cs	Contains the constraints that will be added to the system of constraints of `*this`.

Exceptions

std::invalid_argument Thrown if *this and cs are topology-incompatible or dimension-incompatible.

void Parma_Polyhedra_Library::Polyhedron::add_recycled_constraints ( Constraint_System & cs )

Adds the constraints in cs to the system of constraints of *this (without minimizing the result).

Parameters

cs	The constraint system to be added to `*this`. The constraints in `cs` may be recycled.

Exceptions

std::invalid_argument Thrown if *this and cs are topology-incompatible or dimension-incompatible.

Warning: The only assumption that can be made on cs upon successful or exceptional return is that it can be safely destroyed.

void Parma_Polyhedra_Library::Polyhedron::add_generators ( const Generator_System & gs )

Adds a copy of the generators in gs to the system of generators of *this (without minimizing the result).

Parameters

gs	Contains the generators that will be added to the system of generators of `*this`.

Exceptions

std::invalid_argument Thrown if *this and gs are topology-incompatible or dimension-incompatible, or if *this is empty and the system of generators gs is not empty, but has no points.

void Parma_Polyhedra_Library::Polyhedron::add_recycled_generators ( Generator_System & gs )

Adds the generators in gs to the system of generators of *this (without minimizing the result).

Parameters

gs	The generator system to be added to `*this`. The generators in `gs` may be recycled.

Exceptions

std::invalid_argument Thrown if *this and gs are topology-incompatible or dimension-incompatible, or if *this is empty and the system of generators gs is not empty, but has no points.

Warning: The only assumption that can be made on gs upon successful or exceptional return is that it can be safely destroyed.

void Parma_Polyhedra_Library::Polyhedron::add_congruences ( const Congruence_System & cgs )

Adds a copy of the congruences in cgs to *this, if all the congruences can be exactly represented by a polyhedron.

Parameters

cgs	The congruences to be added.

Exceptions

std::invalid_argument Thrown if *this and cgs are dimension-incompatible, of if there exists in cgs a proper congruence which is neither a tautology, nor a contradiction.

void Parma_Polyhedra_Library::Polyhedron::add_recycled_congruences ( Congruence_System & cgs )

inline

Adds the congruences in cgs to *this, if all the congruences can be exactly represented by a polyhedron.

Parameters

cgs	The congruences to be added. Its elements may be recycled.

Exceptions

std::invalid_argument Thrown if *this and cgs are dimension-incompatible, of if there exists in cgs a proper congruence which is neither a tautology, nor a contradiction

Warning: The only assumption that can be made on cgs upon successful or exceptional return is that it can be safely destroyed.

void Parma_Polyhedra_Library::Polyhedron::refine_with_constraint ( const Constraint & c )

Uses a copy of constraint c to refine *this.

Exceptions

std::invalid_argument Thrown if *this and constraint c are dimension-incompatible.

void Parma_Polyhedra_Library::Polyhedron::refine_with_congruence ( const Congruence & cg )

Uses a copy of congruence cg to refine *this.

Exceptions

std::invalid_argument Thrown if *this and congruence cg are dimension-incompatible.

void Parma_Polyhedra_Library::Polyhedron::refine_with_constraints ( const Constraint_System & cs )

Uses a copy of the constraints in cs to refine *this.

Parameters

cs	Contains the constraints used to refine the system of constraints of `*this`.

Exceptions

std::invalid_argument Thrown if *this and cs are dimension-incompatible.

void Parma_Polyhedra_Library::Polyhedron::refine_with_congruences ( const Congruence_System & cgs )

Uses a copy of the congruences in cgs to refine *this.

Parameters

cgs	Contains the congruences used to refine the system of constraints of `*this`.

Exceptions

std::invalid_argument Thrown if *this and cgs are dimension-incompatible.

template<typename FP_Format , typename Interval_Info >

void Parma_Polyhedra_Library::Polyhedron::refine_with_linear_form_inequality	(	const Linear_Form< Interval< FP_Format, Interval_Info > > &	left,
		const Linear_Form< Interval< FP_Format, Interval_Info > > &	right,
		bool	is_strict = `false`
	)

Refines *this with the constraint expressed by left 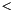$<$ right if is_strict is set, with the constraint left 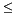$\leq$ right otherwise.

Parameters

left	The linear form on intervals with floating point boundaries that is on the left of the comparison operator. All of its coefficients MUST be bounded.
right	The linear form on intervals with floating point boundaries that is on the right of the comparison operator. All of its coefficients MUST be bounded.
is_strict	True if the comparison is strict.

Exceptions

std::invalid_argument Thrown if left (or right) is dimension-incompatible with *this.

This function is used in abstract interpretation to model a filter that is generated by a comparison of two expressions that are correctly approximated by left and right respectively.

template<typename FP_Format , typename Interval_Info >

void Parma_Polyhedra_Library::Polyhedron::generalized_refine_with_linear_form_inequality	(	const Linear_Form< Interval< FP_Format, Interval_Info > > &	left,
		const Linear_Form< Interval< FP_Format, Interval_Info > > &	right,
		Relation_Symbol	relsym
	)

inline

Refines *this with the constraint expressed by left 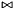$\relsym$ right, where 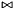$\relsym$ is the relation symbol specified by relsym..

Parameters

left	The linear form on intervals with floating point boundaries that is on the left of the comparison operator. All of its coefficients MUST be bounded.
right	The linear form on intervals with floating point boundaries that is on the right of the comparison operator. All of its coefficients MUST be bounded.
relsym	The relation symbol.

Exceptions

std::invalid_argument	Thrown if `left` (or `right`) is dimension-incompatible with `*this`.
std::runtime_error	Thrown if `relsym` is not a valid relation symbol.

This function is used in abstract interpretation to model a filter that is generated by a comparison of two expressions that are correctly approximated by left and right respectively.

template<typename FP_Format , typename Interval_Info >

void Parma_Polyhedra_Library::Polyhedron::refine_fp_interval_abstract_store ( Box< Interval< FP_Format, Interval_Info > > & store ) const

inline

Refines store with the constraints defining *this.

Parameters

store The interval floating point abstract store to refine.

void Parma_Polyhedra_Library::Polyhedron::unconstrain ( Variable var )

Computes the cylindrification of *this with respect to space dimension var, assigning the result to *this.

Parameters

var	The space dimension that will be unconstrained.

Exceptions

std::invalid_argument Thrown if var is not a space dimension of *this.

void Parma_Polyhedra_Library::Polyhedron::unconstrain ( const Variables_Set & vars )

Computes the cylindrification of *this with respect to the set of space dimensions vars, assigning the result to *this.

Parameters

vars	The set of space dimension that will be unconstrained.

Exceptions

std::invalid_argument Thrown if *this is dimension-incompatible with one of the Variable objects contained in vars.

void Parma_Polyhedra_Library::Polyhedron::intersection_assign ( const Polyhedron & y )

Assigns to *this the intersection of *this and y.

Exceptions

std::invalid_argument Thrown if *this and y are topology-incompatible or dimension-incompatible.

void Parma_Polyhedra_Library::Polyhedron::poly_hull_assign ( const Polyhedron & y )

Assigns to *this the poly-hull of *this and y.

Exceptions

std::invalid_argument Thrown if *this and y are topology-incompatible or dimension-incompatible.

void Parma_Polyhedra_Library::Polyhedron::poly_difference_assign ( const Polyhedron & y )

Assigns to *this the poly-difference of *this and y.

Exceptions

std::invalid_argument Thrown if *this and y are topology-incompatible or dimension-incompatible.

bool Parma_Polyhedra_Library::Polyhedron::simplify_using_context_assign ( const Polyhedron & y )

Assigns to *this a meet-preserving simplification of *this with respect to y. If false is returned, then the intersection is empty.

Exceptions

std::invalid_argument Thrown if *this and y are topology-incompatible or dimension-incompatible.

void Parma_Polyhedra_Library::Polyhedron::affine_image	(	Variable	var,
		const Linear_Expression &	expr,
		Coefficient_traits::const_reference	denominator = `Coefficient_one()`
	)

Assigns to *this the affine image of *this under the function mapping variable var to the affine expression specified by expr and denominator.

Parameters

var	The variable to which the affine expression is assigned;
expr	The numerator of the affine expression;
denominator	The denominator of the affine expression (optional argument with default value 1).

Exceptions

std::invalid_argument Thrown if denominator is zero or if expr and *this are dimension-incompatible or if var is not a space dimension of *this.

template<typename FP_Format , typename Interval_Info >

void Parma_Polyhedra_Library::Polyhedron::affine_form_image	(	Variable	var,
		const Linear_Form< Interval< FP_Format, Interval_Info > > &	lf
	)

Assigns to *this the affine form image of *this under the function mapping variable var into the affine expression(s) specified by lf.

Parameters

var	The variable to which the affine expression is assigned.
lf	The linear form on intervals with floating point boundaries that defines the affine expression(s). ALL of its coefficients MUST be bounded.

Exceptions

std::invalid_argument Thrown if lf and *this are dimension-incompatible or if var is not a space dimension of *this.

This function is used in abstract interpretation to model an assignment of a value that is correctly overapproximated by lf to the floating point variable represented by var.

void Parma_Polyhedra_Library::Polyhedron::affine_preimage	(	Variable	var,
		const Linear_Expression &	expr,
		Coefficient_traits::const_reference	denominator = `Coefficient_one()`
	)

Assigns to *this the affine preimage of *this under the function mapping variable var to the affine expression specified by expr and denominator.

Parameters

var	The variable to which the affine expression is substituted;
expr	The numerator of the affine expression;
denominator	The denominator of the affine expression (optional argument with default value 1).

Exceptions

std::invalid_argument Thrown if denominator is zero or if expr and *this are dimension-incompatible or if var is not a space dimension of *this.

void Parma_Polyhedra_Library::Polyhedron::generalized_affine_image	(	Variable	var,
		Relation_Symbol	relsym,
		const Linear_Expression &	expr,
		Coefficient_traits::const_reference	denominator = `Coefficient_one()`
	)

Assigns to *this the image of *this with respect to the generalized affine relation 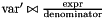$\mathrm{var}' \relsym \frac{\mathrm{expr}}{\mathrm{denominator}}$ , where 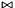$\mathord{\relsym}$ is the relation symbol encoded by relsym.

Parameters

var	The left hand side variable of the generalized affine relation;
relsym	The relation symbol;
expr	The numerator of the right hand side affine expression;
denominator	The denominator of the right hand side affine expression (optional argument with default value 1).

Exceptions

std::invalid_argument Thrown if denominator is zero or if expr and *this are dimension-incompatible or if var is not a space dimension of *this or if *this is a C_Polyhedron and relsym is a strict relation symbol.

void Parma_Polyhedra_Library::Polyhedron::generalized_affine_preimage	(	Variable	var,
		Relation_Symbol	relsym,
		const Linear_Expression &	expr,
		Coefficient_traits::const_reference	denominator = `Coefficient_one()`
	)

Assigns to *this the preimage of *this with respect to the generalized affine relation 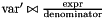$\mathrm{var}' \relsym \frac{\mathrm{expr}}{\mathrm{denominator}}$ , where 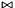$\mathord{\relsym}$ is the relation symbol encoded by relsym.

Parameters

var	The left hand side variable of the generalized affine relation;
relsym	The relation symbol;
expr	The numerator of the right hand side affine expression;
denominator	The denominator of the right hand side affine expression (optional argument with default value 1).

Exceptions

std::invalid_argument Thrown if denominator is zero or if expr and *this are dimension-incompatible or if var is not a space dimension of *this or if *this is a C_Polyhedron and relsym is a strict relation symbol.

void Parma_Polyhedra_Library::Polyhedron::generalized_affine_image	(	const Linear_Expression &	lhs,
		Relation_Symbol	relsym,
		const Linear_Expression &	rhs
	)

Assigns to *this the image of *this with respect to the generalized affine relation 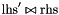$\mathrm{lhs}' \relsym \mathrm{rhs}$ , where 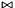$\mathord{\relsym}$ is the relation symbol encoded by relsym.

Parameters

lhs	The left hand side affine expression;
relsym	The relation symbol;
rhs	The right hand side affine expression.

Exceptions

std::invalid_argument Thrown if *this is dimension-incompatible with lhs or rhs or if *this is a C_Polyhedron and relsym is a strict relation symbol.

void Parma_Polyhedra_Library::Polyhedron::generalized_affine_preimage	(	const Linear_Expression &	lhs,
		Relation_Symbol	relsym,
		const Linear_Expression &	rhs
	)

Assigns to *this the preimage of *this with respect to the generalized affine relation 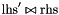$\mathrm{lhs}' \relsym \mathrm{rhs}$ , where 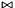$\mathord{\relsym}$ is the relation symbol encoded by relsym.

Parameters

lhs	The left hand side affine expression;
relsym	The relation symbol;
rhs	The right hand side affine expression.

Exceptions

std::invalid_argument Thrown if *this is dimension-incompatible with lhs or rhs or if *this is a C_Polyhedron and relsym is a strict relation symbol.

void Parma_Polyhedra_Library::Polyhedron::bounded_affine_image	(	Variable	var,
		const Linear_Expression &	lb_expr,
		const Linear_Expression &	ub_expr,
		Coefficient_traits::const_reference	denominator = `Coefficient_one()`
	)

Assigns to *this the image of *this with respect to the bounded affine relation 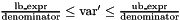$\frac{\mathrm{lb\_expr}}{\mathrm{denominator}} \leq \mathrm{var}' \leq \frac{\mathrm{ub\_expr}}{\mathrm{denominator}}$ .

Parameters

var	The variable updated by the affine relation;
lb_expr	The numerator of the lower bounding affine expression;
ub_expr	The numerator of the upper bounding affine expression;
denominator	The (common) denominator for the lower and upper bounding affine expressions (optional argument with default value 1).

Exceptions

std::invalid_argument Thrown if denominator is zero or if lb_expr (resp., ub_expr) and *this are dimension-incompatible or if var is not a space dimension of *this.

void Parma_Polyhedra_Library::Polyhedron::bounded_affine_preimage	(	Variable	var,
		const Linear_Expression &	lb_expr,
		const Linear_Expression &	ub_expr,
		Coefficient_traits::const_reference	denominator = `Coefficient_one()`
	)

Assigns to *this the preimage of *this with respect to the bounded affine relation 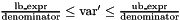$\frac{\mathrm{lb\_expr}}{\mathrm{denominator}} \leq \mathrm{var}' \leq \frac{\mathrm{ub\_expr}}{\mathrm{denominator}}$ .

Parameters

var	The variable updated by the affine relation;
lb_expr	The numerator of the lower bounding affine expression;
ub_expr	The numerator of the upper bounding affine expression;
denominator	The (common) denominator for the lower and upper bounding affine expressions (optional argument with default value 1).

Exceptions

std::invalid_argument Thrown if denominator is zero or if lb_expr (resp., ub_expr) and *this are dimension-incompatible or if var is not a space dimension of *this.

void Parma_Polyhedra_Library::Polyhedron::time_elapse_assign ( const Polyhedron & y )

Assigns to *this the result of computing the time-elapse between *this and y.

Exceptions

std::invalid_argument Thrown if *this and y are topology-incompatible or dimension-incompatible.

void Parma_Polyhedra_Library::Polyhedron::positive_time_elapse_assign ( const Polyhedron & y )

Assigns to *this (the best approximation of) the result of computing the positive time-elapse between *this and y.

Exceptions

std::invalid_argument Thrown if *this and y are dimension-incompatible.

void Parma_Polyhedra_Library::Polyhedron::wrap_assign	(	const Variables_Set &	vars,
		Bounded_Integer_Type_Width	w,
		Bounded_Integer_Type_Representation	r,
		Bounded_Integer_Type_Overflow	o,
		const Constraint_System *	cs_p = `0`,
		unsigned	complexity_threshold = `16`,
		bool	wrap_individually = `true`
	)

Wraps the specified dimensions of the vector space.

Parameters

vars	The set of Variable objects corresponding to the space dimensions to be wrapped.
w	The width of the bounded integer type corresponding to all the dimensions to be wrapped.
r	The representation of the bounded integer type corresponding to all the dimensions to be wrapped.
o	The overflow behavior of the bounded integer type corresponding to all the dimensions to be wrapped.
cs_p	Possibly null pointer to a constraint system whose variables are contained in `vars`. If `cs_p` depends on variables not in `vars`, the behavior is undefined. When non-null, the pointed-to constraint system is assumed to represent the conditional or looping construct guard with respect to which wrapping is performed. Since wrapping requires the computation of upper bounds and due to non-distributivity of constraint refinement over upper bounds, passing a constraint system in this way can be more precise than refining the result of the wrapping operation with the constraints in `cs_p`.
complexity_threshold	A precision parameter of the wrapping operator: higher values result in possibly improved precision.
wrap_individually	`true` if the dimensions should be wrapped individually (something that results in much greater efficiency to the detriment of precision).

Exceptions

std::invalid_argument Thrown if *cs_p is dimension-incompatible with vars, or if *this is dimension-incompatible vars or with *cs_p.

void Parma_Polyhedra_Library::Polyhedron::drop_some_non_integer_points ( Complexity_Class complexity = ANY_COMPLEXITY )

inline

Possibly tightens *this by dropping some points with non-integer coordinates.

Parameters

complexity The maximal complexity of any algorithms used.

Note: Currently there is no optimality guarantee, not even if complexity is ANY_COMPLEXITY.

void Parma_Polyhedra_Library::Polyhedron::drop_some_non_integer_points	(	const Variables_Set &	vars,
		Complexity_Class	complexity = `ANY_COMPLEXITY`
	)

inline

Possibly tightens *this by dropping some points with non-integer coordinates for the space dimensions corresponding to vars.

Parameters

vars	Points with non-integer coordinates for these variables/space-dimensions can be discarded.
complexity	The maximal complexity of any algorithms used.

Note: Currently there is no optimality guarantee, not even if complexity is ANY_COMPLEXITY.

void Parma_Polyhedra_Library::Polyhedron::BHRZ03_widening_assign	(	const Polyhedron &	y,
		unsigned *	tp = `0`
	)

Assigns to *this the result of computing the BHRZ03-widening between *this and y.

Parameters

y	A polyhedron that must be contained in `*this`;
tp	An optional pointer to an unsigned variable storing the number of available tokens (to be used when applying the widening with tokens delay technique).

Exceptions

std::invalid_argument Thrown if *this and y are topology-incompatible or dimension-incompatible.

void Parma_Polyhedra_Library::Polyhedron::limited_BHRZ03_extrapolation_assign	(	const Polyhedron &	y,
		const Constraint_System &	cs,
		unsigned *	tp = `0`
	)

Assigns to *this the result of computing the limited extrapolation between *this and y using the BHRZ03-widening operator.

Parameters

y	A polyhedron that must be contained in `*this`;
cs	The system of constraints used to improve the widened polyhedron;
tp	An optional pointer to an unsigned variable storing the number of available tokens (to be used when applying the widening with tokens delay technique).

Exceptions

std::invalid_argument Thrown if *this, y and cs are topology-incompatible or dimension-incompatible.

void Parma_Polyhedra_Library::Polyhedron::bounded_BHRZ03_extrapolation_assign	(	const Polyhedron &	y,
		const Constraint_System &	cs,
		unsigned *	tp = `0`
	)

Assigns to *this the result of computing the bounded extrapolation between *this and y using the BHRZ03-widening operator.

Parameters

y	A polyhedron that must be contained in `*this`;
cs	The system of constraints used to improve the widened polyhedron;
tp	An optional pointer to an unsigned variable storing the number of available tokens (to be used when applying the widening with tokens delay technique).

Exceptions

std::invalid_argument Thrown if *this, y and cs are topology-incompatible or dimension-incompatible.

void Parma_Polyhedra_Library::Polyhedron::H79_widening_assign	(	const Polyhedron &	y,
		unsigned *	tp = `0`
	)

Assigns to *this the result of computing the H79_widening between *this and y.

Parameters

y	A polyhedron that must be contained in `*this`;
tp	An optional pointer to an unsigned variable storing the number of available tokens (to be used when applying the widening with tokens delay technique).

Exceptions

std::invalid_argument Thrown if *this and y are topology-incompatible or dimension-incompatible.

void Parma_Polyhedra_Library::Polyhedron::limited_H79_extrapolation_assign	(	const Polyhedron &	y,
		const Constraint_System &	cs,
		unsigned *	tp = `0`
	)

Assigns to *this the result of computing the limited extrapolation between *this and y using the H79-widening operator.

Parameters

y	A polyhedron that must be contained in `*this`;
cs	The system of constraints used to improve the widened polyhedron;
tp	An optional pointer to an unsigned variable storing the number of available tokens (to be used when applying the widening with tokens delay technique).

Exceptions

std::invalid_argument Thrown if *this, y and cs are topology-incompatible or dimension-incompatible.

void Parma_Polyhedra_Library::Polyhedron::bounded_H79_extrapolation_assign	(	const Polyhedron &	y,
		const Constraint_System &	cs,
		unsigned *	tp = `0`
	)

Assigns to *this the result of computing the bounded extrapolation between *this and y using the H79-widening operator.

Parameters

y	A polyhedron that must be contained in `*this`;
cs	The system of constraints used to improve the widened polyhedron;
tp	An optional pointer to an unsigned variable storing the number of available tokens (to be used when applying the widening with tokens delay technique).

Exceptions

std::invalid_argument Thrown if *this, y and cs are topology-incompatible or dimension-incompatible.

void Parma_Polyhedra_Library::Polyhedron::add_space_dimensions_and_embed ( dimension_type m )

Adds m new space dimensions and embeds the old polyhedron in the new vector space.

Parameters

m	The number of dimensions to add.

Exceptions

std::length_error Thrown if adding m new space dimensions would cause the vector space to exceed dimension max_space_dimension().

The new space dimensions will be those having the highest indexes in the new polyhedron, which is characterized by a system of constraints in which the variables running through the new dimensions are not constrained. For instance, when starting from the polyhedron 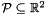$\cP \sseq \Rset^2$ and adding a third space dimension, the result will be the polyhedron

$\bigl\{\, (x, y, z)^\transpose \in \Rset^3 \bigm| (x, y)^\transpose \in \cP \,\bigr\}.$

void Parma_Polyhedra_Library::Polyhedron::add_space_dimensions_and_project ( dimension_type m )

Adds m new space dimensions to the polyhedron and does not embed it in the new vector space.

Parameters

m	The number of space dimensions to add.

Exceptions

std::length_error Thrown if adding m new space dimensions would cause the vector space to exceed dimension max_space_dimension().

The new space dimensions will be those having the highest indexes in the new polyhedron, which is characterized by a system of constraints in which the variables running through the new dimensions are all constrained to be equal to 0. For instance, when starting from the polyhedron 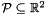$\cP \sseq \Rset^2$ and adding a third space dimension, the result will be the polyhedron

$\bigl\{\, (x, y, 0)^\transpose \in \Rset^3 \bigm| (x, y)^\transpose \in \cP \,\bigr\}.$

void Parma_Polyhedra_Library::Polyhedron::concatenate_assign ( const Polyhedron & y )

Assigns to *this the concatenation of *this and y, taken in this order.

Exceptions

std::invalid_argument	Thrown if `*this` and `y` are topology-incompatible.
std::length_error	Thrown if the concatenation would cause the vector space to exceed dimension `max_space_dimension()`.

void Parma_Polyhedra_Library::Polyhedron::remove_space_dimensions ( const Variables_Set & vars )

Removes all the specified dimensions from the vector space.

Parameters

vars	The set of Variable objects corresponding to the space dimensions to be removed.

Exceptions

std::invalid_argument Thrown if *this is dimension-incompatible with one of the Variable objects contained in vars.

void Parma_Polyhedra_Library::Polyhedron::remove_higher_space_dimensions ( dimension_type new_dimension )

Removes the higher dimensions of the vector space so that the resulting space will have dimension new_dimension.

Exceptions

std::invalid_argument Thrown if new_dimensions is greater than the space dimension of *this.

template<typename Partial_Function >

void Parma_Polyhedra_Library::Polyhedron::map_space_dimensions ( const Partial_Function & pfunc )

Remaps the dimensions of the vector space according to a partial function.

Parameters

pfunc The partial function specifying the destiny of each space dimension.

The template type parameter Partial_Function must provide the following methods.

bool has_empty_codomain() const

returns true if and only if the represented partial function has an empty codomain (i.e., it is always undefined). The has_empty_codomain() method will always be called before the methods below. However, if has_empty_codomain() returns true, none of the functions below will be called.

dimension_type max_in_codomain() const

returns the maximum value that belongs to the codomain of the partial function. The max_in_codomain() method is called at most once.

bool maps(dimension_type i, dimension_type& j) const

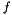Let $f$ be the represented function and 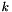$k$ be the value of i. If 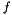$f$ is defined in 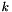$k$ , then $f(k)$ is assigned to j and true is returned. If 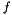$f$ is undefined in 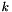$k$ , then false is returned. This method is called at most 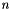$n$ times, where 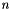$n$ is the dimension of the vector space enclosing the polyhedron.

The result is undefined if pfunc does not encode a partial function with the properties described in the specification of the mapping operator.

void Parma_Polyhedra_Library::Polyhedron::expand_space_dimension	(	Variable	var,
		dimension_type	m
	)

Creates m copies of the space dimension corresponding to var.

Parameters

var	The variable corresponding to the space dimension to be replicated;
m	The number of replicas to be created.

Exceptions

std::invalid_argument	Thrown if `var` does not correspond to a dimension of the vector space.
std::length_error	Thrown if adding `m` new space dimensions would cause the vector space to exceed dimension `max_space_dimension()`.

If *this has space dimension 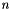$n$ , with 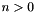$n > 0$ , and var has space dimension 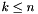$k \leq n$ , then the 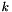$k$ -th space dimension is expanded to m new space dimensions 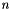$n$ , $n+1$ , $\dots$ , $n+m-1$ .

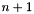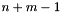void Parma_Polyhedra_Library::Polyhedron::fold_space_dimensions	(	const Variables_Set &	vars,
		Variable	dest
	)

Folds the space dimensions in vars into dest.

Parameters

vars	The set of Variable objects corresponding to the space dimensions to be folded;
dest	The variable corresponding to the space dimension that is the destination of the folding operation.

Exceptions

std::invalid_argument Thrown if *this is dimension-incompatible with dest or with one of the Variable objects contained in vars. Also thrown if dest is contained in vars.

If *this has space dimension 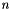$n$ , with 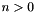$n > 0$ , dest has space dimension 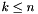$k \leq n$ , vars is a set of variables whose maximum space dimension is also less than or equal to 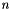$n$ , and dest is not a member of vars, then the space dimensions corresponding to variables in vars are folded into the 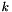$k$ -th space dimension.

void Parma_Polyhedra_Library::Polyhedron::m_swap ( Polyhedron & y )

inline

Swaps *this with polyhedron y. (*this and y can be dimension-incompatible.)

Exceptions

std::invalid_argument Thrown if x and y are topology-incompatible.

int32_t Parma_Polyhedra_Library::Polyhedron::hash_code ( ) const

inline

Returns a 32-bit hash code for *this.

If x and y are such that x == y, then x.hash_code() == y.hash_code().

void Parma_Polyhedra_Library::Polyhedron::drop_some_non_integer_points	(	const Variables_Set *	vars_p,
		Complexity_Class	complexity
	)

protected

Possibly tightens *this by dropping some points with non-integer coordinates for the space dimensions corresponding to *vars_p.

Parameters

vars_p	When nonzero, points with non-integer coordinates for the variables/space-dimensions contained in `*vars_p` can be discarded.
complexity	The maximal complexity of any algorithms used.

Note: Currently there is no optimality guarantee, not even if complexity is ANY_COMPLEXITY.

template<typename FP_Format , typename Interval_Info >

void Parma_Polyhedra_Library::Polyhedron::overapproximate_linear_form	(	const Linear_Form< Interval< FP_Format, Interval_Info > > &	lf,
		const dimension_type	lf_dimension,
		Linear_Form< Interval< FP_Format, Interval_Info > > &	result
	)

protected

Helper function that overapproximates an interval linear form.

Parameters

lf	The linear form on intervals with floating point boundaries to approximate. ALL of its coefficients MUST be bounded.
lf_dimension	Must be the space dimension of `lf`.
result	Used to store the result.

This function makes result become a linear form that is a correct approximation of lf under the constraints specified by *this. The resulting linear form has the property that all of its variable coefficients have a non-significant upper bound and can thus be considered as singletons.

template<typename FP_Format , typename Interval_Info >

void Parma_Polyhedra_Library::Polyhedron::convert_to_integer_expression	(	const Linear_Form< Interval< FP_Format, Interval_Info > > &	lf,
		const dimension_type	lf_dimension,
		Linear_Expression &	result
	)

staticprotected

Helper function that makes result become a Linear_Expression obtained by normalizing the denominators in lf.

Parameters

lf	The linear form on intervals with floating point boundaries to normalize. It should be the result of an application of static method `overapproximate_linear_form`.
lf_dimension	Must be the space dimension of `lf`.
result	Used to store the result.

This function ignores the upper bound of intervals in lf, so that in fact result can be seen as lf multiplied by a proper normalization constant.

template<typename FP_Format , typename Interval_Info >

void Parma_Polyhedra_Library::Polyhedron::convert_to_integer_expressions	(	const Linear_Form< Interval< FP_Format, Interval_Info > > &	lf,
		const dimension_type	lf_dimension,
		Linear_Expression &	res,
		Coefficient &	res_low_coeff,
		Coefficient &	res_hi_coeff,
		Coefficient &	denominator
	)

staticprotected

Normalization helper function.

Parameters

lf	The linear form on intervals with floating point boundaries to normalize. It should be the result of an application of static method `overapproximate_linear_form`.
lf_dimension	Must be the space dimension of `lf`.
res	Stores the normalized linear form, except its inhomogeneous term.
res_low_coeff	Stores the lower boundary of the inhomogeneous term of the result.
res_hi_coeff	Stores the higher boundary of the inhomogeneous term of the result.
denominator	Becomes the common denominator of `res_low_coeff`, `res_hi_coeff` and all coefficients in `res`.

Results are obtained by normalizing denominators in lf, ignoring the upper bounds of variable coefficients in lf.

void Parma_Polyhedra_Library::Polyhedron::positive_time_elapse_assign_impl ( const Polyhedron & y )

protected

Assuming *this is NNC, assigns to *this the result of the "positive time-elapse" between *this and y.

Exceptions

std::invalid_argument Thrown if *this and y are dimension-incompatible.

Friends And Related Function Documentation

std::ostream & operator<<	(	std::ostream &	s,
		const Polyhedron &	ph
	)

Writes a textual representation of ph on s: false is written if ph is an empty polyhedron; true is written if ph is a universe polyhedron; a minimized system of constraints defining ph is written otherwise, all constraints in one row separated by ", ".

void swap	(	Polyhedron &	x,
		Polyhedron &	y
	)

bool operator==	(	const Polyhedron &	x,
		const Polyhedron &	y
	)

Note that x and y may be topology- and/or dimension-incompatible polyhedra: in those cases, the value false is returned.

bool operator!=	(	const Polyhedron &	x,
		const Polyhedron &	y
	)

Note that x and y may be topology- and/or dimension-incompatible polyhedra: in those cases, the value true is returned.

void swap	(	Polyhedron &	x,
		Polyhedron &	y
	)

bool operator!=	(	const Polyhedron &	x,
		const Polyhedron &	y
	)

ppl.hh

Public Types

Public Member Functions

Static Public Member Functions

Protected Member Functions

Static Protected Member Functions

Related Functions

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation

Friends And Related Function Documentation