A cache-oblivious binary search tree of pairs. More...

#include <CO_Tree_defs.hh>

Collaboration diagram for Parma_Polyhedra_Library::CO_Tree:

Classes
class	const_iterator
	A const iterator on the tree elements, ordered by key. More...

class	iterator
	An iterator on the tree elements, ordered by key. More...

class	tree_iterator

Public Types
typedef Coefficient	data_type
	The type of the data elements associated with keys. More...

typedef Coefficient_traits::const_reference	data_type_const_reference

Public Member Functions
	CO_Tree ()
	Constructs an empty tree. More...

	CO_Tree (const CO_Tree &y)
	The copy constructor. More...

template<typename Iterator >
	CO_Tree (Iterator i, dimension_type n)
	A constructor from a sequence of `n` elements. More...

CO_Tree &	operator= (const CO_Tree &y)
	The assignment operator. More...

void	clear ()
	Removes all elements from the tree. More...

	~CO_Tree ()
	The destructor. More...

bool	empty () const
	Returns `true` if the tree has no elements. More...

dimension_type	size () const
	Returns the number of elements stored in the tree. More...

void	dump_tree () const
	Dumps the tree to stdout, for debugging purposes. More...

dimension_type	external_memory_in_bytes () const
	Returns the size in bytes of the memory managed by `*this`. More...

iterator	insert (dimension_type key)
	Inserts an element in the tree. More...

iterator	insert (dimension_type key, data_type_const_reference data)
	Inserts an element in the tree. More...

iterator	insert (iterator itr, dimension_type key)
	Inserts an element in the tree. More...

iterator	insert (iterator itr, dimension_type key, data_type_const_reference data)
	Inserts an element in the tree. More...

iterator	erase (dimension_type key)
	Erases the element with key `key` from the tree. More...

iterator	erase (iterator itr)
	Erases the element pointed to by `itr` from the tree. More...

void	erase_element_and_shift_left (dimension_type key)
	Removes the element with key `key` (if it exists) and decrements by 1 all elements' keys that were greater than `key`. More...

void	increase_keys_from (dimension_type key, dimension_type n)
	Adds `n` to all keys greater than or equal to `key`. More...

void	fast_shift (dimension_type i, iterator itr)

void	m_swap (CO_Tree &x)
	Swaps x with *this. More...

iterator	begin ()
	Returns an iterator that points at the first element. More...

const iterator &	end ()
	Returns an iterator that points after the last element. More...

const_iterator	begin () const
	Equivalent to cbegin(). More...

const const_iterator &	end () const
	Equivalent to cend(). More...

const_iterator	cbegin () const
	Returns a const_iterator that points at the first element. More...

const const_iterator &	cend () const
	Returns a const_iterator that points after the last element. More...

iterator	bisect (dimension_type key)
	Searches an element with key `key` using bisection. More...

const_iterator	bisect (dimension_type key) const
	Searches an element with key `key` using bisection. More...

iterator	bisect_in (iterator first, iterator last, dimension_type key)
	Searches an element with key `key` in [first, last] using bisection. More...

const_iterator	bisect_in (const_iterator first, const_iterator last, dimension_type key) const
	Searches an element with key `key` in [first, last] using bisection. More...

iterator	bisect_near (iterator hint, dimension_type key)
	Searches an element with key `key` near `hint`. More...

const_iterator	bisect_near (const_iterator hint, dimension_type key) const
	Searches an element with key `key` near `hint`. More...

Static Public Member Functions
static dimension_type	max_size ()
	Returns the size() of the largest possible CO_Tree. More...

Private Types
typedef unsigned	height_t
	This is used for node heights and depths in the tree. More...

Private Member Functions
	PPL_COMPILE_TIME_CHECK (C_Integer< height_t >::max >=sizeof_to_bits(sizeof(dimension_type)),"height_t is too small to store depths.")

dimension_type	dfs_index (const_iterator itr) const

dimension_type	dfs_index (iterator itr) const

dimension_type	bisect_in (dimension_type first, dimension_type last, dimension_type key) const
	Searches an element with key `key` in [first, last] using bisection. More...

dimension_type	bisect_near (dimension_type hint, dimension_type key) const
	Searches an element with key `key` near `hint`. More...

tree_iterator	insert_precise (dimension_type key, data_type_const_reference data, tree_iterator itr)
	Inserts an element in the tree. More...

tree_iterator	insert_precise_aux (dimension_type key, data_type_const_reference data, tree_iterator itr)
	Helper for `insert_precise`. More...

void	insert_in_empty_tree (dimension_type key, data_type_const_reference data)
	Inserts an element in the tree. More...

iterator	erase (tree_iterator itr)
	Erases from the tree the element pointed to by `itr` . More...

void	init (dimension_type n)
	Initializes a tree with reserved size at least `n` . More...

void	destroy ()
	Deallocates the tree's dynamic arrays. More...

bool	structure_OK () const
	Checks the internal invariants, but not the densities. More...

bool	OK () const
	Checks the internal invariants. More...

void	rebuild_bigger_tree ()
	Increases the tree's reserved size. More...

void	rebuild_smaller_tree ()
	Decreases the tree's reserved size. More...

void	refresh_cached_iterators ()
	Re-initializes the cached iterators. More...

tree_iterator	rebalance (tree_iterator itr, dimension_type key, data_type_const_reference value)
	Rebalances the tree. More...

dimension_type	compact_elements_in_the_rightmost_end (dimension_type last_in_subtree, dimension_type subtree_size, dimension_type key, data_type_const_reference value, bool add_element)
	Moves all elements of a subtree to the rightmost end. More...

void	redistribute_elements_in_subtree (dimension_type root_index, dimension_type subtree_size, dimension_type last_used, dimension_type key, data_type_const_reference value, bool add_element)
	Redistributes the elements in the subtree rooted at `root_index`. More...

void	move_data_from (CO_Tree &tree)
	Moves all data in the tree `tree` into *this. More...

void	copy_data_from (const CO_Tree &tree)
	Copies all data in the tree `tree` into *this. More...

Static Private Member Functions
static unsigned	integer_log2 (dimension_type n)
	Returns the floor of the base-2 logarithm of `n` . More...

static bool	is_less_than_ratio (dimension_type numer, dimension_type denom, dimension_type ratio)
	Compares the fractions numer/denom with ratio/100. More...

static bool	is_greater_than_ratio (dimension_type numer, dimension_type denom, dimension_type ratio)
	Compares the fractions numer/denom with ratio/100. More...

static void	dump_subtree (tree_iterator itr)
	Dumps the subtree rooted at `itr` to stdout, for debugging purposes. More...

static dimension_type	count_used_in_subtree (tree_iterator itr)
	Counts the number of used elements in the subtree rooted at itr. More...

static void	move_data_element (data_type &to, data_type &from)
	Moves the value of `from` in `to` . More...

Private Attributes
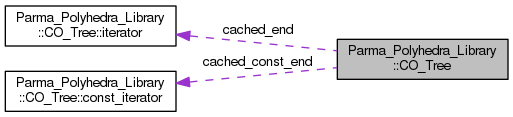
iterator	cached_end
	The iterator returned by end(). More...

const_iterator	cached_const_end
	The iterator returned by the const version of end(). More...

height_t	max_depth
	The depth of the leaves in the complete tree. More...

dimension_type *	indexes
	The vector that contains the keys in the tree. More...

std::allocator< data_type >	data_allocator
	The allocator used to allocate/deallocate data. More...

data_type *	data
	The vector that contains the data of the keys in the tree. More...

dimension_type	reserved_size
	The number of nodes in the complete tree. More...

dimension_type	size_
	The number of values stored in the tree. More...

Static Private Attributes
static const dimension_type	max_density_percent = 91
	The maximum density of used nodes. More...

static const dimension_type	min_density_percent = 38
	The minimum density of used nodes. More...

static const dimension_type	min_leaf_density_percent = 1
	The minimum density at the leaves' depth. More...

static const dimension_type	unused_index = C_Integer<dimension_type>::max
	An index used as a marker for unused nodes in the tree. More...

Related Functions
(Note that these are not member functions.)
void	swap (CO_Tree &x, CO_Tree &y)
	Swaps `x` with `y`. More...

Detailed Description

A cache-oblivious binary search tree of pairs.

This class implements a binary search tree with keys of dimension_type type and data of Coefficient type, laid out in a dynamically-sized array.

The array-based layout saves calls to new/delete (to insert $n$ elements only $O(\log n)$ allocations are performed) and, more importantly, is much more cache-friendly than a standard (pointer-based) tree, because the elements are stored sequentially in memory (leaving some holes to allow fast insertion of new elements). The downside of this representation is that all iterators are invalidated when an element is added or removed, because the array could have been enlarged or shrunk. This is partially addressed by providing references to internal end iterators that are updated when needed.

B-trees are cache-friendly too, but the cache size is fixed (usually at compile-time). This raises two problems: firstly the cache size must be known in advance and those data structures do not perform well with other cache sizes and, secondly, even if the cache size is known, the optimizations target only one level of cache. This kind of data structures are called cache aware. This implementation, instead, is cache oblivious: it performs well with every cache size, and thus exploits all of the available caches.

Assuming n is the number of elements in the tree and B is the number of (dimension_type, Coefficient) pairs that fit in a cache line, the time and cache misses complexities are the following:

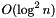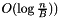Insertions/Queries/Deletions: $O(\log^2 n)$ time, $O(\log \frac{n}{B}))$ cache misses.
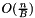Tree traversal from begin() to end(), using an iterator: time, $O(\frac{n}{B})$ cache misses.
Queries with a hint: 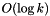$O(\log k)$ time and 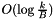$O(\log \frac{k}{B})$ cache misses, where k is the distance between the given iterator and the searched element (or the position where it would have been).

The binary search tree is embedded in a (slightly bigger) complete tree, that is enlarged and shrunk when needed. The complete tree is laid out in an in-order DFS layout in two arrays: one for the keys and one for the associated data. The indexes and values are stored in different arrays to reduce cache-misses during key queries.

The tree can store up to 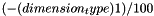$(-(dimension_type)1)/100$ elements. This limit allows faster density computations, but can be removed if needed.

Definition at line 103 of file CO_Tree_defs.hh.

Member Typedef Documentation

typedef Coefficient Parma_Polyhedra_Library::CO_Tree::data_type

The type of the data elements associated with keys.

If this is changed, occurrences of Coefficient_zero() in the CO_Tree implementation have to be replaced with constants of the correct type.

Definition at line 148 of file CO_Tree_defs.hh.

typedef Coefficient_traits::const_reference Parma_Polyhedra_Library::CO_Tree::data_type_const_reference

Definition at line 149 of file CO_Tree_defs.hh.

typedef unsigned Parma_Polyhedra_Library::CO_Tree::height_t

private

This is used for node heights and depths in the tree.

Definition at line 107 of file CO_Tree_defs.hh.

Constructor & Destructor Documentation

Parma_Polyhedra_Library::CO_Tree::CO_Tree ( )

inline

Constructs an empty tree.

This constructor takes $O(1)$ time.

Definition at line 50 of file CO_Tree_inlines.hh.

References init(), and OK().

Referenced by clear().

                  {
   init(0);
   PPL_ASSERT(OK());
 }

Parma_Polyhedra_Library::CO_Tree::CO_Tree ( const CO_Tree & y )

inline

The copy constructor.

Parameters

y	The tree that will be copied.

This constructor takes $O(n)$ time.

Definition at line 56 of file CO_Tree_inlines.hh.

References copy_data_from(), data_allocator, init(), OK(), and reserved_size.

                                  {
   PPL_ASSERT(y.OK());
   data_allocator = y.data_allocator;
   init(y.reserved_size);
   copy_data_from(y);
 }

template<typename Iterator >

Parma_Polyhedra_Library::CO_Tree::CO_Tree	(	Iterator	i,
		dimension_type	n
	)

A constructor from a sequence of n elements.

Parameters

i	An iterator that points to the first element of the sequence.
n	The number of elements in the [i, i_end) sequence.

i must be an input iterator on a sequence of data_type elements, sorted by index. Objects of Iterator type must have an index() method that returns the index with which the element pointed to by the iterator must be inserted.

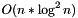This constructor takes $O(n)$ time, so it is more efficient than the construction of an empty tree followed by n insertions, that would take $O(n*\log^2 n)$ time.

Definition at line 30 of file CO_Tree_templates.hh.

References Parma_Polyhedra_Library::CO_Tree::tree_iterator::get_left_child(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::get_parent(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::get_right_child(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::index(), init(), integer_log2(), is_greater_than_ratio(), max_density_percent, OK(), reserved_size, size_, sizeof_to_bits, and unused_index.

                                              {
 
   if (n == 0) {
     init(0);
     PPL_ASSERT(OK());
     return;
   }
 
   const dimension_type new_max_depth = integer_log2(n) + 1;
   reserved_size = (static_cast<dimension_type>(1) << new_max_depth) - 1;
 
   if (is_greater_than_ratio(n, reserved_size, max_density_percent)
       && reserved_size != 3) {
     reserved_size = reserved_size*2 + 1;
   }
 
   init(reserved_size);
 
   tree_iterator root(*this);
 
   // This is static and with static allocation, to improve performance.
   // sizeof_to_bits(sizeof(dimension_type)) is the maximum k such that
   // 2^k-1 is a dimension_type, so it is the maximum tree height.
   // For each node level, the stack may contain up to 4 elements: two elements
   // with operation 0, one element with operation 2 and one element
   // with operation 3. An additional element with operation 1 can be at the
   // top of the tree.
   static std::pair<dimension_type, signed char>
     stack[4U * sizeof_to_bits(sizeof(dimension_type)) + 1U];
 
   dimension_type stack_first_empty = 0;
 
   // A pair (n, operation) in the stack means:
   //
   // * Go to the parent, if operation is 0.
   // * Go to the left child, then fill the current tree with n elements, if
   //   operation is 1.
   // * Go to the right child, then fill the current tree with n elements, if
   //   operation is 2.
   // * Fill the current tree with n elements, if operation is 3.
 
   stack[0].first = n;
   stack[0].second = 3;
   ++stack_first_empty;
 
   while (stack_first_empty != 0) {
 
     // Implement
     //
     // <CODE>
     //   top_n         = stack.top().first;
     //   top_operation = stack.top().second;
     // </CODE>
     const dimension_type top_n = stack[stack_first_empty - 1].first;
     const signed char top_operation = stack[stack_first_empty - 1].second;
 
     switch (top_operation) {
 
     case 0:
       root.get_parent();
       --stack_first_empty;
       continue;
 
     case 1:
       root.get_left_child();
       break;
 
     case 2:
       root.get_right_child();
       break;
 #ifndef NDEBUG
     case 3:
       break;
 
     default:
       // We should not be here
       PPL_UNREACHABLE;
 #endif
     }
 
     // We now visit the current tree
 
     if (top_n == 0) {
       --stack_first_empty;
     }
     else {
       if (top_n == 1) {
         PPL_ASSERT(root.index() == unused_index);
         root.index() = i.index();
         new(&(*root)) data_type(*i);
         ++i;
         --stack_first_empty;
       }
       else {
         PPL_ASSERT(stack_first_empty + 3 < sizeof(stack)/sizeof(stack[0]));
 
         const dimension_type half = (top_n + 1) / 2;
         stack[stack_first_empty - 1].second = 0;
         stack[stack_first_empty    ] = std::make_pair(top_n - half, 2);
         stack[stack_first_empty + 1] = std::make_pair(1, 3);
         stack[stack_first_empty + 2].second = 0;
         stack[stack_first_empty + 3] = std::make_pair(half - 1, 1);
         stack_first_empty += 4;
       }
     }
   }
   size_ = n;
   PPL_ASSERT(OK());
 }

Parma_Polyhedra_Library::CO_Tree::~CO_Tree ( )

inline

The destructor.

This destructor takes $O(n)$ time.

Definition at line 80 of file CO_Tree_inlines.hh.

References destroy().

                   {
 
   destroy();
 }

Member Function Documentation

CO_Tree::iterator Parma_Polyhedra_Library::CO_Tree::begin ( )

inline

Returns an iterator that points at the first element.

This method takes $O(1)$ time.

Definition at line 196 of file CO_Tree_inlines.hh.

Referenced by Parma_Polyhedra_Library::Sparse_Row::begin(), bisect(), and external_memory_in_bytes().

                {
   return iterator(*this);
 }

CO_Tree::const_iterator Parma_Polyhedra_Library::CO_Tree::begin ( ) const

inline

Equivalent to cbegin().

Definition at line 206 of file CO_Tree_inlines.hh.

                      {
   return const_iterator(*this);
 }

CO_Tree::iterator Parma_Polyhedra_Library::CO_Tree::bisect ( dimension_type key )

inline

Searches an element with key key using bisection.

Parameters

key	The key that will be searched for.

If the element is found, an iterator pointing to that element is returned; otherwise, the returned iterator refers to the immediately preceding or succeeding value. If the tree is empty, end() is returned.

This method takes $O(\log n)$ time.

Definition at line 226 of file CO_Tree_inlines.hh.

References begin(), bisect_in(), empty(), and end().

Referenced by bisect_near(), Parma_Polyhedra_Library::Sparse_Row::find(), and Parma_Polyhedra_Library::Sparse_Row::lower_bound().

                                   {
   if (empty()) {
     return end();
   }
   iterator last = end();
   --last;
   return bisect_in(begin(), last, key);
 }

CO_Tree::const_iterator Parma_Polyhedra_Library::CO_Tree::bisect ( dimension_type key ) const

inline

Searches an element with key key using bisection.

Parameters

key	The key that will be searched for.

If the element is found, an iterator pointing to that element is returned; otherwise, the returned iterator refers to the immediately preceding or succeeding value. If the tree is empty, end() is returned.

This method takes $O(\log n)$ time.

Definition at line 236 of file CO_Tree_inlines.hh.

References begin(), bisect_in(), empty(), and end().

                                         {
   if (empty()) {
     return end();
   }
   const_iterator last = end();
   --last;
   return bisect_in(begin(), last, key);
 }

CO_Tree::iterator Parma_Polyhedra_Library::CO_Tree::bisect_in	(	iterator	first,
		iterator	last,
		dimension_type	key
	)

inline

Searches an element with key key in [first, last] using bisection.

Parameters

first	An iterator pointing to the first element in the range. It must not be end().
last	An iterator pointing to the last element in the range. Note that this is included in the search. It must not be end().
key	The key that will be searched for.

Returns: If the specified key is found, an iterator pointing to that element is returned; otherwise, the returned iterator refers to the immediately preceding or succeeding value. If the tree is empty, end() is returned.

This method takes 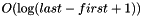$O(\log(last - first + 1))$ time.

Definition at line 246 of file CO_Tree_inlines.hh.

References dfs_index(), and end().

Referenced by bisect(), and bisect_in().

                                                                     {
   PPL_ASSERT(first != end());
   PPL_ASSERT(last != end());
   const dimension_type index
     = bisect_in(dfs_index(first), dfs_index(last), key);
   return iterator(*this, index);
 }

CO_Tree::const_iterator Parma_Polyhedra_Library::CO_Tree::bisect_in	(	const_iterator	first,
		const_iterator	last,
		dimension_type	key
	)		const

inline

Searches an element with key key in [first, last] using bisection.

Parameters

first	An iterator pointing to the first element in the range. It must not be end().
last	An iterator pointing to the last element in the range. Note that this is included in the search. It must not be end().
key	The key that will be searched for.

Returns: If the specified key is found, an iterator pointing to that element is returned; otherwise, the returned iterator refers to the immediately preceding or succeeding value. If the tree is empty, end() is returned.

This method takes 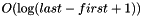$O(\log(last - first + 1))$ time.

Definition at line 255 of file CO_Tree_inlines.hh.

References bisect_in(), dfs_index(), and end().

                                              {
   PPL_ASSERT(first != end());
   PPL_ASSERT(last != end());
   const dimension_type index
     = bisect_in(dfs_index(first), dfs_index(last), key);
   return const_iterator(*this, index);
 }

PPL::dimension_type Parma_Polyhedra_Library::CO_Tree::bisect_in	(	dimension_type	first,
		dimension_type	last,
		dimension_type	key
	)		const

private

Searches an element with key key in [first, last] using bisection.

Parameters

first	The index of the first element in the range. It must be the index of an element with a value.
last	The index of the last element in the range. It must be the index of an element with a value. Note that this is included in the search.
key	The key that will be searched for.

Returns: If the element is found, the index of that element is returned; otherwise, the returned index refers to the immediately preceding or succeeding value.

This method takes $O(\log n)$ time.

Definition at line 215 of file CO_Tree.cc.

                                              {
   PPL_ASSERT(first != 0);
   PPL_ASSERT(last <= reserved_size);
   PPL_ASSERT(first <= last);
   PPL_ASSERT(indexes[first] != unused_index);
   PPL_ASSERT(indexes[last] != unused_index);
 
   while (first < last) {
     dimension_type half = (first + last) / 2;
     dimension_type new_half = half;
 
     while (indexes[new_half] == unused_index) {
       ++new_half;
     }
 
     if (indexes[new_half] == key) {
       return new_half;
     }
 
     if (indexes[new_half] > key) {
 
       while (indexes[half] == unused_index) {
         --half;
       }
 
       last = half;
 
     }
     else {
 
       ++new_half;
       while (indexes[new_half] == unused_index) {
         ++new_half;
       }
 
       first = new_half;
     }
   }
 
   // It is important that last is returned instead of first, because first
   // may have increased beyond last, even beyond the original value of last
   // at the beginning of this method.
   return last;
 }

CO_Tree::iterator Parma_Polyhedra_Library::CO_Tree::bisect_near	(	iterator	hint,
		dimension_type	key
	)

inline

Searches an element with key key near hint.

Parameters

hint	An iterator used as a hint.
key	The key that will be searched for.

If the element is found, the returned iterator points to that element; otherwise, it points to the immediately preceding or succeeding value. If the tree is empty, end() is returned.

The value of itr does not affect the result of this method, as long it is a valid iterator for this tree. itr may even be end().

This method takes $O(\log n)$ time. If the distance between the returned position and hint is $O(1)$ it takes $O(1)$ time.

Definition at line 265 of file CO_Tree_inlines.hh.

References bisect(), dfs_index(), and end().

Referenced by bisect_near(), Parma_Polyhedra_Library::Sparse_Row::find(), and Parma_Polyhedra_Library::Sparse_Row::lower_bound().

                                                       {
   if (hint == end()) {
     return bisect(key);
   }
   const dimension_type index
     = bisect_near(dfs_index(hint), key);
   return iterator(*this, index);
 }

CO_Tree::const_iterator Parma_Polyhedra_Library::CO_Tree::bisect_near	(	const_iterator	hint,
		dimension_type	key
	)		const

inline

Searches an element with key key near hint.

Parameters

hint	An iterator used as a hint.
key	The key that will be searched for.

If the element is found, the returned iterator points to that element; otherwise, it points to the immediately preceding or succeeding value. If the tree is empty, end() is returned.

The value of itr does not affect the result of this method, as long it is a valid iterator for this tree. itr may even be end().

This method takes $O(\log n)$ time. If the distance between the returned position and hint is $O(1)$ it takes $O(1)$ time.

Definition at line 275 of file CO_Tree_inlines.hh.

References bisect(), bisect_near(), dfs_index(), and end().

                                                                   {
   if (hint == end()) {
     return bisect(key);
   }
   const dimension_type index = bisect_near(dfs_index(hint), key);
   return const_iterator(*this, index);
 }

PPL::dimension_type Parma_Polyhedra_Library::CO_Tree::bisect_near	(	dimension_type	hint,
		dimension_type	key
	)		const

private

Searches an element with key key near hint.

Parameters

hint	An index used as a hint. It must be the index of an element with a value.
key	The key that will be searched for.

Returns: If the element is found, the index of that element is returned; otherwise, the returned index refers to the immediately preceding or succeeding value.

This uses a binary progression and then a bisection, so this method is $O(\log n)$ , and it is $O(1)$ if the distance between the returned position and hint is $O(1)$ .

This method takes $O(\log n)$ time. If the distance between the returned position and hint is $O(1)$ it takes $O(1)$ time.

Definition at line 262 of file CO_Tree.cc.

References Parma_Polyhedra_Library::swap().

                                                                      {
   PPL_ASSERT(hint != 0);
   PPL_ASSERT(hint <= reserved_size);
   PPL_ASSERT(indexes[hint] != unused_index);
 
   if (indexes[hint] == key) {
     return hint;
   }
 
   dimension_type new_hint;
   dimension_type offset = 1;
 
   if (indexes[hint] > key) {
     // The searched element is before `hint'.
 
     while (true) {
 
       if (hint <= offset) {
         // The searched element is in (0,hint).
         new_hint = hint;
         hint = 1;
         // The searched element is in [hint,new_hint).
         while (indexes[hint] == unused_index) {
           ++hint;
         }
 
         if (indexes[hint] >= key) {
           return hint;
         }
         // The searched element is in (hint,new_hint) and both indexes point
         // to valid elements.
         break;
       }
       else {
         new_hint = hint - offset;
       }
 
       PPL_ASSERT(new_hint > 0);
       PPL_ASSERT(new_hint <= reserved_size);
 
       // Find the element at `new_hint' (or the first after it).
       while (indexes[new_hint] == unused_index) {
         ++new_hint;
       }
 
       PPL_ASSERT(new_hint <= hint);
 
       if (indexes[new_hint] == key) {
         return new_hint;
       }
       else
         if (indexes[new_hint] < key) {
           // The searched element is in (new_hint,hint)
           using std::swap;
           swap(hint, new_hint);
           // The searched element is now in (hint,new_hint).
           break;
         }
 
       hint = new_hint;
       offset *= 2;
     }
 
   }
   else {
     // The searched element is after `hint'.
     while (true) {
 
       if (hint + offset > reserved_size) {
         // The searched element is in (hint,reserved_size+1).
         new_hint = reserved_size;
         // The searched element is in (hint,new_hint].
         while (indexes[new_hint] == unused_index) {
           --new_hint;
         }
         if (indexes[new_hint] <= key) {
           return new_hint;
         }
         // The searched element is in (hint,new_hint) and both indexes point
         // to valid elements.
         break;
       }
       else {
         new_hint = hint + offset;
       }
 
       PPL_ASSERT(new_hint > 0);
       PPL_ASSERT(new_hint <= reserved_size);
 
       // Find the element at `new_hint' (or the first after it).
       while (indexes[new_hint] == unused_index) {
         --new_hint;
       }
 
       PPL_ASSERT(hint <= new_hint);
 
       if (indexes[new_hint] == key) {
         return new_hint;
       }
       else {
         if (indexes[new_hint] > key) {
           // The searched element is in (hint,new_hint).
           break;
         }
       }
       hint = new_hint;
       offset *= 2;
     }
   }
   // The searched element is in (hint,new_hint).
   PPL_ASSERT(hint > 0);
   PPL_ASSERT(hint < new_hint);
   PPL_ASSERT(new_hint <= reserved_size);
   PPL_ASSERT(indexes[hint] != unused_index);
   PPL_ASSERT(indexes[new_hint] != unused_index);
 
   ++hint;
   while (indexes[hint] == unused_index) {
     ++hint;
   }
 
   if (hint == new_hint) {
     return hint;
   }
 
   --new_hint;
 
   while (indexes[new_hint] == unused_index) {
     --new_hint;
   }
 
   PPL_ASSERT(hint <= new_hint);
   PPL_ASSERT(indexes[hint] != unused_index);
   PPL_ASSERT(indexes[new_hint] != unused_index);
 
   return bisect_in(hint, new_hint, key);
 }

CO_Tree::const_iterator Parma_Polyhedra_Library::CO_Tree::cbegin ( ) const

inline

Returns a const_iterator that points at the first element.

This method takes $O(1)$ time.

Definition at line 216 of file CO_Tree_inlines.hh.

Referenced by Parma_Polyhedra_Library::Sparse_Row::begin(), and Parma_Polyhedra_Library::Sparse_Row::cbegin().

                       {
   return const_iterator(*this);
 }

const CO_Tree::const_iterator & Parma_Polyhedra_Library::CO_Tree::cend ( ) const

inline

Returns a const_iterator that points after the last element.

This method always returns a reference to the same internal iterator, that is updated at each operation that modifies the structure. Client code can keep a const reference to that iterator instead of keep updating a local iterator.

This method takes $O(1)$ time.

Definition at line 221 of file CO_Tree_inlines.hh.

References cached_const_end.

Referenced by Parma_Polyhedra_Library::Sparse_Row::cend(), and Parma_Polyhedra_Library::Sparse_Row::end().

                     {
   return cached_const_end;
 }

void Parma_Polyhedra_Library::CO_Tree::clear ( )

inline

Removes all elements from the tree.

This method takes $O(n)$ time.

Definition at line 75 of file CO_Tree_inlines.hh.

References CO_Tree().

Referenced by Parma_Polyhedra_Library::Sparse_Row::clear().

                {
   *this = CO_Tree();
 }

PPL::dimension_type Parma_Polyhedra_Library::CO_Tree::compact_elements_in_the_rightmost_end	(	dimension_type	last_in_subtree,
		dimension_type	subtree_size,
		dimension_type	key,
		data_type_const_reference	value,
		bool	add_element
	)

private

Moves all elements of a subtree to the rightmost end.

Returns: The index of the rightmost unused node in the subtree after the process.

Parameters

last_in_subtree	It is the index of the last element in the subtree.
subtree_size	It is the number of valid elements in the subtree. It must be greater than zero.
key	The key that may be added to the tree if add_element is `true`.
value	The value that may be added to the tree if add_element is `true`.
add_element	If it is true, it tries to add an element with key `key` and value `value` in the process (but it may not).

This method takes 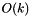$O(k)$ time, where k is subtree_size.

Definition at line 951 of file CO_Tree.cc.

                                                           {
 
   PPL_ASSERT(subtree_size != 0);
 
   PPL_ASSERT(subtree_size != 1 || !add_element);
 
   dimension_type* last_index_in_subtree = &(indexes[last_in_subtree]);
   data_type* last_data_in_subtree = &(data[last_in_subtree]);
 
   dimension_type* first_unused_index = last_index_in_subtree;
   data_type* first_unused_data = last_data_in_subtree;
 
   while (*last_index_in_subtree == unused_index) {
     --last_index_in_subtree;
     --last_data_in_subtree;
   }
 
   // From now on, last_index_in_subtree and last_data_in_subtree point to the
   // rightmost node with a value in the subtree. first_unused_index and
   // first_unused_data point to the rightmost unused node in the subtree.
 
   if (add_element) {
     while (subtree_size != 0) {
       --subtree_size;
       if (last_index_in_subtree == indexes || key > *last_index_in_subtree) {
         if (last_index_in_subtree == indexes
             || last_index_in_subtree != first_unused_index) {
           PPL_ASSERT(first_unused_index != indexes);
           PPL_ASSERT(*first_unused_index == unused_index);
           new(first_unused_data) data_type(value);
           // Set the index only if the construction was successful.
           *first_unused_index = key;
           --first_unused_index;
           --first_unused_data;
         }
         break;
       }
       else {
         if (last_index_in_subtree != first_unused_index) {
           PPL_ASSERT(first_unused_index != indexes);
           PPL_ASSERT(last_index_in_subtree != indexes);
           PPL_ASSERT(*first_unused_index == unused_index);
           *first_unused_index = *last_index_in_subtree;
           *last_index_in_subtree = unused_index;
           move_data_element(*first_unused_data, *last_data_in_subtree);
         }
         --last_index_in_subtree;
         --last_data_in_subtree;
         while (*last_index_in_subtree == unused_index) {
           --last_index_in_subtree;
           --last_data_in_subtree;
         }
         --first_unused_index;
         --first_unused_data;
       }
     }
   }
   while (subtree_size != 0) {
     if (last_index_in_subtree != first_unused_index) {
       PPL_ASSERT(first_unused_index != indexes);
       PPL_ASSERT(last_index_in_subtree != indexes);
       PPL_ASSERT(*first_unused_index == unused_index);
       *first_unused_index = *last_index_in_subtree;
       *last_index_in_subtree = unused_index;
       move_data_element(*first_unused_data, *last_data_in_subtree);
     }
     --last_index_in_subtree;
     --last_data_in_subtree;
     while (*last_index_in_subtree == unused_index) {
       --last_index_in_subtree;
       --last_data_in_subtree;
     }
     --first_unused_index;
     --first_unused_data;
     --subtree_size;
   }
 
   const std::ptrdiff_t distance = first_unused_index - indexes;
   PPL_ASSERT(distance >= 0);
   return static_cast<dimension_type>(distance);
 }

void Parma_Polyhedra_Library::CO_Tree::copy_data_from ( const CO_Tree & tree )

private

Copies all data in the tree tree into *this.

Parameters

tree	The tree from which the element will be copied into *this.

this must be empty and must have the same reserved size of tree. this->OK() may return false before this method is called, but this->structure_OK() must return true.

This method takes $O(n)$ time.

Definition at line 1246 of file CO_Tree.cc.

References data, indexes, reserved_size, and size_.

Referenced by CO_Tree(), and operator=().

                                            {
   PPL_ASSERT(size_ == 0);
   PPL_ASSERT(reserved_size == x.reserved_size);
   PPL_ASSERT(structure_OK());
 
   if (x.size_ == 0) {
     PPL_ASSERT(OK());
     return;
   }
 
   dimension_type i;
   try {
     for (i = x.reserved_size; i > 0; --i) {
       if (x.indexes[i] != unused_index) {
         indexes[i] = x.indexes[i];
         new(&(data[i])) data_type(x.data[i]);
       }
       else {
         PPL_ASSERT(indexes[i] == unused_index);
       }
     }
   } catch (...) {
     // The (used) data elements in (i,x.reserved_size] have been constructed
     // successfully.
     // The constructor of data[i] has thrown an exception, so data[i] has not
     // been constructed.
 
     // 1. Destroy the data elements that have been constructed successfully.
     for (dimension_type j = x.reserved_size; j > i; --j) {
       if (indexes[j] != unused_index) {
         data[j].~data_type();
       }
     }
 
     // 2. Deallocate index[] and data[]
     delete[] indexes;
     data_allocator.deallocate(data, reserved_size + 1);
 
     // 3. Set the tree to an empty tree and rethrow exception.
     init(0);
     throw;
   }
 
   size_ = x.size_;
   PPL_ASSERT(OK());
 }

PPL::dimension_type Parma_Polyhedra_Library::CO_Tree::count_used_in_subtree ( tree_iterator itr )

staticprivate

Counts the number of used elements in the subtree rooted at itr.

Parameters

itr	An iterator pointing to the root of the desired subtree.

This method takes 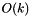$O(k)$ time, where k is the number of elements in the subtree.

Definition at line 1294 of file CO_Tree.cc.

References Parma_Polyhedra_Library::CO_Tree::tree_iterator::dfs_index(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::get_offset(), indexes, and Parma_Polyhedra_Library::CO_Tree::tree_iterator::tree.

                                                    {
   dimension_type n = 0;
 
   const dimension_type k = itr.get_offset();
   const dimension_type root_index = itr.dfs_index();
 
   // The complete subtree rooted at itr has 2*k - 1 nodes.
 
   PPL_ASSERT(root_index > (k - 1));
 
   const dimension_type* current_index
     = &(itr.tree.indexes[root_index - (k - 1)]);
 
   for (dimension_type j = 2*k - 1; j > 0; --j, ++current_index) {
     if (*current_index != unused_index) {
       ++n;
     }
   }
 
   return n;
 }

void Parma_Polyhedra_Library::CO_Tree::destroy ( )

private

Deallocates the tree's dynamic arrays.

After this call, the tree fields are uninitialized, so init() must be called again before using the tree.

This method takes $O(n)$ time.

Definition at line 649 of file CO_Tree.cc.

Referenced by operator=(), and ~CO_Tree().

                     {
 
   if (reserved_size != 0) {
     for (dimension_type i = 1; i <= reserved_size; ++i) {
       if (indexes[i] != unused_index) {
         data[i].~data_type();
       }
     }
 
     delete[] indexes;
     data_allocator.deallocate(data, reserved_size + 1);
   }
 }

dimension_type Parma_Polyhedra_Library::CO_Tree::dfs_index ( const_iterator itr ) const

inlineprivate

Returns the index of the current element in the DFS layout of the complete tree.

Returns: the index of the current element in the DFS layout of the complete tree.

Parameters

itr	the iterator that points to the desired element.

Definition at line 32 of file CO_Tree_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::const_iterator::current_index, indexes, and reserved_size.

Referenced by bisect_in(), bisect_near(), and fast_shift().

                                            {
   PPL_ASSERT(itr.current_index != 0);
   PPL_ASSERT(itr.current_index >= indexes + 1);
   PPL_ASSERT(itr.current_index <= indexes + reserved_size);
   const std::ptrdiff_t index = itr.current_index - indexes;
   return static_cast<dimension_type>(index);
 }

dimension_type Parma_Polyhedra_Library::CO_Tree::dfs_index ( iterator itr ) const

inlineprivate

Returns the index of the current element in the DFS layout of the complete tree.

Returns: the index of the current element in the DFS layout of the complete tree.

Parameters

itr	the iterator that points to the desired element.

Definition at line 41 of file CO_Tree_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::iterator::current_index, indexes, and reserved_size.

                                      {
   PPL_ASSERT(itr.current_index != 0);
   PPL_ASSERT(itr.current_index >= indexes + 1);
   PPL_ASSERT(itr.current_index <= indexes + reserved_size);
   const std::ptrdiff_t index = itr.current_index - indexes;
   return static_cast<dimension_type>(index);
 }

void Parma_Polyhedra_Library::CO_Tree::dump_subtree ( tree_iterator itr )

staticprivate

Dumps the subtree rooted at itr to stdout, for debugging purposes.

Parameters

itr	A tree_iterator pointing to the root of the desired subtree.

Definition at line 798 of file CO_Tree.cc.

References Parma_Polyhedra_Library::CO_Tree::tree_iterator::depth(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::get_left_child(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::get_parent(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::get_right_child(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::index(), and Parma_Polyhedra_Library::CO_Tree::tree_iterator::is_leaf().

Referenced by dump_tree().

                                           {
   if (!itr.is_leaf()) {
     itr.get_left_child();
     dump_subtree(itr);
     itr.get_parent();
   }
   std::cout << "At depth: " << itr.depth();
   if (itr.index() == unused_index) {
     std::cout << " (no data)" << std::endl;
   }
   else {
     std::cout << " pair (" << itr.index() << "," << *itr << ")" << std::endl;
   }
   if (!itr.is_leaf()) {
     itr.get_right_child();
     dump_subtree(itr);
     itr.get_parent();
   }
 }

void Parma_Polyhedra_Library::CO_Tree::dump_tree ( ) const

inline

Dumps the tree to stdout, for debugging purposes.

Definition at line 101 of file CO_Tree_inlines.hh.

References dump_subtree(), and empty().

                          {
   if (empty()) {
     std::cout << "(empty tree)" << std::endl;
   }
   else {
     dump_subtree(tree_iterator(*const_cast<CO_Tree*>(this)));
   }
 }

bool Parma_Polyhedra_Library::CO_Tree::empty ( ) const

inline

Returns true if the tree has no elements.

This method takes $O(1)$ time.

Definition at line 86 of file CO_Tree_inlines.hh.

References size_.

Referenced by bisect(), Parma_Polyhedra_Library::CO_Tree::const_iterator::const_iterator(), dump_tree(), erase(), Parma_Polyhedra_Library::Sparse_Row::get(), insert(), insert_in_empty_tree(), and Parma_Polyhedra_Library::CO_Tree::iterator::iterator().

                      {
   return size_ == 0;
 }

const CO_Tree::iterator & Parma_Polyhedra_Library::CO_Tree::end ( )

inline

Returns an iterator that points after the last element.

This method always returns a reference to the same internal iterator, that is updated at each operation that modifies the structure. Client code can keep a const reference to that iterator instead of keep updating a local iterator.

This method takes $O(1)$ time.

Definition at line 201 of file CO_Tree_inlines.hh.

References cached_end.

Referenced by bisect(), bisect_in(), bisect_near(), Parma_Polyhedra_Library::Sparse_Row::end(), erase(), external_memory_in_bytes(), and fast_shift().

              {
   return cached_end;
 }

const CO_Tree::const_iterator & Parma_Polyhedra_Library::CO_Tree::end ( ) const

inline

Equivalent to cend().

Definition at line 211 of file CO_Tree_inlines.hh.

References cached_const_end.

                    {
   return cached_const_end;
 }

CO_Tree::iterator Parma_Polyhedra_Library::CO_Tree::erase ( dimension_type key )

inline

Erases the element with key key from the tree.

This operation invalidates existing iterators.

Returns: an iterator to the next element (or end() if there are no elements with key greater than key ).

Parameters

key	The key of the element that will be erased from the tree.

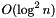This method takes $O(\log n)$ time if the element already exists, and $O(\log^2 n)$ amortized time otherwise.

Definition at line 143 of file CO_Tree_inlines.hh.

References empty(), end(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::go_down_searching_key(), Parma_Polyhedra_Library::CO_Tree::iterator::index(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::index(), and unused_index.

Referenced by erase(), and Parma_Polyhedra_Library::Sparse_Row::reset().

                                  {
   PPL_ASSERT(key != unused_index);
 
   if (empty()) {
     return end();
   }
 
   tree_iterator itr(*this);
   itr.go_down_searching_key(key);
 
   if (itr.index() == key) {
     return erase(itr);
   }
 
   iterator result(itr);
   if (result.index() < key) {
     ++result;
   }
 
   PPL_ASSERT(result == end() || result.index() > key);
 #ifndef NDEBUG
   iterator last = end();
   --last;
   PPL_ASSERT((result == end()) == (last.index() < key));
 #endif
 
   return result;
 }

CO_Tree::iterator Parma_Polyhedra_Library::CO_Tree::erase ( iterator itr )

inline

Erases the element pointed to by itr from the tree.

This operation invalidates existing iterators.

Returns: an iterator to the next element (or end() if there are no elements with key greater than key ).

Parameters

itr	An iterator pointing to the element that will be erased from the tree.

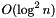This method takes $O(\log n)$ time if the element already exists, and $O(\log^2 n)$ amortized time otherwise.

Definition at line 173 of file CO_Tree_inlines.hh.

References end(), and erase().

                            {
   PPL_ASSERT(itr != end());
   return erase(tree_iterator(itr, *this));
 }

PPL::CO_Tree::iterator Parma_Polyhedra_Library::CO_Tree::erase ( tree_iterator itr )

private

Erases from the tree the element pointed to by itr .

This operation invalidates existing iterators.

Returns: An iterator to the next element (or end() if there are no elements with key greater than key ).

Parameters

itr	An iterator pointing to the element that will be erased.

This method takes 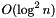$O(\log^2 n)$ amortized time.

Definition at line 503 of file CO_Tree.cc.

                                    {
   PPL_ASSERT(itr.index() != unused_index);
 
   PPL_ASSERT(size_ != 0);
 
   if (size_ == 1) {
     // Deleting the only element of this tree, now it is empty.
     clear();
     return end();
   }
 
   if (is_less_than_ratio(size_ - 1, reserved_size, min_density_percent)
       && !is_greater_than_ratio(size_ - 1, reserved_size/2,
                                 max_density_percent)) {
 
     const dimension_type key = itr.index();
 
     PPL_ASSERT(!is_greater_than_ratio(size_, reserved_size,
                                       max_density_percent));
 
     rebuild_smaller_tree();
     itr.get_root();
     itr.go_down_searching_key(key);
 
     PPL_ASSERT(itr.index() == key);
   }
 
 #ifndef NDEBUG
   if (size_ > 1) {
     PPL_ASSERT(!is_less_than_ratio(size_ - 1, reserved_size,
                                    min_density_percent)
                || is_greater_than_ratio(size_ - 1, reserved_size/2,
                                         max_density_percent));
   }
 #endif
 
   const dimension_type deleted_key = itr.index();
   tree_iterator deleted_node = itr;
   (*itr).~data_type();
   while (true) {
     dimension_type& current_key  = itr.index();
     data_type&      current_data = *itr;
     if (itr.is_leaf()) {
       break;
     }
     itr.get_left_child();
     if (itr.index() != unused_index) {
       // The left child has a value.
       itr.follow_right_children_with_value();
     }
     else {
       // The left child has not a value, try the right child.
       itr.get_parent();
       itr.get_right_child();
       if (itr.index() != unused_index) {
         // The right child has a value.
         itr.follow_left_children_with_value();
       }
       else {
         // The right child has not a value, too.
         itr.get_parent();
         break;
       }
     }
     using std::swap;
     swap(current_key, itr.index());
     move_data_element(current_data, *itr);
   }
 
   PPL_ASSERT(itr.index() != unused_index);
   itr.index() = unused_index;
   --size_;
 
   PPL_ASSERT(OK());
 
   itr = rebalance(itr, 0, Coefficient_zero());
 
   if (itr.get_offset() < deleted_node.get_offset()) {
     // deleted_node is an ancestor of itr
     itr = deleted_node;
   }
 
   itr.go_down_searching_key(deleted_key);
 
   iterator result(itr);
 
   if (result.index() < deleted_key) {
     ++result;
   }
 
   PPL_ASSERT(OK());
   PPL_ASSERT(result == end() || result.index() > deleted_key);
 #ifndef NDEBUG
   if (!empty()) {
     iterator last = end();
     --last;
     PPL_ASSERT((result == end()) == (last.index() < deleted_key));
   }
 #endif
 
   return result;
 }

void Parma_Polyhedra_Library::CO_Tree::erase_element_and_shift_left ( dimension_type key )

Removes the element with key key (if it exists) and decrements by 1 all elements' keys that were greater than key.

Parameters

key	The key of the element that will be erased from the tree.

This operation invalidates existing iterators.

This method takes 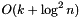$O(k+\log^2 n)$ expected time, where k is the number of elements with keys greater than key.

Definition at line 179 of file CO_Tree.cc.

Referenced by Parma_Polyhedra_Library::Sparse_Row::delete_element_and_shift().

                                                            {
   iterator itr = erase(key);
   if (itr == end()) {
     return;
   }
   const dimension_type i = dfs_index(itr);
   dimension_type* p = indexes + i;
   const dimension_type* const p_end = indexes + (reserved_size + 1);
   for ( ; p != p_end; ++p) {
     if (*p != unused_index) {
       --(*p);
     }
   }
   PPL_ASSERT(OK());
 }

PPL::dimension_type Parma_Polyhedra_Library::CO_Tree::external_memory_in_bytes ( ) const

Returns the size in bytes of the memory managed by *this.

This method takes $O(n)$ time.

Definition at line 30 of file CO_Tree.cc.

References begin(), data, end(), Parma_Polyhedra_Library::external_memory_in_bytes(), indexes, and reserved_size.

Referenced by Parma_Polyhedra_Library::Sparse_Row::external_memory_in_bytes().

                                            {
   dimension_type memory_size = 0;
   if (reserved_size != 0) {
     // Add the size of data[]
     memory_size += (reserved_size + 1)*sizeof(data[0]);
     // Add the size of indexes[]
     memory_size += (reserved_size + 2)*sizeof(indexes[0]);
     for (const_iterator itr = begin(), itr_end = end();
          itr != itr_end; ++itr) {
       memory_size += PPL::external_memory_in_bytes(*itr);
     }
   }
   return memory_size;
 }

void Parma_Polyhedra_Library::CO_Tree::fast_shift	(	dimension_type	i,
		iterator	itr
	)

inline

Sets to i the key of *itr. Assumes that i<=itr.index() and that there are no elements with keys in [i,itr.index()).

All existing iterators remain valid.

This method takes $O(1)$ time.

Definition at line 284 of file CO_Tree_inlines.hh.

References dfs_index(), end(), Parma_Polyhedra_Library::CO_Tree::iterator::index(), indexes, and OK().

Referenced by Parma_Polyhedra_Library::Sparse_Row::fast_swap().

                                                   {
   PPL_ASSERT(itr != end());
   PPL_ASSERT(i <= itr.index());
   indexes[dfs_index(itr)] = i;
   PPL_ASSERT(OK());
 }

void Parma_Polyhedra_Library::CO_Tree::increase_keys_from	(	dimension_type	key,
		dimension_type	n
	)

Adds n to all keys greater than or equal to key.

Parameters

key	The key of the first element whose key will be increased.
n	Specifies how much the keys will be increased.

This method takes 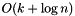$O(k+\log n)$ expected time, where k is the number of elements with keys greater than or equal to key.

Definition at line 196 of file CO_Tree.cc.

References Parma_Polyhedra_Library::Implementation::BD_Shapes::empty.

Referenced by Parma_Polyhedra_Library::Sparse_Row::add_zeroes_and_shift().

                                                                    {
   if (empty()) {
     return;
   }
   dimension_type* p = indexes + reserved_size;
   while (*p == unused_index) {
     --p;
   }
   while (p != indexes && *p >= key) {
     *p += n;
     --p;
     while (*p == unused_index) {
       --p;
     }
   }
   PPL_ASSERT(OK());
 }

void Parma_Polyhedra_Library::CO_Tree::init ( dimension_type n )

private

Initializes a tree with reserved size at least n .

Parameters

n	A lower bound on the tree's desired reserved size.

This method takes $O(n)$ time.

Definition at line 607 of file CO_Tree.cc.

Referenced by CO_Tree(), operator=(), and rebuild_smaller_tree().

                                  {
   indexes = NULL;
   data = NULL;
   size_ = 0;
   reserved_size = 0;
   max_depth = 0;
 
   if (n > 0) {
     const dimension_type max_d = integer_log2(n) + 1;
     const height_t new_max_depth = static_cast<height_t>(max_d);
     const dimension_type new_reserved_size
       = (static_cast<dimension_type>(1) << new_max_depth) - 1;
     // If this throws, *this will be the empty tree.
     indexes = new dimension_type[new_reserved_size + 2];
     try {
       data = data_allocator.allocate(new_reserved_size + 1);
     }
     catch (...) {
       delete[] indexes;
       indexes = 0;
       PPL_ASSERT(OK());
       throw;
     }
     max_depth = new_max_depth;
     reserved_size = new_reserved_size;
 
     // Mark all pairs as unused.
     for (dimension_type i = 1; i <= reserved_size; ++i) {
       indexes[i] = unused_index;
     }
 
     // These are used as markers by iterators.
     indexes[0] = 0;
     indexes[reserved_size + 1] = 0;
   }
 
   refresh_cached_iterators();
 
   PPL_ASSERT(structure_OK());
 }

CO_Tree::iterator Parma_Polyhedra_Library::CO_Tree::insert ( dimension_type key )

inline

Inserts an element in the tree.

Returns: An iterator that points to the inserted pair.

Parameters

key	The key that will be inserted into the tree, associated with the default data.

If such a pair already exists, an iterator pointing to that pair is returned.

This operation invalidates existing iterators.

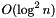This method takes $O(\log n)$ time if the element already exists, and $O(\log^2 n)$ amortized time otherwise.

Definition at line 111 of file CO_Tree_inlines.hh.

References Parma_Polyhedra_Library::Coefficient_zero(), empty(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::go_down_searching_key(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::index(), and insert_precise().

Referenced by Parma_Polyhedra_Library::Sparse_Row::insert().

                                         {
   if (empty()) {
     return insert(key, Coefficient_zero());
   }
   else {
     tree_iterator itr(*this);
     itr.go_down_searching_key(key);
     if (itr.index() == key) {
       return iterator(itr);
     }
     else {
       return iterator(insert_precise(key, Coefficient_zero(), itr));
     }
   }
 }

CO_Tree::iterator Parma_Polyhedra_Library::CO_Tree::insert	(	dimension_type	key,
		data_type_const_reference	data
	)

inline

Inserts an element in the tree.

Returns: An iterator that points to the inserted element.

Parameters

key	The key that will be inserted into the tree..
data	The data that will be inserted into the tree.

If an element with the specified key already exists, its associated data is set to data and an iterator pointing to that pair is returned.

This operation invalidates existing iterators.

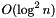This method takes $O(\log n)$ time if the element already exists, and $O(\log^2 n)$ amortized time otherwise.amortized

Definition at line 128 of file CO_Tree_inlines.hh.

References empty(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::go_down_searching_key(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::index(), insert_in_empty_tree(), insert_precise(), and unused_index.

                                                                    {
   if (empty()) {
     insert_in_empty_tree(key, data1);
     tree_iterator itr(*this);
     PPL_ASSERT(itr.index() != unused_index);
     return iterator(itr);
   }
   else {
     tree_iterator itr(*this);
     itr.go_down_searching_key(key);
     return iterator(insert_precise(key, data1, itr));
   }
 }

PPL::CO_Tree::iterator Parma_Polyhedra_Library::CO_Tree::insert	(	iterator	itr,
		dimension_type	key
	)

Inserts an element in the tree.

Returns: An iterator that points to the inserted element.

Parameters

itr	The iterator used as hint
key	The key that will be inserted into the tree, associated with the default data.

This will be faster if itr points near to the place where the new element will be inserted (or where is already stored). However, the value of itr does not affect the result of this method, as long it is a valid iterator for this tree. itr may even be end().

If an element with the specified key already exists, an iterator pointing to that pair is returned.

This operation invalidates existing iterators.

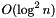This method takes $O(\log n)$ time if the element already exists, and $O(\log^2 n)$ amortized time otherwise.

Definition at line 46 of file CO_Tree.cc.

References Parma_Polyhedra_Library::Coefficient_zero(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::depth(), Parma_Polyhedra_Library::Implementation::BD_Shapes::empty, Parma_Polyhedra_Library::CO_Tree::tree_iterator::get_offset(), and Parma_Polyhedra_Library::CO_Tree::iterator::index().

                                                     {
   PPL_ASSERT(key1 != unused_index);
 
   if (empty()) {
     insert_in_empty_tree(key1, Coefficient_zero());
     return iterator(*this);
   }
 
   if (itr == end()) {
     return insert(key1);
   }
 
   iterator candidate1 = bisect_near(itr, key1);
 
   if (key1 == candidate1.index()) {
     return candidate1;
   }
 
   dimension_type candidate2_index = dfs_index(candidate1);
 
   if (key1 < candidate1.index()) {
     --candidate2_index;
     while (indexes[candidate2_index] == unused_index) {
       --candidate2_index;
     }
   }
   else {
     ++candidate2_index;
     while (indexes[candidate2_index] == unused_index) {
       ++candidate2_index;
     }
   }
 
   tree_iterator candidate1_node(candidate1, *this);
 
   PPL_ASSERT(candidate2_index <= reserved_size + 1);
 
   if (candidate2_index == 0 || candidate2_index > reserved_size) {
     // Use candidate1
     return iterator(insert_precise(key1, Coefficient_zero(),
                                    candidate1_node));
   }
 
   tree_iterator candidate2_node(*this, candidate2_index);
 
   // Adjacent nodes in an in-order visit of a tree always have different
   // heights. This fact can be easily proven by induction on the tree's
   // height, using the definition of the in-order layout.
   PPL_ASSERT(candidate1_node.get_offset() != candidate2_node.get_offset());
 
   if (candidate1_node.get_offset() < candidate2_node.get_offset()) {
     PPL_ASSERT(candidate1_node.depth() > candidate2_node.depth());
     // candidate1_node is deeper in the tree than candidate2_node, so use
     // candidate1_node.
     return iterator(insert_precise(key1, Coefficient_zero(),
                                    candidate1_node));
   }
   else {
     PPL_ASSERT(candidate1_node.depth() < candidate2_node.depth());
     // candidate2_node is deeper in the tree than candidate1_node, so use
     // candidate2_node.
     return iterator(insert_precise(key1, Coefficient_zero(),
                                     candidate2_node));
   }
 }

PPL::CO_Tree::iterator Parma_Polyhedra_Library::CO_Tree::insert	(	iterator	itr,
		dimension_type	key,
		data_type_const_reference	data
	)

Inserts an element in the tree.

Returns: An iterator that points to the inserted element.

Parameters

itr	The iterator used as hint
key	The key that will be inserted into the tree.
data	The data that will be inserted into the tree.

This will be faster if itr points near to the place where the new element will be inserted (or where is already stored). However, the value of itr does not affect the result of this method, as long it is a valid iterator for this tree. itr may even be end().

If an element with the specified key already exists, its associated data is set to data and an iterator pointing to that pair is returned.

This operation invalidates existing iterators.

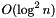This method takes $O(\log n)$ time if the element already exists, and $O(\log^2 n)$ amortized time otherwise.

Definition at line 113 of file CO_Tree.cc.

References Parma_Polyhedra_Library::CO_Tree::tree_iterator::depth(), Parma_Polyhedra_Library::Implementation::BD_Shapes::empty, Parma_Polyhedra_Library::CO_Tree::tree_iterator::get_offset(), and Parma_Polyhedra_Library::CO_Tree::iterator::index().

                                                       {
   PPL_ASSERT(key1 != unused_index);
 
   if (empty()) {
     insert_in_empty_tree(key1, data1);
     return iterator(*this);
   }
 
   if (itr == end()) {
     return insert(key1, data1);
   }
 
   iterator candidate1 = bisect_near(itr, key1);
 
   if (key1 == candidate1.index()) {
     *candidate1 = data1;
     return candidate1;
   }
 
   dimension_type candidate2_index = dfs_index(candidate1);
 
   if (key1 < candidate1.index()) {
     --candidate2_index;
     while (indexes[candidate2_index] == unused_index) {
       --candidate2_index;
     }
 
   }
   else {
     ++candidate2_index;
     while (indexes[candidate2_index] == unused_index) {
       ++candidate2_index;
     }
 
   }
 
   tree_iterator candidate1_node(candidate1, *this);
 
   if (candidate2_index == 0 || candidate2_index > reserved_size) {
     // Use candidate1
     return iterator(insert_precise(key1, data1, candidate1_node));
   }
 
   tree_iterator candidate2_node(*this, candidate2_index);
 
   // Adjacent nodes in an in-order visit of a tree always have different
   // heights. This fact can be easily proven by induction on the tree's
   // height, using the definition of the in-order layout.
   PPL_ASSERT(candidate1_node.get_offset() != candidate2_node.get_offset());
 
   if (candidate1_node.get_offset() < candidate2_node.get_offset()) {
     PPL_ASSERT(candidate1_node.depth() > candidate2_node.depth());
     // candidate1_node is deeper in the tree than candidate2_node, so
     // use candidate1_node.
     return iterator(insert_precise(key1, data1, candidate1_node));
   }
   else {
     PPL_ASSERT(candidate1_node.depth() < candidate2_node.depth());
     // candidate2_node is deeper in the tree than candidate1_node, so
     // use candidate2_node.
     return iterator(insert_precise(key1, data1, candidate2_node));
   }
 }

void Parma_Polyhedra_Library::CO_Tree::insert_in_empty_tree	(	dimension_type	key,
		data_type_const_reference	data
	)

inlineprivate

Inserts an element in the tree.

Parameters

key	The key that will be inserted into the tree.
data	The data that will be associated with `key`.

The tree must be empty.

This operation invalidates existing iterators.

This method takes $O(1)$ time.

Definition at line 292 of file CO_Tree_inlines.hh.

References empty(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::index(), OK(), rebuild_bigger_tree(), size_, and unused_index.

Referenced by insert().

                                                                {
   PPL_ASSERT(empty());
   rebuild_bigger_tree();
   tree_iterator itr(*this);
   PPL_ASSERT(itr.index() == unused_index);
   new(&(*itr)) data_type(data1);
   // Set the index afterwards, so that if the constructor above throws
   // the tree's structure is consistent.
   itr.index() = key;
   ++size_;
 
   PPL_ASSERT(OK());
 }

PPL::CO_Tree::tree_iterator Parma_Polyhedra_Library::CO_Tree::insert_precise	(	dimension_type	key,
		data_type_const_reference	data,
		tree_iterator	itr
	)

private

Inserts an element in the tree.

If there is already an element with key key in the tree, its associated data is set to data.

This operation invalidates existing iterators.

Returns: An iterator that points to the inserted element.

Parameters

key	The key that will be inserted into the tree.
data	The data that will be associated with `key`.
itr	It must point to the element in the tree with key `key` or, if no such element exists, it must point to the node that would be his parent.

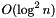This method takes $O(1)$ time if the element already exists, and $O(\log^2 n)$ amortized time otherwise.

Definition at line 401 of file CO_Tree.cc.

References Parma_Polyhedra_Library::Coefficient_zero(), Parma_Polyhedra_Library::Implementation::BD_Shapes::empty, Parma_Polyhedra_Library::CO_Tree::tree_iterator::go_down_searching_key(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::index(), and Parma_Polyhedra_Library::swap().

Referenced by insert().

                                                 {
   PPL_ASSERT(key1 != unused_index);
   PPL_ASSERT(!empty());
 
 #ifndef NDEBUG
   // Check that `itr' is a correct hint.
   tree_iterator itr2(*this);
   itr2.go_down_searching_key(key1);
   PPL_ASSERT(itr == itr2);
 #endif
 
   if (itr.index() == key1) {
     // Replacement, rather than insertion.
     *itr = data1;
     PPL_ASSERT(OK());
     return itr;
   }
 
   // Proper insertion: check if it would invalidate `data1'.
   const bool invalidating
     = (data <= &data1) && (&data1 < data + (reserved_size + 1));
 
   if (!invalidating) {
     return insert_precise_aux(key1, data1, itr);
   }
   // `data1' could be invalidated by the insert, because it is
   // a coefficient of this row. Avoid the issue by copying it.
   data_type data1_copy = data1;
 
 #ifndef NDEBUG
   dimension_type i = &data1 - data;
   dimension_type key2 = indexes[i];
   PPL_ASSERT(key2 != unused_index);
   // This is true since `key1' is not in the tree.
   PPL_ASSERT(key2 != key1);
 #endif
 
   // Insert a dummy coefficient.
   // NOTE: this may invalidate `data1', because it may reallocate the tree
   // and/or move coefficients during rebalancing.
   itr = insert_precise_aux(key1, Coefficient_zero(), itr);
 
   PPL_ASSERT(itr.index() == key1);
 
   // Swap the correct coefficient in place.
   using std::swap;
   swap(*itr, data1_copy);
 
   PPL_ASSERT(OK());
   return itr;
 }

PPL::CO_Tree::tree_iterator Parma_Polyhedra_Library::CO_Tree::insert_precise_aux	(	dimension_type	key,
		data_type_const_reference	data,
		tree_iterator	itr
	)

private

Helper for insert_precise.

This helper method takes the same arguments as insert_precise, but besides assuming that itr is a correct hint, it also assumes that key and data are not in the tree; namely, a proper insertion has to be done and the insertion can not invalidate data.

Definition at line 456 of file CO_Tree.cc.

References Parma_Polyhedra_Library::Implementation::BD_Shapes::empty, Parma_Polyhedra_Library::CO_Tree::tree_iterator::get_left_child(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::get_right_child(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::get_root(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::go_down_searching_key(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::index(), and Parma_Polyhedra_Library::CO_Tree::tree_iterator::is_leaf().

                                                     {
   PPL_ASSERT(key1 != unused_index);
   PPL_ASSERT(!empty());
   // This is a proper insert.
   PPL_ASSERT(itr.index() != key1);
   // `data1' is not going to be invalidated.
   PPL_ASSERT(!(data <= &data1 && &data1 < data + (reserved_size + 1)));
 
   if (is_greater_than_ratio(size_ + 1, reserved_size, max_density_percent)) {
     rebuild_bigger_tree();
     // `itr' was invalidated by the rebuild operation
     itr.get_root();
     itr.go_down_searching_key(key1);
     PPL_ASSERT(itr.index() != key1);
   }
 
   PPL_ASSERT(!is_greater_than_ratio(size_ + 1, reserved_size,
                                     max_density_percent));
 
   ++size_;
 
   if (!itr.is_leaf()) {
     if (key1 < itr.index()) {
       itr.get_left_child();
     }
     else {
       itr.get_right_child();
     }
     PPL_ASSERT(itr.index() == unused_index);
 
     new(&(*itr)) data_type(data1);
     // Set the index only if the construction was successful.
     itr.index() = key1;
   }
   else {
     itr = rebalance(itr, key1, data1);
     itr.go_down_searching_key(key1);
     PPL_ASSERT(itr.index() == key1);
   }
   PPL_ASSERT(OK());
 
   return itr;
 }

unsigned Parma_Polyhedra_Library::CO_Tree::integer_log2 ( dimension_type n )

staticprivate

Returns the floor of the base-2 logarithm of n .

Parameters

n	It must be greater than zero.

This method takes $O(\log n)$ time.

Definition at line 787 of file CO_Tree.cc.

Referenced by CO_Tree(), and Parma_Polyhedra_Library::CO_Tree::tree_iterator::depth().

                                          {
   PPL_ASSERT(n != 0);
   unsigned result = 0;
   while (n != 1) {
     n /= 2;
     ++result;
   }
   return result;
 }

bool Parma_Polyhedra_Library::CO_Tree::is_greater_than_ratio	(	dimension_type	numer,
		dimension_type	denom,
		dimension_type	ratio
	)

inlinestaticprivate

Compares the fractions numer/denom with ratio/100.

Returns: Returns true if the fraction numer/denom is greater than the fraction ratio/100.

Parameters

ratio	It must be less than or equal to 100.
numer	The numerator of the fraction.
denom	The denominator of the fraction.

This method takes $O(1)$ time.

Definition at line 318 of file CO_Tree_inlines.hh.

References unused_index.

Referenced by CO_Tree().

                                                      {
   PPL_ASSERT(ratio <= 100);
   // If these are true, no overflows are possible.
   PPL_ASSERT(denom <= unused_index/100);
   PPL_ASSERT(numer <= unused_index/100);
   return 100*numer > ratio*denom;
 }

bool Parma_Polyhedra_Library::CO_Tree::is_less_than_ratio	(	dimension_type	numer,
		dimension_type	denom,
		dimension_type	ratio
	)

inlinestaticprivate

Compares the fractions numer/denom with ratio/100.

Returns: Returns true if the fraction numer/denom is less than the fraction ratio/100.

Parameters

ratio	It must be less than or equal to 100.
numer	The numerator of the fraction.
denom	The denominator of the fraction.

This method takes $O(1)$ time.

Definition at line 308 of file CO_Tree_inlines.hh.

References unused_index.

                                                   {
   PPL_ASSERT(ratio <= 100);
   // If these are true, no overflows are possible.
   PPL_ASSERT(denom <= unused_index/100);
   PPL_ASSERT(numer <= unused_index/100);
   return 100*numer < ratio*denom;
 }

void Parma_Polyhedra_Library::CO_Tree::m_swap ( CO_Tree & x )

inline

Swaps x with *this.

Parameters

x	The tree that will be swapped with *this.

This operation invalidates existing iterators.

This method takes $O(1)$ time.

Definition at line 179 of file CO_Tree_inlines.hh.

References data, data_allocator, indexes, max_depth, refresh_cached_iterators(), reserved_size, size_, structure_OK(), Parma_Polyhedra_Library::swap(), and swap().

Referenced by Parma_Polyhedra_Library::Sparse_Row::linear_combine(), rebuild_smaller_tree(), and Parma_Polyhedra_Library::swap().

                           {
   using std::swap;
   swap(max_depth, x.max_depth);
   swap(indexes, x.indexes);
   swap(data_allocator, x.data_allocator);
   swap(data, x.data);
   swap(reserved_size, x.reserved_size);
   swap(size_, x.size_);
   // Cached iterators have been invalidated by the swap,
   // they must be refreshed here.
   refresh_cached_iterators();
   x.refresh_cached_iterators();
   PPL_ASSERT(structure_OK());
   PPL_ASSERT(x.structure_OK());
 }

dimension_type Parma_Polyhedra_Library::CO_Tree::max_size ( )

inlinestatic

Returns the size() of the largest possible CO_Tree.

Definition at line 96 of file CO_Tree_inlines.hh.

Referenced by Parma_Polyhedra_Library::Sparse_Row::max_size().

                   {
   return C_Integer<dimension_type>::max/100;
 }

void Parma_Polyhedra_Library::CO_Tree::move_data_element	(	data_type &	to,
		data_type &	from
	)

inlinestaticprivate

Moves the value of from in to .

Parameters

from	It must be a valid value.
to	It must be a non-constructed chunk of memory.

After the move, from becomes a non-constructed chunk of memory and to gets the value previously stored by from.

The implementation of this method assumes that data_type values do not keep pointers to themselves nor to their fields.

This method takes $O(1)$ time.

Definition at line 345 of file CO_Tree_inlines.hh.

                                                          {
   /*
     The following code is equivalent (but slower):
 
     <CODE>
       new(&to) data_type(from);
       from.~data_type();
     </CODE>
   */
   std::memcpy(&to, &from, sizeof(data_type));
 }

void Parma_Polyhedra_Library::CO_Tree::move_data_from ( CO_Tree & tree )

private

Moves all data in the tree tree into *this.

Parameters

tree	The tree from which the element will be moved into *this.

this must be empty and big enough to contain all of tree's data without exceeding max_density.

This method takes $O(n)$ time.

Definition at line 1133 of file CO_Tree.cc.

References data, Parma_Polyhedra_Library::CO_Tree::tree_iterator::get_left_child(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::get_parent(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::get_right_child(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::index(), indexes, reserved_size, size_, sizeof_to_bits, and structure_OK().

Referenced by rebuild_smaller_tree().

                                         {
   PPL_ASSERT(size_ == 0);
   if (tree.size_ == 0) {
     return;
   }
 
   tree_iterator root(*this);
 
   dimension_type source_index = 1;
   while (tree.indexes[source_index] == unused_index) {
     ++source_index;
   }
 
   // This is static and with static allocation, to improve performance.
   // sizeof_to_bits(sizeof(dimension_type)) is the maximum k such that 2^k-1 is a
   // dimension_type, so it is the maximum tree height.
   // For each node level, the stack may contain up to 4 elements: two elements
   // with operation 0, one element with operation 2 and one element
   // with operation 3. An additional element with operation 1 can be at the
   // top of the tree.
   static std::pair<dimension_type, signed char>
     stack[5U * sizeof_to_bits(sizeof(dimension_type))];
 
   dimension_type stack_first_empty = 0;
 
   // A pair (n, operation) in the stack means:
   //
   // * Go to the parent, if operation is 0.
   // * Go to the left child, then visit the current tree (with size n), if
   //   operation is 1.
   // * Go to the right child, then visit the current tree (with size n), if
   //   operation is 2.
   // * Visit the current tree (with size n), if operation is 3.
 
   stack[0].first = tree.size_;
   stack[0].second = 3;
   ++stack_first_empty;
 
   while (stack_first_empty != 0) {
 
     // Implement
     //
     // <CODE>
     //   top_n         = stack.top().first;
     //   top_operation = stack.top().second;
     // </CODE>
     const dimension_type top_n = stack[stack_first_empty - 1].first;
     const signed char top_operation = stack[stack_first_empty - 1].second;
 
     switch (top_operation) {
 
     case 0:
       root.get_parent();
       --stack_first_empty;
       continue;
 
     case 1:
       root.get_left_child();
       break;
 
     case 2:
       root.get_right_child();
       break;
 
 #ifndef NDEBUG
     case 3:
       break;
 
     default:
       PPL_UNREACHABLE;
       break;
 #endif
     }
 
     // We now visit the current tree
 
     if (top_n == 0) {
       --stack_first_empty;
     }
     else {
       if (top_n == 1) {
         PPL_ASSERT(root.index() == unused_index);
         PPL_ASSERT(tree.indexes[source_index] != unused_index);
         root.index() = tree.indexes[source_index];
         tree.indexes[source_index] = unused_index;
         move_data_element(*root, tree.data[source_index]);
         PPL_ASSERT(source_index <= tree.reserved_size);
         ++source_index;
         while (tree.indexes[source_index] == unused_index) {
           ++source_index;
         }
         --stack_first_empty;
       }
       else {
         PPL_ASSERT(stack_first_empty + 3 < sizeof(stack)/sizeof(stack[0]));
 
         const dimension_type half = (top_n + 1) / 2;
         stack[stack_first_empty - 1].second = 0;
         stack[stack_first_empty    ] = std::make_pair(top_n - half, 2);
         stack[stack_first_empty + 1] = std::make_pair(1, 3);
         stack[stack_first_empty + 2].second = 0;
         stack[stack_first_empty + 3] = std::make_pair(half - 1, 1);
         stack_first_empty += 4;
       }
     }
   }
   size_ = tree.size_;
   tree.size_ = 0;
   PPL_ASSERT(tree.structure_OK());
   PPL_ASSERT(structure_OK());
 }

bool Parma_Polyhedra_Library::CO_Tree::OK ( ) const

private

Checks the internal invariants.

Definition at line 752 of file CO_Tree.cc.

                      {
 
   if (!structure_OK()) {
     return false;
   }
   {
     dimension_type real_size = 0;
 
     for (const_iterator itr = begin(), itr_end = end(); itr != itr_end; ++itr) {
       ++real_size;
     }
 
     if (real_size != size_) {
       // There are \p real_size elements in the tree, but size is \p size.
       return false;
     }
   }
 
   if (reserved_size > 0) {
     if (is_greater_than_ratio(size_, reserved_size, max_density_percent)
         && reserved_size != 3) {
       // Found too high density.
       return false;
     }
     if (is_less_than_ratio(size_, reserved_size, min_density_percent)
         && !is_greater_than_ratio(size_, reserved_size/2, max_density_percent)) {
       // Found too low density
       return false;
     }
   }
 
   return true;
 }

CO_Tree & Parma_Polyhedra_Library::CO_Tree::operator= ( const CO_Tree & y )

inline

The assignment operator.

Parameters

y	The tree that will be assigned to *this.

This method takes $O(n)$ time.

Definition at line 64 of file CO_Tree_inlines.hh.

References copy_data_from(), data_allocator, destroy(), init(), and reserved_size.

                                    {
   if (this != &y) {
     destroy();
     data_allocator = y.data_allocator;
     init(y.reserved_size);
     copy_data_from(y);
   }
   return *this;
 }

Parma_Polyhedra_Library::CO_Tree::PPL_COMPILE_TIME_CHECK	(	C_Integer< height_t >::max >=	sizeof_to_bitssizeof(dimension_type),
		"height_t is too small to store depths."
	)

private

PPL::CO_Tree::tree_iterator Parma_Polyhedra_Library::CO_Tree::rebalance	(	tree_iterator	itr,
		dimension_type	key,
		data_type_const_reference	value
	)

private

Rebalances the tree.

For insertions, it adds the pair (key, value) in the process.

This operation invalidates existing iterators that point to nodes in the rebalanced subtree.

Returns: an iterator pointing to the root of the subtree that was rebalanced.

Parameters

itr	It points to the node where the new element has to be inserted or where an element has just been deleted.
key	The index that will be inserted in the tree (for insertions only).
value	The value that will be inserted in the tree (for insertions only).

This method takes 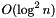$O(\log^2 n)$ amortized time.

Definition at line 868 of file CO_Tree.cc.

                                                          {
   // Trees with reserved size 3 need not to be rebalanced.
   // This check is needed because they can't be shrunk, so they may violate
   // the density thresholds, and this would prevent the following while from
   // working correctly.
   if (reserved_size == 3) {
     PPL_ASSERT(OK());
     return tree_iterator(*this);
   }
   PPL_ASSERT(itr.index() == unused_index || itr.is_leaf());
   height_t itr_depth_minus_1 = itr.depth() - 1;
   const height_t height = max_depth - itr_depth_minus_1;
   dimension_type subtree_size;
   dimension_type subtree_reserved_size = (static_cast<dimension_type>(1)
                                           << height) - 1;
   const bool deleting = itr.index() == unused_index;
   PPL_ASSERT(deleting || key != unused_index);
   if (deleting) {
     subtree_size = 0;
   }
   else {
     // The existing element and the element with index key we want to add.
     subtree_size = 2;
   }
 
   while (is_greater_than_ratio(subtree_size, subtree_reserved_size,
                                max_density_percent
                                + ((itr_depth_minus_1
                                    * (100 - max_density_percent))
                                   / (max_depth - 1)))
          || is_less_than_ratio(subtree_size, subtree_reserved_size,
                                min_density_percent
                                - ((itr_depth_minus_1
                                    * (min_density_percent
                                       - min_leaf_density_percent))
                                   / (max_depth - 1)))) {
     // The density in the tree is correct, so the while condition is always
     // false for the root.
     PPL_ASSERT(itr_depth_minus_1 != 0);
     const bool is_right_brother = itr.is_right_child();
     itr.get_parent();
     if (is_right_brother) {
       itr.get_left_child();
     }
     else {
       itr.get_right_child();
     }
     subtree_size += count_used_in_subtree(itr);
     itr.get_parent();
     PPL_ASSERT(itr.index() != unused_index);
     ++subtree_size;
     subtree_reserved_size = 2*subtree_reserved_size + 1;
     --itr_depth_minus_1;
     PPL_ASSERT(itr.depth() - 1 == itr_depth_minus_1);
   }
 
   // Now the subtree rooted at itr has been chosen as the subtree to be
   // rebalanced.
 
   // Step 1: compact elements of this subtree in the rightmost end, from right
   //         to left.
   const dimension_type last_index_in_subtree
     = itr.dfs_index() + itr.get_offset() - 1;
 
   const dimension_type first_unused
     = compact_elements_in_the_rightmost_end(last_index_in_subtree,
                                             subtree_size, key, value,
                                             !deleting);
 
   // Step 2: redistribute the elements, from left to right.
   redistribute_elements_in_subtree(itr.dfs_index(), subtree_size,
                                    first_unused + 1, key, value,
                                    first_unused != last_index_in_subtree
                                                    - subtree_size);
 
   PPL_ASSERT(OK());
 
   return itr;
 }

void Parma_Polyhedra_Library::CO_Tree::rebuild_bigger_tree ( )

private

Increases the tree's reserved size.

This is called when the density is about to exceed the maximum density (specified by max_density_percent).

This method takes $O(n)$ time.

Definition at line 819 of file CO_Tree.cc.

Referenced by insert_in_empty_tree().

                                 {
   if (reserved_size == 0) {
     init(3);
     PPL_ASSERT(structure_OK());
     return;
   }
 
   const dimension_type new_reserved_size = reserved_size*2 + 1;
 
   dimension_type* const new_indexes = new dimension_type[new_reserved_size + 2];
 
   data_type* new_data;
 
   try {
     new_data = data_allocator.allocate(new_reserved_size + 1);
   } catch (...) {
     delete[] new_indexes;
     throw;
   }
 
   new_indexes[1] = unused_index;
 
   for (dimension_type i = 1, j = 2; i <= reserved_size; ++i, ++j) {
     new_indexes[j] = indexes[i];
     if (indexes[i] != unused_index) {
       move_data_element(new_data[j], data[i]);
     }
     ++j;
     new_indexes[j] = unused_index;
   }
 
   // These are used as markers by iterators.
   new_indexes[0] = 0;
   new_indexes[new_reserved_size + 1] = 0;
 
   delete[] indexes;
   data_allocator.deallocate(data, reserved_size + 1);
 
   indexes = new_indexes;
   data = new_data;
   reserved_size = new_reserved_size;
   ++max_depth;
 
   refresh_cached_iterators();
 
   PPL_ASSERT(structure_OK());
 }

void Parma_Polyhedra_Library::CO_Tree::rebuild_smaller_tree ( )

inlineprivate

Decreases the tree's reserved size.

This is called when the density is about to become less than the minimum allowed density (specified by min_density_percent).

reserved_size must be greater than 3 (otherwise the tree can just be cleared).

This method takes $O(n)$ time.

Definition at line 328 of file CO_Tree_inlines.hh.

References init(), m_swap(), move_data_from(), reserved_size, and structure_OK().

                               {
   PPL_ASSERT(reserved_size > 3);
   CO_Tree new_tree;
   new_tree.init(reserved_size / 2);
   new_tree.move_data_from(*this);
   m_swap(new_tree);
   PPL_ASSERT(new_tree.structure_OK());
   PPL_ASSERT(structure_OK());
 }

void Parma_Polyhedra_Library::CO_Tree::redistribute_elements_in_subtree	(	dimension_type	root_index,
		dimension_type	subtree_size,
		dimension_type	last_used,
		dimension_type	key,
		data_type_const_reference	value,
		bool	add_element
	)

private

Redistributes the elements in the subtree rooted at root_index.

The subtree's elements must be compacted to the rightmost end.

Parameters

root_index	The index of the subtree's root node.
subtree_size	It is the number of used elements in the subtree. It must be greater than zero.
last_used	It points to the leftmost element with a value in the subtree.
add_element	If it is true, this method adds an element with the specified key and value in the process.
key	The key that will be added to the tree if `add_element` is `true`.
value	The data that will be added to the tree if `add_element` is `true`.

This method takes 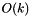$O(k)$ time, where k is subtree_size.

Definition at line 1038 of file CO_Tree.cc.

References sizeof_to_bits.

                       {
 
   // This is static and with static allocation, to improve performance.
   // sizeof_to_bits(sizeof(dimension_type)) is the maximum k such that
   // 2^k-1 is a dimension_type, so it is the maximum tree height.
   // For each node level, the stack may contain up to two element (one for the
   // subtree rooted at the right son of a node of that level, and one for the
   // node itself). An additional element can be at the top of the tree.
   static std::pair<dimension_type,dimension_type>
     stack[2U * sizeof_to_bits(sizeof(dimension_type)) + 1U];
 
   std::pair<dimension_type,dimension_type>* stack_first_empty = stack;
 
   // A pair (n, i) in the stack means to visit the subtree with root index i
   // and size n.
 
   PPL_ASSERT(subtree_size != 0);
 
   stack_first_empty->first  = subtree_size;
   stack_first_empty->second = root_index;
   ++stack_first_empty;
 
   while (stack_first_empty != stack) {
 
     --stack_first_empty;
 
     // Implement
     //
     // <CODE>
     //   top_n = stack.top().first;
     //   top_i = stack.top().second;
     // </CODE>
     const dimension_type top_n = stack_first_empty->first;
     const dimension_type top_i = stack_first_empty->second;
 
     PPL_ASSERT(top_n != 0);
     if (top_n == 1) {
       if (add_element
           && (last_used > reserved_size || indexes[last_used] > key)) {
         PPL_ASSERT(last_used != top_i);
         PPL_ASSERT(indexes[top_i] == unused_index);
         add_element = false;
         new(&(data[top_i])) data_type(value);
         // Set the index only if the construction was successful.
         indexes[top_i] = key;
       }
       else {
         if (last_used != top_i) {
           PPL_ASSERT(indexes[top_i] == unused_index);
           indexes[top_i] = indexes[last_used];
           indexes[last_used] = unused_index;
           move_data_element(data[top_i], data[last_used]);
         }
         ++last_used;
       }
     }
     else {
       PPL_ASSERT(stack_first_empty + 2
                  < stack + sizeof(stack)/sizeof(stack[0]));
 
       const dimension_type offset = (top_i & -top_i) / 2;
       const dimension_type half = (top_n + 1) / 2;
 
       PPL_ASSERT(half > 0);
 
       // Right subtree
       PPL_ASSERT(top_n - half > 0);
       stack_first_empty->first  = top_n - half;
       stack_first_empty->second = top_i + offset;
       ++stack_first_empty;
 
       // Root of the current subtree
       stack_first_empty->first   = 1;
       stack_first_empty->second  = top_i;
       ++stack_first_empty;
 
       // Left subtree
       if (half - 1 != 0) {
         stack_first_empty->first   = half - 1;
         stack_first_empty->second  = top_i - offset;
         ++stack_first_empty;
       }
     }
   }
 
   PPL_ASSERT(!add_element);
 }

void Parma_Polyhedra_Library::CO_Tree::refresh_cached_iterators ( )

inlineprivate

Re-initializes the cached iterators.

This method must be called when the indexes[] and data[] vector are reallocated.

This method takes $O(1)$ time.

Definition at line 339 of file CO_Tree_inlines.hh.

References cached_const_end, cached_end, and reserved_size.

Referenced by m_swap().

                                   {
   cached_end = iterator(*this, reserved_size + 1);
   cached_const_end = const_iterator(*this, reserved_size + 1);
 }

dimension_type Parma_Polyhedra_Library::CO_Tree::size ( ) const

inline

Returns the number of elements stored in the tree.

This method takes $O(1)$ time.

Definition at line 91 of file CO_Tree_inlines.hh.

References size_.

Referenced by Parma_Polyhedra_Library::Sparse_Row::num_stored_elements().

                     {
   return size_;
 }

bool Parma_Polyhedra_Library::CO_Tree::structure_OK ( ) const

private

Checks the internal invariants, but not the densities.

Definition at line 664 of file CO_Tree.cc.

References Parma_Polyhedra_Library::CO_Tree::const_iterator::index(), and Parma_Polyhedra_Library::CO_Tree::tree_iterator::index().

Referenced by m_swap(), move_data_from(), and rebuild_smaller_tree().

                                {
 
   if (size_ > reserved_size) {
     return false;
   }
 
   if (reserved_size == 0) {
     if (indexes != NULL) {
       return false;
     }
     if (data != NULL) {
       return false;
     }
     if (max_depth != 0) {
       return false;
     }
 
     return true;
   }
 
   if (reserved_size < 3) {
     return false;
   }
   if (reserved_size != (static_cast<dimension_type>(1) << max_depth) - 1) {
     return false;
   }
 
   if (data == NULL) {
     return false;
   }
 
   if (indexes == NULL) {
     return false;
   }
 
   if (max_depth == 0) {
     return false;
   }
 
   if (size_ == 0) {
 
     // This const_cast could be removed by adding a const_tree_iterator,
     // but it would add much code duplication without a real need.
     tree_iterator itr(*const_cast<CO_Tree*>(this));
     if (itr.index() != unused_index) {
       return false;
     }
 
   }
   else {
     // This const_cast could be removed by adding a const_tree_iterator,
     // but it would add much code duplication without a real need.
     tree_iterator itr(*const_cast<CO_Tree*>(this));
     const dimension_type real_size = count_used_in_subtree(itr);
     if (real_size != size_) {
       // There are \p real_size elements in the tree that are reachable by the
       // root, but size is \p size.
       return false;
     }
   }
 
   if (size_ != 0) {
     const_iterator itr = begin();
     const_iterator itr_end = end();
 
     if (itr != itr_end) {
       dimension_type last_index = itr.index();
       for (++itr; itr != itr_end; ++itr) {
         if (last_index >= itr.index()) {
           // Found index \p itr->first after index \p last_index.
           return false;
         }
         last_index = itr.index();
       }
     }
   }
 
   if (const_iterator(cached_end) != const_iterator(*this, reserved_size + 1)) {
     return false;
   }
   if (cached_const_end != const_iterator(*this, reserved_size + 1)) {
     return false;
   }
 
   return true;
 }

Friends And Related Function Documentation

void swap	(	CO_Tree &	x,
		CO_Tree &	y
	)

Definition at line 873 of file CO_Tree_inlines.hh.

Referenced by Parma_Polyhedra_Library::CO_Tree::const_iterator::m_swap(), Parma_Polyhedra_Library::CO_Tree::iterator::m_swap(), and m_swap().

                              {
   x.m_swap(y);
 }

Member Data Documentation

const_iterator Parma_Polyhedra_Library::CO_Tree::cached_const_end

private

The iterator returned by the const version of end().

It is updated when needed, to keep it valid.

Definition at line 1289 of file CO_Tree_defs.hh.

Referenced by cend(), end(), and refresh_cached_iterators().

iterator Parma_Polyhedra_Library::CO_Tree::cached_end

private

The iterator returned by end().

It is updated when needed, to keep it valid.

Definition at line 1283 of file CO_Tree_defs.hh.

Referenced by end(), and refresh_cached_iterators().

data_type* Parma_Polyhedra_Library::CO_Tree::data

private

The vector that contains the data of the keys in the tree.

If index[i] is unused_index, data[i] is unused. Otherwise, data[i] contains the data associated to the indexes[i] key.

Its size is reserved_size + 1, because the first element is not used (to allow using the same index in both indexes[] and data[] instead of adding 1 to access data[]).

Definition at line 1316 of file CO_Tree_defs.hh.

Referenced by copy_data_from(), external_memory_in_bytes(), m_swap(), move_data_from(), and Parma_Polyhedra_Library::CO_Tree::iterator::operator=().

std::allocator<data_type> Parma_Polyhedra_Library::CO_Tree::data_allocator

private

The allocator used to allocate/deallocate data.

Definition at line 1305 of file CO_Tree_defs.hh.

Referenced by CO_Tree(), m_swap(), and operator=().

dimension_type* Parma_Polyhedra_Library::CO_Tree::indexes

private

The vector that contains the keys in the tree.

If an element of this vector is unused_index , it means that that element and the corresponding element of data[] are not used.

Its size is reserved_size + 2, because the first and the last elements are used as markers for iterators.

Definition at line 1302 of file CO_Tree_defs.hh.

Referenced by Parma_Polyhedra_Library::CO_Tree::const_iterator::const_iterator(), copy_data_from(), count_used_in_subtree(), dfs_index(), external_memory_in_bytes(), fast_shift(), Parma_Polyhedra_Library::CO_Tree::iterator::iterator(), m_swap(), move_data_from(), and Parma_Polyhedra_Library::CO_Tree::iterator::operator=().

const dimension_type Parma_Polyhedra_Library::CO_Tree::max_density_percent = 91

staticprivate

The maximum density of used nodes.

This must be greater than or equal to 50 and lower than 100.

Definition at line 1255 of file CO_Tree_defs.hh.

Referenced by CO_Tree().

height_t Parma_Polyhedra_Library::CO_Tree::max_depth

private

The depth of the leaves in the complete tree.

Definition at line 1292 of file CO_Tree_defs.hh.

Referenced by m_swap().

const dimension_type Parma_Polyhedra_Library::CO_Tree::min_density_percent = 38

staticprivate

The minimum density of used nodes.

Must be strictly lower than the half of max_density_percent.

Definition at line 1261 of file CO_Tree_defs.hh.

const dimension_type Parma_Polyhedra_Library::CO_Tree::min_leaf_density_percent = 1

staticprivate

The minimum density at the leaves' depth.

Must be greater than zero and strictly lower than min_density_percent.

Increasing the value is safe but leads to time inefficiencies (measured against ppl_lpsol on 24 August 2010), because it forces trees to be more balanced, increasing the cost of rebalancing.

Definition at line 1271 of file CO_Tree_defs.hh.

dimension_type Parma_Polyhedra_Library::CO_Tree::reserved_size

private

The number of nodes in the complete tree.

It is one less than a power of 2. If this is 0, data and indexes are set to NULL.

Definition at line 1323 of file CO_Tree_defs.hh.

Referenced by CO_Tree(), Parma_Polyhedra_Library::CO_Tree::const_iterator::const_iterator(), copy_data_from(), dfs_index(), external_memory_in_bytes(), Parma_Polyhedra_Library::CO_Tree::iterator::iterator(), m_swap(), move_data_from(), operator=(), rebuild_smaller_tree(), refresh_cached_iterators(), and Parma_Polyhedra_Library::CO_Tree::tree_iterator::tree_iterator().

dimension_type Parma_Polyhedra_Library::CO_Tree::size_

private

The number of values stored in the tree.

Definition at line 1326 of file CO_Tree_defs.hh.

Referenced by CO_Tree(), copy_data_from(), empty(), insert_in_empty_tree(), m_swap(), move_data_from(), and size().

const dimension_type Parma_Polyhedra_Library::CO_Tree::unused_index = C_Integer<dimension_type>::max

staticprivate

An index used as a marker for unused nodes in the tree.

This must not be used as a key.

Definition at line 1277 of file CO_Tree_defs.hh.

Referenced by CO_Tree(), Parma_Polyhedra_Library::CO_Tree::const_iterator::const_iterator(), erase(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::follow_left_children_with_value(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::follow_right_children_with_value(), insert(), insert_in_empty_tree(), is_greater_than_ratio(), is_less_than_ratio(), Parma_Polyhedra_Library::CO_Tree::iterator::iterator(), Parma_Polyhedra_Library::CO_Tree::const_iterator::operator++(), Parma_Polyhedra_Library::CO_Tree::iterator::operator++(), Parma_Polyhedra_Library::CO_Tree::const_iterator::operator--(), and Parma_Polyhedra_Library::CO_Tree::iterator::operator--().

The documentation for this class was generated from the following files:

Classes

Public Types

Public Member Functions

Static Public Member Functions

Private Types

Private Member Functions

Static Private Member Functions

Private Attributes

Static Private Attributes

Related Functions

Detailed Description

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation

Friends And Related Function Documentation

Member Data Documentation