The entire library is confined to this namespace. More...
Namespaces | |
| Boundary_NS | |
| Checked | |
| Types and functions implementing checked numbers. | |
| Implementation | |
| Implementation related data and functions. | |
| Interfaces | |
| Data and functions related to language interfaces. | |
| Interval_NS | |
| IO_Operators | |
| All input/output operators are confined to this namespace. | |
Classes | |
| class | Affine_Space |
| An affine space. More... | |
| class | Any_Pointset |
| Any PPL pointset. More... | |
| class | Approximable_Reference |
| A concrete expression representing a reference to some approximable. More... | |
| class | Approximable_Reference_Common |
| Base class for references to some approximable. More... | |
| class | Ask_Tell |
| The ask and tell construction on a base-level domain. More... | |
| class | Ask_Tell_Pair |
| A pair of ask and tell descriptions. More... | |
| class | BD_Shape |
| A bounded difference shape. More... | |
| class | BD_Shape_Helpers |
| class | BHRZ03_Certificate |
| The convergence certificate for the BHRZ03 widening operator. More... | |
| class | Binary_Operator |
| A binary operator applied to two concrete expressions. More... | |
| class | Binary_Operator_Common |
| Base class for binary operator applied to two concrete expressions. More... | |
| class | Bit_Matrix |
| A matrix of bits. More... | |
| class | Bit_Row |
| A row in a matrix of bits. More... | |
| struct | Bool |
A class holding a constant called value that evaluates to b. More... | |
| class | Box |
| A not necessarily closed, iso-oriented hyperrectangle. More... | |
| class | Box_Helpers |
| struct | C_Integer |
| struct | C_Integer< char > |
| struct | C_Integer< signed char > |
| struct | C_Integer< signed int > |
| struct | C_Integer< signed long > |
| struct | C_Integer< signed long long > |
| struct | C_Integer< signed short > |
| struct | C_Integer< unsigned char > |
| struct | C_Integer< unsigned int > |
| struct | C_Integer< unsigned long > |
| struct | C_Integer< unsigned long long > |
| struct | C_Integer< unsigned short > |
| class | C_Polyhedron |
| A closed convex polyhedron. More... | |
| class | c_streambuf |
| class | Cast_Floating_Point_Expression |
| A generic Cast Floating Point Expression. More... | |
| class | Cast_Operator |
| A cast operator converting one concrete expression to some type. More... | |
| class | Cast_Operator_Common |
| Base class for cast operator concrete expressions. More... | |
| struct | Check_Overflow_Policy |
| A policy checking for overflows. More... | |
| class | Checked_Number |
| A wrapper for numeric types implementing a given policy. More... | |
| struct | Checked_Number_Transparent_Policy |
| class | CO_Tree |
| A cache-oblivious binary search tree of pairs. More... | |
| struct | Coefficient_traits_template |
| Coefficient traits. More... | |
| struct | Coefficient_traits_template< GMP_Integer > |
| Coefficient traits specialization for unbounded integers. More... | |
| struct | Compile_Time_Check |
A class that is only defined if b evaluates to true. More... | |
| struct | Compile_Time_Check< true > |
A class that is only defined if b evaluates to true. More... | |
| class | Concrete_Expression |
| The base class of all concrete expressions. More... | |
| class | Concrete_Expression_Common |
| Base class for all concrete expressions. More... | |
| class | Concrete_Expression_Type |
| The type of a concrete expression. More... | |
| class | Congruence |
| A linear congruence. More... | |
| class | Congruence_System |
| A system of congruences. More... | |
| class | Congruences_Reduction |
| This class provides the reduction method for the Congruences_Product domain. More... | |
| class | const_iterator_to_const |
| A const_iterator on a sequence of read-only objects. More... | |
| struct | Constant |
| struct | Constant_ |
| class | Constant_Floating_Point_Expression |
| A generic Constant Floating Point Expression. More... | |
| class | Constraint |
| A linear equality or inequality. More... | |
| class | Constraint_System |
| A system of constraints. More... | |
| class | Constraint_System_const_iterator |
| An iterator over a system of constraints. More... | |
| class | Constraints_Reduction |
| This class provides the reduction method for the Constraints_Product domain. More... | |
| class | DB_Matrix |
| The base class for the square matrices. More... | |
| class | DB_Row |
| The base class for the single rows of matrices. More... | |
| class | DB_Row_Impl_Handler |
| The handler of the actual DB_Row implementation. More... | |
| struct | Debug_WRD_Extended_Number_Policy |
| class | Dense_Row |
| A finite sequence of coefficients. More... | |
| class | Determinate |
| A wrapper for PPL pointsets, providing them with a determinate constraint system interface, as defined in [Bag98]. More... | |
| class | Difference_Floating_Point_Expression |
| A generic Difference Floating Point Expression. More... | |
| class | Dirty_Temp |
| A structure for the efficient handling of temporaries. More... | |
| class | Dirty_Temp< T, typename Enable_If< Slow_Copy< T >::value >::type > |
| Specialization for the handling of temporaries with a free list. More... | |
| class | Dirty_Temp< T, typename Enable_If<!Slow_Copy< T >::value >::type > |
| Specialization for the handling of temporaries with local variables. More... | |
| class | Division_Floating_Point_Expression |
| A generic Division Floating Point Expression. More... | |
| class | Domain_Product |
| This class is temporary and will be removed when template typedefs will be supported in C++. More... | |
| struct | Enable_If |
A class that provides a type member called type equivalent to T if and only if b is true. More... | |
| struct | Enable_If< true, T > |
A class that provides a type member called type equivalent to T if and only if b is true. More... | |
| struct | Enable_If_Is |
| struct | Euclidean_Distance_Specialization |
| class | Expression_Adapter |
| An adapter for Linear_Expression objects. More... | |
| class | Expression_Adapter_Base |
| Adapters' base type (for template meta-programming). More... | |
| class | Expression_Adapter_Transparent |
| A transparent adapter for Linear_Expression objects. More... | |
| class | Expression_Hide_Inhomo |
| An adapter for Linear_Expression that hides the inhomogeneous term. More... | |
| class | Expression_Hide_Last |
| An adapter for Linear_Expression that maybe hides the last coefficient. More... | |
| struct | Extended_Number_Policy |
| struct | False |
A class holding a constant called value that evaluates to false. More... | |
| struct | Fit |
| struct | Fit< T, v, typename Enable_If< C_Integer< T >::value >::type > |
| class | Float |
| struct | float_ibm_double |
| struct | float_ibm_single |
| struct | float_ieee754_double |
| struct | float_ieee754_half |
| struct | float_ieee754_quad |
| struct | float_ieee754_single |
| struct | float_intel_double_extended |
| class | Floating_Point_Constant |
| A floating-point constant concrete expression. More... | |
| class | Floating_Point_Constant_Common |
| Base class for floating-point constant concrete expression. More... | |
| class | Floating_Point_Expression |
| class | FP_Oracle |
| An abstract class to be implemented by an external analyzer such as ECLAIR in order to provide to the PPL the necessary information for performing the analysis of floating point computations. More... | |
| struct | FPU_Related |
| struct | FPU_Related< Checked_Number< T, Policy > > |
| struct | FPU_Related< double > |
| struct | FPU_Related< float > |
| struct | FPU_Related< long double > |
| class | Generator |
| A line, ray, point or closure point. More... | |
| class | Generator_System |
| A system of generators. More... | |
| class | Generator_System_const_iterator |
| An iterator over a system of generators. More... | |
| class | GMP_Integer |
| Unbounded integers as provided by the GMP library. More... | |
| class | Grid |
| A grid. More... | |
| class | Grid_Certificate |
| The convergence certificate for the Grid widening operator. More... | |
| class | Grid_Generator |
| A grid line, parameter or grid point. More... | |
| class | Grid_Generator_System |
| A system of grid generators. More... | |
| class | H79_Certificate |
| A convergence certificate for the H79 widening operator. More... | |
| struct | Has_Assign_Or_Swap |
| struct | Has_Assign_Or_Swap< T, typename Enable_If_Is< void(T::*)(T &x), &T::assign_or_swap >::type > |
| struct | Has_OK |
| struct | Has_OK< T, typename Enable_If_Is< bool(T::*)() const,&T::OK >::type > |
| class | I_Constraint |
| class | I_Constraint_Base |
| class | I_Constraint_Common |
| struct | I_Constraint_Rel |
| struct | ia32_fenv_t |
| class | In_Assert |
| class | Init |
| Class for initialization and finalization. More... | |
| class | Integer_Constant |
| An integer constant concrete expression. More... | |
| class | Integer_Constant_Common |
| Base class for integer constant concrete expressions. More... | |
| struct | Integer_Interval_Info_Policy |
| class | Interval |
| A generic, not necessarily closed, possibly restricted interval. More... | |
| struct | Interval_Base |
| class | Interval_Info_Bitset |
| class | Interval_Info_Null |
| class | Interval_Info_Null_Open |
| struct | Is_Checked |
| struct | Is_Checked< Checked_Number< T, P > > |
| struct | Is_Interval |
| struct | Is_Native |
| struct | Is_Native< char > |
| struct | Is_Native< mpq_class > |
| struct | Is_Native< mpz_class > |
| struct | Is_Native< signed char > |
| struct | Is_Native< signed int > |
| struct | Is_Native< signed long > |
| struct | Is_Native< signed long long > |
| struct | Is_Native< signed short > |
| struct | Is_Native< unsigned char > |
| struct | Is_Native< unsigned int > |
| struct | Is_Native< unsigned long > |
| struct | Is_Native< unsigned long long > |
| struct | Is_Native< unsigned short > |
| struct | Is_Native_Or_Checked |
| struct | Is_Same |
A class holding a constant called value that evaluates to true if and only if T1 is the same type as T2. More... | |
| struct | Is_Same< T, T > |
A class holding a constant called value that evaluates to true if and only if T1 is the same type as T2. More... | |
| struct | Is_Same_Or_Derived |
A class holding a constant called value that evaluates to true if and only if Base is the same type as Derived or Derived is a class derived from Base. More... | |
| struct | Is_Singleton |
| struct | Is_Special |
| struct | Is_Special< Minus_Infinity > |
| struct | Is_Special< Not_A_Number > |
| struct | Is_Special< Plus_Infinity > |
| class | iterator_to_const |
| An iterator on a sequence of read-only objects. More... | |
| struct | L_Infinity_Distance_Specialization |
| class | Limited_Widening_Function |
| Wraps a limited widening method into a function object. More... | |
| class | Linear_Expression |
| A linear expression. More... | |
| class | Linear_Expression_Impl |
| A linear expression. More... | |
| class | Linear_Expression_Interface |
| A linear expression. More... | |
| class | Linear_Form |
| A linear form with interval coefficients. More... | |
| class | Linear_System |
| The base class for systems of constraints and generators. More... | |
| class | Linear_System_With_Bit_Matrix_iterator |
| class | Matrix |
| A sparse matrix of Coefficient. More... | |
| struct | maybe_assign_struct |
| struct | maybe_assign_struct< Type, Type > |
| struct | Minus_Infinity |
| class | MIP_Problem |
| A Mixed Integer (linear) Programming problem. More... | |
| class | Multiplication_Floating_Point_Expression |
| A generic Multiplication Floating Point Expression. More... | |
| struct | Native_Checked_From_Wrapper |
| struct | Native_Checked_From_Wrapper< Checked_Number< T, P > > |
| struct | Native_Checked_From_Wrapper< T, typename Enable_If< Is_Native< T >::value >::type > |
| struct | Native_Checked_To_Wrapper |
| struct | Native_Checked_To_Wrapper< Checked_Number< T, P > > |
| struct | Native_Checked_To_Wrapper< T, typename Enable_If< Is_Native< T >::value >::type > |
| class | NNC_Polyhedron |
| A not necessarily closed convex polyhedron. More... | |
| class | No_Reduction |
| This class provides the reduction method for the Direct_Product domain. More... | |
| struct | Not_A_Number |
| class | Numeric_Format |
| class | Octagonal_Shape |
| An octagonal shape. More... | |
| class | Octagonal_Shape_Helper |
| class | Opposite_Floating_Point_Expression |
| A generic Opposite Floating Point Expression. More... | |
| class | OR_Matrix |
| A matrix representing octagonal constraints. More... | |
| class | Partial_Function |
| class | Partially_Reduced_Product |
| The partially reduced product of two abstractions. More... | |
| class | PIP_Decision_Node |
| A tree node representing a decision in the space of solutions. More... | |
| class | PIP_Problem |
| A Parametric Integer (linear) Programming problem. More... | |
| class | PIP_Solution_Node |
| A tree node representing part of the space of solutions. More... | |
| class | PIP_Tree_Node |
| A node of the PIP solution tree. More... | |
| struct | Plus_Infinity |
| class | Pointset_Ask_Tell |
| The ask-and-tell construction instantiated on PPL polyhedra. More... | |
| class | Pointset_Powerset |
| The powerset construction instantiated on PPL pointset domains. More... | |
| class | Poly_Con_Relation |
| The relation between a polyhedron and a constraint. More... | |
| class | Poly_Gen_Relation |
| The relation between a polyhedron and a generator. More... | |
| class | Polyhedron |
| The base class for convex polyhedra. More... | |
| class | Powerset |
| The powerset construction on a base-level domain. More... | |
| struct | Rational_Interval_Info_Policy |
| struct | Rectilinear_Distance_Specialization |
| struct | Recycle_Input |
| A tag class. More... | |
| class | Scalar_Products |
| A class implementing various scalar product functions. More... | |
| struct | Select_Temp_Boundary_Type |
| Helper class to select the appropriate numerical type to perform boundary computations so as to reduce the chances of overflow without incurring too much overhead. More... | |
| struct | Select_Temp_Boundary_Type< char > |
| struct | Select_Temp_Boundary_Type< signed char > |
| struct | Select_Temp_Boundary_Type< signed int > |
| struct | Select_Temp_Boundary_Type< signed long > |
| struct | Select_Temp_Boundary_Type< signed short > |
| struct | Select_Temp_Boundary_Type< unsigned char > |
| struct | Select_Temp_Boundary_Type< unsigned int > |
| struct | Select_Temp_Boundary_Type< unsigned long > |
| struct | Select_Temp_Boundary_Type< unsigned long long > |
| struct | Select_Temp_Boundary_Type< unsigned short > |
| class | Shape_Preserving_Reduction |
| This class provides the reduction method for the Shape_Preserving_Product domain. More... | |
| struct | Slow_Copy |
| struct | Slow_Copy< Checked_Number< T, P > > |
| struct | Slow_Copy< mpq_class > |
| struct | Slow_Copy< mpz_class > |
| class | Smash_Reduction |
| This class provides the reduction method for the Smash_Product domain. More... | |
| class | Sparse_Row |
| A finite sparse sequence of coefficients. More... | |
| class | stdiobuf |
| class | Sum_Floating_Point_Expression |
| A generic Sum Floating Point Expression. More... | |
| struct | Suppress_Uninitialized_Warnings_Type |
| class | Swapping_Vector |
| struct | TConstant |
| class | Temp_Item |
A pool of temporary items of type T. More... | |
| class | Temp_Reference_Holder |
| An holder for a reference to a temporary object. More... | |
| class | Temp_Value_Holder |
| An (fake) holder for the value of a temporary object. More... | |
| class | Termination_Helpers |
| class | Threshold_Watcher |
| A class of watchdogs controlling the exceeding of a threshold. More... | |
| class | Throwable |
| User objects the PPL can throw. More... | |
| class | Topology_Adjusted_Scalar_Product_Sign |
| Scalar product sign function object depending on topology. More... | |
| struct | True |
A class holding a constant called value that evaluates to true. More... | |
| class | Unary_Operator |
| A unary operator applied to one concrete expression. More... | |
| class | Unary_Operator_Common |
| Base class for unary operator applied to one concrete expression. More... | |
| struct | Use_By_Ref |
| struct | Use_By_Ref< By_Ref, T > |
| struct | Use_By_Ref< By_Value, T > |
| struct | Use_By_Ref< Use_Slow_Copy, T > |
| class | Val_Or_Ref |
| class | Val_Or_Ref< T, Criteria, typename Enable_If< Use_By_Ref< Criteria, T >::value >::type > |
| class | Val_Or_Ref< T, Criteria, typename Enable_If<!Use_By_Ref< Criteria, T >::value >::type > |
| class | Variable |
| A dimension of the vector space. More... | |
| class | Variable_Floating_Point_Expression |
| A generic Variable Floating Point Expression. More... | |
| class | Variables_Set |
| An std::set of variables' indexes. More... | |
| class | Watchdog |
| A watchdog timer. More... | |
| struct | Watchdog_Traits |
| class | Weight_Profiler |
| struct | Weightwatch_Traits |
| Traits class for the deterministic timeout mechanism. More... | |
| class | Widening_Function |
| Wraps a widening method into a function object. More... | |
| struct | WRD_Extended_Number_Policy |
Typedefs | |
| typedef PPL_COEFFICIENT_TYPE | Coefficient |
| An alias for easily naming the type of PPL coefficients. More... | |
| typedef Coefficient_traits_template< Coefficient > | Coefficient_traits |
| An alias for easily naming the coefficient traits. More... | |
| typedef int | Concrete_Expression_Kind |
| Encodes the kind of concrete expression. More... | |
| typedef int | Concrete_Expression_BOP |
| Encodes a binary operator of concrete expressions. More... | |
| typedef int | Concrete_Expression_UOP |
| Encodes a unary operator of concrete expressions. More... | |
| typedef size_t | dimension_type |
| An unsigned integral type for representing space dimensions. More... | |
| typedef size_t | memory_size_type |
| An unsigned integral type for representing memory size in bytes. More... | |
| typedef mpz_class | GMP_Integer |
| typedef Interval_Info_Bitset< unsigned int, Integer_Interval_Info_Policy > | Integer_Interval_Info |
| typedef Interval< mpz_class, Integer_Interval_Info > | Integer_Interval |
| An interval with integral, necessarily closed boundaries. More... | |
| typedef const PIP_Tree_Node * | PIP_Tree |
| typedef Box< Rational_Interval > | Rational_Box |
| A box with rational, possibly open boundaries. More... | |
| typedef Interval_Info_Bitset< unsigned int, Rational_Interval_Info_Policy > | Rational_Interval_Info |
| typedef Interval< mpq_class, Rational_Interval_Info > | Rational_Interval |
| An interval with rational, possibly open boundaries. More... | |
Functions | |
| template<typename T > | |
| Enable_If< Has_Assign_Or_Swap< T >::value, void >::type | assign_or_swap (T &to, T &from) |
| template<typename T > | |
| Enable_If<!Has_Assign_Or_Swap< T >::value &&!Slow_Copy< T >::value, void >::type | assign_or_swap (T &to, T &from) |
| template<typename T > | |
| Enable_If<!Has_Assign_Or_Swap< T >::value &&Slow_Copy< T >::value, void >::type | assign_or_swap (T &to, T &from) |
| template<typename ITV > | |
| Poly_Con_Relation | interval_relation (const ITV &i, const Constraint::Type constraint_type, Coefficient_traits::const_reference numer, Coefficient_traits::const_reference denom=Coefficient_one()) |
| Returns the relations holding between an interval and an interval constraint. More... | |
| template<typename ITV > | |
| bool | operator!= (const Box< ITV > &x, const Box< ITV > &y) |
| template<typename ITV > | |
| bool | operator== (const Box< ITV > &x, const Box< ITV > &y) |
| unsigned | irrational_precision () |
| Returns the precision parameter used for irrational calculations. More... | |
| void | set_irrational_precision (const unsigned p) |
| Sets the precision parameter used for irrational calculations. More... | |
| void | throw_result_exception (Result r) |
| template<typename T > | |
| T | plus_infinity () |
| template<typename T > | |
| T | minus_infinity () |
| template<typename T > | |
| T | not_a_number () |
| template<typename T > | |
| void | maybe_reset_fpu_inexact () |
| template<typename T > | |
| int | maybe_check_fpu_inexact () |
| Rounding_Dir | rounding_dir (Rounding_Dir dir) |
| Result | check_result (Result r, Rounding_Dir dir) |
| template<typename To , typename From > | |
| Enable_If< Is_Native_Or_Checked< To >::value &&Is_Special< From >::value, Result >::type | assign_r (To &to, const From &, Rounding_Dir dir) |
| template<typename To , typename From > | |
| Enable_If< Is_Native_Or_Checked< To >::value &&Is_Special< From >::value, Result >::type | construct (To &to, const From &, Rounding_Dir dir) |
| template<typename T > | |
| Enable_If< Is_Native_Or_Checked< T >::value, bool >::type | is_minus_infinity (const T &x) |
| template<typename T > | |
| Enable_If< Is_Native_Or_Checked< T >::value, bool >::type | is_plus_infinity (const T &x) |
| template<typename T > | |
| Enable_If< Is_Native_Or_Checked< T >::value, int >::type | infinity_sign (const T &x) |
| template<typename T > | |
| Enable_If< Is_Native_Or_Checked< T >::value, bool >::type | is_not_a_number (const T &x) |
| template<typename T > | |
| Enable_If< Is_Native_Or_Checked< T >::value, bool >::type | is_integer (const T &x) |
| template<typename T , typename Policy > | |
| bool | is_not_a_number (const Checked_Number< T, Policy > &x) |
| template<typename T , typename Policy > | |
| bool | is_minus_infinity (const Checked_Number< T, Policy > &x) |
| template<typename T , typename Policy > | |
| bool | is_plus_infinity (const Checked_Number< T, Policy > &x) |
| template<typename T , typename Policy > | |
| void | exact_div_assign (Checked_Number< T, Policy > &x, const Checked_Number< T, Policy > &y, const Checked_Number< T, Policy > &z) |
| template<typename T > | |
| Enable_If< Is_Native_Or_Checked< T >::value, void >::type | ascii_dump (std::ostream &s, const T &t) |
| template<typename T > | |
| Enable_If< Is_Native_Or_Checked< T >::value, bool >::type | ascii_load (std::istream &s, T &t) |
| void | swap (CO_Tree &x, CO_Tree &y) |
| void | swap (CO_Tree::const_iterator &x, CO_Tree::const_iterator &y) |
| void | swap (CO_Tree::iterator &x, CO_Tree::iterator &y) |
| void | Coefficient_constants_initialize () |
| Initializes the Coefficient constants. More... | |
| void | Coefficient_constants_finalize () |
| Finalizes the Coefficient constants. More... | |
| Coefficient_traits::const_reference | Coefficient_zero () |
| Returns a const reference to a Coefficient with value 0. More... | |
| Coefficient_traits::const_reference | Coefficient_one () |
| Returns a const reference to a Coefficient with value 1. More... | |
| template<typename T > | |
| void | PPL_CC_FLUSH (const T &x) |
| No-op function that force the compiler to store the argument and to reread it from memory if needed (thus preventing CSE). More... | |
| unsigned int | clz32 (uint32_t w) |
| unsigned int | clz64 (uint64_t w) |
| unsigned int | ctz32 (uint32_t w) |
| unsigned int | ctz64 (uint64_t w) |
| unsigned int | clz (unsigned int u) |
| unsigned int | clz (unsigned long ul) |
| unsigned int | clz (unsigned long long ull) |
| unsigned int | ctz (unsigned int u) |
| unsigned int | ctz (unsigned long ul) |
| unsigned int | ctz (unsigned long long ull) |
| bool | operator== (const Constraint_System &x, const Constraint_System &y) |
| bool | operator!= (const Constraint_System &x, const Constraint_System &y) |
| void | linear_combine (Dense_Row &x, const Dense_Row &y, Coefficient_traits::const_reference coeff1, Coefficient_traits::const_reference coeff2) |
| void | linear_combine (Dense_Row &x, const Dense_Row &y, Coefficient_traits::const_reference c1, Coefficient_traits::const_reference c2, dimension_type start, dimension_type end) |
| template<typename To , typename From > | |
| Result | maybe_assign (const To *&top, To &tmp, const From &from, Rounding_Dir dir) |
Assigns to top a pointer to a location that holds the conversion, according to dir, of from to type To. When necessary, and only when necessary, the variable tmp is used to hold the result of conversion. More... | |
| unsigned int | msb_position (unsigned long long v) |
If v is nonzero, returns the position of the most significant bit in a. More... | |
| bool | is_less_precise_than (Floating_Point_Format f1, Floating_Point_Format f2) |
| template<typename FP_Interval_Type > | |
| void | affine_form_image (std::map< dimension_type, Linear_Form< FP_Interval_Type > > &lf_store, const Variable var, const Linear_Form< FP_Interval_Type > &lf) |
| template<typename FP_Interval_Type > | |
| const FP_Interval_Type & | compute_absolute_error (const Floating_Point_Format analyzed_format) |
| template<typename FP_Interval_Type > | |
| void | discard_occurrences (std::map< dimension_type, Linear_Form< FP_Interval_Type > > &lf_store, Variable var) |
| template<typename FP_Interval_Type > | |
| void | upper_bound_assign (std::map< dimension_type, Linear_Form< FP_Interval_Type > > &ls1, const std::map< dimension_type, Linear_Form< FP_Interval_Type > > &ls2) |
| int | fpu_get_control () |
| void | fpu_set_control (int c) |
| int | fpu_get_status () |
| void | fpu_clear_status (unsigned short bits) |
| void | fpu_clear_exceptions () |
| void | fpu_set_rounding_direction (int) |
| int | fpu_save_rounding_direction (int) |
| void | fpu_restore_rounding_direction (int) |
| bool | operator== (const Generator_System &x, const Generator_System &y) |
| bool | operator!= (const Generator_System &x, const Generator_System &y) |
| dimension_type | check_space_dimension_overflow (const dimension_type dim, const dimension_type max, const char *domain, const char *method, const char *reason) |
| dimension_type | not_a_dimension () |
| Returns a value that does not designate a valid dimension. More... | |
| int32_t | hash_code_from_dimension (dimension_type dim) |
Returns the hash code for space dimension dim. More... | |
| template<typename T > | |
| Enable_If< Slow_Copy< T >::value, void >::type | swap (T &, T &) |
| Make sure swap() is specialized when needed. More... | |
| dimension_type | compute_capacity (dimension_type requested_size, dimension_type maximum_size) |
| Speculative allocation function. More... | |
| bool | is_space (char c) |
Returns true if c is any kind of space character. More... | |
| template<typename T > | |
| Enable_If< Has_OK< T >::value, bool >::type | f_OK (const T &to) |
| void | ascii_dump (std::ostream &s, Representation r) |
| bool | ascii_load (std::istream &s, Representation &r) |
| template<typename RA_Container > | |
| RA_Container::iterator | nth_iter (RA_Container &cont, dimension_type n) |
| template<typename RA_Container > | |
| RA_Container::const_iterator | nth_iter (const RA_Container &cont, dimension_type n) |
| dimension_type | least_significant_one_mask (dimension_type i) |
| void | maybe_abandon () |
| void | neg_assign (GMP_Integer &x) |
| void | neg_assign (GMP_Integer &x, const GMP_Integer &y) |
| void | abs_assign (GMP_Integer &x) |
| void | abs_assign (GMP_Integer &x, const GMP_Integer &y) |
| void | gcd_assign (GMP_Integer &x, const GMP_Integer &y, const GMP_Integer &z) |
| void | rem_assign (GMP_Integer &x, const GMP_Integer &y, const GMP_Integer &z) |
| void | gcdext_assign (GMP_Integer &x, GMP_Integer &s, GMP_Integer &t, const GMP_Integer &y, const GMP_Integer &z) |
| void | lcm_assign (GMP_Integer &x, const GMP_Integer &y, const GMP_Integer &z) |
| void | add_mul_assign (GMP_Integer &x, const GMP_Integer &y, const GMP_Integer &z) |
| void | sub_mul_assign (GMP_Integer &x, const GMP_Integer &y, const GMP_Integer &z) |
| void | mul_2exp_assign (GMP_Integer &x, const GMP_Integer &y, unsigned int exp) |
| void | div_2exp_assign (GMP_Integer &x, const GMP_Integer &y, unsigned int exp) |
| void | exact_div_assign (GMP_Integer &x, const GMP_Integer &y, const GMP_Integer &z) |
| void | sqrt_assign (GMP_Integer &x, const GMP_Integer &y) |
| int | cmp (const GMP_Integer &x, const GMP_Integer &y) |
| const mpz_class & | raw_value (const GMP_Integer &x) |
| mpz_class & | raw_value (GMP_Integer &x) |
| void | set_rounding_for_PPL () |
| Sets the FPU rounding mode so that the PPL abstractions based on floating point numbers work correctly. More... | |
| void | restore_pre_PPL_rounding () |
| Sets the FPU rounding mode as it was before initialization of the PPL. More... | |
| void | initialize () |
| Initializes the library. More... | |
| void | finalize () |
| Finalizes the library. More... | |
| I_Result | combine (Result l, Result u) |
| template<typename Boundary , typename Info > | |
| bool | f_is_empty (const Interval< Boundary, Info > &x) |
| template<typename Boundary , typename Info > | |
| bool | f_is_singleton (const Interval< Boundary, Info > &x) |
| template<typename Boundary , typename Info > | |
| int | infinity_sign (const Interval< Boundary, Info > &x) |
| template<typename T > | |
| Enable_If< Is_Singleton< T >::value||Is_Interval< T >::value, bool >::type | is_singleton_integer (const T &x) |
| template<typename T > | |
| Enable_If< Is_Singleton< T >::value||Is_Interval< T >::value, bool >::type | check_empty_arg (const T &x) |
| template<typename T1 , typename T2 > | |
| Enable_If<((Is_Singleton< T1 >::value||Is_Interval< T1 >::value)&&(Is_Singleton< T2 >::value||Is_Interval< T2 >::value)&&(Is_Interval< T1 >::value||Is_Interval< T2 >::value)), bool >::type | operator== (const T1 &x, const T2 &y) |
| template<typename T1 , typename T2 > | |
| Enable_If<((Is_Singleton< T1 >::value||Is_Interval< T1 >::value)&&(Is_Singleton< T2 >::value||Is_Interval< T2 >::value)&&(Is_Interval< T1 >::value||Is_Interval< T2 >::value)), bool >::type | operator!= (const T1 &x, const T2 &y) |
| template<typename B , typename Info , typename T > | |
| Enable_If< Is_Singleton< T >::value, Interval< B, Info > >::type | operator+ (const Interval< B, Info > &x, const T &y) |
| template<typename B , typename Info , typename T > | |
| Enable_If< Is_Singleton< T >::value, Interval< B, Info > >::type | operator+ (const T &x, const Interval< B, Info > &y) |
| template<typename B , typename Info > | |
| Interval< B, Info > | operator+ (const Interval< B, Info > &x, const Interval< B, Info > &y) |
| template<typename B , typename Info , typename T > | |
| Enable_If< Is_Singleton< T >::value, Interval< B, Info > >::type | operator- (const Interval< B, Info > &x, const T &y) |
| template<typename B , typename Info , typename T > | |
| Enable_If< Is_Singleton< T >::value, Interval< B, Info > >::type | operator- (const T &x, const Interval< B, Info > &y) |
| template<typename B , typename Info > | |
| Interval< B, Info > | operator- (const Interval< B, Info > &x, const Interval< B, Info > &y) |
| template<typename B , typename Info , typename T > | |
| Enable_If< Is_Singleton< T >::value, Interval< B, Info > >::type | operator* (const Interval< B, Info > &x, const T &y) |
| template<typename B , typename Info , typename T > | |
| Enable_If< Is_Singleton< T >::value, Interval< B, Info > >::type | operator* (const T &x, const Interval< B, Info > &y) |
| template<typename B , typename Info > | |
| Interval< B, Info > | operator* (const Interval< B, Info > &x, const Interval< B, Info > &y) |
| template<typename B , typename Info , typename T > | |
| Enable_If< Is_Singleton< T >::value, Interval< B, Info > >::type | operator/ (const Interval< B, Info > &x, const T &y) |
| template<typename B , typename Info , typename T > | |
| Enable_If< Is_Singleton< T >::value, Interval< B, Info > >::type | operator/ (const T &x, const Interval< B, Info > &y) |
| template<typename B , typename Info > | |
| Interval< B, Info > | operator/ (const Interval< B, Info > &x, const Interval< B, Info > &y) |
| template<typename Boundary , typename Info > | |
| std::ostream & | operator<< (std::ostream &os, const Interval< Boundary, Info > &x) |
| template<typename Boundary , typename Info > | |
| std::istream & | operator>> (std::istream &is, Interval< Boundary, Info > &x) |
| I_Result | operator| (I_Result a, I_Result b) |
| I_Result | operator& (I_Result a, I_Result b) |
| I_Result | operator- (I_Result a, I_Result b) |
| template<typename T > | |
| I_Constraint< T > | i_constraint (I_Constraint_Rel rel, const T &v) |
| template<typename T > | |
| I_Constraint< T > | i_constraint (I_Constraint_Rel rel, const T &v, bool force) |
| template<typename T > | |
| I_Constraint< T > | i_constraint (I_Constraint_Rel rel, T &v) |
| template<typename T , typename Val_Or_Ref_Criteria > | |
| I_Constraint< T, Val_Or_Ref_Criteria > | i_constraint (I_Constraint_Rel rel, const T &v, const Val_Or_Ref_Criteria &) |
| template<typename T , typename Val_Or_Ref_Criteria > | |
| I_Constraint< T, Val_Or_Ref_Criteria > | i_constraint (I_Constraint_Rel rel, const T &v, bool force, const Val_Or_Ref_Criteria &) |
| template<typename T , typename Val_Or_Ref_Criteria > | |
| I_Constraint< T, Val_Or_Ref_Criteria > | i_constraint (I_Constraint_Rel rel, T &v, const Val_Or_Ref_Criteria &) |
| void | add_mul_assign (Linear_Expression &e1, Coefficient_traits::const_reference factor, const Linear_Expression &e2) |
| void | sub_mul_assign (Linear_Expression &e1, Coefficient_traits::const_reference factor, const Linear_Expression &e2) |
| int | compare (const Linear_Expression &x, const Linear_Expression &y) |
| template<typename T > | |
| Enable_If< Is_Native_Or_Checked< T >::value, void >::type | numer_denom (const T &from, Coefficient &numer, Coefficient &denom) |
Extract the numerator and denominator components of from. More... | |
| template<typename T > | |
| Enable_If< Is_Native_Or_Checked< T >::value, void >::type | div_round_up (T &to, Coefficient_traits::const_reference x, Coefficient_traits::const_reference y) |
Divides x by y into to, rounding the result towards plus infinity. More... | |
| template<typename N > | |
| void | min_assign (N &x, const N &y) |
Assigns to x the minimum between x and y. More... | |
| template<typename N > | |
| void | max_assign (N &x, const N &y) |
Assigns to x the maximum between x and y. More... | |
| template<typename T > | |
| Enable_If< Is_Native_Or_Checked< T >::value, bool >::type | is_even (const T &x) |
Returns true if and only if x is an even number. More... | |
| template<typename T > | |
| Enable_If< Is_Native_Or_Checked< T >::value, bool >::type | is_additive_inverse (const T &x, const T &y) |
Returns true if and only if 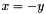 . More... . More... | |
| void | normalize2 (Coefficient_traits::const_reference x, Coefficient_traits::const_reference y, Coefficient &n_x, Coefficient &n_y) |
If 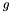 is the GCD of is the GCD of x and y, the values of x and y divided by 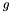 are assigned to are assigned to n_x and n_y, respectively. More... | |
| bool | is_canonical (const mpq_class &x) |
Returns true if and only if x is in canonical form. More... | |
| template<typename T > | |
| T | low_bits_mask (unsigned n) |
Returns a mask for the lowest n bits,. More... | |
| template<typename Row > | |
| void | swap (Matrix< Row > &x, Matrix< Row > &y) |
| dimension_type | max_space_dimension () |
| Returns the maximum space dimension this library can handle. More... | |
| dimension_type | isqrt (dimension_type x) |
Returns the integer square root of x. More... | |
| template<typename D1 , typename D2 > | |
| bool | shrink_to_congruence_no_check (D1 &d1, D2 &d2, const Congruence &cg) |
| int | result_overflow (Result r) |
| bool | result_representable (Result r) |
| void | swap (Parma_Polyhedra_Library::Sparse_Row &x, Parma_Polyhedra_Library::Dense_Row &y) |
| void | swap (Parma_Polyhedra_Library::Dense_Row &x, Parma_Polyhedra_Library::Sparse_Row &y) |
| bool | operator== (const Dense_Row &x, const Sparse_Row &y) |
| bool | operator!= (const Dense_Row &x, const Sparse_Row &y) |
| bool | operator== (const Sparse_Row &x, const Dense_Row &y) |
| bool | operator!= (const Sparse_Row &x, const Dense_Row &y) |
| template<typename T > | |
| void | swap (Swapping_Vector< T > &vec1, Swapping_Vector< T > &vec2) |
| void | swap (Variable &x, Variable &y) |
| void | PPL_handle_timeout (int signum) |
Library Version Control Functions | |
| unsigned | version_major () |
| Returns the major number of the PPL version. More... | |
| unsigned | version_minor () |
| Returns the minor number of the PPL version. More... | |
| unsigned | version_revision () |
| Returns the revision number of the PPL version. More... | |
| unsigned | version_beta () |
| Returns the beta number of the PPL version. More... | |
| const char * | version () |
| Returns a character string containing the PPL version. More... | |
| const char * | banner () |
| Returns a character string containing the PPL banner. More... | |
Functions Controlling Floating Point Unit | |
| void | fpu_initialize_control_functions () |
| Initializes the FPU control functions. More... | |
| fpu_rounding_direction_type | fpu_get_rounding_direction () |
| Returns the current FPU rounding direction. More... | |
| void | fpu_set_rounding_direction (fpu_rounding_direction_type dir) |
Sets the FPU rounding direction to dir. More... | |
| fpu_rounding_control_word_type | fpu_save_rounding_direction (fpu_rounding_direction_type dir) |
Sets the FPU rounding direction to dir and returns the rounding control word previously in use. More... | |
| void | fpu_reset_inexact () |
| Clears the inexact computation status. More... | |
| void | fpu_restore_rounding_direction (fpu_rounding_control_word_type w) |
Restores the FPU rounding rounding control word to cw. More... | |
| int | fpu_check_inexact () |
| Queries the inexact computation status. More... | |
| fpu_rounding_control_word_type | fpu_save_rounding_direction_reset_inexact (fpu_rounding_direction_type dir) |
Sets the FPU rounding direction to dir, clears the inexact computation status, and returns the rounding control word previously in use. More... | |
Memory Size Inspection Functions | |
| template<typename T > | |
| Enable_If< Is_Native< T >::value, memory_size_type >::type | total_memory_in_bytes (const T &) |
| For native types, returns the total size in bytes of the memory occupied by the type of the (unused) parameter, i.e., 0. More... | |
| template<typename T > | |
| Enable_If< Is_Native< T >::value, memory_size_type >::type | external_memory_in_bytes (const T &) |
| For native types, returns the size in bytes of the memory managed by the type of the (unused) parameter, i.e., 0. More... | |
| memory_size_type | total_memory_in_bytes (const mpz_class &x) |
Returns the total size in bytes of the memory occupied by x. More... | |
| memory_size_type | external_memory_in_bytes (const mpz_class &x) |
Returns the size in bytes of the memory managed by x. More... | |
| memory_size_type | total_memory_in_bytes (const mpq_class &x) |
Returns the total size in bytes of the memory occupied by x. More... | |
| memory_size_type | external_memory_in_bytes (const mpq_class &x) |
Returns the size in bytes of the memory managed by x. More... | |
Functions Inspecting and/or Combining Result Values | |
| Result | operator& (Result x, Result y) |
| Result | operator| (Result x, Result y) |
| Result | operator- (Result x, Result y) |
| Result_Class | result_class (Result r) |
| Result_Relation | result_relation (Result r) |
| Result | result_relation_class (Result r) |
Functions Inspecting and/or Combining Rounding_Dir Values | |
| Rounding_Dir | operator& (Rounding_Dir x, Rounding_Dir y) |
| Rounding_Dir | operator| (Rounding_Dir x, Rounding_Dir y) |
| Rounding_Dir | inverse (Rounding_Dir dir) |
| Rounding_Dir | round_dir (Rounding_Dir dir) |
| bool | round_down (Rounding_Dir dir) |
| bool | round_up (Rounding_Dir dir) |
| bool | round_ignore (Rounding_Dir dir) |
| bool | round_not_needed (Rounding_Dir dir) |
| bool | round_not_requested (Rounding_Dir dir) |
| bool | round_direct (Rounding_Dir dir) |
| bool | round_inverse (Rounding_Dir dir) |
| bool | round_strict_relation (Rounding_Dir dir) |
| fpu_rounding_direction_type | round_fpu_dir (Rounding_Dir dir) |
Functions for the Synthesis of Linear Rankings | |
| template<typename PSET > | |
| bool | termination_test_MS (const PSET &pset) |
| template<typename PSET > | |
| bool | termination_test_MS_2 (const PSET &pset_before, const PSET &pset_after) |
| template<typename PSET > | |
| bool | one_affine_ranking_function_MS (const PSET &pset, Generator &mu) |
| template<typename PSET > | |
| bool | one_affine_ranking_function_MS_2 (const PSET &pset_before, const PSET &pset_after, Generator &mu) |
| template<typename PSET > | |
| void | all_affine_ranking_functions_MS (const PSET &pset, C_Polyhedron &mu_space) |
| template<typename PSET > | |
| void | all_affine_ranking_functions_MS_2 (const PSET &pset_before, const PSET &pset_after, C_Polyhedron &mu_space) |
| template<typename PSET > | |
| void | all_affine_quasi_ranking_functions_MS (const PSET &pset, C_Polyhedron &decreasing_mu_space, C_Polyhedron &bounded_mu_space) |
| template<typename PSET > | |
| void | all_affine_quasi_ranking_functions_MS_2 (const PSET &pset_before, const PSET &pset_after, C_Polyhedron &decreasing_mu_space, C_Polyhedron &bounded_mu_space) |
| template<typename PSET > | |
| bool | termination_test_PR (const PSET &pset) |
| template<typename PSET > | |
| bool | termination_test_PR_2 (const PSET &pset_before, const PSET &pset_after) |
| template<typename PSET > | |
| bool | one_affine_ranking_function_PR (const PSET &pset, Generator &mu) |
| template<typename PSET > | |
| bool | one_affine_ranking_function_PR_2 (const PSET &pset_before, const PSET &pset_after, Generator &mu) |
| template<typename PSET > | |
| void | all_affine_ranking_functions_PR (const PSET &pset, NNC_Polyhedron &mu_space) |
| template<typename PSET > | |
| void | all_affine_ranking_functions_PR_2 (const PSET &pset_before, const PSET &pset_after, NNC_Polyhedron &mu_space) |
Variables | |
| Minus_Infinity | MINUS_INFINITY |
| Plus_Infinity | PLUS_INFINITY |
| Not_A_Number | NOT_A_NUMBER |
| const Throwable *volatile | abandon_expensive_computations = 0 |
| A pointer to an exception object. More... | |
| template<typename Unsigned > | |
| Enable_If<(static_cast< Unsigned >-1) > | |
Detailed Description
The entire library is confined to this namespace.
Typedef Documentation
| typedef int Parma_Polyhedra_Library::Concrete_Expression_BOP |
Encodes a binary operator of concrete expressions.
The values should be uniquely defined by the particular instance and named: ADD, SUB, MUL, DIV, REM, BAND, BOR, BXOR, LSHIFT, RSHIFT.
Definition at line 86 of file Concrete_Expression_types.hh.
Encodes the kind of concrete expression.
The values should be defined by the particular instance and uniquely identify one of: Binary_Operator, Unary_Operator, Cast_Operator, Integer_Constant, Floating_Point_Constant, or Approximable_Reference. For example, the Binary_Operator kind integer constant should be defined by an instance as the member Binary_Operator<T>::KIND.
Definition at line 66 of file Concrete_Expression_types.hh.
| typedef int Parma_Polyhedra_Library::Concrete_Expression_UOP |
Encodes a unary operator of concrete expressions.
The values should be uniquely defined by the particular instance and named: PLUS, MINUS, BNOT.
Definition at line 94 of file Concrete_Expression_types.hh.
| typedef mpz_class Parma_Polyhedra_Library::GMP_Integer |
Definition at line 31 of file GMP_Integer_types.hh.
| typedef Interval<mpz_class, Integer_Interval_Info> Parma_Polyhedra_Library::Integer_Interval |
An interval with integral, necessarily closed boundaries.
Definition at line 49 of file Integer_Interval.hh.
| typedef Interval_Info_Bitset<unsigned int, Integer_Interval_Info_Policy> Parma_Polyhedra_Library::Integer_Interval_Info |
Definition at line 44 of file Integer_Interval.hh.
| typedef const PIP_Tree_Node* Parma_Polyhedra_Library::PIP_Tree |
Definition at line 20 of file PIP_Tree_types.hh.
A box with rational, possibly open boundaries.
Definition at line 35 of file Rational_Box.hh.
| typedef Interval<mpq_class, Rational_Interval_Info> Parma_Polyhedra_Library::Rational_Interval |
An interval with rational, possibly open boundaries.
Definition at line 50 of file Rational_Interval.hh.
| typedef Interval_Info_Bitset<unsigned int, Rational_Interval_Info_Policy> Parma_Polyhedra_Library::Rational_Interval_Info |
Definition at line 45 of file Rational_Interval.hh.
Enumeration Type Documentation
Definition at line 23 of file fpu_types.hh.
Definition at line 22 of file fpu_types.hh.
| Enumerator | |
|---|---|
| VC_NORMAL |
Representable number result class. |
| VC_MINUS_INFINITY |
Negative infinity result class. |
| VC_PLUS_INFINITY |
Positive infinity result class. |
| VC_NAN |
Not a number result class. |
| VC_MASK | |
Definition at line 29 of file Result_defs.hh.
Definition at line 46 of file Result_defs.hh.
| Enumerator | |
|---|---|
| T_YES | |
| T_NO | |
| T_MAYBE | |
Definition at line 37 of file Interval_defs.hh.
Function Documentation
|
related |
Definition at line 42 of file GMP_Integer_inlines.hh.
Referenced by Parma_Polyhedra_Library::MIP_Problem::compute_simplex_using_steepest_edge_float(), and Parma_Polyhedra_Library::MIP_Problem::get_exiting_base_index().
|
related |
Definition at line 47 of file GMP_Integer_inlines.hh.
|
related |
Definition at line 75 of file GMP_Integer_inlines.hh.
Referenced by Parma_Polyhedra_Library::PIP_Tree_Node::add_constraint(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::add_mul_assign(), Parma_Polyhedra_Library::MIP_Problem::compute_generator(), Parma_Polyhedra_Library::Grid::expand_space_dimension(), Parma_Polyhedra_Library::Polyhedron::expand_space_dimension(), Parma_Polyhedra_Library::Implementation::Termination::fill_constraint_system_PR(), Parma_Polyhedra_Library::Implementation::Termination::fill_constraint_system_PR_original(), Parma_Polyhedra_Library::Implementation::Termination::fill_constraint_systems_MS(), Parma_Polyhedra_Library::BD_Shape< T >::frequency(), Parma_Polyhedra_Library::PIP_Solution_Node::generate_cut(), Parma_Polyhedra_Library::Dense_Row::linear_combine(), Parma_Polyhedra_Library::Sparse_Row::linear_combine(), Parma_Polyhedra_Library::Grid::map_space_dimensions(), Parma_Polyhedra_Library::Polyhedron::map_space_dimensions(), Parma_Polyhedra_Library::Octagonal_Shape< T >::relation_with(), Parma_Polyhedra_Library::BD_Shape< T >::relation_with(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::scalar_product_assign(), Parma_Polyhedra_Library::PIP_Solution_Node::solve(), Parma_Polyhedra_Library::MIP_Problem::steepest_edge_exact_entering_index(), Parma_Polyhedra_Library::PIP_Solution_Node::update_solution(), and Parma_Polyhedra_Library::PIP_Solution_Node::update_tableau().
|
related |
Definition at line 401 of file Linear_Expression_inlines.hh.
References Parma_Polyhedra_Library::Linear_Expression_Interface::add_mul_assign(), and Parma_Polyhedra_Library::Linear_Expression::impl.
|
related |
Definition at line 524 of file Float_inlines.hh.
References discard_occurrences(), and Parma_Polyhedra_Library::Variable::id().
|
related |
Definition at line 35 of file Checked_Number_templates.hh.
Referenced by Parma_Polyhedra_Library::Congruence_System::ascii_dump(), Parma_Polyhedra_Library::Linear_System< Row >::ascii_dump(), Parma_Polyhedra_Library::Interval< Boundary, Info >::ascii_dump(), Parma_Polyhedra_Library::MIP_Problem::OK(), Parma_Polyhedra_Library::PIP_Problem::OK(), Parma_Polyhedra_Library::Polyhedron::OK(), and Parma_Polyhedra_Library::Grid::OK().
|
inline |
Definition at line 140 of file globals_inlines.hh.
References DENSE.
| Enable_If<Is_Native_Or_Checked<T>::value, bool>::type Parma_Polyhedra_Library::ascii_load | ( | std::istream & | s, |
| T & | t | ||
| ) |
Definition at line 57 of file Checked_Number_templates.hh.
Referenced by Parma_Polyhedra_Library::Congruence_System::ascii_load(), Parma_Polyhedra_Library::Matrix< Row >::ascii_load(), Parma_Polyhedra_Library::Linear_System< Row >::ascii_load(), and Parma_Polyhedra_Library::Interval< Boundary, Info >::ascii_load().
|
inline |
Definition at line 150 of file globals_inlines.hh.
|
inline |
If there is no assign_or_swap() method but copies are not slow, copy.
Definition at line 52 of file assign_or_swap.hh.
|
inline |
If there is no assign_or_swap() and copies are slow, delegate to swap().
Definition at line 64 of file assign_or_swap.hh.
References swap().
|
related |
Definition at line 207 of file Checked_Number_inlines.hh.
References check_result(), and rounding_dir().
Referenced by Parma_Polyhedra_Library::Octagonal_Shape< T >::add_space_dimensions_and_project(), Parma_Polyhedra_Library::BD_Shape< T >::add_space_dimensions_and_project(), Parma_Polyhedra_Library::Octagonal_Shape< T >::affine_form_image(), Parma_Polyhedra_Library::Octagonal_Shape< T >::affine_image(), Parma_Polyhedra_Library::BD_Shape< T >::affine_image(), Parma_Polyhedra_Library::Boundary_NS::assign(), Parma_Polyhedra_Library::BD_Shape< T >::BD_Shape(), Parma_Polyhedra_Library::Octagonal_Shape< T >::BHMZ05_widening_assign(), Parma_Polyhedra_Library::BD_Shape< T >::BHMZ05_widening_assign(), Parma_Polyhedra_Library::BD_Shape< T >::BHZ09_upper_bound_assign_if_exact(), Parma_Polyhedra_Library::Box< ITV >::bounded_affine_image(), Parma_Polyhedra_Library::Octagonal_Shape< T >::bounded_affine_image(), Parma_Polyhedra_Library::BD_Shape< T >::bounded_affine_image(), Parma_Polyhedra_Library::Box< ITV >::bounded_affine_preimage(), Parma_Polyhedra_Library::Box< ITV >::Box(), Parma_Polyhedra_Library::Octagonal_Shape< T >::CC76_extrapolation_assign(), Parma_Polyhedra_Library::BD_Shape< T >::CC76_extrapolation_assign(), Parma_Polyhedra_Library::Boundary_NS::complement(), Parma_Polyhedra_Library::DB_Row_Impl_Handler< T >::Impl::construct_upward_approximation(), Parma_Polyhedra_Library::Polyhedron::contains_integer_point(), Parma_Polyhedra_Library::Octagonal_Shape< T >::contains_integer_point(), Parma_Polyhedra_Library::BD_Shape< T >::contains_integer_point(), Parma_Polyhedra_Library::I_Constraint_Common< I_Constraint< T, Val_Or_Ref_Criteria, extended > >::convert_real(), Parma_Polyhedra_Library::Octagonal_Shape< T >::deduce_minus_v_pm_u_bounds(), Parma_Polyhedra_Library::BD_Shape< T >::deduce_u_minus_v_bounds(), Parma_Polyhedra_Library::BD_Shape< T >::deduce_v_minus_u_bounds(), Parma_Polyhedra_Library::Octagonal_Shape< T >::deduce_v_pm_u_bounds(), div_round_up(), Parma_Polyhedra_Library::Octagonal_Shape< T >::drop_some_non_integer_points(), Parma_Polyhedra_Library::BD_Shape< T >::euclidean_distance_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::euclidean_distance_assign(), Parma_Polyhedra_Library::DB_Row_Impl_Handler< T >::Impl::expand_within_capacity(), Parma_Polyhedra_Library::Octagonal_Shape< T >::export_interval_constraints(), Parma_Polyhedra_Library::BD_Shape< T >::forget_all_dbm_constraints(), Parma_Polyhedra_Library::Octagonal_Shape< T >::forget_all_octagonal_constraints(), Parma_Polyhedra_Library::BD_Shape< T >::forget_binary_dbm_constraints(), Parma_Polyhedra_Library::Octagonal_Shape< T >::forget_binary_octagonal_constraints(), Parma_Polyhedra_Library::Box< ITV >::frequency(), Parma_Polyhedra_Library::BD_Shape< T >::frequency(), Parma_Polyhedra_Library::Polyhedron::frequency(), Parma_Polyhedra_Library::maybe_assign_struct< To, From >::function(), Parma_Polyhedra_Library::BD_Shape< T >::general_refine(), Parma_Polyhedra_Library::Box< ITV >::generalized_affine_image(), Parma_Polyhedra_Library::Octagonal_Shape< T >::generalized_affine_image(), Parma_Polyhedra_Library::BD_Shape< T >::generalized_affine_image(), Parma_Polyhedra_Library::Box< ITV >::has_lower_bound(), Parma_Polyhedra_Library::Box< ITV >::has_upper_bound(), Parma_Polyhedra_Library::BD_Shape< T >::incremental_shortest_path_closure_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::incremental_strong_closure_assign(), Parma_Polyhedra_Library::BD_Shape< T >::inhomogeneous_affine_form_image(), Parma_Polyhedra_Library::Octagonal_Shape< T >::integer_upper_bound_assign_if_exact(), Parma_Polyhedra_Library::Interval< Boundary, Info >::Interval(), Parma_Polyhedra_Library::Octagonal_Shape< T >::interval_coefficient_upper_bound(), interval_relation(), Parma_Polyhedra_Library::MIP_Problem::is_mip_satisfiable(), Parma_Polyhedra_Library::Octagonal_Shape< T >::is_strongly_reduced(), Parma_Polyhedra_Library::BD_Shape< T >::l_infinity_distance_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::l_infinity_distance_assign(), Parma_Polyhedra_Library::DB_Matrix< T >::l_m_distance_assign(), Parma_Polyhedra_Library::Generator::l_m_distance_assign(), Parma_Polyhedra_Library::OR_Matrix< T >::l_m_distance_assign(), Parma_Polyhedra_Library::Box< ITV >::l_m_distance_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::linear_form_upper_bound(), Parma_Polyhedra_Library::BD_Shape< T >::linear_form_upper_bound(), Parma_Polyhedra_Library::BD_Shape< T >::max_min(), Parma_Polyhedra_Library::Box< ITV >::max_min(), Parma_Polyhedra_Library::Octagonal_Shape< T >::max_min(), Parma_Polyhedra_Library::Polyhedron::max_min(), numer_denom(), Parma_Polyhedra_Library::Octagonal_Shape< T >::Octagonal_Shape(), Parma_Polyhedra_Library::BD_Shape< T >::one_variable_affine_form_image(), Parma_Polyhedra_Library::Checked_Number< T, Policy >::operator=(), Parma_Polyhedra_Library::Box< ITV >::propagate_constraint_no_check(), Parma_Polyhedra_Library::BD_Shape< T >::rectilinear_distance_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::rectilinear_distance_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::refine(), Parma_Polyhedra_Library::BD_Shape< T >::refine(), Parma_Polyhedra_Library::Box< ITV >::refine_interval_no_check(), Parma_Polyhedra_Library::Octagonal_Shape< T >::refine_with_linear_form_inequality(), Parma_Polyhedra_Library::Box< ITV >::relation_with(), Parma_Polyhedra_Library::Octagonal_Shape< T >::relation_with(), Parma_Polyhedra_Library::BD_Shape< T >::relation_with(), Parma_Polyhedra_Library::Boundary_NS::set_boundary_infinity(), Parma_Polyhedra_Library::Boundary_NS::set_minus_infinity(), Parma_Polyhedra_Library::Boundary_NS::set_plus_infinity(), Parma_Polyhedra_Library::Boundary_NS::set_unbounded(), Parma_Polyhedra_Library::Boundary_NS::set_zero(), Parma_Polyhedra_Library::BD_Shape< T >::shortest_path_closure_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::simplify_using_context_assign(), Parma_Polyhedra_Library::BD_Shape< T >::simplify_using_context_assign(), Parma_Polyhedra_Library::MIP_Problem::solve_mip(), Parma_Polyhedra_Library::Octagonal_Shape< T >::strong_closure_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::strong_reduction_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::tight_closure_assign(), Parma_Polyhedra_Library::BD_Shape< T >::two_variables_affine_form_image(), Parma_Polyhedra_Library::Octagonal_Shape< T >::upper_bound_assign_if_exact(), and Parma_Polyhedra_Library::Implementation::wrap_assign().
| const char * Parma_Polyhedra_Library::banner | ( | ) |
Returns a character string containing the PPL banner.
The banner provides information about the PPL version, the licensing, the lack of any warranty whatsoever, the C++ compiler used to build the library, where to report bugs and where to look for further information.
Definition at line 106 of file version.cc.
|
inline |
Definition at line 146 of file Interval_inlines.hh.
References Parma_Polyhedra_Library::Interval_NS::f_info(), and f_is_empty().
Referenced by Parma_Polyhedra_Library::Interval< Boundary, Info >::add_assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::contains(), Parma_Polyhedra_Library::Interval< Boundary, Info >::div_assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::is_disjoint_from(), Parma_Polyhedra_Library::Interval< Boundary, Info >::join_assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::mul_assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::neg_assign(), operator<<(), operator==(), Parma_Polyhedra_Library::Interval< Boundary, Info >::refine_existential(), Parma_Polyhedra_Library::Interval< Boundary, Info >::refine_universal(), Parma_Polyhedra_Library::Interval< Boundary, Info >::strictly_contains(), and Parma_Polyhedra_Library::Interval< Boundary, Info >::sub_assign().
|
inline |
Definition at line 48 of file Checked_Number_inlines.hh.
References result_relation(), ROUND_NOT_NEEDED, and VR_EQ.
Referenced by assign_r(), Parma_Polyhedra_Library::Checked_Number< T, Policy >::assign_r(), Parma_Polyhedra_Library::Checked_Number< T, Policy >::Checked_Number(), construct(), Parma_Polyhedra_Library::Checked_Number< T, Policy >::input(), and Parma_Polyhedra_Library::Checked_Number< T, Policy >::output().
| dimension_type Parma_Polyhedra_Library::check_space_dimension_overflow | ( | const dimension_type | dim, |
| const dimension_type | max, | ||
| const char * | domain, | ||
| const char * | method, | ||
| const char * | reason | ||
| ) |
Definition at line 48 of file globals.cc.
Referenced by Parma_Polyhedra_Library::Box< ITV >::add_space_dimensions_and_embed(), Parma_Polyhedra_Library::Grid::add_space_dimensions_and_embed(), Parma_Polyhedra_Library::Box< ITV >::add_space_dimensions_and_project(), Parma_Polyhedra_Library::Grid::add_space_dimensions_and_project(), Parma_Polyhedra_Library::Polyhedron::add_space_dimensions_and_project(), Parma_Polyhedra_Library::Box< ITV >::Box(), Parma_Polyhedra_Library::Polyhedron::check_space_dimension_overflow(), Parma_Polyhedra_Library::Box< ITV >::concatenate_assign(), Parma_Polyhedra_Library::Grid::concatenate_assign(), Parma_Polyhedra_Library::Polyhedron::concatenate_assign(), Parma_Polyhedra_Library::Grid::expand_space_dimension(), Parma_Polyhedra_Library::Polyhedron::expand_space_dimension(), and Parma_Polyhedra_Library::Grid::Grid().
|
inline |
Definition at line 143 of file compiler.hh.
References clz32(), and clz64().
Referenced by Parma_Polyhedra_Library::Implementation::last_one(), and msb_position().
|
inline |
|
inline |
|
inline |
|
inline |
|
related |
Definition at line 106 of file GMP_Integer_inlines.hh.
Referenced by Parma_Polyhedra_Library::Polyhedron::add_and_minimize(), Parma_Polyhedra_Library::Checked::cmp_mp(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::compare(), and Parma_Polyhedra_Library::Linear_System< Row >::sort_pending_and_remove_duplicates().
| void Parma_Polyhedra_Library::Coefficient_constants_finalize | ( | ) |
Finalizes the Coefficient constants.
Referenced by Parma_Polyhedra_Library::Init::~Init().
| void Parma_Polyhedra_Library::Coefficient_constants_initialize | ( | ) |
Initializes the Coefficient constants.
Referenced by Parma_Polyhedra_Library::Init::Init().
| Coefficient_traits::const_reference Parma_Polyhedra_Library::Coefficient_one | ( | ) |
Returns a const reference to a Coefficient with value 1.
Referenced by Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::add_mul_assign(), Parma_Polyhedra_Library::Generator::closure_point(), Parma_Polyhedra_Library::Grid::construct(), Parma_Polyhedra_Library::Constraint::construct_epsilon_geq_zero(), Parma_Polyhedra_Library::Grid::conversion(), Parma_Polyhedra_Library::Generator::Generator(), Parma_Polyhedra_Library::Grid::Grid(), Parma_Polyhedra_Library::Grid_Generator::grid_point(), Parma_Polyhedra_Library::Constraint::initialize(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::operator+=(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::operator-=(), Parma_Polyhedra_Library::Generator::point(), Parma_Polyhedra_Library::MIP_Problem::process_pending_constraints(), Parma_Polyhedra_Library::Grid::reduce_parameter_with_line(), Parma_Polyhedra_Library::Grid::reduce_reduced(), Parma_Polyhedra_Library::Octagonal_Shape< T >::relation_with(), Parma_Polyhedra_Library::MIP_Problem::second_phase(), Parma_Polyhedra_Library::Grid::simplify(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::sub_mul_assign(), Parma_Polyhedra_Library::Implementation::wrap_assign(), Parma_Polyhedra_Library::Box< ITV >::wrap_assign(), and Parma_Polyhedra_Library::Grid::wrap_assign().
| Coefficient_traits::const_reference Parma_Polyhedra_Library::Coefficient_zero | ( | ) |
Returns a const reference to a Coefficient with value 0.
Referenced by Parma_Polyhedra_Library::Congruence_System::add_unit_rows_and_space_dimensions(), Parma_Polyhedra_Library::Congruence::affine_preimage(), Parma_Polyhedra_Library::Constraint_System::affine_preimage(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::coefficient(), Parma_Polyhedra_Library::Grid::conversion(), Parma_Polyhedra_Library::Polyhedron::conversion(), Parma_Polyhedra_Library::CO_Tree::erase(), Parma_Polyhedra_Library::Grid::expand_space_dimension(), Parma_Polyhedra_Library::Polyhedron::expand_space_dimension(), Parma_Polyhedra_Library::Expression_Hide_Inhomo< T >::gcd(), Parma_Polyhedra_Library::Box< ITV >::generalized_affine_preimage(), Parma_Polyhedra_Library::Expression_Hide_Inhomo< T >::get(), Parma_Polyhedra_Library::Sparse_Row::get(), Parma_Polyhedra_Library::Grid_Generator::grid_line(), Parma_Polyhedra_Library::Expression_Hide_Inhomo< T >::inhomogeneous_term(), Parma_Polyhedra_Library::Linear_Expression::initialize(), Parma_Polyhedra_Library::CO_Tree::insert(), Parma_Polyhedra_Library::CO_Tree::insert_precise(), Parma_Polyhedra_Library::Grid_Generator::is_equivalent_to(), Parma_Polyhedra_Library::Polyhedron::modify_according_to_evolution(), Parma_Polyhedra_Library::Congruence::operator<<(), Parma_Polyhedra_Library::Constraint::operator<<(), Parma_Polyhedra_Library::Dense_Row::operator=(), Parma_Polyhedra_Library::Grid_Generator::parameter(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::print(), Parma_Polyhedra_Library::Octagonal_Shape< T >::relation_with(), Parma_Polyhedra_Library::BD_Shape< T >::relation_with(), Parma_Polyhedra_Library::Grid_Generator::set_is_parameter(), and Parma_Polyhedra_Library::Grid::simplify().
Definition at line 40 of file Interval_defs.hh.
Referenced by Parma_Polyhedra_Library::Interval< Boundary, Info >::add_assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::difference_assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::div_assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::join_assign(), Parma_Polyhedra_Library::DB_Matrix< T >::l_m_distance_assign(), Parma_Polyhedra_Library::Generator::l_m_distance_assign(), Parma_Polyhedra_Library::OR_Matrix< T >::l_m_distance_assign(), Parma_Polyhedra_Library::Box< ITV >::l_m_distance_assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::mul_assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::neg_assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::refine_existential(), Parma_Polyhedra_Library::Interval< Boundary, Info >::refine_universal(), Parma_Polyhedra_Library::Interval< Boundary, Info >::set_infinities(), and Parma_Polyhedra_Library::Interval< Boundary, Info >::sub_assign().
|
related |
Definition at line 587 of file Linear_Expression_inlines.hh.
References Parma_Polyhedra_Library::Linear_Expression_Interface::compare(), and Parma_Polyhedra_Library::Linear_Expression::impl.
Referenced by Parma_Polyhedra_Library::Polyhedron::add_and_minimize(), Parma_Polyhedra_Library::Linear_System< Row >::add_universe_rows_and_space_dimensions(), Parma_Polyhedra_Library::Linear_System< Row >::back_substitute(), Parma_Polyhedra_Library::Polyhedron::BHRZ03_evolving_points(), Parma_Polyhedra_Library::Bit_Matrix::check_sorted(), Parma_Polyhedra_Library::Linear_System< Row >::check_sorted(), Parma_Polyhedra_Library::Grid_Generator::check_strong_normalized(), Parma_Polyhedra_Library::Generator::check_strong_normalized(), Parma_Polyhedra_Library::Constraint::check_strong_normalized(), Parma_Polyhedra_Library::Grid_Certificate::compare(), Parma_Polyhedra_Library::Constraint::compare(), Parma_Polyhedra_Library::Generator::compare(), Parma_Polyhedra_Library::Grid_Generator::compare(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::compare(), Parma_Polyhedra_Library::Polyhedron::conversion(), Parma_Polyhedra_Library::Linear_System< Row >::insert(), Parma_Polyhedra_Library::Linear_System< Row >::insert_no_ok(), Parma_Polyhedra_Library::Linear_System< Row >::merge_rows_assign(), Parma_Polyhedra_Library::Bit_Matrix::Bit_Row_Less_Than::operator()(), Parma_Polyhedra_Library::Linear_System< Row >::Row_Less_Than::operator()(), and Parma_Polyhedra_Library::Linear_System< Row >::sort_pending_and_remove_duplicates().
|
related |
Definition at line 35 of file Float_templates.hh.
References Parma_Polyhedra_Library::float_ieee754_half::BASE, Parma_Polyhedra_Library::float_ieee754_single::BASE, Parma_Polyhedra_Library::float_ieee754_double::BASE, Parma_Polyhedra_Library::float_ibm_single::BASE, Parma_Polyhedra_Library::float_intel_double_extended::BASE, Parma_Polyhedra_Library::float_ieee754_quad::BASE, Parma_Polyhedra_Library::float_ieee754_half::EXPONENT_BIAS, Parma_Polyhedra_Library::float_ieee754_single::EXPONENT_BIAS, Parma_Polyhedra_Library::float_ieee754_double::EXPONENT_BIAS, Parma_Polyhedra_Library::float_ibm_single::EXPONENT_BIAS, Parma_Polyhedra_Library::float_intel_double_extended::EXPONENT_BIAS, Parma_Polyhedra_Library::float_ieee754_quad::EXPONENT_BIAS, GREATER_OR_EQUAL, i_constraint(), IBM_SINGLE, IEEE754_DOUBLE, IEEE754_HALF, IEEE754_QUAD, IEEE754_SINGLE, INTEL_DOUBLE_EXTENDED, LESS_OR_EQUAL, Parma_Polyhedra_Library::float_ieee754_half::MANTISSA_BITS, Parma_Polyhedra_Library::float_ieee754_single::MANTISSA_BITS, Parma_Polyhedra_Library::float_ieee754_double::MANTISSA_BITS, Parma_Polyhedra_Library::float_ibm_single::MANTISSA_BITS, Parma_Polyhedra_Library::float_intel_double_extended::MANTISSA_BITS, Parma_Polyhedra_Library::float_ieee754_quad::MANTISSA_BITS, and msb_position().
|
inline |
Speculative allocation function.
- Returns
- The actual capacity to be allocated.
- Parameters
-
requested_size The number of elements we need. maximum_size The maximum number of elements to be allocated. It is assumed to be no less than requested_size.
Computes a capacity given a requested size. Allows for speculative allocation aimed at reducing the number of reallocations enough to guarantee amortized constant insertion time for our vector-like data structures. In all cases, the speculative allocation will not exceed maximum_size.
Definition at line 90 of file globals_inlines.hh.
Referenced by Parma_Polyhedra_Library::MIP_Problem::add_constraint_helper(), Parma_Polyhedra_Library::Bit_Matrix::add_recycled_row(), Parma_Polyhedra_Library::Dense_Row::add_zeroes_and_shift(), Parma_Polyhedra_Library::DB_Row< T >::DB_Row(), Parma_Polyhedra_Library::Linear_Form< C >::extend(), Parma_Polyhedra_Library::DB_Matrix< T >::grow(), Parma_Polyhedra_Library::Linear_Form< C >::Linear_Form(), Parma_Polyhedra_Library::Linear_System< Row >::merge_rows_assign(), Parma_Polyhedra_Library::DB_Matrix< T >::operator=(), Parma_Polyhedra_Library::OR_Matrix< T >::operator=(), Parma_Polyhedra_Library::Swapping_Vector< T >::reserve(), Parma_Polyhedra_Library::Bit_Matrix::resize(), Parma_Polyhedra_Library::DB_Matrix< T >::resize_no_copy(), and Parma_Polyhedra_Library::Polyhedron::simplify().
|
related |
Definition at line 217 of file Checked_Number_inlines.hh.
References check_result(), and rounding_dir().
Referenced by Parma_Polyhedra_Library::DB_Row< T >::construct(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::construct(), Parma_Polyhedra_Library::DB_Row_Impl_Handler< T >::Impl::construct_upward_approximation(), Parma_Polyhedra_Library::DB_Row< T >::DB_Row(), and Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::Linear_Expression_Impl().
|
inline |
Definition at line 186 of file compiler.hh.
References ctz32(), and ctz64().
Referenced by Parma_Polyhedra_Library::Implementation::first_one().
|
inline |
|
inline |
|
inline |
Definition at line 121 of file compiler.hh.
|
inline |
|
related |
|
related |
Definition at line 90 of file GMP_Integer_inlines.hh.
|
inline |
Divides x by y into to, rounding the result towards plus infinity.
Definition at line 65 of file math_utilities_inlines.hh.
References assign_r(), PPL_DIRTY_TEMP, ROUND_NOT_NEEDED, and ROUND_UP.
Referenced by Parma_Polyhedra_Library::BD_Shape< T >::add_constraint(), Parma_Polyhedra_Library::Octagonal_Shape< T >::add_constraint(), Parma_Polyhedra_Library::BD_Shape< T >::add_dbm_constraint(), Parma_Polyhedra_Library::Octagonal_Shape< T >::add_octagonal_constraint(), Parma_Polyhedra_Library::Octagonal_Shape< T >::affine_image(), Parma_Polyhedra_Library::BD_Shape< T >::affine_image(), Parma_Polyhedra_Library::BD_Shape< T >::BD_Shape(), Parma_Polyhedra_Library::BD_Shape< T >::bounded_affine_image(), Parma_Polyhedra_Library::Octagonal_Shape< T >::generalized_affine_image(), Parma_Polyhedra_Library::BD_Shape< T >::generalized_affine_image(), Parma_Polyhedra_Library::Octagonal_Shape< T >::get_limiting_octagon(), Parma_Polyhedra_Library::BD_Shape< T >::get_limiting_shape(), Parma_Polyhedra_Library::Octagonal_Shape< T >::Octagonal_Shape(), Parma_Polyhedra_Library::Octagonal_Shape< T >::refine(), Parma_Polyhedra_Library::BD_Shape< T >::refine(), Parma_Polyhedra_Library::Octagonal_Shape< T >::refine_no_check(), and Parma_Polyhedra_Library::BD_Shape< T >::refine_no_check().
|
related |
Definition at line 95 of file GMP_Integer_inlines.hh.
|
related |
Definition at line 713 of file Checked_Number_inlines.hh.
References ROUND_NOT_NEEDED.
Referenced by Parma_Polyhedra_Library::PIP_Tree_Node::Artificial_Parameter::Artificial_Parameter(), Parma_Polyhedra_Library::PIP_Tree_Node::compatibility_check(), Parma_Polyhedra_Library::MIP_Problem::compute_generator(), Parma_Polyhedra_Library::Grid::conversion(), Parma_Polyhedra_Library::Polyhedron::convert_to_integer_expression(), Parma_Polyhedra_Library::Polyhedron::convert_to_integer_expressions(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::exact_div_assign(), Parma_Polyhedra_Library::Grid::frequency_no_check(), Parma_Polyhedra_Library::MIP_Problem::get_exiting_base_index(), Parma_Polyhedra_Library::Grid::Grid(), Parma_Polyhedra_Library::Generator::is_matching_closure_point(), Parma_Polyhedra_Library::Box< ITV >::max_min(), Parma_Polyhedra_Library::Grid::max_min(), Parma_Polyhedra_Library::Dense_Row::normalize(), Parma_Polyhedra_Library::PIP_Solution_Node::Tableau::normalize(), Parma_Polyhedra_Library::Sparse_Row::normalize(), normalize2(), Parma_Polyhedra_Library::Congruence_System::normalize_moduli(), Parma_Polyhedra_Library::Grid::reduce_congruence_with_equality(), Parma_Polyhedra_Library::Grid::reduce_equality_with_equality(), Parma_Polyhedra_Library::Grid::reduce_line_with_line(), Parma_Polyhedra_Library::Grid::reduce_parameter_with_line(), Parma_Polyhedra_Library::Grid::reduce_pc_with_pc(), Parma_Polyhedra_Library::Grid_Generator::scale_to_divisor(), Parma_Polyhedra_Library::PIP_Solution_Node::solve(), and Parma_Polyhedra_Library::MIP_Problem::steepest_edge_exact_entering_index().
|
inline |
For native types, returns the size in bytes of the memory managed by the type of the (unused) parameter, i.e., 0.
Definition at line 106 of file globals_inlines.hh.
Referenced by Parma_Polyhedra_Library::Pointset_Ask_Tell< PSET >::external_memory_in_bytes(), Parma_Polyhedra_Library::Congruence::external_memory_in_bytes(), Parma_Polyhedra_Library::Checked_Number< T, Policy >::external_memory_in_bytes(), Parma_Polyhedra_Library::PIP_Tree_Node::Artificial_Parameter::external_memory_in_bytes(), Parma_Polyhedra_Library::Dense_Row::external_memory_in_bytes(), Parma_Polyhedra_Library::DB_Row_Impl_Handler< T >::Impl::external_memory_in_bytes(), external_memory_in_bytes(), Parma_Polyhedra_Library::PIP_Solution_Node::Tableau::external_memory_in_bytes(), Parma_Polyhedra_Library::Interval< Boundary, Info >::external_memory_in_bytes(), Parma_Polyhedra_Library::CO_Tree::external_memory_in_bytes(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::external_memory_in_bytes(), Parma_Polyhedra_Library::Pointset_Ask_Tell< PSET >::total_memory_in_bytes(), Parma_Polyhedra_Library::Determinate< PSET >::total_memory_in_bytes(), Parma_Polyhedra_Library::Powerset< D >::total_memory_in_bytes(), Parma_Polyhedra_Library::DB_Matrix< T >::total_memory_in_bytes(), Parma_Polyhedra_Library::DB_Row< T >::total_memory_in_bytes(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::total_memory_in_bytes(), Parma_Polyhedra_Library::Linear_Form< C >::total_memory_in_bytes(), Parma_Polyhedra_Library::Matrix< Row >::total_memory_in_bytes(), Parma_Polyhedra_Library::DB_Row_Impl_Handler< T >::Impl::total_memory_in_bytes(), Parma_Polyhedra_Library::Linear_System< Row >::total_memory_in_bytes(), total_memory_in_bytes(), Parma_Polyhedra_Library::Interval< Boundary, Info >::total_memory_in_bytes(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::total_memory_in_bytes(), Parma_Polyhedra_Library::PIP_Problem::total_memory_in_bytes(), Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::total_memory_in_bytes(), Parma_Polyhedra_Library::Box< ITV >::total_memory_in_bytes(), Parma_Polyhedra_Library::Octagonal_Shape< T >::total_memory_in_bytes(), and Parma_Polyhedra_Library::BD_Shape< T >::total_memory_in_bytes().
|
inline |
Returns the size in bytes of the memory managed by x.
Definition at line 118 of file globals_inlines.hh.
|
inline |
Returns the size in bytes of the memory managed by x.
Definition at line 129 of file globals_inlines.hh.
References external_memory_in_bytes().
|
inline |
Definition at line 53 of file Interval_inlines.hh.
References Parma_Polyhedra_Library::Interval< Boundary, Info >::is_empty().
Referenced by check_empty_arg().
|
inline |
Definition at line 58 of file Interval_inlines.hh.
References Parma_Polyhedra_Library::Interval< Boundary, Info >::is_singleton().
Referenced by Parma_Polyhedra_Library::Interval< Boundary, Info >::refine_existential(), and Parma_Polyhedra_Library::Interval< Boundary, Info >::refine_universal().
|
inline |
Definition at line 518 of file globals_defs.hh.
Referenced by Parma_Polyhedra_Library::Interval< Boundary, Info >::add_assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::contains(), Parma_Polyhedra_Library::Interval< Boundary, Info >::difference_assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::div_assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::intersect_assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::is_disjoint_from(), Parma_Polyhedra_Library::Interval< Boundary, Info >::join_assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::mul_assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::neg_assign(), operator==(), Parma_Polyhedra_Library::Interval< Boundary, Info >::refine_existential(), Parma_Polyhedra_Library::Interval< Boundary, Info >::refine_universal(), Parma_Polyhedra_Library::Interval< Boundary, Info >::strictly_contains(), and Parma_Polyhedra_Library::Interval< Boundary, Info >::sub_assign().
|
inline |
Finalizes the library.
Definition at line 60 of file initializer.hh.
References Parma_Polyhedra_Library::Implementation::finalize_aux().
Referenced by Parma_Polyhedra_Library::DB_Matrix< T >::l_m_distance_assign(), Parma_Polyhedra_Library::Generator::l_m_distance_assign(), Parma_Polyhedra_Library::OR_Matrix< T >::l_m_distance_assign(), Parma_Polyhedra_Library::Box< ITV >::l_m_distance_assign(), and Parma_Polyhedra_Library::Init::~Init().
|
inline |
Queries the inexact computation status.
Returns 0 if the computation was definitely exact, 1 if it was definitely inexact, -1 if definite exactness information is unavailable.
Definition at line 190 of file fpu-ia32_inlines.hh.
References fpu_get_status(), FPU_INEXACT, and SSE_INEXACT.
Referenced by maybe_check_fpu_inexact(), Parma_Polyhedra_Library::Checked::prepare_inexact(), and Parma_Polyhedra_Library::Checked::result_relation().
|
inline |
Definition at line 105 of file fpu-ia32_inlines.hh.
Referenced by fpu_reset_inexact().
|
inline |
Definition at line 96 of file fpu-ia32_inlines.hh.
References Parma_Polyhedra_Library::ia32_fenv_t::status_word.
|
inline |
Definition at line 76 of file fpu-ia32_inlines.hh.
Referenced by fpu_get_rounding_direction().
|
inline |
Returns the current FPU rounding direction.
Definition at line 132 of file fpu-ia32_inlines.hh.
References fpu_get_control(), and FPU_ROUNDING_MASK.
Referenced by Parma_Polyhedra_Library::Init::Init().
|
inline |
Definition at line 89 of file fpu-ia32_inlines.hh.
Referenced by fpu_check_inexact().
|
inline |
Initializes the FPU control functions.
Definition at line 124 of file fpu-ia32_inlines.hh.
Referenced by Parma_Polyhedra_Library::Init::Init().
|
inline |
Clears the inexact computation status.
Definition at line 162 of file fpu-ia32_inlines.hh.
References fpu_clear_exceptions(), and PPL_SSE_CONTROL_DEFAULT.
Referenced by maybe_reset_fpu_inexact(), and Parma_Polyhedra_Library::Checked::prepare_inexact().
|
inline |
Definition at line 62 of file fpu-none_inlines.hh.
|
inline |
Restores the FPU rounding rounding control word to cw.
Definition at line 177 of file fpu-ia32_inlines.hh.
References fpu_set_control(), PPL_FPU_CONTROL_DEFAULT, and PPL_SSE_CONTROL_DEFAULT.
Referenced by Parma_Polyhedra_Library::Checked::add_float(), Parma_Polyhedra_Library::Checked::add_mul_float(), Parma_Polyhedra_Library::Checked::assign_float_float_inexact(), Parma_Polyhedra_Library::Checked::assign_float_int_inexact(), Parma_Polyhedra_Library::Checked::ceil_float(), Parma_Polyhedra_Library::Checked::div_float(), Parma_Polyhedra_Library::Checked::floor_float(), Parma_Polyhedra_Library::Checked::mul_float(), Parma_Polyhedra_Library::Checked::sqrt_float(), Parma_Polyhedra_Library::Checked::sub_float(), and Parma_Polyhedra_Library::Checked::sub_mul_float().
|
inline |
Definition at line 50 of file fpu-none_inlines.hh.
|
inline |
Sets the FPU rounding direction to dir and returns the rounding control word previously in use.
Definition at line 149 of file fpu-ia32_inlines.hh.
References fpu_set_control(), PPL_FPU_CONTROL_DEFAULT_BASE, and PPL_SSE_CONTROL_DEFAULT_BASE.
Referenced by Parma_Polyhedra_Library::Checked::add_float(), Parma_Polyhedra_Library::Checked::add_mul_float(), Parma_Polyhedra_Library::Checked::assign_float_float_inexact(), Parma_Polyhedra_Library::Checked::assign_float_int_inexact(), Parma_Polyhedra_Library::Checked::ceil_float(), Parma_Polyhedra_Library::Checked::div_float(), Parma_Polyhedra_Library::Checked::floor_float(), Parma_Polyhedra_Library::Checked::mul_float(), Parma_Polyhedra_Library::Checked::sqrt_float(), Parma_Polyhedra_Library::Checked::sub_float(), and Parma_Polyhedra_Library::Checked::sub_mul_float().
| fpu_rounding_control_word_type Parma_Polyhedra_Library::fpu_save_rounding_direction_reset_inexact | ( | fpu_rounding_direction_type | dir | ) |
Sets the FPU rounding direction to dir, clears the inexact computation status, and returns the rounding control word previously in use.
|
inline |
Definition at line 83 of file fpu-ia32_inlines.hh.
References c.
Referenced by fpu_restore_rounding_direction(), fpu_save_rounding_direction(), and fpu_set_rounding_direction().
|
inline |
Definition at line 44 of file fpu-none_inlines.hh.
|
inline |
Sets the FPU rounding direction to dir.
Definition at line 137 of file fpu-ia32_inlines.hh.
References fpu_set_control(), PPL_FPU_CONTROL_DEFAULT_BASE, and PPL_SSE_CONTROL_DEFAULT_BASE.
Referenced by Parma_Polyhedra_Library::Init::Init(), restore_pre_PPL_rounding(), set_rounding_for_PPL(), and Parma_Polyhedra_Library::Init::~Init().
|
related |
Definition at line 52 of file GMP_Integer_inlines.hh.
Referenced by Parma_Polyhedra_Library::PIP_Tree_Node::Artificial_Parameter::Artificial_Parameter(), Parma_Polyhedra_Library::MIP_Problem::choose_branching_variable(), Parma_Polyhedra_Library::PIP_Tree_Node::compatibility_check(), Parma_Polyhedra_Library::Polyhedron::contains_integer_point(), Parma_Polyhedra_Library::Grid::conversion(), Parma_Polyhedra_Library::Grid::frequency_no_check(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::gcd(), Parma_Polyhedra_Library::Grid::Grid(), Parma_Polyhedra_Library::Generator::is_matching_closure_point(), Parma_Polyhedra_Library::MIP_Problem::is_mip_satisfiable(), Parma_Polyhedra_Library::Grid::max_min(), Parma_Polyhedra_Library::Dense_Row::normalize(), Parma_Polyhedra_Library::PIP_Solution_Node::Tableau::normalize(), Parma_Polyhedra_Library::Sparse_Row::normalize(), normalize2(), Parma_Polyhedra_Library::MIP_Problem::OK(), Parma_Polyhedra_Library::Grid::reduce_congruence_with_equality(), Parma_Polyhedra_Library::Grid::reduce_equality_with_equality(), Parma_Polyhedra_Library::Grid::reduce_line_with_line(), Parma_Polyhedra_Library::Grid::reduce_parameter_with_line(), Parma_Polyhedra_Library::Grid::relation_with(), Parma_Polyhedra_Library::PIP_Solution_Node::solve(), Parma_Polyhedra_Library::MIP_Problem::solve_mip(), and Parma_Polyhedra_Library::Congruence::strong_normalize().
|
related |
Definition at line 62 of file GMP_Integer_inlines.hh.
Referenced by Parma_Polyhedra_Library::Grid::reduce_pc_with_pc().
|
inline |
Returns the hash code for space dimension dim.
Definition at line 43 of file globals_inlines.hh.
Referenced by Parma_Polyhedra_Library::Pointset_Ask_Tell< PSET >::hash_code(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::hash_code(), Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::hash_code(), Parma_Polyhedra_Library::Box< ITV >::hash_code(), Parma_Polyhedra_Library::Octagonal_Shape< T >::hash_code(), Parma_Polyhedra_Library::BD_Shape< T >::hash_code(), Parma_Polyhedra_Library::Grid::hash_code(), and Parma_Polyhedra_Library::Polyhedron::hash_code().
|
inline |
Definition at line 443 of file intervals_defs.hh.
Referenced by Parma_Polyhedra_Library::Box< ITV >::bounded_affine_image(), Parma_Polyhedra_Library::Box< ITV >::bounded_affine_preimage(), Parma_Polyhedra_Library::Box< ITV >::Box(), compute_absolute_error(), Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >::compute_absolute_error(), Parma_Polyhedra_Library::Constant_Floating_Point_Expression< FP_Interval_Type, FP_Format >::Constant_Floating_Point_Expression(), Parma_Polyhedra_Library::Box< ITV >::generalized_affine_image(), Parma_Polyhedra_Library::Interval< Boundary, Info >::lower_constraint(), Parma_Polyhedra_Library::Box< ITV >::propagate_constraint_no_check(), Parma_Polyhedra_Library::Box< ITV >::refine_interval_no_check(), Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >::relative_error(), Parma_Polyhedra_Library::Linear_Form< C >::relative_error(), Parma_Polyhedra_Library::Interval< Boundary, Info >::upper_constraint(), and Parma_Polyhedra_Library::Box< ITV >::wrap_assign().
|
inline |
Definition at line 449 of file intervals_defs.hh.
|
inline |
Definition at line 455 of file intervals_defs.hh.
|
inline |
Definition at line 461 of file intervals_defs.hh.
|
inline |
Definition at line 467 of file intervals_defs.hh.
|
inline |
Definition at line 474 of file intervals_defs.hh.
|
inline |
Definition at line 63 of file Interval_inlines.hh.
References Parma_Polyhedra_Library::Interval< Boundary, Info >::infinity_sign().
|
related |
Definition at line 241 of file Checked_Number_inlines.hh.
References is_minus_infinity(), and is_plus_infinity().
Referenced by Parma_Polyhedra_Library::Interval< Boundary, Info >::add_assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::div_assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::mul_assign(), and Parma_Polyhedra_Library::Interval< Boundary, Info >::sub_assign().
|
inline |
Initializes the library.
Definition at line 52 of file initializer.hh.
References Parma_Polyhedra_Library::Implementation::initialize_aux().
Referenced by Parma_Polyhedra_Library::Init::Init().
| Poly_Con_Relation Parma_Polyhedra_Library::interval_relation | ( | const ITV & | i, |
| const Constraint::Type | constraint_type, | ||
| Coefficient_traits::const_reference | numer, | ||
| Coefficient_traits::const_reference | denom = Coefficient_one() |
||
| ) |
Returns the relations holding between an interval and an interval constraint.
- Parameters
-
i The interval; constraint_type The constraint type; numer The numerator of the constraint bound; denom The denominator of the constraint bound
The interval constraint has the form denom * Variable(0) relsym numer where relsym is ==, > or >= depending on the constraint_type.
Definition at line 645 of file Box_templates.hh.
References assign_r(), Parma_Polyhedra_Library::Constraint::EQUALITY, Parma_Polyhedra_Library::Poly_Con_Relation::is_disjoint(), Parma_Polyhedra_Library::Poly_Con_Relation::is_included(), Parma_Polyhedra_Library::Constraint::NONSTRICT_INEQUALITY, Parma_Polyhedra_Library::Poly_Con_Relation::nothing(), PPL_DIRTY_TEMP, ROUND_NOT_NEEDED, Parma_Polyhedra_Library::Poly_Con_Relation::saturates(), Parma_Polyhedra_Library::Boundary_NS::sgn(), Parma_Polyhedra_Library::Constraint::STRICT_INEQUALITY, and Parma_Polyhedra_Library::Poly_Con_Relation::strictly_intersects().
Referenced by Parma_Polyhedra_Library::Box< ITV >::get_limiting_box(), and Parma_Polyhedra_Library::Box< ITV >::relation_with().
|
inline |
Returns the precision parameter used for irrational calculations.
Definition at line 535 of file checked_mpq_inlines.hh.
References Parma_Polyhedra_Library::Checked::irrational_precision.
|
inline |
Returns true if and only if 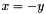 .
.
Definition at line 104 of file math_utilities_inlines.hh.
References ROUND_DIRECT, ROUND_STRICT_RELATION, and V_EQ.
Referenced by Parma_Polyhedra_Library::Octagonal_Shape< T >::compute_leaders(), Parma_Polyhedra_Library::BD_Shape< T >::compute_predecessors(), Parma_Polyhedra_Library::Octagonal_Shape< T >::compute_successors(), Parma_Polyhedra_Library::BD_Shape< T >::constraints(), Parma_Polyhedra_Library::Octagonal_Shape< T >::constraints(), Parma_Polyhedra_Library::BD_Shape< T >::frequency(), Parma_Polyhedra_Library::Octagonal_Shape< T >::frequency(), Parma_Polyhedra_Library::BD_Shape< T >::is_shortest_path_reduced(), Parma_Polyhedra_Library::Octagonal_Shape< T >::minimized_congruences(), Parma_Polyhedra_Library::BD_Shape< T >::operator<<(), Parma_Polyhedra_Library::Octagonal_Shape< T >::operator<<(), Parma_Polyhedra_Library::Octagonal_Shape< T >::relation_with(), Parma_Polyhedra_Library::BD_Shape< T >::relation_with(), Parma_Polyhedra_Library::Octagonal_Shape< T >::simplify_using_context_assign(), and Parma_Polyhedra_Library::Octagonal_Shape< T >::tight_coherence_would_make_empty().
|
inline |
Returns true if and only if x is in canonical form.
Definition at line 111 of file math_utilities_inlines.hh.
References PPL_DIRTY_TEMP.
Referenced by Parma_Polyhedra_Library::Box< ITV >::Box(), Parma_Polyhedra_Library::Polyhedron::contains_integer_point(), Parma_Polyhedra_Library::Box< ITV >::max_min(), and Parma_Polyhedra_Library::MIP_Problem::solve_mip().
|
inline |
Returns true if and only if x is an even number.
Definition at line 96 of file math_utilities_inlines.hh.
References ROUND_DIRECT, ROUND_STRICT_RELATION, and V_EQ.
Referenced by Parma_Polyhedra_Library::Octagonal_Shape< T >::drop_some_non_integer_points(), Parma_Polyhedra_Library::Octagonal_Shape< T >::tight_closure_assign(), and Parma_Polyhedra_Library::Octagonal_Shape< T >::tight_coherence_would_make_empty().
|
related |
Definition at line 254 of file Checked_Number_inlines.hh.
References raw_value().
Referenced by Parma_Polyhedra_Library::BD_Shape< T >::BHZ09_upper_bound_assign_if_exact(), Parma_Polyhedra_Library::Octagonal_Shape< T >::contains_integer_point(), Parma_Polyhedra_Library::BD_Shape< T >::contains_integer_point(), Parma_Polyhedra_Library::I_Constraint_Common< I_Constraint< T, Val_Or_Ref_Criteria, extended > >::convert_integer(), Parma_Polyhedra_Library::Box< ITV >::drop_some_non_integer_points(), Parma_Polyhedra_Library::Octagonal_Shape< T >::drop_some_non_integer_points(), Parma_Polyhedra_Library::BD_Shape< T >::drop_some_non_integer_points(), Parma_Polyhedra_Library::Octagonal_Shape< T >::drop_some_non_integer_points_helper(), Parma_Polyhedra_Library::BD_Shape< T >::drop_some_non_integer_points_helper(), Parma_Polyhedra_Library::Octagonal_Shape< T >::integer_upper_bound_assign_if_exact(), Parma_Polyhedra_Library::BD_Shape< T >::integer_upper_bound_assign_if_exact(), is_singleton_integer(), Parma_Polyhedra_Library::Octagonal_Shape< T >::tight_closure_assign(), and Parma_Polyhedra_Library::Octagonal_Shape< T >::tight_coherence_would_make_empty().
|
related |
Definition at line 513 of file Float_inlines.hh.
Referenced by Parma_Polyhedra_Library::Concrete_Expression< Target >::cast_linearize().
|
related |
Definition at line 227 of file Checked_Number_inlines.hh.
References raw_value().
Referenced by Parma_Polyhedra_Library::DB_Matrix< T >::ascii_load(), Parma_Polyhedra_Library::OR_Matrix< T >::ascii_load(), infinity_sign(), Parma_Polyhedra_Library::Boundary_NS::is_domain_inf(), Parma_Polyhedra_Library::Boundary_NS::normal_is_boundary_infinity(), Parma_Polyhedra_Library::Boundary_NS::normal_is_reverse_infinity(), numer_denom(), Parma_Polyhedra_Library::BD_Shape< T >::OK(), and Parma_Polyhedra_Library::Octagonal_Shape< T >::OK().
|
inline |
Definition at line 313 of file Checked_Number_inlines.hh.
References Parma_Polyhedra_Library::Checked_Number< T, Policy >::raw_value().
|
related |
Definition at line 247 of file Checked_Number_inlines.hh.
References raw_value().
Referenced by Parma_Polyhedra_Library::Interval_NS::f_is_empty(), numer_denom(), Parma_Polyhedra_Library::DB_Row< T >::OK(), and Parma_Polyhedra_Library::Interval< Boundary, Info >::OK().
|
inline |
Definition at line 307 of file Checked_Number_inlines.hh.
References Parma_Polyhedra_Library::Checked_Number< T, Policy >::raw_value().
|
related |
Definition at line 234 of file Checked_Number_inlines.hh.
References raw_value().
Referenced by Parma_Polyhedra_Library::Octagonal_Shape< T >::affine_image(), Parma_Polyhedra_Library::BD_Shape< T >::affine_image(), Parma_Polyhedra_Library::BD_Shape< T >::BFT00_upper_bound_assign_if_exact(), Parma_Polyhedra_Library::Octagonal_Shape< T >::bounded_affine_image(), Parma_Polyhedra_Library::BD_Shape< T >::bounded_affine_image(), Parma_Polyhedra_Library::BD_Shape< T >::bounds(), Parma_Polyhedra_Library::Octagonal_Shape< T >::bounds(), Parma_Polyhedra_Library::Box< ITV >::Box(), Parma_Polyhedra_Library::Octagonal_Shape< T >::CC76_narrowing_assign(), Parma_Polyhedra_Library::BD_Shape< T >::CC76_narrowing_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::constrains(), Parma_Polyhedra_Library::BD_Shape< T >::constrains(), Parma_Polyhedra_Library::BD_Shape< T >::constraints(), Parma_Polyhedra_Library::Octagonal_Shape< T >::constraints(), Parma_Polyhedra_Library::Octagonal_Shape< T >::contains_integer_point(), Parma_Polyhedra_Library::BD_Shape< T >::contains_integer_point(), Parma_Polyhedra_Library::Octagonal_Shape< T >::deduce_minus_v_pm_u_bounds(), Parma_Polyhedra_Library::BD_Shape< T >::deduce_u_minus_v_bounds(), Parma_Polyhedra_Library::BD_Shape< T >::deduce_v_minus_u_bounds(), Parma_Polyhedra_Library::Octagonal_Shape< T >::deduce_v_pm_u_bounds(), Parma_Polyhedra_Library::Octagonal_Shape< T >::drop_some_non_integer_points(), Parma_Polyhedra_Library::BD_Shape< T >::export_interval_constraints(), Parma_Polyhedra_Library::Octagonal_Shape< T >::export_interval_constraints(), Parma_Polyhedra_Library::Octagonal_Shape< T >::frequency(), Parma_Polyhedra_Library::Octagonal_Shape< T >::generalized_affine_image(), Parma_Polyhedra_Library::BD_Shape< T >::generalized_affine_image(), Parma_Polyhedra_Library::BD_Shape< T >::incremental_shortest_path_closure_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::incremental_strong_closure_assign(), infinity_sign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::is_bounded(), Parma_Polyhedra_Library::BD_Shape< T >::is_bounded(), Parma_Polyhedra_Library::Boundary_NS::is_domain_sup(), Parma_Polyhedra_Library::BD_Shape< T >::is_shortest_path_reduced(), Parma_Polyhedra_Library::Octagonal_Shape< T >::is_strong_coherent(), Parma_Polyhedra_Library::Octagonal_Shape< T >::is_strongly_reduced(), Parma_Polyhedra_Library::Octagonal_Shape< T >::is_universe(), Parma_Polyhedra_Library::BD_Shape< T >::is_universe(), Parma_Polyhedra_Library::DB_Matrix< T >::l_m_distance_assign(), Parma_Polyhedra_Library::OR_Matrix< T >::l_m_distance_assign(), Parma_Polyhedra_Library::BD_Shape< T >::left_one_var_refine(), Parma_Polyhedra_Library::BD_Shape< T >::max_min(), Parma_Polyhedra_Library::Octagonal_Shape< T >::max_min(), Parma_Polyhedra_Library::BD_Shape< T >::minimized_congruences(), Parma_Polyhedra_Library::BD_Shape< T >::minimized_constraints(), Parma_Polyhedra_Library::Boundary_NS::normal_is_boundary_infinity(), Parma_Polyhedra_Library::Boundary_NS::normal_is_reverse_infinity(), numer_denom(), Parma_Polyhedra_Library::BD_Shape< T >::OK(), Parma_Polyhedra_Library::Octagonal_Shape< T >::OK(), Parma_Polyhedra_Library::BD_Shape< T >::one_variable_affine_form_image(), Parma_Polyhedra_Library::BD_Shape< T >::operator<<(), Parma_Polyhedra_Library::Octagonal_Shape< T >::operator<<(), Parma_Polyhedra_Library::Octagonal_Shape< T >::refine(), Parma_Polyhedra_Library::BD_Shape< T >::refine(), Parma_Polyhedra_Library::Octagonal_Shape< T >::relation_with(), Parma_Polyhedra_Library::BD_Shape< T >::relation_with(), Parma_Polyhedra_Library::BD_Shape< T >::shortest_path_closure_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::simplify_using_context_assign(), Parma_Polyhedra_Library::BD_Shape< T >::simplify_using_context_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::strong_closure_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::strong_coherence_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::tight_closure_assign(), and Parma_Polyhedra_Library::Octagonal_Shape< T >::tight_coherence_would_make_empty().
|
inline |
Definition at line 319 of file Checked_Number_inlines.hh.
References Parma_Polyhedra_Library::Checked_Number< T, Policy >::raw_value().
|
inline |
Definition at line 139 of file Interval_inlines.hh.
References Parma_Polyhedra_Library::Interval_NS::f_lower(), and is_integer().
|
inline |
Returns true if c is any kind of space character.
Definition at line 168 of file globals_inlines.hh.
Referenced by operator>>(), Parma_Polyhedra_Library::Checked::parse_number_part(), and Parma_Polyhedra_Library::IO_Operators::wrap_string().
|
inline |
Returns the integer square root of x.
Definition at line 452 of file OR_Matrix_inlines.hh.
Referenced by Parma_Polyhedra_Library::OR_Matrix< T >::max_num_rows().
|
related |
Definition at line 70 of file GMP_Integer_inlines.hh.
Referenced by Parma_Polyhedra_Library::MIP_Problem::compute_generator(), Parma_Polyhedra_Library::Grid::conversion(), Parma_Polyhedra_Library::Polyhedron::convert_to_integer_expression(), Parma_Polyhedra_Library::Polyhedron::convert_to_integer_expressions(), Parma_Polyhedra_Library::MIP_Problem::get_exiting_base_index(), Parma_Polyhedra_Library::Box< ITV >::max_min(), Parma_Polyhedra_Library::Grid::normalize_divisors(), Parma_Polyhedra_Library::Congruence_System::normalize_moduli(), and Parma_Polyhedra_Library::MIP_Problem::steepest_edge_exact_entering_index().
|
inline |
Definition at line 187 of file globals_inlines.hh.
Referenced by Parma_Polyhedra_Library::CO_Tree::tree_iterator::follow_left_children_with_value(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::follow_right_children_with_value(), Parma_Polyhedra_Library::CO_Tree::tree_iterator::operator=(), and Parma_Polyhedra_Library::CO_Tree::tree_iterator::tree_iterator().
|
related |
Definition at line 505 of file Dense_Row_inlines.hh.
References Parma_Polyhedra_Library::Dense_Row::linear_combine().
Referenced by Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::add_mul_assign(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::linear_combine(), Parma_Polyhedra_Library::MIP_Problem::linear_combine(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::linear_combine_lax(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::operator+=(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::operator-=(), Parma_Polyhedra_Library::MIP_Problem::pivot(), Parma_Polyhedra_Library::MIP_Problem::process_pending_constraints(), Parma_Polyhedra_Library::MIP_Problem::second_phase(), and Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::sub_mul_assign().
|
related |
Definition at line 512 of file Dense_Row_inlines.hh.
References Parma_Polyhedra_Library::Dense_Row::linear_combine().
|
inline |
Returns a mask for the lowest n bits,.
Definition at line 45 of file math_utilities_inlines.hh.
|
inline |
Assigns to x the maximum between x and y.
Definition at line 88 of file math_utilities_inlines.hh.
Referenced by Parma_Polyhedra_Library::BD_Shape< T >::BD_Shape(), Parma_Polyhedra_Library::Octagonal_Shape< T >::fold_space_dimensions(), Parma_Polyhedra_Library::BD_Shape< T >::fold_space_dimensions(), Parma_Polyhedra_Library::Interval< Boundary, Info >::intersect_assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::join_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::Octagonal_Shape(), Parma_Polyhedra_Library::Octagonal_Shape< T >::upper_bound_assign(), and Parma_Polyhedra_Library::Interval< Boundary, Info >::upper_extend().
|
inline |
Returns the maximum space dimension this library can handle.
Definition at line 40 of file max_space_dimension.hh.
References Parma_Polyhedra_Library::Variable::max_space_dimension(), Parma_Polyhedra_Library::Box< ITV >::max_space_dimension(), Parma_Polyhedra_Library::Grid::max_space_dimension(), Parma_Polyhedra_Library::Polyhedron::max_space_dimension(), and not_a_dimension().
Referenced by Parma_Polyhedra_Library::MIP_Problem::add_space_dimensions_and_embed(), Parma_Polyhedra_Library::PIP_Problem::add_space_dimensions_and_embed(), Parma_Polyhedra_Library::Box< ITV >::add_space_dimensions_and_embed(), Parma_Polyhedra_Library::Grid::add_space_dimensions_and_embed(), Parma_Polyhedra_Library::Box< ITV >::add_space_dimensions_and_project(), Parma_Polyhedra_Library::Grid::add_space_dimensions_and_project(), Parma_Polyhedra_Library::Polyhedron::add_space_dimensions_and_project(), Parma_Polyhedra_Library::Box< ITV >::concatenate_assign(), Parma_Polyhedra_Library::Grid::concatenate_assign(), Parma_Polyhedra_Library::Polyhedron::concatenate_assign(), Parma_Polyhedra_Library::Grid::construct(), Parma_Polyhedra_Library::Box< ITV >::expand_space_dimension(), Parma_Polyhedra_Library::Octagonal_Shape< T >::expand_space_dimension(), Parma_Polyhedra_Library::BD_Shape< T >::expand_space_dimension(), Parma_Polyhedra_Library::Grid::expand_space_dimension(), Parma_Polyhedra_Library::Polyhedron::expand_space_dimension(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::Linear_Expression_Impl(), Parma_Polyhedra_Library::Pointset_Ask_Tell< PSET >::max_space_dimension(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::max_space_dimension(), Parma_Polyhedra_Library::Linear_System< Row >::max_space_dimension(), and Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::max_space_dimension().
|
related |
Definition at line 75 of file globals_inlines.hh.
References abandon_expensive_computations, Parma_Polyhedra_Library::In_Assert::asserting(), and Parma_Polyhedra_Library::Weightwatch_Traits::check_function.
Referenced by Parma_Polyhedra_Library::PIP_Tree_Node::compatibility_check(), Parma_Polyhedra_Library::MIP_Problem::compute_simplex_using_exact_pricing(), Parma_Polyhedra_Library::MIP_Problem::compute_simplex_using_steepest_edge_float(), Parma_Polyhedra_Library::Polyhedron::conversion(), Parma_Polyhedra_Library::Box< ITV >::propagate_constraints_no_check(), and Parma_Polyhedra_Library::PIP_Solution_Node::solve().
|
inline |
Assigns to top a pointer to a location that holds the conversion, according to dir, of from to type To. When necessary, and only when necessary, the variable tmp is used to hold the result of conversion.
Definition at line 64 of file distances_inlines.hh.
References Parma_Polyhedra_Library::maybe_assign_struct< To, From >::function().
Referenced by Parma_Polyhedra_Library::DB_Matrix< T >::l_m_distance_assign(), Parma_Polyhedra_Library::Generator::l_m_distance_assign(), Parma_Polyhedra_Library::OR_Matrix< T >::l_m_distance_assign(), and Parma_Polyhedra_Library::Box< ITV >::l_m_distance_assign().
|
inline |
Definition at line 843 of file Checked_Number_inlines.hh.
References fpu_check_inexact().
|
inline |
Definition at line 835 of file Checked_Number_inlines.hh.
References fpu_reset_inexact().
|
inline |
Assigns to x the minimum between x and y.
Definition at line 80 of file math_utilities_inlines.hh.
Referenced by Parma_Polyhedra_Library::BD_Shape< T >::incremental_shortest_path_closure_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::incremental_strong_closure_assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::intersect_assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::join_assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::lower_extend(), Parma_Polyhedra_Library::BD_Shape< T >::shortest_path_closure_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::strong_closure_assign(), and Parma_Polyhedra_Library::Octagonal_Shape< T >::strong_coherence_assign().
|
inline |
|
inline |
If v is nonzero, returns the position of the most significant bit in a.
The behavior is undefined if v is zero.
Definition at line 518 of file Float_inlines.hh.
References clz(), and sizeof_to_bits.
Referenced by compute_absolute_error(), and Parma_Polyhedra_Library::Linear_Form< C >::relative_error().
|
related |
Definition at line 85 of file GMP_Integer_inlines.hh.
Referenced by Parma_Polyhedra_Library::Implementation::wrap_assign(), Parma_Polyhedra_Library::Box< ITV >::wrap_assign(), Parma_Polyhedra_Library::Grid::wrap_assign(), Parma_Polyhedra_Library::Implementation::wrap_assign_col(), and Parma_Polyhedra_Library::Implementation::wrap_assign_ind().
|
related |
Definition at line 32 of file GMP_Integer_inlines.hh.
Referenced by Parma_Polyhedra_Library::BD_Shape< T >::add_constraint(), Parma_Polyhedra_Library::Octagonal_Shape< T >::add_constraint(), Parma_Polyhedra_Library::BD_Shape< T >::affine_image(), Parma_Polyhedra_Library::Octagonal_Shape< T >::affine_preimage(), Parma_Polyhedra_Library::Linear_System< Row >::back_substitute(), Parma_Polyhedra_Library::BD_Shape< T >::bounded_affine_image(), Parma_Polyhedra_Library::Box< ITV >::bounded_affine_preimage(), Parma_Polyhedra_Library::Octagonal_Shape< T >::bounded_affine_preimage(), Parma_Polyhedra_Library::BD_Shape< T >::bounded_affine_preimage(), Parma_Polyhedra_Library::Generator::closure_point(), Parma_Polyhedra_Library::MIP_Problem::compute_generator(), Parma_Polyhedra_Library::MIP_Problem::compute_simplex_using_steepest_edge_float(), Parma_Polyhedra_Library::Polyhedron::conversion(), Parma_Polyhedra_Library::Octagonal_Shape< T >::deduce_minus_v_pm_u_bounds(), Parma_Polyhedra_Library::Octagonal_Shape< T >::deduce_v_pm_u_bounds(), Parma_Polyhedra_Library::Grid_Generator::fancy_print(), Parma_Polyhedra_Library::Generator::fancy_print(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::gcd(), Parma_Polyhedra_Library::Octagonal_Shape< T >::generalized_affine_image(), Parma_Polyhedra_Library::BD_Shape< T >::generalized_affine_image(), Parma_Polyhedra_Library::Grid::generalized_affine_image(), Parma_Polyhedra_Library::Box< ITV >::generalized_affine_preimage(), Parma_Polyhedra_Library::BD_Shape< T >::generalized_affine_preimage(), Parma_Polyhedra_Library::Octagonal_Shape< T >::generalized_affine_preimage(), Parma_Polyhedra_Library::Grid::generalized_affine_preimage(), Parma_Polyhedra_Library::Polyhedron::generalized_affine_preimage(), Parma_Polyhedra_Library::PIP_Solution_Node::generate_cut(), Parma_Polyhedra_Library::Octagonal_Shape< T >::get_limiting_octagon(), Parma_Polyhedra_Library::BD_Shape< T >::get_limiting_shape(), Parma_Polyhedra_Library::Grid::Grid(), Parma_Polyhedra_Library::Grid_Generator::grid_point(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::linear_combine(), Parma_Polyhedra_Library::MIP_Problem::linear_combine(), Parma_Polyhedra_Library::Sparse_Row::linear_combine(), Parma_Polyhedra_Library::BD_Shape< T >::max_min(), Parma_Polyhedra_Library::Octagonal_Shape< T >::max_min(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::negate(), Parma_Polyhedra_Library::Dense_Row::normalize(), Parma_Polyhedra_Library::Sparse_Row::normalize(), Parma_Polyhedra_Library::Linear_Expression::operator-(), Parma_Polyhedra_Library::Congruence::operator<<(), Parma_Polyhedra_Library::Constraint::operator<<(), Parma_Polyhedra_Library::Constraint::operator==(), Parma_Polyhedra_Library::Constraint::operator>(), Parma_Polyhedra_Library::Constraint::operator>=(), Parma_Polyhedra_Library::Grid_Generator::parameter(), Parma_Polyhedra_Library::Generator::point(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::print(), Parma_Polyhedra_Library::MIP_Problem::process_pending_constraints(), Parma_Polyhedra_Library::Grid::reduce_congruence_with_equality(), Parma_Polyhedra_Library::Grid::reduce_equality_with_equality(), Parma_Polyhedra_Library::Grid::reduce_line_with_line(), Parma_Polyhedra_Library::Grid::reduce_parameter_with_line(), Parma_Polyhedra_Library::Octagonal_Shape< T >::refine(), Parma_Polyhedra_Library::BD_Shape< T >::refine(), Parma_Polyhedra_Library::Octagonal_Shape< T >::refine_no_check(), Parma_Polyhedra_Library::BD_Shape< T >::refine_no_check(), Parma_Polyhedra_Library::Octagonal_Shape< T >::relation_with(), Parma_Polyhedra_Library::BD_Shape< T >::relation_with(), Parma_Polyhedra_Library::MIP_Problem::second_phase(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::sign_normalize(), Parma_Polyhedra_Library::PIP_Problem::solve(), Parma_Polyhedra_Library::PIP_Solution_Node::update_tableau(), Parma_Polyhedra_Library::Implementation::wrap_assign(), Parma_Polyhedra_Library::Box< ITV >::wrap_assign(), and Parma_Polyhedra_Library::Grid::wrap_assign().
|
related |
Definition at line 37 of file GMP_Integer_inlines.hh.
|
inline |
If 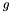 is the GCD of
is the GCD of x and y, the values of x and y divided by 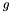 are assigned to
are assigned to n_x and n_y, respectively.
- Note
xandn_xmay be the same object and likewise foryandn_y. Any other aliasing results in undefined behavior.
Definition at line 34 of file math_utilities_inlines.hh.
References exact_div_assign(), gcd_assign(), and PPL_DIRTY_TEMP_COEFFICIENT.
Referenced by Parma_Polyhedra_Library::Polyhedron::conversion(), Parma_Polyhedra_Library::MIP_Problem::evaluate_objective_function(), Parma_Polyhedra_Library::Box< ITV >::frequency(), Parma_Polyhedra_Library::BD_Shape< T >::frequency(), Parma_Polyhedra_Library::Octagonal_Shape< T >::frequency(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::linear_combine(), and Parma_Polyhedra_Library::MIP_Problem::linear_combine().
|
inline |
Returns a value that does not designate a valid dimension.
Definition at line 38 of file globals_inlines.hh.
Referenced by Parma_Polyhedra_Library::PIP_Problem::clear(), Parma_Polyhedra_Library::PIP_Tree_Node::compatibility_check(), Parma_Polyhedra_Library::PIP_Solution_Node::generate_cut(), Parma_Polyhedra_Library::Partial_Function::insert(), Parma_Polyhedra_Library::Concrete_Expression< Target >::linearize(), Parma_Polyhedra_Library::Grid::map_space_dimensions(), Parma_Polyhedra_Library::Polyhedron::map_space_dimensions(), Parma_Polyhedra_Library::Partial_Function::maps(), max_space_dimension(), Parma_Polyhedra_Library::Variable::max_space_dimension(), Parma_Polyhedra_Library::MIP_Problem::merge_split_variable(), Parma_Polyhedra_Library::PIP_Problem::OK(), Parma_Polyhedra_Library::PIP_Problem::operator<<(), Parma_Polyhedra_Library::Partial_Function::print(), Parma_Polyhedra_Library::MIP_Problem::process_pending_constraints(), Parma_Polyhedra_Library::PIP_Solution_Node::row_sign(), Parma_Polyhedra_Library::PIP_Solution_Node::solve(), and Parma_Polyhedra_Library::PIP_Solution_Node::update_tableau().
|
inline |
|
inline |
|
inline |
Definition at line 181 of file globals_inlines.hh.
|
inline |
Extract the numerator and denominator components of from.
Definition at line 52 of file math_utilities_inlines.hh.
References assign_r(), is_minus_infinity(), is_not_a_number(), is_plus_infinity(), PPL_DIRTY_TEMP, and ROUND_NOT_NEEDED.
Referenced by Parma_Polyhedra_Library::BD_Shape< T >::BFT00_upper_bound_assign_if_exact(), Parma_Polyhedra_Library::BD_Shape< T >::constraints(), Parma_Polyhedra_Library::Octagonal_Shape< T >::constraints(), Parma_Polyhedra_Library::Polyhedron::convert_to_integer_expression(), Parma_Polyhedra_Library::Polyhedron::convert_to_integer_expressions(), Parma_Polyhedra_Library::BD_Shape< T >::frequency(), Parma_Polyhedra_Library::Octagonal_Shape< T >::frequency(), Parma_Polyhedra_Library::BD_Shape< T >::max_min(), Parma_Polyhedra_Library::Octagonal_Shape< T >::max_min(), Parma_Polyhedra_Library::BD_Shape< T >::minimized_congruences(), Parma_Polyhedra_Library::Octagonal_Shape< T >::minimized_congruences(), Parma_Polyhedra_Library::BD_Shape< T >::minimized_constraints(), Parma_Polyhedra_Library::Octagonal_Shape< T >::relation_with(), and Parma_Polyhedra_Library::BD_Shape< T >::relation_with().
|
related |
Definition at line 185 of file Interval_inlines.hh.
|
related |
Definition at line 264 of file Box_inlines.hh.
|
related |
Definition at line 286 of file Generator_System_inlines.hh.
|
related |
Definition at line 416 of file Constraint_System_inlines.hh.
| bool Parma_Polyhedra_Library::operator!= | ( | const Dense_Row & | x, |
| const Sparse_Row & | y | ||
| ) |
Definition at line 832 of file Sparse_Row.cc.
| bool Parma_Polyhedra_Library::operator!= | ( | const Sparse_Row & | x, |
| const Dense_Row & | y | ||
| ) |
Definition at line 842 of file Sparse_Row.cc.
Definition at line 101 of file intervals_defs.hh.
|
inline |
Definition at line 1037 of file Interval_inlines.hh.
References Parma_Polyhedra_Library::Interval< Boundary, Info >::mul_assign().
|
inline |
Definition at line 1045 of file Interval_inlines.hh.
References Parma_Polyhedra_Library::Interval< Boundary, Info >::mul_assign().
|
inline |
Definition at line 1053 of file Interval_inlines.hh.
References Parma_Polyhedra_Library::Interval< Boundary, Info >::mul_assign().
|
inline |
Definition at line 989 of file Interval_inlines.hh.
References Parma_Polyhedra_Library::Interval< Boundary, Info >::add_assign().
|
inline |
Definition at line 997 of file Interval_inlines.hh.
References Parma_Polyhedra_Library::Interval< Boundary, Info >::add_assign().
|
inline |
Definition at line 1005 of file Interval_inlines.hh.
References Parma_Polyhedra_Library::Interval< Boundary, Info >::add_assign().
Definition at line 107 of file intervals_defs.hh.
|
inline |
Definition at line 1013 of file Interval_inlines.hh.
References Parma_Polyhedra_Library::Interval< Boundary, Info >::sub_assign().
|
inline |
Definition at line 1021 of file Interval_inlines.hh.
References Parma_Polyhedra_Library::Interval< Boundary, Info >::sub_assign().
|
inline |
Definition at line 1029 of file Interval_inlines.hh.
References Parma_Polyhedra_Library::Interval< Boundary, Info >::sub_assign().
|
inline |
Definition at line 1061 of file Interval_inlines.hh.
References Parma_Polyhedra_Library::Interval< Boundary, Info >::div_assign().
|
inline |
Definition at line 1069 of file Interval_inlines.hh.
References Parma_Polyhedra_Library::Interval< Boundary, Info >::div_assign().
|
inline |
Definition at line 1077 of file Interval_inlines.hh.
References Parma_Polyhedra_Library::Interval< Boundary, Info >::div_assign().
|
inline |
Definition at line 1085 of file Interval_inlines.hh.
References check_empty_arg(), Parma_Polyhedra_Library::Boundary_NS::LOWER, ROUND_NOT_NEEDED, Parma_Polyhedra_Library::Boundary_NS::SPECIAL, and Parma_Polyhedra_Library::Boundary_NS::UPPER.
|
related |
Definition at line 164 of file Interval_inlines.hh.
References check_empty_arg(), Parma_Polyhedra_Library::Boundary_NS::eq(), Parma_Polyhedra_Library::Interval_NS::f_info(), Parma_Polyhedra_Library::Interval_NS::f_lower(), f_OK(), Parma_Polyhedra_Library::Interval_NS::f_upper(), Parma_Polyhedra_Library::Boundary_NS::LOWER, and Parma_Polyhedra_Library::Boundary_NS::UPPER.
|
related |
Definition at line 281 of file Generator_System_inlines.hh.
References Parma_Polyhedra_Library::Generator_System::sys.
|
related |
Definition at line 411 of file Constraint_System_inlines.hh.
References Parma_Polyhedra_Library::Constraint_System::sys.
|
related |
Definition at line 581 of file Box_templates.hh.
References Parma_Polyhedra_Library::Box< ITV >::is_empty(), Parma_Polyhedra_Library::Box< ITV >::seq, and Parma_Polyhedra_Library::Box< ITV >::space_dimension().
Referenced by Parma_Polyhedra_Library::iterator_to_const< Container >::operator!=(), Parma_Polyhedra_Library::const_iterator_to_const< Container >::operator!=(), and Parma_Polyhedra_Library::PIP_Tree_Node::Artificial_Parameter::operator!=().
| bool Parma_Polyhedra_Library::operator== | ( | const Dense_Row & | x, |
| const Sparse_Row & | y | ||
| ) |
Definition at line 810 of file Sparse_Row.cc.
References Parma_Polyhedra_Library::Sparse_Row::end(), Parma_Polyhedra_Library::CO_Tree::const_iterator::index(), Parma_Polyhedra_Library::Sparse_Row::lower_bound(), Parma_Polyhedra_Library::Sparse_Row::size(), and Parma_Polyhedra_Library::Dense_Row::size().
| bool Parma_Polyhedra_Library::operator== | ( | const Sparse_Row & | x, |
| const Dense_Row & | y | ||
| ) |
Definition at line 837 of file Sparse_Row.cc.
|
inline |
Definition at line 244 of file Interval_templates.hh.
References Parma_Polyhedra_Library::Interval< Boundary, Info >::assign(), Parma_Polyhedra_Library::Boundary_NS::assign(), c, EMPTY, Parma_Polyhedra_Library::Interval< Boundary, Info >::info(), is_space(), Parma_Polyhedra_Library::Boundary_NS::LOWER, Parma_Polyhedra_Library::Interval< Boundary, Info >::lower(), result_relation_class(), ROUND_DOWN, ROUND_UP, Parma_Polyhedra_Library::Interval_NS::SCALAR_INFO, Parma_Polyhedra_Library::Boundary_NS::set_minus_infinity(), Parma_Polyhedra_Library::Boundary_NS::set_plus_infinity(), UNIVERSE, Parma_Polyhedra_Library::Boundary_NS::UPPER, Parma_Polyhedra_Library::Interval< Boundary, Info >::upper(), V_CVT_STR_UNK, V_EQ, V_EQ_MINUS_INFINITY, V_EQ_PLUS_INFINITY, V_GE, V_GT, V_GT_MINUS_INFINITY, V_LE, V_LT, V_LT_PLUS_INFINITY, and V_NAN.
Definition at line 95 of file intervals_defs.hh.
|
inline |
|
inline |
No-op function that force the compiler to store the argument and to reread it from memory if needed (thus preventing CSE).
Definition at line 49 of file compiler.hh.
References PPL_USED.
Referenced by Parma_Polyhedra_Library::Checked::limit_precision().
| void Parma_Polyhedra_Library::PPL_handle_timeout | ( | int | signum | ) |
|
related |
Definition at line 111 of file GMP_Integer_inlines.hh.
Referenced by Parma_Polyhedra_Library::Checked_Number< T, Policy >::cmp(), is_integer(), is_minus_infinity(), is_not_a_number(), is_plus_infinity(), and Parma_Polyhedra_Library::Checked_Number< T, Policy >::sgn().
|
related |
Definition at line 116 of file GMP_Integer_inlines.hh.
|
related |
Definition at line 57 of file GMP_Integer_inlines.hh.
Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::approximate_partition_aux().
|
inline |
Sets the FPU rounding mode as it was before initialization of the PPL.
This is important if the application uses floating-point computations outside the PPL. It is crucial when the application uses functions from a mathematical library that are not guaranteed to work correctly under all rounding modes.
After calling this function it is absolutely necessary to call set_rounding_for_PPL() before using any PPL abstractions based on floating point numbers. This is performed automatically at finalization-time.
Definition at line 40 of file Init_inlines.hh.
References fpu_set_rounding_direction(), and Parma_Polyhedra_Library::Init::old_rounding_direction.
|
inline |
Definition at line 73 of file Result_inlines.hh.
References result_class(), V_GT_SUP, V_LT_INF, VC_MINUS_INFINITY, VC_NORMAL, and VC_PLUS_INFINITY.
Referenced by Parma_Polyhedra_Library::Checked::add_mul_int(), Parma_Polyhedra_Library::Checked::sub_mul_int(), Parma_Polyhedra_Library::Implementation::wrap_assign(), and Parma_Polyhedra_Library::Interval< Boundary, Info >::wrap_assign().
|
inline |
Definition at line 96 of file Result_inlines.hh.
References V_UNREPRESENTABLE.
Referenced by Parma_Polyhedra_Library::Boundary_NS::set_boundary_infinity(), Parma_Polyhedra_Library::Boundary_NS::set_minus_infinity(), and Parma_Polyhedra_Library::Boundary_NS::set_plus_infinity().
|
inline |
Definition at line 38 of file Checked_Number_inlines.hh.
References ROUND_CHECK, and ROUND_NOT_NEEDED.
Referenced by assign_r(), Parma_Polyhedra_Library::Checked_Number< T, Policy >::assign_r(), Parma_Polyhedra_Library::Checked_Number< T, Policy >::Checked_Number(), construct(), Parma_Polyhedra_Library::Checked_Number< T, Policy >::input(), and Parma_Polyhedra_Library::Checked_Number< T, Policy >::output().
|
inline |
Sets the precision parameter used for irrational calculations.
The lesser between numerator and denominator is limited to 2**p.
If p is less than or equal to INT_MAX, sets the precision parameter used for irrational calculations to p.
- Exceptions
-
std::invalid_argument Thrown if pis greater thanINT_MAX.
Definition at line 549 of file checked_mpq_inlines.hh.
References Parma_Polyhedra_Library::Checked::irrational_precision.
Referenced by Parma_Polyhedra_Library::Init::Init().
|
inline |
Sets the FPU rounding mode so that the PPL abstractions based on floating point numbers work correctly.
This is performed automatically at initialization-time. Calling this function is needed only if restore_pre_PPL_rounding() has been previously called.
Definition at line 33 of file Init_inlines.hh.
References fpu_set_rounding_direction(), ROUND_DIRECT, and round_fpu_dir().
| bool Parma_Polyhedra_Library::shrink_to_congruence_no_check | ( | D1 & | d1, |
| D2 & | d2, | ||
| const Congruence & | cg | ||
| ) |
Definition at line 551 of file Partially_Reduced_Product_templates.hh.
References EMPTY, Parma_Polyhedra_Library::Congruence::expression(), Parma_Polyhedra_Library::Poly_Con_Relation::is_included(), Parma_Polyhedra_Library::Congruence::modulus(), PPL_DIRTY_TEMP_COEFFICIENT, and swap().
Referenced by Parma_Polyhedra_Library::Congruences_Reduction< D1, D2 >::product_reduce().
|
related |
Definition at line 101 of file GMP_Integer_inlines.hh.
|
related |
Definition at line 80 of file GMP_Integer_inlines.hh.
Referenced by Parma_Polyhedra_Library::MIP_Problem::compute_generator(), Parma_Polyhedra_Library::Grid::conversion(), Parma_Polyhedra_Library::Implementation::Termination::fill_constraint_system_PR(), Parma_Polyhedra_Library::Implementation::Termination::fill_constraint_system_PR_original(), Parma_Polyhedra_Library::Implementation::Termination::fill_constraint_systems_MS(), Parma_Polyhedra_Library::BD_Shape< T >::frequency(), Parma_Polyhedra_Library::Box< ITV >::generalized_affine_preimage(), Parma_Polyhedra_Library::Polyhedron::modify_according_to_evolution(), Parma_Polyhedra_Library::Grid::reduce_congruence_with_equality(), and Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::sub_mul_assign().
|
related |
Definition at line 408 of file Linear_Expression_inlines.hh.
References Parma_Polyhedra_Library::Linear_Expression::impl, and Parma_Polyhedra_Library::Linear_Expression_Interface::sub_mul_assign().
Definition at line 94 of file Variable_inlines.hh.
References Parma_Polyhedra_Library::Variable::m_swap().
Referenced by Parma_Polyhedra_Library::Variable::m_swap().
|
inline |
Make sure swap() is specialized when needed.
This will cause a compile-time error whenever a specialization for T is beneficial but missing.
Definition at line 122 of file globals_defs.hh.
References PPL_COMPILE_TIME_CHECK.
|
related |
Definition at line 194 of file Matrix_inlines.hh.
References Parma_Polyhedra_Library::Matrix< Row >::m_swap().
Referenced by Parma_Polyhedra_Library::Matrix< Row >::m_swap().
|
related |
Definition at line 233 of file Swapping_Vector_inlines.hh.
References Parma_Polyhedra_Library::Swapping_Vector< T >::m_swap().
Referenced by Parma_Polyhedra_Library::Swapping_Vector< T >::erase(), Parma_Polyhedra_Library::Swapping_Vector< T >::m_swap(), and Parma_Polyhedra_Library::Swapping_Vector< T >::reserve().
| void Parma_Polyhedra_Library::swap | ( | Parma_Polyhedra_Library::Sparse_Row & | x, |
| Parma_Polyhedra_Library::Dense_Row & | y | ||
| ) |
Definition at line 1171 of file Sparse_Row.cc.
References Parma_Polyhedra_Library::Sparse_Row::begin(), Parma_Polyhedra_Library::Sparse_Row::end(), Parma_Polyhedra_Library::Sparse_Row::size(), and swap().
| void Parma_Polyhedra_Library::swap | ( | Parma_Polyhedra_Library::Dense_Row & | x, |
| Parma_Polyhedra_Library::Sparse_Row & | y | ||
| ) |
Definition at line 1189 of file Sparse_Row.cc.
References swap().
Definition at line 873 of file CO_Tree_inlines.hh.
References Parma_Polyhedra_Library::CO_Tree::m_swap().
Referenced by Parma_Polyhedra_Library::Polyhedron::add_recycled_generators(), Parma_Polyhedra_Library::Bit_Matrix::add_recycled_row(), Parma_Polyhedra_Library::Matrix< Row >::add_recycled_row(), Parma_Polyhedra_Library::Matrix< Row >::add_row(), Parma_Polyhedra_Library::Congruence_System::add_unit_rows_and_space_dimensions(), Parma_Polyhedra_Library::Linear_System< Row >::add_universe_rows_and_space_dimensions(), Parma_Polyhedra_Library::Dense_Row::add_zeroes_and_shift(), Parma_Polyhedra_Library::Octagonal_Shape< T >::affine_form_image(), Parma_Polyhedra_Library::Octagonal_Shape< T >::affine_image(), Parma_Polyhedra_Library::BD_Shape< T >::affine_image(), Parma_Polyhedra_Library::Pointset_Ask_Tell< PSET >::ascii_load(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::ascii_load(), assign_or_swap(), Parma_Polyhedra_Library::Linear_System< Row >::assign_with_pending(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::BGP99_heuristics_assign(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::BHZ03_widening_assign(), Parma_Polyhedra_Library::CO_Tree::bisect_near(), Parma_Polyhedra_Library::Bit_Matrix::clear(), Parma_Polyhedra_Library::PIP_Tree_Node::compatibility_check(), Parma_Polyhedra_Library::Congruence_System::concatenate(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::concatenate_assign(), Parma_Polyhedra_Library::Polyhedron::concatenate_assign(), Parma_Polyhedra_Library::Polyhedron::constraints(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::construct(), Parma_Polyhedra_Library::Polyhedron::conversion(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::difference_assign(), Parma_Polyhedra_Library::Swapping_Vector< T >::erase(), Parma_Polyhedra_Library::CO_Tree::erase(), Parma_Polyhedra_Library::Octagonal_Shape< T >::extract_octagonal_difference(), Parma_Polyhedra_Library::Linear_System< Row >::gauss(), Parma_Polyhedra_Library::Polyhedron::generators(), Parma_Polyhedra_Library::DB_Matrix< T >::grow(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::has_a_free_dimension_helper(), Parma_Polyhedra_Library::Congruence_System::insert(), Parma_Polyhedra_Library::Linear_System< Row >::insert_pending_no_ok(), Parma_Polyhedra_Library::CO_Tree::insert_precise(), Parma_Polyhedra_Library::Congruence_System::insert_verbatim(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::intersection_preserving_enlarge_element(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::is_universe(), Parma_Polyhedra_Library::Bit_Row::iter_swap(), Parma_Polyhedra_Library::DB_Row< T >::iter_swap(), Parma_Polyhedra_Library::Linear_Expression::Linear_Expression(), Parma_Polyhedra_Library::Swapping_Vector< T >::m_swap(), Parma_Polyhedra_Library::Bit_Matrix::m_swap(), Parma_Polyhedra_Library::Matrix< Row >::m_swap(), Parma_Polyhedra_Library::Dense_Row::m_swap(), Parma_Polyhedra_Library::Linear_System< Row >::m_swap(), Parma_Polyhedra_Library::Interval< Boundary, Info >::m_swap(), Parma_Polyhedra_Library::Sparse_Row::m_swap(), Parma_Polyhedra_Library::Constant_Floating_Point_Expression< FP_Interval_Type, FP_Format >::m_swap(), Parma_Polyhedra_Library::Cast_Floating_Point_Expression< FP_Interval_Type, FP_Format >::m_swap(), Parma_Polyhedra_Library::Variable_Floating_Point_Expression< FP_Interval_Type, FP_Format >::m_swap(), Parma_Polyhedra_Library::Opposite_Floating_Point_Expression< FP_Interval_Type, FP_Format >::m_swap(), Parma_Polyhedra_Library::DB_Matrix< T >::m_swap(), Parma_Polyhedra_Library::Sum_Floating_Point_Expression< FP_Interval_Type, FP_Format >::m_swap(), Parma_Polyhedra_Library::Difference_Floating_Point_Expression< FP_Interval_Type, FP_Format >::m_swap(), Parma_Polyhedra_Library::DB_Row< T >::m_swap(), Parma_Polyhedra_Library::Determinate< PSET >::m_swap(), Parma_Polyhedra_Library::Division_Floating_Point_Expression< FP_Interval_Type, FP_Format >::m_swap(), Parma_Polyhedra_Library::Multiplication_Floating_Point_Expression< FP_Interval_Type, FP_Format >::m_swap(), Parma_Polyhedra_Library::Interval_Info_Bitset< T, Policy >::m_swap(), Parma_Polyhedra_Library::PIP_Tree_Node::Artificial_Parameter::m_swap(), Parma_Polyhedra_Library::Ask_Tell< D >::m_swap(), Parma_Polyhedra_Library::Linear_Form< C >::m_swap(), Parma_Polyhedra_Library::Congruence::m_swap(), Parma_Polyhedra_Library::Pointset_Ask_Tell< PSET >::m_swap(), Parma_Polyhedra_Library::Powerset< D >::m_swap(), Parma_Polyhedra_Library::Congruence_System::m_swap(), Parma_Polyhedra_Library::OR_Matrix< T >::m_swap(), Parma_Polyhedra_Library::Linear_Expression::const_iterator::m_swap(), Parma_Polyhedra_Library::MIP_Problem::m_swap(), Parma_Polyhedra_Library::Box< ITV >::m_swap(), Parma_Polyhedra_Library::Constraint::m_swap(), Parma_Polyhedra_Library::Grid_Generator::m_swap(), Parma_Polyhedra_Library::Generator::m_swap(), Parma_Polyhedra_Library::BD_Shape< T >::m_swap(), Parma_Polyhedra_Library::Octagonal_Shape< T >::m_swap(), Parma_Polyhedra_Library::Linear_Expression::m_swap(), Parma_Polyhedra_Library::PIP_Problem::m_swap(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::m_swap(), Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::m_swap(), Parma_Polyhedra_Library::Grid::m_swap(), Parma_Polyhedra_Library::Polyhedron::m_swap(), Parma_Polyhedra_Library::Box< ITV >::map_space_dimensions(), Parma_Polyhedra_Library::Octagonal_Shape< T >::map_space_dimensions(), Parma_Polyhedra_Library::BD_Shape< T >::map_space_dimensions(), Parma_Polyhedra_Library::Linear_System< Row >::merge_rows_assign(), Parma_Polyhedra_Library::BD_Shape< T >::one_variable_affine_form_image(), Parma_Polyhedra_Library::Implementation::Indirect_Swapper< RA_Container >::operator()(), Parma_Polyhedra_Library::Implementation::Indirect_Swapper2< RA_Container1, RA_Container2 >::operator()(), Parma_Polyhedra_Library::Pointset_Ask_Tell< PSET >::operator=(), Parma_Polyhedra_Library::Linear_System< Row >::operator=(), Parma_Polyhedra_Library::Sparse_Row::operator=(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::operator=(), Parma_Polyhedra_Library::Linear_Expression::const_iterator::operator=(), Parma_Polyhedra_Library::Constraint::operator==(), Parma_Polyhedra_Library::Powerset< D >::pairwise_apply_assign(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::pairwise_reduce(), Parma_Polyhedra_Library::Matrix< Row >::permute_columns(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::permute_space_dimensions(), Parma_Polyhedra_Library::Polyhedron::Polyhedron(), Parma_Polyhedra_Library::Polyhedron::positive_time_elapse_assign_impl(), Parma_Polyhedra_Library::Smash_Reduction< D1, D2 >::product_reduce(), Parma_Polyhedra_Library::Constraints_Reduction< D1, D2 >::product_reduce(), Parma_Polyhedra_Library::MIP_Problem::RAII_Temporary_Real_Relaxation::RAII_Temporary_Real_Relaxation(), Parma_Polyhedra_Library::Grid::remove_higher_space_dimensions(), Parma_Polyhedra_Library::Linear_System< Row >::remove_row_no_ok(), Parma_Polyhedra_Library::Linear_System< Row >::remove_rows(), Parma_Polyhedra_Library::Congruence_System::remove_rows(), Parma_Polyhedra_Library::Box< ITV >::remove_space_dimensions(), Parma_Polyhedra_Library::BD_Shape< T >::remove_space_dimensions(), Parma_Polyhedra_Library::Swapping_Vector< T >::reserve(), Parma_Polyhedra_Library::Bit_Matrix::resize(), Parma_Polyhedra_Library::DB_Matrix< T >::resize_no_copy(), Parma_Polyhedra_Library::MIP_Problem::second_phase(), Parma_Polyhedra_Library::Polyhedron::select_H79_constraints(), Parma_Polyhedra_Library::Grid::set_empty(), Parma_Polyhedra_Library::Linear_Expression::set_representation(), Parma_Polyhedra_Library::BD_Shape< T >::shortest_path_reduction_assign(), shrink_to_congruence_no_check(), Parma_Polyhedra_Library::Linear_System< Row >::simplify(), Parma_Polyhedra_Library::Grid::simplify(), Parma_Polyhedra_Library::Polyhedron::simplify(), Parma_Polyhedra_Library::Polyhedron::simplify_using_context_assign(), Parma_Polyhedra_Library::PIP_Solution_Node::solve(), Parma_Polyhedra_Library::PIP_Decision_Node::solve(), Parma_Polyhedra_Library::Linear_System< Row >::sort_and_remove_with_sat(), Parma_Polyhedra_Library::Linear_System< Row >::sort_pending_and_remove_duplicates(), Parma_Polyhedra_Library::MIP_Problem::steepest_edge_exact_entering_index(), Parma_Polyhedra_Library::Polyhedron::strongly_minimize_constraints(), Parma_Polyhedra_Library::Polyhedron::strongly_minimize_generators(), Parma_Polyhedra_Library::Checked_Number< T, Policy >::swap(), swap(), Parma_Polyhedra_Library::Dense_Row::swap_coefficients(), Parma_Polyhedra_Library::Sparse_Row::swap_coefficients(), Parma_Polyhedra_Library::Linear_System< Row >::swap_row_intervals(), Parma_Polyhedra_Library::Polyhedron::time_elapse_assign(), Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::upper_bound_assign_if_exact(), and Parma_Polyhedra_Library::MIP_Problem::RAII_Temporary_Real_Relaxation::~RAII_Temporary_Real_Relaxation().
|
related |
Definition at line 878 of file CO_Tree_inlines.hh.
References Parma_Polyhedra_Library::CO_Tree::const_iterator::m_swap().
|
related |
Definition at line 883 of file CO_Tree_inlines.hh.
References Parma_Polyhedra_Library::CO_Tree::iterator::m_swap().
Referenced by Parma_Polyhedra_Library::CO_Tree::const_iterator::m_swap(), Parma_Polyhedra_Library::CO_Tree::iterator::m_swap(), and Parma_Polyhedra_Library::CO_Tree::m_swap().
| void Parma_Polyhedra_Library::throw_result_exception | ( | Result | r | ) |
Definition at line 30 of file Checked_Number.cc.
References V_CVT_STR_UNK, V_DIV_ZERO, V_EMPTY, V_EQ, V_EQ_MINUS_INFINITY, V_EQ_PLUS_INFINITY, V_GE, V_GT, V_GT_MINUS_INFINITY, V_GT_SUP, V_INF_ADD_INF, V_INF_DIV_INF, V_INF_MOD, V_INF_MUL_ZERO, V_INF_SUB_INF, V_LE, V_LGE, V_LT, V_LT_INF, V_LT_PLUS_INFINITY, V_MOD_ZERO, V_NAN, V_NE, V_SQRT_NEG, V_UNKNOWN_NEG_OVERFLOW, V_UNKNOWN_POS_OVERFLOW, and V_UNREPRESENTABLE.
Referenced by Parma_Polyhedra_Library::Extended_Number_Policy::handle_result(), Parma_Polyhedra_Library::WRD_Extended_Number_Policy::handle_result(), and Parma_Polyhedra_Library::Debug_WRD_Extended_Number_Policy::handle_result().
|
inline |
For native types, returns the total size in bytes of the memory occupied by the type of the (unused) parameter, i.e., 0.
Definition at line 113 of file globals_inlines.hh.
Referenced by Parma_Polyhedra_Library::Checked_Number< T, Policy >::total_memory_in_bytes().
|
inline |
Returns the total size in bytes of the memory occupied by x.
Definition at line 124 of file globals_inlines.hh.
References external_memory_in_bytes().
|
inline |
Returns the total size in bytes of the memory occupied by x.
Definition at line 135 of file globals_inlines.hh.
References external_memory_in_bytes().
|
related |
Definition at line 153 of file Float_templates.hh.
Referenced by Parma_Polyhedra_Library::Polyhedron::BFT00_poly_hull_assign_if_exact(), Parma_Polyhedra_Library::BD_Shape< T >::BFT00_upper_bound_assign_if_exact(), Parma_Polyhedra_Library::BD_Shape< T >::BHZ09_upper_bound_assign_if_exact(), Parma_Polyhedra_Library::Grid::fold_space_dimensions(), Parma_Polyhedra_Library::Octagonal_Shape< T >::integer_upper_bound_assign_if_exact(), Parma_Polyhedra_Library::Octagonal_Shape< T >::upper_bound_assign_if_exact(), and Parma_Polyhedra_Library::Grid::upper_bound_assign_if_exact().
| const char * Parma_Polyhedra_Library::version | ( | ) |
Returns a character string containing the PPL version.
Definition at line 101 of file version.cc.
| unsigned Parma_Polyhedra_Library::version_beta | ( | ) |
Returns the beta number of the PPL version.
Definition at line 96 of file version.cc.
References PPL_VERSION_BETA.
| unsigned Parma_Polyhedra_Library::version_major | ( | ) |
Returns the major number of the PPL version.
Definition at line 81 of file version.cc.
References PPL_VERSION_MAJOR.
| unsigned Parma_Polyhedra_Library::version_minor | ( | ) |
Returns the minor number of the PPL version.
Definition at line 86 of file version.cc.
References PPL_VERSION_MINOR.
| unsigned Parma_Polyhedra_Library::version_revision | ( | ) |
Returns the revision number of the PPL version.
Definition at line 91 of file version.cc.
References PPL_VERSION_REVISION.
Variable Documentation
|
inline |
Definition at line 270 of file OR_Matrix_inlines.hh.
| Minus_Infinity Parma_Polyhedra_Library::MINUS_INFINITY |
Definition at line 30 of file checked.cc.
Referenced by Parma_Polyhedra_Library::Interval< Boundary, Info >::add_assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::div_assign(), minus_infinity(), Parma_Polyhedra_Library::Interval< Boundary, Info >::mul_assign(), Parma_Polyhedra_Library::Boundary_NS::set_boundary_infinity(), Parma_Polyhedra_Library::Boundary_NS::set_minus_infinity(), Parma_Polyhedra_Library::Boundary_NS::set_unbounded(), and Parma_Polyhedra_Library::Interval< Boundary, Info >::sub_assign().
| Not_A_Number Parma_Polyhedra_Library::NOT_A_NUMBER |
Definition at line 32 of file checked.cc.
Referenced by not_a_number().
| Plus_Infinity Parma_Polyhedra_Library::PLUS_INFINITY |
Definition at line 31 of file checked.cc.
Referenced by Parma_Polyhedra_Library::Interval< Boundary, Info >::add_assign(), Parma_Polyhedra_Library::BD_Shape< T >::BD_Shape(), Parma_Polyhedra_Library::Octagonal_Shape< T >::BHMZ05_widening_assign(), Parma_Polyhedra_Library::BD_Shape< T >::BHMZ05_widening_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::CC76_extrapolation_assign(), Parma_Polyhedra_Library::BD_Shape< T >::CC76_extrapolation_assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::div_assign(), Parma_Polyhedra_Library::BD_Shape< T >::euclidean_distance_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::euclidean_distance_assign(), Parma_Polyhedra_Library::DB_Row_Impl_Handler< T >::Impl::expand_within_capacity(), Parma_Polyhedra_Library::BD_Shape< T >::forget_all_dbm_constraints(), Parma_Polyhedra_Library::Octagonal_Shape< T >::forget_all_octagonal_constraints(), Parma_Polyhedra_Library::BD_Shape< T >::forget_binary_dbm_constraints(), Parma_Polyhedra_Library::Octagonal_Shape< T >::forget_binary_octagonal_constraints(), Parma_Polyhedra_Library::Octagonal_Shape< T >::generalized_affine_image(), Parma_Polyhedra_Library::BD_Shape< T >::generalized_affine_image(), Parma_Polyhedra_Library::BD_Shape< T >::incremental_shortest_path_closure_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::incremental_strong_closure_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::is_strongly_reduced(), Parma_Polyhedra_Library::BD_Shape< T >::l_infinity_distance_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::l_infinity_distance_assign(), Parma_Polyhedra_Library::DB_Matrix< T >::l_m_distance_assign(), Parma_Polyhedra_Library::OR_Matrix< T >::l_m_distance_assign(), Parma_Polyhedra_Library::Box< ITV >::l_m_distance_assign(), Parma_Polyhedra_Library::Interval< Boundary, Info >::mul_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::Octagonal_Shape(), plus_infinity(), Parma_Polyhedra_Library::BD_Shape< T >::rectilinear_distance_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::rectilinear_distance_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::refine_with_linear_form_inequality(), Parma_Polyhedra_Library::Boundary_NS::set_boundary_infinity(), Parma_Polyhedra_Library::Boundary_NS::set_plus_infinity(), Parma_Polyhedra_Library::Boundary_NS::set_unbounded(), Parma_Polyhedra_Library::BD_Shape< T >::shortest_path_closure_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::strong_closure_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::strong_reduction_assign(), and Parma_Polyhedra_Library::Interval< Boundary, Info >::sub_assign().
