A not necessarily closed, iso-oriented hyperrectangle. More...
#include <Box_defs.hh>
Classes | |
| class | Status |
Public Types | |
| typedef ITV | interval_type |
| The type of intervals used to implement the box. More... | |
Public Member Functions | |
| const ITV & | get_interval (Variable var) const |
Returns a reference the interval that bounds var. More... | |
| void | set_interval (Variable var, const ITV &i) |
Sets to i the interval that bounds var. More... | |
| bool | has_lower_bound (Variable var, Coefficient &n, Coefficient &d, bool &closed) const |
If the space dimension of var is unbounded below, return false. Otherwise return true and set n, d and closed accordingly. More... | |
| bool | has_upper_bound (Variable var, Coefficient &n, Coefficient &d, bool &closed) const |
If the space dimension of var is unbounded above, return false. Otherwise return true and set n, d and closed accordingly. More... | |
| Constraint_System | constraints () const |
Returns a system of constraints defining *this. More... | |
| Constraint_System | minimized_constraints () const |
Returns a minimized system of constraints defining *this. More... | |
| Congruence_System | congruences () const |
Returns a system of congruences approximating *this. More... | |
| Congruence_System | minimized_congruences () const |
Returns a minimized system of congruences approximating *this. More... | |
| memory_size_type | total_memory_in_bytes () const |
Returns the total size in bytes of the memory occupied by *this. More... | |
| memory_size_type | external_memory_in_bytes () const |
Returns the size in bytes of the memory managed by *this. More... | |
| int32_t | hash_code () const |
Returns a 32-bit hash code for *this. More... | |
| void | ascii_dump () const |
Writes to std::cerr an ASCII representation of *this. More... | |
| void | ascii_dump (std::ostream &s) const |
Writes to s an ASCII representation of *this. More... | |
| void | print () const |
Prints *this to std::cerr using operator<<. More... | |
| bool | ascii_load (std::istream &s) |
Loads from s an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets *this accordingly. Returns true if successful, false otherwise. More... | |
| void | set_empty () |
| Causes the box to become empty, i.e., to represent the empty set. More... | |
| template<typename T , typename Iterator > | |
| Enable_If< Is_Same< T, Box< ITV > >::value &&Is_Same_Or_Derived< Interval_Base, ITV >::value, void >::type | CC76_widening_assign (const T &y, Iterator first, Iterator last) |
| template<typename T > | |
| Enable_If< Is_Same< T, Box< ITV > >::value &&Is_Same_Or_Derived< Interval_Base, ITV >::value, void >::type | CC76_widening_assign (const T &y, unsigned *tp) |
| template<typename T > | |
| Enable_If< Is_Same< T, Box< ITV > >::value &&Is_Same_Or_Derived< Interval_Base, ITV >::value, void >::type | CC76_narrowing_assign (const T &y) |
Constructors, Assignment, Swap and Destructor | |
| Box (dimension_type num_dimensions=0, Degenerate_Element kind=UNIVERSE) | |
| Builds a universe or empty box of the specified space dimension. More... | |
| Box (const Box &y, Complexity_Class complexity=ANY_COMPLEXITY) | |
| Ordinary copy constructor. More... | |
| template<typename Other_ITV > | |
| Box (const Box< Other_ITV > &y, Complexity_Class complexity=ANY_COMPLEXITY) | |
Builds a conservative, upward approximation of y. More... | |
| Box (const Constraint_System &cs) | |
Builds a box from the system of constraints cs. More... | |
| Box (const Constraint_System &cs, Recycle_Input dummy) | |
Builds a box recycling a system of constraints cs. More... | |
| Box (const Generator_System &gs) | |
Builds a box from the system of generators gs. More... | |
| Box (const Generator_System &gs, Recycle_Input dummy) | |
Builds a box recycling the system of generators gs. More... | |
| Box (const Congruence_System &cgs) | |
| Box (const Congruence_System &cgs, Recycle_Input dummy) | |
| template<typename T > | |
| Box (const BD_Shape< T > &bds, Complexity_Class complexity=POLYNOMIAL_COMPLEXITY) | |
Builds a box containing the BDS bds. More... | |
| template<typename T > | |
| Box (const Octagonal_Shape< T > &oct, Complexity_Class complexity=POLYNOMIAL_COMPLEXITY) | |
Builds a box containing the octagonal shape oct. More... | |
| Box (const Polyhedron &ph, Complexity_Class complexity=ANY_COMPLEXITY) | |
Builds a box containing the polyhedron ph. More... | |
| Box (const Grid &gr, Complexity_Class complexity=POLYNOMIAL_COMPLEXITY) | |
Builds a box containing the grid gr. More... | |
| template<typename D1 , typename D2 , typename R > | |
| Box (const Partially_Reduced_Product< D1, D2, R > &dp, Complexity_Class complexity=ANY_COMPLEXITY) | |
Builds a box containing the partially reduced product dp. More... | |
| Box & | operator= (const Box &y) |
The assignment operator (*this and y can be dimension-incompatible). More... | |
| void | m_swap (Box &y) |
Swaps *this with y (*this and y can be dimension-incompatible). More... | |
Member Functions that Do Not Modify the Box | |
| dimension_type | space_dimension () const |
Returns the dimension of the vector space enclosing *this. More... | |
| dimension_type | affine_dimension () const |
Returns  , if , if *this is empty; otherwise, returns the affine dimension of *this. More... | |
| bool | is_empty () const |
Returns true if and only if *this is an empty box. More... | |
| bool | is_universe () const |
Returns true if and only if *this is a universe box. More... | |
| bool | is_topologically_closed () const |
Returns true if and only if *this is a topologically closed subset of the vector space. More... | |
| bool | is_discrete () const |
Returns true if and only if *this is discrete. More... | |
| bool | is_bounded () const |
Returns true if and only if *this is a bounded box. More... | |
| bool | contains_integer_point () const |
Returns true if and only if *this contains at least one integer point. More... | |
| bool | constrains (Variable var) const |
Returns true if and only if var is constrained in *this. More... | |
| Poly_Con_Relation | relation_with (const Constraint &c) const |
Returns the relations holding between *this and the constraint c. More... | |
| Poly_Con_Relation | relation_with (const Congruence &cg) const |
Returns the relations holding between *this and the congruence cg. More... | |
| Poly_Gen_Relation | relation_with (const Generator &g) const |
Returns the relations holding between *this and the generator g. More... | |
| bool | bounds_from_above (const Linear_Expression &expr) const |
Returns true if and only if expr is bounded from above in *this. More... | |
| bool | bounds_from_below (const Linear_Expression &expr) const |
Returns true if and only if expr is bounded from below in *this. More... | |
| bool | maximize (const Linear_Expression &expr, Coefficient &sup_n, Coefficient &sup_d, bool &maximum) const |
Returns true if and only if *this is not empty and expr is bounded from above in *this, in which case the supremum value is computed. More... | |
| bool | maximize (const Linear_Expression &expr, Coefficient &sup_n, Coefficient &sup_d, bool &maximum, Generator &g) const |
Returns true if and only if *this is not empty and expr is bounded from above in *this, in which case the supremum value and a point where expr reaches it are computed. More... | |
| bool | minimize (const Linear_Expression &expr, Coefficient &inf_n, Coefficient &inf_d, bool &minimum) const |
Returns true if and only if *this is not empty and expr is bounded from below in *this, in which case the infimum value is computed. More... | |
| bool | minimize (const Linear_Expression &expr, Coefficient &inf_n, Coefficient &inf_d, bool &minimum, Generator &g) const |
Returns true if and only if *this is not empty and expr is bounded from below in *this, in which case the infimum value and a point where expr reaches it are computed. More... | |
| bool | frequency (const Linear_Expression &expr, Coefficient &freq_n, Coefficient &freq_d, Coefficient &val_n, Coefficient &val_d) const |
Returns true if and only if there exist a unique value val such that *this saturates the equality expr = val. More... | |
| bool | contains (const Box &y) const |
Returns true if and only if *this contains y. More... | |
| bool | strictly_contains (const Box &y) const |
Returns true if and only if *this strictly contains y. More... | |
| bool | is_disjoint_from (const Box &y) const |
Returns true if and only if *this and y are disjoint. More... | |
| bool | OK () const |
Returns true if and only if *this satisfies all its invariants. More... | |
Space-Dimension Preserving Member Functions that May Modify the Box | |
| void | add_constraint (const Constraint &c) |
Adds a copy of constraint c to the system of constraints defining *this. More... | |
| void | add_constraints (const Constraint_System &cs) |
Adds the constraints in cs to the system of constraints defining *this. More... | |
| void | add_recycled_constraints (Constraint_System &cs) |
Adds the constraints in cs to the system of constraints defining *this. More... | |
| void | add_congruence (const Congruence &cg) |
Adds to *this a constraint equivalent to the congruence cg. More... | |
| void | add_congruences (const Congruence_System &cgs) |
Adds to *this constraints equivalent to the congruences in cgs. More... | |
| void | add_recycled_congruences (Congruence_System &cgs) |
Adds to *this constraints equivalent to the congruences in cgs. More... | |
| void | refine_with_constraint (const Constraint &c) |
Use the constraint c to refine *this. More... | |
| void | refine_with_constraints (const Constraint_System &cs) |
Use the constraints in cs to refine *this. More... | |
| void | refine_with_congruence (const Congruence &cg) |
Use the congruence cg to refine *this. More... | |
| void | refine_with_congruences (const Congruence_System &cgs) |
Use the congruences in cgs to refine *this. More... | |
| void | propagate_constraint (const Constraint &c) |
Use the constraint c for constraint propagation on *this. More... | |
| void | propagate_constraints (const Constraint_System &cs, dimension_type max_iterations=0) |
Use the constraints in cs for constraint propagation on *this. More... | |
| void | unconstrain (Variable var) |
Computes the cylindrification of *this with respect to space dimension var, assigning the result to *this. More... | |
| void | unconstrain (const Variables_Set &vars) |
Computes the cylindrification of *this with respect to the set of space dimensions vars, assigning the result to *this. More... | |
| void | intersection_assign (const Box &y) |
Assigns to *this the intersection of *this and y. More... | |
| void | upper_bound_assign (const Box &y) |
Assigns to *this the smallest box containing the union of *this and y. More... | |
| bool | upper_bound_assign_if_exact (const Box &y) |
If the upper bound of *this and y is exact, it is assigned to *this and true is returned, otherwise false is returned. More... | |
| void | difference_assign (const Box &y) |
Assigns to *this the difference of *this and y. More... | |
| bool | simplify_using_context_assign (const Box &y) |
Assigns to *this a meet-preserving simplification of *this with respect to y. If false is returned, then the intersection is empty. More... | |
| void | affine_image (Variable var, const Linear_Expression &expr, Coefficient_traits::const_reference denominator=Coefficient_one()) |
Assigns to *this the affine image of *this under the function mapping variable var to the affine expression specified by expr and denominator. More... | |
| void | affine_form_image (Variable var, const Linear_Form< ITV > &lf) |
Assigns to *this the affine form image of *this under the function mapping variable var into the affine expression(s) specified by lf. More... | |
| void | affine_preimage (Variable var, const Linear_Expression &expr, Coefficient_traits::const_reference denominator=Coefficient_one()) |
Assigns to *this the affine preimage of *this under the function mapping variable var to the affine expression specified by expr and denominator. More... | |
| void | generalized_affine_image (Variable var, Relation_Symbol relsym, const Linear_Expression &expr, Coefficient_traits::const_reference denominator=Coefficient_one()) |
Assigns to *this the image of *this with respect to the generalized affine relation  , where , where  is the relation symbol encoded by is the relation symbol encoded by relsym. More... | |
| void | generalized_affine_preimage (Variable var, Relation_Symbol relsym, const Linear_Expression &expr, Coefficient_traits::const_reference denominator=Coefficient_one()) |
Assigns to *this the preimage of *this with respect to the generalized affine relation  , where , where  is the relation symbol encoded by is the relation symbol encoded by relsym. More... | |
| void | generalized_affine_image (const Linear_Expression &lhs, Relation_Symbol relsym, const Linear_Expression &rhs) |
Assigns to *this the image of *this with respect to the generalized affine relation  , where , where  is the relation symbol encoded by is the relation symbol encoded by relsym. More... | |
| void | generalized_affine_preimage (const Linear_Expression &lhs, Relation_Symbol relsym, const Linear_Expression &rhs) |
Assigns to *this the preimage of *this with respect to the generalized affine relation  , where , where  is the relation symbol encoded by is the relation symbol encoded by relsym. More... | |
| void | bounded_affine_image (Variable var, const Linear_Expression &lb_expr, const Linear_Expression &ub_expr, Coefficient_traits::const_reference denominator=Coefficient_one()) |
Assigns to *this the image of *this with respect to the bounded affine relation  . More... . More... | |
| void | bounded_affine_preimage (Variable var, const Linear_Expression &lb_expr, const Linear_Expression &ub_expr, Coefficient_traits::const_reference denominator=Coefficient_one()) |
Assigns to *this the preimage of *this with respect to the bounded affine relation  . More... . More... | |
| void | time_elapse_assign (const Box &y) |
Assigns to *this the result of computing the time-elapse between *this and y. More... | |
| void | topological_closure_assign () |
Assigns to *this its topological closure. More... | |
| void | wrap_assign (const Variables_Set &vars, Bounded_Integer_Type_Width w, Bounded_Integer_Type_Representation r, Bounded_Integer_Type_Overflow o, const Constraint_System *cs_p=0, unsigned complexity_threshold=16, bool wrap_individually=true) |
| Wraps the specified dimensions of the vector space. More... | |
| void | drop_some_non_integer_points (Complexity_Class complexity=ANY_COMPLEXITY) |
Possibly tightens *this by dropping some points with non-integer coordinates. More... | |
| void | drop_some_non_integer_points (const Variables_Set &vars, Complexity_Class complexity=ANY_COMPLEXITY) |
Possibly tightens *this by dropping some points with non-integer coordinates for the space dimensions corresponding to vars. More... | |
| template<typename T > | |
| Enable_If< Is_Same< T, Box >::value &&Is_Same_Or_Derived< Interval_Base, ITV >::value, void >::type | CC76_widening_assign (const T &y, unsigned *tp=0) |
Assigns to *this the result of computing the CC76-widening between *this and y. More... | |
| template<typename T , typename Iterator > | |
| Enable_If< Is_Same< T, Box >::value &&Is_Same_Or_Derived< Interval_Base, ITV >::value, void >::type | CC76_widening_assign (const T &y, Iterator first, Iterator last) |
Assigns to *this the result of computing the CC76-widening between *this and y. More... | |
| void | widening_assign (const Box &y, unsigned *tp=0) |
| Same as CC76_widening_assign(y, tp). More... | |
| void | limited_CC76_extrapolation_assign (const Box &y, const Constraint_System &cs, unsigned *tp=0) |
Improves the result of the CC76-extrapolation computation by also enforcing those constraints in cs that are satisfied by all the points of *this. More... | |
| template<typename T > | |
| Enable_If< Is_Same< T, Box >::value &&Is_Same_Or_Derived< Interval_Base, ITV >::value, void >::type | CC76_narrowing_assign (const T &y) |
Assigns to *this the result of restoring in y the constraints of *this that were lost by CC76-extrapolation applications. More... | |
Member Functions that May Modify the Dimension of the Vector Space | |
| void | add_space_dimensions_and_embed (dimension_type m) |
Adds m new dimensions and embeds the old box into the new space. More... | |
| void | add_space_dimensions_and_project (dimension_type m) |
Adds m new dimensions to the box and does not embed it in the new vector space. More... | |
| void | concatenate_assign (const Box &y) |
Seeing a box as a set of tuples (its points), assigns to *this all the tuples that can be obtained by concatenating, in the order given, a tuple of *this with a tuple of y. More... | |
| void | remove_space_dimensions (const Variables_Set &vars) |
| Removes all the specified dimensions. More... | |
| void | remove_higher_space_dimensions (dimension_type new_dimension) |
Removes the higher dimensions so that the resulting space will have dimension new_dimension. More... | |
| template<typename Partial_Function > | |
| void | map_space_dimensions (const Partial_Function &pfunc) |
| Remaps the dimensions of the vector space according to a partial function. More... | |
| void | expand_space_dimension (Variable var, dimension_type m) |
Creates m copies of the space dimension corresponding to var. More... | |
| void | fold_space_dimensions (const Variables_Set &vars, Variable dest) |
Folds the space dimensions in vars into dest. More... | |
Static Public Member Functions | |
| static dimension_type | max_space_dimension () |
| Returns the maximum space dimension that a Box can handle. More... | |
| static bool | can_recycle_constraint_systems () |
| Returns false indicating that this domain does not recycle constraints. More... | |
| static bool | can_recycle_congruence_systems () |
| Returns false indicating that this domain does not recycle congruences. More... | |
Private Types | |
| typedef std::vector< ITV > | Sequence |
| The type of sequence used to implement the box. More... | |
| typedef ITV | Tmp_Interval_Type |
| The type of intervals used by inner computations when trying to limit the cumulative effect of approximation errors. More... | |
Private Member Functions | |
| bool | marked_empty () const |
Returns true if and only if the box is known to be empty. More... | |
| void | set_nonempty () |
Marks *this as definitely not empty. More... | |
| void | set_empty_up_to_date () |
Asserts the validity of the empty flag of *this. More... | |
| void | reset_empty_up_to_date () |
Invalidates empty flag of *this. More... | |
| bool | check_empty () const |
Checks the hard way whether *this is an empty box: returns true if and only if it is so. More... | |
| const ITV & | operator[] (dimension_type k) const |
Returns a reference the interval that bounds the box on the k-th space dimension. More... | |
| void | add_interval_constraint_no_check (dimension_type var_id, Constraint::Type type, Coefficient_traits::const_reference numer, Coefficient_traits::const_reference denom) |
| WRITE ME. More... | |
| void | add_constraint_no_check (const Constraint &c) |
| WRITE ME. More... | |
| void | add_constraints_no_check (const Constraint_System &cs) |
| WRITE ME. More... | |
| void | add_congruence_no_check (const Congruence &cg) |
| WRITE ME. More... | |
| void | add_congruences_no_check (const Congruence_System &cgs) |
| WRITE ME. More... | |
| void | refine_no_check (const Constraint &c) |
Uses the constraint c to refine *this. More... | |
| void | refine_no_check (const Constraint_System &cs) |
Uses the constraints in cs to refine *this. More... | |
| void | refine_no_check (const Congruence &cg) |
Uses the congruence cg to refine *this. More... | |
| void | refine_no_check (const Congruence_System &cgs) |
Uses the congruences in cgs to refine *this. More... | |
| void | propagate_constraint_no_check (const Constraint &c) |
Propagates the constraint c to refine *this. More... | |
| void | propagate_constraints_no_check (const Constraint_System &cs, dimension_type max_iterations) |
Propagates the constraints in cs to refine *this. More... | |
| bool | bounds (const Linear_Expression &expr, bool from_above) const |
Checks if and how expr is bounded in *this. More... | |
| bool | max_min (const Linear_Expression &expr, bool maximize, Coefficient &ext_n, Coefficient &ext_d, bool &included, Generator &g) const |
Maximizes or minimizes expr subject to *this. More... | |
| bool | max_min (const Linear_Expression &expr, bool maximize, Coefficient &ext_n, Coefficient &ext_d, bool &included) const |
Maximizes or minimizes expr subject to *this. More... | |
| void | get_limiting_box (const Constraint_System &cs, Box &limiting_box) const |
Adds to limiting_box the interval constraints in cs that are satisfied by *this. More... | |
Static Private Member Functions | |
| static I_Result | refine_interval_no_check (ITV &itv, Constraint::Type type, Coefficient_traits::const_reference numer, Coefficient_traits::const_reference denom) |
| WRITE ME. More... | |
Private Attributes | |
| Sequence | seq |
| A sequence of intervals, one for each dimension of the vector space. More... | |
| Status | status |
| The status flags to keep track of the internal state. More... | |
Friends | |
| template<typename Other_ITV > | |
| class | Parma_Polyhedra_Library::Box |
| bool | operator== (const Box< ITV > &x, const Box< ITV > &y) |
| std::ostream & | Parma_Polyhedra_Library::IO_Operators::operator<< (std::ostream &s, const Box< ITV > &box) |
| template<typename Specialization , typename Temp , typename To , typename I > | |
| bool | Parma_Polyhedra_Library::l_m_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Box< I > &x, const Box< I > &y, const Rounding_Dir dir, Temp &tmp0, Temp &tmp1, Temp &tmp2) |
Related Functions | |
(Note that these are not member functions.) | |
| template<typename ITV > | |
| void | swap (Box< ITV > &x, Box< ITV > &y) |
Swaps x with y. More... | |
| template<typename ITV > | |
| bool | operator== (const Box< ITV > &x, const Box< ITV > &y) |
Returns true if and only if x and y are the same box. More... | |
| template<typename ITV > | |
| bool | operator!= (const Box< ITV > &x, const Box< ITV > &y) |
Returns true if and only if x and y are not the same box. More... | |
| template<typename ITV > | |
| std::ostream & | operator<< (std::ostream &s, const Box< ITV > &box) |
| Output operator. More... | |
| template<typename To , typename ITV > | |
| bool | rectilinear_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Box< ITV > &x, const Box< ITV > &y, Rounding_Dir dir) |
Computes the rectilinear (or Manhattan) distance between x and y. More... | |
| template<typename Temp , typename To , typename ITV > | |
| bool | rectilinear_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Box< ITV > &x, const Box< ITV > &y, Rounding_Dir dir) |
Computes the rectilinear (or Manhattan) distance between x and y. More... | |
| template<typename Temp , typename To , typename ITV > | |
| bool | rectilinear_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Box< ITV > &x, const Box< ITV > &y, Rounding_Dir dir, Temp &tmp0, Temp &tmp1, Temp &tmp2) |
Computes the rectilinear (or Manhattan) distance between x and y. More... | |
| template<typename To , typename ITV > | |
| bool | euclidean_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Box< ITV > &x, const Box< ITV > &y, Rounding_Dir dir) |
Computes the euclidean distance between x and y. More... | |
| template<typename Temp , typename To , typename ITV > | |
| bool | euclidean_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Box< ITV > &x, const Box< ITV > &y, Rounding_Dir dir) |
Computes the euclidean distance between x and y. More... | |
| template<typename Temp , typename To , typename ITV > | |
| bool | euclidean_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Box< ITV > &x, const Box< ITV > &y, Rounding_Dir dir, Temp &tmp0, Temp &tmp1, Temp &tmp2) |
Computes the euclidean distance between x and y. More... | |
| template<typename To , typename ITV > | |
| bool | l_infinity_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Box< ITV > &x, const Box< ITV > &y, Rounding_Dir dir) |
Computes the  distance between distance between x and y. More... | |
| template<typename Temp , typename To , typename ITV > | |
| bool | l_infinity_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Box< ITV > &x, const Box< ITV > &y, Rounding_Dir dir) |
Computes the  distance between distance between x and y. More... | |
| template<typename Temp , typename To , typename ITV > | |
| bool | l_infinity_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Box< ITV > &x, const Box< ITV > &y, Rounding_Dir dir, Temp &tmp0, Temp &tmp1, Temp &tmp2) |
Computes the  distance between distance between x and y. More... | |
| template<typename Specialization , typename Temp , typename To , typename ITV > | |
| bool | l_m_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Box< ITV > &x, const Box< ITV > &y, Rounding_Dir dir, Temp &tmp0, Temp &tmp1, Temp &tmp2) |
| template<typename Temp , typename To , typename ITV > | |
| bool | rectilinear_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Box< ITV > &x, const Box< ITV > &y, const Rounding_Dir dir, Temp &tmp0, Temp &tmp1, Temp &tmp2) |
| template<typename Temp , typename To , typename ITV > | |
| bool | rectilinear_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Box< ITV > &x, const Box< ITV > &y, const Rounding_Dir dir) |
| template<typename To , typename ITV > | |
| bool | rectilinear_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Box< ITV > &x, const Box< ITV > &y, const Rounding_Dir dir) |
| template<typename Temp , typename To , typename ITV > | |
| bool | euclidean_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Box< ITV > &x, const Box< ITV > &y, const Rounding_Dir dir, Temp &tmp0, Temp &tmp1, Temp &tmp2) |
| template<typename Temp , typename To , typename ITV > | |
| bool | euclidean_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Box< ITV > &x, const Box< ITV > &y, const Rounding_Dir dir) |
| template<typename To , typename ITV > | |
| bool | euclidean_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Box< ITV > &x, const Box< ITV > &y, const Rounding_Dir dir) |
| template<typename Temp , typename To , typename ITV > | |
| bool | l_infinity_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Box< ITV > &x, const Box< ITV > &y, const Rounding_Dir dir, Temp &tmp0, Temp &tmp1, Temp &tmp2) |
| template<typename Temp , typename To , typename ITV > | |
| bool | l_infinity_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Box< ITV > &x, const Box< ITV > &y, const Rounding_Dir dir) |
| template<typename To , typename ITV > | |
| bool | l_infinity_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Box< ITV > &x, const Box< ITV > &y, const Rounding_Dir dir) |
| template<typename ITV > | |
| void | swap (Box< ITV > &x, Box< ITV > &y) |
| template<typename ITV > | |
| std::ostream & | operator<< (std::ostream &s, const Box< ITV > &box) |
| template<typename Specialization , typename Temp , typename To , typename ITV > | |
| bool | l_m_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Box< ITV > &x, const Box< ITV > &y, const Rounding_Dir dir, Temp &tmp0, Temp &tmp1, Temp &tmp2) |
Exception Throwers | |
| void | throw_dimension_incompatible (const char *method, const Box &y) const |
| void | throw_dimension_incompatible (const char *method, dimension_type required_dim) const |
| void | throw_dimension_incompatible (const char *method, const Constraint &c) const |
| void | throw_dimension_incompatible (const char *method, const Congruence &cg) const |
| void | throw_dimension_incompatible (const char *method, const Constraint_System &cs) const |
| void | throw_dimension_incompatible (const char *method, const Congruence_System &cgs) const |
| void | throw_dimension_incompatible (const char *method, const Generator &g) const |
| void | throw_dimension_incompatible (const char *method, const char *le_name, const Linear_Expression &le) const |
| template<typename C > | |
| void | throw_dimension_incompatible (const char *method, const char *lf_name, const Linear_Form< C > &lf) const |
| static void | throw_constraint_incompatible (const char *method) |
| static void | throw_expression_too_complex (const char *method, const Linear_Expression &le) |
| static void | throw_invalid_argument (const char *method, const char *reason) |
Detailed Description
template<typename ITV>
class Parma_Polyhedra_Library::Box< ITV >
A not necessarily closed, iso-oriented hyperrectangle.
A Box object represents the smash product of  not necessarily closed and possibly unbounded intervals represented by objects of class
not necessarily closed and possibly unbounded intervals represented by objects of class ITV, where  is the space dimension of the box.
is the space dimension of the box.
An interval constraint (resp., interval congruence) is a syntactic constraint (resp., congruence) that only mentions a single space dimension.
The Box domain optimally supports:
- tautological and inconsistent constraints and congruences;
- the interval constraints that are optimally supported by the template argument class
ITV; - the interval congruences that are optimally supported by the template argument class
ITV.
Depending on the method, using a constraint or congruence that is not optimally supported by the domain will either raise an exception or result in a (possibly non-optimal) upward approximation.
The user interface for the Box domain is meant to be as similar as possible to the one developed for the polyhedron class C_Polyhedron.
Definition at line 299 of file Box_defs.hh.
Member Typedef Documentation
| typedef ITV Parma_Polyhedra_Library::Box< ITV >::interval_type |
The type of intervals used to implement the box.
Definition at line 302 of file Box_defs.hh.
|
private |
The type of sequence used to implement the box.
Definition at line 1756 of file Box_defs.hh.
|
private |
The type of intervals used by inner computations when trying to limit the cumulative effect of approximation errors.
Definition at line 1762 of file Box_defs.hh.
Constructor & Destructor Documentation
|
inlineexplicit |
Builds a universe or empty box of the specified space dimension.
- Parameters
-
num_dimensions The number of dimensions of the vector space enclosing the box; kind Specifies whether the universe or the empty box has to be built.
Definition at line 50 of file Box_templates.hh.
References Parma_Polyhedra_Library::Box< ITV >::OK(), Parma_Polyhedra_Library::Box< ITV >::seq, Parma_Polyhedra_Library::Box< ITV >::set_empty(), Parma_Polyhedra_Library::Box< ITV >::set_empty_up_to_date(), and Parma_Polyhedra_Library::UNIVERSE.
|
inline |
Ordinary copy constructor.
The complexity argument is ignored.
Definition at line 70 of file Box_inlines.hh.
|
inlineexplicit |
Builds a conservative, upward approximation of y.
The complexity argument is ignored.
Definition at line 109 of file Box_templates.hh.
References Parma_Polyhedra_Library::Box< ITV >::marked_empty(), Parma_Polyhedra_Library::Box< ITV >::OK(), Parma_Polyhedra_Library::Box< ITV >::seq, Parma_Polyhedra_Library::Box< ITV >::set_empty(), and Parma_Polyhedra_Library::Box< ITV >::space_dimension().
|
inlineexplicit |
Builds a box from the system of constraints cs.
The box inherits the space dimension of cs.
- Parameters
-
cs A system of constraints: constraints that are not interval constraints are ignored (even though they may have contributed to the space dimension).
Definition at line 74 of file Box_templates.hh.
References Parma_Polyhedra_Library::Box< ITV >::add_constraints_no_check(), Parma_Polyhedra_Library::Box< ITV >::seq, Parma_Polyhedra_Library::Constraint_System::space_dimension(), and Parma_Polyhedra_Library::UNIVERSE.
|
inline |
Builds a box recycling a system of constraints cs.
The box inherits the space dimension of cs.
- Parameters
-
cs A system of constraints: constraints that are not interval constraints are ignored (even though they may have contributed to the space dimension). dummy A dummy tag to syntactically differentiate this one from the other constructors.
Definition at line 93 of file Box_inlines.hh.
|
explicit |
Builds a box from the system of generators gs.
Builds the smallest box containing the polyhedron defined by gs. The box inherits the space dimension of gs.
- Exceptions
-
std::invalid_argument Thrown if the system of generators is not empty but has no points.
Definition at line 128 of file Box_templates.hh.
References Parma_Polyhedra_Library::assign_r(), Parma_Polyhedra_Library::Expression_Adapter< T >::begin(), Parma_Polyhedra_Library::Generator_System::begin(), Parma_Polyhedra_Library::Generator::CLOSURE_POINT, Parma_Polyhedra_Library::Generator::coefficient(), Parma_Polyhedra_Library::Generator::divisor(), Parma_Polyhedra_Library::Expression_Hide_Last< T >::end(), Parma_Polyhedra_Library::Generator_System::end(), Parma_Polyhedra_Library::EQUAL, Parma_Polyhedra_Library::Generator::expression(), Parma_Polyhedra_Library::GREATER_THAN, Parma_Polyhedra_Library::i_constraint(), Parma_Polyhedra_Library::Generator::is_point(), Parma_Polyhedra_Library::LESS_THAN, Parma_Polyhedra_Library::Generator::LINE, Parma_Polyhedra_Library::Box< ITV >::OK(), PPL_DIRTY_TEMP, Parma_Polyhedra_Library::Generator::RAY, Parma_Polyhedra_Library::ROUND_NOT_NEEDED, Parma_Polyhedra_Library::Box< ITV >::seq, Parma_Polyhedra_Library::Box< ITV >::set_empty(), Parma_Polyhedra_Library::Box< ITV >::set_empty_up_to_date(), Parma_Polyhedra_Library::Boundary_NS::sgn(), Parma_Polyhedra_Library::Box< ITV >::space_dimension(), Parma_Polyhedra_Library::Generator::type(), and Parma_Polyhedra_Library::UNIVERSE.
|
inline |
Builds a box recycling the system of generators gs.
Builds the smallest box containing the polyhedron defined by gs. The box inherits the space dimension of gs.
- Parameters
-
gs The generator system describing the polyhedron to be approximated. dummy A dummy tag to syntactically differentiate this one from the other constructors.
- Exceptions
-
std::invalid_argument Thrown if the system of generators is not empty but has no points.
Definition at line 101 of file Box_inlines.hh.
|
inlineexplicit |
Builds the smallest box containing the grid defined by a system of congruences cgs. The box inherits the space dimension of cgs.
- Parameters
-
cgs A system of congruences: congruences that are not non-relational equality constraints are ignored (though they may have contributed to the space dimension).
Definition at line 91 of file Box_templates.hh.
References Parma_Polyhedra_Library::Box< ITV >::add_congruences_no_check(), Parma_Polyhedra_Library::Box< ITV >::seq, Parma_Polyhedra_Library::Congruence_System::space_dimension(), and Parma_Polyhedra_Library::UNIVERSE.
|
inline |
Builds the smallest box containing the grid defined by a system of congruences cgs, recycling cgs. The box inherits the space dimension of cgs.
- Parameters
-
cgs A system of congruences: congruences that are not non-relational equality constraints are ignored (though they will contribute to the space dimension). dummy A dummy tag to syntactically differentiate this one from the other constructors.
Definition at line 109 of file Box_inlines.hh.
|
explicit |
Builds a box containing the BDS bds.
Builds the smallest box containing bds using a polynomial algorithm. The complexity argument is ignored.
Definition at line 248 of file Box_templates.hh.
References Parma_Polyhedra_Library::BD_Shape< T >::dbm, Parma_Polyhedra_Library::GREATER_OR_EQUAL, Parma_Polyhedra_Library::is_plus_infinity(), Parma_Polyhedra_Library::LESS_OR_EQUAL, Parma_Polyhedra_Library::BD_Shape< T >::marked_empty(), Parma_Polyhedra_Library::Box< ITV >::OK(), PPL_DIRTY_TEMP, Parma_Polyhedra_Library::ROUND_DOWN, Parma_Polyhedra_Library::Box< ITV >::seq, Parma_Polyhedra_Library::I_Constraint< T, Val_Or_Ref_Criteria, extended >::set(), Parma_Polyhedra_Library::Box< ITV >::set_empty(), Parma_Polyhedra_Library::Box< ITV >::set_empty_up_to_date(), Parma_Polyhedra_Library::BD_Shape< T >::shortest_path_closure_assign(), and Parma_Polyhedra_Library::Box< ITV >::space_dimension().
|
explicit |
Builds a box containing the octagonal shape oct.
Builds the smallest box containing oct using a polynomial algorithm. The complexity argument is ignored.
Definition at line 301 of file Box_templates.hh.
References Parma_Polyhedra_Library::assign_r(), Parma_Polyhedra_Library::GREATER_OR_EQUAL, Parma_Polyhedra_Library::is_plus_infinity(), Parma_Polyhedra_Library::LESS_OR_EQUAL, Parma_Polyhedra_Library::Octagonal_Shape< T >::marked_empty(), Parma_Polyhedra_Library::Octagonal_Shape< T >::matrix, PPL_DIRTY_TEMP, Parma_Polyhedra_Library::ROUND_NOT_NEEDED, Parma_Polyhedra_Library::Box< ITV >::seq, Parma_Polyhedra_Library::I_Constraint< T, Val_Or_Ref_Criteria, extended >::set(), Parma_Polyhedra_Library::Box< ITV >::set_empty(), Parma_Polyhedra_Library::Box< ITV >::set_empty_up_to_date(), Parma_Polyhedra_Library::Box< ITV >::space_dimension(), and Parma_Polyhedra_Library::Octagonal_Shape< T >::strong_closure_assign().
|
explicit |
Builds a box containing the polyhedron ph.
Builds a box containing ph using algorithms whose complexity does not exceed the one specified by complexity. If complexity is ANY_COMPLEXITY, then the built box is the smallest one containing ph.
Definition at line 355 of file Box_templates.hh.
References Parma_Polyhedra_Library::MIP_Problem::add_constraint(), Parma_Polyhedra_Library::MIP_Problem::add_constraints(), Parma_Polyhedra_Library::ANY_COMPLEXITY, Parma_Polyhedra_Library::assign_r(), Parma_Polyhedra_Library::Constraint_System::begin(), c, Parma_Polyhedra_Library::Polyhedron::constraints(), Parma_Polyhedra_Library::Polyhedron::constraints_are_up_to_date(), Parma_Polyhedra_Library::Constraint_System::end(), Parma_Polyhedra_Library::MIP_Problem::evaluate_objective_function(), Parma_Polyhedra_Library::Constraint::expression(), Parma_Polyhedra_Library::Polyhedron::generators(), Parma_Polyhedra_Library::Polyhedron::generators_are_up_to_date(), Parma_Polyhedra_Library::GREATER_OR_EQUAL, Parma_Polyhedra_Library::Polyhedron::has_pending_constraints(), Parma_Polyhedra_Library::Constraint_System::has_strict_inequalities(), Parma_Polyhedra_Library::is_canonical(), Parma_Polyhedra_Library::Polyhedron::is_empty(), Parma_Polyhedra_Library::MIP_Problem::is_satisfiable(), Parma_Polyhedra_Library::Constraint::is_strict_inequality(), Parma_Polyhedra_Library::LESS_OR_EQUAL, Parma_Polyhedra_Library::Box< ITV >::m_swap(), Parma_Polyhedra_Library::Polyhedron::marked_empty(), Parma_Polyhedra_Library::MAXIMIZATION, Parma_Polyhedra_Library::MINIMIZATION, Parma_Polyhedra_Library::OPTIMIZED_MIP_PROBLEM, Parma_Polyhedra_Library::MIP_Problem::optimizing_point(), Parma_Polyhedra_Library::POLYNOMIAL_COMPLEXITY, PPL_DIRTY_TEMP, PPL_DIRTY_TEMP_COEFFICIENT, Parma_Polyhedra_Library::Box< ITV >::propagate_constraints_no_check(), Parma_Polyhedra_Library::ROUND_NOT_NEEDED, Parma_Polyhedra_Library::Box< ITV >::seq, Parma_Polyhedra_Library::I_Constraint< T, Val_Or_Ref_Criteria, extended >::set(), Parma_Polyhedra_Library::Box< ITV >::set_empty(), Parma_Polyhedra_Library::Box< ITV >::set_empty_up_to_date(), Parma_Polyhedra_Library::MIP_Problem::set_objective_function(), Parma_Polyhedra_Library::MIP_Problem::set_optimization_mode(), Parma_Polyhedra_Library::SIMPLEX_COMPLEXITY, Parma_Polyhedra_Library::Polyhedron::simplified_constraints(), Parma_Polyhedra_Library::MIP_Problem::solve(), Parma_Polyhedra_Library::Polyhedron::space_dimension(), and Parma_Polyhedra_Library::UNIVERSE.
|
explicit |
Builds a box containing the grid gr.
Builds the smallest box containing gr using a polynomial algorithm. The complexity argument is ignored.
Definition at line 474 of file Box_templates.hh.
References Parma_Polyhedra_Library::assign_r(), Parma_Polyhedra_Library::Grid_Generator_System::empty(), Parma_Polyhedra_Library::EQUAL, Parma_Polyhedra_Library::Grid::gen_sys, Parma_Polyhedra_Library::Grid::generators_are_up_to_date(), Parma_Polyhedra_Library::i_constraint(), Parma_Polyhedra_Library::Grid::marked_empty(), Parma_Polyhedra_Library::Grid::maximize(), PPL_DIRTY_TEMP, PPL_DIRTY_TEMP_COEFFICIENT, Parma_Polyhedra_Library::ROUND_NOT_NEEDED, Parma_Polyhedra_Library::Box< ITV >::seq, Parma_Polyhedra_Library::Box< ITV >::set_empty(), Parma_Polyhedra_Library::Box< ITV >::set_empty_up_to_date(), Parma_Polyhedra_Library::Grid::space_dimension(), Parma_Polyhedra_Library::UNIVERSE, and Parma_Polyhedra_Library::Grid::update_generators().
|
explicit |
Builds a box containing the partially reduced product dp.
Builds a box containing ph using algorithms whose complexity does not exceed the one specified by complexity.
Definition at line 529 of file Box_templates.hh.
References Parma_Polyhedra_Library::check_space_dimension_overflow(), Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::domain1(), Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::domain2(), Parma_Polyhedra_Library::Box< ITV >::intersection_assign(), Parma_Polyhedra_Library::Box< ITV >::m_swap(), Parma_Polyhedra_Library::Box< ITV >::max_space_dimension(), and Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::space_dimension().
Member Function Documentation
|
inline |
Adds to *this a constraint equivalent to the congruence cg.
- Parameters
-
cg The congruence to be added.
- Exceptions
-
std::invalid_argument Thrown if *thisand congruencecgare dimension-incompatible, orcgis not optimally supported by the box domain.
Definition at line 348 of file Box_inlines.hh.
References Parma_Polyhedra_Library::Congruence::space_dimension().
|
private |
WRITE ME.
Definition at line 2411 of file Box_templates.hh.
References Parma_Polyhedra_Library::Congruence::coefficient(), Parma_Polyhedra_Library::Constraint::EQUALITY, Parma_Polyhedra_Library::Box_Helpers::extract_interval_congruence(), Parma_Polyhedra_Library::Congruence::inhomogeneous_term(), Parma_Polyhedra_Library::Congruence::is_equality(), Parma_Polyhedra_Library::Congruence::is_inconsistent(), Parma_Polyhedra_Library::Congruence::is_proper_congruence(), Parma_Polyhedra_Library::Congruence::is_tautological(), and Parma_Polyhedra_Library::Congruence::space_dimension().
|
inline |
Adds to *this constraints equivalent to the congruences in cgs.
- Parameters
-
cgs The congruences to be added.
- Exceptions
-
std::invalid_argument Thrown if *thisandcgsare dimension-incompatible, orcgscontains a congruence which is not optimally supported by the box domain.
Definition at line 360 of file Box_inlines.hh.
References Parma_Polyhedra_Library::Congruence_System::space_dimension().
|
private |
WRITE ME.
Definition at line 2459 of file Box_templates.hh.
References Parma_Polyhedra_Library::Congruence_System::begin(), Parma_Polyhedra_Library::Congruence_System::end(), and Parma_Polyhedra_Library::Congruence_System::space_dimension().
Referenced by Parma_Polyhedra_Library::Box< ITV >::Box().
|
inline |
Adds a copy of constraint c to the system of constraints defining *this.
- Parameters
-
c The constraint to be added.
- Exceptions
-
std::invalid_argument Thrown if *thisand constraintcare dimension-incompatible, orcis not optimally supported by the Box domain.
Definition at line 319 of file Box_inlines.hh.
References Parma_Polyhedra_Library::Constraint::space_dimension().
|
private |
WRITE ME.
Definition at line 2355 of file Box_templates.hh.
References Parma_Polyhedra_Library::Constraint::coefficient(), Parma_Polyhedra_Library::Box_Helpers::extract_interval_constraint(), Parma_Polyhedra_Library::Constraint::inhomogeneous_term(), Parma_Polyhedra_Library::Constraint::is_equality(), Parma_Polyhedra_Library::Constraint::is_strict_inequality(), Parma_Polyhedra_Library::Constraint::space_dimension(), and Parma_Polyhedra_Library::Constraint::type().
|
inline |
Adds the constraints in cs to the system of constraints defining *this.
- Parameters
-
cs The constraints to be added.
- Exceptions
-
std::invalid_argument Thrown if *thisandcsare dimension-incompatible, orcscontains a constraint which is not optimally supported by the box domain.
Definition at line 331 of file Box_inlines.hh.
References Parma_Polyhedra_Library::Constraint_System::space_dimension().
|
private |
WRITE ME.
Definition at line 2397 of file Box_templates.hh.
References Parma_Polyhedra_Library::Constraint_System::begin(), Parma_Polyhedra_Library::Constraint_System::end(), and Parma_Polyhedra_Library::Constraint_System::space_dimension().
Referenced by Parma_Polyhedra_Library::Box< ITV >::Box().
|
inlineprivate |
WRITE ME.
Definition at line 442 of file Box_inlines.hh.
Referenced by Parma_Polyhedra_Library::Box< ITV >::get_limiting_box().
|
inline |
Adds to *this constraints equivalent to the congruences in cgs.
- Parameters
-
cgs The congruence system to be added to *this. The congruences incgsmay be recycled.
- Exceptions
-
std::invalid_argument Thrown if *thisandcgsare dimension-incompatible, orcgscontains a congruence which is not optimally supported by the box domain.
- Warning
- The only assumption that can be made on
cgsupon successful or exceptional return is that it can be safely destroyed.
Definition at line 369 of file Box_inlines.hh.
|
inline |
Adds the constraints in cs to the system of constraints defining *this.
- Parameters
-
cs The constraints to be added. They may be recycled.
- Exceptions
-
std::invalid_argument Thrown if *thisandcsare dimension-incompatible, orcscontains a constraint which is not optimally supported by the box domain.
- Warning
- The only assumption that can be made on
csupon successful or exceptional return is that it can be safely destroyed.
Definition at line 342 of file Box_inlines.hh.
|
inline |
Adds m new dimensions and embeds the old box into the new space.
- Parameters
-
m The number of dimensions to add.
The new dimensions will be those having the highest indexes in the new box, which is defined by a system of interval constraints in which the variables running through the new dimensions are unconstrained. For instance, when starting from the box 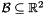 and adding a third dimension, the result will be the box
and adding a third dimension, the result will be the box
![\[ \bigl\{\, (x, y, z)^\transpose \in \Rset^3 \bigm| (x, y)^\transpose \in \cB \,\bigr\}. \]](form_753.png)
Definition at line 546 of file Box_templates.hh.
References Parma_Polyhedra_Library::check_space_dimension_overflow(), Parma_Polyhedra_Library::max_space_dimension(), and Parma_Polyhedra_Library::UNIVERSE.
|
inline |
Adds m new dimensions to the box and does not embed it in the new vector space.
- Parameters
-
m The number of dimensions to add.
The new dimensions will be those having the highest indexes in the new box, which is defined by a system of bounded differences in which the variables running through the new dimensions are all constrained to be equal to 0. For instance, when starting from the box 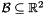 and adding a third dimension, the result will be the box
and adding a third dimension, the result will be the box
![\[ \bigl\{\, (x, y, 0)^\transpose \in \Rset^3 \bigm| (x, y)^\transpose \in \cB \,\bigr\}. \]](form_754.png)
Definition at line 564 of file Box_templates.hh.
References Parma_Polyhedra_Library::check_space_dimension_overflow(), and Parma_Polyhedra_Library::max_space_dimension().
| dimension_type Parma_Polyhedra_Library::Box< ITV >::affine_dimension | ( | ) | const |
Returns  , if
, if *this is empty; otherwise, returns the affine dimension of *this.
Definition at line 1427 of file Box_templates.hh.
| void Parma_Polyhedra_Library::Box< ITV >::affine_form_image | ( | Variable | var, |
| const Linear_Form< ITV > & | lf | ||
| ) |
Assigns to *this the affine form image of *this under the function mapping variable var into the affine expression(s) specified by lf.
- Parameters
-
var The variable to which the affine expression is assigned. lf The linear form on intervals with floating point boundaries that defines the affine expression(s). ALL of its coefficients MUST be bounded.
- Exceptions
-
std::invalid_argument Thrown if lfand*thisare dimension-incompatible or ifvaris not a dimension of*this.
This function is used in abstract interpretation to model an assignment of a value that is correctly overapproximated by lf to the floating point variable represented by var.
Definition at line 3115 of file Box_templates.hh.
References Parma_Polyhedra_Library::Linear_Form< C >::coefficient(), Parma_Polyhedra_Library::Variable::id(), Parma_Polyhedra_Library::Linear_Form< C >::inhomogeneous_term(), PPL_COMPILE_TIME_CHECK, Parma_Polyhedra_Library::Variable::space_dimension(), and Parma_Polyhedra_Library::Linear_Form< C >::space_dimension().
| void Parma_Polyhedra_Library::Box< ITV >::affine_image | ( | Variable | var, |
| const Linear_Expression & | expr, | ||
| Coefficient_traits::const_reference | denominator = Coefficient_one() |
||
| ) |
Assigns to *this the affine image of *this under the function mapping variable var to the affine expression specified by expr and denominator.
- Parameters
-
var The variable to which the affine expression is assigned; expr The numerator of the affine expression; denominator The denominator of the affine expression (optional argument with default value 1).
- Exceptions
-
std::invalid_argument Thrown if denominatoris zero or ifexprand*thisare dimension-incompatible or ifvaris not a space dimension of*this.
Definition at line 3069 of file Box_templates.hh.
References Parma_Polyhedra_Library::Linear_Expression::begin(), Parma_Polyhedra_Library::Linear_Expression::end(), Parma_Polyhedra_Library::Variable::id(), Parma_Polyhedra_Library::Linear_Expression::inhomogeneous_term(), Parma_Polyhedra_Library::Variable::space_dimension(), and Parma_Polyhedra_Library::Linear_Expression::space_dimension().
| void Parma_Polyhedra_Library::Box< ITV >::affine_preimage | ( | Variable | var, |
| const Linear_Expression & | expr, | ||
| Coefficient_traits::const_reference | denominator = Coefficient_one() |
||
| ) |
Assigns to *this the affine preimage of *this under the function mapping variable var to the affine expression specified by expr and denominator.
- Parameters
-
var The variable to which the affine expression is substituted; expr The numerator of the affine expression; denominator The denominator of the affine expression (optional argument with default value 1).
- Exceptions
-
std::invalid_argument Thrown if denominatoris zero or ifexprand*thisare dimension-incompatible or ifvaris not a space dimension of*this.
Definition at line 3155 of file Box_templates.hh.
References Parma_Polyhedra_Library::Linear_Expression::begin(), Parma_Polyhedra_Library::Linear_Expression::coefficient(), Parma_Polyhedra_Library::Linear_Expression::end(), Parma_Polyhedra_Library::Variable::id(), Parma_Polyhedra_Library::Linear_Expression::inhomogeneous_term(), Parma_Polyhedra_Library::inverse(), Parma_Polyhedra_Library::Variable::space_dimension(), Parma_Polyhedra_Library::Linear_Expression::space_dimension(), and Parma_Polyhedra_Library::UNIVERSE.
| void Parma_Polyhedra_Library::Box< ITV >::ascii_dump | ( | ) | const |
Writes to std::cerr an ASCII representation of *this.
| void Parma_Polyhedra_Library::Box< ITV >::ascii_dump | ( | std::ostream & | s | ) | const |
Writes to s an ASCII representation of *this.
Definition at line 4414 of file Box_templates.hh.
References Parma_Polyhedra_Library::Implementation::BD_Shapes::separator.
| bool Parma_Polyhedra_Library::Box< ITV >::ascii_load | ( | std::istream & | s | ) |
Loads from s an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets *this accordingly. Returns true if successful, false otherwise.
Definition at line 4429 of file Box_templates.hh.
| void Parma_Polyhedra_Library::Box< ITV >::bounded_affine_image | ( | Variable | var, |
| const Linear_Expression & | lb_expr, | ||
| const Linear_Expression & | ub_expr, | ||
| Coefficient_traits::const_reference | denominator = Coefficient_one() |
||
| ) |
Assigns to *this the image of *this with respect to the bounded affine relation  .
.
- Parameters
-
var The variable updated by the affine relation; lb_expr The numerator of the lower bounding affine expression; ub_expr The numerator of the upper bounding affine expression; denominator The (common) denominator for the lower and upper bounding affine expressions (optional argument with default value 1).
- Exceptions
-
std::invalid_argument Thrown if denominatoris zero or iflb_expr(resp.,ub_expr) and*thisare dimension-incompatible or ifvaris not a space dimension of*this.
Definition at line 3223 of file Box_templates.hh.
References Parma_Polyhedra_Library::assign_r(), Parma_Polyhedra_Library::Linear_Expression::coefficient(), Parma_Polyhedra_Library::GREATER_OR_EQUAL, Parma_Polyhedra_Library::GREATER_THAN, Parma_Polyhedra_Library::i_constraint(), Parma_Polyhedra_Library::Variable::id(), Parma_Polyhedra_Library::LESS_OR_EQUAL, Parma_Polyhedra_Library::LESS_THAN, PPL_DIRTY_TEMP, PPL_DIRTY_TEMP_COEFFICIENT, Parma_Polyhedra_Library::ROUND_NOT_NEEDED, Parma_Polyhedra_Library::Variable::space_dimension(), Parma_Polyhedra_Library::Linear_Expression::space_dimension(), and Parma_Polyhedra_Library::UNIVERSE.
| void Parma_Polyhedra_Library::Box< ITV >::bounded_affine_preimage | ( | Variable | var, |
| const Linear_Expression & | lb_expr, | ||
| const Linear_Expression & | ub_expr, | ||
| Coefficient_traits::const_reference | denominator = Coefficient_one() |
||
| ) |
Assigns to *this the preimage of *this with respect to the bounded affine relation  .
.
- Parameters
-
var The variable updated by the affine relation; lb_expr The numerator of the lower bounding affine expression; ub_expr The numerator of the upper bounding affine expression; denominator The (common) denominator for the lower and upper bounding affine expressions (optional argument with default value 1).
- Exceptions
-
std::invalid_argument Thrown if denominatoris zero or iflb_expr(resp.,ub_expr) and*thisare dimension-incompatible or ifvaris not a space dimension of*this.
Definition at line 3374 of file Box_templates.hh.
References Parma_Polyhedra_Library::assign_r(), Parma_Polyhedra_Library::Linear_Expression::coefficient(), Parma_Polyhedra_Library::GREATER_OR_EQUAL, Parma_Polyhedra_Library::GREATER_THAN, Parma_Polyhedra_Library::i_constraint(), Parma_Polyhedra_Library::Variable::id(), Parma_Polyhedra_Library::LESS_OR_EQUAL, Parma_Polyhedra_Library::LESS_THAN, Parma_Polyhedra_Library::neg_assign(), PPL_DIRTY_TEMP, PPL_DIRTY_TEMP_COEFFICIENT, Parma_Polyhedra_Library::ROUND_NOT_NEEDED, Parma_Polyhedra_Library::Variable::space_dimension(), and Parma_Polyhedra_Library::Linear_Expression::space_dimension().
|
private |
Checks if and how expr is bounded in *this.
Returns true if and only if from_above is true and expr is bounded from above in *this, or from_above is false and expr is bounded from below in *this.
- Parameters
-
expr The linear expression to test; from_above trueif and only if the boundedness of interest is "from above".
- Exceptions
-
std::invalid_argument Thrown if exprand*thisare dimension-incompatible.
Definition at line 605 of file Box_templates.hh.
References Parma_Polyhedra_Library::Linear_Expression::begin(), Parma_Polyhedra_Library::Linear_Expression::end(), Parma_Polyhedra_Library::Variable::id(), Parma_Polyhedra_Library::Boundary_NS::sgn(), and Parma_Polyhedra_Library::Linear_Expression::space_dimension().
|
inline |
Returns true if and only if expr is bounded from above in *this.
- Exceptions
-
std::invalid_argument Thrown if exprand*thisare dimension-incompatible.
Definition at line 189 of file Box_inlines.hh.
|
inline |
Returns true if and only if expr is bounded from below in *this.
- Exceptions
-
std::invalid_argument Thrown if exprand*thisare dimension-incompatible.
Definition at line 195 of file Box_inlines.hh.
|
inlinestatic |
Returns false indicating that this domain does not recycle congruences.
Definition at line 381 of file Box_inlines.hh.
|
inlinestatic |
Returns false indicating that this domain does not recycle constraints.
Definition at line 375 of file Box_inlines.hh.
| Enable_If<Is_Same<T, Box>::value && Is_Same_Or_Derived<Interval_Base, ITV>::value, void>::type Parma_Polyhedra_Library::Box< ITV >::CC76_narrowing_assign | ( | const T & | y | ) |
Assigns to *this the result of restoring in y the constraints of *this that were lost by CC76-extrapolation applications.
- Parameters
-
y A Box that must contain *this.
- Exceptions
-
std::invalid_argument Thrown if *thisandyare dimension-incompatible.
- Note
- As was the case for widening operators, the argument
yis meant to denote the value computed in the previous iteration step, whereas*thisdenotes the value computed in the current iteration step (in the decreasing iteration sequence). Hence, the callx.CC76_narrowing_assign(y)will assign toxthe result of the computation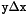 .
.
| Enable_If<Is_Same<T, Box<ITV> >::value && Is_Same_Or_Derived<Interval_Base, ITV>::value, void>::type Parma_Polyhedra_Library::Box< ITV >::CC76_narrowing_assign | ( | const T & | y | ) |
Definition at line 4203 of file Box_templates.hh.
| Enable_If<Is_Same<T, Box>::value && Is_Same_Or_Derived<Interval_Base, ITV>::value, void>::type Parma_Polyhedra_Library::Box< ITV >::CC76_widening_assign | ( | const T & | y, |
| unsigned * | tp = 0 |
||
| ) |
Assigns to *this the result of computing the CC76-widening between *this and y.
- Parameters
-
y A box that must be contained in *this.tp An optional pointer to an unsigned variable storing the number of available tokens (to be used when applying the widening with tokens delay technique).
- Exceptions
-
std::invalid_argument Thrown if *thisandyare dimension-incompatible.
Referenced by Parma_Polyhedra_Library::Polyhedron::bounded_BHRZ03_extrapolation_assign(), Parma_Polyhedra_Library::Polyhedron::bounded_H79_extrapolation_assign(), Parma_Polyhedra_Library::Box< ITV >::CC76_widening_assign(), and Parma_Polyhedra_Library::Box< ITV >::limited_CC76_extrapolation_assign().
| Enable_If<Is_Same<T, Box>::value && Is_Same_Or_Derived<Interval_Base, ITV>::value, void>::type Parma_Polyhedra_Library::Box< ITV >::CC76_widening_assign | ( | const T & | y, |
| Iterator | first, | ||
| Iterator | last | ||
| ) |
Assigns to *this the result of computing the CC76-widening between *this and y.
- Parameters
-
y A box that must be contained in *this.first An iterator that points to the first stop-point. last An iterator that points one past the last stop-point.
- Exceptions
-
std::invalid_argument Thrown if *thisandyare dimension-incompatible.
| Enable_If<Is_Same<T, Box<ITV> >::value && Is_Same_Or_Derived<Interval_Base, ITV>::value, void>::type Parma_Polyhedra_Library::Box< ITV >::CC76_widening_assign | ( | const T & | y, |
| Iterator | first, | ||
| Iterator | last | ||
| ) |
Definition at line 4080 of file Box_templates.hh.
| Enable_If<Is_Same<T, Box<ITV> >::value && Is_Same_Or_Derived<Interval_Base, ITV>::value, void>::type Parma_Polyhedra_Library::Box< ITV >::CC76_widening_assign | ( | const T & | y, |
| unsigned * | tp | ||
| ) |
Definition at line 4096 of file Box_templates.hh.
References Parma_Polyhedra_Library::Box< ITV >::CC76_widening_assign(), and Parma_Polyhedra_Library::Box< ITV >::contains().
|
private |
Checks the hard way whether *this is an empty box: returns true if and only if it is so.
Definition at line 1450 of file Box_templates.hh.
References Parma_Polyhedra_Library::Box< ITV >::set_empty(), and Parma_Polyhedra_Library::Box< ITV >::set_nonempty().
Referenced by Parma_Polyhedra_Library::Box< ITV >::OK().
| void Parma_Polyhedra_Library::Box< ITV >::concatenate_assign | ( | const Box< ITV > & | y | ) |
Seeing a box as a set of tuples (its points), assigns to *this all the tuples that can be obtained by concatenating, in the order given, a tuple of *this with a tuple of y.
Let 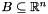 and
and  be the boxes corresponding, on entry, to
be the boxes corresponding, on entry, to *this and y, respectively. Upon successful completion, *this will represent the box 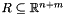 such that
such that
![\[ R \defeq \Bigl\{\, (x_1, \ldots, x_n, y_1, \ldots, y_m)^\transpose \Bigm| (x_1, \ldots, x_n)^\transpose \in B, (y_1, \ldots, y_m)^\transpose \in D \,\Bigl\}. \]](form_764.png)
Another way of seeing it is as follows: first increases the space dimension of *this by adding y.space_dimension() new dimensions; then adds to the system of constraints of *this a renamed-apart version of the constraints of y.
Definition at line 1964 of file Box_templates.hh.
References Parma_Polyhedra_Library::check_space_dimension_overflow(), Parma_Polyhedra_Library::EMPTY, Parma_Polyhedra_Library::Box< ITV >::marked_empty(), Parma_Polyhedra_Library::max_space_dimension(), Parma_Polyhedra_Library::Box< ITV >::OK(), Parma_Polyhedra_Library::Box< ITV >::seq, Parma_Polyhedra_Library::Box< ITV >::set_empty(), Parma_Polyhedra_Library::Box< ITV >::space_dimension(), Parma_Polyhedra_Library::Box< ITV >::status, and Parma_Polyhedra_Library::Box< ITV >::Status::test_empty_up_to_date().
| Congruence_System Parma_Polyhedra_Library::Box< ITV >::congruences | ( | ) | const |
Returns a system of congruences approximating *this.
Definition at line 4344 of file Box_templates.hh.
References Parma_Polyhedra_Library::Congruence_System::insert(), PPL_DIRTY_TEMP_COEFFICIENT, Parma_Polyhedra_Library::Congruence_System::zero_dim_empty(), and Parma_Polyhedra_Library::Congruence::zero_dim_false().
| bool Parma_Polyhedra_Library::Box< ITV >::constrains | ( | Variable | var | ) | const |
Returns true if and only if var is constrained in *this.
- Exceptions
-
std::invalid_argument Thrown if varis not a space dimension of*this.
Definition at line 1606 of file Box_templates.hh.
References Parma_Polyhedra_Library::Variable::space_dimension().
| Constraint_System Parma_Polyhedra_Library::Box< ITV >::constraints | ( | ) | const |
Returns a system of constraints defining *this.
Definition at line 4248 of file Box_templates.hh.
References Parma_Polyhedra_Library::Constraint_System::insert(), PPL_DIRTY_TEMP_COEFFICIENT, Parma_Polyhedra_Library::Constraint_System::set_space_dimension(), Parma_Polyhedra_Library::Constraint_System::zero_dim_empty(), and Parma_Polyhedra_Library::Constraint::zero_dim_false().
Referenced by Parma_Polyhedra_Library::BD_Shape< T >::BD_Shape(), Parma_Polyhedra_Library::Polyhedron::bounded_BHRZ03_extrapolation_assign(), Parma_Polyhedra_Library::Polyhedron::bounded_H79_extrapolation_assign(), and Parma_Polyhedra_Library::Octagonal_Shape< T >::Octagonal_Shape().
| bool Parma_Polyhedra_Library::Box< ITV >::contains | ( | const Box< ITV > & | y | ) | const |
Returns true if and only if *this contains y.
- Exceptions
-
std::invalid_argument Thrown if xandyare dimension-incompatible.
Definition at line 1291 of file Box_templates.hh.
References Parma_Polyhedra_Library::Box< ITV >::is_empty(), Parma_Polyhedra_Library::Box< ITV >::seq, Parma_Polyhedra_Library::Box< ITV >::space_dimension(), and Parma_Polyhedra_Library::Box< ITV >::throw_dimension_incompatible().
Referenced by Parma_Polyhedra_Library::Box< ITV >::CC76_widening_assign(), and Parma_Polyhedra_Library::Box< ITV >::strictly_contains().
| bool Parma_Polyhedra_Library::Box< ITV >::contains_integer_point | ( | ) | const |
Returns true if and only if *this contains at least one integer point.
Definition at line 1522 of file Box_templates.hh.
| void Parma_Polyhedra_Library::Box< ITV >::difference_assign | ( | const Box< ITV > & | y | ) |
Assigns to *this the difference of *this and y.
- Exceptions
-
std::invalid_argument Thrown if *thisandyare dimension-incompatible.
Definition at line 2010 of file Box_templates.hh.
References Parma_Polyhedra_Library::Box< ITV >::is_empty(), Parma_Polyhedra_Library::Box< ITV >::seq, Parma_Polyhedra_Library::Box< ITV >::set_empty(), and Parma_Polyhedra_Library::Box< ITV >::space_dimension().
| void Parma_Polyhedra_Library::Box< ITV >::drop_some_non_integer_points | ( | Complexity_Class | complexity = ANY_COMPLEXITY | ) |
Possibly tightens *this by dropping some points with non-integer coordinates.
- Parameters
-
complexity The maximal complexity of any algorithms used.
- Note
- Currently there is no optimality guarantee, not even if
complexityisANY_COMPLEXITY.
Definition at line 1855 of file Box_templates.hh.
References Parma_Polyhedra_Library::is_integer().
| void Parma_Polyhedra_Library::Box< ITV >::drop_some_non_integer_points | ( | const Variables_Set & | vars, |
| Complexity_Class | complexity = ANY_COMPLEXITY |
||
| ) |
Possibly tightens *this by dropping some points with non-integer coordinates for the space dimensions corresponding to vars.
- Parameters
-
vars Points with non-integer coordinates for these variables/space-dimensions can be discarded. complexity The maximal complexity of any algorithms used.
- Note
- Currently there is no optimality guarantee, not even if
complexityisANY_COMPLEXITY.
Definition at line 1874 of file Box_templates.hh.
References Parma_Polyhedra_Library::is_integer(), and Parma_Polyhedra_Library::Variables_Set::space_dimension().
|
inline |
Creates m copies of the space dimension corresponding to var.
- Parameters
-
var The variable corresponding to the space dimension to be replicated; m The number of replicas to be created.
- Exceptions
-
std::invalid_argument Thrown if vardoes not correspond to a dimension of the vector space.std::length_error Thrown if adding mnew space dimensions would cause the vector space to exceed dimensionmax_space_dimension().
If *this has space dimension  , with
, with 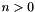 , and
, and var has space dimension 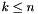 , then the
, then the  -th space dimension is expanded to
-th space dimension is expanded to m new space dimensions  ,
, 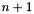 ,
,  ,
, 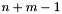 .
.
Definition at line 240 of file Box_inlines.hh.
References Parma_Polyhedra_Library::Variable::id(), Parma_Polyhedra_Library::max_space_dimension(), and Parma_Polyhedra_Library::Variable::space_dimension().
| memory_size_type Parma_Polyhedra_Library::Box< ITV >::external_memory_in_bytes | ( | ) | const |
Returns the size in bytes of the memory managed by *this.
Definition at line 4378 of file Box_templates.hh.
| void Parma_Polyhedra_Library::Box< ITV >::fold_space_dimensions | ( | const Variables_Set & | vars, |
| Variable | dest | ||
| ) |
Folds the space dimensions in vars into dest.
- Parameters
-
vars The set of Variable objects corresponding to the space dimensions to be folded; dest The variable corresponding to the space dimension that is the destination of the folding operation.
- Exceptions
-
std::invalid_argument Thrown if *thisis dimension-incompatible withdestor with one of the Variable objects contained invars. Also thrown ifdestis contained invars.
If *this has space dimension  , with
, with 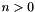 ,
, dest has space dimension 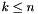 ,
, vars is a set of variables whose maximum space dimension is also less than or equal to  , and
, and dest is not a member of vars, then the space dimensions corresponding to variables in vars are folded into the  -th space dimension.
-th space dimension.
Definition at line 2316 of file Box_templates.hh.
References Parma_Polyhedra_Library::Variable::id(), Parma_Polyhedra_Library::Variables_Set::space_dimension(), and Parma_Polyhedra_Library::Variable::space_dimension().
| bool Parma_Polyhedra_Library::Box< ITV >::frequency | ( | const Linear_Expression & | expr, |
| Coefficient & | freq_n, | ||
| Coefficient & | freq_d, | ||
| Coefficient & | val_n, | ||
| Coefficient & | val_d | ||
| ) | const |
Returns true if and only if there exist a unique value val such that *this saturates the equality expr = val.
- Parameters
-
expr The linear expression for which the frequency is needed; freq_n If trueis returned, the value is set to ; Present for interface compatibility with class Grid, where the frequency can have a non-zero value;
; Present for interface compatibility with class Grid, where the frequency can have a non-zero value;freq_d If trueis returned, the value is set to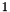 ;
;val_n The numerator of val;val_d The denominator of val;
- Exceptions
-
std::invalid_argument Thrown if exprand*thisare dimension-incompatible.
If false is returned, then freq_n, freq_d, val_n and val_d are left untouched.
Definition at line 1536 of file Box_templates.hh.
References Parma_Polyhedra_Library::assign_r(), Parma_Polyhedra_Library::Linear_Expression::begin(), c, Parma_Polyhedra_Library::Linear_Expression::end(), Parma_Polyhedra_Library::Linear_Expression::inhomogeneous_term(), Parma_Polyhedra_Library::normalize2(), PPL_DIRTY_TEMP, PPL_DIRTY_TEMP_COEFFICIENT, Parma_Polyhedra_Library::ROUND_NOT_NEEDED, and Parma_Polyhedra_Library::Linear_Expression::space_dimension().
| void Parma_Polyhedra_Library::Box< ITV >::generalized_affine_image | ( | Variable | var, |
| Relation_Symbol | relsym, | ||
| const Linear_Expression & | expr, | ||
| Coefficient_traits::const_reference | denominator = Coefficient_one() |
||
| ) |
Assigns to *this the image of *this with respect to the generalized affine relation  , where
, where  is the relation symbol encoded by
is the relation symbol encoded by relsym.
- Parameters
-
var The left hand side variable of the generalized affine relation; relsym The relation symbol; expr The numerator of the right hand side affine expression; denominator The denominator of the right hand side affine expression (optional argument with default value 1).
- Exceptions
-
std::invalid_argument Thrown if denominatoris zero or ifexprand*thisare dimension-incompatible or ifvaris not a space dimension of*this.
Definition at line 3562 of file Box_templates.hh.
References Parma_Polyhedra_Library::EQUAL, Parma_Polyhedra_Library::GREATER_OR_EQUAL, Parma_Polyhedra_Library::GREATER_THAN, Parma_Polyhedra_Library::Variable::id(), Parma_Polyhedra_Library::LESS_OR_EQUAL, Parma_Polyhedra_Library::LESS_THAN, Parma_Polyhedra_Library::NOT_EQUAL, Parma_Polyhedra_Library::Variable::space_dimension(), and Parma_Polyhedra_Library::Linear_Expression::space_dimension().
| void Parma_Polyhedra_Library::Box< ITV >::generalized_affine_image | ( | const Linear_Expression & | lhs, |
| Relation_Symbol | relsym, | ||
| const Linear_Expression & | rhs | ||
| ) |
Assigns to *this the image of *this with respect to the generalized affine relation  , where
, where  is the relation symbol encoded by
is the relation symbol encoded by relsym.
- Parameters
-
lhs The left hand side affine expression; relsym The relation symbol; rhs The right hand side affine expression.
- Exceptions
-
std::invalid_argument Thrown if *thisis dimension-incompatible withlhsorrhs.
Definition at line 3788 of file Box_templates.hh.
References Parma_Polyhedra_Library::assign_r(), Parma_Polyhedra_Library::Linear_Expression::coefficient(), Parma_Polyhedra_Library::EQUAL, Parma_Polyhedra_Library::Linear_Expression::first_nonzero(), Parma_Polyhedra_Library::GREATER_OR_EQUAL, Parma_Polyhedra_Library::GREATER_THAN, Parma_Polyhedra_Library::i_constraint(), Parma_Polyhedra_Library::Linear_Expression::inhomogeneous_term(), Parma_Polyhedra_Library::Linear_Expression::last_nonzero(), Parma_Polyhedra_Library::LESS_OR_EQUAL, Parma_Polyhedra_Library::LESS_THAN, Parma_Polyhedra_Library::NOT_EQUAL, PPL_DIRTY_TEMP, PPL_DIRTY_TEMP_COEFFICIENT, Parma_Polyhedra_Library::ROUND_NOT_NEEDED, Parma_Polyhedra_Library::I_Constraint< T, Val_Or_Ref_Criteria, extended >::set(), Parma_Polyhedra_Library::Linear_Expression::space_dimension(), and Parma_Polyhedra_Library::UNIVERSE.
| void Parma_Polyhedra_Library::Box< ITV >::generalized_affine_preimage | ( | Variable | var, |
| Relation_Symbol | relsym, | ||
| const Linear_Expression & | expr, | ||
| Coefficient_traits::const_reference | denominator = Coefficient_one() |
||
| ) |
Assigns to *this the preimage of *this with respect to the generalized affine relation  , where
, where  is the relation symbol encoded by
is the relation symbol encoded by relsym.
- Parameters
-
var The left hand side variable of the generalized affine relation; relsym The relation symbol; expr The numerator of the right hand side affine expression; denominator The denominator of the right hand side affine expression (optional argument with default value 1).
- Exceptions
-
std::invalid_argument Thrown if denominatoris zero or ifexprand*thisare dimension-incompatible or ifvaris not a space dimension of*this.
Definition at line 3635 of file Box_templates.hh.
References Parma_Polyhedra_Library::Linear_Expression::coefficient(), Parma_Polyhedra_Library::Coefficient_zero(), Parma_Polyhedra_Library::EQUAL, Parma_Polyhedra_Library::GREATER_OR_EQUAL, Parma_Polyhedra_Library::GREATER_THAN, Parma_Polyhedra_Library::LESS_OR_EQUAL, Parma_Polyhedra_Library::LESS_THAN, Parma_Polyhedra_Library::neg_assign(), Parma_Polyhedra_Library::NOT_EQUAL, PPL_DIRTY_TEMP_COEFFICIENT, Parma_Polyhedra_Library::Linear_Expression::set_inhomogeneous_term(), Parma_Polyhedra_Library::Boundary_NS::sgn(), Parma_Polyhedra_Library::Variable::space_dimension(), Parma_Polyhedra_Library::Linear_Expression::space_dimension(), and Parma_Polyhedra_Library::UNIVERSE.
| void Parma_Polyhedra_Library::Box< ITV >::generalized_affine_preimage | ( | const Linear_Expression & | lhs, |
| Relation_Symbol | relsym, | ||
| const Linear_Expression & | rhs | ||
| ) |
Assigns to *this the preimage of *this with respect to the generalized affine relation  , where
, where  is the relation symbol encoded by
is the relation symbol encoded by relsym.
- Parameters
-
lhs The left hand side affine expression; relsym The relation symbol; rhs The right hand side affine expression.
- Exceptions
-
std::invalid_argument Thrown if *thisis dimension-incompatible withlhsorrhs.
Definition at line 4028 of file Box_templates.hh.
References Parma_Polyhedra_Library::Linear_Expression::begin(), Parma_Polyhedra_Library::Linear_Expression::coefficient(), Parma_Polyhedra_Library::Linear_Expression::end(), Parma_Polyhedra_Library::NOT_EQUAL, PPL_DIRTY_TEMP_COEFFICIENT, Parma_Polyhedra_Library::Linear_Expression::space_dimension(), and Parma_Polyhedra_Library::sub_mul_assign().
|
inline |
Returns a reference the interval that bounds var.
- Exceptions
-
std::invalid_argument Thrown if varis not a space dimension of*this.
Definition at line 150 of file Box_inlines.hh.
References Parma_Polyhedra_Library::EMPTY, Parma_Polyhedra_Library::Variable::id(), and Parma_Polyhedra_Library::Variable::space_dimension().
Referenced by Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >::intervalize(), and Parma_Polyhedra_Library::Polyhedron::overapproximate_linear_form().
|
private |
Adds to limiting_box the interval constraints in cs that are satisfied by *this.
Definition at line 4124 of file Box_templates.hh.
References Parma_Polyhedra_Library::Box< ITV >::add_interval_constraint_no_check(), Parma_Polyhedra_Library::Constraint_System::begin(), Parma_Polyhedra_Library::Constraint::coefficient(), Parma_Polyhedra_Library::Constraint_System::end(), Parma_Polyhedra_Library::Box_Helpers::extract_interval_constraint(), Parma_Polyhedra_Library::Constraint::inhomogeneous_term(), Parma_Polyhedra_Library::interval_relation(), Parma_Polyhedra_Library::Poly_Con_Relation::is_included(), Parma_Polyhedra_Library::Constraint_System::space_dimension(), and Parma_Polyhedra_Library::Constraint::type().
|
inline |
If the space dimension of var is unbounded below, return false. Otherwise return true and set n, d and closed accordingly.
- Note
- It is assumed that
*thisis a non-empty box having space dimension greater than or equal to that ofvar. An undefined behavior is obtained if this assumption is not met. To be more precise, if*thisis an empty box (having space dimension greater than or equal to that ofvar) such that!marked_empty()holds, then the method can be called without incurring in undefined behavior: it will return unspecified boundary values that, if queried systematically on all space dimensions, will encode the box emptiness.
Let 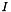 be the interval corresponding to variable
be the interval corresponding to variable var in the non-empty box *this. If 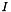 is not bounded from below, simply return
is not bounded from below, simply return false (leaving all other parameters unchanged). Otherwise, set n, d and closed as follows:
nanddare assigned the integers and
and 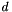 such that the fraction
such that the fraction 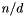 corresponds to the greatest lower bound of
corresponds to the greatest lower bound of 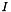 . The fraction
. The fraction 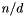 is in canonical form, meaning that
is in canonical form, meaning that  and
and 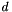 have no common factors,
have no common factors, 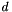 is positive, and if
is positive, and if  is zero then
is zero then 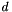 is one;
is one;closedis set totrueif and only if the lower boundary of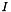 is closed (i.e., it is included in the interval).
is closed (i.e., it is included in the interval).
Definition at line 270 of file Box_inlines.hh.
References Parma_Polyhedra_Library::assign_r(), Parma_Polyhedra_Library::Variable::id(), PPL_DIRTY_TEMP, and Parma_Polyhedra_Library::ROUND_NOT_NEEDED.
Referenced by Parma_Polyhedra_Library::Grid::Grid(), and Parma_Polyhedra_Library::Polyhedron::Polyhedron().
|
inline |
If the space dimension of var is unbounded above, return false. Otherwise return true and set n, d and closed accordingly.
- Note
- It is assumed that
*thisis a non-empty box having space dimension greater than or equal to that ofvar. An undefined behavior is obtained if this assumption is not met. To be more precise, if*thisis an empty box (having space dimension greater than or equal to that ofvar) such that!marked_empty()holds, then the method can be called without incurring in undefined behavior: it will return unspecified boundary values that, if queried systematically on all space dimensions, will encode the box emptiness.
Let 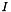 be the interval corresponding to variable
be the interval corresponding to variable var in the non-empty box *this. If 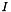 is not bounded from above, simply return
is not bounded from above, simply return false (leaving all other parameters unchanged). Otherwise, set n, d and closed as follows:
nanddare assigned the integers and
and 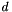 such that the fraction
such that the fraction 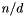 corresponds to the least upper bound of
corresponds to the least upper bound of 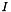 . The fraction
. The fraction 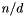 is in canonical form, meaning that
is in canonical form, meaning that  and
and 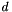 have no common factors,
have no common factors, 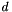 is positive, and if
is positive, and if  is zero then
is zero then 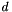 is one;
is one;closedis set totrueif and only if the upper boundary of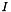 is closed (i.e., it is included in the interval).
is closed (i.e., it is included in the interval).
Definition at line 294 of file Box_inlines.hh.
References Parma_Polyhedra_Library::assign_r(), Parma_Polyhedra_Library::Variable::id(), PPL_DIRTY_TEMP, and Parma_Polyhedra_Library::ROUND_NOT_NEEDED.
Referenced by Parma_Polyhedra_Library::Grid::Grid(), and Parma_Polyhedra_Library::Polyhedron::Polyhedron().
|
inline |
Returns a 32-bit hash code for *this.
If x and y are such that x == y, then x.hash_code() == y.hash_code().
Definition at line 137 of file Box_inlines.hh.
References Parma_Polyhedra_Library::hash_code_from_dimension().
| void Parma_Polyhedra_Library::Box< ITV >::intersection_assign | ( | const Box< ITV > & | y | ) |
Assigns to *this the intersection of *this and y.
- Exceptions
-
std::invalid_argument Thrown if *thisandyare dimension-incompatible.
Definition at line 1901 of file Box_templates.hh.
References Parma_Polyhedra_Library::Box< ITV >::marked_empty(), Parma_Polyhedra_Library::Box< ITV >::OK(), Parma_Polyhedra_Library::Box< ITV >::seq, Parma_Polyhedra_Library::Box< ITV >::set_empty(), Parma_Polyhedra_Library::Box< ITV >::space_dimension(), and Parma_Polyhedra_Library::Box< ITV >::throw_dimension_incompatible().
Referenced by Parma_Polyhedra_Library::Box< ITV >::Box().
| bool Parma_Polyhedra_Library::Box< ITV >::is_bounded | ( | ) | const |
Returns true if and only if *this is a bounded box.
Definition at line 1508 of file Box_templates.hh.
| bool Parma_Polyhedra_Library::Box< ITV >::is_discrete | ( | ) | const |
Returns true if and only if *this is discrete.
Definition at line 1494 of file Box_templates.hh.
| bool Parma_Polyhedra_Library::Box< ITV >::is_disjoint_from | ( | const Box< ITV > & | y | ) | const |
Returns true if and only if *this and y are disjoint.
- Exceptions
-
std::invalid_argument Thrown if xandyare dimension-incompatible.
Definition at line 1319 of file Box_templates.hh.
References Parma_Polyhedra_Library::Box< ITV >::marked_empty(), Parma_Polyhedra_Library::Box< ITV >::seq, Parma_Polyhedra_Library::Box< ITV >::space_dimension(), and Parma_Polyhedra_Library::Box< ITV >::throw_dimension_incompatible().
|
inline |
Returns true if and only if *this is an empty box.
Definition at line 183 of file Box_inlines.hh.
Referenced by Parma_Polyhedra_Library::BD_Shape< T >::BD_Shape(), Parma_Polyhedra_Library::Box< ITV >::contains(), Parma_Polyhedra_Library::Box< ITV >::difference_assign(), Parma_Polyhedra_Library::Grid::Grid(), Parma_Polyhedra_Library::Box< ITV >::l_m_distance_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::Octagonal_Shape(), Parma_Polyhedra_Library::operator==(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::Pointset_Powerset(), Parma_Polyhedra_Library::Polyhedron::Polyhedron(), Parma_Polyhedra_Library::Box< ITV >::simplify_using_context_assign(), Parma_Polyhedra_Library::Box< ITV >::time_elapse_assign(), Parma_Polyhedra_Library::Box< ITV >::upper_bound_assign(), Parma_Polyhedra_Library::Box< ITV >::upper_bound_assign_if_exact(), and Parma_Polyhedra_Library::Box< ITV >::wrap_assign().
| bool Parma_Polyhedra_Library::Box< ITV >::is_topologically_closed | ( | ) | const |
Returns true if and only if *this is a topologically closed subset of the vector space.
Definition at line 1479 of file Box_templates.hh.
| bool Parma_Polyhedra_Library::Box< ITV >::is_universe | ( | ) | const |
Returns true if and only if *this is a universe box.
Definition at line 1465 of file Box_templates.hh.
| void Parma_Polyhedra_Library::Box< ITV >::limited_CC76_extrapolation_assign | ( | const Box< ITV > & | y, |
| const Constraint_System & | cs, | ||
| unsigned * | tp = 0 |
||
| ) |
Improves the result of the CC76-extrapolation computation by also enforcing those constraints in cs that are satisfied by all the points of *this.
- Parameters
-
y A box that must be contained in *this.cs The system of constraints used to improve the widened box. tp An optional pointer to an unsigned variable storing the number of available tokens (to be used when applying the widening with tokens delay technique).
- Exceptions
-
std::invalid_argument Thrown if *this,yandcsare dimension-incompatible or ifcscontains a strict inequality.
Definition at line 4155 of file Box_templates.hh.
References Parma_Polyhedra_Library::Box< ITV >::CC76_widening_assign(), Parma_Polyhedra_Library::Box< ITV >::marked_empty(), Parma_Polyhedra_Library::Constraint_System::space_dimension(), Parma_Polyhedra_Library::Box< ITV >::space_dimension(), and Parma_Polyhedra_Library::UNIVERSE.
|
inline |
Swaps *this with y (*this and y can be dimension-incompatible).
Definition at line 84 of file Box_inlines.hh.
References Parma_Polyhedra_Library::Box< ITV >::seq, Parma_Polyhedra_Library::Box< ITV >::status, and Parma_Polyhedra_Library::swap().
Referenced by Parma_Polyhedra_Library::Box< ITV >::Box(), and Parma_Polyhedra_Library::Box< ITV >::swap().
| void Parma_Polyhedra_Library::Box< ITV >::map_space_dimensions | ( | const Partial_Function & | pfunc | ) |
Remaps the dimensions of the vector space according to a partial function.
- Parameters
-
pfunc The partial function specifying the destiny of each dimension.
The template type parameter Partial_Function must provide the following methods.
returns true if and only if the represented partial function has an empty co-domain (i.e., it is always undefined). The has_empty_codomain() method will always be called before the methods below. However, if has_empty_codomain() returns true, none of the functions below will be called.
returns the maximum value that belongs to the co-domain of the partial function.
Let 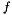 be the represented function and
be the represented function and  be the value of
be the value of i. If 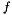 is defined in
is defined in  , then
, then 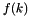 is assigned to
is assigned to j and true is returned. If 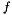 is undefined in
is undefined in  , then
, then false is returned.
The result is undefined if pfunc does not encode a partial function with the properties described in the specification of the mapping operator.
Definition at line 2282 of file Box_templates.hh.
References Parma_Polyhedra_Library::Partial_Function::has_empty_codomain(), Parma_Polyhedra_Library::Partial_Function::maps(), Parma_Polyhedra_Library::Partial_Function::max_in_codomain(), Parma_Polyhedra_Library::Box< ITV >::seq, and Parma_Polyhedra_Library::swap().
|
inlineprivate |
Returns true if and only if the box is known to be empty.
The return value false does not necessarily implies that *this is non-empty.
Definition at line 38 of file Box_inlines.hh.
Referenced by Parma_Polyhedra_Library::Box< ITV >::Box(), Parma_Polyhedra_Library::Box< ITV >::concatenate_assign(), Parma_Polyhedra_Library::Box< ITV >::intersection_assign(), Parma_Polyhedra_Library::Box< ITV >::is_disjoint_from(), Parma_Polyhedra_Library::Box< ITV >::l_m_distance_assign(), Parma_Polyhedra_Library::Box< ITV >::limited_CC76_extrapolation_assign(), Parma_Polyhedra_Library::Box< ITV >::simplify_using_context_assign(), and Parma_Polyhedra_Library::Box< ITV >::time_elapse_assign().
|
private |
Maximizes or minimizes expr subject to *this.
- Parameters
-
expr The linear expression to be maximized or minimized subject to *this;maximize trueif maximization is what is wanted;ext_n The numerator of the extremum value; ext_d The denominator of the extremum value; included trueif and only if the extremum ofexprcan actually be reached in*this;g When maximization or minimization succeeds, will be assigned a point or closure point where exprreaches the corresponding extremum value.
- Exceptions
-
std::invalid_argument Thrown if exprand*thisare dimension-incompatible.
If *this is empty or expr is not bounded in the appropriate direction, false is returned and ext_n, ext_d, included and g are left untouched.
Definition at line 1200 of file Box_templates.hh.
References Parma_Polyhedra_Library::assign_r(), Parma_Polyhedra_Library::Linear_Expression::coefficient(), Parma_Polyhedra_Library::exact_div_assign(), Parma_Polyhedra_Library::lcm_assign(), Parma_Polyhedra_Library::Generator::point(), PPL_DIRTY_TEMP, PPL_DIRTY_TEMP_COEFFICIENT, Parma_Polyhedra_Library::ROUND_NOT_NEEDED, and Parma_Polyhedra_Library::Boundary_NS::sgn().
|
private |
Maximizes or minimizes expr subject to *this.
- Parameters
-
expr The linear expression to be maximized or minimized subject to *this;maximize trueif maximization is what is wanted;ext_n The numerator of the extremum value; ext_d The denominator of the extremum value; included trueif and only if the extremum ofexprcan actually be reached in*this;
- Exceptions
-
std::invalid_argument Thrown if exprand*thisare dimension-incompatible.
If *this is empty or expr is not bounded in the appropriate direction, false is returned and ext_n, ext_d, included and point are left untouched.
Definition at line 1123 of file Box_templates.hh.
References Parma_Polyhedra_Library::assign_r(), Parma_Polyhedra_Library::Linear_Expression::begin(), Parma_Polyhedra_Library::Linear_Expression::end(), Parma_Polyhedra_Library::Linear_Expression::inhomogeneous_term(), Parma_Polyhedra_Library::is_canonical(), PPL_DIRTY_TEMP, Parma_Polyhedra_Library::ROUND_NOT_NEEDED, Parma_Polyhedra_Library::Boundary_NS::sgn(), and Parma_Polyhedra_Library::Linear_Expression::space_dimension().
|
inlinestatic |
Returns the maximum space dimension that a Box can handle.
Definition at line 129 of file Box_inlines.hh.
Referenced by Parma_Polyhedra_Library::Box< ITV >::Box(), and Parma_Polyhedra_Library::max_space_dimension().
|
inline |
Returns true if and only if *this is not empty and expr is bounded from above in *this, in which case the supremum value is computed.
- Parameters
-
expr The linear expression to be maximized subject to *this;sup_n The numerator of the supremum value; sup_d The denominator of the supremum value; maximum trueif and only if the supremum is also the maximum value.
- Exceptions
-
std::invalid_argument Thrown if exprand*thisare dimension-incompatible.
If *this is empty or expr is not bounded from above, false is returned and sup_n, sup_d and maximum are left untouched.
Definition at line 201 of file Box_inlines.hh.
|
inline |
Returns true if and only if *this is not empty and expr is bounded from above in *this, in which case the supremum value and a point where expr reaches it are computed.
- Parameters
-
expr The linear expression to be maximized subject to *this;sup_n The numerator of the supremum value; sup_d The denominator of the supremum value; maximum trueif and only if the supremum is also the maximum value;g When maximization succeeds, will be assigned the point or closure point where exprreaches its supremum value.
- Exceptions
-
std::invalid_argument Thrown if exprand*thisare dimension-incompatible.
If *this is empty or expr is not bounded from above, false is returned and sup_n, sup_d, maximum and g are left untouched.
Definition at line 209 of file Box_inlines.hh.
|
inline |
Returns true if and only if *this is not empty and expr is bounded from below in *this, in which case the infimum value is computed.
- Parameters
-
expr The linear expression to be minimized subject to *this;inf_n The numerator of the infimum value; inf_d The denominator of the infimum value; minimum trueif and only if the infimum is also the minimum value.
- Exceptions
-
std::invalid_argument Thrown if exprand*thisare dimension-incompatible.
If *this is empty or expr is not bounded from below, false is returned and inf_n, inf_d and minimum are left untouched.
Definition at line 217 of file Box_inlines.hh.
|
inline |
Returns true if and only if *this is not empty and expr is bounded from below in *this, in which case the infimum value and a point where expr reaches it are computed.
- Parameters
-
expr The linear expression to be minimized subject to *this;inf_n The numerator of the infimum value; inf_d The denominator of the infimum value; minimum trueif and only if the infimum is also the minimum value;g When minimization succeeds, will be assigned a point or closure point where exprreaches its infimum value.
- Exceptions
-
std::invalid_argument Thrown if exprand*thisare dimension-incompatible.
If *this is empty or expr is not bounded from below, false is returned and inf_n, inf_d, minimum and g are left untouched.
Definition at line 225 of file Box_inlines.hh.
|
inline |
Returns a minimized system of congruences approximating *this.
Definition at line 393 of file Box_inlines.hh.
| Constraint_System Parma_Polyhedra_Library::Box< ITV >::minimized_constraints | ( | ) | const |
Returns a minimized system of constraints defining *this.
Definition at line 4292 of file Box_templates.hh.
References Parma_Polyhedra_Library::Constraint_System::insert(), PPL_DIRTY_TEMP_COEFFICIENT, Parma_Polyhedra_Library::Constraint_System::set_space_dimension(), Parma_Polyhedra_Library::Constraint_System::zero_dim_empty(), and Parma_Polyhedra_Library::Constraint::zero_dim_false().
| bool Parma_Polyhedra_Library::Box< ITV >::OK | ( | ) | const |
Returns true if and only if *this satisfies all its invariants.
Definition at line 1400 of file Box_templates.hh.
References Parma_Polyhedra_Library::Box< ITV >::check_empty(), and Parma_Polyhedra_Library::Box< ITV >::reset_empty_up_to_date().
Referenced by Parma_Polyhedra_Library::Box< ITV >::Status::ascii_load(), Parma_Polyhedra_Library::Box< ITV >::Box(), Parma_Polyhedra_Library::Box< ITV >::concatenate_assign(), Parma_Polyhedra_Library::Box< ITV >::intersection_assign(), Parma_Polyhedra_Library::Box< ITV >::simplify_using_context_assign(), Parma_Polyhedra_Library::Box< ITV >::time_elapse_assign(), Parma_Polyhedra_Library::Box< ITV >::upper_bound_assign(), and Parma_Polyhedra_Library::Box< ITV >::wrap_assign().
|
inline |
The assignment operator (*this and y can be dimension-incompatible).
Definition at line 76 of file Box_inlines.hh.
References Parma_Polyhedra_Library::Box< ITV >::seq, and Parma_Polyhedra_Library::Box< ITV >::status.
|
inlineprivate |
Returns a reference the interval that bounds the box on the k-th space dimension.
Definition at line 143 of file Box_inlines.hh.
| void Parma_Polyhedra_Library::Box< ITV >::print | ( | ) | const |
Prints *this to std::cerr using operator<<.
|
inline |
Use the constraint c for constraint propagation on *this.
- Parameters
-
c The constraint to be used for constraint propagation.
- Exceptions
-
std::invalid_argument Thrown if *thisandcare dimension-incompatible.
Definition at line 522 of file Box_inlines.hh.
References Parma_Polyhedra_Library::Constraint::space_dimension().
|
private |
Propagates the constraint c to refine *this.
- Parameters
-
c The constraint to be propagated.
- Warning
- If
cand*thisare dimension-incompatible, the behavior is undefined. - This method may lead to non-termination.
For any expression 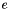 , we denote by
, we denote by 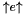 (resp.,
(resp., 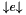 ) the result of any computation that is guaranteed to yield an upper (resp., lower) approximation of
) the result of any computation that is guaranteed to yield an upper (resp., lower) approximation of 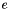 . So there exists
. So there exists 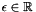 with
with 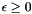 such that
such that 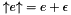 . If
. If 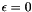 we say that the computation of
we say that the computation of 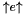 is exact; we say it is inexact otherwise. Similarly for
is exact; we say it is inexact otherwise. Similarly for 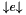 .
.
Consider a constraint of the general form
![\[ z + \sum_{i \in I}{a_ix_i} \relsym 0, \]](form_774.png)
where 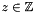 ,
, 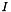 is a set of indices,
is a set of indices, 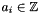 with
with 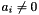 for each
for each 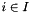 , and
, and 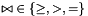 . The set
. The set 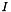 is subdivided into the disjoint sets
is subdivided into the disjoint sets  and
and  such that, for each
such that, for each 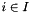 ,
, 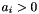 if
if 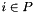 and
and 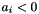 if
if 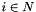 . Suppose that, for each
. Suppose that, for each 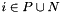 a variation interval
a variation interval 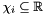 is known for
is known for 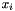 and that the infimum and the supremum of
and that the infimum and the supremum of 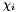 are denoted, respectively, by
are denoted, respectively, by 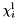 and
and 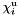 , where
, where 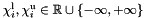 .
.
For each 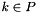 , we have
, we have
![\[ x_k \relsym \frac{1}{a_k} \Biggl( - z - \sum_{i \in N}{a_ix_i} - \sum_{\genfrac{}{}{0pt}{} {\scriptstyle i \in P} {\scriptstyle i \neq k}}{a_ix_i} \Biggr). \]](form_792.png)
Thus, if 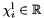 for each
for each 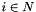 and
and 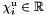 for each
for each 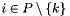 , we have
, we have
![\[ x_k \geq \Biggl\downarrow \frac{1}{a_k} \Biggl( - z - \sum_{i \in N}{a_i\chi_i^\mathrm{l}} - \sum_{\genfrac{}{}{0pt}{} {\scriptstyle i \in P} {\scriptstyle i \neq k}}{a_i\chi_i^\mathrm{u}} \Biggr) \Biggr\downarrow \]](form_796.png)
and, if 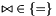 ,
, 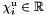 for each
for each 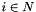 and
and 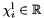 for each
for each 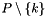 ,
,
![\[ x_k \leq \Biggl\uparrow \frac{1}{a_k} \Biggl( - z - \sum_{i \in N}{a_i\chi_i^\mathrm{u}} - \sum_{\genfrac{}{}{0pt}{} {\scriptstyle i \in P} {\scriptstyle i \neq k}}{a_i\chi_i^\mathrm{l}} \Biggr) \Biggl\uparrow. \]](form_799.png)
In the first inequality, the relation is strict if 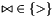 , or if
, or if 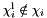 for some
for some 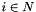 , or if
, or if 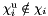 for some
for some 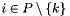 , or if the computation is inexact. In the second inequality, the relation is strict if
, or if the computation is inexact. In the second inequality, the relation is strict if 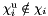 for some
for some 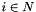 , or if
, or if 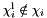 for some
for some 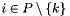 , or if the computation is inexact.
, or if the computation is inexact.
For each 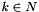 , we have
, we have
![\[ \frac{1}{a_k} \Biggl( - z - \sum_{\genfrac{}{}{0pt}{} {\scriptstyle i \in N} {\scriptstyle i \neq k}}{a_ix_i} - \sum_{i \in P}{a_ix_i} \Biggr) \relsym x_k. \]](form_804.png)
Thus, if 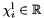 for each
for each 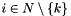 and
and 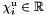 for each
for each 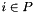 , we have
, we have
![\[ \Biggl\uparrow \frac{1}{a_k} \Biggl( - z - \sum_{\genfrac{}{}{0pt}{} {\scriptstyle i \in N} {\scriptstyle i \neq k}}{a_i\chi_i^\mathrm{l}} - \sum_{i \in P}{a_i\chi_i^\mathrm{u}} \Biggr) \Biggl\uparrow \geq x_k \]](form_806.png)
and, if 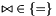 ,
, 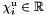 for each
for each 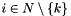 and
and 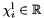 for each
for each 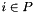 ,
,
![\[ \Biggl\downarrow \frac{1}{a_k} \Biggl( - z - \sum_{\genfrac{}{}{0pt}{} {\scriptstyle i \in N} {\scriptstyle i \neq k}}{a_i\chi_i^\mathrm{u}} - \sum_{i \in P}{a_i\chi_i^\mathrm{l}} \Biggr) \Biggl\downarrow \leq x_k. \]](form_807.png)
In the first inequality, the relation is strict if 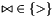 , or if
, or if 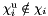 for some
for some 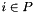 , or if
, or if 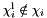 for some
for some 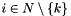 , or if the computation is inexact. In the second inequality, the relation is strict if
, or if the computation is inexact. In the second inequality, the relation is strict if 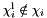 for some
for some 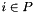 , or if
, or if 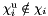 for some
for some 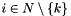 , or if the computation is inexact.
, or if the computation is inexact.
Definition at line 2581 of file Box_templates.hh.
References Parma_Polyhedra_Library::assign_r(), Parma_Polyhedra_Library::Expression_Adapter< T >::begin(), Parma_Polyhedra_Library::Constraint::EQUALITY, Parma_Polyhedra_Library::Constraint::expression(), Parma_Polyhedra_Library::GREATER_OR_EQUAL, Parma_Polyhedra_Library::GREATER_THAN, Parma_Polyhedra_Library::i_constraint(), Parma_Polyhedra_Library::Variable::id(), Parma_Polyhedra_Library::Constraint::inhomogeneous_term(), Parma_Polyhedra_Library::Expression_Hide_Last< T >::last_nonzero(), Parma_Polyhedra_Library::LESS_OR_EQUAL, Parma_Polyhedra_Library::LESS_THAN, Parma_Polyhedra_Library::Expression_Hide_Last< T >::lower_bound(), Parma_Polyhedra_Library::Constraint::NONSTRICT_INEQUALITY, Parma_Polyhedra_Library::Implementation::Boxes::propagate_constraint_check_result(), Parma_Polyhedra_Library::ROUND_DOWN, Parma_Polyhedra_Library::ROUND_UP, Parma_Polyhedra_Library::Boundary_NS::sgn(), Parma_Polyhedra_Library::Constraint::space_dimension(), Parma_Polyhedra_Library::Constraint::STRICT_INEQUALITY, Parma_Polyhedra_Library::T_MAYBE, Parma_Polyhedra_Library::T_NO, Parma_Polyhedra_Library::T_YES, and Parma_Polyhedra_Library::Constraint::type().
|
inline |
Use the constraints in cs for constraint propagation on *this.
- Parameters
-
cs The constraints to be used for constraint propagation. max_iterations The maximum number of propagation steps for each constraint in cs. If zero (the default), the number of propagation steps will be unbounded, possibly resulting in an infinite loop.
- Exceptions
-
std::invalid_argument Thrown if *thisandcsare dimension-incompatible.
- Warning
- This method may lead to non-termination if
max_iterationsis 0.
Definition at line 538 of file Box_inlines.hh.
References Parma_Polyhedra_Library::Constraint_System::space_dimension().
|
private |
Propagates the constraints in cs to refine *this.
- Parameters
-
cs The constraints to be propagated. max_iterations The maximum number of propagation steps for each constraint in cs. If zero, the number of propagation steps will be unbounded, possibly resulting in an infinite loop.
- Warning
- If
csand*thisare dimension-incompatible, the behavior is undefined. -
This method may lead to non-termination if
max_iterationsis 0.
Definition at line 3030 of file Box_templates.hh.
References Parma_Polyhedra_Library::Constraint_System::begin(), Parma_Polyhedra_Library::Constraint_System::end(), Parma_Polyhedra_Library::maybe_abandon(), Parma_Polyhedra_Library::Implementation::num_constraints(), Parma_Polyhedra_Library::Constraint_System::space_dimension(), WEIGHT_ADD_MUL, and WEIGHT_BEGIN.
Referenced by Parma_Polyhedra_Library::Box< ITV >::Box().
|
inlinestaticprivate |
WRITE ME.
Definition at line 401 of file Box_inlines.hh.
References Parma_Polyhedra_Library::assign_r(), Parma_Polyhedra_Library::EQUAL, Parma_Polyhedra_Library::Constraint::EQUALITY, Parma_Polyhedra_Library::GREATER_OR_EQUAL, Parma_Polyhedra_Library::GREATER_THAN, Parma_Polyhedra_Library::I_ANY, Parma_Polyhedra_Library::i_constraint(), Parma_Polyhedra_Library::LESS_OR_EQUAL, Parma_Polyhedra_Library::LESS_THAN, Parma_Polyhedra_Library::Constraint::NONSTRICT_INEQUALITY, PPL_DIRTY_TEMP, Parma_Polyhedra_Library::ROUND_NOT_NEEDED, and Parma_Polyhedra_Library::Constraint::STRICT_INEQUALITY.
|
private |
Uses the constraint c to refine *this.
- Parameters
-
c The constraint to be used for the refinement.
- Warning
- If
cand*thisare dimension-incompatible, the behavior is undefined.
Definition at line 2473 of file Box_templates.hh.
References Parma_Polyhedra_Library::Constraint::coefficient(), Parma_Polyhedra_Library::Box_Helpers::extract_interval_constraint(), Parma_Polyhedra_Library::Constraint::inhomogeneous_term(), Parma_Polyhedra_Library::Constraint::is_equality(), Parma_Polyhedra_Library::Constraint::is_strict_inequality(), Parma_Polyhedra_Library::Constraint::space_dimension(), and Parma_Polyhedra_Library::Constraint::type().
|
private |
Uses the constraints in cs to refine *this.
- Parameters
-
cs The constraints to be used for the refinement. To avoid termination problems, each constraint in cswill be used for a single refinement step.
- Warning
- If
csand*thisare dimension-incompatible, the behavior is undefined.
Definition at line 2503 of file Box_templates.hh.
References Parma_Polyhedra_Library::Constraint_System::begin(), Parma_Polyhedra_Library::Constraint_System::end(), and Parma_Polyhedra_Library::Constraint_System::space_dimension().
|
private |
Uses the congruence cg to refine *this.
- Parameters
-
cg The congruence to be added. Nontrivial proper congruences are ignored.
- Warning
- If
cgand*thisare dimension-incompatible, the behavior is undefined.
Definition at line 2514 of file Box_templates.hh.
References c, Parma_Polyhedra_Library::Congruence::is_equality(), Parma_Polyhedra_Library::Congruence::is_inconsistent(), Parma_Polyhedra_Library::Congruence::is_proper_congruence(), and Parma_Polyhedra_Library::Congruence::space_dimension().
|
private |
Uses the congruences in cgs to refine *this.
- Parameters
-
cgs The congruences to be added. Nontrivial proper congruences are ignored.
- Warning
- If
cgsand*thisare dimension-incompatible, the behavior is undefined.
Definition at line 2535 of file Box_templates.hh.
References Parma_Polyhedra_Library::Congruence_System::begin(), Parma_Polyhedra_Library::Congruence_System::end(), and Parma_Polyhedra_Library::Congruence_System::space_dimension().
|
inline |
Use the congruence cg to refine *this.
- Parameters
-
cg The congruence to be used for refinement.
- Exceptions
-
std::invalid_argument Thrown if *thisandcgare dimension-incompatible.
Definition at line 491 of file Box_inlines.hh.
References Parma_Polyhedra_Library::Congruence::space_dimension().
|
inline |
Use the congruences in cgs to refine *this.
- Parameters
-
cgs The congruences to be used for refinement.
- Exceptions
-
std::invalid_argument Thrown if *thisandcgsare dimension-incompatible.
Definition at line 506 of file Box_inlines.hh.
References Parma_Polyhedra_Library::Congruence_System::space_dimension().
|
inline |
Use the constraint c to refine *this.
- Parameters
-
c The constraint to be used for refinement.
- Exceptions
-
std::invalid_argument Thrown if *thisandcare dimension-incompatible.
Definition at line 459 of file Box_inlines.hh.
References Parma_Polyhedra_Library::Constraint::space_dimension().
|
inline |
Use the constraints in cs to refine *this.
- Parameters
-
cs The constraints to be used for refinement. To avoid termination problems, each constraint in cswill be used for a single refinement step.
- Exceptions
-
std::invalid_argument Thrown if *thisandcsare dimension-incompatible.
- Note
- The user is warned that the accuracy of this refinement operator depends on the order of evaluation of the constraints in
cs, which is in general unpredictable. If a fine control on such an order is needed, the user should consider calling the methodrefine_with_constraint(const Constraint& c)inside an appropriate looping construct.
Definition at line 476 of file Box_inlines.hh.
References Parma_Polyhedra_Library::Constraint_System::space_dimension().
| Poly_Con_Relation Parma_Polyhedra_Library::Box< ITV >::relation_with | ( | const Constraint & | c | ) | const |
Returns the relations holding between *this and the constraint c.
- Exceptions
-
std::invalid_argument Thrown if *thisand constraintcare dimension-incompatible.
Definition at line 920 of file Box_templates.hh.
References Parma_Polyhedra_Library::assign_r(), Parma_Polyhedra_Library::Expression_Adapter< T >::begin(), Parma_Polyhedra_Library::Constraint::coefficient(), Parma_Polyhedra_Library::Expression_Hide_Last< T >::end(), Parma_Polyhedra_Library::Constraint::expression(), Parma_Polyhedra_Library::Box_Helpers::extract_interval_constraint(), Parma_Polyhedra_Library::Variable::id(), Parma_Polyhedra_Library::Constraint::inhomogeneous_term(), Parma_Polyhedra_Library::interval_relation(), Parma_Polyhedra_Library::Poly_Con_Relation::is_disjoint(), Parma_Polyhedra_Library::Constraint::is_equality(), Parma_Polyhedra_Library::Poly_Con_Relation::is_included(), Parma_Polyhedra_Library::Constraint::is_inequality(), Parma_Polyhedra_Library::Constraint::is_strict_inequality(), Parma_Polyhedra_Library::Poly_Con_Relation::nothing(), PPL_DIRTY_TEMP, Parma_Polyhedra_Library::ROUND_NOT_NEEDED, Parma_Polyhedra_Library::Poly_Con_Relation::saturates(), Parma_Polyhedra_Library::Boundary_NS::sgn(), Parma_Polyhedra_Library::Constraint::space_dimension(), and Parma_Polyhedra_Library::Constraint::type().
| Poly_Con_Relation Parma_Polyhedra_Library::Box< ITV >::relation_with | ( | const Congruence & | cg | ) | const |
Returns the relations holding between *this and the congruence cg.
- Exceptions
-
std::invalid_argument Thrown if *thisand constraintcgare dimension-incompatible.
Definition at line 854 of file Box_templates.hh.
References Parma_Polyhedra_Library::assign_r(), Parma_Polyhedra_Library::Expression_Adapter< T >::begin(), c, Parma_Polyhedra_Library::Expression_Adapter< T >::end(), Parma_Polyhedra_Library::Constraint::EQUALITY, Parma_Polyhedra_Library::Congruence::expression(), Parma_Polyhedra_Library::Variable::id(), Parma_Polyhedra_Library::Congruence::inhomogeneous_term(), Parma_Polyhedra_Library::interval_relation(), Parma_Polyhedra_Library::Poly_Con_Relation::is_disjoint(), Parma_Polyhedra_Library::Congruence::is_equality(), Parma_Polyhedra_Library::Poly_Con_Relation::is_included(), Parma_Polyhedra_Library::Congruence::is_inconsistent(), Parma_Polyhedra_Library::Congruence::modulus(), PPL_DIRTY_TEMP, PPL_DIRTY_TEMP_COEFFICIENT, Parma_Polyhedra_Library::ROUND_DOWN, Parma_Polyhedra_Library::ROUND_NOT_NEEDED, Parma_Polyhedra_Library::Poly_Con_Relation::saturates(), Parma_Polyhedra_Library::Congruence::space_dimension(), and Parma_Polyhedra_Library::Poly_Con_Relation::strictly_intersects().
| Poly_Gen_Relation Parma_Polyhedra_Library::Box< ITV >::relation_with | ( | const Generator & | g | ) | const |
Returns the relations holding between *this and the generator g.
- Exceptions
-
std::invalid_argument Thrown if *thisand generatorgare dimension-incompatible.
Definition at line 1016 of file Box_templates.hh.
References Parma_Polyhedra_Library::assign_r(), Parma_Polyhedra_Library::Expression_Adapter< T >::begin(), Parma_Polyhedra_Library::Generator::coefficient(), Parma_Polyhedra_Library::Generator::divisor(), Parma_Polyhedra_Library::Expression_Hide_Last< T >::end(), Parma_Polyhedra_Library::Generator::expression(), Parma_Polyhedra_Library::Variable::id(), Parma_Polyhedra_Library::Generator::is_line(), Parma_Polyhedra_Library::Generator::is_line_or_ray(), Parma_Polyhedra_Library::Generator::is_point(), Parma_Polyhedra_Library::Generator::is_ray(), Parma_Polyhedra_Library::Poly_Gen_Relation::nothing(), PPL_DIRTY_TEMP, Parma_Polyhedra_Library::ROUND_NOT_NEEDED, Parma_Polyhedra_Library::Boundary_NS::sgn(), Parma_Polyhedra_Library::Generator::space_dimension(), and Parma_Polyhedra_Library::Poly_Gen_Relation::subsumes().
| void Parma_Polyhedra_Library::Box< ITV >::remove_higher_space_dimensions | ( | dimension_type | new_dimension | ) |
Removes the higher dimensions so that the resulting space will have dimension new_dimension.
- Exceptions
-
std::invalid_argument Thrown if new_dimensionis greater than the space dimension of*this.
Definition at line 2258 of file Box_templates.hh.
|
inline |
Removes all the specified dimensions.
- Parameters
-
vars The set of Variable objects corresponding to the dimensions to be removed.
- Exceptions
-
std::invalid_argument Thrown if *thisis dimension-incompatible with one of the Variable objects contained invars.
Definition at line 2201 of file Box_templates.hh.
References Parma_Polyhedra_Library::Variables_Set::space_dimension(), and Parma_Polyhedra_Library::swap().
|
inlineprivate |
Invalidates empty flag of *this.
Definition at line 64 of file Box_inlines.hh.
Referenced by Parma_Polyhedra_Library::Box< ITV >::OK().
|
inline |
Causes the box to become empty, i.e., to represent the empty set.
Definition at line 44 of file Box_inlines.hh.
Referenced by Parma_Polyhedra_Library::Box< ITV >::Status::ascii_load(), Parma_Polyhedra_Library::Box< ITV >::Box(), Parma_Polyhedra_Library::Box< ITV >::check_empty(), Parma_Polyhedra_Library::Box< ITV >::concatenate_assign(), Parma_Polyhedra_Library::Box< ITV >::difference_assign(), Parma_Polyhedra_Library::Box< ITV >::intersection_assign(), Parma_Polyhedra_Library::Box< ITV >::time_elapse_assign(), and Parma_Polyhedra_Library::Box< ITV >::wrap_assign().
|
inlineprivate |
Asserts the validity of the empty flag of *this.
Definition at line 58 of file Box_inlines.hh.
Referenced by Parma_Polyhedra_Library::Box< ITV >::Status::ascii_load(), and Parma_Polyhedra_Library::Box< ITV >::Box().
|
inline |
Sets to i the interval that bounds var.
- Exceptions
-
std::invalid_argument Thrown if varis not a space dimension of*this.
Definition at line 164 of file Box_inlines.hh.
References Parma_Polyhedra_Library::Variable::id(), and Parma_Polyhedra_Library::Variable::space_dimension().
|
inlineprivate |
Marks *this as definitely not empty.
Definition at line 51 of file Box_inlines.hh.
Referenced by Parma_Polyhedra_Library::Box< ITV >::check_empty(), and Parma_Polyhedra_Library::Box< ITV >::simplify_using_context_assign().
| bool Parma_Polyhedra_Library::Box< ITV >::simplify_using_context_assign | ( | const Box< ITV > & | y | ) |
Assigns to *this a meet-preserving simplification of *this with respect to y. If false is returned, then the intersection is empty.
- Exceptions
-
std::invalid_argument Thrown if *thisandyare dimension-incompatible.
Definition at line 2075 of file Box_templates.hh.
References Parma_Polyhedra_Library::Box< ITV >::is_empty(), Parma_Polyhedra_Library::Box< ITV >::marked_empty(), Parma_Polyhedra_Library::Box< ITV >::OK(), Parma_Polyhedra_Library::Box< ITV >::seq, Parma_Polyhedra_Library::Box< ITV >::set_nonempty(), Parma_Polyhedra_Library::Box< ITV >::space_dimension(), Parma_Polyhedra_Library::Box< ITV >::throw_dimension_incompatible(), and Parma_Polyhedra_Library::UNIVERSE.
|
inline |
Returns the dimension of the vector space enclosing *this.
Definition at line 123 of file Box_inlines.hh.
Referenced by Parma_Polyhedra_Library::BD_Shape< T >::BD_Shape(), Parma_Polyhedra_Library::Box< ITV >::Box(), Parma_Polyhedra_Library::Box< ITV >::concatenate_assign(), Parma_Polyhedra_Library::Box< ITV >::contains(), Parma_Polyhedra_Library::Box< ITV >::difference_assign(), Parma_Polyhedra_Library::Grid::Grid(), Parma_Polyhedra_Library::Box< ITV >::intersection_assign(), Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >::intervalize(), Parma_Polyhedra_Library::Box< ITV >::is_disjoint_from(), Parma_Polyhedra_Library::Box< ITV >::l_m_distance_assign(), Parma_Polyhedra_Library::Box< ITV >::limited_CC76_extrapolation_assign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::Octagonal_Shape(), Parma_Polyhedra_Library::operator==(), Parma_Polyhedra_Library::Polyhedron::Polyhedron(), Parma_Polyhedra_Library::Box< ITV >::simplify_using_context_assign(), Parma_Polyhedra_Library::Box< ITV >::throw_dimension_incompatible(), Parma_Polyhedra_Library::Box< ITV >::time_elapse_assign(), Parma_Polyhedra_Library::Box< ITV >::upper_bound_assign(), Parma_Polyhedra_Library::Box< ITV >::upper_bound_assign_if_exact(), and Parma_Polyhedra_Library::Box< ITV >::wrap_assign().
|
inline |
Returns true if and only if *this strictly contains y.
- Exceptions
-
std::invalid_argument Thrown if xandyare dimension-incompatible.
Definition at line 233 of file Box_inlines.hh.
References Parma_Polyhedra_Library::Box< ITV >::contains().
|
staticprivate |
Definition at line 4537 of file Box_templates.hh.
|
private |
Definition at line 4459 of file Box_templates.hh.
References Parma_Polyhedra_Library::Box< ITV >::space_dimension().
Referenced by Parma_Polyhedra_Library::Box< ITV >::contains(), Parma_Polyhedra_Library::Box< ITV >::intersection_assign(), Parma_Polyhedra_Library::Box< ITV >::is_disjoint_from(), Parma_Polyhedra_Library::Box< ITV >::simplify_using_context_assign(), Parma_Polyhedra_Library::Box< ITV >::time_elapse_assign(), Parma_Polyhedra_Library::Box< ITV >::upper_bound_assign(), and Parma_Polyhedra_Library::Box< ITV >::upper_bound_assign_if_exact().
|
private |
Definition at line 4471 of file Box_templates.hh.
|
private |
Definition at line 4482 of file Box_templates.hh.
References Parma_Polyhedra_Library::Constraint::space_dimension().
|
private |
Definition at line 4493 of file Box_templates.hh.
References Parma_Polyhedra_Library::Congruence::space_dimension().
|
private |
Definition at line 4504 of file Box_templates.hh.
References Parma_Polyhedra_Library::Constraint_System::space_dimension().
|
private |
Definition at line 4515 of file Box_templates.hh.
References Parma_Polyhedra_Library::Congruence_System::space_dimension().
|
private |
Definition at line 4526 of file Box_templates.hh.
References Parma_Polyhedra_Library::Generator::space_dimension().
|
private |
Definition at line 4557 of file Box_templates.hh.
References Parma_Polyhedra_Library::Linear_Expression::space_dimension().
|
private |
Definition at line 4571 of file Box_templates.hh.
References Parma_Polyhedra_Library::Linear_Form< C >::space_dimension().
|
staticprivate |
Definition at line 4546 of file Box_templates.hh.
|
staticprivate |
Definition at line 4584 of file Box_templates.hh.
| void Parma_Polyhedra_Library::Box< ITV >::time_elapse_assign | ( | const Box< ITV > & | y | ) |
Assigns to *this the result of computing the time-elapse between *this and y.
- Exceptions
-
std::invalid_argument Thrown if *thisandyare dimension-incompatible.
Definition at line 2157 of file Box_templates.hh.
References Parma_Polyhedra_Library::Box< ITV >::is_empty(), Parma_Polyhedra_Library::Box< ITV >::marked_empty(), Parma_Polyhedra_Library::Box< ITV >::OK(), Parma_Polyhedra_Library::Box< ITV >::seq, Parma_Polyhedra_Library::Box< ITV >::set_empty(), Parma_Polyhedra_Library::Box< ITV >::space_dimension(), and Parma_Polyhedra_Library::Box< ITV >::throw_dimension_incompatible().
| void Parma_Polyhedra_Library::Box< ITV >::topological_closure_assign | ( | ) |
Assigns to *this its topological closure.
Definition at line 1659 of file Box_templates.hh.
|
inline |
Returns the total size in bytes of the memory occupied by *this.
Definition at line 117 of file Box_inlines.hh.
References Parma_Polyhedra_Library::external_memory_in_bytes().
|
inline |
Computes the cylindrification of *this with respect to space dimension var, assigning the result to *this.
- Parameters
-
var The space dimension that will be unconstrained.
- Exceptions
-
std::invalid_argument Thrown if varis not a space dimension of*this.
Definition at line 555 of file Box_inlines.hh.
References Parma_Polyhedra_Library::Variable::id(), and Parma_Polyhedra_Library::UNIVERSE.
| void Parma_Polyhedra_Library::Box< ITV >::unconstrain | ( | const Variables_Set & | vars | ) |
Computes the cylindrification of *this with respect to the set of space dimensions vars, assigning the result to *this.
- Parameters
-
vars The set of space dimension that will be unconstrained.
- Exceptions
-
std::invalid_argument Thrown if *thisis dimension-incompatible with one of the Variable objects contained invars.
Definition at line 1622 of file Box_templates.hh.
References Parma_Polyhedra_Library::Variables_Set::space_dimension(), and Parma_Polyhedra_Library::UNIVERSE.
| void Parma_Polyhedra_Library::Box< ITV >::upper_bound_assign | ( | const Box< ITV > & | y | ) |
Assigns to *this the smallest box containing the union of *this and y.
- Exceptions
-
std::invalid_argument Thrown if *thisandyare dimension-incompatible.
Definition at line 1938 of file Box_templates.hh.
References Parma_Polyhedra_Library::Box< ITV >::is_empty(), Parma_Polyhedra_Library::Box< ITV >::OK(), Parma_Polyhedra_Library::Box< ITV >::seq, Parma_Polyhedra_Library::Box< ITV >::space_dimension(), and Parma_Polyhedra_Library::Box< ITV >::throw_dimension_incompatible().
|
inline |
If the upper bound of *this and y is exact, it is assigned to *this and true is returned, otherwise false is returned.
- Exceptions
-
std::invalid_argument Thrown if *thisandyare dimension-incompatible.
Definition at line 1343 of file Box_templates.hh.
References Parma_Polyhedra_Library::Box< ITV >::is_empty(), Parma_Polyhedra_Library::Box< ITV >::seq, Parma_Polyhedra_Library::Box< ITV >::space_dimension(), and Parma_Polyhedra_Library::Box< ITV >::throw_dimension_incompatible().
|
inline |
Same as CC76_widening_assign(y, tp).
Definition at line 387 of file Box_inlines.hh.
| void Parma_Polyhedra_Library::Box< ITV >::wrap_assign | ( | const Variables_Set & | vars, |
| Bounded_Integer_Type_Width | w, | ||
| Bounded_Integer_Type_Representation | r, | ||
| Bounded_Integer_Type_Overflow | o, | ||
| const Constraint_System * | cs_p = 0, |
||
| unsigned | complexity_threshold = 16, |
||
| bool | wrap_individually = true |
||
| ) |
Wraps the specified dimensions of the vector space.
- Parameters
-
vars The set of Variable objects corresponding to the space dimensions to be wrapped. w The width of the bounded integer type corresponding to all the dimensions to be wrapped. r The representation of the bounded integer type corresponding to all the dimensions to be wrapped. o The overflow behavior of the bounded integer type corresponding to all the dimensions to be wrapped. cs_p Possibly null pointer to a constraint system. When non-null, the pointed-to constraint system is assumed to represent the conditional or looping construct guard with respect to which wrapping is performed. Since wrapping requires the computation of upper bounds and due to non-distributivity of constraint refinement over upper bounds, passing a constraint system in this way can be more precise than refining the result of the wrapping operation with the constraints in *cs_p.complexity_threshold A precision parameter which is ignored for the Box domain. wrap_individually A precision parameter which is ignored for the Box domain.
- Exceptions
-
std::invalid_argument Thrown if *thisis dimension-incompatible with one of the Variable objects contained invarsor with*cs_p.
Definition at line 1671 of file Box_templates.hh.
References Parma_Polyhedra_Library::Constraint_System::begin(), c, Parma_Polyhedra_Library::Constraint::coefficient(), Parma_Polyhedra_Library::Coefficient_one(), Parma_Polyhedra_Library::Constraint_System::end(), Parma_Polyhedra_Library::Box_Helpers::extract_interval_constraint(), Parma_Polyhedra_Library::GREATER_OR_EQUAL, Parma_Polyhedra_Library::i_constraint(), Parma_Polyhedra_Library::Constraint::inhomogeneous_term(), Parma_Polyhedra_Library::Box< ITV >::is_empty(), Parma_Polyhedra_Library::Constraint::is_inconsistent(), Parma_Polyhedra_Library::LESS_OR_EQUAL, Parma_Polyhedra_Library::LESS_THAN, Parma_Polyhedra_Library::mul_2exp_assign(), Parma_Polyhedra_Library::neg_assign(), Parma_Polyhedra_Library::Box< ITV >::OK(), Parma_Polyhedra_Library::OVERFLOW_IMPOSSIBLE, Parma_Polyhedra_Library::OVERFLOW_UNDEFINED, Parma_Polyhedra_Library::OVERFLOW_WRAPS, PPL_DIRTY_TEMP, PPL_DIRTY_TEMP_COEFFICIENT, PPL_USED, Parma_Polyhedra_Library::Box< ITV >::seq, Parma_Polyhedra_Library::Box< ITV >::set_empty(), Parma_Polyhedra_Library::SIGNED_2_COMPLEMENT, Parma_Polyhedra_Library::Variables_Set::space_dimension(), Parma_Polyhedra_Library::Constraint_System::space_dimension(), Parma_Polyhedra_Library::Box< ITV >::space_dimension(), Parma_Polyhedra_Library::Constraint::type(), Parma_Polyhedra_Library::UNIVERSE, Parma_Polyhedra_Library::UNSIGNED, and Parma_Polyhedra_Library::Implementation::wrap_assign().
Friends And Related Function Documentation
|
related |
Computes the euclidean distance between x and y.
If the euclidean distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.
The direction of the approximation is specified by dir.
All computations are performed using variables of type Checked_Number<To, Extended_Number_Policy>.
|
related |
Computes the euclidean distance between x and y.
If the euclidean distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.
The direction of the approximation is specified by dir.
All computations are performed using variables of type Checked_Number<Temp, Extended_Number_Policy>.
|
related |
Computes the euclidean distance between x and y.
If the euclidean distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.
The direction of the approximation is specified by dir.
All computations are performed using the temporary variables tmp0, tmp1 and tmp2.
|
related |
Definition at line 624 of file Box_inlines.hh.
|
related |
Definition at line 638 of file Box_inlines.hh.
References PPL_DIRTY_TEMP.
|
related |
Definition at line 652 of file Box_inlines.hh.
|
related |
Computes the  distance between
distance between x and y.
If the  distance between
distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.
The direction of the approximation is specified by dir.
All computations are performed using variables of type Checked_Number<To, Extended_Number_Policy>.
|
related |
Computes the  distance between
distance between x and y.
If the  distance between
distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.
The direction of the approximation is specified by dir.
All computations are performed using variables of type Checked_Number<Temp, Extended_Number_Policy>.
|
related |
Computes the  distance between
distance between x and y.
If the  distance between
distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.
The direction of the approximation is specified by dir.
All computations are performed using the temporary variables tmp0, tmp1 and tmp2.
|
related |
Definition at line 665 of file Box_inlines.hh.
|
related |
Definition at line 679 of file Box_inlines.hh.
References PPL_DIRTY_TEMP.
|
related |
Definition at line 693 of file Box_inlines.hh.
|
related |
Helper function for computing distances.
|
related |
Definition at line 4597 of file Box_templates.hh.
References Parma_Polyhedra_Library::assign_r(), Parma_Polyhedra_Library::combine(), Parma_Polyhedra_Library::finalize(), Parma_Polyhedra_Library::inverse(), Parma_Polyhedra_Library::Box< ITV >::is_empty(), Parma_Polyhedra_Library::Box< ITV >::marked_empty(), Parma_Polyhedra_Library::maybe_assign(), Parma_Polyhedra_Library::PLUS_INFINITY, Parma_Polyhedra_Library::ROUND_NOT_NEEDED, Parma_Polyhedra_Library::Box< ITV >::seq, Parma_Polyhedra_Library::Boundary_NS::sgn(), and Parma_Polyhedra_Library::Box< ITV >::space_dimension().
Returns true if and only if x and y are not the same box.
Note that x and y may be dimension-incompatible boxes: in this case, the value true is returned.
Definition at line 264 of file Box_inlines.hh.
|
related |
Output operator.
|
related |
Definition at line 4389 of file Box_templates.hh.
Returns true if and only if x and y are the same box.
Note that x and y may be dimension-incompatible boxes: in this case, the value false is returned.
Definition at line 581 of file Box_templates.hh.
Definition at line 581 of file Box_templates.hh.
|
friend |
Definition at line 1739 of file Box_defs.hh.
|
friend |
|
friend |
|
related |
Computes the rectilinear (or Manhattan) distance between x and y.
If the rectilinear distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.
The direction of the approximation is specified by dir.
All computations are performed using variables of type Checked_Number<To, Extended_Number_Policy>.
|
related |
Computes the rectilinear (or Manhattan) distance between x and y.
If the rectilinear distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.
The direction of the approximation is specified by dir.
All computations are performed using variables of type Checked_Number<Temp, Extended_Number_Policy>.
|
related |
Computes the rectilinear (or Manhattan) distance between x and y.
If the rectilinear distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.
The direction of the approximation is specified by dir.
All computations are performed using the temporary variables tmp0, tmp1 and tmp2.
|
related |
Definition at line 583 of file Box_inlines.hh.
|
related |
Definition at line 597 of file Box_inlines.hh.
References PPL_DIRTY_TEMP.
|
related |
Definition at line 611 of file Box_inlines.hh.
Definition at line 706 of file Box_inlines.hh.
References Parma_Polyhedra_Library::Box< ITV >::m_swap().
Member Data Documentation
|
private |
A sequence of intervals, one for each dimension of the vector space.
Definition at line 1765 of file Box_defs.hh.
Referenced by Parma_Polyhedra_Library::Box< ITV >::Box(), Parma_Polyhedra_Library::Box< ITV >::concatenate_assign(), Parma_Polyhedra_Library::Box< ITV >::contains(), Parma_Polyhedra_Library::Box< ITV >::difference_assign(), Parma_Polyhedra_Library::Box< ITV >::intersection_assign(), Parma_Polyhedra_Library::Box< ITV >::is_disjoint_from(), Parma_Polyhedra_Library::Box< ITV >::l_m_distance_assign(), Parma_Polyhedra_Library::Box< ITV >::m_swap(), Parma_Polyhedra_Library::Box< ITV >::map_space_dimensions(), Parma_Polyhedra_Library::Box< ITV >::operator=(), Parma_Polyhedra_Library::operator==(), Parma_Polyhedra_Library::Box< ITV >::simplify_using_context_assign(), Parma_Polyhedra_Library::Box< ITV >::time_elapse_assign(), Parma_Polyhedra_Library::Box< ITV >::upper_bound_assign(), Parma_Polyhedra_Library::Box< ITV >::upper_bound_assign_if_exact(), and Parma_Polyhedra_Library::Box< ITV >::wrap_assign().
|
private |
The status flags to keep track of the internal state.
Definition at line 1772 of file Box_defs.hh.
Referenced by Parma_Polyhedra_Library::Box< ITV >::concatenate_assign(), Parma_Polyhedra_Library::Box< ITV >::m_swap(), and Parma_Polyhedra_Library::Box< ITV >::operator=().
The documentation for this class was generated from the following files:
