PPL  1.2
Public Member Functions | Static Public Member Functions | Private Types | Private Member Functions | Private Attributes | Static Private Attributes | Friends | Related Functions | List of all members
Parma_Polyhedra_Library::Linear_Form< C > Class Template Reference
C++ Language Interface

A linear form with interval coefficients. More...

#include <Linear_Form_defs.hh>

Public Member Functions

 Linear_Form ()
 Default constructor: returns a copy of Linear_Form::zero(). More...
 
 Linear_Form (const Linear_Form &f)
 Ordinary copy constructor. More...
 
 ~Linear_Form ()
 Destructor. More...
 
 Linear_Form (const C &n)
 Builds the linear form corresponding to the inhomogeneous term n. More...
 
 Linear_Form (Variable v)
 Builds the linear form corresponding to the variable v. More...
 
 Linear_Form (const Linear_Expression &e)
 Builds a linear form approximating the linear expression e. More...
 
dimension_type space_dimension () const
 Returns the dimension of the vector space enclosing *this. More...
 
const C & coefficient (Variable v) const
 Returns the coefficient of v in *this. More...
 
const C & inhomogeneous_term () const
 Returns the inhomogeneous term of *this. More...
 
void negate ()
 Negates all the coefficients of *this. More...
 
memory_size_type total_memory_in_bytes () const
 Returns a lower bound to the total size in bytes of the memory occupied by *this. More...
 
memory_size_type external_memory_in_bytes () const
 Returns the size in bytes of the memory managed by *this. More...
 
void ascii_dump () const
 Writes to std::cerr an ASCII representation of *this. More...
 
void ascii_dump (std::ostream &s) const
 Writes to s an ASCII representation of *this. More...
 
void print () const
 Prints *this to std::cerr using operator<<. More...
 
bool ascii_load (std::istream &s)
 Loads from s an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets *this accordingly. Returns true if successful, false otherwise. More...
 
bool OK () const
 Checks if all the invariants are satisfied. More...
 
void m_swap (Linear_Form &y)
 Swaps *this with y. More...
 
bool overflows () const
 Verifies if the linear form overflows. More...
 
void relative_error (Floating_Point_Format analyzed_format, Linear_Form &result) const
 Computes the relative error associated to floating point computations that operate on a quantity that is overapproximated by *this. More...
 
template<typename Target >
bool intervalize (const FP_Oracle< Target, C > &oracle, C &result) const
 Makes result become an interval that overapproximates all the possible values of *this. More...
 

Static Public Member Functions

static dimension_type max_space_dimension ()
 Returns the maximum space dimension a Linear_Form can handle. More...
 

Private Types

typedef std::vector< C > vec_type
 Type of the container vector. More...
 

Private Member Functions

 Linear_Form (dimension_type sz, bool)
 Implementation sizing constructor. More...
 
 Linear_Form (Variable v, Variable w)
 Builds the linear form corresponding to the difference of v and w. More...
 
dimension_type size () const
 Gives the number of generic coefficients currently in use. More...
 
void extend (dimension_type sz)
 Extends the vector of *this to size sz. More...
 
C & operator[] (dimension_type i)
 Returns a reference to vec[i]. More...
 
const C & operator[] (dimension_type i) const
 Returns a const reference to vec[i]. More...
 

Private Attributes

vec_type vec
 The container vector. More...
 

Static Private Attributes

static C zero
 The generic coefficient equal to the singleton zero. More...
 

Friends

Linear_Form< C > operator+ (const Linear_Form< C > &f1, const Linear_Form< C > &f2)
 
Linear_Form< C > operator+ (const C &n, const Linear_Form< C > &f)
 
Linear_Form< C > operator+ (const Linear_Form< C > &f, const C &n)
 
Linear_Form< C > operator+ (Variable v, const Linear_Form< C > &f)
 
Linear_Form< C > operator- (const Linear_Form< C > &f)
 
Linear_Form< C > operator- (const Linear_Form< C > &f1, const Linear_Form< C > &f2)
 
Linear_Form< C > operator- (const C &n, const Linear_Form< C > &f)
 
Linear_Form< C > operator- (const Linear_Form< C > &f, const C &n)
 
Linear_Form< C > operator- (Variable v, const Linear_Form< C > &f)
 
Linear_Form< C > operator- (const Linear_Form< C > &f, Variable v)
 
Linear_Form< C > operator* (const C &n, const Linear_Form< C > &f)
 
Linear_Form< C > operator* (const Linear_Form< C > &f, const C &n)
 
Linear_Form< C > & operator+= (Linear_Form< C > &f1, const Linear_Form< C > &f2)
 
Linear_Form< C > & operator+= (Linear_Form< C > &f, Variable v)
 
Linear_Form< C > & operator+= (Linear_Form< C > &f, const C &n)
 
Linear_Form< C > & operator-= (Linear_Form< C > &f1, const Linear_Form< C > &f2)
 
Linear_Form< C > & operator-= (Linear_Form< C > &f, Variable v)
 
Linear_Form< C > & operator-= (Linear_Form< C > &f, const C &n)
 
Linear_Form< C > & operator*= (Linear_Form< C > &f, const C &n)
 
Linear_Form< C > & operator/= (Linear_Form< C > &f, const C &n)
 
bool operator== (const Linear_Form< C > &x, const Linear_Form< C > &y)
 
std::ostream & Parma_Polyhedra_Library::IO_Operators::operator (std::ostream &s, const Linear_Form< C > &f)
 

Related Functions

(Note that these are not member functions.)

template<typename FP_Interval_Type >
void discard_occurrences (std::map< dimension_type, Linear_Form< FP_Interval_Type > > &lf_store, Variable var)
 
template<typename FP_Interval_Type >
void affine_form_image (std::map< dimension_type, Linear_Form< FP_Interval_Type > > &lf_store, Variable var, const Linear_Form< FP_Interval_Type > &lf)
 
template<typename FP_Interval_Type >
void upper_bound_assign (std::map< dimension_type, Linear_Form< FP_Interval_Type > > &ls1, const std::map< dimension_type, Linear_Form< FP_Interval_Type > > &ls2)
 
template<typename C >
void swap (Linear_Form< C > &x, Linear_Form< C > &y)
 Swaps x with y. More...
 
template<typename C >
Linear_Form< C > operator+ (const Linear_Form< C > &f1, const Linear_Form< C > &f2)
 Returns the linear form f1 + f2. More...
 
template<typename C >
Linear_Form< C > operator+ (Variable v, const Linear_Form< C > &f)
 Returns the linear form v + f. More...
 
template<typename C >
Linear_Form< C > operator+ (const Linear_Form< C > &f, Variable v)
 Returns the linear form f + v. More...
 
template<typename C >
Linear_Form< C > operator+ (const C &n, const Linear_Form< C > &f)
 Returns the linear form n + f. More...
 
template<typename C >
Linear_Form< C > operator+ (const Linear_Form< C > &f, const C &n)
 Returns the linear form f + n. More...
 
template<typename C >
Linear_Form< C > operator+ (const Linear_Form< C > &f)
 Returns the linear form f. More...
 
template<typename C >
Linear_Form< C > operator- (const Linear_Form< C > &f)
 Returns the linear form - f. More...
 
template<typename C >
Linear_Form< C > operator- (const Linear_Form< C > &f1, const Linear_Form< C > &f2)
 Returns the linear form f1 - f2. More...
 
template<typename C >
Linear_Form< C > operator- (Variable v, const Linear_Form< C > &f)
 Returns the linear form v - f. More...
 
template<typename C >
Linear_Form< C > operator- (const Linear_Form< C > &f, Variable v)
 Returns the linear form f - v. More...
 
template<typename C >
Linear_Form< C > operator- (const C &n, const Linear_Form< C > &f)
 Returns the linear form n - f. More...
 
template<typename C >
Linear_Form< C > operator- (const Linear_Form< C > &f, const C &n)
 Returns the linear form f - n. More...
 
template<typename C >
Linear_Form< C > operator* (const C &n, const Linear_Form< C > &f)
 Returns the linear form n * f. More...
 
template<typename C >
Linear_Form< C > operator* (const Linear_Form< C > &f, const C &n)
 Returns the linear form f * n. More...
 
template<typename C >
Linear_Form< C > & operator+= (Linear_Form< C > &f1, const Linear_Form< C > &f2)
 Returns the linear form f1 + f2 and assigns it to e1. More...
 
template<typename C >
Linear_Form< C > & operator+= (Linear_Form< C > &f, Variable v)
 Returns the linear form f + v and assigns it to f. More...
 
template<typename C >
Linear_Form< C > & operator+= (Linear_Form< C > &f, const C &n)
 Returns the linear form f + n and assigns it to f. More...
 
template<typename C >
Linear_Form< C > & operator-= (Linear_Form< C > &f1, const Linear_Form< C > &f2)
 Returns the linear form f1 - f2 and assigns it to f1. More...
 
template<typename C >
Linear_Form< C > & operator-= (Linear_Form< C > &f, Variable v)
 Returns the linear form f - v and assigns it to f. More...
 
template<typename C >
Linear_Form< C > & operator-= (Linear_Form< C > &f, const C &n)
 Returns the linear form f - n and assigns it to f. More...
 
template<typename C >
Linear_Form< C > & operator*= (Linear_Form< C > &f, const C &n)
 Returns the linear form n * f and assigns it to f. More...
 
template<typename C >
Linear_Form< C > & operator/= (Linear_Form< C > &f, const C &n)
 Returns the linear form f / n and assigns it to f. More...
 
template<typename C >
bool operator== (const Linear_Form< C > &x, const Linear_Form< C > &y)
 Returns true if and only if x and y are equal. More...
 
template<typename C >
bool operator!= (const Linear_Form< C > &x, const Linear_Form< C > &y)
 Returns true if and only if x and y are different. More...
 
template<typename C >
std::ostream & operator<< (std::ostream &s, const Linear_Form< C > &f)
 Output operator. More...
 
template<typename C >
Linear_Form< C > operator+ (const Linear_Form< C > &f)
 
template<typename C >
Linear_Form< C > operator+ (const Linear_Form< C > &f, const C &n)
 
template<typename C >
Linear_Form< C > operator+ (const Linear_Form< C > &f, const Variable v)
 
template<typename C >
Linear_Form< C > operator- (const Linear_Form< C > &f, const C &n)
 
template<typename C >
Linear_Form< C > operator- (const Variable v, const Variable w)
 
template<typename C >
Linear_Form< C > operator* (const Linear_Form< C > &f, const C &n)
 
template<typename C >
Linear_Form< C > & operator+= (Linear_Form< C > &f, const C &n)
 
template<typename C >
Linear_Form< C > & operator-= (Linear_Form< C > &f, const C &n)
 
template<typename C >
bool operator!= (const Linear_Form< C > &x, const Linear_Form< C > &y)
 
template<typename C >
void swap (Linear_Form< C > &x, Linear_Form< C > &y)
 
template<typename C >
Linear_Form< C > operator+ (const Linear_Form< C > &f1, const Linear_Form< C > &f2)
 
template<typename C >
Linear_Form< C > operator+ (const Variable v, const Linear_Form< C > &f)
 
template<typename C >
Linear_Form< C > operator+ (const C &n, const Linear_Form< C > &f)
 
template<typename C >
Linear_Form< C > operator- (const Linear_Form< C > &f)
 
template<typename C >
Linear_Form< C > operator- (const Linear_Form< C > &f1, const Linear_Form< C > &f2)
 
template<typename C >
Linear_Form< C > operator- (const Variable v, const Linear_Form< C > &f)
 
template<typename C >
Linear_Form< C > operator- (const Linear_Form< C > &f, const Variable v)
 
template<typename C >
Linear_Form< C > operator- (const C &n, const Linear_Form< C > &f)
 
template<typename C >
Linear_Form< C > operator* (const C &n, const Linear_Form< C > &f)
 
template<typename C >
Linear_Form< C > & operator+= (Linear_Form< C > &f1, const Linear_Form< C > &f2)
 
template<typename C >
Linear_Form< C > & operator+= (Linear_Form< C > &f, const Variable v)
 
template<typename C >
Linear_Form< C > & operator-= (Linear_Form< C > &f1, const Linear_Form< C > &f2)
 
template<typename C >
Linear_Form< C > & operator-= (Linear_Form< C > &f, const Variable v)
 
template<typename C >
Linear_Form< C > & operator*= (Linear_Form< C > &f, const C &n)
 
template<typename C >
Linear_Form< C > & operator/= (Linear_Form< C > &f, const C &n)
 
template<typename C >
bool operator== (const Linear_Form< C > &x, const Linear_Form< C > &y)
 
template<typename C >
std::ostream & operator<< (std::ostream &s, const Linear_Form< C > &f)
 

Detailed Description

template<typename C>
class Parma_Polyhedra_Library::Linear_Form< C >

A linear form with interval coefficients.

An object of the class Linear_Form represents the interval linear form

\[ \sum_{i=0}^{n-1} a_i x_i + b \]

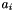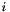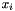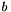where $n$ is the dimension of the vector space, each $a_i$ is the coefficient of the $i$-th variable $x_i$ and $b$ is the inhomogeneous term. The coefficients and the inhomogeneous term of the linear form have the template parameter C as their type. C must be the type of an Interval.

How to build a linear form.
A full set of functions is defined in order to provide a convenient interface for building complex linear forms starting from simpler ones and from objects of the classes Variable and C. Available operators include binary addition and subtraction, as well as multiplication and division by a coefficient. The space dimension of a linear form is defined as the highest variable dimension among variables that have a nonzero coefficient in the linear form, or zero if no such variable exists. The space dimension for each variable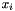 $x_i$ is given by $i + 1$.
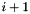Example
Given the type T of an Interval with floating point coefficients (though any integral type may also be used), the following code builds the interval linear form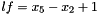 $lf = x_5 - x_2 + 1$ with space dimension 6:
Variable x5(5);
Variable x2(2);
T x5_coefficient;
x5_coefficient.lower() = 2.0;
x5_coefficient.upper() = 3.0;
T inhomogeneous_term;
inhomogeneous_term.lower() = 4.0;
inhomogeneous_term.upper() = 8.0;
Linear_Form<T> lf(x2);
lf = -lf;
lf += Linear_Form<T>(x2);
Linear_Form<T> lf_x5(x5);
lf_x5 *= x5_coefficient;
lf += lf_x5;
Note that lf_x5 is created with space dimension 6, while lf is created with space dimension 0 and then extended first to space dimension 2 when x2 is subtracted and finally to space dimension 6 when lf_x5 is added.

Definition at line 261 of file Linear_Form_defs.hh.

Member Typedef Documentation

template<typename C>
typedef std::vector<C> Parma_Polyhedra_Library::Linear_Form< C >::vec_type
private

Type of the container vector.

Definition at line 406 of file Linear_Form_defs.hh.

Constructor & Destructor Documentation

template<typename C >
Parma_Polyhedra_Library::Linear_Form< C >::Linear_Form ( )
inline

Default constructor: returns a copy of Linear_Form::zero().

Definition at line 41 of file Linear_Form_inlines.hh.

References Parma_Polyhedra_Library::compute_capacity(), and Parma_Polyhedra_Library::Linear_Form< C >::vec.

42  : vec(1, zero) {
43  vec.reserve(compute_capacity(1, vec_type().max_size()));
44 }
Parma_Polyhedra_Library::Linear_Form::vec_type
std::vector< C > vec_type
Type of the container vector.
Definition: Linear_Form_defs.hh:406
Parma_Polyhedra_Library::compute_capacity
dimension_type compute_capacity(dimension_type requested_size, dimension_type maximum_size)
Speculative allocation function.
Definition: globals_inlines.hh:90
Parma_Polyhedra_Library::Linear_Form::zero
static C zero
The generic coefficient equal to the singleton zero.
Definition: Linear_Form_defs.hh:403
Parma_Polyhedra_Library::Linear_Form::vec
vec_type vec
The container vector.
Definition: Linear_Form_defs.hh:409
template<typename C >
Parma_Polyhedra_Library::Linear_Form< C >::Linear_Form ( const Linear_Form< C > &  f)
inline

Ordinary copy constructor.

Definition at line 55 of file Linear_Form_inlines.hh.

56  : vec(f.vec) {
57 }
Parma_Polyhedra_Library::Linear_Form::vec
vec_type vec
The container vector.
Definition: Linear_Form_defs.hh:409
template<typename C >
Parma_Polyhedra_Library::Linear_Form< C >::~Linear_Form ( )
inline

Destructor.

Definition at line 61 of file Linear_Form_inlines.hh.

61  {
62 }
template<typename C >
Parma_Polyhedra_Library::Linear_Form< C >::Linear_Form ( const C &  n)
inlineexplicit

Builds the linear form corresponding to the inhomogeneous term n.

Definition at line 80 of file Linear_Form_inlines.hh.

References Parma_Polyhedra_Library::compute_capacity(), and Parma_Polyhedra_Library::Linear_Form< C >::vec.

81  : vec(1, n) {
82  vec.reserve(compute_capacity(1, vec_type().max_size()));
83 }
Parma_Polyhedra_Library::Linear_Form::vec_type
std::vector< C > vec_type
Type of the container vector.
Definition: Linear_Form_defs.hh:406
Parma_Polyhedra_Library::compute_capacity
dimension_type compute_capacity(dimension_type requested_size, dimension_type maximum_size)
Speculative allocation function.
Definition: globals_inlines.hh:90
Parma_Polyhedra_Library::Linear_Form::vec
vec_type vec
The container vector.
Definition: Linear_Form_defs.hh:409
template<typename C >
Parma_Polyhedra_Library::Linear_Form< C >::Linear_Form ( Variable  v)

Builds the linear form corresponding to the variable v.

Exceptions
std::length_errorThrown if the space dimension of v exceeds Linear_Form::max_space_dimension().

Definition at line 37 of file Linear_Form_templates.hh.

References Parma_Polyhedra_Library::compute_capacity(), Parma_Polyhedra_Library::Linear_Form< C >::max_space_dimension(), Parma_Polyhedra_Library::Variable::space_dimension(), Parma_Polyhedra_Library::Linear_Form< C >::vec, and Parma_Polyhedra_Library::Linear_Form< C >::zero.

38  : vec() {
39  const dimension_type space_dim = v.space_dimension();
40  if (space_dim > max_space_dimension()) {
41  throw std::length_error("Linear_Form<C>::"
42  "Linear_Form(v):\n"
43  "v exceeds the maximum allowed "
44  "space dimension.");
45  }
46  vec.reserve(compute_capacity(space_dim+1, vec_type().max_size()));
47  vec.resize(space_dim+1, zero);
48  vec[v.space_dimension()] = C(typename C::boundary_type(1));
49 }
Parma_Polyhedra_Library::Linear_Form::vec_type
std::vector< C > vec_type
Type of the container vector.
Definition: Linear_Form_defs.hh:406
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
Parma_Polyhedra_Library::compute_capacity
dimension_type compute_capacity(dimension_type requested_size, dimension_type maximum_size)
Speculative allocation function.
Definition: globals_inlines.hh:90
Parma_Polyhedra_Library::Linear_Form::zero
static C zero
The generic coefficient equal to the singleton zero.
Definition: Linear_Form_defs.hh:403
Parma_Polyhedra_Library::Linear_Form::vec
vec_type vec
The container vector.
Definition: Linear_Form_defs.hh:409
Parma_Polyhedra_Library::Linear_Form::max_space_dimension
static dimension_type max_space_dimension()
Returns the maximum space dimension a Linear_Form can handle.
Definition: Linear_Form_inlines.hh:35
template<typename C >
Parma_Polyhedra_Library::Linear_Form< C >::Linear_Form ( const Linear_Expression &  e)

Builds a linear form approximating the linear expression e.

Definition at line 72 of file Linear_Form_templates.hh.

References Parma_Polyhedra_Library::Linear_Expression::coefficient(), Parma_Polyhedra_Library::compute_capacity(), Parma_Polyhedra_Library::Linear_Expression::inhomogeneous_term(), Parma_Polyhedra_Library::Linear_Form< C >::max_space_dimension(), Parma_Polyhedra_Library::Linear_Expression::space_dimension(), and Parma_Polyhedra_Library::Linear_Form< C >::vec.

73  : vec() {
74  const dimension_type space_dim = e.space_dimension();
75  if (space_dim > max_space_dimension()) {
76  throw std::length_error("Linear_Form<C>::"
77  "Linear_Form(e):\n"
78  "e exceeds the maximum allowed "
79  "space dimension.");
80  }
81  vec.reserve(compute_capacity(space_dim+1, vec_type().max_size()));
82  vec.resize(space_dim+1);
83  for (dimension_type i = space_dim; i-- > 0; )
84  vec[i+1] = e.coefficient(Variable(i));
85  vec[0] = e.inhomogeneous_term();
86 }
Parma_Polyhedra_Library::Linear_Form::vec_type
std::vector< C > vec_type
Type of the container vector.
Definition: Linear_Form_defs.hh:406
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
Parma_Polyhedra_Library::compute_capacity
dimension_type compute_capacity(dimension_type requested_size, dimension_type maximum_size)
Speculative allocation function.
Definition: globals_inlines.hh:90
Parma_Polyhedra_Library::Linear_Form::vec
vec_type vec
The container vector.
Definition: Linear_Form_defs.hh:409
Parma_Polyhedra_Library::Linear_Form::max_space_dimension
static dimension_type max_space_dimension()
Returns the maximum space dimension a Linear_Form can handle.
Definition: Linear_Form_inlines.hh:35
template<typename C >
Parma_Polyhedra_Library::Linear_Form< C >::Linear_Form ( dimension_type  sz,
bool   
)
inlineprivate

Implementation sizing constructor.

The bool parameter is just to avoid problems with the constructor Linear_Form(const C& n).

Definition at line 48 of file Linear_Form_inlines.hh.

References Parma_Polyhedra_Library::compute_capacity(), and Parma_Polyhedra_Library::Linear_Form< C >::vec.

49  : vec(sz, zero) {
50  vec.reserve(compute_capacity(sz, vec_type().max_size()));
51 }
Parma_Polyhedra_Library::Linear_Form::vec_type
std::vector< C > vec_type
Type of the container vector.
Definition: Linear_Form_defs.hh:406
Parma_Polyhedra_Library::compute_capacity
dimension_type compute_capacity(dimension_type requested_size, dimension_type maximum_size)
Speculative allocation function.
Definition: globals_inlines.hh:90
Parma_Polyhedra_Library::Linear_Form::zero
static C zero
The generic coefficient equal to the singleton zero.
Definition: Linear_Form_defs.hh:403
Parma_Polyhedra_Library::Linear_Form::vec
vec_type vec
The container vector.
Definition: Linear_Form_defs.hh:409
template<typename C >
Parma_Polyhedra_Library::Linear_Form< C >::Linear_Form ( Variable  v,
Variable  w 
)
private

Builds the linear form corresponding to the difference of v and w.

Exceptions
std::length_errorThrown if the space dimension of v or the one of w exceed Linear_Form::max_space_dimension().

Definition at line 52 of file Linear_Form_templates.hh.

References Parma_Polyhedra_Library::compute_capacity(), Parma_Polyhedra_Library::Linear_Form< C >::max_space_dimension(), Parma_Polyhedra_Library::Variable::space_dimension(), Parma_Polyhedra_Library::Linear_Form< C >::vec, and Parma_Polyhedra_Library::Linear_Form< C >::zero.

53  : vec() {
54  const dimension_type v_space_dim = v.space_dimension();
55  const dimension_type w_space_dim = w.space_dimension();
56  const dimension_type space_dim = std::max(v_space_dim, w_space_dim);
57  if (space_dim > max_space_dimension()) {
58  throw std::length_error("Linear_Form<C>::"
59  "Linear_Form(v, w):\n"
60  "v or w exceed the maximum allowed "
61  "space dimension.");
62  }
63  vec.reserve(compute_capacity(space_dim+1, vec_type().max_size()));
64  vec.resize(space_dim+1, zero);
65  if (v_space_dim != w_space_dim) {
66  vec[v_space_dim] = C(typename C::boundary_type(1));
67  vec[w_space_dim] = C(typename C::boundary_type(-1));
68  }
69 }
Parma_Polyhedra_Library::Linear_Form::vec_type
std::vector< C > vec_type
Type of the container vector.
Definition: Linear_Form_defs.hh:406
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
Parma_Polyhedra_Library::compute_capacity
dimension_type compute_capacity(dimension_type requested_size, dimension_type maximum_size)
Speculative allocation function.
Definition: globals_inlines.hh:90
Parma_Polyhedra_Library::Linear_Form::zero
static C zero
The generic coefficient equal to the singleton zero.
Definition: Linear_Form_defs.hh:403
Parma_Polyhedra_Library::Linear_Form::vec
vec_type vec
The container vector.
Definition: Linear_Form_defs.hh:409
Parma_Polyhedra_Library::Linear_Form::max_space_dimension
static dimension_type max_space_dimension()
Returns the maximum space dimension a Linear_Form can handle.
Definition: Linear_Form_inlines.hh:35

Member Function Documentation

template<typename C>
void Parma_Polyhedra_Library::Linear_Form< C >::ascii_dump ( ) const

Writes to std::cerr an ASCII representation of *this.

template<typename C >
void Parma_Polyhedra_Library::Linear_Form< C >::ascii_dump ( std::ostream &  s) const
inline

Writes to s an ASCII representation of *this.

Definition at line 200 of file Linear_Form_inlines.hh.

References Parma_Polyhedra_Library::Implementation::BD_Shapes::separator.

200  {
201  using namespace IO_Operators;
202  dimension_type space_dim = space_dimension();
203  s << space_dim << "\n";
204  for (dimension_type i = 0; i <= space_dim; ++i) {
205  const char separator = ' ';
206  s << vec[i] << separator;
207  }
208  s << "\n";
209 }
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
Parma_Polyhedra_Library::Linear_Form::space_dimension
dimension_type space_dimension() const
Returns the dimension of the vector space enclosing *this.
Definition: Linear_Form_inlines.hh:87
Parma_Polyhedra_Library::Implementation::BD_Shapes::separator
const char separator
Definition: BDS_Status_inlines.hh:198
Parma_Polyhedra_Library::Linear_Form::vec
vec_type vec
The container vector.
Definition: Linear_Form_defs.hh:409
template<typename C >
bool Parma_Polyhedra_Library::Linear_Form< C >::ascii_load ( std::istream &  s)
inline

Loads from s an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets *this accordingly. Returns true if successful, false otherwise.

Definition at line 213 of file Linear_Form_inlines.hh.

213  {
214  using namespace IO_Operators;
215  dimension_type new_dim;
216  if (!(s >> new_dim)) {
217  return false;
218  }
219 
220  vec.resize(new_dim + 1, zero);
221  for (dimension_type i = 0; i <= new_dim; ++i) {
222  if (!(s >> vec[i])) {
223  return false;
224  }
225  }
226 
227  PPL_ASSERT(OK());
228  return true;
229 }
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
Parma_Polyhedra_Library::Linear_Form::OK
bool OK() const
Checks if all the invariants are satisfied.
Definition: Linear_Form_templates.hh:404
Parma_Polyhedra_Library::Linear_Form::zero
static C zero
The generic coefficient equal to the singleton zero.
Definition: Linear_Form_defs.hh:403
Parma_Polyhedra_Library::Linear_Form::vec
vec_type vec
The container vector.
Definition: Linear_Form_defs.hh:409
template<typename C >
const C & Parma_Polyhedra_Library::Linear_Form< C >::coefficient ( Variable  v) const
inline

Returns the coefficient of v in *this.

Definition at line 93 of file Linear_Form_inlines.hh.

References Parma_Polyhedra_Library::Variable::id(), and Parma_Polyhedra_Library::Variable::space_dimension().

Referenced by Parma_Polyhedra_Library::Box< ITV >::affine_form_image(), Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >::intervalize(), Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >::overflows(), and Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >::relative_error().

93  {
94  if (v.space_dimension() > space_dimension()) {
95  return zero;
96  }
97  return vec[v.id()+1];
98 }
Parma_Polyhedra_Library::Linear_Form::space_dimension
dimension_type space_dimension() const
Returns the dimension of the vector space enclosing *this.
Definition: Linear_Form_inlines.hh:87
Parma_Polyhedra_Library::Linear_Form::zero
static C zero
The generic coefficient equal to the singleton zero.
Definition: Linear_Form_defs.hh:403
Parma_Polyhedra_Library::Linear_Form::vec
vec_type vec
The container vector.
Definition: Linear_Form_defs.hh:409
template<typename C >
void Parma_Polyhedra_Library::Linear_Form< C >::extend ( dimension_type  sz)
inlineprivate

Extends the vector of *this to size sz.

Definition at line 72 of file Linear_Form_inlines.hh.

References Parma_Polyhedra_Library::compute_capacity().

Referenced by Parma_Polyhedra_Library::Linear_Form< C >::operator+(), Parma_Polyhedra_Library::Linear_Form< C >::operator+=(), Parma_Polyhedra_Library::Linear_Form< C >::operator-(), and Parma_Polyhedra_Library::Linear_Form< C >::operator-=().

72  {
73  assert(sz > size());
74  vec.reserve(compute_capacity(sz, vec_type().max_size()));
75  vec.resize(sz, zero);
76 }
Parma_Polyhedra_Library::Linear_Form::vec_type
std::vector< C > vec_type
Type of the container vector.
Definition: Linear_Form_defs.hh:406
Parma_Polyhedra_Library::compute_capacity
dimension_type compute_capacity(dimension_type requested_size, dimension_type maximum_size)
Speculative allocation function.
Definition: globals_inlines.hh:90
Parma_Polyhedra_Library::Linear_Form::zero
static C zero
The generic coefficient equal to the singleton zero.
Definition: Linear_Form_defs.hh:403
Parma_Polyhedra_Library::Linear_Form::vec
vec_type vec
The container vector.
Definition: Linear_Form_defs.hh:409
Parma_Polyhedra_Library::Linear_Form::size
dimension_type size() const
Gives the number of generic coefficients currently in use.
Definition: Linear_Form_inlines.hh:66
template<typename C >
memory_size_type Parma_Polyhedra_Library::Linear_Form< C >::external_memory_in_bytes ( ) const
inline

Returns the size in bytes of the memory managed by *this.

Definition at line 393 of file Linear_Form_templates.hh.

393  {
394  memory_size_type n = 0;
395  for (dimension_type i = size(); i-- > 0; ) {
396  n += vec[i].external_memory_in_bytes();
397  }
398  n += vec.capacity()*sizeof(C);
399  return n;
400 }
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
Parma_Polyhedra_Library::Linear_Form::vec
vec_type vec
The container vector.
Definition: Linear_Form_defs.hh:409
Parma_Polyhedra_Library::Linear_Form::size
dimension_type size() const
Gives the number of generic coefficients currently in use.
Definition: Linear_Form_inlines.hh:66
Parma_Polyhedra_Library::memory_size_type
size_t memory_size_type
An unsigned integral type for representing memory size in bytes.
Definition: globals_types.hh:26
template<typename C >
const C & Parma_Polyhedra_Library::Linear_Form< C >::inhomogeneous_term ( ) const
inline

Returns the inhomogeneous term of *this.

Definition at line 116 of file Linear_Form_inlines.hh.

Referenced by Parma_Polyhedra_Library::Box< ITV >::affine_form_image(), Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >::intervalize(), Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >::overflows(), and Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >::relative_error().

116  {
117  return vec[0];
118 }
Parma_Polyhedra_Library::Linear_Form::vec
vec_type vec
The container vector.
Definition: Linear_Form_defs.hh:409
template<typename C >
template<typename Target >
bool Parma_Polyhedra_Library::Linear_Form< C >::intervalize ( const FP_Oracle< Target, C > &  oracle,
C &  result 
) const

Makes result become an interval that overapproximates all the possible values of *this.

Parameters
oracleThe FP_Oracle to be queried.
resultThe linear form that will store the result.
Returns
true if the operation was successful, false otherwise (the possibility of failure depends on the oracle's implementation).
Template type parameters
  • The class template parameter Target specifies the implementation of Concrete_Expression to be used.

This method makes result become 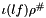$\iota(lf)\rho^{\#}$, that is an interval defined as:

\[ \iota\left(i + \sum_{v \in \cV}i_{v}v\right)\rho^{\#} \defeq i \asifp \left(\bigoplus_{v \in \cV}{}^{\#}i_{v} \amifp \rho^{\#}(v)\right) \]

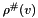where $\rho^{\#}(v)$ is an interval (provided by the oracle) that correctly approximates the value of $v$.

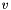The result is undefined if C is not the type of an interval with floating point boundaries.

Definition at line 492 of file Linear_Form_templates.hh.

References Parma_Polyhedra_Library::FP_Oracle< Target, FP_Interval_Type >::get_interval().

493  {
494  result = C(inhomogeneous_term());
495  dimension_type dimension = space_dimension();
496  for (dimension_type i = 0; i < dimension; ++i) {
497  C current_addend = coefficient(Variable(i));
498  C curr_int;
499  if (!oracle.get_interval(i, curr_int)) {
500  return false;
501  }
502  current_addend *= curr_int;
503  result += current_addend;
504  }
505 
506  return true;
507 }
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
Parma_Polyhedra_Library::Linear_Form::coefficient
const C & coefficient(Variable v) const
Returns the coefficient of v in *this.
Definition: Linear_Form_inlines.hh:93
Parma_Polyhedra_Library::Linear_Form::space_dimension
dimension_type space_dimension() const
Returns the dimension of the vector space enclosing *this.
Definition: Linear_Form_inlines.hh:87
Parma_Polyhedra_Library::Linear_Form::inhomogeneous_term
const C & inhomogeneous_term() const
Returns the inhomogeneous term of *this.
Definition: Linear_Form_inlines.hh:116
template<typename C >
void Parma_Polyhedra_Library::Linear_Form< C >::m_swap ( Linear_Form< C > &  y)
inline

Swaps *this with y.

Definition at line 193 of file Linear_Form_inlines.hh.

References Parma_Polyhedra_Library::swap(), and Parma_Polyhedra_Library::Linear_Form< C >::vec.

Referenced by Parma_Polyhedra_Library::Linear_Form< C >::swap().

193  {
194  using std::swap;
195  swap(vec, y.vec);
196 }
Parma_Polyhedra_Library::Linear_Form::swap
void swap(Linear_Form< C > &x, Linear_Form< C > &y)
Swaps x with y.
Parma_Polyhedra_Library::swap
void swap(CO_Tree &x, CO_Tree &y)
Definition: CO_Tree_inlines.hh:873
Parma_Polyhedra_Library::Linear_Form::vec
vec_type vec
The container vector.
Definition: Linear_Form_defs.hh:409
template<typename C >
dimension_type Parma_Polyhedra_Library::Linear_Form< C >::max_space_dimension ( )
inlinestatic

Returns the maximum space dimension a Linear_Form can handle.

Definition at line 35 of file Linear_Form_inlines.hh.

Referenced by Parma_Polyhedra_Library::Linear_Form< C >::Linear_Form().

35  {
36  return vec_type().max_size() - 1;
37 }
Parma_Polyhedra_Library::Linear_Form::vec_type
std::vector< C > vec_type
Type of the container vector.
Definition: Linear_Form_defs.hh:406
template<typename C >
void Parma_Polyhedra_Library::Linear_Form< C >::negate ( )

Negates all the coefficients of *this.

Definition at line 384 of file Linear_Form_templates.hh.

Referenced by Parma_Polyhedra_Library::Octagonal_Shape< T >::affine_form_image(), Parma_Polyhedra_Library::Opposite_Floating_Point_Expression< FP_Interval_Type, FP_Format >::linearize(), Parma_Polyhedra_Library::Concrete_Expression< Target >::linearize(), and Parma_Polyhedra_Library::BD_Shape< T >::two_variables_affine_form_image().

384  {
385  for (dimension_type i = vec.size(); i-- > 0; ) {
386  vec[i].neg_assign(vec[i]);
387  }
388  return;
389 }
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
Parma_Polyhedra_Library::Linear_Form::vec
vec_type vec
The container vector.
Definition: Linear_Form_defs.hh:409
template<typename C >
bool Parma_Polyhedra_Library::Linear_Form< C >::OK ( ) const

Checks if all the invariants are satisfied.

Definition at line 404 of file Linear_Form_templates.hh.

404  {
405  for (dimension_type i = size(); i-- > 0; ) {
406  if (!vec[i].OK()) {
407  return false;
408  }
409  }
410  return true;
411 }
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
Parma_Polyhedra_Library::Linear_Form::OK
bool OK() const
Checks if all the invariants are satisfied.
Definition: Linear_Form_templates.hh:404
Parma_Polyhedra_Library::Linear_Form::vec
vec_type vec
The container vector.
Definition: Linear_Form_defs.hh:409
Parma_Polyhedra_Library::Linear_Form::size
dimension_type size() const
Gives the number of generic coefficients currently in use.
Definition: Linear_Form_inlines.hh:66
template<typename C >
C & Parma_Polyhedra_Library::Linear_Form< C >::operator[] ( dimension_type  i)
inlineprivate

Returns a reference to vec[i].

Definition at line 102 of file Linear_Form_inlines.hh.

102  {
103  assert(i < size());
104  return vec[i];
105 }
Parma_Polyhedra_Library::Linear_Form::vec
vec_type vec
The container vector.
Definition: Linear_Form_defs.hh:409
Parma_Polyhedra_Library::Linear_Form::size
dimension_type size() const
Gives the number of generic coefficients currently in use.
Definition: Linear_Form_inlines.hh:66
template<typename C >
const C & Parma_Polyhedra_Library::Linear_Form< C >::operator[] ( dimension_type  i) const
inlineprivate

Returns a const reference to vec[i].

Definition at line 109 of file Linear_Form_inlines.hh.

109  {
110  assert(i < size());
111  return vec[i];
112 }
Parma_Polyhedra_Library::Linear_Form::vec
vec_type vec
The container vector.
Definition: Linear_Form_defs.hh:409
Parma_Polyhedra_Library::Linear_Form::size
dimension_type size() const
Gives the number of generic coefficients currently in use.
Definition: Linear_Form_inlines.hh:66
template<typename C >
bool Parma_Polyhedra_Library::Linear_Form< C >::overflows ( ) const
inline

Verifies if the linear form overflows.

Returns
Returns false if all coefficients in lf are bounded, true otherwise.

T must be the type of possibly unbounded quantities.

Definition at line 234 of file Linear_Form_inlines.hh.

Referenced by Parma_Polyhedra_Library::Concrete_Expression< Target >::add_linearize(), Parma_Polyhedra_Library::Concrete_Expression< Target >::cast_linearize(), Parma_Polyhedra_Library::Concrete_Expression< Target >::div_linearize(), Parma_Polyhedra_Library::Concrete_Expression< Target >::linearize(), Parma_Polyhedra_Library::Concrete_Expression< Target >::mul_linearize(), and Parma_Polyhedra_Library::Concrete_Expression< Target >::sub_linearize().

234  {
235  if (!inhomogeneous_term().is_bounded()) {
236  return true;
237  }
238  for (dimension_type i = space_dimension(); i-- > 0; ) {
239  if (!coefficient(Variable(i)).is_bounded()) {
240  return true;
241  }
242  }
243 
244  return false;
245 }
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
Parma_Polyhedra_Library::Linear_Form::coefficient
const C & coefficient(Variable v) const
Returns the coefficient of v in *this.
Definition: Linear_Form_inlines.hh:93
Parma_Polyhedra_Library::Linear_Form::space_dimension
dimension_type space_dimension() const
Returns the dimension of the vector space enclosing *this.
Definition: Linear_Form_inlines.hh:87
Parma_Polyhedra_Library::Linear_Form::inhomogeneous_term
const C & inhomogeneous_term() const
Returns the inhomogeneous term of *this.
Definition: Linear_Form_inlines.hh:116
template<typename C>
void Parma_Polyhedra_Library::Linear_Form< C >::print ( ) const

Prints *this to std::cerr using operator<<.

template<typename C >
void Parma_Polyhedra_Library::Linear_Form< C >::relative_error ( Floating_Point_Format  analyzed_format,
Linear_Form< C > &  result 
) const

Computes the relative error associated to floating point computations that operate on a quantity that is overapproximated by *this.

Parameters
analyzed_formatThe floating point format used by the analyzed program.
resultBecomes the linear form corresponding to the relative error committed.

This method makes result become a linear form obtained by evaluating the function 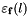$\varepsilon_{\mathbf{f}}(l)$ on the linear form. This function is defined as:

\[ \varepsilon_{\mathbf{f}}\left([a, b]+\sum_{v \in \cV}[a_{v}, b_{v}]v\right) \defeq (\textrm{max}(|a|, |b|) \amifp [-\beta^{-\textrm{p}}, \beta^{-\textrm{p}}]) + \sum_{v \in \cV}(\textrm{max}(|a_{v}|,|b_{v}|) \amifp [-\beta^{-\textrm{p}}, \beta^{-\textrm{p}}])v \]

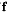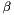where p is the fraction size in bits for the format $\mathbf{f}$ and $\beta$ the base.

The result is undefined if T is not the type of an interval with floating point boundaries.

Definition at line 416 of file Linear_Form_templates.hh.

References Parma_Polyhedra_Library::float_ieee754_half::BASE, Parma_Polyhedra_Library::float_ieee754_single::BASE, Parma_Polyhedra_Library::float_ieee754_double::BASE, Parma_Polyhedra_Library::float_ibm_single::BASE, Parma_Polyhedra_Library::float_intel_double_extended::BASE, Parma_Polyhedra_Library::float_ieee754_quad::BASE, Parma_Polyhedra_Library::GREATER_OR_EQUAL, Parma_Polyhedra_Library::i_constraint(), Parma_Polyhedra_Library::IBM_SINGLE, Parma_Polyhedra_Library::IEEE754_DOUBLE, Parma_Polyhedra_Library::IEEE754_HALF, Parma_Polyhedra_Library::IEEE754_QUAD, Parma_Polyhedra_Library::IEEE754_SINGLE, Parma_Polyhedra_Library::INTEL_DOUBLE_EXTENDED, Parma_Polyhedra_Library::LESS_OR_EQUAL, Parma_Polyhedra_Library::float_ieee754_half::MANTISSA_BITS, Parma_Polyhedra_Library::float_ieee754_single::MANTISSA_BITS, Parma_Polyhedra_Library::float_ieee754_double::MANTISSA_BITS, Parma_Polyhedra_Library::float_ibm_single::MANTISSA_BITS, Parma_Polyhedra_Library::float_intel_double_extended::MANTISSA_BITS, Parma_Polyhedra_Library::float_ieee754_quad::MANTISSA_BITS, and Parma_Polyhedra_Library::msb_position().

Referenced by Parma_Polyhedra_Library::Concrete_Expression< Target >::add_linearize(), Parma_Polyhedra_Library::Concrete_Expression< Target >::cast_linearize(), Parma_Polyhedra_Library::Concrete_Expression< Target >::div_linearize(), Parma_Polyhedra_Library::Concrete_Expression< Target >::mul_linearize(), and Parma_Polyhedra_Library::Concrete_Expression< Target >::sub_linearize().

418  {
419  typedef typename C::boundary_type analyzer_format;
420 
421  // Get the necessary information on the analyzed's format.
422  unsigned int f_base;
423  unsigned int f_mantissa_bits;
424  switch (analyzed_format) {
425  case IEEE754_HALF:
426  f_base = float_ieee754_half::BASE;
427  f_mantissa_bits = float_ieee754_half::MANTISSA_BITS;
428  break;
429  case IEEE754_SINGLE:
430  f_base = float_ieee754_single::BASE;
431  f_mantissa_bits = float_ieee754_single::MANTISSA_BITS;
432  break;
433  case IEEE754_DOUBLE:
434  f_base = float_ieee754_double::BASE;
435  f_mantissa_bits = float_ieee754_double::MANTISSA_BITS;
436  break;
437  case IBM_SINGLE:
438  f_base = float_ibm_single::BASE;
439  f_mantissa_bits = float_ibm_single::MANTISSA_BITS;
440  break;
441  case IEEE754_QUAD:
442  f_base = float_ieee754_quad::BASE;
443  f_mantissa_bits = float_ieee754_quad::MANTISSA_BITS;
444  break;
445  case INTEL_DOUBLE_EXTENDED:
446  f_base = float_intel_double_extended::BASE;
447  f_mantissa_bits = float_intel_double_extended::MANTISSA_BITS;
448  break;
449  default:
450  PPL_UNREACHABLE;
451  break;
452  }
453 
454  C error_propagator;
455  // We assume that f_base is a power of 2.
456  unsigned int u_power = msb_position(f_base) * f_mantissa_bits;
457  int neg_power = -static_cast<int>(u_power);
458  analyzer_format lb = static_cast<analyzer_format>(ldexp(1.0, neg_power));
459 
460  error_propagator.build(i_constraint(GREATER_OR_EQUAL, -lb),
461  i_constraint(LESS_OR_EQUAL, lb));
462 
463  // Handle the inhomogeneous term.
464  const C* current_term = &inhomogeneous_term();
465  assert(current_term->is_bounded());
466 
467  C current_multiplier(std::max(std::abs(current_term->lower()),
468  std::abs(current_term->upper())));
469  Linear_Form current_result_term(current_multiplier);
470  current_result_term *= error_propagator;
471  result = Linear_Form(current_result_term);
472 
473  // Handle the other terms.
474  dimension_type dimension = space_dimension();
475  for (dimension_type i = 0; i < dimension; ++i) {
476  current_term = &coefficient(Variable(i));
477  assert(current_term->is_bounded());
478  current_multiplier = C(std::max(std::abs(current_term->lower()),
479  std::abs(current_term->upper())));
480  current_result_term = Linear_Form(Variable(i));
481  current_result_term *= current_multiplier;
482  current_result_term *= error_propagator;
483  result += current_result_term;
484  }
485 
486  return;
487 }
Parma_Polyhedra_Library::float_ieee754_quad::BASE
static const unsigned int BASE
Definition: Float_defs.hh:261
Parma_Polyhedra_Library::i_constraint
I_Constraint< T > i_constraint(I_Constraint_Rel rel, const T &v)
Definition: intervals_defs.hh:443
Parma_Polyhedra_Library::float_intel_double_extended::BASE
static const unsigned int BASE
Definition: Float_defs.hh:220
Parma_Polyhedra_Library::float_ieee754_single::MANTISSA_BITS
static const unsigned int MANTISSA_BITS
Definition: Float_defs.hh:93
Parma_Polyhedra_Library::LESS_OR_EQUAL
Less than or equal to.
Definition: globals_types.hh:46
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
Parma_Polyhedra_Library::float_ibm_single::MANTISSA_BITS
static const unsigned int MANTISSA_BITS
Definition: Float_defs.hh:171
Parma_Polyhedra_Library::Linear_Form::coefficient
const C & coefficient(Variable v) const
Returns the coefficient of v in *this.
Definition: Linear_Form_inlines.hh:93
Parma_Polyhedra_Library::IEEE754_HALF
IEEE 754 half precision, 16 bits (5 exponent, 10 mantissa).
Definition: globals_types.hh:189
Parma_Polyhedra_Library::IEEE754_QUAD
IEEE 754 quad precision, 128 bits (15 exponent, 112 mantissa).
Definition: globals_types.hh:198
Parma_Polyhedra_Library::IBM_SINGLE
IBM single precision, 32 bits (7 exponent, 24 mantissa).
Definition: globals_types.hh:204
Parma_Polyhedra_Library::float_ibm_single::BASE
static const unsigned int BASE
Definition: Float_defs.hh:169
Parma_Polyhedra_Library::float_ieee754_single::BASE
static const unsigned int BASE
Definition: Float_defs.hh:91
Parma_Polyhedra_Library::float_ieee754_double::BASE
static const unsigned int BASE
Definition: Float_defs.hh:137
Parma_Polyhedra_Library::Linear_Form::space_dimension
dimension_type space_dimension() const
Returns the dimension of the vector space enclosing *this.
Definition: Linear_Form_inlines.hh:87
Parma_Polyhedra_Library::msb_position
unsigned int msb_position(unsigned long long v)
If v is nonzero, returns the position of the most significant bit in a.
Definition: Float_inlines.hh:518
Parma_Polyhedra_Library::INTEL_DOUBLE_EXTENDED
Intel double extended precision, 80 bits (15 exponent, 64 mantissa)
Definition: globals_types.hh:201
Parma_Polyhedra_Library::GREATER_OR_EQUAL
Greater than or equal to.
Definition: globals_types.hh:50
Parma_Polyhedra_Library::float_intel_double_extended::MANTISSA_BITS
static const unsigned int MANTISSA_BITS
Definition: Float_defs.hh:222
Parma_Polyhedra_Library::float_ieee754_half::BASE
static const unsigned int BASE
Definition: Float_defs.hh:58
Parma_Polyhedra_Library::float_ieee754_quad::MANTISSA_BITS
static const unsigned int MANTISSA_BITS
Definition: Float_defs.hh:263
Parma_Polyhedra_Library::IEEE754_DOUBLE
IEEE 754 double precision, 64 bits (11 exponent, 52 mantissa).
Definition: globals_types.hh:195
Parma_Polyhedra_Library::Linear_Form::inhomogeneous_term
const C & inhomogeneous_term() const
Returns the inhomogeneous term of *this.
Definition: Linear_Form_inlines.hh:116
Parma_Polyhedra_Library::Linear_Form::Linear_Form
Linear_Form()
Default constructor: returns a copy of Linear_Form::zero().
Definition: Linear_Form_inlines.hh:41
Parma_Polyhedra_Library::IEEE754_SINGLE
IEEE 754 single precision, 32 bits (8 exponent, 23 mantissa).
Definition: globals_types.hh:192
Parma_Polyhedra_Library::float_ieee754_double::MANTISSA_BITS
static const unsigned int MANTISSA_BITS
Definition: Float_defs.hh:139
Parma_Polyhedra_Library::float_ieee754_half::MANTISSA_BITS
static const unsigned int MANTISSA_BITS
Definition: Float_defs.hh:60
template<typename C >
dimension_type Parma_Polyhedra_Library::Linear_Form< C >::size ( ) const
inlineprivate

Gives the number of generic coefficients currently in use.

Definition at line 66 of file Linear_Form_inlines.hh.

Referenced by Parma_Polyhedra_Library::Linear_Form< C >::operator*(), Parma_Polyhedra_Library::Linear_Form< C >::operator*=(), Parma_Polyhedra_Library::Linear_Form< C >::operator+(), Parma_Polyhedra_Library::Linear_Form< C >::operator+=(), Parma_Polyhedra_Library::Linear_Form< C >::operator-(), Parma_Polyhedra_Library::Linear_Form< C >::operator-=(), Parma_Polyhedra_Library::Linear_Form< C >::operator/=(), and Parma_Polyhedra_Library::Linear_Form< C >::operator==().

66  {
67  return vec.size();
68 }
Parma_Polyhedra_Library::Linear_Form::vec
vec_type vec
The container vector.
Definition: Linear_Form_defs.hh:409
template<typename C >
dimension_type Parma_Polyhedra_Library::Linear_Form< C >::space_dimension ( ) const
inline

Returns the dimension of the vector space enclosing *this.

Definition at line 87 of file Linear_Form_inlines.hh.

Referenced by Parma_Polyhedra_Library::Box< ITV >::affine_form_image(), Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >::intervalize(), Parma_Polyhedra_Library::Linear_Form< C >::operator+(), Parma_Polyhedra_Library::Linear_Form< C >::operator+=(), Parma_Polyhedra_Library::Linear_Form< C >::operator-(), Parma_Polyhedra_Library::Linear_Form< C >::operator-=(), Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >::overflows(), Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >::relative_error(), Parma_Polyhedra_Library::Box< ITV >::throw_dimension_incompatible(), Parma_Polyhedra_Library::Octagonal_Shape< T >::throw_dimension_incompatible(), and Parma_Polyhedra_Library::Polyhedron::throw_dimension_incompatible().

87  {
88  return size() - 1;
89 }
Parma_Polyhedra_Library::Linear_Form::size
dimension_type size() const
Gives the number of generic coefficients currently in use.
Definition: Linear_Form_inlines.hh:66
template<typename C >
memory_size_type Parma_Polyhedra_Library::Linear_Form< C >::total_memory_in_bytes ( ) const
inline

Returns a lower bound to the total size in bytes of the memory occupied by *this.

Definition at line 122 of file Linear_Form_inlines.hh.

References Parma_Polyhedra_Library::external_memory_in_bytes().

122  {
123  return sizeof(*this) + external_memory_in_bytes();
124 }
Parma_Polyhedra_Library::Linear_Form::external_memory_in_bytes
memory_size_type external_memory_in_bytes() const
Returns the size in bytes of the memory managed by *this.
Definition: Linear_Form_templates.hh:393

Friends And Related Function Documentation

template<typename FP_Interval_Type >
void affine_form_image ( std::map< dimension_type, Linear_Form< FP_Interval_Type > > &  lf_store,
Variable  var,
const Linear_Form< FP_Interval_Type > &  lf 
)
related

Assigns the linear form lf to var in the linear form abstract store lf_store, then discards all occurrences of var from it.

Definition at line 524 of file Float_inlines.hh.

527  {
528  // Assign the new linear form for var.
529  lf_store[var.id()] = lf;
530  // Now invalidate all linear forms in which var occurs.
531  discard_occurrences(lf_store, var);
532 }
Parma_Polyhedra_Library::Linear_Form::discard_occurrences
void discard_occurrences(std::map< dimension_type, Linear_Form< FP_Interval_Type > > &lf_store, Variable var)
Definition: Float_templates.hh:135
template<typename FP_Interval_Type >
void discard_occurrences ( std::map< dimension_type, Linear_Form< FP_Interval_Type > > &  lf_store,
Variable  var 
)
related

Discards all linear forms containing variable var from the linear form abstract store lf_store.

Definition at line 135 of file Float_templates.hh.

137  {
138  typedef Linear_Form<FP_Interval_Type> FP_Linear_Form;
139  typedef typename std::map<dimension_type, FP_Linear_Form>::iterator Iter;
140  for (Iter i = lf_store.begin(); i != lf_store.end(); ) {
141  if ((i->second).coefficient(var) != 0) {
142  i = lf_store.erase(i);
143  }
144  else {
145  ++i;
146  }
147  }
148 }
template<typename C >
bool operator!= ( const Linear_Form< C > &  x,
const Linear_Form< C > &  y 
)
related

Definition at line 187 of file Linear_Form_inlines.hh.

187  {
188  return !(x == y);
189 }
template<typename C >
bool operator!= ( const Linear_Form< C > &  x,
const Linear_Form< C > &  y 
)
related

Returns true if and only if x and y are different.

template<typename C >
Linear_Form< C > operator* ( const C &  n,
const Linear_Form< C > &  f 
)
related

Returns the linear form n * f.

template<typename C >
Linear_Form< C > operator* ( const Linear_Form< C > &  f,
const C &  n 
)
related

Returns the linear form f * n.

template<typename C >
Linear_Form< C > operator* ( const Linear_Form< C > &  f,
const C &  n 
)
related

Definition at line 164 of file Linear_Form_inlines.hh.

164  {
165  return n * f;
166 }
template<typename C >
Linear_Form< C > operator* ( const C &  n,
const Linear_Form< C > &  f 
)
related

Definition at line 253 of file Linear_Form_templates.hh.

References Parma_Polyhedra_Library::Linear_Form< C >::size().

253  {
254  Linear_Form<C> r(f);
255  for (dimension_type i = f.size(); i-- > 0; ) {
256  r[i] *= n;
257  }
258  return r;
259 }
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
template<typename C>
Linear_Form<C> operator* ( const C &  n,
const Linear_Form< C > &  f 
)
friend
template<typename C>
Linear_Form<C> operator* ( const Linear_Form< C > &  f,
const C &  n 
)
friend
template<typename C >
Linear_Form< C > & operator*= ( Linear_Form< C > &  f,
const C &  n 
)
related

Returns the linear form n * f and assigns it to f.

template<typename C >
Linear_Form< C > & operator*= ( Linear_Form< C > &  f,
const C &  n 
)
related

Definition at line 328 of file Linear_Form_templates.hh.

References Parma_Polyhedra_Library::Linear_Form< C >::size().

328  {
329  dimension_type f_size = f.size();
330  for (dimension_type i = f_size; i-- > 0; ) {
331  f[i] *= n;
332  }
333  return f;
334 }
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
template<typename C>
Linear_Form<C>& operator*= ( Linear_Form< C > &  f,
const C &  n 
)
friend
template<typename C >
Linear_Form< C > operator+ ( const Linear_Form< C > &  f1,
const Linear_Form< C > &  f2 
)
related

Returns the linear form f1 + f2.

template<typename C >
Linear_Form< C > operator+ ( Variable  v,
const Linear_Form< C > &  f 
)
related

Returns the linear form v + f.

template<typename C >
Linear_Form< C > operator+ ( const Linear_Form< C > &  f,
Variable  v 
)
related

Returns the linear form f + v.

template<typename C >
Linear_Form< C > operator+ ( const C &  n,
const Linear_Form< C > &  f 
)
related

Returns the linear form n + f.

template<typename C >
Linear_Form< C > operator+ ( const Linear_Form< C > &  f,
const C &  n 
)
related

Returns the linear form f + n.

template<typename C >
Linear_Form< C > operator+ ( const Linear_Form< C > &  f)
related

Returns the linear form f.

template<typename C >
Linear_Form< C > operator+ ( const Linear_Form< C > &  f1,
const Linear_Form< C > &  f2 
)
related

Definition at line 91 of file Linear_Form_templates.hh.

References Parma_Polyhedra_Library::Linear_Form< C >::size(), and Parma_Polyhedra_Library::Linear_Form< C >::vec.

91  {
92  dimension_type f1_size = f1.size();
93  dimension_type f2_size = f2.size();
94  dimension_type min_size;
95  dimension_type max_size;
96  const Linear_Form<C>* p_e_max;
97  if (f1_size > f2_size) {
98  min_size = f2_size;
99  max_size = f1_size;
100  p_e_max = &f1;
101  }
102  else {
103  min_size = f1_size;
104  max_size = f2_size;
105  p_e_max = &f2;
106  }
107 
108  Linear_Form<C> r(max_size, false);
109  dimension_type i = max_size;
110  while (i > min_size) {
111  --i;
112  r[i] = p_e_max->vec[i];
113  }
114  while (i > 0) {
115  --i;
116  r[i] = f1[i];
117  r[i] += f2[i];
118  }
119  return r;
120 }
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
template<typename C >
Linear_Form< C > operator+ ( const Variable  v,
const Linear_Form< C > &  f 
)
related

Definition at line 125 of file Linear_Form_templates.hh.

References Parma_Polyhedra_Library::Linear_Form< C >::extend(), Parma_Polyhedra_Library::Variable::space_dimension(), and Parma_Polyhedra_Library::Linear_Form< C >::space_dimension().

125  {
126  const dimension_type v_space_dim = v.space_dimension();
127  if (v_space_dim > Linear_Form<C>::max_space_dimension()) {
128  throw std::length_error("Linear_Form "
129  "operator+(v, f):\n"
130  "v exceeds the maximum allowed "
131  "space dimension.");
132  }
133  Linear_Form<C> r(f);
134  if (v_space_dim > f.space_dimension()) {
135  r.extend(v_space_dim+1);
136  }
137  r[v_space_dim] += C(typename C::boundary_type(1));
138  return r;
139 }
Parma_Polyhedra_Library::max_space_dimension
dimension_type max_space_dimension()
Returns the maximum space dimension this library can handle.
Definition: max_space_dimension.hh:40
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
template<typename C >
Linear_Form< C > operator+ ( const Linear_Form< C > &  f)
related

Definition at line 129 of file Linear_Form_inlines.hh.

129  {
130  return f;
131 }
template<typename C >
Linear_Form< C > operator+ ( const Linear_Form< C > &  f,
const C &  n 
)
related

Definition at line 136 of file Linear_Form_inlines.hh.

136  {
137  return n + f;
138 }
template<typename C >
Linear_Form< C > operator+ ( const Linear_Form< C > &  f,
const Variable  v 
)
related

Definition at line 143 of file Linear_Form_inlines.hh.

143  {
144  return v + f;
145 }
template<typename C >
Linear_Form< C > operator+ ( const C &  n,
const Linear_Form< C > &  f 
)
related

Definition at line 144 of file Linear_Form_templates.hh.

144  {
145  Linear_Form<C> r(f);
146  r[0] += n;
147  return r;
148 }
template<typename C>
Linear_Form<C> operator+ ( const Linear_Form< C > &  f1,
const Linear_Form< C > &  f2 
)
friend
template<typename C>
Linear_Form<C> operator+ ( const C &  n,
const Linear_Form< C > &  f 
)
friend
template<typename C>
Linear_Form<C> operator+ ( const Linear_Form< C > &  f,
const C &  n 
)
friend
template<typename C>
Linear_Form<C> operator+ ( Variable  v,
const Linear_Form< C > &  f 
)
friend
template<typename C >
Linear_Form< C > & operator+= ( Linear_Form< C > &  f1,
const Linear_Form< C > &  f2 
)
related

Returns the linear form f1 + f2 and assigns it to e1.

template<typename C >
Linear_Form< C > & operator+= ( Linear_Form< C > &  f,
Variable  v 
)
related

Returns the linear form f + v and assigns it to f.

Exceptions
std::length_errorThrown if the space dimension of v exceeds Linear_Form::max_space_dimension().
template<typename C >
Linear_Form< C > & operator+= ( Linear_Form< C > &  f,
const C &  n 
)
related

Returns the linear form f + n and assigns it to f.

template<typename C >
Linear_Form< C > & operator+= ( Linear_Form< C > &  f,
const C &  n 
)
related

Definition at line 171 of file Linear_Form_inlines.hh.

171  {
172  f[0] += n;
173  return f;
174 }
template<typename C >
Linear_Form< C > & operator+= ( Linear_Form< C > &  f1,
const Linear_Form< C > &  f2 
)
related

Definition at line 264 of file Linear_Form_templates.hh.

References Parma_Polyhedra_Library::Linear_Form< C >::extend(), and Parma_Polyhedra_Library::Linear_Form< C >::size().

264  {
265  dimension_type f1_size = f1.size();
266  dimension_type f2_size = f2.size();
267  if (f1_size < f2_size) {
268  f1.extend(f2_size);
269  }
270  for (dimension_type i = f2_size; i-- > 0; ) {
271  f1[i] += f2[i];
272  }
273  return f1;
274 }
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
template<typename C >
Linear_Form< C > & operator+= ( Linear_Form< C > &  f,
const Variable  v 
)
related

Definition at line 279 of file Linear_Form_templates.hh.

References Parma_Polyhedra_Library::Linear_Form< C >::extend(), Parma_Polyhedra_Library::Variable::space_dimension(), and Parma_Polyhedra_Library::Linear_Form< C >::space_dimension().

279  {
280  const dimension_type v_space_dim = v.space_dimension();
281  if (v_space_dim > Linear_Form<C>::max_space_dimension()) {
282  throw std::length_error("Linear_Form<C>& "
283  "operator+=(e, v):\n"
284  "v exceeds the maximum allowed space dimension.");
285  }
286  if (v_space_dim > f.space_dimension()) {
287  f.extend(v_space_dim+1);
288  }
289  f[v_space_dim] += C(typename C::boundary_type(1));
290  return f;
291 }
Parma_Polyhedra_Library::max_space_dimension
dimension_type max_space_dimension()
Returns the maximum space dimension this library can handle.
Definition: max_space_dimension.hh:40
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
template<typename C>
Linear_Form<C>& operator+= ( Linear_Form< C > &  f1,
const Linear_Form< C > &  f2 
)
friend
template<typename C>
Linear_Form<C>& operator+= ( Linear_Form< C > &  f,
Variable  v 
)
friend
template<typename C>
Linear_Form<C>& operator+= ( Linear_Form< C > &  f,
const C &  n 
)
friend
template<typename C >
Linear_Form< C > operator- ( const Linear_Form< C > &  f)
related

Returns the linear form - f.

template<typename C >
Linear_Form< C > operator- ( const Linear_Form< C > &  f1,
const Linear_Form< C > &  f2 
)
related

Returns the linear form f1 - f2.

template<typename C >
Linear_Form< C > operator- ( Variable  v,
const Linear_Form< C > &  f 
)
related

Returns the linear form v - f.

template<typename C >
Linear_Form< C > operator- ( const Linear_Form< C > &  f,
Variable  v 
)
related

Returns the linear form f - v.

template<typename C >
Linear_Form< C > operator- ( const C &  n,
const Linear_Form< C > &  f 
)
related

Returns the linear form n - f.

template<typename C >
Linear_Form< C > operator- ( const Linear_Form< C > &  f,
const C &  n 
)
related

Returns the linear form f - n.

template<typename C >
Linear_Form< C > operator- ( const Linear_Form< C > &  f,
const C &  n 
)
related

Definition at line 150 of file Linear_Form_inlines.hh.

150  {
151  return -n + f;
152 }
template<typename C >
Linear_Form< C > operator- ( const Linear_Form< C > &  f)
related

Definition at line 153 of file Linear_Form_templates.hh.

References Parma_Polyhedra_Library::Linear_Form< C >::size().

153  {
154  Linear_Form<C> r(f);
155  for (dimension_type i = f.size(); i-- > 0; ) {
156  r[i].neg_assign(r[i]);
157  }
158  return r;
159 }
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
template<typename C >
Linear_Form< C > operator- ( const Variable  v,
const Variable  w 
)
related

Definition at line 157 of file Linear_Form_inlines.hh.

157  {
158  return Linear_Form<C>(v, w);
159 }
template<typename C >
Linear_Form< C > operator- ( const Linear_Form< C > &  f1,
const Linear_Form< C > &  f2 
)
related

Definition at line 164 of file Linear_Form_templates.hh.

References Parma_Polyhedra_Library::Linear_Form< C >::size().

164  {
165  dimension_type f1_size = f1.size();
166  dimension_type f2_size = f2.size();
167  if (f1_size > f2_size) {
168  Linear_Form<C> r(f1_size, false);
169  dimension_type i = f1_size;
170  while (i > f2_size) {
171  --i;
172  r[i] = f1[i];
173  }
174  while (i > 0) {
175  --i;
176  r[i] = f1[i];
177  r[i] -= f2[i];
178  }
179  return r;
180  }
181  else {
182  Linear_Form<C> r(f2_size, false);
183  dimension_type i = f2_size;
184  while (i > f1_size) {
185  --i;
186  r[i].neg_assign(f2[i]);
187  }
188  while (i > 0) {
189  --i;
190  r[i] = f1[i];
191  r[i] -= f2[i];
192  }
193  return r;
194  }
195 }
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
template<typename C >
Linear_Form< C > operator- ( const Variable  v,
const Linear_Form< C > &  f 
)
related

Definition at line 200 of file Linear_Form_templates.hh.

References Parma_Polyhedra_Library::Linear_Form< C >::extend(), Parma_Polyhedra_Library::Linear_Form< C >::size(), Parma_Polyhedra_Library::Variable::space_dimension(), and Parma_Polyhedra_Library::Linear_Form< C >::space_dimension().

200  {
201  const dimension_type v_space_dim = v.space_dimension();
202  if (v_space_dim > Linear_Form<C>::max_space_dimension()) {
203  throw std::length_error("Linear_Form "
204  "operator-(v, e):\n"
205  "v exceeds the maximum allowed "
206  "space dimension.");
207  }
208  Linear_Form<C> r(f);
209  if (v_space_dim > f.space_dimension()) {
210  r.extend(v_space_dim+1);
211  }
212  for (dimension_type i = f.size(); i-- > 0; ) {
213  r[i].neg_assign(r[i]);
214  }
215  r[v_space_dim] += C(typename C::boundary_type(1));
216  return r;
217 }
Parma_Polyhedra_Library::max_space_dimension
dimension_type max_space_dimension()
Returns the maximum space dimension this library can handle.
Definition: max_space_dimension.hh:40
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
template<typename C >
Linear_Form< C > operator- ( const Linear_Form< C > &  f,
const Variable  v 
)
related

Definition at line 222 of file Linear_Form_templates.hh.

References Parma_Polyhedra_Library::Linear_Form< C >::extend(), Parma_Polyhedra_Library::Variable::space_dimension(), and Parma_Polyhedra_Library::Linear_Form< C >::space_dimension().

222  {
223  const dimension_type v_space_dim = v.space_dimension();
224  if (v_space_dim > Linear_Form<C>::max_space_dimension()) {
225  throw std::length_error("Linear_Form "
226  "operator-(e, v):\n"
227  "v exceeds the maximum allowed "
228  "space dimension.");
229  }
230  Linear_Form<C> r(f);
231  if (v_space_dim > f.space_dimension()) {
232  r.extend(v_space_dim+1);
233  }
234  r[v_space_dim] -= C(typename C::boundary_type(1));
235  return r;
236 }
Parma_Polyhedra_Library::max_space_dimension
dimension_type max_space_dimension()
Returns the maximum space dimension this library can handle.
Definition: max_space_dimension.hh:40
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
template<typename C >
Linear_Form< C > operator- ( const C &  n,
const Linear_Form< C > &  f 
)
related

Definition at line 241 of file Linear_Form_templates.hh.

References Parma_Polyhedra_Library::Linear_Form< C >::size().

241  {
242  Linear_Form<C> r(f);
243  for (dimension_type i = f.size(); i-- > 0; ) {
244  r[i].neg_assign(r[i]);
245  }
246  r[0] += n;
247  return r;
248 }
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
template<typename C>
Linear_Form<C> operator- ( const Linear_Form< C > &  f)
friend
template<typename C>
Linear_Form<C> operator- ( const Linear_Form< C > &  f1,
const Linear_Form< C > &  f2 
)
friend
template<typename C>
Linear_Form<C> operator- ( const C &  n,
const Linear_Form< C > &  f 
)
friend
template<typename C>
Linear_Form<C> operator- ( const Linear_Form< C > &  f,
const C &  n 
)
friend
template<typename C>
Linear_Form<C> operator- ( Variable  v,
const Linear_Form< C > &  f 
)
friend
template<typename C>
Linear_Form<C> operator- ( const Linear_Form< C > &  f,
Variable  v 
)
friend
template<typename C >
Linear_Form< C > & operator-= ( Linear_Form< C > &  f1,
const Linear_Form< C > &  f2 
)
related

Returns the linear form f1 - f2 and assigns it to f1.

template<typename C >
Linear_Form< C > & operator-= ( Linear_Form< C > &  f,
Variable  v 
)
related

Returns the linear form f - v and assigns it to f.

Exceptions
std::length_errorThrown if the space dimension of v exceeds Linear_Form::max_space_dimension().
template<typename C >
Linear_Form< C > & operator-= ( Linear_Form< C > &  f,
const C &  n 
)
related

Returns the linear form f - n and assigns it to f.

template<typename C >
Linear_Form< C > & operator-= ( Linear_Form< C > &  f,
const C &  n 
)
related

Definition at line 179 of file Linear_Form_inlines.hh.

179  {
180  f[0] -= n;
181  return f;
182 }
template<typename C >
Linear_Form< C > & operator-= ( Linear_Form< C > &  f1,
const Linear_Form< C > &  f2 
)
related

Definition at line 296 of file Linear_Form_templates.hh.

References Parma_Polyhedra_Library::Linear_Form< C >::extend(), and Parma_Polyhedra_Library::Linear_Form< C >::size().

296  {
297  dimension_type f1_size = f1.size();
298  dimension_type f2_size = f2.size();
299  if (f1_size < f2_size) {
300  f1.extend(f2_size);
301  }
302  for (dimension_type i = f2_size; i-- > 0; ) {
303  f1[i] -= f2[i];
304  }
305  return f1;
306 }
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
template<typename C >
Linear_Form< C > & operator-= ( Linear_Form< C > &  f,
const Variable  v 
)
related

Definition at line 311 of file Linear_Form_templates.hh.

References Parma_Polyhedra_Library::Linear_Form< C >::extend(), Parma_Polyhedra_Library::Variable::space_dimension(), and Parma_Polyhedra_Library::Linear_Form< C >::space_dimension().

311  {
312  const dimension_type v_space_dim = v.space_dimension();
313  if (v_space_dim > Linear_Form<C>::max_space_dimension()) {
314  throw std::length_error("Linear_Form<C>& "
315  "operator-=(e, v):\n"
316  "v exceeds the maximum allowed space dimension.");
317  }
318  if (v_space_dim > f.space_dimension()) {
319  f.extend(v_space_dim+1);
320  }
321  f[v_space_dim] -= C(typename C::boundary_type(1));
322  return f;
323 }
Parma_Polyhedra_Library::max_space_dimension
dimension_type max_space_dimension()
Returns the maximum space dimension this library can handle.
Definition: max_space_dimension.hh:40
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
template<typename C>
Linear_Form<C>& operator-= ( Linear_Form< C > &  f1,
const Linear_Form< C > &  f2 
)
friend
template<typename C>
Linear_Form<C>& operator-= ( Linear_Form< C > &  f,
Variable  v 
)
friend
template<typename C>
Linear_Form<C>& operator-= ( Linear_Form< C > &  f,
const C &  n 
)
friend
template<typename C >
Linear_Form< C > & operator/= ( Linear_Form< C > &  f,
const C &  n 
)
related

Returns the linear form f / n and assigns it to f.

Performs the division of a linear form by a scalar. It is up to the user to ensure that division by 0 is not performed.

template<typename C >
Linear_Form< C > & operator/= ( Linear_Form< C > &  f,
const C &  n 
)
related

Definition at line 339 of file Linear_Form_templates.hh.

References Parma_Polyhedra_Library::Linear_Form< C >::size().

339  {
340  dimension_type f_size = f.size();
341  for (dimension_type i = f_size; i-- > 0; ) {
342  f[i] /= n;
343  }
344  return f;
345 }
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
template<typename C>
Linear_Form<C>& operator/= ( Linear_Form< C > &  f,
const C &  n 
)
friend
template<typename C >
std::ostream & operator<< ( std::ostream &  s,
const Linear_Form< C > &  f 
)
related

Output operator.

template<typename C >
std::ostream & operator<< ( std::ostream &  s,
const Linear_Form< C > &  f 
)
related

Definition at line 512 of file Linear_Form_templates.hh.

512  {
513  const dimension_type num_variables = f.space_dimension();
514  bool first = true;
515  for (dimension_type v = 0; v < num_variables; ++v) {
516  const C& fv = f[v+1];
517  if (fv != typename C::boundary_type(0)) {
518  if (first) {
519  if (fv == typename C::boundary_type(-1)) {
520  s << "-";
521  }
522  else if (fv != typename C::boundary_type(1)) {
523  s << fv << "*";
524  }
525  first = false;
526  }
527  else {
528  if (fv == typename C::boundary_type(-1)) {
529  s << " - ";
530  }
531  else {
532  s << " + ";
533  if (fv != typename C::boundary_type(1)) {
534  s << fv << "*";
535  }
536  }
537  }
538  s << Variable(v);
539  }
540  }
541  // Inhomogeneous term.
542  const C& it = f[0];
543  if (it != 0) {
544  if (!first) {
545  s << " + ";
546  }
547  else {
548  first = false;
549  }
550  s << it;
551  }
552 
553  if (first) {
554  // The null linear form.
555  s << Linear_Form<C>::zero;
556  }
557  return s;
558 }
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
template<typename C >
bool operator== ( const Linear_Form< C > &  x,
const Linear_Form< C > &  y 
)
related

Returns true if and only if x and y are equal.

template<typename C >
bool operator== ( const Linear_Form< C > &  x,
const Linear_Form< C > &  y 
)
related

Definition at line 350 of file Linear_Form_templates.hh.

References Parma_Polyhedra_Library::Linear_Form< C >::size(), and Parma_Polyhedra_Library::Linear_Form< C >::zero.

350  {
351  const dimension_type x_size = x.size();
352  const dimension_type y_size = y.size();
353  if (x_size >= y_size) {
354  for (dimension_type i = y_size; i-- > 0; ) {
355  if (x[i] != y[i]) {
356  return false;
357  }
358  }
359  for (dimension_type i = x_size; --i >= y_size; ) {
360  if (x[i] != x.zero) {
361  return false;
362  }
363  }
364  }
365  else {
366  for (dimension_type i = x_size; i-- > 0; ) {
367  if (x[i] != y[i]) {
368  return false;
369  }
370  }
371  for (dimension_type i = y_size; --i >= x_size; ) {
372  if (y[i] != x.zero) {
373  return false;
374  }
375  }
376 
377  }
378 
379  return true;
380 }
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22
template<typename C>
bool operator== ( const Linear_Form< C > &  x,
const Linear_Form< C > &  y 
)
friend
template<typename C>
std::ostream& Parma_Polyhedra_Library::IO_Operators::operator ( std::ostream &  s,
const Linear_Form< C > &  f 
)
friend
template<typename C >
void swap ( Linear_Form< C > &  x,
Linear_Form< C > &  y 
)
related

Swaps x with y.

template<typename C >
void swap ( Linear_Form< C > &  x,
Linear_Form< C > &  y 
)
related

Definition at line 250 of file Linear_Form_inlines.hh.

References Parma_Polyhedra_Library::Linear_Form< C >::m_swap().

250  {
251  x.m_swap(y);
252 }
template<typename FP_Interval_Type >
void upper_bound_assign ( std::map< dimension_type, Linear_Form< FP_Interval_Type > > &  ls1,
const std::map< dimension_type, Linear_Form< FP_Interval_Type > > &  ls2 
)
related

Discards from ls1 all linear forms but those that are associated to the same variable in ls2.

Definition at line 153 of file Float_templates.hh.

156  {
157  typedef Linear_Form<FP_Interval_Type> FP_Linear_Form;
158  typedef typename std::map<dimension_type, FP_Linear_Form>::iterator Iter;
159  typedef typename std::map<dimension_type,
160  FP_Linear_Form>::const_iterator Const_Iter;
161 
162  Const_Iter i2_end = ls2.end();
163  for (Iter i1 = ls1.begin(), i1_end = ls1.end(); i1 != i1_end; ) {
164  Const_Iter i2 = ls2.find(i1->first);
165  if ((i2 == i2_end) || (i1->second != i2->second)) {
166  i1 = ls1.erase(i1);
167  }
168  else {
169  ++i1;
170  }
171  }
172 }
Parma_Polyhedra_Library::dimension_type
size_t dimension_type
An unsigned integral type for representing space dimensions.
Definition: globals_types.hh:22

Member Data Documentation

template<typename C>
vec_type Parma_Polyhedra_Library::Linear_Form< C >::vec
private

The container vector.

Definition at line 409 of file Linear_Form_defs.hh.

Referenced by Parma_Polyhedra_Library::Linear_Form< C >::Linear_Form(), Parma_Polyhedra_Library::Linear_Form< C >::m_swap(), and Parma_Polyhedra_Library::Linear_Form< C >::operator+().

template<typename C>
C Parma_Polyhedra_Library::Linear_Form< C >::zero
staticprivate

The generic coefficient equal to the singleton zero.

Definition at line 403 of file Linear_Form_defs.hh.

Referenced by Parma_Polyhedra_Library::Linear_Form< C >::Linear_Form(), and Parma_Polyhedra_Library::Linear_Form< C >::operator==().

The documentation for this class was generated from the following files: