Types and functions implementing checked numbers. More...
Classes | |
| struct | Extended_Int |
| struct | Float_2exp |
| struct | Larger |
| struct | Larger< char > |
| struct | Larger< signed char > |
| struct | Larger< signed int > |
| struct | Larger< signed long > |
| struct | Larger< signed long long > |
| struct | Larger< signed short > |
| struct | Larger< unsigned char > |
| struct | Larger< unsigned int > |
| struct | Larger< unsigned long > |
| struct | Larger< unsigned long long > |
| struct | Larger< unsigned short > |
| struct | number_struct |
| struct | Safe_Conversion |
| struct | Safe_Conversion< T, T > |
| struct | Safe_Int_Comparison |
| struct | Safe_Int_Comparison< T1, T2, typename Enable_If<(C_Integer< T1 >::value &&C_Integer< T2 >::value)>::type > |
Typedefs | |
| typedef int16_t | int_fast16_t |
| typedef int32_t | int_fast32_t |
| typedef int64_t | int_fast64_t |
| typedef uint16_t | uint_fast16_t |
| typedef uint32_t | uint_fast32_t |
| typedef uint64_t | uint_fast64_t |
| typedef int | mp_size_field_t |
| This is assumed to be the type of the _mp_size field of GMP's __mpz_struct. More... | |
Functions | |
| int | get_digit (char c, unsigned int base=10) |
Returns the integer value associated with the ASCII code c, in the base base positional number system, if there is such an association; returns 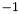 otherwise. More... otherwise. More... | |
| bool | sum_sign (bool &a_neg, unsigned long &a_mod, bool b_neg, unsigned long b_mod) |
Adds the number represented (in the modulus-and-sign representation) by b_neg and b_mod to the number represented by a_neg and a_mod, assigning the result to the latter. Returns false is the result cannot be represented; returns true otherwise. More... | |
| Result | parse_number_part (std::istream &is, number_struct &numer) |
Helper function for parse_number(): reads the numerator or denominator part of a number from is into numer, returning the appropriate Result value. More... | |
| Result | parse_number (std::istream &is, number_struct &numer, number_struct &denom) |
Reads a number from is writing it into numer, the numerator, and denom, the denominator; the appropriate Result value is returned. More... | |
| Result | input_mpq (mpq_class &to, std::istream &is) |
| std::string | float_mpq_to_string (mpq_class &q) |
| PPL_DECLARE_FUN2_0_0 (copy, void, nonconst, Type1, const, Type2) PPL_DECLARE_FUN1_0_0(sgn | |
| From | PPL_DECLARE_FUN2_0_0 (cmp, Result_Relation, const, Type1, const, Type2) PPL_DECLARE_FUN1_0_3(classify |
| From bool | PPL_DECLARE_FUN1_0_0 (is_nan, bool, const, Type) PPL_DECLARE_FUN1_0_0(is_minf |
| From bool Type | PPL_DECLARE_FUN1_0_0 (is_pinf, bool, const, Type) PPL_DECLARE_FUN1_0_0(is_int |
| From bool Type Type | PPL_DECLARE_FUN1_0_2 (assign_special, Result, nonconst, Type, Result_Class, Rounding_Dir) PPL_DECLARE_FUN1_0_2(construct_special |
| From bool Type Type Rounding_Dir | PPL_DECLARE_FUN2_0_1 (construct, Result, nonconst, To, const, From, Rounding_Dir) PPL_DECLARE_FUN2_0_1(assign |
| From bool Type Type Rounding_Dir Rounding_Dir | PPL_DECLARE_FUN2_0_1 (floor, Result, nonconst, To, const, From, Rounding_Dir) PPL_DECLARE_FUN2_0_1(ceil |
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir | PPL_DECLARE_FUN2_0_1 (trunc, Result, nonconst, To, const, From, Rounding_Dir) PPL_DECLARE_FUN2_0_1(neg |
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir | PPL_DECLARE_FUN2_0_1 (abs, Result, nonconst, To, const, From, Rounding_Dir) PPL_DECLARE_FUN2_0_1(sqrt |
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir | PPL_DECLARE_FUN3_0_1 (add, Result, nonconst, To, const, From1, const, From2, Rounding_Dir) PPL_DECLARE_FUN3_0_1(sub |
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir | PPL_DECLARE_FUN3_0_1 (mul, Result, nonconst, To, const, From1, const, From2, Rounding_Dir) PPL_DECLARE_FUN3_0_1(div |
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir | PPL_DECLARE_FUN3_0_1 (rem, Result, nonconst, To, const, From1, const, From2, Rounding_Dir) PPL_DECLARE_FUN3_0_1(idiv |
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir | PPL_DECLARE_FUN2_0_2 (add_2exp, Result, nonconst, To, const, From, unsigned int, Rounding_Dir) PPL_DECLARE_FUN2_0_2(sub_2exp |
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir unsigned Rounding_Dir | PPL_DECLARE_FUN2_0_2 (mul_2exp, Result, nonconst, To, const, From, unsigned int, Rounding_Dir) PPL_DECLARE_FUN2_0_2(div_2exp |
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir | PPL_DECLARE_FUN2_0_2 (smod_2exp, Result, nonconst, To, const, From, unsigned int, Rounding_Dir) PPL_DECLARE_FUN2_0_2(umod_2exp |
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir | PPL_DECLARE_FUN3_0_1 (add_mul, Result, nonconst, To, const, From1, const, From2, Rounding_Dir) PPL_DECLARE_FUN3_0_1(sub_mul |
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir Rounding_Dir | PPL_DECLARE_FUN3_0_1 (gcd, Result, nonconst, To, const, From1, const, From2, Rounding_Dir) PPL_DECLARE_FUN5_0_1(gcdext |
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir Rounding_Dir Rounding_Dir | PPL_DECLARE_FUN3_0_1 (lcm, Result, nonconst, To, const, From1, const, From2, Rounding_Dir) PPL_DECLARE_FUN1_0_2(input |
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir Rounding_Dir Rounding_Dir std::istream Rounding_Dir | PPL_DECLARE_FUN1_1_2 (output, Result, std::ostream &, const, Type, const Numeric_Format &, Rounding_Dir) template< typename Policy |
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir Rounding_Dir Rounding_Dir std::istream Rounding_Dir To Result | round (To &to, Result r, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| Result | assign_ext (To &to, const From &from, Rounding_Dir dir) |
| template<typename Policy , typename Type > | |
| Result | sgn_ext (const Type &x) |
| template<typename Policy1 , typename Policy2 , typename Type1 , typename Type2 > | |
| Result | cmp_ext (const Type1 &x, const Type2 &y) |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| Result | neg_ext (To &to, const From &x, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| Result | abs_ext (To &to, const From &x, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename To , typename From1 , typename From2 > | |
| Result | add_ext (To &to, const From1 &x, const From2 &y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename To , typename From1 , typename From2 > | |
| Result | sub_ext (To &to, const From1 &x, const From2 &y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename To , typename From1 , typename From2 > | |
| Result | mul_ext (To &to, const From1 &x, const From2 &y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename To , typename From1 , typename From2 > | |
| Result | div_ext (To &to, const From1 &x, const From2 &y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename To , typename From1 , typename From2 > | |
| Result | rem_ext (To &to, const From1 &x, const From2 &y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename To , typename From1 , typename From2 > | |
| Result | add_mul_ext (To &to, const From1 &x, const From2 &y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename To , typename From1 , typename From2 > | |
| Result | sub_mul_ext (To &to, const From1 &x, const From2 &y, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| Result | sqrt_ext (To &to, const From &x, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename To , typename From1 , typename From2 > | |
| Result | gcd_ext (To &to, const From1 &x, const From2 &y, Rounding_Dir dir) |
| template<typename To1_Policy , typename To2_Policy , typename To3_Policy , typename From1_Policy , typename From2_Policy , typename To1 , typename To2 , typename To3 , typename From1 , typename From2 > | |
| Result | gcdext_ext (To1 &to, To2 &s, To3 &t, const From1 &x, const From2 &y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename To , typename From1 , typename From2 > | |
| Result | lcm_ext (To &to, const From1 &x, const From2 &y, Rounding_Dir dir) |
| template<typename Policy , typename Type > | |
| Result | output_ext (std::ostream &os, const Type &x, const Numeric_Format &format, Rounding_Dir dir) |
| template<typename Policy , typename Type > | |
| Result | input_ext (Type &x, std::istream &is, Rounding_Dir dir) |
| template<typename T > | |
| bool | handle_ext_natively (const T &) |
| template<typename Policy , typename Type > | |
| bool | ext_to_handle (const Type &x) |
| template<typename Policy , typename Type > | |
| Result_Relation | sgn_ext (const Type &x) |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| Result | construct_ext (To &to, const From &x, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| Result | floor_ext (To &to, const From &x, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| Result | ceil_ext (To &to, const From &x, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| Result | trunc_ext (To &to, const From &x, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename To , typename From1 , typename From2 > | |
| Result | idiv_ext (To &to, const From1 &x, const From2 &y, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| Result | add_2exp_ext (To &to, const From &x, unsigned int exp, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| Result | sub_2exp_ext (To &to, const From &x, unsigned int exp, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| Result | mul_2exp_ext (To &to, const From &x, unsigned int exp, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| Result | div_2exp_ext (To &to, const From &x, unsigned int exp, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| Result | smod_2exp_ext (To &to, const From &x, unsigned int exp, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| Result | umod_2exp_ext (To &to, const From &x, unsigned int exp, Rounding_Dir dir) |
| template<typename Policy1 , typename Policy2 , typename Type1 , typename Type2 > | |
| Result_Relation | cmp_ext (const Type1 &x, const Type2 &y) |
| template<typename Policy1 , typename Policy2 , typename Type1 , typename Type2 > | |
| bool | lt_ext (const Type1 &x, const Type2 &y) |
| template<typename Policy1 , typename Policy2 , typename Type1 , typename Type2 > | |
| bool | gt_ext (const Type1 &x, const Type2 &y) |
| template<typename Policy1 , typename Policy2 , typename Type1 , typename Type2 > | |
| bool | le_ext (const Type1 &x, const Type2 &y) |
| template<typename Policy1 , typename Policy2 , typename Type1 , typename Type2 > | |
| bool | ge_ext (const Type1 &x, const Type2 &y) |
| template<typename Policy1 , typename Policy2 , typename Type1 , typename Type2 > | |
| bool | eq_ext (const Type1 &x, const Type2 &y) |
| template<typename Policy1 , typename Policy2 , typename Type1 , typename Type2 > | |
| bool | ne_ext (const Type1 &x, const Type2 &y) |
| template<typename To_Policy , typename To > | |
| Result | input_ext (To &to, std::istream &is, Rounding_Dir dir) |
| float | multiply_add (float x, float y, float z) |
| double | multiply_add (double x, double y, double z) |
| long double | multiply_add (long double x, long double y, long double z) |
| double | round_to_integer (double x) |
| long double | round_to_integer (long double x) |
| bool | fpu_direct_rounding (Rounding_Dir dir) |
| bool | fpu_inverse_rounding (Rounding_Dir dir) |
| void | limit_precision (const float &v) |
| void | limit_precision (const double &v) |
| void | limit_precision (const long double &) |
| template<typename Policy , typename T > | |
| Result | classify_float (const T v, bool nan, bool inf, bool sign) |
| template<typename Policy , typename T > | |
| bool | is_nan_float (const T v) |
| template<typename Policy , typename T > | |
| bool | is_inf_float (const T v) |
| template<typename Policy , typename T > | |
| bool | is_minf_float (const T v) |
| template<typename Policy , typename T > | |
| bool | is_pinf_float (const T v) |
| template<typename Policy , typename T > | |
| bool | is_int_float (const T v) |
| template<typename Policy , typename T > | |
| Result | assign_special_float (T &v, Result_Class c, Rounding_Dir) |
| template<typename T > | |
| void | pred_float (T &v) |
| template<typename T > | |
| void | succ_float (T &v) |
| template<typename Policy , typename To > | |
| Result | round_lt_float (To &to, Rounding_Dir dir) |
| template<typename Policy , typename To > | |
| Result | round_gt_float (To &to, Rounding_Dir dir) |
| template<typename Policy > | |
| void | prepare_inexact (Rounding_Dir dir) |
| template<typename Policy > | |
| Result | result_relation (Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| Result | assign_float_float_exact (To &to, const From from, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| Result | assign_float_float_inexact (To &to, const From from, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| Result | assign_float_float (To &to, const From from, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | floor_float (Type &to, const Type from, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | ceil_float (Type &to, const Type from, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | trunc_float (Type &to, const Type from, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | neg_float (Type &to, const Type from, Rounding_Dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename Type > | |
| Result | add_float (Type &to, const Type x, const Type y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename Type > | |
| Result | sub_float (Type &to, const Type x, const Type y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename Type > | |
| Result | mul_float (Type &to, const Type x, const Type y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename Type > | |
| Result | div_float (Type &to, const Type x, const Type y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename Type > | |
| Result | idiv_float (Type &to, const Type x, const Type y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename Type > | |
| Result | rem_float (Type &to, const Type x, const Type y, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | add_2exp_float (Type &to, const Type x, unsigned int exp, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | sub_2exp_float (Type &to, const Type x, unsigned int exp, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | mul_2exp_float (Type &to, const Type x, unsigned int exp, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | div_2exp_float (Type &to, const Type x, unsigned int exp, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | smod_2exp_float (Type &to, const Type x, unsigned int exp, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | umod_2exp_float (Type &to, const Type x, unsigned int exp, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | abs_float (Type &to, const Type from, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | sqrt_float (Type &to, const Type from, Rounding_Dir dir) |
| template<typename Policy , typename Type > | |
| Result_Relation | sgn_float (const Type x) |
| template<typename Policy1 , typename Policy2 , typename Type > | |
| Result_Relation | cmp_float (const Type x, const Type y) |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| Result | assign_float_int_inexact (To &to, const From from, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| Result | assign_float_int (To &to, const From from, Rounding_Dir dir) |
| template<typename Policy , typename T > | |
| Result | set_neg_overflow_float (T &to, Rounding_Dir dir) |
| template<typename Policy , typename T > | |
| Result | set_pos_overflow_float (T &to, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename T > | |
| Result | assign_float_mpz (T &to, const mpz_class &from, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename T > | |
| Result | assign_float_mpq (T &to, const mpq_class &from, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename Type > | |
| Result | add_mul_float (Type &to, const Type x, const Type y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename Type > | |
| Result | sub_mul_float (Type &to, const Type x, const Type y, Rounding_Dir dir) |
| template<typename From > | |
| void | assign_mpq_numeric_float (mpq_class &to, const From from) |
| template<> | |
| void | assign_mpq_numeric_float (mpq_class &to, const long double from) |
| template<typename Policy , typename Type > | |
| Result | output_float (std::ostream &os, const Type from, const Numeric_Format &, Rounding_Dir) |
| PPL_SAFE_CONVERSION (signed short, signed char) | |
| PPL_SAFE_CONVERSION (signed long long, signed char) | |
| PPL_SAFE_CONVERSION (signed long long, signed short) | |
| PPL_SAFE_CONVERSION (unsigned short, char) | |
| PPL_SAFE_CONVERSION (unsigned short, unsigned char) | |
| PPL_SAFE_CONVERSION (unsigned long, char) | |
| PPL_SAFE_CONVERSION (unsigned long, unsigned char) | |
| PPL_SAFE_CONVERSION (unsigned long long, char) | |
| PPL_SAFE_CONVERSION (unsigned long long, unsigned char) | |
| PPL_SAFE_CONVERSION (double, float) | |
| PPL_SAFE_CONVERSION (long double, float) | |
| PPL_SAFE_CONVERSION (long double, double) | |
| PPL_SAFE_CONVERSION (mpz_class, char) | |
| PPL_SAFE_CONVERSION (mpz_class, signed char) | |
| PPL_SAFE_CONVERSION (mpz_class, unsigned char) | |
| PPL_SAFE_CONVERSION (mpq_class, char) | |
| PPL_SAFE_CONVERSION (mpq_class, signed char) | |
| PPL_SAFE_CONVERSION (mpq_class, unsigned char) | |
| PPL_SAFE_CONVERSION (mpq_class, float) | |
| PPL_SAFE_CONVERSION (mpq_class, double) | |
| template<typename Policy , typename Type > | |
| struct | PPL_FUNCTION_CLASS (construct)< Policy |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| struct | PPL_FUNCTION_CLASS (construct) |
| template<typename To_Policy , typename To > | |
| struct | PPL_FUNCTION_CLASS (construct_special) |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| Result | assign_exact (To &to, const From &from, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Enable_If< Is_Same< To_Policy, From_Policy >::value, void >::type | copy_generic (Type &to, const Type &from) |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| Result | abs_generic (To &to, const From &from, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename To , typename From > | |
| void | gcd_exact_no_abs (To &to, const From &x, const From &y) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename To , typename From1 , typename From2 > | |
| Result | gcd_exact (To &to, const From1 &x, const From2 &y, Rounding_Dir dir) |
| template<typename To1_Policy , typename To2_Policy , typename To3_Policy , typename From1_Policy , typename From2_Policy , typename To1 , typename To2 , typename To3 , typename From1 , typename From2 > | |
| Result | gcdext_exact (To1 &to, To2 &s, To3 &t, const From1 &x, const From2 &y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename To , typename From1 , typename From2 > | |
| Result | lcm_gcd_exact (To &to, const From1 &x, const From2 &y, Rounding_Dir dir) |
| template<typename Policy , typename Type > | |
| Result_Relation | sgn_generic (const Type &x) |
| template<typename T1 , typename T2 > | |
| Enable_If<(Safe_Int_Comparison< T1, T2 >::value||Safe_Conversion< T1, T2 >::value||Safe_Conversion< T2, T1 >::value), bool >::type | lt (const T1 &x, const T2 &y) |
| template<typename T1 , typename T2 > | |
| Enable_If<(Safe_Int_Comparison< T1, T2 >::value||Safe_Conversion< T1, T2 >::value||Safe_Conversion< T2, T1 >::value), bool >::type | le (const T1 &x, const T2 &y) |
| template<typename T1 , typename T2 > | |
| Enable_If<(Safe_Int_Comparison< T1, T2 >::value||Safe_Conversion< T1, T2 >::value||Safe_Conversion< T2, T1 >::value), bool >::type | eq (const T1 &x, const T2 &y) |
| template<typename S , typename U > | |
| Enable_If<(!Safe_Int_Comparison< S, U >::value &&C_Integer< U >::value &&C_Integer< S >::is_signed), bool >::type | lt (const S &x, const U &y) |
| template<typename U , typename S > | |
| Enable_If<(!Safe_Int_Comparison< S, U >::value &&C_Integer< U >::value &&C_Integer< S >::is_signed), bool >::type | lt (const U &x, const S &y) |
| template<typename S , typename U > | |
| Enable_If<(!Safe_Int_Comparison< S, U >::value &&C_Integer< U >::value &&C_Integer< S >::is_signed), bool >::type | le (const S &x, const U &y) |
| template<typename U , typename S > | |
| Enable_If<(!Safe_Int_Comparison< S, U >::value &&C_Integer< U >::value &&C_Integer< S >::is_signed), bool >::type | le (const U &x, const S &y) |
| template<typename S , typename U > | |
| Enable_If<(!Safe_Int_Comparison< S, U >::value &&C_Integer< U >::value &&C_Integer< S >::is_signed), bool >::type | eq (const S &x, const U &y) |
| template<typename U , typename S > | |
| Enable_If<(!Safe_Int_Comparison< S, U >::value &&C_Integer< U >::value &&C_Integer< S >::is_signed), bool >::type | eq (const U &x, const S &y) |
| template<typename T1 , typename T2 > | |
| Enable_If<(!Safe_Conversion< T1, T2 >::value &&!Safe_Conversion< T2, T1 >::value &&(!C_Integer< T1 >::value||!C_Integer< T2 >::value)), bool >::type | eq (const T1 &x, const T2 &y) |
| template<typename T1 , typename T2 > | |
| Enable_If<(!Safe_Conversion< T1, T2 >::value &&!Safe_Conversion< T2, T1 >::value &&(!C_Integer< T1 >::value||!C_Integer< T2 >::value)), bool >::type | lt (const T1 &x, const T2 &y) |
| template<typename T1 , typename T2 > | |
| Enable_If<(!Safe_Conversion< T1, T2 >::value &&!Safe_Conversion< T2, T1 >::value &&(!C_Integer< T1 >::value||!C_Integer< T2 >::value)), bool >::type | le (const T1 &x, const T2 &y) |
| template<typename Policy1 , typename Policy2 , typename Type1 , typename Type2 > | |
| bool | lt_p (const Type1 &x, const Type2 &y) |
| template<typename Policy1 , typename Policy2 , typename Type1 , typename Type2 > | |
| bool | le_p (const Type1 &x, const Type2 &y) |
| template<typename Policy1 , typename Policy2 , typename Type1 , typename Type2 > | |
| bool | eq_p (const Type1 &x, const Type2 &y) |
| template<typename Policy1 , typename Policy2 , typename Type1 , typename Type2 > | |
| Result_Relation | cmp_generic (const Type1 &x, const Type2 &y) |
| template<typename Policy , typename Type > | |
| Result | assign_nan (Type &to, Result r) |
| template<typename Policy , typename Type > | |
| Result | input_generic (Type &to, std::istream &is, Rounding_Dir dir) |
| template<typename Policy , typename To > | |
| Result | set_neg_overflow_int (To &to, Rounding_Dir dir) |
| template<typename Policy , typename To > | |
| Result | set_pos_overflow_int (To &to, Rounding_Dir dir) |
| template<typename Policy , typename To > | |
| Result | round_lt_int_no_overflow (To &to, Rounding_Dir dir) |
| template<typename Policy , typename To > | |
| Result | round_gt_int_no_overflow (To &to, Rounding_Dir dir) |
| template<typename Policy , typename To > | |
| Result | round_lt_int (To &to, Rounding_Dir dir) |
| template<typename Policy , typename To > | |
| Result | round_gt_int (To &to, Rounding_Dir dir) |
| template<typename Policy , typename Type > | |
| Result | classify_int (const Type v, bool nan, bool inf, bool sign) |
| template<typename Policy , typename Type > | |
| bool | is_nan_int (const Type v) |
| template<typename Policy , typename Type > | |
| bool | is_minf_int (const Type v) |
| template<typename Policy , typename Type > | |
| bool | is_pinf_int (const Type v) |
| template<typename Policy , typename Type > | |
| bool | is_int_int (const Type v) |
| template<typename Policy , typename Type > | |
| Result | assign_special_int (Type &v, Result_Class c, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| Result | assign_signed_int_signed_int (To &to, const From from, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| Result | assign_signed_int_unsigned_int (To &to, const From from, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| Result | assign_unsigned_int_signed_int (To &to, const From from, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| Result | assign_unsigned_int_unsigned_int (To &to, const From from, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename To , typename From > | |
| Result | assign_int_float (To &to, const From from, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename To > | |
| Result | assign_signed_int_mpz (To &to, const mpz_class &from, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename To > | |
| Result | assign_unsigned_int_mpz (To &to, const mpz_class &from, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename To > | |
| Result | assign_int_mpq (To &to, const mpq_class &from, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | neg_int_larger (Type &to, const Type x, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename Type > | |
| Result | add_int_larger (Type &to, const Type x, const Type y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename Type > | |
| Result | sub_int_larger (Type &to, const Type x, const Type y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename Type > | |
| Result | mul_int_larger (Type &to, const Type x, const Type y, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | neg_signed_int (Type &to, const Type from, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | neg_unsigned_int (Type &to, const Type from, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename Type > | |
| Result | add_signed_int (Type &to, const Type x, const Type y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename Type > | |
| Result | add_unsigned_int (Type &to, const Type x, const Type y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename Type > | |
| Result | sub_signed_int (Type &to, const Type x, const Type y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename Type > | |
| Result | sub_unsigned_int (Type &to, const Type x, const Type y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename Type > | |
| Result | mul_signed_int (Type &to, const Type x, const Type y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename Type > | |
| Result | mul_unsigned_int (Type &to, const Type x, const Type y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename Type > | |
| Result | div_signed_int (Type &to, const Type x, const Type y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename Type > | |
| Result | div_unsigned_int (Type &to, const Type x, const Type y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename Type > | |
| Result | idiv_signed_int (Type &to, const Type x, const Type y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename Type > | |
| Result | idiv_unsigned_int (Type &to, const Type x, const Type y, Rounding_Dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename Type > | |
| Result | rem_signed_int (Type &to, const Type x, const Type y, Rounding_Dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename Type > | |
| Result | rem_unsigned_int (Type &to, const Type x, const Type y, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | div_2exp_unsigned_int (Type &to, const Type x, unsigned int exp, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | div_2exp_signed_int (Type &to, const Type x, unsigned int exp, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | add_2exp_unsigned_int (Type &to, const Type x, unsigned int exp, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | add_2exp_signed_int (Type &to, const Type x, unsigned int exp, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | sub_2exp_unsigned_int (Type &to, const Type x, unsigned int exp, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | sub_2exp_signed_int (Type &to, const Type x, unsigned int exp, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | mul_2exp_unsigned_int (Type &to, const Type x, unsigned int exp, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | mul_2exp_signed_int (Type &to, const Type x, unsigned int exp, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | smod_2exp_unsigned_int (Type &to, const Type x, unsigned int exp, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | smod_2exp_signed_int (Type &to, const Type x, unsigned int exp, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | umod_2exp_unsigned_int (Type &to, const Type x, unsigned int exp, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | umod_2exp_signed_int (Type &to, const Type x, unsigned int exp, Rounding_Dir dir) |
| template<typename Type > | |
| void | isqrt_rem (Type &q, Type &r, const Type from) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | sqrt_unsigned_int (Type &to, const Type from, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename Type > | |
| Result | sqrt_signed_int (Type &to, const Type from, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename Type > | |
| Result | add_mul_int (Type &to, const Type x, const Type y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy , typename Type > | |
| Result | sub_mul_int (Type &to, const Type x, const Type y, Rounding_Dir dir) |
| template<typename Policy , typename Type > | |
| Result | output_char (std::ostream &os, Type &from, const Numeric_Format &, Rounding_Dir) |
| template<typename Policy , typename Type > | |
| Result | output_int (std::ostream &os, Type &from, const Numeric_Format &, Rounding_Dir) |
| PPL_SPECIALIZE_GCDEXT (gcdext_exact, char, char, char, char, char) PPL_SPECIALIZE_GCDEXT(gcdext_exact | |
| signed signed signed signed signed char | PPL_SPECIALIZE_GCDEXT (gcdext_exact, signed short, signed short, signed short, signed short, signed short) PPL_SPECIALIZE_GCDEXT(gcdext_exact |
| signed signed signed signed signed char signed signed signed signed signed int signed long signed long signed long signed long signed long long | PPL_SPECIALIZE_GCDEXT (gcdext_exact, unsigned char, unsigned char, unsigned char, unsigned char, unsigned char) PPL_SPECIALIZE_GCDEXT(gcdext_exact |
| template<typename Policy > | |
| Result | classify_mpq (const mpq_class &v, bool nan, bool inf, bool sign) |
| template<typename Policy > | |
| bool | is_nan_mpq (const mpq_class &v) |
| template<typename Policy > | |
| bool | is_minf_mpq (const mpq_class &v) |
| template<typename Policy > | |
| bool | is_pinf_mpq (const mpq_class &v) |
| template<typename Policy > | |
| bool | is_int_mpq (const mpq_class &v) |
| template<typename Policy > | |
| Result | assign_special_mpq (mpq_class &v, Result_Class c, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy , typename From > | |
| Result | construct_mpq_base (mpq_class &to, const From &from, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy , typename From > | |
| Result | construct_mpq_float (mpq_class &to, const From &from, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename From > | |
| Result | assign_mpq_float (mpq_class &to, const From &from, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename From > | |
| Result | assign_mpq_signed_int (mpq_class &to, const From from, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy , typename From > | |
| Result | assign_mpq_unsigned_int (mpq_class &to, const From from, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy > | |
| Result | floor_mpq (mpq_class &to, const mpq_class &from, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy > | |
| Result | ceil_mpq (mpq_class &to, const mpq_class &from, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy > | |
| Result | trunc_mpq (mpq_class &to, const mpq_class &from, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy > | |
| Result | neg_mpq (mpq_class &to, const mpq_class &from, Rounding_Dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy > | |
| Result | add_mpq (mpq_class &to, const mpq_class &x, const mpq_class &y, Rounding_Dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy > | |
| Result | sub_mpq (mpq_class &to, const mpq_class &x, const mpq_class &y, Rounding_Dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy > | |
| Result | mul_mpq (mpq_class &to, const mpq_class &x, const mpq_class &y, Rounding_Dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy > | |
| Result | div_mpq (mpq_class &to, const mpq_class &x, const mpq_class &y, Rounding_Dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy > | |
| Result | idiv_mpq (mpq_class &to, const mpq_class &x, const mpq_class &y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy > | |
| Result | rem_mpq (mpq_class &to, const mpq_class &x, const mpq_class &y, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy > | |
| Result | add_2exp_mpq (mpq_class &to, const mpq_class &x, unsigned int exp, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy > | |
| Result | sub_2exp_mpq (mpq_class &to, const mpq_class &x, unsigned int exp, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy > | |
| Result | mul_2exp_mpq (mpq_class &to, const mpq_class &x, unsigned int exp, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy > | |
| Result | div_2exp_mpq (mpq_class &to, const mpq_class &x, unsigned int exp, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy > | |
| Result | smod_2exp_mpq (mpq_class &to, const mpq_class &x, unsigned int exp, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy > | |
| Result | umod_2exp_mpq (mpq_class &to, const mpq_class &x, unsigned int exp, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy > | |
| Result | abs_mpq (mpq_class &to, const mpq_class &from, Rounding_Dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy > | |
| Result | add_mul_mpq (mpq_class &to, const mpq_class &x, const mpq_class &y, Rounding_Dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy > | |
| Result | sub_mul_mpq (mpq_class &to, const mpq_class &x, const mpq_class &y, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy > | |
| Result | sqrt_mpq (mpq_class &to, const mpq_class &from, Rounding_Dir dir) |
| template<typename Policy > | |
| Result | input_mpq (mpq_class &to, std::istream &is, Rounding_Dir dir) |
| template<typename Policy > | |
| Result | output_mpq (std::ostream &os, const mpq_class &from, const Numeric_Format &, Rounding_Dir) |
| template<typename Policy > | |
| Result | round_lt_mpz (mpz_class &to, Rounding_Dir dir) |
| template<typename Policy > | |
| Result | round_gt_mpz (mpz_class &to, Rounding_Dir dir) |
| mp_size_field_t | get_mp_size (const mpz_class &v) |
| void | set_mp_size (mpz_class &v, mp_size_field_t size) |
| template<typename Policy > | |
| Result | classify_mpz (const mpz_class &v, bool nan, bool inf, bool sign) |
| template<typename Policy > | |
| bool | is_nan_mpz (const mpz_class &v) |
| template<typename Policy > | |
| bool | is_minf_mpz (const mpz_class &v) |
| template<typename Policy > | |
| bool | is_pinf_mpz (const mpz_class &v) |
| template<typename Policy > | |
| bool | is_int_mpz (const mpz_class &v) |
| template<typename Policy > | |
| Result | assign_special_mpz (mpz_class &v, Result_Class c, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy > | |
| void | copy_mpz (mpz_class &to, const mpz_class &from) |
| template<typename To_Policy , typename From_Policy , typename From > | |
| Result | construct_mpz_base (mpz_class &to, const From from, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy , typename From > | |
| Result | construct_mpz_float (mpz_class &to, const From &from, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename From > | |
| Result | assign_mpz_signed_int (mpz_class &to, const From from, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy , typename From > | |
| Result | assign_mpz_unsigned_int (mpz_class &to, const From from, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy , typename From > | |
| Result | assign_mpz_float (mpz_class &to, const From from, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy , typename From > | |
| Result | assign_mpz_long_double (mpz_class &to, const From &from, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy > | |
| Result | assign_mpz_mpq (mpz_class &to, const mpq_class &from, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy > | |
| Result | neg_mpz (mpz_class &to, const mpz_class &from, Rounding_Dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy > | |
| Result | add_mpz (mpz_class &to, const mpz_class &x, const mpz_class &y, Rounding_Dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy > | |
| Result | sub_mpz (mpz_class &to, const mpz_class &x, const mpz_class &y, Rounding_Dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy > | |
| Result | mul_mpz (mpz_class &to, const mpz_class &x, const mpz_class &y, Rounding_Dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy > | |
| Result | div_mpz (mpz_class &to, const mpz_class &x, const mpz_class &y, Rounding_Dir dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy > | |
| Result | idiv_mpz (mpz_class &to, const mpz_class &x, const mpz_class &y, Rounding_Dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy > | |
| Result | rem_mpz (mpz_class &to, const mpz_class &x, const mpz_class &y, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy > | |
| Result | add_2exp_mpz (mpz_class &to, const mpz_class &x, unsigned int exp, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy > | |
| Result | sub_2exp_mpz (mpz_class &to, const mpz_class &x, unsigned int exp, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy > | |
| Result | mul_2exp_mpz (mpz_class &to, const mpz_class &x, unsigned int exp, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy > | |
| Result | div_2exp_mpz (mpz_class &to, const mpz_class &x, unsigned int exp, Rounding_Dir dir) |
| template<typename To_Policy , typename From_Policy > | |
| Result | smod_2exp_mpz (mpz_class &to, const mpz_class &x, unsigned int exp, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy > | |
| Result | umod_2exp_mpz (mpz_class &to, const mpz_class &x, unsigned int exp, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy > | |
| Result | abs_mpz (mpz_class &to, const mpz_class &from, Rounding_Dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy > | |
| Result | add_mul_mpz (mpz_class &to, const mpz_class &x, const mpz_class &y, Rounding_Dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy > | |
| Result | sub_mul_mpz (mpz_class &to, const mpz_class &x, const mpz_class &y, Rounding_Dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy > | |
| Result | gcd_mpz (mpz_class &to, const mpz_class &x, const mpz_class &y, Rounding_Dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy > | |
| Result | gcdext_mpz (mpz_class &to, mpz_class &s, mpz_class &t, const mpz_class &x, const mpz_class &y, Rounding_Dir) |
| template<typename To_Policy , typename From1_Policy , typename From2_Policy > | |
| Result | lcm_mpz (mpz_class &to, const mpz_class &x, const mpz_class &y, Rounding_Dir) |
| template<typename To_Policy , typename From_Policy > | |
| Result | sqrt_mpz (mpz_class &to, const mpz_class &from, Rounding_Dir dir) |
| template<typename Policy , typename Type > | |
| Result_Relation | sgn_mp (const Type &x) |
| template<typename Policy1 , typename Policy2 , typename Type > | |
| Result_Relation | cmp_mp (const Type &x, const Type &y) |
| template<typename Policy > | |
| Result | output_mpz (std::ostream &os, const mpz_class &from, const Numeric_Format &, Rounding_Dir) |
Detailed Description
Types and functions implementing checked numbers.
Typedef Documentation
| typedef int16_t Parma_Polyhedra_Library::Checked::int_fast16_t |
Definition at line 48 of file checked_int_inlines.hh.
| typedef int32_t Parma_Polyhedra_Library::Checked::int_fast32_t |
Definition at line 52 of file checked_int_inlines.hh.
| typedef int64_t Parma_Polyhedra_Library::Checked::int_fast64_t |
Definition at line 56 of file checked_int_inlines.hh.
This is assumed to be the type of the _mp_size field of GMP's __mpz_struct.
Definition at line 61 of file checked_mpz_inlines.hh.
| typedef uint16_t Parma_Polyhedra_Library::Checked::uint_fast16_t |
Definition at line 60 of file checked_int_inlines.hh.
| typedef uint32_t Parma_Polyhedra_Library::Checked::uint_fast32_t |
Definition at line 64 of file checked_int_inlines.hh.
| typedef uint64_t Parma_Polyhedra_Library::Checked::uint_fast64_t |
Definition at line 68 of file checked_int_inlines.hh.
Function Documentation
|
inline |
Definition at line 205 of file checked_ext_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::VC_NAN, and Parma_Polyhedra_Library::VC_PLUS_INFINITY.
|
inline |
Definition at line 733 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::V_EQ, and Parma_Polyhedra_Library::VC_NAN.
|
inline |
Definition at line 288 of file checked_inlines.hh.
|
inline |
|
inline |
|
inline |
Definition at line 685 of file checked_ext_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, and Parma_Polyhedra_Library::VC_PLUS_INFINITY.
|
inline |
Definition at line 637 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, sizeof_to_bits, Type, and Parma_Polyhedra_Library::VC_NAN.
|
inline |
Definition at line 360 of file checked_mpq_inlines.hh.
References PPL_DIRTY_TEMP, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 485 of file checked_mpz_inlines.hh.
References PPL_DIRTY_TEMP, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 1349 of file checked_int_inlines.hh.
References sizeof_to_bits, Type, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 1334 of file checked_int_inlines.hh.
References sizeof_to_bits, Type, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 224 of file checked_ext_inlines.hh.
References CHECK_P, Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::V_INF_ADD_INF, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, and Parma_Polyhedra_Library::VC_PLUS_INFINITY.
|
inline |
Definition at line 462 of file checked_float_inlines.hh.
References fpu_direct_rounding(), fpu_inverse_rounding(), Parma_Polyhedra_Library::fpu_restore_rounding_direction(), Parma_Polyhedra_Library::fpu_save_rounding_direction(), limit_precision(), Parma_Polyhedra_Library::round_fpu_dir(), Parma_Polyhedra_Library::V_INF_ADD_INF, and Parma_Polyhedra_Library::V_NAN.
|
inline |
Definition at line 973 of file checked_int_inlines.hh.
|
inline |
|
inline |
|
inline |
Definition at line 373 of file checked_ext_inlines.hh.
References CHECK_P, Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::V_INF_ADD_INF, Parma_Polyhedra_Library::V_INF_MUL_ZERO, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, Parma_Polyhedra_Library::VC_PLUS_INFINITY, Parma_Polyhedra_Library::VR_GT, and Parma_Polyhedra_Library::VR_LT.
|
inline |
Definition at line 995 of file checked_float_inlines.hh.
References fpu_direct_rounding(), fpu_inverse_rounding(), Parma_Polyhedra_Library::fpu_restore_rounding_direction(), Parma_Polyhedra_Library::fpu_save_rounding_direction(), limit_precision(), multiply_add(), Parma_Polyhedra_Library::round_fpu_dir(), Parma_Polyhedra_Library::V_INF_MUL_ZERO, and Parma_Polyhedra_Library::V_NAN.
|
inline |
Definition at line 1575 of file checked_int_inlines.hh.
References Parma_Polyhedra_Library::result_overflow(), Type, Parma_Polyhedra_Library::V_NAN, Parma_Polyhedra_Library::V_UNKNOWN_NEG_OVERFLOW, and Parma_Polyhedra_Library::V_UNKNOWN_POS_OVERFLOW.
|
inline |
|
inline |
|
inline |
|
inline |
Definition at line 1048 of file checked_int_inlines.hh.
References CHECK_P, and Parma_Polyhedra_Library::V_EQ.
|
inline |
|
inline |
Definition at line 95 of file checked_ext_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, and Parma_Polyhedra_Library::VC_PLUS_INFINITY.
|
inline |
Definition at line 376 of file checked_float_inlines.hh.
|
inline |
Definition at line 339 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::V_EQ, and Parma_Polyhedra_Library::VC_NAN.
|
inline |
Definition at line 349 of file checked_float_inlines.hh.
References fpu_direct_rounding(), fpu_inverse_rounding(), Parma_Polyhedra_Library::fpu_restore_rounding_direction(), Parma_Polyhedra_Library::fpu_save_rounding_direction(), From, limit_precision(), Parma_Polyhedra_Library::round_fpu_dir(), Parma_Polyhedra_Library::ROUND_IGNORE, and Parma_Polyhedra_Library::VC_NAN.
|
inline |
Definition at line 814 of file checked_float_inlines.hh.
References From, and sizeof_to_bits.
|
inline |
Definition at line 797 of file checked_float_inlines.hh.
References fpu_direct_rounding(), Parma_Polyhedra_Library::fpu_restore_rounding_direction(), Parma_Polyhedra_Library::fpu_save_rounding_direction(), limit_precision(), and Parma_Polyhedra_Library::round_fpu_dir().
|
inline |
Definition at line 912 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::Boundary_NS::sgn(), Parma_Polyhedra_Library::V_EQ, and Parma_Polyhedra_Library::Bool< false >::value.
|
inline |
Definition at line 867 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::Boundary_NS::sgn(), Parma_Polyhedra_Library::V_EQ, and Parma_Polyhedra_Library::Bool< false >::value.
|
inline |
Definition at line 542 of file checked_int_inlines.hh.
References CHECK_P, From, le(), lt(), Parma_Polyhedra_Library::round_direct(), Parma_Polyhedra_Library::ROUND_DOWN, Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::round_not_requested(), Parma_Polyhedra_Library::ROUND_UP, Parma_Polyhedra_Library::V_EQ, Parma_Polyhedra_Library::V_LGE, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, and Parma_Polyhedra_Library::VC_PLUS_INFINITY.
|
inline |
Definition at line 739 of file checked_int_inlines.hh.
References PPL_DIRTY_TEMP, Parma_Polyhedra_Library::round_not_requested(), Parma_Polyhedra_Library::V_EQ, and Parma_Polyhedra_Library::V_LGE.
|
inline |
Definition at line 194 of file checked_mpq_inlines.hh.
References assign_mpq_numeric_float(), Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::V_EQ, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, and Parma_Polyhedra_Library::VC_PLUS_INFINITY.
|
inline |
Definition at line 1065 of file checked_float_inlines.hh.
Referenced by assign_mpq_float(), and output_float().
|
inline |
Definition at line 1071 of file checked_float_inlines.hh.
References long.
|
inline |
Definition at line 214 of file checked_mpq_inlines.hh.
References From, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 237 of file checked_mpq_inlines.hh.
References From, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 284 of file checked_mpz_inlines.hh.
References From, Parma_Polyhedra_Library::round_direct(), Parma_Polyhedra_Library::ROUND_DOWN, Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::round_not_requested(), Parma_Polyhedra_Library::ROUND_UP, Parma_Polyhedra_Library::V_EQ, Parma_Polyhedra_Library::V_LGE, Parma_Polyhedra_Library::V_NAN, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, and Parma_Polyhedra_Library::VC_PLUS_INFINITY.
|
inline |
Definition at line 324 of file checked_mpz_inlines.hh.
References input_mpq(), PPL_DIRTY_TEMP, Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::V_EQ, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, and Parma_Polyhedra_Library::VC_PLUS_INFINITY.
|
inline |
Definition at line 350 of file checked_mpz_inlines.hh.
References Parma_Polyhedra_Library::round_down(), Parma_Polyhedra_Library::round_ignore(), Parma_Polyhedra_Library::round_not_needed(), Parma_Polyhedra_Library::round_strict_relation(), Parma_Polyhedra_Library::round_up(), Parma_Polyhedra_Library::V_EQ, Parma_Polyhedra_Library::V_GE, Parma_Polyhedra_Library::V_GT, Parma_Polyhedra_Library::V_LE, Parma_Polyhedra_Library::V_LGE, and Parma_Polyhedra_Library::V_LT.
|
inline |
Definition at line 248 of file checked_mpz_inlines.hh.
References From, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 270 of file checked_mpz_inlines.hh.
References From, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 648 of file checked_inlines.hh.
|
inline |
Definition at line 641 of file checked_int_inlines.hh.
References PPL_GT_SILENT, PPL_LT_SILENT, Parma_Polyhedra_Library::Boundary_NS::sgn(), To, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 363 of file checked_int_inlines.hh.
References CHECK_P, From, PPL_GT_SILENT, PPL_LT_SILENT, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 385 of file checked_int_inlines.hh.
References CHECK_P, From, To, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 216 of file checked_float_inlines.hh.
References PPL_NAN, Parma_Polyhedra_Library::V_EQ_MINUS_INFINITY, Parma_Polyhedra_Library::V_EQ_PLUS_INFINITY, Parma_Polyhedra_Library::V_NAN, Parma_Polyhedra_Library::V_UNREPRESENTABLE, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, and Parma_Polyhedra_Library::VC_PLUS_INFINITY.
|
inline |
Definition at line 314 of file checked_int_inlines.hh.
References Parma_Polyhedra_Library::round_down(), Parma_Polyhedra_Library::round_up(), Parma_Polyhedra_Library::V_EQ_MINUS_INFINITY, Parma_Polyhedra_Library::V_EQ_PLUS_INFINITY, Parma_Polyhedra_Library::V_GT_SUP, Parma_Polyhedra_Library::V_LT_INF, Parma_Polyhedra_Library::V_NAN, Parma_Polyhedra_Library::V_UNREPRESENTABLE, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, and Parma_Polyhedra_Library::VC_PLUS_INFINITY.
|
inline |
Definition at line 110 of file checked_mpq_inlines.hh.
References Parma_Polyhedra_Library::V_EQ_MINUS_INFINITY, Parma_Polyhedra_Library::V_EQ_PLUS_INFINITY, Parma_Polyhedra_Library::V_NAN, Parma_Polyhedra_Library::V_UNREPRESENTABLE, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, and Parma_Polyhedra_Library::VC_PLUS_INFINITY.
|
inline |
Definition at line 141 of file checked_mpz_inlines.hh.
References set_mp_size(), Parma_Polyhedra_Library::V_EQ_MINUS_INFINITY, Parma_Polyhedra_Library::V_EQ_PLUS_INFINITY, Parma_Polyhedra_Library::V_NAN, Parma_Polyhedra_Library::V_UNREPRESENTABLE, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, and Parma_Polyhedra_Library::VC_PLUS_INFINITY.
|
inline |
Definition at line 694 of file checked_int_inlines.hh.
References CHECK_P, long, PPL_GT_SILENT, Parma_Polyhedra_Library::Boundary_NS::sgn(), To, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 398 of file checked_int_inlines.hh.
References CHECK_P, From, To, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 414 of file checked_int_inlines.hh.
References CHECK_P, From, PPL_GT_SILENT, To, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 161 of file checked_ext_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, and Parma_Polyhedra_Library::VC_PLUS_INFINITY.
|
inline |
Definition at line 412 of file checked_float_inlines.hh.
References fpu_direct_rounding(), fpu_inverse_rounding(), Parma_Polyhedra_Library::fpu_restore_rounding_direction(), Parma_Polyhedra_Library::fpu_save_rounding_direction(), limit_precision(), Parma_Polyhedra_Library::round_fpu_dir(), Parma_Polyhedra_Library::ROUND_IGNORE, round_to_integer(), Parma_Polyhedra_Library::ROUND_UP, Parma_Polyhedra_Library::V_EQ, and Parma_Polyhedra_Library::VC_NAN.
|
inline |
|
inline |
Definition at line 149 of file checked_float_inlines.hh.
References CHECK_P, Parma_Polyhedra_Library::V_EQ, Parma_Polyhedra_Library::V_EQ_MINUS_INFINITY, Parma_Polyhedra_Library::V_EQ_PLUS_INFINITY, Parma_Polyhedra_Library::V_GT, Parma_Polyhedra_Library::V_LGE, Parma_Polyhedra_Library::V_LT, and Parma_Polyhedra_Library::V_NAN.
|
inline |
Definition at line 197 of file checked_int_inlines.hh.
References Parma_Polyhedra_Library::V_EQ, Parma_Polyhedra_Library::V_EQ_MINUS_INFINITY, Parma_Polyhedra_Library::V_EQ_PLUS_INFINITY, Parma_Polyhedra_Library::V_GT, Parma_Polyhedra_Library::V_LGE, Parma_Polyhedra_Library::V_LT, and Parma_Polyhedra_Library::V_NAN.
|
inline |
Definition at line 37 of file checked_mpq_inlines.hh.
References Parma_Polyhedra_Library::Boundary_NS::sgn(), Parma_Polyhedra_Library::V_EQ_MINUS_INFINITY, Parma_Polyhedra_Library::V_EQ_PLUS_INFINITY, Parma_Polyhedra_Library::V_GT, Parma_Polyhedra_Library::V_LGE, Parma_Polyhedra_Library::V_LT, and Parma_Polyhedra_Library::V_NAN.
|
inline |
Definition at line 76 of file checked_mpz_inlines.hh.
References get_mp_size(), Parma_Polyhedra_Library::V_EQ_MINUS_INFINITY, Parma_Polyhedra_Library::V_EQ_PLUS_INFINITY, Parma_Polyhedra_Library::V_GT, Parma_Polyhedra_Library::V_LGE, Parma_Polyhedra_Library::V_LT, and Parma_Polyhedra_Library::V_NAN.
|
inline |
Definition at line 894 of file checked_ext_inlines.hh.
References Parma_Polyhedra_Library::VR_EMPTY, Parma_Polyhedra_Library::VR_EQ, Parma_Polyhedra_Library::VR_GT, and Parma_Polyhedra_Library::VR_LT.
|
inline |
Definition at line 894 of file checked_ext_inlines.hh.
References Parma_Polyhedra_Library::VR_EMPTY, Parma_Polyhedra_Library::VR_EQ, Parma_Polyhedra_Library::VR_GT, and Parma_Polyhedra_Library::VR_LT.
|
inline |
Definition at line 782 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::VR_EMPTY, Parma_Polyhedra_Library::VR_EQ, Parma_Polyhedra_Library::VR_GT, and Parma_Polyhedra_Library::VR_LT.
|
inline |
Definition at line 636 of file checked_inlines.hh.
|
inline |
Definition at line 663 of file checked_mpz_inlines.hh.
References Parma_Polyhedra_Library::cmp(), Parma_Polyhedra_Library::VR_EQ, Parma_Polyhedra_Library::VR_GT, and Parma_Polyhedra_Library::VR_LT.
|
inline |
Definition at line 73 of file checked_ext_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, and Parma_Polyhedra_Library::VC_PLUS_INFINITY.
|
inline |
|
inline |
Definition at line 163 of file checked_mpq_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::V_EQ, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, and Parma_Polyhedra_Library::VC_PLUS_INFINITY.
|
inline |
|
inline |
Definition at line 205 of file checked_mpz_inlines.hh.
References From, Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::round_not_requested(), Parma_Polyhedra_Library::V_EQ, Parma_Polyhedra_Library::V_LGE, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, and Parma_Polyhedra_Library::VC_PLUS_INFINITY.
|
inline |
Definition at line 282 of file checked_inlines.hh.
|
inline |
Definition at line 170 of file checked_mpz_inlines.hh.
References get_mp_size(), and set_mp_size().
|
inline |
Definition at line 751 of file checked_ext_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, and Parma_Polyhedra_Library::VC_PLUS_INFINITY.
|
inline |
Definition at line 679 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, sizeof_to_bits, Type, and Parma_Polyhedra_Library::VC_NAN.
|
inline |
|
inline |
Definition at line 521 of file checked_mpz_inlines.hh.
References Parma_Polyhedra_Library::round_down(), Parma_Polyhedra_Library::round_not_requested(), Parma_Polyhedra_Library::round_strict_relation(), Parma_Polyhedra_Library::round_up(), Parma_Polyhedra_Library::V_EQ, Parma_Polyhedra_Library::V_GE, Parma_Polyhedra_Library::V_GT, Parma_Polyhedra_Library::V_LE, Parma_Polyhedra_Library::V_LGE, and Parma_Polyhedra_Library::V_LT.
|
inline |
Definition at line 1286 of file checked_int_inlines.hh.
References Parma_Polyhedra_Library::round_not_requested(), sizeof_to_bits, Type, Parma_Polyhedra_Library::V_EQ, Parma_Polyhedra_Library::V_GE, and Parma_Polyhedra_Library::V_LE.
|
inline |
Definition at line 1260 of file checked_int_inlines.hh.
References Parma_Polyhedra_Library::round_not_requested(), sizeof_to_bits, Type, Parma_Polyhedra_Library::V_EQ, and Parma_Polyhedra_Library::V_GE.
|
inline |
Definition at line 539 of file checked_ext_inlines.hh.
References CHECK_P, Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::V_DIV_ZERO, Parma_Polyhedra_Library::V_EQ, Parma_Polyhedra_Library::V_INF_DIV_INF, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, Parma_Polyhedra_Library::VC_PLUS_INFINITY, Parma_Polyhedra_Library::VR_GT, and Parma_Polyhedra_Library::VR_LT.
|
inline |
Definition at line 560 of file checked_float_inlines.hh.
References fpu_direct_rounding(), fpu_inverse_rounding(), Parma_Polyhedra_Library::fpu_restore_rounding_direction(), Parma_Polyhedra_Library::fpu_save_rounding_direction(), limit_precision(), Parma_Polyhedra_Library::round_fpu_dir(), Parma_Polyhedra_Library::V_DIV_ZERO, Parma_Polyhedra_Library::V_INF_DIV_INF, and Parma_Polyhedra_Library::V_NAN.
|
inline |
Definition at line 321 of file checked_mpq_inlines.hh.
References CHECK_P, Parma_Polyhedra_Library::Boundary_NS::sgn(), Parma_Polyhedra_Library::V_DIV_ZERO, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 422 of file checked_mpz_inlines.hh.
References CHECK_P, Parma_Polyhedra_Library::round_down(), Parma_Polyhedra_Library::round_ignore(), Parma_Polyhedra_Library::round_not_needed(), Parma_Polyhedra_Library::round_strict_relation(), Parma_Polyhedra_Library::round_up(), Parma_Polyhedra_Library::Boundary_NS::sgn(), Parma_Polyhedra_Library::V_DIV_ZERO, Parma_Polyhedra_Library::V_EQ, Parma_Polyhedra_Library::V_GE, Parma_Polyhedra_Library::V_GT, Parma_Polyhedra_Library::V_LE, Parma_Polyhedra_Library::V_LGE, and Parma_Polyhedra_Library::V_LT.
|
inline |
Definition at line 1167 of file checked_int_inlines.hh.
References CHECK_P, Parma_Polyhedra_Library::round_not_requested(), Type, Parma_Polyhedra_Library::V_DIV_ZERO, Parma_Polyhedra_Library::V_EQ, and Parma_Polyhedra_Library::V_LGE.
|
inline |
Definition at line 1196 of file checked_int_inlines.hh.
References CHECK_P, Parma_Polyhedra_Library::round_not_requested(), Type, Parma_Polyhedra_Library::V_DIV_ZERO, Parma_Polyhedra_Library::V_EQ, and Parma_Polyhedra_Library::V_GE.
|
inline |
Definition at line 493 of file checked_inlines.hh.
|
inline |
Definition at line 533 of file checked_inlines.hh.
|
inline |
Definition at line 541 of file checked_inlines.hh.
|
inline |
Definition at line 549 of file checked_inlines.hh.
|
inline |
Definition at line 976 of file checked_ext_inlines.hh.
|
inline |
Definition at line 629 of file checked_inlines.hh.
|
inline |
Definition at line 44 of file checked_ext_inlines.hh.
References handle_ext_natively().
| std::string Parma_Polyhedra_Library::Checked::float_mpq_to_string | ( | mpq_class & | q | ) |
|
inline |
Definition at line 139 of file checked_ext_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, and Parma_Polyhedra_Library::VC_PLUS_INFINITY.
|
inline |
Definition at line 387 of file checked_float_inlines.hh.
References fpu_direct_rounding(), fpu_inverse_rounding(), Parma_Polyhedra_Library::fpu_restore_rounding_direction(), Parma_Polyhedra_Library::fpu_save_rounding_direction(), limit_precision(), Parma_Polyhedra_Library::ROUND_DOWN, Parma_Polyhedra_Library::round_fpu_dir(), Parma_Polyhedra_Library::ROUND_IGNORE, round_to_integer(), Parma_Polyhedra_Library::V_EQ, and Parma_Polyhedra_Library::VC_NAN.
|
inline |
|
inline |
Definition at line 100 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::round_direct(), and Parma_Polyhedra_Library::round_not_requested().
Referenced by add_float(), add_mul_float(), assign_float_float_inexact(), assign_float_int_inexact(), ceil_float(), div_float(), floor_float(), mul_float(), sqrt_float(), sub_float(), and sub_mul_float().
|
inline |
Definition at line 105 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::round_inverse().
Referenced by add_float(), add_mul_float(), assign_float_float_inexact(), ceil_float(), div_float(), floor_float(), mul_float(), sub_float(), and sub_mul_float().
|
inline |
Definition at line 319 of file checked_inlines.hh.
|
inline |
Definition at line 300 of file checked_inlines.hh.
References Parma_Polyhedra_Library::ROUND_NOT_NEEDED.
|
inline |
Definition at line 835 of file checked_ext_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, and Parma_Polyhedra_Library::VC_NAN.
|
inline |
|
inline |
Definition at line 329 of file checked_inlines.hh.
References From2, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 855 of file checked_ext_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, and Parma_Polyhedra_Library::VC_NAN.
|
inline |
|
inline |
Definition at line 969 of file checked_ext_inlines.hh.
Returns the integer value associated with the ASCII code c, in the base base positional number system, if there is such an association; returns 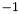 otherwise.
otherwise.
Definition at line 54 of file checked.cc.
Referenced by parse_number_part().
|
inline |
Definition at line 65 of file checked_mpz_inlines.hh.
Referenced by classify_mpz(), copy_mpz(), is_minf_mpz(), is_nan_mpz(), and is_pinf_mpz().
|
inline |
Definition at line 942 of file checked_ext_inlines.hh.
|
inline |
Definition at line 38 of file checked_ext_inlines.hh.
Referenced by ext_to_handle().
|
inline |
Definition at line 599 of file checked_ext_inlines.hh.
References CHECK_P, Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::V_DIV_ZERO, Parma_Polyhedra_Library::V_EQ, Parma_Polyhedra_Library::V_INF_DIV_INF, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, Parma_Polyhedra_Library::VC_PLUS_INFINITY, Parma_Polyhedra_Library::VR_GT, and Parma_Polyhedra_Library::VR_LT.
|
inline |
Definition at line 595 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::result_class(), Parma_Polyhedra_Library::round_dir(), Parma_Polyhedra_Library::ROUND_NOT_NEEDED, Parma_Polyhedra_Library::ROUND_UP, Type, Parma_Polyhedra_Library::V_EQ, Parma_Polyhedra_Library::V_GE, Parma_Polyhedra_Library::V_LE, and Parma_Polyhedra_Library::VC_NORMAL.
|
inline |
Definition at line 333 of file checked_mpq_inlines.hh.
References CHECK_P, Parma_Polyhedra_Library::Boundary_NS::sgn(), and Parma_Polyhedra_Library::V_DIV_ZERO.
|
inline |
Definition at line 458 of file checked_mpz_inlines.hh.
References CHECK_P, Parma_Polyhedra_Library::Boundary_NS::sgn(), Parma_Polyhedra_Library::V_DIV_ZERO, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 1214 of file checked_int_inlines.hh.
References CHECK_P, Parma_Polyhedra_Library::V_DIV_ZERO, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 1228 of file checked_int_inlines.hh.
References CHECK_P, Parma_Polyhedra_Library::V_DIV_ZERO, and Parma_Polyhedra_Library::V_EQ.
| Result Parma_Polyhedra_Library::Checked::input_ext | ( | Type & | x, |
| std::istream & | is, | ||
| Rounding_Dir | dir | ||
| ) |
|
inline |
Definition at line 1028 of file checked_ext_inlines.hh.
|
inline |
Definition at line 655 of file checked_inlines.hh.
| Result Parma_Polyhedra_Library::Checked::input_mpq | ( | mpq_class & | to, |
| std::istream & | is | ||
| ) |
Definition at line 429 of file checked.cc.
References Parma_Polyhedra_Library::Checked::number_struct::base, Parma_Polyhedra_Library::Checked::number_struct::base_for_exponent, Parma_Polyhedra_Library::Checked::number_struct::exponent, Parma_Polyhedra_Library::Checked::number_struct::mantissa, Parma_Polyhedra_Library::Checked::number_struct::neg_exponent, Parma_Polyhedra_Library::Checked::number_struct::neg_mantissa, parse_number(), Parma_Polyhedra_Library::V_CVT_STR_UNK, Parma_Polyhedra_Library::V_EQ, and Parma_Polyhedra_Library::V_NAN.
Referenced by assign_mpz_long_double(), and input_mpq().
|
inline |
Definition at line 503 of file checked_mpq_inlines.hh.
References c, input_mpq(), Parma_Polyhedra_Library::result_class(), Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, and Parma_Polyhedra_Library::VC_PLUS_INFINITY.
|
inline |
|
inline |
Definition at line 210 of file checked_float_inlines.hh.
References round_to_integer().
|
inline |
Definition at line 296 of file checked_int_inlines.hh.
|
inline |
Definition at line 96 of file checked_mpq_inlines.hh.
References Parma_Polyhedra_Library::Boundary_NS::sgn().
|
inline |
Definition at line 133 of file checked_mpz_inlines.hh.
|
inline |
|
inline |
Definition at line 258 of file checked_int_inlines.hh.
|
inline |
Definition at line 76 of file checked_mpq_inlines.hh.
References Parma_Polyhedra_Library::Boundary_NS::sgn().
|
inline |
Definition at line 115 of file checked_mpz_inlines.hh.
References get_mp_size().
|
inline |
|
inline |
Definition at line 240 of file checked_int_inlines.hh.
|
inline |
Definition at line 66 of file checked_mpq_inlines.hh.
References Parma_Polyhedra_Library::Boundary_NS::sgn().
|
inline |
Definition at line 106 of file checked_mpz_inlines.hh.
References get_mp_size().
|
inline |
|
inline |
Definition at line 277 of file checked_int_inlines.hh.
|
inline |
Definition at line 86 of file checked_mpq_inlines.hh.
References Parma_Polyhedra_Library::Boundary_NS::sgn().
|
inline |
Definition at line 124 of file checked_mpz_inlines.hh.
References get_mp_size().
|
inline |
Definition at line 1535 of file checked_int_inlines.hh.
References sizeof_to_bits, and Type.
Referenced by sqrt_unsigned_int().
|
inline |
Definition at line 878 of file checked_ext_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::VC_NAN, and Parma_Polyhedra_Library::VC_PLUS_INFINITY.
|
inline |
Definition at line 422 of file checked_inlines.hh.
References Parma_Polyhedra_Library::ROUND_NOT_NEEDED, and Parma_Polyhedra_Library::V_EQ.
|
inline |
|
inline |
Definition at line 486 of file checked_inlines.hh.
Referenced by assign_int_float().
|
inline |
Definition at line 517 of file checked_inlines.hh.
|
inline |
Definition at line 525 of file checked_inlines.hh.
|
inline |
Definition at line 585 of file checked_inlines.hh.
|
inline |
Definition at line 949 of file checked_ext_inlines.hh.
|
inline |
Definition at line 622 of file checked_inlines.hh.
|
inline |
Definition at line 134 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::PPL_CC_FLUSH().
Referenced by add_float(), add_mul_float(), assign_float_float_inexact(), assign_float_int_inexact(), ceil_float(), div_float(), floor_float(), mul_float(), sqrt_float(), sub_float(), and sub_mul_float().
|
inline |
Definition at line 139 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::PPL_CC_FLUSH().
Definition at line 144 of file checked_float_inlines.hh.
|
inline |
Definition at line 479 of file checked_inlines.hh.
Referenced by assign_int_float().
|
inline |
Definition at line 501 of file checked_inlines.hh.
|
inline |
Definition at line 509 of file checked_inlines.hh.
|
inline |
Definition at line 564 of file checked_inlines.hh.
|
inline |
Definition at line 922 of file checked_ext_inlines.hh.
|
inline |
Definition at line 615 of file checked_inlines.hh.
|
inline |
Definition at line 729 of file checked_ext_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, and Parma_Polyhedra_Library::VC_PLUS_INFINITY.
|
inline |
Definition at line 665 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, sizeof_to_bits, Type, and Parma_Polyhedra_Library::VC_NAN.
|
inline |
|
inline |
|
inline |
Definition at line 1428 of file checked_int_inlines.hh.
References PPL_LT_SILENT, sizeof_to_bits, Type, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 1406 of file checked_int_inlines.hh.
References sizeof_to_bits, Type, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 310 of file checked_ext_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::V_INF_MUL_ZERO, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, Parma_Polyhedra_Library::VC_PLUS_INFINITY, Parma_Polyhedra_Library::VR_GT, and Parma_Polyhedra_Library::VR_LT.
|
inline |
Definition at line 526 of file checked_float_inlines.hh.
References fpu_direct_rounding(), fpu_inverse_rounding(), Parma_Polyhedra_Library::fpu_restore_rounding_direction(), Parma_Polyhedra_Library::fpu_save_rounding_direction(), limit_precision(), Parma_Polyhedra_Library::round_fpu_dir(), Parma_Polyhedra_Library::V_INF_MUL_ZERO, and Parma_Polyhedra_Library::V_NAN.
|
inline |
Definition at line 991 of file checked_int_inlines.hh.
|
inline |
|
inline |
|
inline |
|
inline |
|
inline |
Definition at line 35 of file checked_float_inlines.hh.
Referenced by add_mul_float(), and sub_mul_float().
|
inline |
Definition at line 45 of file checked_float_inlines.hh.
|
inline |
Definition at line 55 of file checked_float_inlines.hh.
|
inline |
Definition at line 999 of file checked_ext_inlines.hh.
|
inline |
Definition at line 117 of file checked_ext_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, and Parma_Polyhedra_Library::VC_PLUS_INFINITY.
|
inline |
Definition at line 451 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::V_EQ, and Parma_Polyhedra_Library::VC_NAN.
|
inline |
Definition at line 964 of file checked_int_inlines.hh.
|
inline |
|
inline |
|
inline |
Definition at line 999 of file checked_int_inlines.hh.
References CHECK_P, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 1013 of file checked_int_inlines.hh.
References CHECK_P, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 1624 of file checked_int_inlines.hh.
References int, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 1005 of file checked_ext_inlines.hh.
References Parma_Polyhedra_Library::V_EQ, and Parma_Polyhedra_Library::V_NAN.
Referenced by Parma_Polyhedra_Library::Checked_Number< T, Policy >::output().
|
inline |
Definition at line 1112 of file checked_float_inlines.hh.
References assign_mpq_numeric_float(), float_mpq_to_string(), and Parma_Polyhedra_Library::V_EQ.
|
inline |
|
inline |
|
inline |
| Result Parma_Polyhedra_Library::Checked::parse_number | ( | std::istream & | is, |
| number_struct & | numer, | ||
| number_struct & | denom | ||
| ) |
Reads a number from is writing it into numer, the numerator, and denom, the denominator; the appropriate Result value is returned.
Definition at line 385 of file checked.cc.
References Parma_Polyhedra_Library::Checked::number_struct::base, Parma_Polyhedra_Library::Checked::number_struct::base_for_exponent, c, Parma_Polyhedra_Library::Checked::number_struct::exponent, Parma_Polyhedra_Library::Checked::number_struct::neg_exponent, parse_number_part(), sum_sign(), Parma_Polyhedra_Library::V_CVT_STR_UNK, and Parma_Polyhedra_Library::V_EQ.
Referenced by input_mpq().
| Result Parma_Polyhedra_Library::Checked::parse_number_part | ( | std::istream & | is, |
| number_struct & | numer | ||
| ) |
Helper function for parse_number(): reads the numerator or denominator part of a number from is into numer, returning the appropriate Result value.
Definition at line 135 of file checked.cc.
References Parma_Polyhedra_Library::Checked::number_struct::base, Parma_Polyhedra_Library::Checked::number_struct::base_for_exponent, c, Parma_Polyhedra_Library::Checked::number_struct::exponent, get_digit(), Parma_Polyhedra_Library::is_space(), Parma_Polyhedra_Library::Checked::number_struct::mantissa, Parma_Polyhedra_Library::Checked::number_struct::neg_exponent, Parma_Polyhedra_Library::Checked::number_struct::neg_mantissa, PPL_UNINITIALIZED, sum_sign(), Parma_Polyhedra_Library::V_CVT_STR_UNK, Parma_Polyhedra_Library::V_EQ, Parma_Polyhedra_Library::V_EQ_MINUS_INFINITY, Parma_Polyhedra_Library::V_EQ_PLUS_INFINITY, and Parma_Polyhedra_Library::V_NAN.
Referenced by parse_number().
| From bool Type Parma_Polyhedra_Library::Checked::PPL_DECLARE_FUN1_0_0 | ( | is_pinf | , |
| bool | , | ||
| const | , | ||
| Type | |||
| ) |
| From bool Type Type Parma_Polyhedra_Library::Checked::PPL_DECLARE_FUN1_0_2 | ( | assign_special | , |
| Result | , | ||
| nonconst | , | ||
| Type | , | ||
| Result_Class | , | ||
| Rounding_Dir | |||
| ) |
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir Rounding_Dir Rounding_Dir std::istream Rounding_Dir Parma_Polyhedra_Library::Checked::PPL_DECLARE_FUN1_1_2 | ( | output | , |
| Result | , | ||
| std::ostream & | , | ||
| const | , | ||
| Type | , | ||
| const Numeric_Format & | , | ||
| Rounding_Dir | |||
| ) |
| Parma_Polyhedra_Library::Checked::PPL_DECLARE_FUN2_0_0 | ( | copy | , |
| void | , | ||
| nonconst | , | ||
| Type1 | , | ||
| const | , | ||
| Type2 | |||
| ) |
| From Parma_Polyhedra_Library::Checked::PPL_DECLARE_FUN2_0_0 | ( | cmp | , |
| Result_Relation | , | ||
| const | , | ||
| Type1 | , | ||
| const | , | ||
| Type2 | |||
| ) |
| From bool Type Type Rounding_Dir Parma_Polyhedra_Library::Checked::PPL_DECLARE_FUN2_0_1 | ( | construct | , |
| Result | , | ||
| nonconst | , | ||
| To | , | ||
| const | , | ||
| From | , | ||
| Rounding_Dir | |||
| ) |
| From bool Type Type Rounding_Dir Rounding_Dir Parma_Polyhedra_Library::Checked::PPL_DECLARE_FUN2_0_1 | ( | floor | , |
| Result | , | ||
| nonconst | , | ||
| To | , | ||
| const | , | ||
| From | , | ||
| Rounding_Dir | |||
| ) |
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Parma_Polyhedra_Library::Checked::PPL_DECLARE_FUN2_0_1 | ( | trunc | , |
| Result | , | ||
| nonconst | , | ||
| To | , | ||
| const | , | ||
| From | , | ||
| Rounding_Dir | |||
| ) |
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Parma_Polyhedra_Library::Checked::PPL_DECLARE_FUN2_0_1 | ( | abs | , |
| Result | , | ||
| nonconst | , | ||
| To | , | ||
| const | , | ||
| From | , | ||
| Rounding_Dir | |||
| ) |
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Parma_Polyhedra_Library::Checked::PPL_DECLARE_FUN2_0_2 | ( | add_2exp | , |
| Result | , | ||
| nonconst | , | ||
| To | , | ||
| const | , | ||
| From | , | ||
| unsigned | int, | ||
| Rounding_Dir | |||
| ) |
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir unsigned Rounding_Dir Parma_Polyhedra_Library::Checked::PPL_DECLARE_FUN2_0_2 | ( | mul_2exp | , |
| Result | , | ||
| nonconst | , | ||
| To | , | ||
| const | , | ||
| From | , | ||
| unsigned | int, | ||
| Rounding_Dir | |||
| ) |
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir Parma_Polyhedra_Library::Checked::PPL_DECLARE_FUN2_0_2 | ( | smod_2exp | , |
| Result | , | ||
| nonconst | , | ||
| To | , | ||
| const | , | ||
| From | , | ||
| unsigned | int, | ||
| Rounding_Dir | |||
| ) |
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Parma_Polyhedra_Library::Checked::PPL_DECLARE_FUN3_0_1 | ( | add | , |
| Result | , | ||
| nonconst | , | ||
| To | , | ||
| const | , | ||
| From1 | , | ||
| const | , | ||
| From2 | , | ||
| Rounding_Dir | |||
| ) |
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Parma_Polyhedra_Library::Checked::PPL_DECLARE_FUN3_0_1 | ( | mul | , |
| Result | , | ||
| nonconst | , | ||
| To | , | ||
| const | , | ||
| From1 | , | ||
| const | , | ||
| From2 | , | ||
| Rounding_Dir | |||
| ) |
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Parma_Polyhedra_Library::Checked::PPL_DECLARE_FUN3_0_1 | ( | rem | , |
| Result | , | ||
| nonconst | , | ||
| To | , | ||
| const | , | ||
| From1 | , | ||
| const | , | ||
| From2 | , | ||
| Rounding_Dir | |||
| ) |
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir Parma_Polyhedra_Library::Checked::PPL_DECLARE_FUN3_0_1 | ( | add_mul | , |
| Result | , | ||
| nonconst | , | ||
| To | , | ||
| const | , | ||
| From1 | , | ||
| const | , | ||
| From2 | , | ||
| Rounding_Dir | |||
| ) |
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir Rounding_Dir Parma_Polyhedra_Library::Checked::PPL_DECLARE_FUN3_0_1 | ( | gcd | , |
| Result | , | ||
| nonconst | , | ||
| To | , | ||
| const | , | ||
| From1 | , | ||
| const | , | ||
| From2 | , | ||
| Rounding_Dir | |||
| ) |
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir Rounding_Dir Rounding_Dir Parma_Polyhedra_Library::Checked::PPL_DECLARE_FUN3_0_1 | ( | lcm | , |
| Result | , | ||
| nonconst | , | ||
| To | , | ||
| const | , | ||
| From1 | , | ||
| const | , | ||
| From2 | , | ||
| Rounding_Dir | |||
| ) |
| struct Parma_Polyhedra_Library::Checked::PPL_FUNCTION_CLASS | ( | construct | ) |
| struct Parma_Polyhedra_Library::Checked::PPL_FUNCTION_CLASS | ( | construct | ) |
Definition at line 258 of file checked_inlines.hh.
| struct Parma_Polyhedra_Library::Checked::PPL_FUNCTION_CLASS | ( | construct_special | ) |
Definition at line 266 of file checked_inlines.hh.
References To.
| Parma_Polyhedra_Library::Checked::PPL_SAFE_CONVERSION | ( | signed | short, |
| signed | char | ||
| ) |
| Parma_Polyhedra_Library::Checked::PPL_SAFE_CONVERSION | ( | signed long | long, |
| signed | char | ||
| ) |
| Parma_Polyhedra_Library::Checked::PPL_SAFE_CONVERSION | ( | signed long | long, |
| signed | short | ||
| ) |
| Parma_Polyhedra_Library::Checked::PPL_SAFE_CONVERSION | ( | unsigned | short, |
| char | |||
| ) |
| Parma_Polyhedra_Library::Checked::PPL_SAFE_CONVERSION | ( | unsigned | short, |
| unsigned | char | ||
| ) |
| Parma_Polyhedra_Library::Checked::PPL_SAFE_CONVERSION | ( | unsigned | long, |
| char | |||
| ) |
| Parma_Polyhedra_Library::Checked::PPL_SAFE_CONVERSION | ( | unsigned | long, |
| unsigned | char | ||
| ) |
| Parma_Polyhedra_Library::Checked::PPL_SAFE_CONVERSION | ( | unsigned long | long, |
| unsigned | char | ||
| ) |
| Parma_Polyhedra_Library::Checked::PPL_SAFE_CONVERSION | ( | double | , |
| float | |||
| ) |
| Parma_Polyhedra_Library::Checked::PPL_SAFE_CONVERSION | ( | long | double, |
| float | |||
| ) |
| Parma_Polyhedra_Library::Checked::PPL_SAFE_CONVERSION | ( | long | double, |
| double | |||
| ) |
| Parma_Polyhedra_Library::Checked::PPL_SAFE_CONVERSION | ( | mpz_class | , |
| char | |||
| ) |
| Parma_Polyhedra_Library::Checked::PPL_SAFE_CONVERSION | ( | mpz_class | , |
| signed | char | ||
| ) |
| Parma_Polyhedra_Library::Checked::PPL_SAFE_CONVERSION | ( | mpz_class | , |
| unsigned | char | ||
| ) |
| Parma_Polyhedra_Library::Checked::PPL_SAFE_CONVERSION | ( | mpq_class | , |
| char | |||
| ) |
| Parma_Polyhedra_Library::Checked::PPL_SAFE_CONVERSION | ( | mpq_class | , |
| signed | char | ||
| ) |
| Parma_Polyhedra_Library::Checked::PPL_SAFE_CONVERSION | ( | mpq_class | , |
| unsigned | char | ||
| ) |
| Parma_Polyhedra_Library::Checked::PPL_SAFE_CONVERSION | ( | mpq_class | , |
| float | |||
| ) |
| Parma_Polyhedra_Library::Checked::PPL_SAFE_CONVERSION | ( | mpq_class | , |
| double | |||
| ) |
| Parma_Polyhedra_Library::Checked::PPL_SPECIALIZE_GCDEXT | ( | gcdext_exact | , |
| char | , | ||
| char | , | ||
| char | , | ||
| char | , | ||
| char | |||
| ) |
| signed signed signed signed signed char signed signed signed signed signed int Parma_Polyhedra_Library::Checked::PPL_SPECIALIZE_GCDEXT | ( | gcdext_exact | , |
| signed | short, | ||
| signed | short, | ||
| signed | short, | ||
| signed | short, | ||
| signed | short | ||
| ) |
| signed signed signed signed signed char signed signed signed signed signed int signed long signed long signed long signed long signed long long unsigned unsigned unsigned unsigned unsigned short Parma_Polyhedra_Library::Checked::PPL_SPECIALIZE_GCDEXT | ( | gcdext_exact | , |
| unsigned | char, | ||
| unsigned | char, | ||
| unsigned | char, | ||
| unsigned | char, | ||
| unsigned | char | ||
| ) |
|
inline |
Definition at line 236 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::Bool< false >::value.
Referenced by round_lt_float().
|
inline |
Definition at line 295 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::fpu_check_inexact(), Parma_Polyhedra_Library::fpu_reset_inexact(), Parma_Polyhedra_Library::round_not_needed(), and Parma_Polyhedra_Library::round_strict_relation().
|
inline |
Definition at line 659 of file checked_ext_inlines.hh.
References CHECK_P, Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::V_EQ, Parma_Polyhedra_Library::V_INF_MOD, and Parma_Polyhedra_Library::VC_NAN.
|
inline |
Definition at line 616 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::V_EQ, Parma_Polyhedra_Library::V_INF_MOD, Parma_Polyhedra_Library::V_MOD_ZERO, and Parma_Polyhedra_Library::V_NAN.
|
inline |
Definition at line 345 of file checked_mpq_inlines.hh.
References CHECK_P, PPL_DIRTY_TEMP, Parma_Polyhedra_Library::Boundary_NS::sgn(), Parma_Polyhedra_Library::V_EQ, and Parma_Polyhedra_Library::V_MOD_ZERO.
|
inline |
Definition at line 473 of file checked_mpz_inlines.hh.
References CHECK_P, Parma_Polyhedra_Library::Boundary_NS::sgn(), Parma_Polyhedra_Library::V_EQ, and Parma_Polyhedra_Library::V_MOD_ZERO.
|
inline |
Definition at line 1239 of file checked_int_inlines.hh.
References CHECK_P, Parma_Polyhedra_Library::V_EQ, and Parma_Polyhedra_Library::V_MOD_ZERO.
|
inline |
Definition at line 1250 of file checked_int_inlines.hh.
References CHECK_P, Parma_Polyhedra_Library::V_EQ, and Parma_Polyhedra_Library::V_MOD_ZERO.
|
inline |
Definition at line 304 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::fpu_check_inexact(), Parma_Polyhedra_Library::round_dir(), Parma_Polyhedra_Library::ROUND_DOWN, Parma_Polyhedra_Library::round_not_needed(), Parma_Polyhedra_Library::round_strict_relation(), Parma_Polyhedra_Library::ROUND_UP, Parma_Polyhedra_Library::V_EQ, Parma_Polyhedra_Library::V_GE, Parma_Polyhedra_Library::V_GT, Parma_Polyhedra_Library::V_LE, Parma_Polyhedra_Library::V_LGE, Parma_Polyhedra_Library::V_LT, and Parma_Polyhedra_Library::V_NE.
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir Rounding_Dir Rounding_Dir std::istream Rounding_Dir To Result Parma_Polyhedra_Library::Checked::round | ( | To & | to, |
| Result | r, | ||
| Rounding_Dir | dir | ||
| ) |
|
inline |
Definition at line 284 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::round_up(), succ_float(), Parma_Polyhedra_Library::V_GT, and Parma_Polyhedra_Library::V_LT.
|
inline |
Definition at line 166 of file checked_int_inlines.hh.
References Parma_Polyhedra_Library::round_up(), Parma_Polyhedra_Library::V_GT, Parma_Polyhedra_Library::V_LT, Parma_Polyhedra_Library::V_LT_PLUS_INFINITY, and Parma_Polyhedra_Library::V_UNREPRESENTABLE.
|
inline |
Definition at line 137 of file checked_int_inlines.hh.
References Parma_Polyhedra_Library::round_up(), Parma_Polyhedra_Library::V_GT, and Parma_Polyhedra_Library::V_LT.
|
inline |
Definition at line 45 of file checked_mpz_inlines.hh.
References Parma_Polyhedra_Library::round_up(), Parma_Polyhedra_Library::V_GT, and Parma_Polyhedra_Library::V_LT.
|
inline |
Definition at line 274 of file checked_float_inlines.hh.
References pred_float(), Parma_Polyhedra_Library::round_down(), Parma_Polyhedra_Library::V_GT, and Parma_Polyhedra_Library::V_LT.
|
inline |
Definition at line 147 of file checked_int_inlines.hh.
References Parma_Polyhedra_Library::round_down(), Parma_Polyhedra_Library::V_GT, Parma_Polyhedra_Library::V_GT_MINUS_INFINITY, Parma_Polyhedra_Library::V_LT, and Parma_Polyhedra_Library::V_UNREPRESENTABLE.
|
inline |
Definition at line 127 of file checked_int_inlines.hh.
References Parma_Polyhedra_Library::round_down(), Parma_Polyhedra_Library::V_GT, and Parma_Polyhedra_Library::V_LT.
|
inline |
Definition at line 35 of file checked_mpz_inlines.hh.
References Parma_Polyhedra_Library::round_down(), Parma_Polyhedra_Library::V_GT, and Parma_Polyhedra_Library::V_LT.
|
inline |
Definition at line 72 of file checked_float_inlines.hh.
Referenced by ceil_float(), floor_float(), and is_int_float().
Definition at line 85 of file checked_float_inlines.hh.
|
inline |
Definition at line 70 of file checked_mpz_inlines.hh.
Referenced by assign_special_mpz(), and copy_mpz().
|
inline |
Definition at line 825 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::round_dir(), Parma_Polyhedra_Library::ROUND_DOWN, Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::ROUND_UP, Parma_Polyhedra_Library::V_GT_MINUS_INFINITY, Parma_Polyhedra_Library::V_LT_INF, and Parma_Polyhedra_Library::Bool< false >::value.
|
inline |
Definition at line 95 of file checked_int_inlines.hh.
References Parma_Polyhedra_Library::round_up(), Parma_Polyhedra_Library::V_GT_MINUS_INFINITY, Parma_Polyhedra_Library::V_LT_INF, and Parma_Polyhedra_Library::V_UNREPRESENTABLE.
|
inline |
Definition at line 846 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::round_dir(), Parma_Polyhedra_Library::ROUND_DOWN, Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::ROUND_UP, Parma_Polyhedra_Library::V_GT_SUP, Parma_Polyhedra_Library::V_LT_PLUS_INFINITY, and Parma_Polyhedra_Library::Bool< false >::value.
|
inline |
Definition at line 111 of file checked_int_inlines.hh.
References Parma_Polyhedra_Library::round_down(), Parma_Polyhedra_Library::V_GT_SUP, Parma_Polyhedra_Library::V_LT_PLUS_INFINITY, and Parma_Polyhedra_Library::V_UNREPRESENTABLE.
|
inline |
Definition at line 51 of file checked_ext_inlines.hh.
References Parma_Polyhedra_Library::VR_EMPTY, Parma_Polyhedra_Library::VR_GT, and Parma_Polyhedra_Library::VR_LT.
|
inline |
Definition at line 51 of file checked_ext_inlines.hh.
References Parma_Polyhedra_Library::VR_EMPTY, Parma_Polyhedra_Library::VR_GT, and Parma_Polyhedra_Library::VR_LT.
|
inline |
Definition at line 767 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::VR_EMPTY, Parma_Polyhedra_Library::VR_EQ, Parma_Polyhedra_Library::VR_GT, and Parma_Polyhedra_Library::VR_LT.
|
inline |
Definition at line 449 of file checked_inlines.hh.
References Parma_Polyhedra_Library::VR_EQ, Parma_Polyhedra_Library::VR_GT, and Parma_Polyhedra_Library::VR_LT.
|
inline |
Definition at line 653 of file checked_mpz_inlines.hh.
References Parma_Polyhedra_Library::Boundary_NS::sgn(), Parma_Polyhedra_Library::VR_EQ, Parma_Polyhedra_Library::VR_GT, and Parma_Polyhedra_Library::VR_LT.
|
inline |
Definition at line 773 of file checked_ext_inlines.hh.
References CHECK_P, Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::V_INF_MOD, and Parma_Polyhedra_Library::VC_NAN.
|
inline |
Definition at line 693 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, sizeof_to_bits, Type, Parma_Polyhedra_Library::V_EQ, Parma_Polyhedra_Library::V_INF_MOD, and Parma_Polyhedra_Library::VC_NAN.
|
inline |
|
inline |
|
inline |
Definition at line 1492 of file checked_int_inlines.hh.
References sizeof_to_bits, Type, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 1473 of file checked_int_inlines.hh.
References sizeof_to_bits, Type, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 813 of file checked_ext_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::V_SQRT_NEG, Parma_Polyhedra_Library::VC_NAN, and Parma_Polyhedra_Library::VC_PLUS_INFINITY.
|
inline |
Definition at line 743 of file checked_float_inlines.hh.
References fpu_direct_rounding(), Parma_Polyhedra_Library::fpu_restore_rounding_direction(), Parma_Polyhedra_Library::fpu_save_rounding_direction(), limit_precision(), Parma_Polyhedra_Library::round_fpu_dir(), Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::V_SQRT_NEG, and Parma_Polyhedra_Library::VC_NAN.
|
inline |
Definition at line 473 of file checked_mpq_inlines.hh.
References CHECK_P, Parma_Polyhedra_Library::inverse(), irrational_precision, Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::V_EQ, and Parma_Polyhedra_Library::V_SQRT_NEG.
|
inline |
Definition at line 633 of file checked_mpz_inlines.hh.
References CHECK_P, PPL_DIRTY_TEMP, Parma_Polyhedra_Library::round_not_requested(), Parma_Polyhedra_Library::V_EQ, Parma_Polyhedra_Library::V_GE, and Parma_Polyhedra_Library::V_SQRT_NEG.
|
inline |
Definition at line 1565 of file checked_int_inlines.hh.
References CHECK_P, and Parma_Polyhedra_Library::V_SQRT_NEG.
|
inline |
Definition at line 1551 of file checked_int_inlines.hh.
References isqrt_rem(), Parma_Polyhedra_Library::round_not_requested(), Type, Parma_Polyhedra_Library::V_EQ, and Parma_Polyhedra_Library::V_GE.
|
inline |
Definition at line 707 of file checked_ext_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, and Parma_Polyhedra_Library::VC_PLUS_INFINITY.
|
inline |
Definition at line 651 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, sizeof_to_bits, Type, and Parma_Polyhedra_Library::VC_NAN.
|
inline |
Definition at line 373 of file checked_mpq_inlines.hh.
References PPL_DIRTY_TEMP, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 498 of file checked_mpz_inlines.hh.
References PPL_DIRTY_TEMP, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 1385 of file checked_int_inlines.hh.
References sizeof_to_bits, Type, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 1370 of file checked_int_inlines.hh.
References sizeof_to_bits, Type, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 267 of file checked_ext_inlines.hh.
References CHECK_P, Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::V_INF_SUB_INF, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, and Parma_Polyhedra_Library::VC_PLUS_INFINITY.
|
inline |
Definition at line 494 of file checked_float_inlines.hh.
References fpu_direct_rounding(), fpu_inverse_rounding(), Parma_Polyhedra_Library::fpu_restore_rounding_direction(), Parma_Polyhedra_Library::fpu_save_rounding_direction(), limit_precision(), Parma_Polyhedra_Library::round_fpu_dir(), Parma_Polyhedra_Library::V_INF_SUB_INF, and Parma_Polyhedra_Library::V_NAN.
|
inline |
Definition at line 982 of file checked_int_inlines.hh.
|
inline |
|
inline |
|
inline |
Definition at line 456 of file checked_ext_inlines.hh.
References CHECK_P, Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::V_INF_MUL_ZERO, Parma_Polyhedra_Library::V_INF_SUB_INF, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, Parma_Polyhedra_Library::VC_PLUS_INFINITY, Parma_Polyhedra_Library::VR_GT, and Parma_Polyhedra_Library::VR_LT.
|
inline |
Definition at line 1030 of file checked_float_inlines.hh.
References fpu_direct_rounding(), fpu_inverse_rounding(), Parma_Polyhedra_Library::fpu_restore_rounding_direction(), Parma_Polyhedra_Library::fpu_save_rounding_direction(), limit_precision(), multiply_add(), Parma_Polyhedra_Library::round_fpu_dir(), Parma_Polyhedra_Library::V_INF_MUL_ZERO, and Parma_Polyhedra_Library::V_NAN.
|
inline |
Definition at line 1600 of file checked_int_inlines.hh.
References Parma_Polyhedra_Library::result_overflow(), Type, Parma_Polyhedra_Library::V_NAN, Parma_Polyhedra_Library::V_UNKNOWN_NEG_OVERFLOW, and Parma_Polyhedra_Library::V_UNKNOWN_POS_OVERFLOW.
|
inline |
|
inline |
|
inline |
|
inline |
Definition at line 1084 of file checked_int_inlines.hh.
References CHECK_P, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 255 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::Bool< false >::value.
Referenced by round_gt_float().
|
inline |
Adds the number represented (in the modulus-and-sign representation) by b_neg and b_mod to the number represented by a_neg and a_mod, assigning the result to the latter. Returns false is the result cannot be represented; returns true otherwise.
Definition at line 110 of file checked.cc.
Referenced by parse_number(), and parse_number_part().
|
inline |
Definition at line 183 of file checked_ext_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::VC_MINUS_INFINITY, Parma_Polyhedra_Library::VC_NAN, and Parma_Polyhedra_Library::VC_PLUS_INFINITY.
|
inline |
Definition at line 437 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, and Parma_Polyhedra_Library::VC_NAN.
|
inline |
|
inline |
Definition at line 793 of file checked_ext_inlines.hh.
References CHECK_P, Parma_Polyhedra_Library::ROUND_IGNORE, Parma_Polyhedra_Library::V_INF_MOD, and Parma_Polyhedra_Library::VC_NAN.
|
inline |
Definition at line 715 of file checked_float_inlines.hh.
References Parma_Polyhedra_Library::ROUND_IGNORE, sizeof_to_bits, Type, Parma_Polyhedra_Library::V_EQ, Parma_Polyhedra_Library::V_INF_MOD, and Parma_Polyhedra_Library::VC_NAN.
|
inline |
|
inline |
|
inline |
Definition at line 1519 of file checked_int_inlines.hh.
References sizeof_to_bits, Type, and Parma_Polyhedra_Library::V_EQ.
|
inline |
Definition at line 1506 of file checked_int_inlines.hh.
References sizeof_to_bits, Type, and Parma_Polyhedra_Library::V_EQ.
Variable Documentation
Definition at line 478 of file checked_defs.hh.
Referenced by Parma_Polyhedra_Library::PIP_Solution_Node::external_memory_in_bytes().
| signed signed signed signed Parma_Polyhedra_Library::Checked::char |
Definition at line 1958 of file checked_int_inlines.hh.
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir Rounding_Dir Parma_Polyhedra_Library::Checked::const |
Definition at line 474 of file checked_defs.hh.
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir Parma_Polyhedra_Library::Checked::From |
Definition at line 494 of file checked_defs.hh.
Referenced by assign_float_float(), assign_float_float_inexact(), assign_float_int(), assign_int_float(), assign_mpq_signed_int(), assign_mpq_unsigned_int(), assign_mpz_float(), assign_mpz_signed_int(), assign_mpz_unsigned_int(), assign_signed_int_signed_int(), assign_signed_int_unsigned_int(), assign_unsigned_int_signed_int(), assign_unsigned_int_unsigned_int(), construct_mpz_float(), and PPL_FUNCTION_CLASS().
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir Rounding_Dir Parma_Polyhedra_Library::Checked::From1 |
Definition at line 511 of file checked_defs.hh.
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir Rounding_Dir Parma_Polyhedra_Library::Checked::From2 |
Definition at line 511 of file checked_defs.hh.
Referenced by gcdext_exact().
| signed signed signed signed signed char signed signed signed signed Parma_Polyhedra_Library::Checked::int |
Definition at line 529 of file checked_defs.hh.
Referenced by output_char().
| unsigned Parma_Polyhedra_Library::Checked::irrational_precision |
Holds the precision parameter used for irrational calculations.
Definition at line 37 of file checked.cc.
Referenced by Parma_Polyhedra_Library::irrational_precision(), Parma_Polyhedra_Library::set_irrational_precision(), and sqrt_mpq().
| signed signed signed signed signed char signed signed signed signed signed int signed long signed long signed long signed long signed long long unsigned unsigned unsigned unsigned unsigned short unsigned unsigned unsigned unsigned Parma_Polyhedra_Library::Checked::long |
Definition at line 1970 of file checked_int_inlines.hh.
Referenced by assign_mpq_numeric_float(), and assign_unsigned_int_mpz().
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir Rounding_Dir Rounding_Dir Parma_Polyhedra_Library::Checked::nonconst |
Definition at line 490 of file checked_defs.hh.
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir Rounding_Dir Rounding_Dir Parma_Polyhedra_Library::Checked::Result |
Definition at line 478 of file checked_defs.hh.
Definition at line 490 of file checked_defs.hh.
| Parma_Polyhedra_Library::Checked::Result_Relation |
Definition at line 474 of file checked_defs.hh.
| signed signed signed signed signed char signed signed signed signed signed int signed long signed long signed long signed long signed long long unsigned unsigned unsigned unsigned Parma_Polyhedra_Library::Checked::short |
Definition at line 1976 of file checked_int_inlines.hh.
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir Parma_Polyhedra_Library::Checked::To |
Definition at line 494 of file checked_defs.hh.
Referenced by assign_float_float(), assign_signed_int_mpz(), assign_signed_int_unsigned_int(), assign_unsigned_int_mpz(), assign_unsigned_int_signed_int(), assign_unsigned_int_unsigned_int(), and PPL_FUNCTION_CLASS().
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir Rounding_Dir Parma_Polyhedra_Library::Checked::To1 |
Definition at line 553 of file checked_defs.hh.
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir Rounding_Dir Parma_Polyhedra_Library::Checked::To2 |
Definition at line 553 of file checked_defs.hh.
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir Rounding_Dir Parma_Polyhedra_Library::Checked::To3 |
Definition at line 553 of file checked_defs.hh.
| From bool Type Type Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir unsigned Rounding_Dir Rounding_Dir Rounding_Dir Parma_Polyhedra_Library::Checked::Type |
Definition at line 478 of file checked_defs.hh.
Referenced by add_2exp_float(), add_2exp_signed_int(), add_2exp_unsigned_int(), add_mul_int(), div_2exp_float(), div_2exp_signed_int(), div_2exp_unsigned_int(), div_signed_int(), div_unsigned_int(), idiv_float(), isqrt_rem(), mul_2exp_float(), mul_2exp_signed_int(), mul_2exp_unsigned_int(), smod_2exp_float(), smod_2exp_signed_int(), smod_2exp_unsigned_int(), sqrt_unsigned_int(), sub_2exp_float(), sub_2exp_signed_int(), sub_2exp_unsigned_int(), sub_mul_int(), umod_2exp_float(), umod_2exp_signed_int(), and umod_2exp_unsigned_int().
