The partially reduced product of two abstractions. More...

#include <Partially_Reduced_Product_defs.hh>

Public Member Functions
	Partially_Reduced_Product (dimension_type num_dimensions=0, Degenerate_Element kind=UNIVERSE)
	Builds an object having the specified properties. More...

	Partially_Reduced_Product (const Congruence_System &cgs)
	Builds a pair, copying a system of congruences. More...

	Partially_Reduced_Product (Congruence_System &cgs)
	Builds a pair, recycling a system of congruences. More...

	Partially_Reduced_Product (const Constraint_System &cs)
	Builds a pair, copying a system of constraints. More...

	Partially_Reduced_Product (Constraint_System &cs)
	Builds a pair, recycling a system of constraints. More...

	Partially_Reduced_Product (const C_Polyhedron &ph, Complexity_Class complexity=ANY_COMPLEXITY)
	Builds a product, from a C polyhedron. More...

	Partially_Reduced_Product (const NNC_Polyhedron &ph, Complexity_Class complexity=ANY_COMPLEXITY)
	Builds a product, from an NNC polyhedron. More...

	Partially_Reduced_Product (const Grid &gr, Complexity_Class complexity=ANY_COMPLEXITY)
	Builds a product, from a grid. More...

template<typename Interval >
	Partially_Reduced_Product (const Box< Interval > &box, Complexity_Class complexity=ANY_COMPLEXITY)
	Builds a product out of a box. More...

template<typename U >
	Partially_Reduced_Product (const BD_Shape< U > &bd, Complexity_Class complexity=ANY_COMPLEXITY)
	Builds a product out of a BD shape. More...

template<typename U >
	Partially_Reduced_Product (const Octagonal_Shape< U > &os, Complexity_Class complexity=ANY_COMPLEXITY)
	Builds a product out of an octagonal shape. More...

	Partially_Reduced_Product (const Partially_Reduced_Product &y, Complexity_Class complexity=ANY_COMPLEXITY)
	Ordinary copy constructor. More...

template<typename E1 , typename E2 , typename S >
	Partially_Reduced_Product (const Partially_Reduced_Product< E1, E2, S > &y, Complexity_Class complexity=ANY_COMPLEXITY)
	Builds a conservative, upward approximation of `y`. More...

Partially_Reduced_Product &	operator= (const Partially_Reduced_Product &y)
	The assignment operator. (`*this` and `y` can be dimension-incompatible.) More...

bool	reduce () const
	Reduce. More...

Member Functions that Do Not Modify the Partially_Reduced_Product
dimension_type	space_dimension () const
	Returns the dimension of the vector space enclosing `*this`. More...

dimension_type	affine_dimension () const
	Returns the minimum affine dimension (see also grid affine dimension) of the components of `*this`. More...

const D1 &	domain1 () const
	Returns a constant reference to the first of the pair. More...

const D2 &	domain2 () const
	Returns a constant reference to the second of the pair. More...

Constraint_System	constraints () const
	Returns a system of constraints which approximates `*this`. More...

Constraint_System	minimized_constraints () const
	Returns a system of constraints which approximates `*this`, in reduced form. More...

Congruence_System	congruences () const
	Returns a system of congruences which approximates `*this`. More...

Congruence_System	minimized_congruences () const
	Returns a system of congruences which approximates `*this`, in reduced form. More...

Poly_Con_Relation	relation_with (const Constraint &c) const
	Returns the relations holding between `*this` and `c`. More...

Poly_Con_Relation	relation_with (const Congruence &cg) const
	Returns the relations holding between `*this` and `cg`. More...

Poly_Gen_Relation	relation_with (const Generator &g) const
	Returns the relations holding between `*this` and `g`. More...

bool	is_empty () const
	Returns `true` if and only if either of the components of `*this` are empty. More...

bool	is_universe () const
	Returns `true` if and only if both of the components of `*this` are the universe. More...

bool	is_topologically_closed () const
	Returns `true` if and only if both of the components of `*this` are topologically closed subsets of the vector space. More...

bool	is_disjoint_from (const Partially_Reduced_Product &y) const
	Returns `true` if and only if `*this` and `y` are componentwise disjoint. More...

bool	is_discrete () const
	Returns `true` if and only if a component of `*this` is discrete. More...

bool	is_bounded () const
	Returns `true` if and only if a component of `*this` is bounded. More...

bool	constrains (Variable var) const
	Returns `true` if and only if `var` is constrained in `*this`. More...

bool	bounds_from_above (const Linear_Expression &expr) const
	Returns `true` if and only if `expr` is bounded in `*this`. More...

bool	bounds_from_below (const Linear_Expression &expr) const
	Returns `true` if and only if `expr` is bounded in `*this`. More...

bool	maximize (const Linear_Expression &expr, Coefficient &sup_n, Coefficient &sup_d, bool &maximum) const
	Returns `true` if and only if `this` is not empty and `expr` is bounded from above in `this`, in which case the supremum value is computed. More...

bool	maximize (const Linear_Expression &expr, Coefficient &sup_n, Coefficient &sup_d, bool &maximum, Generator &g) const
	Returns `true` if and only if `this` is not empty and `expr` is bounded from above in `this`, in which case the supremum value and a point where `expr` reaches it are computed. More...

bool	minimize (const Linear_Expression &expr, Coefficient &inf_n, Coefficient &inf_d, bool &minimum) const
	Returns `true` if and only if `this` is not empty and `expr` is bounded from below i `this`, in which case the infimum value is computed. More...

bool	minimize (const Linear_Expression &expr, Coefficient &inf_n, Coefficient &inf_d, bool &minimum, Generator &g) const
	Returns `true` if and only if `this` is not empty and `expr` is bounded from below in `this`, in which case the infimum value and a point where `expr` reaches it are computed. More...

bool	contains (const Partially_Reduced_Product &y) const
	Returns `true` if and only if each component of `*this` contains the corresponding component of `y`. More...

bool	strictly_contains (const Partially_Reduced_Product &y) const
	Returns `true` if and only if each component of `*this` strictly contains the corresponding component of `y`. More...

bool	OK () const
	Checks if all the invariants are satisfied. More...

Space Dimension Preserving Member Functions that May Modify the Partially_Reduced_Product
void	add_constraint (const Constraint &c)
	Adds constraint `c` to `*this`. More...

void	refine_with_constraint (const Constraint &c)
	Use the constraint `c` to refine `*this`. More...

void	add_congruence (const Congruence &cg)
	Adds a copy of congruence `cg` to `*this`. More...

void	refine_with_congruence (const Congruence &cg)
	Use the congruence `cg` to refine `*this`. More...

void	add_congruences (const Congruence_System &cgs)
	Adds a copy of the congruences in `cgs` to `*this`. More...

void	refine_with_congruences (const Congruence_System &cgs)
	Use the congruences in `cgs` to refine `*this`. More...

void	add_recycled_congruences (Congruence_System &cgs)
	Adds the congruences in `cgs` to *this. More...

void	add_constraints (const Constraint_System &cs)
	Adds a copy of the constraint system in `cs` to `*this`. More...

void	refine_with_constraints (const Constraint_System &cs)
	Use the constraints in `cs` to refine `*this`. More...

void	add_recycled_constraints (Constraint_System &cs)
	Adds the constraint system in `cs` to `*this`. More...

void	unconstrain (Variable var)
	Computes the cylindrification of `this` with respect to space dimension `var`, assigning the result to `this`. More...

void	unconstrain (const Variables_Set &vars)
	Computes the cylindrification of `this` with respect to the set of space dimensions `vars`, assigning the result to `this`. More...

void	intersection_assign (const Partially_Reduced_Product &y)
	Assigns to `this` the componentwise intersection of `this` and `y`. More...

void	upper_bound_assign (const Partially_Reduced_Product &y)
	Assigns to `this` an upper bound of `this` and `y` computed on the corresponding components. More...

bool	upper_bound_assign_if_exact (const Partially_Reduced_Product &y)
	Assigns to `this` an upper bound of `this` and `y` computed on the corresponding components. If it is exact on each of the components of `*this`, `true` is returned, otherwise `false` is returned. More...

void	difference_assign (const Partially_Reduced_Product &y)
	Assigns to `this` an approximation of the set-theoretic difference of `this` and `y`. More...

void	affine_image (Variable var, const Linear_Expression &expr, Coefficient_traits::const_reference denominator=Coefficient_one())
	Assigns to `*this` the affine image of `this` under the function mapping variable `var` to the affine expression specified by `expr` and `denominator`. More...

void	affine_preimage (Variable var, const Linear_Expression &expr, Coefficient_traits::const_reference denominator=Coefficient_one())
	Assigns to `this` the affine preimage of `this` under the function mapping variable `var` to the affine expression specified by `expr` and `denominator`. More...

void	generalized_affine_image (Variable var, Relation_Symbol relsym, const Linear_Expression &expr, Coefficient_traits::const_reference denominator=Coefficient_one())
	Assigns to `this` the image of `this` with respect to the generalized affine relation $\mathrm{var}' \relsym \frac{\mathrm{expr}}{\mathrm{denominator}}$ , where $\mathord{\relsym}$ is the relation symbol encoded by `relsym` (see also generalized affine relation.) More...

void	generalized_affine_preimage (Variable var, Relation_Symbol relsym, const Linear_Expression &expr, Coefficient_traits::const_reference denominator=Coefficient_one())
	Assigns to `this` the preimage of `this` with respect to the generalized affine relation $\mathrm{var}' \relsym \frac{\mathrm{expr}}{\mathrm{denominator}}$ , where $\mathord{\relsym}$ is the relation symbol encoded by `relsym`. (see also generalized affine relation.) More...

void	generalized_affine_image (const Linear_Expression &lhs, Relation_Symbol relsym, const Linear_Expression &rhs)
	Assigns to `this` the image of `this` with respect to the generalized affine relation $\mathrm{lhs}' \relsym \mathrm{rhs}$ , where $\mathord{\relsym}$ is the relation symbol encoded by `relsym`. (see also generalized affine relation.) More...

void	generalized_affine_preimage (const Linear_Expression &lhs, Relation_Symbol relsym, const Linear_Expression &rhs)
	Assigns to `this` the preimage of `this` with respect to the generalized affine relation $\mathrm{lhs}' \relsym \mathrm{rhs}$ , where $\mathord{\relsym}$ is the relation symbol encoded by `relsym`. (see also generalized affine relation.) More...

void	bounded_affine_image (Variable var, const Linear_Expression &lb_expr, const Linear_Expression &ub_expr, Coefficient_traits::const_reference denominator=Coefficient_one())
	Assigns to `this` the image of `this` with respect to the bounded affine relation $\frac{\mathrm{lb\_expr}}{\mathrm{denominator}} \leq \mathrm{var}' \leq \frac{\mathrm{ub\_expr}}{\mathrm{denominator}}$ . More...

void	bounded_affine_preimage (Variable var, const Linear_Expression &lb_expr, const Linear_Expression &ub_expr, Coefficient_traits::const_reference denominator=Coefficient_one())
	Assigns to `this` the preimage of `this` with respect to the bounded affine relation $\frac{\mathrm{lb\_expr}}{\mathrm{denominator}} \leq \mathrm{var}' \leq \frac{\mathrm{ub\_expr}}{\mathrm{denominator}}$ . More...

void	time_elapse_assign (const Partially_Reduced_Product &y)
	Assigns to `this` the result of computing the time-elapse between `this` and `y`. (See also time-elapse.) More...

void	topological_closure_assign ()
	Assigns to `*this` its topological closure. More...

void	widening_assign (const Partially_Reduced_Product &y, unsigned *tp=NULL)
	Assigns to `this` the result of computing the "widening" between `this` and `y`. More...

void	drop_some_non_integer_points (Complexity_Class complexity=ANY_COMPLEXITY)
	Possibly tightens `*this` by dropping some points with non-integer coordinates. More...

void	drop_some_non_integer_points (const Variables_Set &vars, Complexity_Class complexity=ANY_COMPLEXITY)
	Possibly tightens `*this` by dropping some points with non-integer coordinates for the space dimensions corresponding to `vars`. More...

Member Functions that May Modify the Dimension of the Vector Space
void	add_space_dimensions_and_embed (dimension_type m)
	Adds `m` new space dimensions and embeds the components of `*this` in the new vector space. More...

void	add_space_dimensions_and_project (dimension_type m)
	Adds `m` new space dimensions and does not embed the components in the new vector space. More...

void	concatenate_assign (const Partially_Reduced_Product &y)
	Assigns to the first (resp., second) component of `this` the "concatenation" of the first (resp., second) components of `this` and `y`, taken in this order. See also Concatenating Polyhedra. More...

void	remove_space_dimensions (const Variables_Set &vars)
	Removes all the specified dimensions from the vector space. More...

void	remove_higher_space_dimensions (dimension_type new_dimension)
	Removes the higher dimensions of the vector space so that the resulting space will have dimension `new_dimension`. More...

template<typename Partial_Function >
void	map_space_dimensions (const Partial_Function &pfunc)
	Remaps the dimensions of the vector space according to a partial function. More...

void	expand_space_dimension (Variable var, dimension_type m)
	Creates `m` copies of the space dimension corresponding to `var`. More...

void	fold_space_dimensions (const Variables_Set &vars, Variable dest)
	Folds the space dimensions in `vars` into `dest`. More...

Miscellaneous Member Functions
	~Partially_Reduced_Product ()
	Destructor. More...

void	m_swap (Partially_Reduced_Product &y)
	Swaps `this` with product `y`. (`this` and `y` can be dimension-incompatible.) More...

void	ascii_dump () const
	Writes to `std::cerr` an ASCII representation of `*this`. More...

void	ascii_dump (std::ostream &s) const
	Writes to `s` an ASCII representation of `*this`. More...

void	print () const
	Prints `*this` to `std::cerr` using `operator<<`. More...

bool	ascii_load (std::istream &s)
	Loads from `s` an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets `*this` accordingly. Returns `true` if successful, `false` otherwise. More...

memory_size_type	total_memory_in_bytes () const
	Returns the total size in bytes of the memory occupied by `*this`. More...

memory_size_type	external_memory_in_bytes () const
	Returns the size in bytes of the memory managed by `*this`. More...

int32_t	hash_code () const
	Returns a 32-bit hash code for `*this`. More...

Static Public Member Functions
static dimension_type	max_space_dimension ()
	Returns the maximum space dimension this product can handle. More...

Protected Types
typedef D1	Domain1
	The type of the first component. More...

typedef D2	Domain2
	The type of the second component. More...

Protected Member Functions
void	clear_reduced_flag () const
	Clears the reduced flag. More...

void	set_reduced_flag () const
	Sets the reduced flag. More...

bool	is_reduced () const
	Return `true` if and only if the reduced flag is set. More...

Protected Attributes
D1	d1
	The first component. More...

D2	d2
	The second component. More...

bool	reduced
	Flag to record whether the components are reduced with respect to each other and the reduction class. More...

Private Member Functions
void	throw_space_dimension_overflow (const char method, const char reason)

Friends
bool	operator== (const Partially_Reduced_Product< D1, D2, R > &x, const Partially_Reduced_Product< D1, D2, R > &y)

std::ostream &	Parma_Polyhedra_Library::IO_Operators::operator<< (std::ostream &s, const Partially_Reduced_Product< D1, D2, R > &dp)

Related Functions
(Note that these are not member functions.)
template<typename D1 , typename D2 , typename R >
std::ostream &	operator<< (std::ostream &s, const Partially_Reduced_Product< D1, D2, R > &dp)
	Output operator. More...

template<typename D1 , typename D2 , typename R >
void	swap (Partially_Reduced_Product< D1, D2, R > &x, Partially_Reduced_Product< D1, D2, R > &y)
	Swaps `x` with `y`. More...

template<typename D1 , typename D2 , typename R >
bool	operator== (const Partially_Reduced_Product< D1, D2, R > &x, const Partially_Reduced_Product< D1, D2, R > &y)
	Returns `true` if and only if the components of `x` and `y` are pairwise equal. More...

template<typename D1 , typename D2 , typename R >
bool	operator!= (const Partially_Reduced_Product< D1, D2, R > &x, const Partially_Reduced_Product< D1, D2, R > &y)
	Returns `true` if and only if the components of `x` and `y` are not pairwise equal. More...

template<typename D1 , typename D2 , typename R >
bool	operator== (const Partially_Reduced_Product< D1, D2, R > &x, const Partially_Reduced_Product< D1, D2, R > &y)

template<typename D1 , typename D2 , typename R >
bool	operator!= (const Partially_Reduced_Product< D1, D2, R > &x, const Partially_Reduced_Product< D1, D2, R > &y)

template<typename D1 , typename D2 , typename R >
std::ostream &	operator<< (std::ostream &s, const Partially_Reduced_Product< D1, D2, R > &dp)

template<typename D1 , typename D2 , typename R >
void	swap (Partially_Reduced_Product< D1, D2, R > &x, Partially_Reduced_Product< D1, D2, R > &y)

Detailed Description

template<typename D1, typename D2, typename R>
class Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >

The partially reduced product of two abstractions.

Warning: At present, the supported instantiations for the two domain templates D1 and D2 are the simple pointset domains: C_Polyhedron, NNC_Polyhedron, Grid, Octagonal_Shape<T>, BD_Shape<T>, Box<T>.

An object of the class Partially_Reduced_Product<D1, D2, R> represents the (partially reduced) product of two pointset domains D1 and D2 where the form of any reduction is defined by the reduction class R.

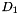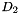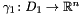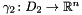Suppose $D_1$ and $D_2$ are two abstract domains with concretization functions: $\fund{\gamma_1}{D_1}{\Rset^n}$ and $\fund{\gamma_2}{D_2}{\Rset^n}$ , respectively.

The partially reduced product 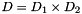$D = D_1 \times D_2$ , for any reduction class R, has a concretization 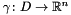$\fund{\gamma}{D}{\Rset^n}$ where, if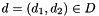 $d = (d_1, d_2) \in D$

$\gamma(d) = \gamma_1(d_1) \inters \gamma_2(d_2).$

The operations are defined to be the result of applying the corresponding operations on each of the components provided the product is already reduced by the reduction method defined by R. In particular, if R is the No_Reduction<D1, D2> class, then the class Partially_Reduced_Product<D1, D2, R> domain is the direct product as defined in [CC79].

How the results on the components are interpreted and combined depend on the specific test. For example, the test for emptiness will first make sure the product is reduced (using the reduction method provided by R if it is not already known to be reduced) and then test if either component is empty; thus, if R defines no reduction between its components and 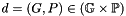$d = (G, P) \in (\Gset \times \Pset)$ is a direct product in one dimension where 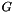$G$ denotes the set of numbers that are integral multiples of 3 while 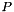$P$ denotes the set of numbers between 1 and 2, then an operation that tests for emptiness should return false. However, the test for the universe returns true if and only if the test is_universe() on both components returns true.

: In all the examples it is assumed that the template R is the No_Reduction<D1, D2> class and that variables x and y are defined (where they are used) as follows:
Variable x(0);

Variable y(1);

Example 1: The following code builds a direct product of a Grid and NNC Polyhedron, corresponding to the positive even integer pairs in 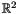$\Rset^2$ , given as a system of congruences:
Congruence_System cgs;

cgs.insert((x %= 0) / 2);

cgs.insert((y %= 0) / 2);

Partially_Reduced_Product<Grid, NNC_Polyhedron, No_Reduction<D1, D2> >

dp(cgs);

dp.add_constraint(x >= 0);

dp.add_constraint(y >= 0);

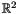Example 2: The following code builds the same product in $\Rset^2$ :
Partially_Reduced_Product<Grid, NNC_Polyhedron, No_Reduction<D1, D2> > dp(2);

dp.add_constraint(x >= 0);

dp.add_constraint(y >= 0);

dp.add_congruence((x %= 0) / 2);

dp.add_congruence((y %= 0) / 2);

Example 3: The following code will write "dp is empty":
Partially_Reduced_Product<Grid, NNC_Polyhedron, No_Reduction<D1, D2> > dp(1);

dp.add_congruence((x %= 0) / 2);

dp.add_congruence((x %= 1) / 2);

if (dp.is_empty())

cout << "dp is empty." << endl;

else

cout << "dp is not empty." << endl;

Example 4: The following code will write "dp is not empty":
Partially_Reduced_Product<Grid, NNC_Polyhedron, No_Reduction<D1, D2> > dp(1);

dp.add_congruence((x %= 0) / 2);

dp.add_constraint(x >= 1);

dp.add_constraint(x <= 1);

if (dp.is_empty())

cout << "dp is empty." << endl;

else

cout << "dp is not empty." << endl;

Definition at line 418 of file Partially_Reduced_Product_defs.hh.

Member Typedef Documentation

template<typename D1, typename D2, typename R>

typedef D1 Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::Domain1

protected

The type of the first component.

Definition at line 1623 of file Partially_Reduced_Product_defs.hh.

template<typename D1, typename D2, typename R>

typedef D2 Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::Domain2

protected

The type of the second component.

Definition at line 1626 of file Partially_Reduced_Product_defs.hh.

Constructor & Destructor Documentation

template<typename D1 , typename D2 , typename R >

Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::Partially_Reduced_Product	(	dimension_type	num_dimensions = `0`,
		Degenerate_Element	kind = `UNIVERSE`
	)

inlineexplicit

Builds an object having the specified properties.

Parameters

num_dimensions	The number of dimensions of the vector space enclosing the pair;
kind	Specifies whether a universe or an empty pair has to be built.

Exceptions

std::length_error Thrown if num_dimensions exceeds the maximum allowed space dimension.

Definition at line 46 of file Partially_Reduced_Product_inlines.hh.

   : d1(num_dimensions <= max_space_dimension()
        ? num_dimensions
        : (throw_space_dimension_overflow("Partially_Reduced_Product(n, k)",
                                          "n exceeds the maximum "
                                          "allowed space dimension"),
           num_dimensions),
        kind),
     d2(num_dimensions, kind) {
   set_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::Partially_Reduced_Product ( const Congruence_System & cgs )

inlineexplicit

Builds a pair, copying a system of congruences.

The pair inherits the space dimension of the congruence system.

Parameters

cgs	The system of congruences to be approximated by the pair.

Exceptions

std::length_error Thrown if num_dimensions exceeds the maximum allowed space dimension.

Definition at line 62 of file Partially_Reduced_Product_inlines.hh.

   : d1(cgs), d2(cgs) {
   clear_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::Partially_Reduced_Product ( Congruence_System & cgs )

inlineexplicit

Builds a pair, recycling a system of congruences.

The pair inherits the space dimension of the congruence system.

Parameters

cgs	The system of congruences to be approximates by the pair. Its data-structures may be recycled to build the pair.

Exceptions

std::length_error Thrown if num_dimensions exceeds the maximum allowed space dimension.

Definition at line 70 of file Partially_Reduced_Product_inlines.hh.

   : d1(const_cast<const Congruence_System&>(cgs)), d2(cgs) {
   clear_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::Partially_Reduced_Product ( const Constraint_System & cs )

inlineexplicit

Builds a pair, copying a system of constraints.

The pair inherits the space dimension of the constraint system.

Parameters

cs	The system of constraints to be approximated by the pair.

Exceptions

std::length_error Thrown if num_dimensions exceeds the maximum allowed space dimension.

Definition at line 78 of file Partially_Reduced_Product_inlines.hh.

   : d1(cs), d2(cs) {
   clear_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::Partially_Reduced_Product ( Constraint_System & cs )

inlineexplicit

Builds a pair, recycling a system of constraints.

The pair inherits the space dimension of the constraint system.

Parameters

cs	The system of constraints to be approximated by the pair.

Exceptions

std::length_error Thrown if the space dimension of cs exceeds the maximum allowed space dimension.

Definition at line 86 of file Partially_Reduced_Product_inlines.hh.

   : d1(const_cast<const Constraint_System&>(cs)), d2(cs) {
   clear_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::Partially_Reduced_Product	(	const C_Polyhedron &	ph,
		Complexity_Class	complexity = `ANY_COMPLEXITY`
	)

inlineexplicit

Builds a product, from a C polyhedron.

Builds a product containing ph using algorithms whose complexity does not exceed the one specified by complexity. If complexity is ANY_COMPLEXITY, then the built product is the smallest one containing ph. The product inherits the space dimension of the polyhedron.

Parameters

ph	The polyhedron to be approximated by the product.
complexity	The complexity that will not be exceeded.

Exceptions

std::length_error Thrown if the space dimension of ph exceeds the maximum allowed space dimension.

Definition at line 94 of file Partially_Reduced_Product_inlines.hh.

   : d1(ph, complexity), d2(ph, complexity) {
   set_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::Partially_Reduced_Product	(	const NNC_Polyhedron &	ph,
		Complexity_Class	complexity = `ANY_COMPLEXITY`
	)

inlineexplicit

Builds a product, from an NNC polyhedron.

Builds a product containing ph using algorithms whose complexity does not exceed the one specified by complexity. If complexity is ANY_COMPLEXITY, then the built product is the smallest one containing ph. The product inherits the space dimension of the polyhedron.

Parameters

ph	The polyhedron to be approximated by the product.
complexity	The complexity that will not be exceeded.

Exceptions

std::length_error Thrown if the space dimension of ph exceeds the maximum allowed space dimension.

Definition at line 103 of file Partially_Reduced_Product_inlines.hh.

   : d1(ph, complexity), d2(ph, complexity) {
   set_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::Partially_Reduced_Product	(	const Grid &	gr,
		Complexity_Class	complexity = `ANY_COMPLEXITY`
	)

inlineexplicit

Builds a product, from a grid.

Builds a product containing gr. The product inherits the space dimension of the grid.

Parameters

gr	The grid to be approximated by the product.
complexity	The complexity is ignored.

Exceptions

std::length_error Thrown if the space dimension of gr exceeds the maximum allowed space dimension.

Definition at line 112 of file Partially_Reduced_Product_inlines.hh.

   : d1(gr), d2(gr) {
   set_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

template<typename Interval >

Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::Partially_Reduced_Product	(	const Box< Interval > &	box,
		Complexity_Class	complexity = `ANY_COMPLEXITY`
	)

inline

Builds a product out of a box.

Builds a product containing box. The product inherits the space dimension of the box.

Parameters

box	The box representing the pair to be built.
complexity	The complexity is ignored.

Exceptions

std::length_error Thrown if the space dimension of box exceeds the maximum allowed space dimension.

Definition at line 121 of file Partially_Reduced_Product_inlines.hh.

   : d1(box), d2(box) {
   set_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

template<typename U >

Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::Partially_Reduced_Product	(	const BD_Shape< U > &	bd,
		Complexity_Class	complexity = `ANY_COMPLEXITY`
	)

inline

Builds a product out of a BD shape.

Builds a product containing bd. The product inherits the space dimension of the BD shape.

Parameters

bd	The BD shape representing the product to be built.
complexity	The complexity is ignored.

Exceptions

std::length_error Thrown if the space dimension of bd exceeds the maximum allowed space dimension.

Definition at line 130 of file Partially_Reduced_Product_inlines.hh.

   : d1(bd), d2(bd) {
   set_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

template<typename U >

Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::Partially_Reduced_Product	(	const Octagonal_Shape< U > &	os,
		Complexity_Class	complexity = `ANY_COMPLEXITY`
	)

inline

Builds a product out of an octagonal shape.

Builds a product containing os. The product inherits the space dimension of the octagonal shape.

Parameters

os	The octagonal shape representing the product to be built.
complexity	The complexity is ignored.

Exceptions

std::length_error Thrown if the space dimension of os exceeds the maximum allowed space dimension.

Definition at line 139 of file Partially_Reduced_Product_inlines.hh.

   : d1(os), d2(os) {
   set_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::Partially_Reduced_Product	(	const Partially_Reduced_Product< D1, D2, R > &	y,
		Complexity_Class	complexity = `ANY_COMPLEXITY`
	)

inline

Ordinary copy constructor.

Definition at line 147 of file Partially_Reduced_Product_inlines.hh.

References Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::reduced.

   : d1(y.d1), d2(y.d2) {
   reduced = y.reduced;
 }

template<typename D1 , typename D2 , typename R >

template<typename E1 , typename E2 , typename S >

Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::Partially_Reduced_Product	(	const Partially_Reduced_Product< E1, E2, S > &	y,
		Complexity_Class	complexity = `ANY_COMPLEXITY`
	)

inlineexplicit

Builds a conservative, upward approximation of y.

The complexity argument is ignored.

Definition at line 157 of file Partially_Reduced_Product_inlines.hh.

References Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::domain1(), Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::domain2(), and Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::intersection_assign().

   : d1(y.space_dimension()), d2(y.space_dimension()), reduced(false) {
   Partially_Reduced_Product<D1, D2, R> pg1(y.domain1(), complexity);
   Partially_Reduced_Product<D1, D2, R> pg2(y.domain2(), complexity);
   pg1.intersection_assign(pg2);
   m_swap(pg1);
 }

template<typename D1 , typename D2 , typename R >

Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::~Partially_Reduced_Product ( )

inline

Destructor.

Definition at line 168 of file Partially_Reduced_Product_inlines.hh.

168 {

169 }

Member Function Documentation

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::add_congruence ( const Congruence & cg )

inline

Adds a copy of congruence cg to *this.

Exceptions

std::invalid_argument Thrown if *this and congruence cg are dimension-incompatible.

Definition at line 404 of file Partially_Reduced_Product_inlines.hh.

                                                                          {
   d1.add_congruence(cg);
   d2.add_congruence(cg);
   clear_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::add_congruences ( const Congruence_System & cgs )

inline

Adds a copy of the congruences in cgs to *this.

Parameters

cgs	The congruence system to be added.

Exceptions

std::invalid_argument Thrown if *this and cgs are dimension-incompatible.

Definition at line 439 of file Partially_Reduced_Product_inlines.hh.

                                               {
   d1.add_congruences(cgs);
   d2.add_congruences(cgs);
   clear_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::add_constraint ( const Constraint & c )

inline

Adds constraint c to *this.

Exceptions

std::invalid_argument Thrown if *this and c are dimension-incompatible.

Definition at line 388 of file Partially_Reduced_Product_inlines.hh.

                                                                         {
   d1.add_constraint(c);
   d2.add_constraint(c);
   clear_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::add_constraints ( const Constraint_System & cs )

inline

Adds a copy of the constraint system in cs to *this.

Parameters

cs	The constraint system to be added.

Exceptions

std::invalid_argument Thrown if *this and cs are dimension-incompatible.

Definition at line 421 of file Partially_Reduced_Product_inlines.hh.

                                              {
   d1.add_constraints(cs);
   d2.add_constraints(cs);
   clear_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::add_recycled_congruences ( Congruence_System & cgs )

Adds the congruences in cgs to *this.

Parameters

cgs	The congruence system to be added that may be recycled.

Exceptions

std::invalid_argument Thrown if *this and cs are dimension-incompatible.

Warning: The only assumption that can be made about cgs upon successful or exceptional return is that it can be safely destroyed.

Definition at line 131 of file Partially_Reduced_Product_templates.hh.

                                                  {
   if (d1.can_recycle_congruence_systems()) {
     d2.refine_with_congruences(cgs);
     d1.add_recycled_congruences(cgs);
   }
   else {
     if (d2.can_recycle_congruence_systems()) {
       d1.refine_with_congruences(cgs);
       d2.add_recycled_congruences(cgs);
     }
     else {
       d1.add_congruences(cgs);
       d2.add_congruences(cgs);
     }
   }
   clear_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::add_recycled_constraints ( Constraint_System & cs )

Adds the constraint system in cs to *this.

Parameters

cs	The constraint system to be added that may be recycled.

Exceptions

std::invalid_argument Thrown if *this and cs are dimension-incompatible.

Warning: The only assumption that can be made about cs upon successful or exceptional return is that it can be safely destroyed.

Definition at line 110 of file Partially_Reduced_Product_templates.hh.

                                                 {
   if (d1.can_recycle_constraint_systems()) {
     d2.refine_with_constraints(cs);
     d1.add_recycled_constraints(cs);
   }
   else {
     if (d2.can_recycle_constraint_systems()) {
       d1.refine_with_constraints(cs);
       d2.add_recycled_constraints(cs);
     }
     else {
       d1.add_constraints(cs);
       d2.add_constraints(cs);
     }
   }
   clear_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::add_space_dimensions_and_embed ( dimension_type m )

inline

Adds m new space dimensions and embeds the components of *this in the new vector space.

Parameters

m	The number of dimensions to add.

Exceptions

std::length_error Thrown if adding m new space dimensions would cause the vector space to exceed dimension max_space_dimension().

Definition at line 584 of file Partially_Reduced_Product_inlines.hh.

                                                  {
   d1.add_space_dimensions_and_embed(m);
   d2.add_space_dimensions_and_embed(m);
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::add_space_dimensions_and_project ( dimension_type m )

inline

Adds m new space dimensions and does not embed the components in the new vector space.

Parameters

m	The number of space dimensions to add.

Exceptions

std::length_error Thrown if adding m new space dimensions would cause the vector space to exceed dimension max_space_dimension().

Definition at line 592 of file Partially_Reduced_Product_inlines.hh.

                                                    {
   d1.add_space_dimensions_and_project(m);
   d2.add_space_dimensions_and_project(m);
 }

template<typename D1 , typename D2 , typename R >

dimension_type Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::affine_dimension ( ) const

inline

Returns the minimum affine dimension (see also grid affine dimension) of the components of *this.

Definition at line 192 of file Partially_Reduced_Product_inlines.hh.

                                                              {
   reduce();
   const dimension_type d1_dim = d1.affine_dimension();
   const dimension_type d2_dim = d2.affine_dimension();
   return std::min(d1_dim, d2_dim);
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::affine_image	(	Variable	var,
		const Linear_Expression &	expr,
		Coefficient_traits::const_reference	denominator = `Coefficient_one()`
	)

inline

Assigns to *this the affine image of this under the function mapping variable var to the affine expression specified by expr and denominator.

Parameters

var	The variable to which the affine expression is assigned;
expr	The numerator of the affine expression;
denominator	The denominator of the affine expression (optional argument with default value 1).

Exceptions

std::invalid_argument Thrown if denominator is zero or if expr and *this are dimension-incompatible or if var is not a space dimension of *this.

Definition at line 269 of file Partially_Reduced_Product_inlines.hh.

                                                               {
   d1.affine_image(var, expr, denominator);
   d2.affine_image(var, expr, denominator);
   clear_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::affine_preimage	(	Variable	var,
		const Linear_Expression &	expr,
		Coefficient_traits::const_reference	denominator = `Coefficient_one()`
	)

inline

Assigns to *this the affine preimage of *this under the function mapping variable var to the affine expression specified by expr and denominator.

Parameters

var	The variable to which the affine expression is substituted;
expr	The numerator of the affine expression;
denominator	The denominator of the affine expression (optional argument with default value 1).

Exceptions

std::invalid_argument Thrown if denominator is zero or if expr and *this are dimension-incompatible or if var is not a space dimension of *this.

Definition at line 280 of file Partially_Reduced_Product_inlines.hh.

                                                                  {
   d1.affine_preimage(var, expr, denominator);
   d2.affine_preimage(var, expr, denominator);
   clear_reduced_flag();
 }

template<typename D1, typename D2, typename R>

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::ascii_dump ( ) const

Writes to std::cerr an ASCII representation of *this.

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::ascii_dump ( std::ostream & s ) const

inline

Writes to s an ASCII representation of *this.

Definition at line 705 of file Partially_Reduced_Product_inlines.hh.

References Parma_Polyhedra_Library::Implementation::BD_Shapes::no, and Parma_Polyhedra_Library::Implementation::BD_Shapes::yes.

                                                                     {
   const char yes = '+';
   const char no = '-';
   s << "Partially_Reduced_Product\n";
   s << (reduced ? yes : no) << "reduced\n";
   s << "Domain 1:\n";
   d1.ascii_dump(s);
   s << "Domain 2:\n";
   d2.ascii_dump(s);
 }

template<typename D1 , typename D2 , typename R >

bool Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::ascii_load ( std::istream & s )

Loads from s an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets *this accordingly. Returns true if successful, false otherwise.

Definition at line 474 of file Partially_Reduced_Product_templates.hh.

References Parma_Polyhedra_Library::Implementation::BD_Shapes::no, and Parma_Polyhedra_Library::Implementation::BD_Shapes::yes.

                                                               {
   const char yes = '+';
   const char no = '-';
   std::string str;
   if (!(s >> str) || str != "Partially_Reduced_Product") {
     return false;
   }
   if (!(s >> str)
       || (str[0] != yes && str[0] != no)
       || str.substr(1) != "reduced") {
     return false;
   }
   reduced = (str[0] == yes);
   if (!(s >> str) || str != "Domain") {
     return false;
   }
   if (!(s >> str) || str != "1:") {
     return false;
   }
   if (!d1.ascii_load(s)) {
     return false;
   }
   if (!(s >> str) || str != "Domain") {
     return false;
   }
   if (!(s >> str) || str != "2:") {
     return false;
   }
   return d2.ascii_load(s);
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::bounded_affine_image	(	Variable	var,
		const Linear_Expression &	lb_expr,
		const Linear_Expression &	ub_expr,
		Coefficient_traits::const_reference	denominator = `Coefficient_one()`
	)

inline

Assigns to *this the image of *this with respect to the bounded affine relation $\frac{\mathrm{lb\_expr}}{\mathrm{denominator}} \leq \mathrm{var}' \leq \frac{\mathrm{ub\_expr}}{\mathrm{denominator}}$ .

Parameters

var	The variable updated by the affine relation;
lb_expr	The numerator of the lower bounding affine expression;
ub_expr	The numerator of the upper bounding affine expression;
denominator	The (common) denominator for the lower and upper bounding affine expressions (optional argument with default value 1).

Exceptions

std::invalid_argument Thrown if denominator is zero or if lb_expr (resp., ub_expr) and *this are dimension-incompatible or if var is not a space dimension of *this.

Definition at line 338 of file Partially_Reduced_Product_inlines.hh.

                                                                       {
   d1.bounded_affine_image(var, lb_expr, ub_expr, denominator);
   d2.bounded_affine_image(var, lb_expr, ub_expr, denominator);
   clear_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::bounded_affine_preimage	(	Variable	var,
		const Linear_Expression &	lb_expr,
		const Linear_Expression &	ub_expr,
		Coefficient_traits::const_reference	denominator = `Coefficient_one()`
	)

inline

Assigns to *this the preimage of *this with respect to the bounded affine relation $\frac{\mathrm{lb\_expr}}{\mathrm{denominator}} \leq \mathrm{var}' \leq \frac{\mathrm{ub\_expr}}{\mathrm{denominator}}$ .

Parameters

var	The variable updated by the affine relation;
lb_expr	The numerator of the lower bounding affine expression;
ub_expr	The numerator of the upper bounding affine expression;
denominator	The (common) denominator for the lower and upper bounding affine expressions (optional argument with default value 1).

Exceptions

std::invalid_argument Thrown if denominator is zero or if lb_expr (resp., ub_expr) and *this are dimension-incompatible or if var is not a space dimension of *this.

Definition at line 350 of file Partially_Reduced_Product_inlines.hh.

                                                                          {
   d1.bounded_affine_preimage(var, lb_expr, ub_expr, denominator);
   d2.bounded_affine_preimage(var, lb_expr, ub_expr, denominator);
   clear_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

bool Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::bounds_from_above ( const Linear_Expression & expr ) const

inline

Returns true if and only if expr is bounded in *this.

This method is the same as bounds_from_below.

Exceptions

std::invalid_argument Thrown if expr and *this are dimension-incompatible.

Definition at line 545 of file Partially_Reduced_Product_inlines.hh.

                                                        {
   reduce();
   return d1.bounds_from_above(expr) || d2.bounds_from_above(expr);
 }

template<typename D1 , typename D2 , typename R >

bool Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::bounds_from_below ( const Linear_Expression & expr ) const

inline

Returns true if and only if expr is bounded in *this.

This method is the same as bounds_from_above.

Exceptions

std::invalid_argument Thrown if expr and *this are dimension-incompatible.

Definition at line 553 of file Partially_Reduced_Product_inlines.hh.

                                                        {
   reduce();
   return d1.bounds_from_below(expr) || d2.bounds_from_below(expr);
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::clear_reduced_flag ( ) const

inlineprotected

Clears the reduced flag.

Definition at line 691 of file Partially_Reduced_Product_inlines.hh.

References Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::reduced.

Referenced by Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::OK().

                                                                {
   const_cast<Partially_Reduced_Product&>(*this).reduced = false;
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::concatenate_assign ( const Partially_Reduced_Product< D1, D2, R > & y )

inline

Assigns to the first (resp., second) component of *this the "concatenation" of the first (resp., second) components of *this and y, taken in this order. See also Concatenating Polyhedra.

Exceptions

std::length_error Thrown if the concatenation would cause the vector space to exceed dimension max_space_dimension().

Definition at line 600 of file Partially_Reduced_Product_inlines.hh.

References Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d1, Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d2, and Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::is_reduced().

                                                        {
   d1.concatenate_assign(y.d1);
   d2.concatenate_assign(y.d2);
   if (!is_reduced() || !y.is_reduced()) {
     clear_reduced_flag();
   }
 }

template<typename D1 , typename D2 , typename R >

Congruence_System Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::congruences ( ) const

Returns a system of congruences which approximates *this.

Definition at line 82 of file Partially_Reduced_Product_templates.hh.

References Parma_Polyhedra_Library::Congruence_System::begin(), Parma_Polyhedra_Library::Congruence_System::end(), and Parma_Polyhedra_Library::Congruence_System::insert().

                                                         {
   reduce();
   Congruence_System cgs = d2.congruences();
   const Congruence_System& cgs1 = d1.congruences();
   for (Congruence_System::const_iterator i = cgs1.begin(),
          cgs_end = cgs1.end(); i != cgs_end; ++i) {
     cgs.insert(*i);
   }
   return cgs;
 }

template<typename D1 , typename D2 , typename R >

bool Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::constrains ( Variable var ) const

inline

Returns true if and only if var is constrained in *this.

Exceptions

std::invalid_argument Thrown if var is not a space dimension of *this.

Definition at line 560 of file Partially_Reduced_Product_inlines.hh.

                                                                    {
   reduce();
   return d1.constrains(var) || d2.constrains(var);
 }

template<typename D1 , typename D2 , typename R >

Constraint_System Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::constraints ( ) const

Returns a system of constraints which approximates *this.

Definition at line 49 of file Partially_Reduced_Product_templates.hh.

References Parma_Polyhedra_Library::Constraint_System::begin(), Parma_Polyhedra_Library::Constraint_System::end(), and Parma_Polyhedra_Library::Constraint_System::insert().

                                                         {
   reduce();
   Constraint_System cs = d2.constraints();
   const Constraint_System& cs1 = d1.constraints();
   for (Constraint_System::const_iterator i = cs1.begin(),
          cs_end = cs1.end(); i != cs_end; ++i) {
     cs.insert(*i);
   }
   return cs;
 }

template<typename D1 , typename D2 , typename R >

bool Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::contains ( const Partially_Reduced_Product< D1, D2, R > & y ) const

inline

Returns true if and only if each component of *this contains the corresponding component of y.

Exceptions

std::invalid_argument Thrown if *this and y are dimension-incompatible.

Definition at line 653 of file Partially_Reduced_Product_inlines.hh.

References Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d1, Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d2, and Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::reduce().

                                                    {
   reduce();
   y.reduce();
   return d1.contains(y.d1) && d2.contains(y.d2);
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::difference_assign ( const Partially_Reduced_Product< D1, D2, R > & y )

inline

Assigns to *this an approximation of the set-theoretic difference of *this and y.

Exceptions

std::invalid_argument Thrown if *this and y are dimension-incompatible.

Definition at line 228 of file Partially_Reduced_Product_inlines.hh.

References Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d1, Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d2, and Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::reduce().

                                                       {
   reduce();
   y.reduce();
   d1.difference_assign(y.d1);
   d2.difference_assign(y.d2);
   clear_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

const D1 & Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::domain1 ( ) const

inline

Returns a constant reference to the first of the pair.

Definition at line 487 of file Partially_Reduced_Product_inlines.hh.

Referenced by Parma_Polyhedra_Library::Box< ITV >::Box(), and Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::Partially_Reduced_Product().

                                                     {
   reduce();
   return d1;
 }

template<typename D1 , typename D2 , typename R >

const D2 & Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::domain2 ( ) const

inline

Returns a constant reference to the second of the pair.

Definition at line 494 of file Partially_Reduced_Product_inlines.hh.

Referenced by Parma_Polyhedra_Library::Box< ITV >::Box(), and Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::Partially_Reduced_Product().

                                                     {
   reduce();
   return d2;
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::drop_some_non_integer_points ( Complexity_Class complexity = ANY_COMPLEXITY )

inline

Possibly tightens *this by dropping some points with non-integer coordinates.

Parameters

complexity The maximal complexity of any algorithms used.

Note: Currently there is no optimality guarantee, not even if complexity is ANY_COMPLEXITY.

Definition at line 457 of file Partially_Reduced_Product_inlines.hh.

                                                           {
   reduce();
   d1.drop_some_non_integer_points(complexity);
   d2.drop_some_non_integer_points(complexity);
   clear_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::drop_some_non_integer_points	(	const Variables_Set &	vars,
		Complexity_Class	complexity = `ANY_COMPLEXITY`
	)

inline

Possibly tightens *this by dropping some points with non-integer coordinates for the space dimensions corresponding to vars.

Parameters

vars	Points with non-integer coordinates for these variables/space-dimensions can be discarded.
complexity	The maximal complexity of any algorithms used.

Note: Currently there is no optimality guarantee, not even if complexity is ANY_COMPLEXITY.

Definition at line 467 of file Partially_Reduced_Product_inlines.hh.

                                                                  {
   reduce();
   d1.drop_some_non_integer_points(vars, complexity);
   d2.drop_some_non_integer_points(vars, complexity);
   clear_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::expand_space_dimension	(	Variable	var,
		dimension_type	m
	)

inline

Creates m copies of the space dimension corresponding to var.

Parameters

var	The variable corresponding to the space dimension to be replicated;
m	The number of replicas to be created.

Exceptions

std::invalid_argument	Thrown if `var` does not correspond to a dimension of the vector space.
std::length_error	Thrown if adding `m` new space dimensions would cause the vector space to exceed dimension `max_space_dimension()`.

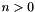If *this has space dimension $n$ , with $n > 0$ , and var has space dimension 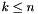$k \leq n$ , then the $k$ -th space dimension is expanded to m new space dimensions $n$ , $n+1$ , $\dots$ , $n+m-1$ .

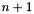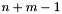Definition at line 636 of file Partially_Reduced_Product_inlines.hh.

                                                        {
   d1.expand_space_dimension(var, m);
   d2.expand_space_dimension(var, m);
 }

template<typename D1 , typename D2 , typename R >

memory_size_type Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::external_memory_in_bytes ( ) const

inline

Returns the size in bytes of the memory managed by *this.

Definition at line 173 of file Partially_Reduced_Product_inlines.hh.

                                                                      {
   return d1.external_memory_in_bytes() + d2.external_memory_in_bytes();
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::fold_space_dimensions	(	const Variables_Set &	vars,
		Variable	dest
	)

inline

Folds the space dimensions in vars into dest.

Parameters

vars	The set of Variable objects corresponding to the space dimensions to be folded;
dest	The variable corresponding to the space dimension that is the destination of the folding operation.

Exceptions

std::invalid_argument Thrown if *this is dimension-incompatible with dest or with one of the Variable objects contained in vars. Also thrown if dest is contained in vars.

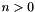If *this has space dimension $n$ , with $n > 0$ , dest has space dimension 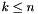$k \leq n$ , vars is a set of variables whose maximum space dimension is also less than or equal to $n$ , and dest is not a member of vars, then the space dimensions corresponding to variables in vars are folded into the $k$ -th space dimension.

Definition at line 644 of file Partially_Reduced_Product_inlines.hh.

                                        {
   d1.fold_space_dimensions(vars, dest);
   d2.fold_space_dimensions(vars, dest);
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::generalized_affine_image	(	Variable	var,
		Relation_Symbol	relsym,
		const Linear_Expression &	expr,
		Coefficient_traits::const_reference	denominator = `Coefficient_one()`
	)

inline

Assigns to *this the image of *this with respect to the generalized affine relation $\mathrm{var}' \relsym \frac{\mathrm{expr}}{\mathrm{denominator}}$ , where $\mathord{\relsym}$ is the relation symbol encoded by relsym (see also generalized affine relation.)

Parameters

var	The left hand side variable of the generalized affine relation;
relsym	The relation symbol;
expr	The numerator of the right hand side affine expression;
denominator	The denominator of the right hand side affine expression (optional argument with default value 1).

Exceptions

std::invalid_argument Thrown if denominator is zero or if expr and *this are dimension-incompatible or if var is not a space dimension of *this or if *this is a C_Polyhedron and relsym is a strict relation symbol.

Definition at line 291 of file Partially_Reduced_Product_inlines.hh.

                                                                           {
   d1.generalized_affine_image(var, relsym, expr, denominator);
   d2.generalized_affine_image(var, relsym, expr, denominator);
   clear_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::generalized_affine_image	(	const Linear_Expression &	lhs,
		Relation_Symbol	relsym,
		const Linear_Expression &	rhs
	)

inline

Assigns to *this the image of *this with respect to the generalized affine relation $\mathrm{lhs}' \relsym \mathrm{rhs}$ , where $\mathord{\relsym}$ is the relation symbol encoded by relsym. (see also generalized affine relation.)

Parameters

lhs	The left hand side affine expression;
relsym	The relation symbol;
rhs	The right hand side affine expression.

Exceptions

std::invalid_argument Thrown if *this is dimension-incompatible with lhs or rhs or if *this is a C_Polyhedron and relsym is a strict relation symbol.

Definition at line 315 of file Partially_Reduced_Product_inlines.hh.

                                                          {
   d1.generalized_affine_image(lhs, relsym, rhs);
   d2.generalized_affine_image(lhs, relsym, rhs);
   clear_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::generalized_affine_preimage	(	Variable	var,
		Relation_Symbol	relsym,
		const Linear_Expression &	expr,
		Coefficient_traits::const_reference	denominator = `Coefficient_one()`
	)

inline

Assigns to *this the preimage of *this with respect to the generalized affine relation $\mathrm{var}' \relsym \frac{\mathrm{expr}}{\mathrm{denominator}}$ , where $\mathord{\relsym}$ is the relation symbol encoded by relsym. (see also generalized affine relation.)

Parameters

var	The left hand side variable of the generalized affine relation;
relsym	The relation symbol;
expr	The numerator of the right hand side affine expression;
denominator	The denominator of the right hand side affine expression (optional argument with default value 1).

Exceptions

std::invalid_argument Thrown if denominator is zero or if expr and *this are dimension-incompatible or if var is not a space dimension of *this or if *this is a C_Polyhedron and relsym is a strict relation symbol.

Definition at line 303 of file Partially_Reduced_Product_inlines.hh.

                                                                              {
   d1.generalized_affine_preimage(var, relsym, expr, denominator);
   d2.generalized_affine_preimage(var, relsym, expr, denominator);
   clear_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::generalized_affine_preimage	(	const Linear_Expression &	lhs,
		Relation_Symbol	relsym,
		const Linear_Expression &	rhs
	)

inline

Assigns to *this the preimage of *this with respect to the generalized affine relation $\mathrm{lhs}' \relsym \mathrm{rhs}$ , where $\mathord{\relsym}$ is the relation symbol encoded by relsym. (see also generalized affine relation.)

Parameters

lhs	The left hand side affine expression;
relsym	The relation symbol;
rhs	The right hand side affine expression.

Exceptions

std::invalid_argument Thrown if *this is dimension-incompatible with lhs or rhs or if *this is a C_Polyhedron and relsym is a strict relation symbol.

Definition at line 326 of file Partially_Reduced_Product_inlines.hh.

                                                             {
   d1.generalized_affine_preimage(lhs, relsym, rhs);
   d2.generalized_affine_preimage(lhs, relsym, rhs);
   clear_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

int32_t Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::hash_code ( ) const

inline

Returns a 32-bit hash code for *this.

If x and y are such that x == y, then x.hash_code() == y.hash_code().

Definition at line 718 of file Partially_Reduced_Product_inlines.hh.

References Parma_Polyhedra_Library::hash_code_from_dimension().

                                                       {
   return hash_code_from_dimension(space_dimension());
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::intersection_assign ( const Partially_Reduced_Product< D1, D2, R > & y )

inline

Assigns to *this the componentwise intersection of *this and y.

Exceptions

std::invalid_argument Thrown if *this and y are dimension-incompatible.

Definition at line 219 of file Partially_Reduced_Product_inlines.hh.

References Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d1, and Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d2.

Referenced by Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::Partially_Reduced_Product().

                                                         {
   d1.intersection_assign(y.d1);
   d2.intersection_assign(y.d2);
   clear_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

bool Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::is_bounded ( ) const

inline

Returns true if and only if a component of *this is bounded.

Definition at line 537 of file Partially_Reduced_Product_inlines.hh.

                                                        {
   reduce();
   return d1.is_bounded() || d2.is_bounded();
 }

template<typename D1 , typename D2 , typename R >

bool Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::is_discrete ( ) const

inline

Returns true if and only if a component of *this is discrete.

Definition at line 530 of file Partially_Reduced_Product_inlines.hh.

                                                         {
   reduce();
   return d1.is_discrete() || d2.is_discrete();
 }

template<typename D1 , typename D2 , typename R >

bool Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::is_disjoint_from ( const Partially_Reduced_Product< D1, D2, R > & y ) const

inline

Returns true if and only if *this and y are componentwise disjoint.

Exceptions

std::invalid_argument Thrown if x and y are dimension-incompatible.

Definition at line 522 of file Partially_Reduced_Product_inlines.hh.

References Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d1, Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d2, and Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::reduce().

                                                            {
   reduce();
   y.reduce();
   return d1.is_disjoint_from(y.d1) || d2.is_disjoint_from(y.d2);
 }

template<typename D1 , typename D2 , typename R >

bool Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::is_empty ( ) const

inline

Returns true if and only if either of the components of *this are empty.

Definition at line 501 of file Partially_Reduced_Product_inlines.hh.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::Pointset_Powerset().

                                                      {
   reduce();
   return d1.is_empty() || d2.is_empty();
 }

template<typename D1 , typename D2 , typename R >

bool Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::is_reduced ( ) const

inlineprotected

Return true if and only if the reduced flag is set.

Definition at line 685 of file Partially_Reduced_Product_inlines.hh.

Referenced by Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::concatenate_assign(), and Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::reduce().

                                                        {
   return reduced;
 }

template<typename D1 , typename D2 , typename R >

bool Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::is_topologically_closed ( ) const

inline

Returns true if and only if both of the components of *this are topologically closed subsets of the vector space.

Definition at line 514 of file Partially_Reduced_Product_inlines.hh.

                                                                     {
   reduce();
   return d1.is_topologically_closed() && d2.is_topologically_closed();
 }

template<typename D1 , typename D2 , typename R >

bool Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::is_universe ( ) const

inline

Returns true if and only if both of the components of *this are the universe.

Definition at line 508 of file Partially_Reduced_Product_inlines.hh.

                                                         {
   return d1.is_universe() && d2.is_universe();
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::m_swap ( Partially_Reduced_Product< D1, D2, R > & y )

inline

Swaps *this with product y. (*this and y can be dimension-incompatible.)

Definition at line 379 of file Partially_Reduced_Product_inlines.hh.

References Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d1, Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d2, Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::reduced, and Parma_Polyhedra_Library::swap().

Referenced by Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::swap().

                                                                          {
   using std::swap;
   swap(d1, y.d1);
   swap(d2, y.d2);
   swap(reduced, y.reduced);
 }

template<typename D1 , typename D2 , typename R >

template<typename Partial_Function >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::map_space_dimensions ( const Partial_Function & pfunc )

inline

Remaps the dimensions of the vector space according to a partial function.

If pfunc maps only some of the dimensions of *this then the rest will be projected away.

If the highest dimension mapped to by pfunc is higher than the highest dimension in *this then the number of dimensions in this will be increased to the highest dimension mapped to by pfunc.

Parameters

pfunc The partial function specifying the destiny of each space dimension.

The template class Partial_Function must provide the following methods.

bool has_empty_codomain() const

returns true if and only if the represented partial function has an empty codomain (i.e., it is always undefined). The has_empty_codomain() method will always be called before the methods below. However, if has_empty_codomain() returns true, none of the functions below will be called.

dimension_type max_in_codomain() const

returns the maximum value that belongs to the codomain of the partial function. The max_in_codomain() method is called at most once.

bool maps(dimension_type i, dimension_type& j) const

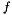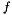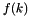Let $f$ be the represented function and $k$ be the value of i. If $f$ is defined in $k$ , then $f(k)$ is assigned to j and true is returned. If 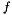$f$ is undefined in $k$ , then false is returned. This method is called at most $n$ times, where $n$ is the dimension of the vector space enclosing *this.

The result is undefined if pfunc does not encode a partial function with the properties described in specification of the mapping operator.

Definition at line 628 of file Partially_Reduced_Product_inlines.hh.

                                                     {
   d1.map_space_dimensions(pfunc);
   d2.map_space_dimensions(pfunc);
 }

template<typename D1 , typename D2 , typename R >

dimension_type Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::max_space_dimension ( )

inlinestatic

Returns the maximum space dimension this product can handle.

Definition at line 37 of file Partially_Reduced_Product_inlines.hh.

References Parma_Polyhedra_Library::max_space_dimension().

                                                           {
   return (D1::max_space_dimension() < D2::max_space_dimension())
     ? D1::max_space_dimension()
     : D2::max_space_dimension();
 }

template<typename D1 , typename D2 , typename R >

bool Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::maximize	(	const Linear_Expression &	expr,
		Coefficient &	sup_n,
		Coefficient &	sup_d,
		bool &	maximum
	)		const

Returns true if and only if *this is not empty and expr is bounded from above in *this, in which case the supremum value is computed.

Parameters

expr	The linear expression to be maximized subject to `*this`;
sup_n	The numerator of the supremum value;
sup_d	The denominator of the supremum value;
maximum	`true` if the supremum value can be reached in `this`.

Exceptions

std::invalid_argument Thrown if expr and *this are dimension-incompatible.

If *this is empty or expr is not bounded by *this, false is returned and sup_n, sup_d and maximum are left untouched.

Definition at line 230 of file Partially_Reduced_Product_templates.hh.

References PPL_DIRTY_TEMP_COEFFICIENT.

                                 {
   reduce();
 
   if (is_empty()) {
     return false;
   }
 
   PPL_DIRTY_TEMP_COEFFICIENT(sup1_n);
   PPL_DIRTY_TEMP_COEFFICIENT(sup1_d);
   PPL_DIRTY_TEMP_COEFFICIENT(sup2_n);
   PPL_DIRTY_TEMP_COEFFICIENT(sup2_d);
   bool maximum1;
   bool maximum2;
   bool r1 = d1.maximize(expr, sup1_n, sup1_d, maximum1);
   bool r2 = d2.maximize(expr, sup2_n, sup2_d, maximum2);
   // If neither is bounded from above, return false.
   if (!r1 && !r2) {
     return false;
   }
   // If only d2 is bounded from above, then use the values for d2.
   if (!r1) {
     sup_n = sup2_n;
     sup_d = sup2_d;
     maximum = maximum2;
     return true;
   }
   // If only d1 is bounded from above, then use the values for d1.
   if (!r2) {
     sup_n = sup1_n;
     sup_d = sup1_d;
     maximum = maximum1;
     return true;
   }
   // If both d1 and d2 are bounded from above, then use the minimum values.
   if (sup2_d * sup1_n >= sup1_d * sup2_n) {
     sup_n = sup1_n;
     sup_d = sup1_d;
     maximum = maximum1;
   }
   else {
     sup_n = sup2_n;
     sup_d = sup2_d;
     maximum = maximum2;
   }
   return true;
 }

template<typename D1 , typename D2 , typename R >

bool Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::maximize	(	const Linear_Expression &	expr,
		Coefficient &	sup_n,
		Coefficient &	sup_d,
		bool &	maximum,
		Generator &	g
	)		const

Returns true if and only if *this is not empty and expr is bounded from above in *this, in which case the supremum value and a point where expr reaches it are computed.

Parameters

expr	The linear expression to be maximized subject to `*this`;
sup_n	The numerator of the supremum value;
sup_d	The denominator of the supremum value;
maximum	`true` if the supremum value can be reached in `this`.
g	When maximization succeeds, will be assigned the point or closure point where `expr` reaches its supremum value.

Exceptions

std::invalid_argument Thrown if expr and *this are dimension-incompatible.

If *this is empty or expr is not bounded by *this, false is returned and sup_n, sup_d, maximum and g are left untouched.

Definition at line 337 of file Partially_Reduced_Product_templates.hh.

References PPL_DIRTY_TEMP_COEFFICIENT.

                                {
   reduce();
 
   if (is_empty()) {
     return false;
   }
   PPL_ASSERT(reduced);
 
   PPL_DIRTY_TEMP_COEFFICIENT(sup1_n);
   PPL_DIRTY_TEMP_COEFFICIENT(sup1_d);
   PPL_DIRTY_TEMP_COEFFICIENT(sup2_n);
   PPL_DIRTY_TEMP_COEFFICIENT(sup2_d);
   bool maximum1;
   bool maximum2;
   Generator g1(point());
   Generator g2(point());
   bool r1 = d1.maximize(expr, sup1_n, sup1_d, maximum1, g1);
   bool r2 = d2.maximize(expr, sup2_n, sup2_d, maximum2, g2);
   // If neither is bounded from above, return false.
   if (!r1 && !r2) {
     return false;
   }
   // If only d2 is bounded from above, then use the values for d2.
   if (!r1) {
     sup_n = sup2_n;
     sup_d = sup2_d;
     maximum = maximum2;
     g = g2;
     return true;
   }
   // If only d1 is bounded from above, then use the values for d1.
   if (!r2) {
     sup_n = sup1_n;
     sup_d = sup1_d;
     maximum = maximum1;
     g = g1;
     return true;
   }
   // If both d1 and d2 are bounded from above, then use the minimum values.
   if (sup2_d * sup1_n >= sup1_d * sup2_n) {
     sup_n = sup1_n;
     sup_d = sup1_d;
     maximum = maximum1;
     g = g1;
   }
   else {
     sup_n = sup2_n;
     sup_d = sup2_d;
     maximum = maximum2;
     g = g2;
   }
   return true;
 }

template<typename D1 , typename D2 , typename R >

bool Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::minimize	(	const Linear_Expression &	expr,
		Coefficient &	inf_n,
		Coefficient &	inf_d,
		bool &	minimum
	)		const

Returns true if and only if *this is not empty and expr is bounded from below i *this, in which case the infimum value is computed.

Parameters

expr	The linear expression to be minimized subject to `*this`;
inf_n	The numerator of the infimum value;
inf_d	The denominator of the infimum value;
minimum	`true` if the infimum value can be reached in `this`.

Exceptions

std::invalid_argument Thrown if expr and *this are dimension-incompatible.

If *this is empty or expr is not bounded from below, false is returned and inf_n, inf_d and minimum are left untouched.

Definition at line 283 of file Partially_Reduced_Product_templates.hh.

References PPL_DIRTY_TEMP_COEFFICIENT.

                                 {
   reduce();
 
   if (is_empty()) {
     return false;
   }
   PPL_ASSERT(reduced);
 
   PPL_DIRTY_TEMP_COEFFICIENT(inf1_n);
   PPL_DIRTY_TEMP_COEFFICIENT(inf1_d);
   PPL_DIRTY_TEMP_COEFFICIENT(inf2_n);
   PPL_DIRTY_TEMP_COEFFICIENT(inf2_d);
   bool minimum1;
   bool minimum2;
   bool r1 = d1.minimize(expr, inf1_n, inf1_d, minimum1);
   bool r2 = d2.minimize(expr, inf2_n, inf2_d, minimum2);
   // If neither is bounded from below, return false.
   if (!r1 && !r2) {
     return false;
   }
   // If only d2 is bounded from below, then use the values for d2.
   if (!r1) {
     inf_n = inf2_n;
     inf_d = inf2_d;
     minimum = minimum2;
     return true;
   }
   // If only d1 is bounded from below, then use the values for d1.
   if (!r2) {
     inf_n = inf1_n;
     inf_d = inf1_d;
     minimum = minimum1;
     return true;
   }
   // If both d1 and d2 are bounded from below, then use the minimum values.
   if (inf2_d * inf1_n <= inf1_d * inf2_n) {
     inf_n = inf1_n;
     inf_d = inf1_d;
     minimum = minimum1;
   }
   else {
     inf_n = inf2_n;
     inf_d = inf2_d;
     minimum = minimum2;
   }
   return true;
 }

template<typename D1 , typename D2 , typename R >

bool Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::minimize	(	const Linear_Expression &	expr,
		Coefficient &	inf_n,
		Coefficient &	inf_d,
		bool &	minimum,
		Generator &	g
	)		const

Returns true if and only if *this is not empty and expr is bounded from below in *this, in which case the infimum value and a point where expr reaches it are computed.

Parameters

expr	The linear expression to be minimized subject to `*this`;
inf_n	The numerator of the infimum value;
inf_d	The denominator of the infimum value;
minimum	`true` if the infimum value can be reached in `this`.
g	When minimization succeeds, will be assigned the point or closure point where `expr` reaches its infimum value.

Exceptions

std::invalid_argument Thrown if expr and *this are dimension-incompatible.

If *this is empty or expr is not bounded from below, false is returned and inf_n, inf_d, minimum and point are left untouched.

Definition at line 398 of file Partially_Reduced_Product_templates.hh.

References PPL_DIRTY_TEMP_COEFFICIENT.

                                {
   reduce();
 
   if (is_empty()) {
     return false;
   }
   PPL_ASSERT(reduced);
 
   PPL_DIRTY_TEMP_COEFFICIENT(inf1_n);
   PPL_DIRTY_TEMP_COEFFICIENT(inf1_d);
   PPL_DIRTY_TEMP_COEFFICIENT(inf2_n);
   PPL_DIRTY_TEMP_COEFFICIENT(inf2_d);
   bool minimum1;
   bool minimum2;
   Generator g1(point());
   Generator g2(point());
   bool r1 = d1.minimize(expr, inf1_n, inf1_d, minimum1, g1);
   bool r2 = d2.minimize(expr, inf2_n, inf2_d, minimum2, g2);
   // If neither is bounded from below, return false.
   if (!r1 && !r2) {
     return false;
   }
   // If only d2 is bounded from below, then use the values for d2.
   if (!r1) {
     inf_n = inf2_n;
     inf_d = inf2_d;
     minimum = minimum2;
     g = g2;
     return true;
   }
   // If only d1 is bounded from below, then use the values for d1.
   if (!r2) {
     inf_n = inf1_n;
     inf_d = inf1_d;
     minimum = minimum1;
     g = g1;
     return true;
   }
   // If both d1 and d2 are bounded from below, then use the minimum values.
   if (inf2_d * inf1_n <= inf1_d * inf2_n) {
     inf_n = inf1_n;
     inf_d = inf1_d;
     minimum = minimum1;
     g = g1;
   }
   else {
     inf_n = inf2_n;
     inf_d = inf2_d;
     minimum = minimum2;
     g = g2;
   }
   return true;
 }

template<typename D1 , typename D2 , typename R >

Congruence_System Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::minimized_congruences ( ) const

Returns a system of congruences which approximates *this, in reduced form.

Definition at line 95 of file Partially_Reduced_Product_templates.hh.

References Parma_Polyhedra_Library::Congruence_System::begin(), Parma_Polyhedra_Library::Congruence_System::end(), Parma_Polyhedra_Library::Congruence_System::insert(), and Parma_Polyhedra_Library::Grid::minimized_congruences().

                                                                   {
   reduce();
   Congruence_System cgs = d2.congruences();
   const Congruence_System& cgs1 = d1.congruences();
   for (Congruence_System::const_iterator i = cgs1.begin(),
          cgs_end = cgs1.end(); i != cgs_end; ++i) {
     cgs.insert(*i);
   }
   Grid gr(cgs);
   return gr.minimized_congruences();
 }

template<typename D1 , typename D2 , typename R >

Constraint_System Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::minimized_constraints ( ) const

Returns a system of constraints which approximates *this, in reduced form.

Definition at line 62 of file Partially_Reduced_Product_templates.hh.

References Parma_Polyhedra_Library::Constraint_System::begin(), Parma_Polyhedra_Library::Constraint_System::end(), Parma_Polyhedra_Library::Constraint_System::has_strict_inequalities(), Parma_Polyhedra_Library::Constraint_System::insert(), and Parma_Polyhedra_Library::Polyhedron::minimized_constraints().

                                                                   {
   reduce();
   Constraint_System cs = d2.constraints();
   const Constraint_System& cs1 = d1.constraints();
   for (Constraint_System::const_iterator i = cs1.begin(),
          cs_end = cs1.end(); i != cs_end; ++i) {
     cs.insert(*i);
   }
   if (cs.has_strict_inequalities()) {
     NNC_Polyhedron ph(cs);
     return ph.minimized_constraints();
   }
   else {
     C_Polyhedron ph(cs);
     return ph.minimized_constraints();
   }
 }

template<typename D1 , typename D2 , typename R >

bool Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::OK ( ) const

inline

Checks if all the invariants are satisfied.

Definition at line 458 of file Partially_Reduced_Product_templates.hh.

References Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::clear_reduced_flag(), and Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::reduce().

                                                {
   if (reduced) {
     Partially_Reduced_Product<D1, D2, R> dp1 = *this;
     Partially_Reduced_Product<D1, D2, R> dp2 = *this;
     /* Force dp1 reduction */
     dp1.clear_reduced_flag();
     dp1.reduce();
     if (dp1 != dp2) {
       return false;
     }
   }
   return d1.OK() && d2.OK();
 }

template<typename D1 , typename D2 , typename R >

Partially_Reduced_Product< D1, D2, R > & Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::operator= ( const Partially_Reduced_Product< D1, D2, R > & y )

inline

The assignment operator. (*this and y can be dimension-incompatible.)

Definition at line 478 of file Partially_Reduced_Product_inlines.hh.

References Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d1, Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d2, and Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::reduced.

                                               {
   d1 = y.d1;
   d2 = y.d2;
   reduced = y.reduced;
   return *this;
 }

template<typename D1, typename D2, typename R>

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::print ( ) const

Prints *this to std::cerr using operator<<.

template<typename D1 , typename D2 , typename R >

bool Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::reduce ( ) const

inline

Reduce.

Definition at line 671 of file Partially_Reduced_Product_inlines.hh.

References Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d1, Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d2, and Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::is_reduced().

                                                    {
   Partially_Reduced_Product& dp
     = const_cast<Partially_Reduced_Product&>(*this);
   if (dp.is_reduced()) {
     return false;
   }
   R r;
   r.product_reduce(dp.d1, dp.d2);
   set_reduced_flag();
   return true;
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::refine_with_congruence ( const Congruence & cg )

inline

Use the congruence cg to refine *this.

Parameters

cg	The congruence to be used for refinement.

Exceptions

std::invalid_argument Thrown if *this and cg are dimension-incompatible.

Definition at line 412 of file Partially_Reduced_Product_inlines.hh.

                                                                                  {
   d1.refine_with_congruence(cg);
   d2.refine_with_congruence(cg);
   clear_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::refine_with_congruences ( const Congruence_System & cgs )

inline

Use the congruences in cgs to refine *this.

Parameters

cgs	The congruences to be used for refinement.

Exceptions

std::invalid_argument Thrown if *this and cgs are dimension-incompatible.

Definition at line 448 of file Partially_Reduced_Product_inlines.hh.

                                                       {
   d1.refine_with_congruences(cgs);
   d2.refine_with_congruences(cgs);
   clear_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::refine_with_constraint ( const Constraint & c )

inline

Use the constraint c to refine *this.

Parameters

c	The constraint to be used for refinement.

Exceptions

std::invalid_argument Thrown if *this and c are dimension-incompatible.

Definition at line 396 of file Partially_Reduced_Product_inlines.hh.

                                                                                 {
   d1.refine_with_constraint(c);
   d2.refine_with_constraint(c);
   clear_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::refine_with_constraints ( const Constraint_System & cs )

inline

Use the constraints in cs to refine *this.

Parameters

cs	The constraints to be used for refinement.

Exceptions

std::invalid_argument Thrown if *this and cs are dimension-incompatible.

Definition at line 430 of file Partially_Reduced_Product_inlines.hh.

                                                      {
   d1.refine_with_constraints(cs);
   d2.refine_with_constraints(cs);
   clear_reduced_flag();
 }

template<typename D1 , typename D2 , typename R >

Poly_Con_Relation Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::relation_with ( const Constraint & c ) const

Returns the relations holding between *this and c.

Definition at line 166 of file Partially_Reduced_Product_templates.hh.

References Parma_Polyhedra_Library::Poly_Con_Relation::implies(), Parma_Polyhedra_Library::Poly_Con_Relation::is_disjoint(), Parma_Polyhedra_Library::Poly_Con_Relation::is_included(), Parma_Polyhedra_Library::Poly_Con_Relation::nothing(), and Parma_Polyhedra_Library::Poly_Con_Relation::saturates().

                                          {
   reduce();
   Poly_Con_Relation relation1 = d1.relation_with(c);
   Poly_Con_Relation relation2 = d2.relation_with(c);
 
   Poly_Con_Relation result = Poly_Con_Relation::nothing();
 
   if (relation1.implies(Poly_Con_Relation::is_included())) {
     result = result && Poly_Con_Relation::is_included();
   }
   else if (relation2.implies(Poly_Con_Relation::is_included())) {
     result = result && Poly_Con_Relation::is_included();
   }
   if (relation1.implies(Poly_Con_Relation::saturates())) {
     result = result && Poly_Con_Relation::saturates();
   }
   else if (relation2.implies(Poly_Con_Relation::saturates())) {
     result = result && Poly_Con_Relation::saturates();
   }
   if (relation1.implies(Poly_Con_Relation::is_disjoint())) {
     result = result && Poly_Con_Relation::is_disjoint();
   }
   else if (relation2.implies(Poly_Con_Relation::is_disjoint())) {
     result = result && Poly_Con_Relation::is_disjoint();
   }
 
   return result;
 }

template<typename D1 , typename D2 , typename R >

Poly_Con_Relation Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::relation_with ( const Congruence & cg ) const

Returns the relations holding between *this and cg.

Definition at line 198 of file Partially_Reduced_Product_templates.hh.

References Parma_Polyhedra_Library::Poly_Con_Relation::implies(), Parma_Polyhedra_Library::Poly_Con_Relation::is_disjoint(), Parma_Polyhedra_Library::Poly_Con_Relation::is_included(), Parma_Polyhedra_Library::Poly_Con_Relation::nothing(), and Parma_Polyhedra_Library::Poly_Con_Relation::saturates().

                                           {
   reduce();
   Poly_Con_Relation relation1 = d1.relation_with(cg);
   Poly_Con_Relation relation2 = d2.relation_with(cg);
 
   Poly_Con_Relation result = Poly_Con_Relation::nothing();
 
   if (relation1.implies(Poly_Con_Relation::is_included())) {
     result = result && Poly_Con_Relation::is_included();
   }
   else if (relation2.implies(Poly_Con_Relation::is_included())) {
     result = result && Poly_Con_Relation::is_included();
   }
   if (relation1.implies(Poly_Con_Relation::saturates())) {
     result = result && Poly_Con_Relation::saturates();
   }
   else if (relation2.implies(Poly_Con_Relation::saturates())) {
     result = result && Poly_Con_Relation::saturates();
   }
   if (relation1.implies(Poly_Con_Relation::is_disjoint())) {
     result = result && Poly_Con_Relation::is_disjoint();
   }
   else if (relation2.implies(Poly_Con_Relation::is_disjoint())) {
     result = result && Poly_Con_Relation::is_disjoint();
   }
 
   return result;
 }

template<typename D1 , typename D2 , typename R >

Poly_Gen_Relation Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::relation_with ( const Generator & g ) const

Returns the relations holding between *this and g.

Definition at line 152 of file Partially_Reduced_Product_templates.hh.

References Parma_Polyhedra_Library::Poly_Gen_Relation::nothing(), and Parma_Polyhedra_Library::Poly_Gen_Relation::subsumes().

                                         {
   reduce();
   if (Poly_Gen_Relation::nothing() == d1.relation_with(g)
       || Poly_Gen_Relation::nothing() == d2.relation_with(g)) {
     return Poly_Gen_Relation::nothing();
   }
   else {
     return Poly_Gen_Relation::subsumes();
   }
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::remove_higher_space_dimensions ( dimension_type new_dimension )

inline

Removes the higher dimensions of the vector space so that the resulting space will have dimension new_dimension.

Exceptions

std::invalid_argument Thrown if new_dimensions is greater than the space dimension of *this.

Definition at line 619 of file Partially_Reduced_Product_inlines.hh.

                                                              {
   d1.remove_higher_space_dimensions(new_dimension);
   d2.remove_higher_space_dimensions(new_dimension);
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::remove_space_dimensions ( const Variables_Set & vars )

inline

Removes all the specified dimensions from the vector space.

Parameters

vars	The set of Variable objects corresponding to the space dimensions to be removed.

Exceptions

std::invalid_argument Thrown if *this is dimension-incompatible with one of the Variable objects contained in vars.

Definition at line 611 of file Partially_Reduced_Product_inlines.hh.

                                                    {
   d1.remove_space_dimensions(vars);
   d2.remove_space_dimensions(vars);
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::set_reduced_flag ( ) const

inlineprotected

Sets the reduced flag.

Definition at line 697 of file Partially_Reduced_Product_inlines.hh.

References Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::reduced.

                                                              {
   const_cast<Partially_Reduced_Product&>(*this).reduced = true;
 }

template<typename D1 , typename D2 , typename R >

dimension_type Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::space_dimension ( ) const

inline

Returns the dimension of the vector space enclosing *this.

Definition at line 185 of file Partially_Reduced_Product_inlines.hh.

Referenced by Parma_Polyhedra_Library::Box< ITV >::Box().

                                                             {
   PPL_ASSERT(d1.space_dimension() == d2.space_dimension());
   return d1.space_dimension();
 }

template<typename D1 , typename D2 , typename R >

bool Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::strictly_contains ( const Partially_Reduced_Product< D1, D2, R > & y ) const

inline

Returns true if and only if each component of *this strictly contains the corresponding component of y.

Exceptions

std::invalid_argument Thrown if *this and y are dimension-incompatible.

Definition at line 662 of file Partially_Reduced_Product_inlines.hh.

References Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d1, Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d2, and Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::reduce().

                                                             {
   reduce();
   y.reduce();
   return (d1.contains(y.d1) && d2.strictly_contains(y.d2))
     || (d2.contains(y.d2) && d1.strictly_contains(y.d1));
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::throw_space_dimension_overflow	(	const char *	method,
		const char *	reason
	)

private

Definition at line 39 of file Partially_Reduced_Product_templates.hh.

                                                      {
   std::ostringstream s;
   s << "PPL::Partially_Reduced_Product::" << method << ":" << std::endl
     << reason << ".";
   throw std::length_error(s.str());
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::time_elapse_assign ( const Partially_Reduced_Product< D1, D2, R > & y )

inline

Assigns to *this the result of computing the time-elapse between *this and y. (See also time-elapse.)

Exceptions

std::invalid_argument Thrown if *this and y are dimension-incompatible.

Definition at line 362 of file Partially_Reduced_Product_inlines.hh.

References Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d1, Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d2, and Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::reduce().

                                                        {
   reduce();
   y.reduce();
   d1.time_elapse_assign(y.d1);
   d2.time_elapse_assign(y.d2);
   PPL_ASSERT_HEAVY(OK());
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::topological_closure_assign ( )

inline

Assigns to *this its topological closure.

Definition at line 372 of file Partially_Reduced_Product_inlines.hh.

                                                                  {
   d1.topological_closure_assign();
   d2.topological_closure_assign();
 }

template<typename D1 , typename D2 , typename R >

memory_size_type Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::total_memory_in_bytes ( ) const

inline

Returns the total size in bytes of the memory occupied by *this.

Definition at line 179 of file Partially_Reduced_Product_inlines.hh.

References Parma_Polyhedra_Library::external_memory_in_bytes().

                                                                   {
   return sizeof(*this) + external_memory_in_bytes();
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::unconstrain ( Variable var )

inline

Computes the cylindrification of *this with respect to space dimension var, assigning the result to *this.

Parameters

var	The space dimension that will be unconstrained.

Exceptions

std::invalid_argument Thrown if var is not a space dimension of *this.

Definition at line 202 of file Partially_Reduced_Product_inlines.hh.

                                 {
   reduce();
   d1.unconstrain(var);
   d2.unconstrain(var);
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::unconstrain ( const Variables_Set & vars )

inline

Computes the cylindrification of *this with respect to the set of space dimensions vars, assigning the result to *this.

Parameters

vars	The set of space dimension that will be unconstrained.

Exceptions

std::invalid_argument Thrown if *this is dimension-incompatible with one of the Variable objects contained in vars.

Definition at line 210 of file Partially_Reduced_Product_inlines.hh.

                                                                            {
   reduce();
   d1.unconstrain(vars);
   d2.unconstrain(vars);
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::upper_bound_assign ( const Partially_Reduced_Product< D1, D2, R > & y )

inline

Assigns to *this an upper bound of *this and y computed on the corresponding components.

Exceptions

std::invalid_argument Thrown if *this and y are dimension-incompatible.

Definition at line 239 of file Partially_Reduced_Product_inlines.hh.

References Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d1, Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d2, and Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::reduce().

                                                        {
   reduce();
   y.reduce();
   d1.upper_bound_assign(y.d1);
   d2.upper_bound_assign(y.d2);
 }

template<typename D1 , typename D2 , typename R >

bool Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::upper_bound_assign_if_exact ( const Partially_Reduced_Product< D1, D2, R > & y )

inline

Assigns to *this an upper bound of *this and y computed on the corresponding components. If it is exact on each of the components of *this, true is returned, otherwise false is returned.

Exceptions

std::invalid_argument Thrown if *this and y are dimension-incompatible.

Definition at line 249 of file Partially_Reduced_Product_inlines.hh.

References Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d1, Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d2, Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::reduce(), and Parma_Polyhedra_Library::swap().

                                                                 {
   reduce();
   y.reduce();
   D1 d1_copy = d1;
   bool ub_exact = d1_copy.upper_bound_assign_if_exact(y.d1);
   if (!ub_exact) {
     return false;
   }
   ub_exact = d2.upper_bound_assign_if_exact(y.d2);
   if (!ub_exact) {
     return false;
   }
   using std::swap;
   swap(d1, d1_copy);
   return true;
 }

template<typename D1 , typename D2 , typename R >

void Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::widening_assign	(	const Partially_Reduced_Product< D1, D2, R > &	y,
		unsigned *	tp = `NULL`
	)

inline

Assigns to *this the result of computing the "widening" between *this and y.

This widening uses either the congruence or generator systems depending on which of the systems describing x and y are up to date and minimized.

Parameters

y	A product that must be contained in `*this`;
tp	An optional pointer to an unsigned variable storing the number of available tokens (to be used when applying the widening with tokens delay technique).

Exceptions

std::invalid_argument Thrown if *this and y are dimension-incompatible.

Definition at line 568 of file Partially_Reduced_Product_inlines.hh.

References Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d1, Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d2, and Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::reduce().

                                 {
   // FIXME(0.10.1): In general this is _NOT_ a widening since the reduction
   //        may mean that the sequence does not satisfy the ascending
   //        chain condition.
   //        However, for the direct, smash and constraints product
   //        it may be ok - but this still needs checking.
   reduce();
   y.reduce();
   d1.widening_assign(y.d1, tp);
   d2.widening_assign(y.d2, tp);
 }

Friends And Related Function Documentation

template<typename D1 , typename D2 , typename R >

bool operator!=	(	const Partially_Reduced_Product< D1, D2, R > &	x,
		const Partially_Reduced_Product< D1, D2, R > &	y
	)

Note that x and y may be dimension-incompatible: in those cases, the value true is returned.

template<typename D1 , typename D2 , typename R >

bool operator!=	(	const Partially_Reduced_Product< D1, D2, R > &	x,
		const Partially_Reduced_Product< D1, D2, R > &	y
	)

                                                           {
   return !(x == y);
 }

template<typename D1 , typename D2 , typename R >

std::ostream & operator<<	(	std::ostream &	s,
		const Partially_Reduced_Product< D1, D2, R > &	dp
	)

Writes a textual representation of dp on s.

template<typename D1 , typename D2 , typename R >

std::ostream & operator<<	(	std::ostream &	s,
		const Partially_Reduced_Product< D1, D2, R > &	dp
	)

References Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d1, and Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d2.

                                                                          {
   return s << "Domain 1:\n"
            << dp.d1
            << "Domain 2:\n"
            << dp.d2;
 }

template<typename D1 , typename D2 , typename R >

bool operator==	(	const Partially_Reduced_Product< D1, D2, R > &	x,
		const Partially_Reduced_Product< D1, D2, R > &	y
	)

Note that x and y may be dimension-incompatible: in those cases, the value false is returned.

template<typename D1 , typename D2 , typename R >

bool operator==	(	const Partially_Reduced_Product< D1, D2, R > &	x,
		const Partially_Reduced_Product< D1, D2, R > &	y
	)

References Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d1, Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d2, and Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::reduce().

                                                           {
   x.reduce();
   y.reduce();
   return x.d1 == y.d1 && x.d2 == y.d2;
 }

template<typename D1, typename D2, typename R>

bool operator==	(	const Partially_Reduced_Product< D1, D2, R > &	x,
		const Partially_Reduced_Product< D1, D2, R > &	y
	)

friend

template<typename D1, typename D2, typename R>

std::ostream& Parma_Polyhedra_Library::IO_Operators::operator<<	(	std::ostream &	s,
		const Partially_Reduced_Product< D1, D2, R > &	dp
	)

friend

template<typename D1 , typename D2 , typename R >

void swap	(	Partially_Reduced_Product< D1, D2, R > &	x,
		Partially_Reduced_Product< D1, D2, R > &	y
	)

template<typename D1 , typename D2 , typename R >

void swap	(	Partially_Reduced_Product< D1, D2, R > &	x,
		Partially_Reduced_Product< D1, D2, R > &	y
	)

References Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::m_swap().

                                               {
   x.m_swap(y);
 }

Member Data Documentation

template<typename D1, typename D2, typename R>

D1 Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d1

protected

The first component.

Definition at line 1629 of file Partially_Reduced_Product_defs.hh.

template<typename D1, typename D2, typename R>

D2 Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::d2

protected

The second component.

Definition at line 1632 of file Partially_Reduced_Product_defs.hh.

template<typename D1, typename D2, typename R>

bool Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::reduced

protected

Flag to record whether the components are reduced with respect to each other and the reduction class.

Definition at line 1648 of file Partially_Reduced_Product_defs.hh.

Referenced by Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::clear_reduced_flag(), Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::m_swap(), Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::operator=(), Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::Partially_Reduced_Product(), and Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::set_reduced_flag().

The documentation for this class was generated from the following files:

Public Member Functions

Static Public Member Functions

Protected Types

Protected Member Functions

Protected Attributes

Private Member Functions

Friends

Related Functions

Detailed Description

template<typename D1, typename D2, typename R> class Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation

Friends And Related Function Documentation

Member Data Documentation

template<typename D1, typename D2, typename R>
class Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >