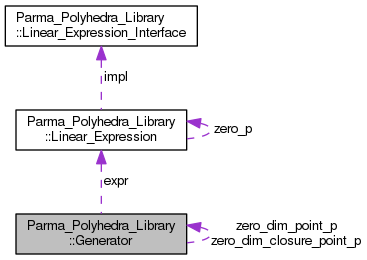
A line, ray, point or closure point. More...

#include <Generator_defs.hh>

Collaboration diagram for Parma_Polyhedra_Library::Generator:

Public Types
enum	Type { LINE, RAY, POINT, CLOSURE_POINT }
	The generator type. More...

typedef Expression_Hide_Last< Expression_Hide_Inhomo< Linear_Expression > >	expr_type
	The type of the (adapted) internal expression. More...

Public Member Functions
	Generator (Representation r=default_representation)
	Constructs the point at the origin. More...

	Generator (const Generator &g)

	Generator (const Generator &g, Representation r)
	Copy constructor with given representation. More...

	Generator (const Generator &g, dimension_type space_dim)

	Generator (const Generator &g, dimension_type space_dim, Representation r)
	Copy constructor with given representation and space dimension. More...

	~Generator ()
	Destructor. More...

Generator &	operator= (const Generator &g)
	Assignment operator. More...

Representation	representation () const
	Returns the current representation of *this. More...

void	set_representation (Representation r)
	Converts *this to the specified representation. More...

dimension_type	space_dimension () const
	Returns the dimension of the vector space enclosing `*this`. More...

void	set_space_dimension (dimension_type space_dim)

void	swap_space_dimensions (Variable v1, Variable v2)
	Swaps the coefficients of the variables `v1` and `v2` . More...

bool	remove_space_dimensions (const Variables_Set &vars)
	Removes all the specified dimensions from the generator. More...

void	permute_space_dimensions (const std::vector< Variable > &cycle)
	Permutes the space dimensions of the generator. More...

void	shift_space_dimensions (Variable v, dimension_type n)

Type	type () const
	Returns the generator type of `*this`. More...

bool	is_line () const
	Returns `true` if and only if `*this` is a line. More...

bool	is_ray () const
	Returns `true` if and only if `*this` is a ray. More...

bool	is_line_or_ray () const
	Returns `true` if and only if `*this` is a line or a ray. More...

bool	is_point () const
	Returns `true` if and only if `*this` is a point. More...

bool	is_closure_point () const
	Returns `true` if and only if `*this` is a closure point. More...

Coefficient_traits::const_reference	coefficient (Variable v) const
	Returns the coefficient of `v` in `*this`. More...

Coefficient_traits::const_reference	divisor () const
	If `*this` is either a point or a closure point, returns its divisor. More...

memory_size_type	total_memory_in_bytes () const
	Returns a lower bound to the total size in bytes of the memory occupied by `*this`. More...

memory_size_type	external_memory_in_bytes () const
	Returns the size in bytes of the memory managed by `*this`. More...

bool	is_equivalent_to (const Generator &y) const
	Returns `true` if and only if `*this` and `y` are equivalent generators. More...

bool	is_equal_to (const Generator &y) const
	Returns `true` if `*this` is identical to `y`. More...

bool	OK () const
	Checks if all the invariants are satisfied. More...

void	ascii_dump () const
	Writes to `std::cerr` an ASCII representation of `*this`. More...

void	ascii_dump (std::ostream &s) const
	Writes to `s` an ASCII representation of `*this`. More...

void	print () const
	Prints `*this` to `std::cerr` using `operator<<`. More...

bool	ascii_load (std::istream &s)
	Loads from `s` an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets `*this` accordingly. Returns `true` if successful, `false` otherwise. More...

void	m_swap (Generator &y)
	Swaps `*this` with `y`. More...

expr_type	expression () const
	Partial read access to the (adapted) internal expression. More...

Static Public Member Functions
static Generator	line (const Linear_Expression &e, Representation r=default_representation)
	Returns the line of direction `e`. More...

static Generator	ray (const Linear_Expression &e, Representation r=default_representation)
	Returns the ray of direction `e`. More...

static Generator	point (const Linear_Expression &e=Linear_Expression::zero(), Coefficient_traits::const_reference d=Coefficient_one(), Representation r=default_representation)
	Returns the point at `e` / `d`. More...

static Generator	point (Representation r)
	Returns the origin. More...

static Generator	point (const Linear_Expression &e, Representation r)
	Returns the point at `e`. More...

static Generator	closure_point (const Linear_Expression &e=Linear_Expression::zero(), Coefficient_traits::const_reference d=Coefficient_one(), Representation r=default_representation)
	Returns the closure point at `e` / `d`. More...

static Generator	closure_point (Representation r)
	Returns the closure point at the origin. More...

static Generator	closure_point (const Linear_Expression &e, Representation r)
	Returns the closure point at `e`. More...

static dimension_type	max_space_dimension ()
	Returns the maximum space dimension a Generator can handle. More...

static void	initialize ()
	Initializes the class. More...

static void	finalize ()
	Finalizes the class. More...

static const Generator &	zero_dim_point ()
	Returns the origin of the zero-dimensional space 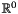$\Rset^0$ . More...

static const Generator &	zero_dim_closure_point ()
	Returns, as a closure point, the origin of the zero-dimensional space 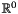$\Rset^0$ . More...

Static Public Attributes
static const Representation	default_representation = SPARSE
	The representation used for new Generators. More...

Private Types
enum	Kind { LINE_OR_EQUALITY = 0, RAY_OR_POINT_OR_INEQUALITY = 1 }
	The possible kinds of Generator objects. More...

Private Member Functions
	Generator (Linear_Expression &e, Type type, Topology topology)
	Builds a generator of type `type` and topology `topology`, stealing the coefficients from `e`. More...

	Generator (Linear_Expression &e, Kind kind, Topology topology)

	Generator (dimension_type space_dim, Kind kind, Topology topology, Representation r=default_representation)

bool	is_line_or_equality () const
	Returns `true` if and only if `*this` row represents a line or an equality. More...

bool	is_ray_or_point_or_inequality () const
	Returns `true` if and only if `*this` row represents a ray, a point or an inequality. More...

void	set_is_line_or_equality ()
	Sets to `LINE_OR_EQUALITY` the kind of `*this` row. More...

void	set_is_ray_or_point_or_inequality ()
	Sets to `RAY_OR_POINT_OR_INEQUALITY` the kind of `*this` row. More...

void	mark_as_necessarily_closed ()
	Marks the epsilon dimension as a standard dimension. More...

void	mark_as_not_necessarily_closed ()
	Marks the last dimension as the epsilon dimension. More...

void	linear_combine (const Generator &y, dimension_type i)
	Linearly combines `*this` with `y` so that i-th coefficient is 0. More...

void	set_space_dimension_no_ok (dimension_type space_dim)

void	throw_dimension_incompatible (const char method, const char v_name, Variable v) const
	Throw a `std::invalid_argument` exception containing the appropriate error message. More...

void	throw_invalid_argument (const char method, const char reason) const
	Throw a `std::invalid_argument` exception containing the appropriate error message. More...

bool	is_ray_or_point () const
	Returns `true` if and only if `*this` is not a line. More...

void	set_is_line ()
	Sets the Generator kind to `LINE_OR_EQUALITY`. More...

void	set_is_ray_or_point ()
	Sets the Generator kind to `RAY_OR_POINT_OR_INEQUALITY`. More...

bool	is_matching_closure_point (const Generator &p) const
	Returns `true` if and only if the closure point `this` has the same coordinates* of the point `p`. More...

Coefficient_traits::const_reference	epsilon_coefficient () const
	Returns the epsilon coefficient. The generator must be NNC. More...

void	set_epsilon_coefficient (Coefficient_traits::const_reference n)
	Sets the epsilon coefficient to `n`. The generator must be NNC. More...

void	sign_normalize ()
	Normalizes the sign of the coefficients so that the first non-zero (homogeneous) coefficient of a line-or-equality is positive. More...

void	strong_normalize ()
	Strong normalization: ensures that different Generator objects represent different hyperplanes or hyperspaces. More...

bool	check_strong_normalized () const
	Returns `true` if and only if the coefficients are strongly normalized. More...

void	fancy_print (std::ostream &s) const
	A print function, with fancy, more human-friendly output. More...

Flags inspection methods
Topology	topology () const
	Returns the topological kind of `*this`. More...

bool	is_not_necessarily_closed () const
	Returns `true` if and only if the topology of `*this` row is not necessarily closed. More...

bool	is_necessarily_closed () const
	Returns `true` if and only if the topology of `*this` row is necessarily closed. More...

Flags coercion methods
void	set_topology (Topology x)
	Sets to `x` the topological kind of `*this` row. More...

void	set_necessarily_closed ()
	Sets to `NECESSARILY_CLOSED` the topological kind of `*this` row. More...

void	set_not_necessarily_closed ()
	Sets to `NOT_NECESSARILY_CLOSED` the topological kind of `*this` row. More...

Private Attributes
Linear_Expression	expr
	The linear expression encoding `*this`. More...

Kind	kind_
	The kind of `*this`. More...

Topology	topology_
	The topology of `*this`. More...

Static Private Attributes
static const Generator *	zero_dim_point_p = 0
	Holds (between class initialization and finalization) a pointer to the origin of the zero-dimensional space 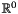$\Rset^0$ . More...

static const Generator *	zero_dim_closure_point_p = 0
	Holds (between class initialization and finalization) a pointer to the origin of the zero-dimensional space 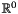$\Rset^0$ , as a closure point. More...

Friends
class	Expression_Adapter< Generator >

class	Linear_System< Generator >

class	Parma_Polyhedra_Library::Scalar_Products

class	Parma_Polyhedra_Library::Topology_Adjusted_Scalar_Product_Sign

class	Parma_Polyhedra_Library::Topology_Adjusted_Scalar_Product_Assign

class	Parma_Polyhedra_Library::Generator_System

class	Parma_Polyhedra_Library::Generator_System_const_iterator

class	Parma_Polyhedra_Library::Polyhedron

class	Parma_Polyhedra_Library::Grid_Generator_System

class	Parma_Polyhedra_Library::MIP_Problem

class	Parma_Polyhedra_Library::Grid

std::ostream &	Parma_Polyhedra_Library::IO_Operators::operator<< (std::ostream &s, const Generator &g)

int	compare (const Generator &x, const Generator &y)

Related Functions
(Note that these are not member functions.)
int	compare (const Generator &x, const Generator &y)

std::ostream &	operator<< (std::ostream &s, const Generator &g)

std::ostream &	operator<< (std::ostream &s, const Generator::Type &t)

int	compare (const Generator &x, const Generator &y)
	The basic comparison function. More...

std::ostream &	operator<< (std::ostream &s, const Generator &g)
	Output operator. More...

void	swap (Generator &x, Generator &y)
	Swaps `x` with `y`. More...

Generator	line (const Linear_Expression &e, Representation r=Generator::default_representation)
	Shorthand for Generator::line(const Linear_Expression& e, Representation r). More...

Generator	ray (const Linear_Expression &e, Representation r=Generator::default_representation)
	Shorthand for Generator::ray(const Linear_Expression& e, Representation r). More...

Generator	point (const Linear_Expression &e=Linear_Expression::zero(), Coefficient_traits::const_reference d=Coefficient_one(), Representation r=Generator::default_representation)
	Shorthand for Generator::point(const Linear_Expression& e, Coefficient_traits::const_reference d, Representation r). More...

Generator	point (Representation r)
	Shorthand for Generator::point(Representation r). More...

Generator	point (const Linear_Expression &e, Representation r)
	Shorthand for Generator::point(const Linear_Expression& e, Representation r). More...

Generator	closure_point (const Linear_Expression &e=Linear_Expression::zero(), Coefficient_traits::const_reference d=Coefficient_one(), Representation r=Generator::default_representation)
	Shorthand for Generator::closure_point(const Linear_Expression& e, Coefficient_traits::const_reference d, Representation r). More...

Generator	closure_point (Representation r)
	Shorthand for Generator::closure_point(Representation r). More...

Generator	closure_point (const Linear_Expression &e, Representation r)
	Shorthand for Generator::closure_point(const Linear_Expression& e, Representation r). More...

bool	operator== (const Generator &x, const Generator &y)
	Returns `true` if and only if `x` is equivalent to `y`. More...

bool	operator!= (const Generator &x, const Generator &y)
	Returns `true` if and only if `x` is not equivalent to `y`. More...

template<typename To >
bool	rectilinear_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, Rounding_Dir dir)
	Computes the rectilinear (or Manhattan) distance between `x` and `y`. More...

template<typename Temp , typename To >
bool	rectilinear_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, Rounding_Dir dir)
	Computes the rectilinear (or Manhattan) distance between `x` and `y`. More...

template<typename Temp , typename To >
bool	rectilinear_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, Rounding_Dir dir, Temp &tmp0, Temp &tmp1, Temp &tmp2)
	Computes the rectilinear (or Manhattan) distance between `x` and `y`. More...

template<typename To >
bool	euclidean_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, Rounding_Dir dir)
	Computes the euclidean distance between `x` and `y`. More...

template<typename Temp , typename To >
bool	rectilinear_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, Rounding_Dir dir)
	Computes the euclidean distance between `x` and `y`. More...

template<typename Temp , typename To >
bool	euclidean_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, Rounding_Dir dir, Temp &tmp0, Temp &tmp1, Temp &tmp2)
	Computes the euclidean distance between `x` and `y`. More...

template<typename To >
bool	l_infinity_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, Rounding_Dir dir)
	Computes the $L_\infty$ distance between `x` and `y`. More...

template<typename Temp , typename To >
bool	l_infinity_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, Rounding_Dir dir)
	Computes the $L_\infty$ distance between `x` and `y`. More...

template<typename Temp , typename To >
bool	l_infinity_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, Rounding_Dir dir, Temp &tmp0, Temp &tmp1, Temp &tmp2)
	Computes the $L_\infty$ distance between `x` and `y`. More...

std::ostream &	operator<< (std::ostream &s, const Generator::Type &t)
	Output operator. More...

Generator	line (const Linear_Expression &e, Representation r)

Generator	ray (const Linear_Expression &e, Representation r)

Generator	point (const Linear_Expression &e, Coefficient_traits::const_reference d, Representation r)

Generator	point (Representation r)

Generator	point (const Linear_Expression &e, Representation r)

Generator	closure_point (const Linear_Expression &e, Coefficient_traits::const_reference d, Representation r)

Generator	closure_point (Representation r)

Generator	closure_point (const Linear_Expression &e, Representation r)

bool	operator== (const Generator &x, const Generator &y)

bool	operator!= (const Generator &x, const Generator &y)

template<typename Specialization , typename Temp , typename To >
bool	l_m_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, const Rounding_Dir dir, Temp &tmp0, Temp &tmp1, Temp &tmp2)

template<typename Temp , typename To >
bool	rectilinear_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, const Rounding_Dir dir, Temp &tmp0, Temp &tmp1, Temp &tmp2)

template<typename Temp , typename To >
bool	rectilinear_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, const Rounding_Dir dir)

template<typename To >
bool	rectilinear_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, const Rounding_Dir dir)

template<typename Temp , typename To >
bool	euclidean_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, const Rounding_Dir dir, Temp &tmp0, Temp &tmp1, Temp &tmp2)

template<typename Temp , typename To >
bool	euclidean_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, const Rounding_Dir dir)

template<typename To >
bool	euclidean_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, const Rounding_Dir dir)

template<typename Temp , typename To >
bool	l_infinity_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, const Rounding_Dir dir, Temp &tmp0, Temp &tmp1, Temp &tmp2)

template<typename Temp , typename To >
bool	l_infinity_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, const Rounding_Dir dir)

template<typename To >
bool	l_infinity_distance_assign (Checked_Number< To, Extended_Number_Policy > &r, const Generator &x, const Generator &y, const Rounding_Dir dir)

void	swap (Generator &x, Generator &y)

Detailed Description

A line, ray, point or closure point.

An object of the class Generator is one of the following:

a line $\vect{l} = (a_0, \ldots, a_{n-1})^\transpose$ ;
a ray $\vect{r} = (a_0, \ldots, a_{n-1})^\transpose$ ;
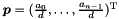a point $\vect{p} = (\frac{a_0}{d}, \ldots, \frac{a_{n-1}}{d})^\transpose$ ;
a closure point $\vect{c} = (\frac{a_0}{d}, \ldots, \frac{a_{n-1}}{d})^\transpose$ ;

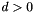where $n$ is the dimension of the space and, for points and closure points, $d > 0$ is the divisor.

A note on terminology.: As observed in Section Representations of Convex Polyhedra, there are cases when, in order to represent a polyhedron 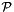$\cP$ using the generator system 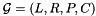$\cG = (L, R, P, C)$ , we need to include in the finite set 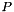even points of 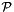$\cP$ that are not vertices of 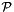$\cP$ . This situation is even more frequent when working with NNC polyhedra and it is the reason why we prefer to use the word `point' where other libraries use the word `vertex'.

How to build a generator.: Each type of generator is built by applying the corresponding function (line, ray, point or closure_point) to a linear expression, representing a direction in the space; the space dimension of the generator is defined as the space dimension of the corresponding linear expression. Linear expressions used to define a generator should be homogeneous (any constant term will be simply ignored). When defining points and closure points, an optional Coefficient argument can be used as a common divisor for all the coefficients occurring in the provided linear expression; the default value for this argument is 1.

: In all the following examples it is assumed that variables x, y and z are defined as follows:
Variable x(0);

Variable y(1);

Variable z(2);

Example 1: The following code builds a line with direction 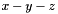and having space dimension :
Generator l = line(x - y - z);

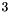As mentioned above, the constant term of the linear expression is not relevant. Thus, the following code has the same effect:
Generator l = line(x - y - z + 15);

By definition, the origin of the space is not a line, so that the following code throws an exception:
Generator l = line(0*x);

Example 2: The following code builds a ray with the same direction as the line in Example 1:
Generator r = ray(x - y - z);

As is the case for lines, when specifying a ray the constant term of the linear expression is not relevant; also, an exception is thrown when trying to build a ray from the origin of the space.

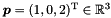Example 3: The following code builds the point $\vect{p} = (1, 0, 2)^\transpose \in \Rset^3$ :
Generator p = point(1*x + 0*y + 2*z);

The same effect can be obtained by using the following code:
Generator p = point(x + 2*z);

Similarly, the origin $\vect{0} \in \Rset^3$ can be defined using either one of the following lines of code:
Generator origin3 = point(0*x + 0*y + 0*z);

Generator origin3_alt = point(0*z);

Note however that the following code would have defined a different point, namely $\vect{0} \in \Rset^2$ :
Generator origin2 = point(0*y);

The following two lines of code both define the only point having space dimension zero, namely $\vect{0} \in \Rset^0$ . In the second case we exploit the fact that the first argument of the function point is optional.
Generator origin0 = Generator::zero_dim_point();

Generator origin0_alt = point();

Example 4: The point 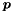$\vect{p}$ specified in Example 3 above can also be obtained with the following code, where we provide a non-default value for the second argument of the function point (the divisor):
Generator p = point(2*x + 0*y + 4*z, 2);

Obviously, the divisor can be usefully exploited to specify points having some non-integer (but rational) coordinates. For instance, the point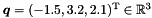 $\vect{q} = (-1.5, 3.2, 2.1)^\transpose \in \Rset^3$ can be specified by the following code:
Generator q = point(-15*x + 32*y + 21*z, 10);

If a zero divisor is provided, an exception is thrown.

Example 5: Closure points are specified in the same way we defined points, but invoking their specific constructor function. For instance, the closure point 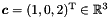$\vect{c} = (1, 0, 2)^\transpose \in \Rset^3$ is defined by
Generator c = closure_point(1*x + 0*y + 2*z);

For the particular case of the (only) closure point having space dimension zero, we can use any of the following:
Generator closure_origin0 = Generator::zero_dim_closure_point();

Generator closure_origin0_alt = closure_point();

How to inspect a generator: Several methods are provided to examine a generator and extract all the encoded information: its space dimension, its type and the value of its integer coefficients.

Example 6: The following code shows how it is possible to access each single coefficient of a generator. If g1 is a point having coordinates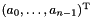 $(a_0, \ldots, a_{n-1})^\transpose$ , we construct the closure point g2 having coordinates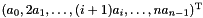 $(a_0, 2 a_1, \ldots, (i+1)a_i, \ldots, n a_{n-1})^\transpose$ .
if (g1.is_point()) {

cout << "Point g1: " << g1 << endl;

Linear_Expression e;

for (dimension_type i = g1.space_dimension(); i-- > 0; )

e += (i + 1) * g1.coefficient(Variable(i)) * Variable(i);

Generator g2 = closure_point(e, g1.divisor());

cout << "Closure point g2: " << g2 << endl;

}

else

cout << "Generator g1 is not a point." << endl;

Therefore, for the point
Generator g1 = point(2*x - y + 3*z, 2);

we would obtain the following output:
Point g1: p((2*A - B + 3*C)/2)

Closure point g2: cp((2*A - 2*B + 9*C)/2)

When working with (closure) points, be careful not to confuse the notion of coefficient with the notion of coordinate: these are equivalent only when the divisor of the (closure) point is 1.

Definition at line 285 of file Generator_defs.hh.

Member Typedef Documentation

typedef Expression_Hide_Last<Expression_Hide_Inhomo<Linear_Expression> > Parma_Polyhedra_Library::Generator::expr_type

The type of the (adapted) internal expression.

Definition at line 531 of file Generator_defs.hh.

Constructor & Destructor Documentation

Parma_Polyhedra_Library::Generator::Generator ( Representation r = default_representation )

inlineexplicit

Constructs the point at the origin.

Definition at line 113 of file Generator_inlines.hh.

References Parma_Polyhedra_Library::Coefficient_one(), expr, OK(), Parma_Polyhedra_Library::Linear_Expression::set_inhomogeneous_term(), and space_dimension().

   : expr(r),
     kind_(RAY_OR_POINT_OR_INEQUALITY),
     topology_(NECESSARILY_CLOSED) {
   expr.set_inhomogeneous_term(Coefficient_one());
   PPL_ASSERT(space_dimension() == 0);
   PPL_ASSERT(OK());
 }

Parma_Polyhedra_Library::Generator::Generator ( const Generator & g )

inline

Ordinary copy constructor. The representation of the new Generator will be the same as g.

Definition at line 167 of file Generator_inlines.hh.

   : expr(g.expr),
     kind_(g.kind_),
     topology_(g.topology_) {
 }

Parma_Polyhedra_Library::Generator::Generator	(	const Generator &	g,
		Representation	r
	)

inline

Copy constructor with given representation.

Definition at line 174 of file Generator_inlines.hh.

References OK().

   : expr(g.expr, r),
     kind_(g.kind_),
     topology_(g.topology_) {
   // This does not assert OK() because it's called by OK().
   PPL_ASSERT(OK());
 }

Parma_Polyhedra_Library::Generator::Generator	(	const Generator &	g,
		dimension_type	space_dim
	)

inline

Copy constructor with given space dimension. The representation of the new Generator will be the same as g.

Definition at line 183 of file Generator_inlines.hh.

References OK(), and space_dimension().

   : expr(g.expr, g.is_necessarily_closed() ? space_dim : (space_dim + 1)),
     kind_(g.kind_),
     topology_(g.topology_) {
   PPL_ASSERT(OK());
   PPL_ASSERT(space_dimension() == space_dim);
 }

Parma_Polyhedra_Library::Generator::Generator	(	const Generator &	g,
		dimension_type	space_dim,
		Representation	r
	)

inline

Copy constructor with given representation and space dimension.

Definition at line 192 of file Generator_inlines.hh.

References OK(), and space_dimension().

   : expr(g.expr, g.is_necessarily_closed() ? space_dim : (space_dim + 1), r),
     kind_(g.kind_),
     topology_(g.topology_) {
   PPL_ASSERT(OK());
   PPL_ASSERT(space_dimension() == space_dim);
 }

Parma_Polyhedra_Library::Generator::~Generator ( )

inline

Destructor.

Definition at line 202 of file Generator_inlines.hh.

202 {

203 }

Parma_Polyhedra_Library::Generator::Generator	(	Linear_Expression &	e,
		Type	type,
		Topology	topology
	)

inlineprivate

Builds a generator of type type and topology topology, stealing the coefficients from e.

If the topology is NNC, the last dimension of e is used as the epsilon coefficient.

Definition at line 139 of file Generator_inlines.hh.

References CLOSURE_POINT, expr, kind_, LINE, LINE_OR_EQUALITY, Parma_Polyhedra_Library::NOT_NECESSARILY_CLOSED, RAY_OR_POINT_OR_INEQUALITY, Parma_Polyhedra_Library::Linear_Expression::set_space_dimension(), Parma_Polyhedra_Library::Linear_Expression::space_dimension(), strong_normalize(), and swap().

   : topology_(topology) {
   PPL_ASSERT(type != CLOSURE_POINT || topology == NOT_NECESSARILY_CLOSED);
   swap(expr, e);
   if (topology == NOT_NECESSARILY_CLOSED) {
     expr.set_space_dimension(expr.space_dimension() + 1);
   }
   if (type == LINE) {
     kind_ = LINE_OR_EQUALITY;
   }
   else {
     kind_ = RAY_OR_POINT_OR_INEQUALITY;
   }
   strong_normalize();
 }

Parma_Polyhedra_Library::Generator::Generator	(	Linear_Expression &	e,
		Kind	kind,
		Topology	topology
	)

inlineprivate

Definition at line 156 of file Generator_inlines.hh.

References expr, Parma_Polyhedra_Library::NOT_NECESSARILY_CLOSED, Parma_Polyhedra_Library::Linear_Expression::set_space_dimension(), Parma_Polyhedra_Library::Linear_Expression::space_dimension(), strong_normalize(), and swap().

   : kind_(kind),
     topology_(topology) {
   swap(expr, e);
   if (topology == NOT_NECESSARILY_CLOSED) {
     expr.set_space_dimension(expr.space_dimension() + 1);
   }
   strong_normalize();
 }

Parma_Polyhedra_Library::Generator::Generator	(	dimension_type	space_dim,
		Kind	kind,
		Topology	topology,
		Representation	r = `default_representation`
	)

inlineprivate

Definition at line 123 of file Generator_inlines.hh.

References expr, is_necessarily_closed(), OK(), Parma_Polyhedra_Library::Linear_Expression::set_space_dimension(), and space_dimension().

   : expr(r),
     kind_(kind),
     topology_(topology) {
   if (is_necessarily_closed()) {
     expr.set_space_dimension(space_dim);
   }
   else {
     expr.set_space_dimension(space_dim + 1);
   }
   PPL_ASSERT(space_dimension() == space_dim);
   PPL_ASSERT(OK());
 }

Member Function Documentation

void Parma_Polyhedra_Library::Generator::ascii_dump ( ) const

Writes to std::cerr an ASCII representation of *this.

void Parma_Polyhedra_Library::Generator::ascii_dump ( std::ostream & s ) const

inline

Writes to s an ASCII representation of *this.

Definition at line 449 of file Generator_inlines.hh.

References Parma_Polyhedra_Library::Linear_Expression::ascii_dump(), CLOSURE_POINT, expr, is_necessarily_closed(), LINE, POINT, RAY, and type().

                                          {
 
   expr.ascii_dump(s);
 
   s << " ";
 
   switch (type()) {
   case Generator::LINE:
     s << "L ";
     break;
   case Generator::RAY:
     s << "R ";
     break;
   case Generator::POINT:
     s << "P ";
     break;
   case Generator::CLOSURE_POINT:
     s << "C ";
     break;
   }
   if (is_necessarily_closed()) {
     s << "(C)";
   }
   else {
     s << "(NNC)";
   }
   s << "\n";
 }

bool Parma_Polyhedra_Library::Generator::ascii_load ( std::istream & s )

inline

Loads from s an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets *this accordingly. Returns true if successful, false otherwise.

Definition at line 479 of file Generator_inlines.hh.

References Parma_Polyhedra_Library::Linear_Expression::ascii_load(), CLOSURE_POINT, expr, is_necessarily_closed(), is_not_necessarily_closed(), LINE, mark_as_necessarily_closed(), mark_as_not_necessarily_closed(), POINT, RAY, set_is_line(), set_is_ray_or_point(), and type().

                                    {
   std::string str;
 
   expr.ascii_load(s);
 
   if (!(s >> str)) {
     return false;
   }
   if (str == "L") {
     set_is_line();
   }
   else if (str == "R" || str == "P" || str == "C") {
     set_is_ray_or_point();
   }
   else {
     return false;
   }
 
   std::string str2;
 
   if (!(s >> str2)) {
     return false;
   }
   if (str2 == "(C)") {
     if (is_not_necessarily_closed()) {
       // TODO: Avoid using the mark_as_*() methods if possible.
       mark_as_necessarily_closed();
     }
   }
   else {
     if (str2 == "(NNC)") {
       if (is_necessarily_closed()) {
         // TODO: Avoid using the mark_as_*() methods if possible.
         mark_as_not_necessarily_closed();
       }
     }
     else {
       return false;
     }
   }
 
   // Checking for equality of actual and declared types.
   switch (type()) {
   case Generator::LINE:
     if (str != "L") {
       return false;
     }
     break;
   case Generator::RAY:
     if (str != "R") {
       return false;
     }
     break;
   case Generator::POINT:
     if (str != "P") {
       return false;
     }
     break;
   case Generator::CLOSURE_POINT:
     if (str != "C") {
       return false;
     }
     break;
   }
 
   return true;
 }

bool Parma_Polyhedra_Library::Generator::check_strong_normalized ( ) const

private

Returns true if and only if the coefficients are strongly normalized.

Definition at line 271 of file Generator.cc.

References Parma_Polyhedra_Library::compare(), and strong_normalize().

                                             {
   Generator tmp = *this;
   tmp.strong_normalize();
   return compare(*this, tmp) == 0;
 }

PPL::Generator Parma_Polyhedra_Library::Generator::closure_point	(	const Linear_Expression &	e = `Linear_Expression::zero()`,
		Coefficient_traits::const_reference	d = `Coefficient_one()`,
		Representation	r = `default_representation`
	)

static

Returns the closure point at e / d.

Both e and d are optional arguments, with default values Linear_Expression::zero() and Coefficient_one(), respectively.

Exceptions

std::invalid_argument Thrown if d is zero.

Definition at line 92 of file Generator.cc.

References expr, Parma_Polyhedra_Library::neg_assign(), Parma_Polyhedra_Library::Linear_Expression::normalize(), Parma_Polyhedra_Library::NOT_NECESSARILY_CLOSED, POINT, and Parma_Polyhedra_Library::Linear_Expression::set_inhomogeneous_term().

Referenced by closure_point().

                                                 {
   if (d == 0) {
     throw std::invalid_argument("PPL::closure_point(e, d):\n"
                                 "d == 0.");
   }
   Linear_Expression ec(e, r);
   ec.set_inhomogeneous_term(d);
 
   Generator g(ec, Generator::POINT, NOT_NECESSARILY_CLOSED);
 
   // If the divisor is negative, we negate it as well as
   // all the coefficients of the point, because we want to preserve
   // the invariant: the divisor of a point is strictly positive.
   if (d < 0) {
     neg_assign(g.expr);
   }
 
   // Enforce normalization.
   g.expr.normalize();
   return g;
 }

PPL::Generator Parma_Polyhedra_Library::Generator::closure_point ( Representation r )

static

Returns the closure point at the origin.

Definition at line 123 of file Generator.cc.

References Parma_Polyhedra_Library::Coefficient_one(), and Parma_Polyhedra_Library::Linear_Expression::zero().

                                             {
   return closure_point(Linear_Expression::zero(), Coefficient_one(), r);
 }

PPL::Generator Parma_Polyhedra_Library::Generator::closure_point	(	const Linear_Expression &	e,
		Representation	r
	)

static

Returns the closure point at e.

Definition at line 117 of file Generator.cc.

References Parma_Polyhedra_Library::Coefficient_one().

                                                 {
   return closure_point(e, Coefficient_one(), r);
 }

Coefficient_traits::const_reference Parma_Polyhedra_Library::Generator::coefficient ( Variable v ) const

inline

Returns the coefficient of v in *this.

Exceptions

std::invalid_argument Thrown if the index of v is greater than or equal to the space dimension of *this.

Definition at line 325 of file Generator_inlines.hh.

References Parma_Polyhedra_Library::Linear_Expression::coefficient(), expr, Parma_Polyhedra_Library::Variable::space_dimension(), space_dimension(), and throw_dimension_incompatible().

                                              {
   if (v.space_dimension() > space_dimension()) {
     throw_dimension_incompatible("coefficient(v)", "v", v);
   }
   return expr.coefficient(v);
 }

Coefficient_traits::const_reference Parma_Polyhedra_Library::Generator::divisor ( ) const

inline

If *this is either a point or a closure point, returns its divisor.

Exceptions

std::invalid_argument Thrown if *this is neither a point nor a closure point.

Definition at line 333 of file Generator_inlines.hh.

References expr, Parma_Polyhedra_Library::Linear_Expression::inhomogeneous_term(), is_ray_or_point(), and throw_invalid_argument().

                          {
   Coefficient_traits::const_reference d = expr.inhomogeneous_term();
   if (!is_ray_or_point() || d == 0) {
     throw_invalid_argument("divisor()",
                            "*this is neither a point nor a closure point");
   }
   return d;
 }

Coefficient_traits::const_reference Parma_Polyhedra_Library::Generator::epsilon_coefficient ( ) const

inlineprivate

Returns the epsilon coefficient. The generator must be NNC.

Definition at line 343 of file Generator_inlines.hh.

References Parma_Polyhedra_Library::Linear_Expression::coefficient(), expr, is_not_necessarily_closed(), and Parma_Polyhedra_Library::Linear_Expression::space_dimension().

Referenced by Parma_Polyhedra_Library::Generator_System::add_corresponding_closure_points(), Parma_Polyhedra_Library::Generator_System::add_corresponding_points(), Parma_Polyhedra_Library::Polyhedron::positive_time_elapse_assign_impl(), Parma_Polyhedra_Library::Polyhedron::strongly_minimize_generators(), and type().

                                      {
   PPL_ASSERT(is_not_necessarily_closed());
   return expr.coefficient(Variable(expr.space_dimension() - 1));
 }

Generator::expr_type Parma_Polyhedra_Library::Generator::expression ( ) const

inline

Partial read access to the (adapted) internal expression.

Definition at line 40 of file Generator_inlines.hh.

References expr, and is_not_necessarily_closed().

                             {
   return expr_type(expr, is_not_necessarily_closed());
 }

memory_size_type Parma_Polyhedra_Library::Generator::external_memory_in_bytes ( ) const

inline

Returns the size in bytes of the memory managed by *this.

Definition at line 357 of file Generator_inlines.hh.

References expr, and Parma_Polyhedra_Library::Linear_Expression::external_memory_in_bytes().

Referenced by Parma_Polyhedra_Library::MIP_Problem::external_memory_in_bytes(), and total_memory_in_bytes().

                                           {
   return expr.external_memory_in_bytes();
 }

void Parma_Polyhedra_Library::Generator::fancy_print ( std::ostream & s ) const

private

A print function, with fancy, more human-friendly output.

This is used by operator<<().

Definition at line 303 of file Generator.cc.

References c, CLOSURE_POINT, LINE, Parma_Polyhedra_Library::neg_assign(), Parma_Polyhedra_Library::IO_Operators::operator<<(), POINT, PPL_DIRTY_TEMP_COEFFICIENT, and RAY.

Referenced by operator<<().

                                              {
     bool needed_divisor = false;
   bool extra_parentheses = false;
   const dimension_type num_variables = space_dimension();
   const Generator::Type t = type();
   switch (t) {
   case Generator::LINE:
     s << "l(";
     break;
   case Generator::RAY:
     s << "r(";
     break;
   case Generator::POINT:
     s << "p(";
     goto any_point;
   case Generator::CLOSURE_POINT:
     s << "c(";
   any_point:
     if (expr.inhomogeneous_term() != 1) {
       needed_divisor = true;
       if (!expr.all_zeroes(1, num_variables + 1)) {
         extra_parentheses = true;
         s << "(";
       }
     }
     break;
   }
 
   PPL_DIRTY_TEMP_COEFFICIENT(c);
   bool first = true;
   for (Linear_Expression::const_iterator i = expr.begin(),
           i_end = expr.lower_bound(Variable(num_variables)); i != i_end; ++i) {
     c = *i;
     if (!first) {
       if (c > 0) {
         s << " + ";
       }
       else {
         s << " - ";
         neg_assign(c);
       }
     }
     else {
       first = false;
     }
     if (c == -1) {
       s << "-";
     }
     else if (c != 1) {
       s << c << "*";
     }
     IO_Operators::operator<<(s, i.variable());
   }
   if (first) {
     // A point or closure point in the origin.
     s << 0;
   }
   if (extra_parentheses) {
     s << ")";
   }
   if (needed_divisor) {
     s << "/" << expr.inhomogeneous_term();
   }
   s << ")";
 }

void Parma_Polyhedra_Library::Generator::finalize ( )

static

Finalizes the class.

Definition at line 292 of file Generator.cc.

Referenced by Parma_Polyhedra_Library::Init::~Init().

                        {
   PPL_ASSERT(zero_dim_point_p != 0);
   delete zero_dim_point_p;
   zero_dim_point_p = 0;
 
   PPL_ASSERT(zero_dim_closure_point_p != 0);
   delete zero_dim_closure_point_p;
   zero_dim_closure_point_p = 0;
 }

void Parma_Polyhedra_Library::Generator::initialize ( )

static

Initializes the class.

Definition at line 281 of file Generator.cc.

Referenced by Parma_Polyhedra_Library::Init::Init().

                          {
   PPL_ASSERT(zero_dim_point_p == 0);
   zero_dim_point_p
     = new Generator(point());
 
   PPL_ASSERT(zero_dim_closure_point_p == 0);
   zero_dim_closure_point_p
     = new Generator(closure_point());
 }

bool Parma_Polyhedra_Library::Generator::is_closure_point ( ) const

inline

Returns true if and only if *this is a closure point.

Definition at line 310 of file Generator_inlines.hh.

References CLOSURE_POINT, and type().

                                   {
   return type() == CLOSURE_POINT;
 }

bool Parma_Polyhedra_Library::Generator::is_equal_to ( const Generator & y ) const

Returns true if *this is identical to y.

This is faster than is_equivalent_to(), but it may return `false' even for equivalent generators.

Definition at line 258 of file Generator.cc.

References expr, kind_, and topology_.

                                                   {
   return expr.is_equal_to(y.expr) && kind_ == y.kind_
          && topology_ == y.topology_;
 }

bool Parma_Polyhedra_Library::Generator::is_equivalent_to ( const Generator & y ) const

Returns true if and only if *this and y are equivalent generators.

Generators having different space dimensions are not equivalent.

Definition at line 226 of file Generator.cc.

References expr, expression(), Parma_Polyhedra_Library::Linear_Expression::is_equal_to(), is_necessarily_closed(), Parma_Polyhedra_Library::Linear_Expression::normalize(), space_dimension(), and type().

Referenced by operator!=(), and operator==().

                                                        {
   const Generator& x = *this;
   const dimension_type x_space_dim = x.space_dimension();
   if (x_space_dim != y.space_dimension()) {
     return false;
   }
 
   const Type x_type = x.type();
   if (x_type != y.type()) {
     return false;
   }
 
   if (x_type == POINT
       && !(x.is_necessarily_closed() && y.is_necessarily_closed())) {
     // Due to the presence of epsilon-coefficients, syntactically
     // different points may actually encode the same generator.
     // First, drop the epsilon-coefficient ...
     Linear_Expression x_expr(x.expression());
     Linear_Expression y_expr(y.expression());
     // ... second, re-normalize ...
     x_expr.normalize();
     y_expr.normalize();
     // ... and finally check for syntactic equality.
     return x_expr.is_equal_to(y_expr);
   }
 
   // Here the epsilon-coefficient, if present, is zero.
   // It is sufficient to check for syntactic equality.
   return x.expr.is_equal_to(y.expr);
 }

bool Parma_Polyhedra_Library::Generator::is_line ( ) const

inline

Returns true if and only if *this is a line.

Definition at line 263 of file Generator_inlines.hh.

References is_line_or_equality().

                          {
   return is_line_or_equality();
 }

bool Parma_Polyhedra_Library::Generator::is_line_or_equality ( ) const

inlineprivate

Returns true if and only if *this row represents a line or an equality.

Definition at line 50 of file Generator_inlines.hh.

References kind_, and LINE_OR_EQUALITY.

Referenced by Parma_Polyhedra_Library::Polyhedron::BFT00_poly_hull_assign_if_exact(), compare(), and is_line().

                                      {
   return (kind_ == LINE_OR_EQUALITY);
 }

bool Parma_Polyhedra_Library::Generator::is_line_or_ray ( ) const

inline

Returns true if and only if *this is a line or a ray.

Definition at line 273 of file Generator_inlines.hh.

References expr, and Parma_Polyhedra_Library::Linear_Expression::inhomogeneous_term().

                                 {
   return expr.inhomogeneous_term() == 0;
 }

bool Parma_Polyhedra_Library::Generator::is_matching_closure_point ( const Generator & p ) const

private

Returns true if and only if the closure point *this has the same coordinates of the point p.

It is assumed that *this is a closure point, p is a point and both topologies and space dimensions agree.

Definition at line 399 of file Generator.cc.

References Parma_Polyhedra_Library::exact_div_assign(), expr, Parma_Polyhedra_Library::gcd_assign(), Parma_Polyhedra_Library::Linear_Expression::inhomogeneous_term(), Parma_Polyhedra_Library::Linear_Expression::is_equal_to(), PPL_DIRTY_TEMP_COEFFICIENT, space_dimension(), Parma_Polyhedra_Library::Linear_Expression::space_dimension(), topology(), and type().

Referenced by Parma_Polyhedra_Library::Polyhedron::is_topologically_closed(), and Parma_Polyhedra_Library::Generator_System_const_iterator::skip_forward().

                                                                 {
   PPL_ASSERT(topology() == p.topology()
          && space_dimension() == p.space_dimension()
          && type() == CLOSURE_POINT
          && p.type() == POINT);
   const Generator& cp = *this;
   if (cp.expr.inhomogeneous_term() == p.expr.inhomogeneous_term()) {
     // Divisors are equal: we can simply compare coefficients
     // (disregarding the epsilon coefficient).
     return cp.expr.is_equal_to(p.expr, 1, cp.expr.space_dimension());
   }
   else {
     // Divisors are different: divide them by their GCD
     // to simplify the following computation.
     PPL_DIRTY_TEMP_COEFFICIENT(gcd);
     gcd_assign(gcd, cp.expr.inhomogeneous_term(), p.expr.inhomogeneous_term());
     const bool rel_prime = (gcd == 1);
     PPL_DIRTY_TEMP_COEFFICIENT(cp_0_scaled);
     PPL_DIRTY_TEMP_COEFFICIENT(p_0_scaled);
     if (!rel_prime) {
       exact_div_assign(cp_0_scaled, cp.expr.inhomogeneous_term(), gcd);
       exact_div_assign(p_0_scaled, p.expr.inhomogeneous_term(), gcd);
     }
     const Coefficient& cp_div = rel_prime ? cp.expr.inhomogeneous_term() : cp_0_scaled;
     const Coefficient& p_div = rel_prime ? p.expr.inhomogeneous_term() : p_0_scaled;
     return cp.expr.is_equal_to(p.expr, p_div, cp_div, 1, cp.expr.space_dimension());
   }
 }

bool Parma_Polyhedra_Library::Generator::is_necessarily_closed ( ) const

inlineprivate

Returns true if and only if the topology of *this row is necessarily closed.

Definition at line 30 of file Generator_inlines.hh.

References Parma_Polyhedra_Library::NECESSARILY_CLOSED, and topology().

Referenced by Parma_Polyhedra_Library::Polyhedron::add_generator(), ascii_dump(), ascii_load(), Generator(), is_equivalent_to(), mark_as_not_necessarily_closed(), Parma_Polyhedra_Library::Topology_Adjusted_Scalar_Product_Sign::operator()(), and type().

                                        {
   return (topology() == NECESSARILY_CLOSED);
 }

bool Parma_Polyhedra_Library::Generator::is_not_necessarily_closed ( ) const

inlineprivate

Returns true if and only if the topology of *this row is not necessarily closed.

Definition at line 35 of file Generator_inlines.hh.

References Parma_Polyhedra_Library::NOT_NECESSARILY_CLOSED, and topology().

Referenced by ascii_load(), epsilon_coefficient(), expression(), mark_as_necessarily_closed(), and set_epsilon_coefficient().

                                            {
   return (topology() == NOT_NECESSARILY_CLOSED);
 }

bool Parma_Polyhedra_Library::Generator::is_point ( ) const

inline

Returns true if and only if *this is a point.

Definition at line 305 of file Generator_inlines.hh.

References POINT, and type().

                           {
   return type() == POINT;
 }

bool Parma_Polyhedra_Library::Generator::is_ray ( ) const

inline

Returns true if and only if *this is a ray.

Definition at line 278 of file Generator_inlines.hh.

References is_line_or_ray(), and is_ray_or_point().

Referenced by Parma_Polyhedra_Library::Polyhedron::BHRZ03_evolving_rays(), and Parma_Polyhedra_Library::Box< ITV >::relation_with().

                         {
   return is_ray_or_point() && is_line_or_ray();
 }

bool Parma_Polyhedra_Library::Generator::is_ray_or_point ( ) const

inlineprivate

Returns true if and only if *this is not a line.

Definition at line 268 of file Generator_inlines.hh.

References is_ray_or_point_or_inequality().

Referenced by divisor(), and is_ray().

                                  {
   return is_ray_or_point_or_inequality();
 }

bool Parma_Polyhedra_Library::Generator::is_ray_or_point_or_inequality ( ) const

inlineprivate

Returns true if and only if *this row represents a ray, a point or an inequality.

Definition at line 55 of file Generator_inlines.hh.

References kind_, and RAY_OR_POINT_OR_INEQUALITY.

Referenced by is_ray_or_point().

                                                {
   return (kind_ == RAY_OR_POINT_OR_INEQUALITY);
 }

PPL::Generator Parma_Polyhedra_Library::Generator::line	(	const Linear_Expression &	e,
		Representation	r = `default_representation`
	)

static

Returns the line of direction e.

Exceptions

std::invalid_argument Thrown if the homogeneous part of e represents the origin of the vector space.

Definition at line 143 of file Generator.cc.

References Parma_Polyhedra_Library::Linear_Expression::all_homogeneous_terms_are_zero(), LINE, Parma_Polyhedra_Library::NECESSARILY_CLOSED, and Parma_Polyhedra_Library::Linear_Expression::set_inhomogeneous_term().

Referenced by Parma_Polyhedra_Library::Polyhedron::add_generator(), line(), and Parma_Polyhedra_Library::Polyhedron::unconstrain().

                                                                {
   // The origin of the space cannot be a line.
   if (e.all_homogeneous_terms_are_zero()) {
     throw std::invalid_argument("PPL::line(e):\n"
                                 "e == 0, but the origin cannot be a line.");
   }
 
   Linear_Expression ec(e, r);
   ec.set_inhomogeneous_term(0);
   const Generator g(ec, Generator::LINE, NECESSARILY_CLOSED);
 
   return g;
 }

void Parma_Polyhedra_Library::Generator::linear_combine	(	const Generator &	y,
		dimension_type	i
	)

private

Linearly combines *this with y so that i-th coefficient is 0.

Parameters

y	The Generator that will be combined with `*this` object;
i	The index of the coefficient that has to become .

Computes a linear combination of *this and y having the i-th coefficient equal to $0$ . Then it assigns the resulting Generator to *this and normalizes it.

Definition at line 207 of file Generator.cc.

References expr.

Referenced by Parma_Polyhedra_Library::Polyhedron::BHRZ03_evolving_points().

                                                                  {
   expr.linear_combine(y.expr, i);
   strong_normalize();
 }

void Parma_Polyhedra_Library::Generator::m_swap ( Generator & y )

inline

Swaps *this with y.

Definition at line 548 of file Generator_inlines.hh.

References expr, kind_, swap(), Parma_Polyhedra_Library::swap(), and topology_.

Referenced by swap().

                               {
   using std::swap;
   swap(expr, y.expr);
   swap(kind_, y.kind_);
   swap(topology_, y.topology_);
 }

void Parma_Polyhedra_Library::Generator::mark_as_necessarily_closed ( )

inlineprivate

Marks the epsilon dimension as a standard dimension.

The row topology is changed to NECESSARILY_CLOSED, and the number of space dimensions is increased by 1.

Definition at line 91 of file Generator_inlines.hh.

References is_not_necessarily_closed(), Parma_Polyhedra_Library::NECESSARILY_CLOSED, and topology_.

Referenced by ascii_load().

                                       {
   PPL_ASSERT(is_not_necessarily_closed());
   topology_ = NECESSARILY_CLOSED;
 }

void Parma_Polyhedra_Library::Generator::mark_as_not_necessarily_closed ( )

inlineprivate

Marks the last dimension as the epsilon dimension.

The row topology is changed to NOT_NECESSARILY_CLOSED, and the number of space dimensions is decreased by 1.

Definition at line 97 of file Generator_inlines.hh.

References is_necessarily_closed(), Parma_Polyhedra_Library::NOT_NECESSARILY_CLOSED, and topology_.

Referenced by ascii_load().

                                           {
   PPL_ASSERT(is_necessarily_closed());
   topology_ = NOT_NECESSARILY_CLOSED;
 }

dimension_type Parma_Polyhedra_Library::Generator::max_space_dimension ( )

inlinestatic

Returns the maximum space dimension a Generator can handle.

Definition at line 224 of file Generator_inlines.hh.

References Parma_Polyhedra_Library::Linear_Expression::max_space_dimension().

                                {
   return Linear_Expression::max_space_dimension();
 }

bool Parma_Polyhedra_Library::Generator::OK ( ) const

Checks if all the invariants are satisfied.

Definition at line 432 of file Generator.cc.

References strong_normalize().

Referenced by Parma_Polyhedra_Library::Polyhedron::BFT00_poly_hull_assign_if_exact(), Parma_Polyhedra_Library::Polyhedron::BHRZ03_evolving_rays(), Parma_Polyhedra_Library::Polyhedron::generalized_affine_image(), Generator(), Parma_Polyhedra_Library::Polyhedron::positive_time_elapse_assign_impl(), set_space_dimension(), Parma_Polyhedra_Library::Polyhedron::strongly_minimize_generators(), and Parma_Polyhedra_Library::Polyhedron::time_elapse_assign().

                        {
   // Topology consistency checks.
   if (is_not_necessarily_closed() && expr.space_dimension() == 0) {
 #ifndef NDEBUG
     std::cerr << "Generator has fewer coefficients than the minimum "
               << "allowed by its topology."
               << std::endl;
 #endif
     return false;
   }
 
   // Normalization check.
   Generator tmp = *this;
   tmp.strong_normalize();
   if (tmp != *this) {
 #ifndef NDEBUG
     std::cerr << "Generators should be strongly normalized!"
               << std::endl;
 #endif
     return false;
   }
 
   switch (type()) {
   case LINE:
     // Intentionally fall through.
   case RAY:
     if (expr.inhomogeneous_term() != 0) {
 #ifndef NDEBUG
       std::cerr << "Lines must have a zero inhomogeneous term!"
                 << std::endl;
 #endif
       return false;
     }
     if (!is_necessarily_closed() && epsilon_coefficient() != 0) {
 #ifndef NDEBUG
       std::cerr << "Lines and rays must have a zero coefficient "
                 << "for the epsilon dimension!"
                 << std::endl;
 #endif
       return false;
     }
     // The following test is correct, since we already checked
     // that the epsilon coordinate is zero.
     if (expr.all_homogeneous_terms_are_zero()) {
 #ifndef NDEBUG
       std::cerr << "The origin of the vector space cannot be a line or a ray!"
                 << std::endl;
 #endif
       return false;
     }
     break;
 
   case POINT:
     if (expr.inhomogeneous_term() <= 0) {
 #ifndef NDEBUG
       std::cerr << "Points must have a positive divisor!"
                 << std::endl;
 #endif
       return false;
     }
     if (!is_necessarily_closed()) {
       if (epsilon_coefficient() <= 0) {
 #ifndef NDEBUG
         std::cerr << "In the NNC topology, points must have epsilon > 0"
                   << std::endl;
 #endif
         return false;
       }
     }
     break;
 
   case CLOSURE_POINT:
     if (expr.inhomogeneous_term() <= 0) {
 #ifndef NDEBUG
       std::cerr << "Closure points must have a positive divisor!"
                 << std::endl;
 #endif
       return false;
     }
     break;
   }
 
   // All tests passed.
   return true;
 }

Generator & Parma_Polyhedra_Library::Generator::operator= ( const Generator & g )

inline

Assignment operator.

Definition at line 206 of file Generator_inlines.hh.

References swap().

                                        {
   Generator tmp = g;
   swap(*this, tmp);
 
   return *this;
 }

void Parma_Polyhedra_Library::Generator::permute_space_dimensions ( const std::vector< Variable > & cycle )

Permutes the space dimensions of the generator.

Parameters

cycle A vector representing a cycle of the permutation according to which the space dimensions must be rearranged.

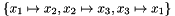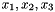The cycle vector represents a cycle of a permutation of space dimensions. For example, the permutation $\{ x_1 \mapsto x_2, x_2 \mapsto x_3, x_3 \mapsto x_1 \}$ can be represented by the vector containing $ x_1, x_2, x_3 $ .

Definition at line 192 of file Generator.cc.

                                                            {
   if (cycle.size() < 2) {
     // No-op. No need to call sign_normalize().
     return;
   }
 
   expr.permute_space_dimensions(cycle);
 
   // *this is still normalized but may be not strongly normalized: sign
   // normalization is necessary.
   sign_normalize();
   PPL_ASSERT(OK());
 }

PPL::Generator Parma_Polyhedra_Library::Generator::point	(	const Linear_Expression &	e = `Linear_Expression::zero()`,
		Coefficient_traits::const_reference	d = `Coefficient_one()`,
		Representation	r = `default_representation`
	)

static

Returns the point at e / d.

Both e and d are optional arguments, with default values Linear_Expression::zero() and Coefficient_one(), respectively.

Exceptions

std::invalid_argument Thrown if d is zero.

Definition at line 57 of file Generator.cc.

References expr, Parma_Polyhedra_Library::NECESSARILY_CLOSED, Parma_Polyhedra_Library::neg_assign(), Parma_Polyhedra_Library::Linear_Expression::normalize(), POINT, and Parma_Polyhedra_Library::Linear_Expression::set_inhomogeneous_term().

Referenced by Parma_Polyhedra_Library::Polyhedron::add_generator(), Parma_Polyhedra_Library::Box< ITV >::max_min(), Parma_Polyhedra_Library::Grid::max_min(), and point().

                                         {
   if (d == 0) {
     throw std::invalid_argument("PPL::point(e, d):\n"
                                 "d == 0.");
   }
   Linear_Expression ec(e, r);
   ec.set_inhomogeneous_term(d);
   Generator g(ec, Generator::POINT, NECESSARILY_CLOSED);
 
   // If the divisor is negative, we negate it as well as
   // all the coefficients of the point, because we want to preserve
   // the invariant: the divisor of a point is strictly positive.
   if (d < 0) {
     neg_assign(g.expr);
   }
 
   // Enforce normalization.
   g.expr.normalize();
   return g;
 }

PPL::Generator Parma_Polyhedra_Library::Generator::point ( Representation r )

static

Returns the origin.

Definition at line 87 of file Generator.cc.

References Parma_Polyhedra_Library::Coefficient_one(), and Parma_Polyhedra_Library::Linear_Expression::zero().

                                     {
   return point(Linear_Expression::zero(), Coefficient_one(), r);
 }

PPL::Generator Parma_Polyhedra_Library::Generator::point	(	const Linear_Expression &	e,
		Representation	r
	)

static

Returns the point at e.

Definition at line 81 of file Generator.cc.

References Parma_Polyhedra_Library::Coefficient_one().

                                         {
   return point(e, Coefficient_one(), r);
 }

void Parma_Polyhedra_Library::Generator::print ( ) const

Prints *this to std::cerr using operator<<.

PPL::Generator Parma_Polyhedra_Library::Generator::ray	(	const Linear_Expression &	e,
		Representation	r = `default_representation`
	)

static

Returns the ray of direction e.

Exceptions

std::invalid_argument Thrown if the homogeneous part of e represents the origin of the vector space.

Definition at line 128 of file Generator.cc.

References Parma_Polyhedra_Library::Linear_Expression::all_homogeneous_terms_are_zero(), Parma_Polyhedra_Library::NECESSARILY_CLOSED, RAY, and Parma_Polyhedra_Library::Linear_Expression::set_inhomogeneous_term().

Referenced by Parma_Polyhedra_Library::Polyhedron::add_generator(), and ray().

                                                               {
   // The origin of the space cannot be a ray.
   if (e.all_homogeneous_terms_are_zero()) {
     throw std::invalid_argument("PPL::ray(e):\n"
                                 "e == 0, but the origin cannot be a ray.");
   }
 
   Linear_Expression ec(e, r);
   ec.set_inhomogeneous_term(0);
   const Generator g(ec, Generator::RAY, NECESSARILY_CLOSED);
 
   return g;
 }

bool Parma_Polyhedra_Library::Generator::remove_space_dimensions ( const Variables_Set & vars )

Removes all the specified dimensions from the generator.

The space dimension of the variable with the highest space dimension in vars must be at most the space dimension of this.

If all dimensions with nonzero coefficients are removed from a ray or a line, it is changed into a point and this method returns false . Otherwise, it returns true .

Definition at line 168 of file Generator.cc.

References Parma_Polyhedra_Library::Variables_Set::space_dimension().

                                                                {
   PPL_ASSERT(vars.space_dimension() <= space_dimension());
   expr.remove_space_dimensions(vars);
 
   if (is_line_or_ray() && expr.all_homogeneous_terms_are_zero()) {
     // Become a point.
     set_is_ray_or_point();
     expr.set_inhomogeneous_term(1);
     if (is_not_necessarily_closed()) {
       set_epsilon_coefficient(1);
     }
 
     PPL_ASSERT(OK());
     return false;
   }
   else {
     strong_normalize();
     PPL_ASSERT(OK());
     return true;
   }
 }

Representation Parma_Polyhedra_Library::Generator::representation ( ) const

inline

Returns the current representation of *this.

Definition at line 214 of file Generator_inlines.hh.

References expr, and Parma_Polyhedra_Library::Linear_Expression::representation().

                                 {
   return expr.representation();
 }

void Parma_Polyhedra_Library::Generator::set_epsilon_coefficient ( Coefficient_traits::const_reference n )

inlineprivate

Sets the epsilon coefficient to n. The generator must be NNC.

Definition at line 350 of file Generator_inlines.hh.

References expr, is_not_necessarily_closed(), Parma_Polyhedra_Library::Linear_Expression::set_coefficient(), and Parma_Polyhedra_Library::Linear_Expression::space_dimension().

Referenced by Parma_Polyhedra_Library::Generator_System::add_corresponding_closure_points(), Parma_Polyhedra_Library::Generator_System::add_corresponding_points(), Parma_Polyhedra_Library::Generator_System::convert_into_non_necessarily_closed(), Parma_Polyhedra_Library::Polyhedron::generalized_affine_image(), Parma_Polyhedra_Library::Generator_System::insert(), Parma_Polyhedra_Library::Generator_System::insert_pending(), and Parma_Polyhedra_Library::Polyhedron::strongly_minimize_generators().

                                                                       {
   PPL_ASSERT(is_not_necessarily_closed());
   expr.set_coefficient(Variable(expr.space_dimension() - 1), n);
 }

void Parma_Polyhedra_Library::Generator::set_is_line ( )

inlineprivate

Sets the Generator kind to LINE_OR_EQUALITY.

Definition at line 315 of file Generator_inlines.hh.

References set_is_line_or_equality().

Referenced by ascii_load().

                        {
   set_is_line_or_equality();
 }

void Parma_Polyhedra_Library::Generator::set_is_line_or_equality ( )

inlineprivate

Sets to LINE_OR_EQUALITY the kind of *this row.

Definition at line 65 of file Generator_inlines.hh.

References kind_, and LINE_OR_EQUALITY.

Referenced by set_is_line().

                                    {
   kind_ = LINE_OR_EQUALITY;
 }

void Parma_Polyhedra_Library::Generator::set_is_ray_or_point ( )

inlineprivate

Sets the Generator kind to RAY_OR_POINT_OR_INEQUALITY.

Definition at line 320 of file Generator_inlines.hh.

References set_is_ray_or_point_or_inequality().

Referenced by ascii_load().

                                {
   set_is_ray_or_point_or_inequality();
 }

void Parma_Polyhedra_Library::Generator::set_is_ray_or_point_or_inequality ( )

inlineprivate

Sets to RAY_OR_POINT_OR_INEQUALITY the kind of *this row.

Definition at line 70 of file Generator_inlines.hh.

References kind_, and RAY_OR_POINT_OR_INEQUALITY.

Referenced by Parma_Polyhedra_Library::Polyhedron::BFT00_poly_hull_assign_if_exact(), and set_is_ray_or_point().

                                              {
   kind_ = RAY_OR_POINT_OR_INEQUALITY;
 }

void Parma_Polyhedra_Library::Generator::set_necessarily_closed ( )

inlineprivate

Sets to NECESSARILY_CLOSED the topological kind of *this row.

Definition at line 103 of file Generator_inlines.hh.

References Parma_Polyhedra_Library::NECESSARILY_CLOSED, and set_topology().

                                   {
   set_topology(NECESSARILY_CLOSED);
 }

void Parma_Polyhedra_Library::Generator::set_not_necessarily_closed ( )

inlineprivate

Sets to NOT_NECESSARILY_CLOSED the topological kind of *this row.

Definition at line 108 of file Generator_inlines.hh.

References Parma_Polyhedra_Library::NOT_NECESSARILY_CLOSED, and set_topology().

Referenced by Parma_Polyhedra_Library::Generator_System::insert().

                                       {
   set_topology(NOT_NECESSARILY_CLOSED);
 }

void Parma_Polyhedra_Library::Generator::set_representation ( Representation r )

inline

Converts *this to the specified representation.

Definition at line 219 of file Generator_inlines.hh.

References expr, and Parma_Polyhedra_Library::Linear_Expression::set_representation().

                                               {
   expr.set_representation(r);
 }

void Parma_Polyhedra_Library::Generator::set_space_dimension ( dimension_type space_dim )

inline

Sets the dimension of the vector space enclosing *this to space_dim .

Definition at line 252 of file Generator_inlines.hh.

References OK(), and set_space_dimension_no_ok().

Referenced by Parma_Polyhedra_Library::Generator_System::insert(), and Parma_Polyhedra_Library::Generator_System::insert_pending().

                                                        {
   set_space_dimension_no_ok(space_dim);
   PPL_ASSERT(OK());
 }

void Parma_Polyhedra_Library::Generator::set_space_dimension_no_ok ( dimension_type space_dim )

inlineprivate

Sets the dimension of the vector space enclosing *this to space_dim . Sets the space dimension of the rows in the system to space_dim .

This method is for internal use, it does *not* assert OK() at the end, so it can be used for invalid objects.

Definition at line 229 of file Generator_inlines.hh.

References expr, Parma_Polyhedra_Library::NECESSARILY_CLOSED, Parma_Polyhedra_Library::Linear_Expression::set_space_dimension(), space_dimension(), Parma_Polyhedra_Library::Linear_Expression::space_dimension(), strong_normalize(), Parma_Polyhedra_Library::Linear_Expression::swap_space_dimensions(), and topology().

Referenced by set_space_dimension().

                                                              {
   const dimension_type old_expr_space_dim = expr.space_dimension();
   if (topology() == NECESSARILY_CLOSED) {
     expr.set_space_dimension(space_dim);
   }
   else {
     const dimension_type old_space_dim = space_dimension();
     if (space_dim > old_space_dim) {
       expr.set_space_dimension(space_dim + 1);
       expr.swap_space_dimensions(Variable(space_dim), Variable(old_space_dim));
     }
     else {
       expr.swap_space_dimensions(Variable(space_dim), Variable(old_space_dim));
       expr.set_space_dimension(space_dim + 1);
     }
   }
   PPL_ASSERT(space_dimension() == space_dim);
   if (expr.space_dimension() < old_expr_space_dim) {
     strong_normalize();
   }
 }

void Parma_Polyhedra_Library::Generator::set_topology ( Topology x )

inlineprivate

Sets to x the topological kind of *this row.

Definition at line 75 of file Generator_inlines.hh.

References expr, Parma_Polyhedra_Library::NECESSARILY_CLOSED, Parma_Polyhedra_Library::Linear_Expression::set_space_dimension(), Parma_Polyhedra_Library::Linear_Expression::space_dimension(), topology(), and topology_.

Referenced by Parma_Polyhedra_Library::Generator_System::insert_pending(), set_necessarily_closed(), and set_not_necessarily_closed().

                                   {
   if (topology() == x) {
     return;
   }
   if (topology() == NECESSARILY_CLOSED) {
     // Add a column for the epsilon dimension.
     expr.set_space_dimension(expr.space_dimension() + 1);
   }
   else {
     PPL_ASSERT(expr.space_dimension() > 0);
     expr.set_space_dimension(expr.space_dimension() - 1);
   }
   topology_ = x;
 }

void Parma_Polyhedra_Library::Generator::shift_space_dimensions	(	Variable	v,
		dimension_type	n
	)

inline

Shift by n positions the coefficients of variables, starting from the coefficient of v. This increases the space dimension by n.

Definition at line 258 of file Generator_inlines.hh.

References expr, and Parma_Polyhedra_Library::Linear_Expression::shift_space_dimensions().

                                                               {
   expr.shift_space_dimensions(v, n);
 }

void Parma_Polyhedra_Library::Generator::sign_normalize ( )

private

Normalizes the sign of the coefficients so that the first non-zero (homogeneous) coefficient of a line-or-equality is positive.

Definition at line 264 of file Generator.cc.

Referenced by Parma_Polyhedra_Library::Polyhedron::BFT00_poly_hull_assign_if_exact(), and strong_normalize().

                              {
   if (is_line_or_equality()) {
     expr.sign_normalize();
   }
 }

dimension_type Parma_Polyhedra_Library::Generator::space_dimension ( ) const

inline

Returns the dimension of the vector space enclosing *this.

Definition at line 45 of file Generator_inlines.hh.

References expression(), and Parma_Polyhedra_Library::Expression_Hide_Last< T >::space_dimension().

                                  {
   return expression().space_dimension();
 }

void Parma_Polyhedra_Library::Generator::strong_normalize ( )

inlineprivate

Strong normalization: ensures that different Generator objects represent different hyperplanes or hyperspaces.

Applies both Generator::normalize() and Generator::sign_normalize().

Definition at line 367 of file Generator_inlines.hh.

References expr, Parma_Polyhedra_Library::Linear_Expression::normalize(), and sign_normalize().

Referenced by check_strong_normalized(), Generator(), OK(), and set_space_dimension_no_ok().

                             {
   expr.normalize();
   sign_normalize();
 }

void Parma_Polyhedra_Library::Generator::swap_space_dimensions	(	Variable	v1,
		Variable	v2
	)

Swaps the coefficients of the variables v1 and v2 .

Definition at line 158 of file Generator.cc.

References Parma_Polyhedra_Library::Variable::space_dimension().

                                                             {
   PPL_ASSERT(v1.space_dimension() <= space_dimension());
   PPL_ASSERT(v2.space_dimension() <= space_dimension());
   expr.swap_space_dimensions(v1, v2);
   // *this is still normalized but it may not be strongly normalized.
   sign_normalize();
   PPL_ASSERT(OK());
 }

void Parma_Polyhedra_Library::Generator::throw_dimension_incompatible	(	const char *	method,
		const char *	v_name,
		Variable	v
	)		const

private

Throw a std::invalid_argument exception containing the appropriate error message.

Definition at line 37 of file Generator.cc.

References Parma_Polyhedra_Library::Variable::space_dimension(), and space_dimension().

Referenced by coefficient().

                                                                      {
   std::ostringstream s;
   s << "PPL::Generator::" << method << ":" << std::endl
     << "this->space_dimension() == " << space_dimension() << ", "
     << v_name << ".space_dimension() == " << v.space_dimension() << ".";
   throw std::invalid_argument(s.str());
 }

void Parma_Polyhedra_Library::Generator::throw_invalid_argument	(	const char *	method,
		const char *	reason
	)		const

private

Throw a std::invalid_argument exception containing the appropriate error message.

Definition at line 48 of file Generator.cc.

Referenced by divisor().

                                                                  {
   std::ostringstream s;
   s << "PPL::Generator::" << method << ":" << std::endl
     << reason << ".";
   throw std::invalid_argument(s.str());
 }

Topology Parma_Polyhedra_Library::Generator::topology ( ) const

inlineprivate

Returns the topological kind of *this.

Definition at line 60 of file Generator_inlines.hh.

References topology_.

Referenced by Parma_Polyhedra_Library::Generator_System::insert(), Parma_Polyhedra_Library::Generator_System::insert_pending(), is_matching_closure_point(), is_necessarily_closed(), is_not_necessarily_closed(), set_space_dimension_no_ok(), and set_topology().

                           {
   return topology_;
 }

memory_size_type Parma_Polyhedra_Library::Generator::total_memory_in_bytes ( ) const

inline

Returns a lower bound to the total size in bytes of the memory occupied by *this.

Definition at line 362 of file Generator_inlines.hh.

References external_memory_in_bytes().

                                        {
   return sizeof(*this) + external_memory_in_bytes();
 }

Generator::Type Parma_Polyhedra_Library::Generator::type ( ) const

inline

Returns the generator type of *this.

Definition at line 283 of file Generator_inlines.hh.

References CLOSURE_POINT, epsilon_coefficient(), is_line(), is_line_or_ray(), is_necessarily_closed(), LINE, POINT, and RAY.

                       {
   if (is_line()) {
     return LINE;
   }
   if (is_line_or_ray()) {
     return RAY;
   }
   if (is_necessarily_closed()) {
     return POINT;
   }
   else {
     // Checking the value of the epsilon coefficient.
     if (epsilon_coefficient() == 0) {
       return CLOSURE_POINT;
     }
     else {
       return POINT;
     }
   }
 }

const Generator & Parma_Polyhedra_Library::Generator::zero_dim_closure_point ( )

inlinestatic

Returns, as a closure point, the origin of the zero-dimensional space 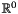$\Rset^0$ .

Definition at line 379 of file Generator_inlines.hh.

References zero_dim_closure_point_p.

Referenced by Parma_Polyhedra_Library::Polyhedron::add_space_dimensions_and_project().

                                   {
   PPL_ASSERT(zero_dim_closure_point_p != 0);
   return *zero_dim_closure_point_p;
 }

const Generator & Parma_Polyhedra_Library::Generator::zero_dim_point ( )

inlinestatic

Returns the origin of the zero-dimensional space 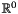$\Rset^0$ .

Definition at line 373 of file Generator_inlines.hh.

References zero_dim_point_p.

Referenced by Parma_Polyhedra_Library::Polyhedron::add_space_dimensions_and_project(), and Parma_Polyhedra_Library::Generator_System::initialize().

                           {
   PPL_ASSERT(zero_dim_point_p != 0);
   return *zero_dim_point_p;
 }

Friends And Related Function Documentation

Generator closure_point	(	const Linear_Expression &	e,
		Coefficient_traits::const_reference	d,
		Representation	r
	)

References closure_point().

                                 {
   return Generator::closure_point(e, d, r);
 }

Generator closure_point ( Representation r )

References closure_point().

                                 {
   return Generator::closure_point(r);
 }

Generator closure_point	(	const Linear_Expression &	e,
		Representation	r
	)

References closure_point().

                                 {
   return Generator::closure_point(e, r);
 }

Generator closure_point	(	const Linear_Expression &	e = `Linear_Expression::zero()`,
		Coefficient_traits::const_reference	d = `Coefficient_one()`,
		Representation	r = `Generator::default_representation`
	)

Generator closure_point ( Representation r )

Generator closure_point	(	const Linear_Expression &	e,
		Representation	r
	)

int compare	(	const Generator &	x,
		const Generator &	y
	)

Returns: The returned absolute value can be , 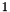or .

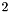Parameters

x	A row of coefficients;
y	Another row.

Compares x and y, where x and y may be of different size, in which case the "missing" coefficients are assumed to be zero. The comparison is such that:

equalities are smaller than inequalities;
lines are smaller than points and rays;
the ordering is lexicographic;
the positions compared are, in decreasing order of significance, 1, 2, ..., size(), 0;
the result is negative, zero, or positive if x is smaller than, equal to, or greater than y, respectively;
when x and y are different, the absolute value of the result is 1 if the difference is due to the coefficient in position 0; it is 2 otherwise.

When x and y represent the hyper-planes associated to two equality or inequality constraints, the coefficient at 0 is the known term. In this case, the return value can be characterized as follows:

-2, if x is smaller than y and they are not parallel;
-1, if x is smaller than y and they are parallel;
0, if x and y are equal;
+1, if y is smaller than x and they are parallel;
+2, if y is smaller than x and they are not parallel.

int compare	(	const Generator &	x,
		const Generator &	y
	)

References Parma_Polyhedra_Library::compare(), expr, and is_line_or_equality().

                                                    {
   const bool x_is_line_or_equality = x.is_line_or_equality();
   const bool y_is_line_or_equality = y.is_line_or_equality();
   if (x_is_line_or_equality != y_is_line_or_equality) {
     // Equalities (lines) precede inequalities (ray/point).
     return y_is_line_or_equality ? 2 : -2;
   }
 
   return compare(x.expr, y.expr);
 }

int compare	(	const Generator &	x,
		const Generator &	y
	)

friend

template<typename Temp , typename To >

bool euclidean_distance_assign	(	Checked_Number< To, Extended_Number_Policy > &	r,
		const Generator &	x,
		const Generator &	y,
		const Rounding_Dir	dir,
		Temp &	tmp0,
		Temp &	tmp1,
		Temp &	tmp2
	)

                                       {
   return l_m_distance_assign<Euclidean_Distance_Specialization<Temp> >
     (r, x, y, dir, tmp0, tmp1, tmp2);
 }

template<typename Temp , typename To >

bool euclidean_distance_assign	(	Checked_Number< To, Extended_Number_Policy > &	r,
		const Generator &	x,
		const Generator &	y,
		const Rounding_Dir	dir
	)

References PPL_DIRTY_TEMP.

                                                   {
   typedef Checked_Number<Temp, Extended_Number_Policy> Checked_Temp;
   PPL_DIRTY_TEMP(Checked_Temp, tmp0);
   PPL_DIRTY_TEMP(Checked_Temp, tmp1);
   PPL_DIRTY_TEMP(Checked_Temp, tmp2);
   return euclidean_distance_assign(r, x, y, dir, tmp0, tmp1, tmp2);
 }

template<typename To >

bool euclidean_distance_assign	(	Checked_Number< To, Extended_Number_Policy > &	r,
		const Generator &	x,
		const Generator &	y,
		const Rounding_Dir	dir
	)

                                                   {
   return euclidean_distance_assign<To, To>(r, x, y, dir);
 }

template<typename To >

bool euclidean_distance_assign	(	Checked_Number< To, Extended_Number_Policy > &	r,
		const Generator &	x,
		const Generator &	y,
		Rounding_Dir	dir
	)

If the euclidean distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.

The direction of the approximation is specified by dir.

All computations are performed using variables of type Checked_Number<To, Extended_Number_Policy>.

Note: Distances are only defined between generators that are points and/or closure points; for rays or lines, false is returned.

template<typename Temp , typename To >

bool euclidean_distance_assign	(	Checked_Number< To, Extended_Number_Policy > &	r,
		const Generator &	x,
		const Generator &	y,
		Rounding_Dir	dir,
		Temp &	tmp0,
		Temp &	tmp1,
		Temp &	tmp2
	)

If the euclidean distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.

The direction of the approximation is specified by dir.

All computations are performed using the temporary variables tmp0, tmp1 and tmp2.

Note: Distances are only defined between generators that are points and/or closure points; for rays or lines, false is returned.

friend class Expression_Adapter< Generator >

friend

Definition at line 730 of file Generator_defs.hh.

template<typename Temp , typename To >

bool l_infinity_distance_assign	(	Checked_Number< To, Extended_Number_Policy > &	r,
		const Generator &	x,
		const Generator &	y,
		const Rounding_Dir	dir,
		Temp &	tmp0,
		Temp &	tmp1,
		Temp &	tmp2
	)

                                        {
   return l_m_distance_assign<L_Infinity_Distance_Specialization<Temp> >
     (r, x, y, dir, tmp0, tmp1, tmp2);
 }

template<typename Temp , typename To >

bool l_infinity_distance_assign	(	Checked_Number< To, Extended_Number_Policy > &	r,
		const Generator &	x,
		const Generator &	y,
		const Rounding_Dir	dir
	)

References PPL_DIRTY_TEMP.

                                                    {
   typedef Checked_Number<Temp, Extended_Number_Policy> Checked_Temp;
   PPL_DIRTY_TEMP(Checked_Temp, tmp0);
   PPL_DIRTY_TEMP(Checked_Temp, tmp1);
   PPL_DIRTY_TEMP(Checked_Temp, tmp2);
   return l_infinity_distance_assign(r, x, y, dir, tmp0, tmp1, tmp2);
 }

template<typename To >

bool l_infinity_distance_assign	(	Checked_Number< To, Extended_Number_Policy > &	r,
		const Generator &	x,
		const Generator &	y,
		const Rounding_Dir	dir
	)

                                                    {
   return l_infinity_distance_assign<To, To>(r, x, y, dir);
 }

template<typename To >

bool l_infinity_distance_assign	(	Checked_Number< To, Extended_Number_Policy > &	r,
		const Generator &	x,
		const Generator &	y,
		Rounding_Dir	dir
	)

If the $L_\infty$ distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.

The direction of the approximation is specified by dir.

All computations are performed using variables of type Checked_Number<To, Extended_Number_Policy>.

Note: Distances are only defined between generators that are points and/or closure points; for rays or lines, false is returned.

template<typename Temp , typename To >

bool l_infinity_distance_assign	(	Checked_Number< To, Extended_Number_Policy > &	r,
		const Generator &	x,
		const Generator &	y,
		Rounding_Dir	dir
	)

If the $L_\infty$ distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.

The direction of the approximation is specified by dir.

All computations are performed using variables of type Checked_Number<Temp, Extended_Number_Policy>.

Note: Distances are only defined between generators that are points and/or closure points; for rays or lines, false is returned.

template<typename Temp , typename To >

bool l_infinity_distance_assign	(	Checked_Number< To, Extended_Number_Policy > &	r,
		const Generator &	x,
		const Generator &	y,
		Rounding_Dir	dir,
		Temp &	tmp0,
		Temp &	tmp1,
		Temp &	tmp2
	)

If the $L_\infty$ distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.

The direction of the approximation is specified by dir.

All computations are performed using the temporary variables tmp0, tmp1 and tmp2.

Note: Distances are only defined between generators that are points and/or closure points; for rays or lines, false is returned.

template<typename Specialization , typename Temp , typename To >

bool l_m_distance_assign	(	Checked_Number< To, Extended_Number_Policy > &	r,
		const Generator &	x,
		const Generator &	y,
		const Rounding_Dir	dir,
		Temp &	tmp0,
		Temp &	tmp1,
		Temp &	tmp2
	)

References Parma_Polyhedra_Library::assign_r(), coefficient(), Parma_Polyhedra_Library::combine(), divisor(), Parma_Polyhedra_Library::finalize(), Parma_Polyhedra_Library::inverse(), is_line_or_ray(), Parma_Polyhedra_Library::maybe_assign(), PPL_DIRTY_TEMP, Parma_Polyhedra_Library::ROUND_NOT_NEEDED, Parma_Polyhedra_Library::Boundary_NS::sgn(), and space_dimension().

                                 {
   // Generator kind compatibility check: we only compute distances
   // between (closure) points.
   if (x.is_line_or_ray() || y.is_line_or_ray()) {
     return false;
   }
   const dimension_type x_space_dim = x.space_dimension();
   // Dimension-compatibility check.
   if (x_space_dim != y.space_dimension()) {
     return false;
   }
 
   // All zero-dim generators have distance zero.
   if (x_space_dim == 0) {
     assign_r(r, 0, ROUND_NOT_NEEDED);
     return true;
   }
 
   PPL_DIRTY_TEMP(mpq_class, x_coord);
   PPL_DIRTY_TEMP(mpq_class, y_coord);
   PPL_DIRTY_TEMP(mpq_class, x_div);
   PPL_DIRTY_TEMP(mpq_class, y_div);
   assign_r(x_div, x.divisor(), ROUND_NOT_NEEDED);
   assign_r(y_div, y.divisor(), ROUND_NOT_NEEDED);
 
   assign_r(tmp0, 0, ROUND_NOT_NEEDED);
   // TODO: This loop can be optimized more, if needed.
   for (dimension_type i = x_space_dim; i-- > 0; ) {
     assign_r(x_coord, x.coefficient(Variable(i)), ROUND_NOT_NEEDED);
     div_assign_r(x_coord, x_coord, x_div, ROUND_NOT_NEEDED);
     assign_r(y_coord, y.coefficient(Variable(i)), ROUND_NOT_NEEDED);
     div_assign_r(y_coord, y_coord, y_div, ROUND_NOT_NEEDED);
     const Temp* tmp1p;
     const Temp* tmp2p;
 
     if (x_coord > y_coord) {
       maybe_assign(tmp1p, tmp1, x_coord, dir);
       maybe_assign(tmp2p, tmp2, y_coord, inverse(dir));
     }
     else {
       maybe_assign(tmp1p, tmp1, y_coord, dir);
       maybe_assign(tmp2p, tmp2, x_coord, inverse(dir));
     }
     sub_assign_r(tmp1, *tmp1p, *tmp2p, dir);
     PPL_ASSERT(sgn(tmp1) >= 0);
     Specialization::combine(tmp0, tmp1, dir);
   }
   Specialization::finalize(tmp0, dir);
   assign_r(r, tmp0, dir);
   return true;
 }

Generator line	(	const Linear_Expression &	e,
		Representation	r
	)

References line().

                                                    {
   return Generator::line(e, r);
 }

Generator line	(	const Linear_Expression &	e,
		Representation	r = `Generator::default_representation`
	)

friend class Linear_System< Generator >

friend

Definition at line 731 of file Generator_defs.hh.

bool operator!=	(	const Generator &	x,
		const Generator &	y
	)

References is_equivalent_to().

                                                    {
   return !x.is_equivalent_to(y);
 }

bool operator!=	(	const Generator &	x,
		const Generator &	y
	)

std::ostream & operator<<	(	std::ostream &	s,
		const Generator &	g
	)

std::ostream & operator<<	(	std::ostream &	s,
		const Generator &	g
	)

References fancy_print().

                                                              {
   g.fancy_print(s);
   return s;
 }

std::ostream & operator<<	(	std::ostream &	s,
		const Generator::Type &	t
	)

References CLOSURE_POINT, LINE, POINT, and RAY.

                                                                  {
   const char* n = 0;
   switch (t) {
   case Generator::LINE:
     n = "LINE";
     break;
   case Generator::RAY:
     n = "RAY";
     break;
   case Generator::POINT:
     n = "POINT";
     break;
   case Generator::CLOSURE_POINT:
     n = "CLOSURE_POINT";
     break;
   }
   s << n;
   return s;
 }

std::ostream & operator<<	(	std::ostream &	s,
		const Generator::Type &	t
	)

bool operator==	(	const Generator &	x,
		const Generator &	y
	)

References is_equivalent_to().

                                                    {
   return x.is_equivalent_to(y);
 }

bool operator==	(	const Generator &	x,
		const Generator &	y
	)

friend class Parma_Polyhedra_Library::Generator_System

friend

Definition at line 735 of file Generator_defs.hh.

friend class Parma_Polyhedra_Library::Generator_System_const_iterator

friend

Definition at line 736 of file Generator_defs.hh.

friend class Parma_Polyhedra_Library::Grid

friend

Definition at line 742 of file Generator_defs.hh.

friend class Parma_Polyhedra_Library::Grid_Generator_System

friend

Definition at line 740 of file Generator_defs.hh.

std::ostream& Parma_Polyhedra_Library::IO_Operators::operator<<	(	std::ostream &	s,
		const Generator &	g
	)

friend

friend class Parma_Polyhedra_Library::MIP_Problem

friend

Definition at line 741 of file Generator_defs.hh.

friend class Parma_Polyhedra_Library::Polyhedron

friend

Definition at line 738 of file Generator_defs.hh.

friend class Parma_Polyhedra_Library::Scalar_Products

friend

Definition at line 732 of file Generator_defs.hh.

friend class Parma_Polyhedra_Library::Topology_Adjusted_Scalar_Product_Assign

friend

Definition at line 734 of file Generator_defs.hh.

friend class Parma_Polyhedra_Library::Topology_Adjusted_Scalar_Product_Sign

friend

Definition at line 733 of file Generator_defs.hh.

Generator point	(	const Linear_Expression &	e,
		Coefficient_traits::const_reference	d,
		Representation	r
	)

References point().

                         {
   return Generator::point(e, d, r);
 }

Generator point ( Representation r )

References point().

                         {
   return Generator::point(r);
 }

Generator point	(	const Linear_Expression &	e,
		Representation	r
	)

References point().

                                                     {
   return Generator::point(e, r);
 }

Generator point	(	const Linear_Expression &	e = `Linear_Expression::zero()`,
		Coefficient_traits::const_reference	d = `Coefficient_one()`,
		Representation	r = `Generator::default_representation`
	)

Generator point ( Representation r )

Generator point	(	const Linear_Expression &	e,
		Representation	r
	)

Generator ray	(	const Linear_Expression &	e,
		Representation	r
	)

References ray().

                                                   {
   return Generator::ray(e, r);
 }

Generator ray	(	const Linear_Expression &	e,
		Representation	r = `Generator::default_representation`
	)

template<typename Temp , typename To >

bool rectilinear_distance_assign	(	Checked_Number< To, Extended_Number_Policy > &	r,
		const Generator &	x,
		const Generator &	y,
		const Rounding_Dir	dir,
		Temp &	tmp0,
		Temp &	tmp1,
		Temp &	tmp2
	)

                                         {
   return l_m_distance_assign<Rectilinear_Distance_Specialization<Temp> >
     (r, x, y, dir, tmp0, tmp1, tmp2);
 }

template<typename Temp , typename To >

bool rectilinear_distance_assign	(	Checked_Number< To, Extended_Number_Policy > &	r,
		const Generator &	x,
		const Generator &	y,
		const Rounding_Dir	dir
	)

References PPL_DIRTY_TEMP.

                                                     {
   typedef Checked_Number<Temp, Extended_Number_Policy> Checked_Temp;
   PPL_DIRTY_TEMP(Checked_Temp, tmp0);
   PPL_DIRTY_TEMP(Checked_Temp, tmp1);
   PPL_DIRTY_TEMP(Checked_Temp, tmp2);
   return rectilinear_distance_assign(r, x, y, dir, tmp0, tmp1, tmp2);
 }

template<typename To >

bool rectilinear_distance_assign	(	Checked_Number< To, Extended_Number_Policy > &	r,
		const Generator &	x,
		const Generator &	y,
		const Rounding_Dir	dir
	)

                                                     {
   return rectilinear_distance_assign<To, To>(r, x, y, dir);
 }

template<typename To >

bool rectilinear_distance_assign	(	Checked_Number< To, Extended_Number_Policy > &	r,
		const Generator &	x,
		const Generator &	y,
		Rounding_Dir	dir
	)

If the rectilinear distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.

The direction of the approximation is specified by dir.

All computations are performed using variables of type Checked_Number<To, Extended_Number_Policy>.

Note: Distances are only defined between generators that are points and/or closure points; for rays or lines, false is returned.

template<typename Temp , typename To >

bool rectilinear_distance_assign	(	Checked_Number< To, Extended_Number_Policy > &	r,
		const Generator &	x,
		const Generator &	y,
		Rounding_Dir	dir
	)

If the rectilinear distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.

The direction of the approximation is specified by dir.

All computations are performed using variables of type Checked_Number<Temp, Extended_Number_Policy>.

Note: Distances are only defined between generators that are points and/or closure points; for rays or lines, false is returned.

template<typename Temp , typename To >

bool rectilinear_distance_assign	(	Checked_Number< To, Extended_Number_Policy > &	r,
		const Generator &	x,
		const Generator &	y,
		Rounding_Dir	dir,
		Temp &	tmp0,
		Temp &	tmp1,
		Temp &	tmp2
	)

If the rectilinear distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.

The direction of the approximation is specified by dir.

All computations are performed using the temporary variables tmp0, tmp1 and tmp2.

Note: Distances are only defined between generators that are points and/or closure points; for rays or lines, false is returned.

template<typename Temp , typename To >

bool rectilinear_distance_assign	(	Checked_Number< To, Extended_Number_Policy > &	r,
		const Generator &	x,
		const Generator &	y,
		Rounding_Dir	dir
	)

If the euclidean distance between x and y is defined, stores an approximation of it into r and returns true; returns false otherwise.

The direction of the approximation is specified by dir.

All computations are performed using variables of type Checked_Number<Temp, Extended_Number_Policy>.

Note: Distances are only defined between generators that are points and/or closure points; for rays or lines, false is returned.

void swap	(	Generator &	x,
		Generator &	y
	)

Referenced by Generator(), m_swap(), and operator=().

void swap	(	Generator &	x,
		Generator &	y
	)

References m_swap().

                                  {
   x.m_swap(y);
 }

Member Data Documentation

const Representation Parma_Polyhedra_Library::Generator::default_representation = SPARSE

static

The representation used for new Generators.

Note: The copy constructor and the copy constructor with specified size use the representation of the original object, so that it is indistinguishable from the original object.

Definition at line 294 of file Generator_defs.hh.

Linear_Expression Parma_Polyhedra_Library::Generator::expr

private

The linear expression encoding *this.

Definition at line 543 of file Generator_defs.hh.

Kind Parma_Polyhedra_Library::Generator::kind_

private

The kind of *this.

Definition at line 546 of file Generator_defs.hh.

Referenced by Generator(), is_equal_to(), is_line_or_equality(), is_ray_or_point_or_inequality(), m_swap(), set_is_line_or_equality(), and set_is_ray_or_point_or_inequality().

Topology Parma_Polyhedra_Library::Generator::topology_

private

The topology of *this.

Definition at line 549 of file Generator_defs.hh.

Referenced by is_equal_to(), m_swap(), mark_as_necessarily_closed(), mark_as_not_necessarily_closed(), set_topology(), and topology().

const PPL::Generator * Parma_Polyhedra_Library::Generator::zero_dim_closure_point_p = 0

staticprivate

Holds (between class initialization and finalization) a pointer to the origin of the zero-dimensional space 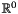$\Rset^0$ , as a closure point.

Definition at line 561 of file Generator_defs.hh.

Referenced by zero_dim_closure_point().

const PPL::Generator * Parma_Polyhedra_Library::Generator::zero_dim_point_p = 0

staticprivate

Holds (between class initialization and finalization) a pointer to the origin of the zero-dimensional space 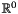$\Rset^0$ .

Definition at line 555 of file Generator_defs.hh.

Referenced by zero_dim_point().

The documentation for this class was generated from the following files:

Public Types

Public Member Functions

Static Public Member Functions

Static Public Attributes

Private Types

Private Member Functions

Private Attributes

Static Private Attributes

Friends

Related Functions

Detailed Description

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation

Friends And Related Function Documentation

Member Data Documentation