Parma_Polyhedra_Library::MIP_Problem Class Reference

A Mixed Integer (linear) Programming problem. More...

#include <MIP_Problem_defs.hh>

Collaboration diagram for Parma_Polyhedra_Library::MIP_Problem:

Classes
class	const_iterator
	A read-only iterator on the constraints defining the feasible region. More...
struct	Inherit_Constraints
	A tag type to distinguish normal vs. inheriting copy constructor. More...
struct	RAII_Temporary_Real_Relaxation
	A helper class to temporarily relax a MIP problem using RAII. More...

Public Types
enum	Control_Parameter_Name { PRICING }
	Names of MIP problems' control parameters. More...
enum	Control_Parameter_Value { PRICING_STEEPEST_EDGE_FLOAT, PRICING_STEEPEST_EDGE_EXACT, PRICING_TEXTBOOK }
	Possible values for MIP problem's control parameters. More...

Public Member Functions
	MIP_Problem (dimension_type dim=0)
	Builds a trivial MIP problem. More...
template<typename In >
	MIP_Problem (dimension_type dim, In first, In last, const Variables_Set &int_vars, const Linear_Expression &obj=Linear_Expression::zero(), Optimization_Mode mode=MAXIMIZATION)
	Builds an MIP problem having space dimension dim from the sequence of constraints in the range 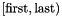, the objective function obj and optimization mode mode; those dimensions whose indices occur in int_vars are constrained to take an integer value. More...
template<typename In >
	MIP_Problem (dimension_type dim, In first, In last, const Linear_Expression &obj=Linear_Expression::zero(), Optimization_Mode mode=MAXIMIZATION)
	Builds an MIP problem having space dimension dim from the sequence of constraints in the range 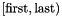, the objective function obj and optimization mode mode. More...
	MIP_Problem (dimension_type dim, const Constraint_System &cs, const Linear_Expression &obj=Linear_Expression::zero(), Optimization_Mode mode=MAXIMIZATION)
	Builds an MIP problem having space dimension dim from the constraint system cs, the objective function obj and optimization mode mode. More...
	MIP_Problem (const MIP_Problem &y)
	Ordinary copy constructor. More...
	~MIP_Problem ()
	Destructor. More...
MIP_Problem &	operator= (const MIP_Problem &y)
	Assignment operator. More...
dimension_type	space_dimension () const
	Returns the space dimension of the MIP problem. More...
const Variables_Set &	integer_space_dimensions () const
	Returns a set containing all the variables' indexes constrained to be integral. More...
const_iterator	constraints_begin () const
	Returns a read-only iterator to the first constraint defining the feasible region. More...
const_iterator	constraints_end () const
	Returns a past-the-end read-only iterator to the sequence of constraints defining the feasible region. More...
const Linear_Expression &	objective_function () const
	Returns the objective function. More...
Optimization_Mode	optimization_mode () const
	Returns the optimization mode. More...
void	clear ()
	Resets *this to be equal to the trivial MIP problem. More...
void	add_space_dimensions_and_embed (dimension_type m)
	Adds m new space dimensions and embeds the old MIP problem in the new vector space. More...
void	add_to_integer_space_dimensions (const Variables_Set &i_vars)
	Sets the variables whose indexes are in set i_vars to be integer space dimensions. More...
void	add_constraint (const Constraint &c)
	Adds a copy of constraint c to the MIP problem. More...
void	add_constraints (const Constraint_System &cs)
	Adds a copy of the constraints in cs to the MIP problem. More...
void	set_objective_function (const Linear_Expression &obj)
	Sets the objective function to obj. More...
void	set_optimization_mode (Optimization_Mode mode)
	Sets the optimization mode to mode. More...
bool	is_satisfiable () const
	Checks satisfiability of *this. More...
MIP_Problem_Status	solve () const
	Optimizes the MIP problem. More...
void	evaluate_objective_function (const Generator &evaluating_point, Coefficient &numer, Coefficient &denom) const
	Sets num and denom so that is the result of evaluating the objective function on evaluating_point. More...
const Generator &	feasible_point () const
	Returns a feasible point for *this, if it exists. More...
const Generator &	optimizing_point () const
	Returns an optimal point for *this, if it exists. More...
void	optimal_value (Coefficient &numer, Coefficient &denom) const
	Sets numer and denom so that is the solution of the optimization problem. More...
bool	OK () const
	Checks if all the invariants are satisfied. More...
void	ascii_dump () const
	Writes to std::cerr an ASCII representation of *this. More...
void	ascii_dump (std::ostream &s) const
	Writes to s an ASCII representation of *this. More...
void	print () const
	Prints *this to std::cerr using operator<<. More...
bool	ascii_load (std::istream &s)
	Loads from s an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets *this accordingly. Returns true if successful, false otherwise. More...
memory_size_type	total_memory_in_bytes () const
	Returns the total size in bytes of the memory occupied by *this. More...
memory_size_type	external_memory_in_bytes () const
	Returns the size in bytes of the memory managed by *this. More...
void	m_swap (MIP_Problem &y)
	Swaps *this with y. More...
Control_Parameter_Value	get_control_parameter (Control_Parameter_Name name) const
	Returns the value of the control parameter name. More...
void	set_control_parameter (Control_Parameter_Value value)
	Sets control parameter value. More...

Static Public Member Functions
static dimension_type	max_space_dimension ()
	Returns the maximum space dimension an MIP_Problem can handle. More...

Private Types
enum	Status {   UNSATISFIABLE, SATISFIABLE, UNBOUNDED, OPTIMIZED,   PARTIALLY_SATISFIABLE }
	An enumerated type describing the internal status of the MIP problem. More...
typedef std::vector< Constraint * >	Constraint_Sequence
	A type alias for a sequence of constraints. More...
typedef Sparse_Row	Row
typedef Row	working_cost_type

Private Member Functions
	MIP_Problem (const MIP_Problem &y, Inherit_Constraints)
	Copy constructor inheriting constraints. More...
void	add_constraint_helper (const Constraint &c)
	Helper method: implements exception safe addition. More...
void	process_pending_constraints ()
	Processes the pending constraints of *this. More...
void	second_phase ()
	Optimizes the MIP problem using the second phase of the primal simplex algorithm. More...
MIP_Problem_Status	compute_tableau (std::vector< dimension_type > &worked_out_row)
	Assigns to this->tableau a simplex tableau representing the MIP problem, inserting into this->mapping the information that is required to recover the original MIP problem. More...
bool	parse_constraints (dimension_type &additional_tableau_rows, dimension_type &additional_slack_variables, std::deque< bool > &is_tableau_constraint, std::deque< bool > &is_satisfied_inequality, std::deque< bool > &is_nonnegative_variable, std::deque< bool > &is_remergeable_variable) const
	Parses the pending constraints to gather information on how to resize the tableau. More...
dimension_type	get_exiting_base_index (dimension_type entering_var_index) const
	Computes the row index of the variable exiting the base of the MIP problem. Implemented with anti-cycling rule. More...
void	pivot (dimension_type entering_var_index, dimension_type exiting_base_index)
	Performs the pivoting operation on the tableau. More...
dimension_type	textbook_entering_index () const
	Computes the column index of the variable entering the base, using the textbook algorithm with anti-cycling rule. More...
dimension_type	steepest_edge_exact_entering_index () const
	Computes the column index of the variable entering the base, using an exact steepest-edge algorithm with anti-cycling rule. More...
dimension_type	steepest_edge_float_entering_index () const
	Same as steepest_edge_exact_entering_index, but using floating points. More...
bool	compute_simplex_using_exact_pricing ()
	Returns true if and if only the algorithm successfully computed a feasible solution. More...
bool	compute_simplex_using_steepest_edge_float ()
	Returns true if and if only the algorithm successfully computed a feasible solution. More...
void	erase_artificials (dimension_type begin_artificials, dimension_type end_artificials)
	Drop unnecessary artificial variables from the tableau and get ready for the second phase of the simplex algorithm. More...
bool	is_in_base (dimension_type var_index, dimension_type &row_index) const
void	compute_generator () const
	Computes a valid generator that satisfies all the constraints of the Linear Programming problem associated to *this. More...
dimension_type	merge_split_variable (dimension_type var_index)
	Merges back the positive and negative part of a (previously split) variable after detecting a corresponding nonnegativity constraint. More...
bool	is_lp_satisfiable () const
	Returns true if and if only the LP problem is satisfiable. More...

Static Private Member Functions
static void	linear_combine (Row &x, const Row &y, const dimension_type k)
	Linearly combines x with y so that *this[k] is 0. More...
static void	linear_combine (Dense_Row &x, const Sparse_Row &y, const dimension_type k)
	Linearly combines x with y so that *this[k] is 0. More...
static bool	is_unbounded_obj_function (const Linear_Expression &obj_function, const std::vector< std::pair< dimension_type, dimension_type > > &mapping, Optimization_Mode optimization_mode)
static bool	is_satisfied (const Constraint &c, const Generator &g)
	Returns true if and only if c is satisfied by g. More...
static bool	is_saturated (const Constraint &c, const Generator &g)
	Returns true if and only if c is saturated by g. More...
static MIP_Problem_Status	solve_mip (bool &have_incumbent_solution, mpq_class &incumbent_solution_value, Generator &incumbent_solution_point, MIP_Problem &mip, const Variables_Set &i_vars)
	Returns a status that encodes the solution of the MIP problem. More...
static bool	is_mip_satisfiable (MIP_Problem &mip, const Variables_Set &i_vars, Generator &p)
	Returns true if and if only the MIP problem mip is satisfiable when variables in i_vars can only take integral values. More...
static bool	choose_branching_variable (const MIP_Problem &mip, const Variables_Set &i_vars, dimension_type &branching_index)
	Returns true if and if only mip.last_generator satisfies all the integrality conditions implicitly stated using by i_vars. More...

Private Attributes
dimension_type	external_space_dim
	The dimension of the vector space. More...
dimension_type	internal_space_dim
	The space dimension of the current (partial) solution of the MIP problem; it may be smaller than external_space_dim. More...
Matrix< Row >	tableau
	The matrix encoding the current feasible region in tableau form. More...
working_cost_type	working_cost
	The working cost function. More...
std::vector< std::pair< dimension_type, dimension_type > >	mapping
	A map between the variables of `input_cs' and `tableau'. More...
std::vector< dimension_type >	base
	The current basic solution. More...
Status	status
	The internal state of the MIP problem. More...
Control_Parameter_Value	pricing
	The pricing method in use. More...
bool	initialized
	A Boolean encoding whether or not internal data structures have already been properly sized and populated: useful to allow for deeper checks in method OK(). More...
std::vector< Constraint * >	input_cs
	The sequence of constraints describing the feasible region. More...
dimension_type	inherited_constraints
	The number of constraints that are inherited from our parent in the recursion tree built when solving via branch-and-bound. More...
dimension_type	first_pending_constraint
	The first index of `input_cs' containing a pending constraint. More...
Linear_Expression	input_obj_function
	The objective function to be optimized. More...
Optimization_Mode	opt_mode
	The optimization mode requested. More...
Generator	last_generator
	The last successfully computed feasible or optimizing point. More...
Variables_Set	i_variables
	A set containing all the indexes of variables that are constrained to have an integer value. More...

Friends
struct	RAII_Temporary_Real_Relaxation

Related Functions
(Note that these are not member functions.)
std::ostream &	operator<< (std::ostream &s, const MIP_Problem &mip)
std::ostream &	operator<< (std::ostream &s, const MIP_Problem &mip)
	Output operator. More...
void	swap (MIP_Problem &x, MIP_Problem &y)
	Swaps x with y. More...
void	swap (MIP_Problem &x, MIP_Problem &y)

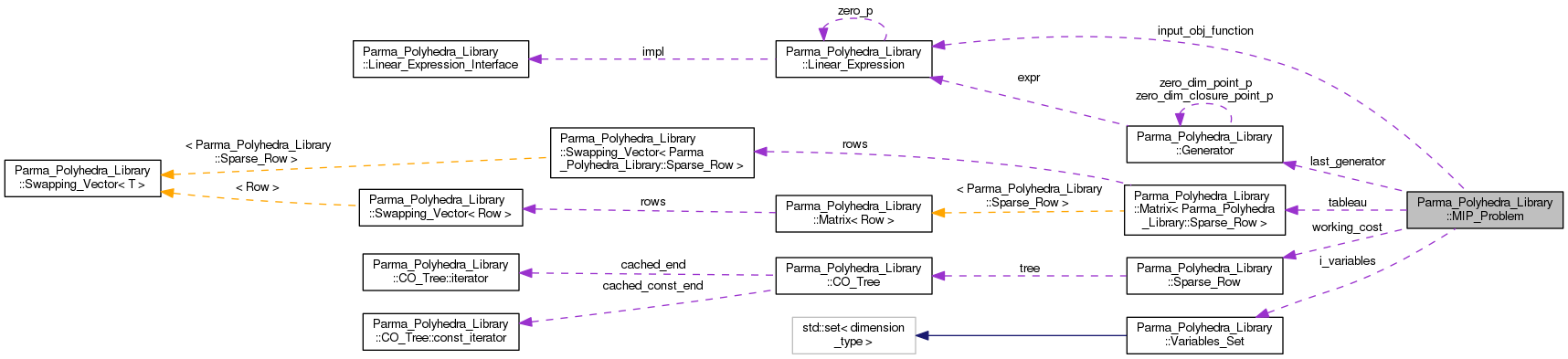
Detailed Description

A Mixed Integer (linear) Programming problem.

An object of this class encodes a mixed integer (linear) programming problem. The MIP problem is specified by providing:

• the dimension of the vector space;
• the feasible region, by means of a finite set of linear equality and non-strict inequality constraints;
• the subset of the unknown variables that range over the integers (the other variables implicitly ranging over the reals);
• the objective function, described by a Linear_Expression;
• the optimization mode (either maximization or minimization).

The class provides support for the (incremental) solution of the MIP problem based on variations of the revised simplex method and on branch-and-bound techniques. The result of the resolution process is expressed in terms of an enumeration, encoding the feasibility and the unboundedness of the optimization problem. The class supports simple feasibility tests (i.e., no optimization), as well as the extraction of an optimal (resp., feasible) point, provided the MIP_Problem is optimizable (resp., feasible).

By exploiting the incremental nature of the solver, it is possible to reuse part of the computational work already done when solving variants of a given MIP_Problem: currently, incremental resolution supports the addition of space dimensions, the addition of constraints, the change of objective function and the change of optimization mode.

Definition at line 87 of file MIP_Problem_defs.hh.

Member Typedef Documentation

typedef std::vector<Constraint*> Parma_Polyhedra_Library::MIP_Problem::Constraint_Sequence

private

A type alias for a sequence of constraints.

Definition at line 237 of file MIP_Problem_defs.hh.

typedef Sparse_Row Parma_Polyhedra_Library::MIP_Problem::Row

private

Definition at line 508 of file MIP_Problem_defs.hh.

typedef Row Parma_Polyhedra_Library::MIP_Problem::working_cost_type

private

Definition at line 516 of file MIP_Problem_defs.hh.

Constructor & Destructor Documentation

Parma_Polyhedra_Library::MIP_Problem::MIP_Problem ( dimension_type  dim = 0 )

explicit

Builds a trivial MIP problem.

A trivial MIP problem requires to maximize the objective function on a vector space under no constraints at all: the origin of the vector space is an optimal solution.

Parameters

dim	The dimension of the vector space enclosing *this (optional argument with default value ).

Exceptions

std::length_error

Thrown if dim exceeds max_space_dimension().

Definition at line 78 of file MIP_Problem.cc.

References max_space_dimension(), and OK().

  : external_space_dim(dim),
    internal_space_dim(0),
    tableau(),
    working_cost(0),
    mapping(),
    base(),
    status(PARTIALLY_SATISFIABLE),
    pricing(PRICING_STEEPEST_EDGE_FLOAT),
    initialized(false),
    input_cs(),
    inherited_constraints(0),
    first_pending_constraint(0),
    input_obj_function(),
    opt_mode(MAXIMIZATION),
    last_generator(point()),
    i_variables() {
  // Check for space dimension overflow.
  if (dim > max_space_dimension()) {
    throw std::length_error("PPL::MIP_Problem::MIP_Problem(dim, cs, obj, "
                            "mode):\n"
                            "dim exceeds the maximum allowed "
                            "space dimension.");
  }
  PPL_ASSERT(OK());
}

template<typename In >

Parma_Polyhedra_Library::MIP_Problem::MIP_Problem	(	dimension_type	dim,
		In	first,
		In	last,
		const Variables_Set &	int_vars,
		const Linear_Expression &	obj = Linear_Expression::zero(),
		Optimization_Mode	mode = MAXIMIZATION
	)

Builds an MIP problem having space dimension dim from the sequence of constraints in the range 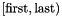, the objective function obj and optimization mode mode; those dimensions whose indices occur in int_vars are constrained to take an integer value.

Parameters

dim	The dimension of the vector space enclosing *this.
first	An input iterator to the start of the sequence of constraints.
last	A past-the-end input iterator to the sequence of constraints.
int_vars	The set of variables' indexes that are constrained to take integer values.
obj	The objective function (optional argument with default value ).
mode	The optimization mode (optional argument with default value MAXIMIZATION).

Exceptions

std::length_error	Thrown if dim exceeds max_space_dimension().
std::invalid_argument	Thrown if a constraint in the sequence is a strict inequality, if the space dimension of a constraint (resp., of the objective function or of the integer variables) or the space dimension of the integer variable set is strictly greater than dim.

Definition at line 32 of file MIP_Problem_templates.hh.

References add_constraint_helper(), external_space_dim, i_variables, input_cs, max_space_dimension(), OK(), Parma_Polyhedra_Library::Variables_Set::space_dimension(), and Parma_Polyhedra_Library::Linear_Expression::space_dimension().

  : external_space_dim(dim),
    internal_space_dim(0),
    tableau(),
    working_cost(0),
    mapping(),
    base(),
    status(PARTIALLY_SATISFIABLE),
    pricing(PRICING_STEEPEST_EDGE_FLOAT),
    initialized(false),
    input_cs(),
    inherited_constraints(0),
    first_pending_constraint(0),
    input_obj_function(obj),
    opt_mode(mode),
    last_generator(point()),
    i_variables(int_vars) {
  // Check that integer Variables_Set does not exceed the space dimension
  // of the problem.
  if (i_variables.space_dimension() > external_space_dim) {
    std::ostringstream s;
    s << "PPL::MIP_Problem::MIP_Problem"
      << "(dim, first, last, int_vars, obj, mode):\n"
      << "dim == "<< external_space_dim << " and int_vars.space_dimension() =="
      << " " << i_variables.space_dimension() << " are dimension"
      "incompatible.";
    throw std::invalid_argument(s.str());
  }

  // Check for space dimension overflow.
  if (dim > max_space_dimension()) {
    throw std::length_error("PPL::MIP_Problem:: MIP_Problem(dim, first, "
                            "last, int_vars, obj, mode):\n"
                            "dim exceeds the maximum allowed"
                            "space dimension.");
  }
  // Check the objective function.
  if (obj.space_dimension() > dim) {
    std::ostringstream s;
    s << "PPL::MIP_Problem::MIP_Problem(dim, first, last,"
      << "int_vars, obj, mode):\n"
      << "obj.space_dimension() == "<< obj.space_dimension()
      << " exceeds d == "<< dim << ".";
    throw std::invalid_argument(s.str());
  }
  // Check the constraints.
  try {
    for (In i = first; i != last; ++i) {
      if (i->is_strict_inequality()) {
        throw std::invalid_argument("PPL::MIP_Problem::"
                                    "MIP_Problem(dim, first, last, int_vars,"
                                    "obj, mode):\nrange [first, last) contains"
                                    "a strict inequality constraint.");
      }
      if (i->space_dimension() > dim) {
        std::ostringstream s;
        s << "PPL::MIP_Problem::"
          << "MIP_Problem(dim, first, last, int_vars, obj, mode):\n"
          << "range [first, last) contains a constraint having space"
          << "dimension  == " << i->space_dimension() << " that exceeds"
          "this->space_dimension == " << dim << ".";
        throw std::invalid_argument(s.str());
      }
      add_constraint_helper(*i);
    }
  } catch (...) {
    // Delete the allocated constraints, to avoid memory leaks.

    for (Constraint_Sequence::const_iterator
          i = input_cs.begin(), i_end = input_cs.end();
          i != i_end; ++i) {
      delete *i;
    }

    throw;
  }
  PPL_ASSERT(OK());
}

template<typename In >

Parma_Polyhedra_Library::MIP_Problem::MIP_Problem	(	dimension_type	dim,
		In	first,
		In	last,
		const Linear_Expression &	obj = Linear_Expression::zero(),
		Optimization_Mode	mode = MAXIMIZATION
	)

Builds an MIP problem having space dimension dim from the sequence of constraints in the range 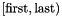, the objective function obj and optimization mode mode.

Parameters

dim	The dimension of the vector space enclosing *this.
first	An input iterator to the start of the sequence of constraints.
last	A past-the-end input iterator to the sequence of constraints.
obj	The objective function (optional argument with default value ).
mode	The optimization mode (optional argument with default value MAXIMIZATION).

Exceptions

std::length_error	Thrown if dim exceeds max_space_dimension().
std::invalid_argument	Thrown if a constraint in the sequence is a strict inequality or if the space dimension of a constraint (resp., of the objective function or of the integer variables) is strictly greater than dim.

Definition at line 116 of file MIP_Problem_templates.hh.

References add_constraint_helper(), input_cs, max_space_dimension(), OK(), and Parma_Polyhedra_Library::Linear_Expression::space_dimension().

  : external_space_dim(dim),
    internal_space_dim(0),
    tableau(),
    working_cost(0),
    mapping(),
    base(),
    status(PARTIALLY_SATISFIABLE),
    pricing(PRICING_STEEPEST_EDGE_FLOAT),
    initialized(false),
    input_cs(),
    inherited_constraints(0),
    first_pending_constraint(0),
    input_obj_function(obj),
    opt_mode(mode),
    last_generator(point()),
    i_variables() {
  // Check for space dimension overflow.
  if (dim > max_space_dimension()) {
    throw std::length_error("PPL::MIP_Problem::"
                            "MIP_Problem(dim, first, last, obj, mode):\n"
                            "dim exceeds the maximum allowed space "
                            "dimension.");
  }
  // Check the objective function.
  if (obj.space_dimension() > dim) {
    std::ostringstream s;
    s << "PPL::MIP_Problem::MIP_Problem(dim, first, last,"
      << " obj, mode):\n"
      << "obj.space_dimension() == "<< obj.space_dimension()
      << " exceeds d == "<< dim << ".";
    throw std::invalid_argument(s.str());
  }
  // Check the constraints.
  try {
    for (In i = first; i != last; ++i) {
      if (i->is_strict_inequality()) {
        throw std::invalid_argument("PPL::MIP_Problem::"
                                    "MIP_Problem(dim, first, last, obj, mode):"
                                    "\n"
                                    "range [first, last) contains a strict "
                                    "inequality constraint.");
      }
      if (i->space_dimension() > dim) {
        std::ostringstream s;
        s << "PPL::MIP_Problem::"
          << "MIP_Problem(dim, first, last, obj, mode):\n"
          << "range [first, last) contains a constraint having space"
          << "dimension" << " == " << i->space_dimension() << " that exceeds"
          "this->space_dimension == " << dim << ".";
        throw std::invalid_argument(s.str());
      }
      add_constraint_helper(*i);
    }
  } catch (...) {
    // Delete the allocated constraints, to avoid memory leaks.

    for (Constraint_Sequence::const_iterator
          i = input_cs.begin(), i_end = input_cs.end();
          i != i_end; ++i) {
      delete *i;
    }

    throw;
  }
  PPL_ASSERT(OK());
}

Parma_Polyhedra_Library::MIP_Problem::MIP_Problem	(	dimension_type	dim,
		const Constraint_System &	cs,
		const Linear_Expression &	obj = Linear_Expression::zero(),
		Optimization_Mode	mode = MAXIMIZATION
	)

Builds an MIP problem having space dimension dim from the constraint system cs, the objective function obj and optimization mode mode.

Parameters

dim	The dimension of the vector space enclosing *this.
cs	The constraint system defining the feasible region.
obj	The objective function (optional argument with default value ).
mode	The optimization mode (optional argument with default value MAXIMIZATION).

Exceptions

std::length_error	Thrown if dim exceeds max_space_dimension().
std::invalid_argument	Thrown if the constraint system contains any strict inequality or if the space dimension of the constraint system (resp., the objective function) is strictly greater than dim.

Definition at line 105 of file MIP_Problem.cc.

References add_constraint_helper(), Parma_Polyhedra_Library::Constraint_System::begin(), Parma_Polyhedra_Library::Constraint_System::end(), Parma_Polyhedra_Library::Constraint_System::has_strict_inequalities(), max_space_dimension(), OK(), Parma_Polyhedra_Library::Constraint_System::space_dimension(), and Parma_Polyhedra_Library::Linear_Expression::space_dimension().

  : external_space_dim(dim),
    internal_space_dim(0),
    tableau(),
    working_cost(0),
    mapping(),
    base(),
    status(PARTIALLY_SATISFIABLE),
    pricing(PRICING_STEEPEST_EDGE_FLOAT),
    initialized(false),
    input_cs(),
    inherited_constraints(0),
    first_pending_constraint(0),
    input_obj_function(obj),
    opt_mode(mode),
    last_generator(point()),
    i_variables() {
  // Check for space dimension overflow.
  if (dim > max_space_dimension()) {
    throw std::length_error("PPL::MIP_Problem::MIP_Problem(dim, cs, obj, "
                            "mode):\n"
                            "dim exceeds the maximum allowed"
                            "space dimension.");
  }
  // Check the objective function.
  if (obj.space_dimension() > dim) {
    std::ostringstream s;
    s << "PPL::MIP_Problem::MIP_Problem(dim, cs, obj,"
      << " mode):\n"
      << "obj.space_dimension() == "<< obj.space_dimension()
      << " exceeds dim == "<< dim << ".";
    throw std::invalid_argument(s.str());
  }
  // Check the constraint system.
  if (cs.space_dimension() > dim) {
    std::ostringstream s;
    s << "PPL::MIP_Problem::MIP_Problem(dim, cs, obj, mode):\n"
      << "cs.space_dimension == " << cs.space_dimension()
      << " exceeds dim == " << dim << ".";
    throw std::invalid_argument(s.str());
  }
  if (cs.has_strict_inequalities()) {
    throw std::invalid_argument("PPL::MIP_Problem::"
                                "MIP_Problem(d, cs, obj, m):\n"
                                "cs contains strict inequalities.");
  }
  // Actually copy the constraints.
  for (Constraint_System::const_iterator
         i = cs.begin(), i_end = cs.end(); i != i_end; ++i) {
    add_constraint_helper(*i);
  }

  PPL_ASSERT(OK());
}

Parma_Polyhedra_Library::MIP_Problem::MIP_Problem ( const MIP_Problem &  y )

inline

Ordinary copy constructor.

Definition at line 44 of file MIP_Problem_inlines.hh.

References add_constraint_helper(), input_cs, and OK().

  : external_space_dim(y.external_space_dim),
    internal_space_dim(y.internal_space_dim),
    tableau(y.tableau),
    working_cost(y.working_cost),
    mapping(y.mapping),
    base(y.base),
    status(y.status),
    pricing(y.pricing),
    initialized(y.initialized),
    input_cs(),
    inherited_constraints(0),
    first_pending_constraint(),
    input_obj_function(y.input_obj_function),
    opt_mode(y.opt_mode),
    last_generator(y.last_generator),
    i_variables(y.i_variables) {
  input_cs.reserve(y.input_cs.size());
  for (Constraint_Sequence::const_iterator i = y.input_cs.begin(),
         i_end = y.input_cs.end(); i != i_end; ++i) {
    add_constraint_helper(*(*i));
  }
  PPL_ASSERT(OK());
}

Parma_Polyhedra_Library::MIP_Problem::~MIP_Problem ( )

inline

Destructor.

Definition at line 111 of file MIP_Problem_inlines.hh.

References inherited_constraints, input_cs, and Parma_Polyhedra_Library::nth_iter().

                          {
  // NOTE: do NOT delete inherited constraints; they are owned
  // (and will eventually be deleted) by ancestors.
  for (Constraint_Sequence::const_iterator
         i = nth_iter(input_cs, inherited_constraints),
         i_end = input_cs.end(); i != i_end; ++i) {
    delete *i;
  }
}

Parma_Polyhedra_Library::MIP_Problem::MIP_Problem ( const MIP_Problem &  y, Inherit_Constraints    )

inlineprivate

Copy constructor inheriting constraints.

Definition at line 70 of file MIP_Problem_inlines.hh.

References OK().

  : external_space_dim(y.external_space_dim),
    internal_space_dim(y.internal_space_dim),
    tableau(y.tableau),
    working_cost(y.working_cost),
    mapping(y.mapping),
    base(y.base),
    status(y.status),
    pricing(y.pricing),
    initialized(y.initialized),
    input_cs(y.input_cs),
    // NOTE: The constraints are inherited, NOT copied!
    inherited_constraints(y.input_cs.size()),
    first_pending_constraint(y.first_pending_constraint),
    input_obj_function(y.input_obj_function),
    opt_mode(y.opt_mode),
    last_generator(y.last_generator),
    i_variables(y.i_variables) {
  PPL_ASSERT(OK());
}

Member Function Documentation

void Parma_Polyhedra_Library::MIP_Problem::add_constraint

(

const Constraint &

c

)

Adds a copy of constraint c to the MIP problem.

Exceptions

std::invalid_argument

Thrown if the constraint c is a strict inequality or if its space dimension is strictly greater than the space dimension of *this.

Definition at line 164 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::Constraint::is_strict_inequality(), and Parma_Polyhedra_Library::Constraint::space_dimension().

Referenced by Parma_Polyhedra_Library::BD_Shape< T >::BD_Shape(), Parma_Polyhedra_Library::BD_Shape< T >::BFT00_upper_bound_assign_if_exact(), Parma_Polyhedra_Library::Box< ITV >::Box(), is_mip_satisfiable(), Parma_Polyhedra_Library::Octagonal_Shape< T >::Octagonal_Shape(), Parma_Polyhedra_Library::Polyhedron::simplify_using_context_assign(), and solve_mip().

                                                  {
  if (space_dimension() < c.space_dimension()) {
    std::ostringstream s;
    s << "PPL::MIP_Problem::add_constraint(c):\n"
      << "c.space_dimension() == "<< c.space_dimension() << " exceeds "
         "this->space_dimension == " << space_dimension() << ".";
    throw std::invalid_argument(s.str());
  }
  if (c.is_strict_inequality()) {
    throw std::invalid_argument("PPL::MIP_Problem::add_constraint(c):\n"
                                "c is a strict inequality.");
  }
  add_constraint_helper(c);
  if (status != UNSATISFIABLE) {
    status = PARTIALLY_SATISFIABLE;
  }
  PPL_ASSERT(OK());
}

void Parma_Polyhedra_Library::MIP_Problem::add_constraint_helper ( const Constraint &  c )

inlineprivate

Helper method: implements exception safe addition.

Definition at line 92 of file MIP_Problem_inlines.hh.

References Parma_Polyhedra_Library::compute_capacity(), and input_cs.

Referenced by MIP_Problem().

                                                      {
  // For exception safety, reserve space for the new element.
  const dimension_type size = input_cs.size();
  if (size == input_cs.capacity()) {
    const dimension_type max_size = input_cs.max_size();
    if (size == max_size) {
      throw std::length_error("MIP_Problem::add_constraint(): "
                              "too many constraints");
    }
    // Use an exponential grow policy to avoid too many reallocations.
    input_cs.reserve(compute_capacity(size + 1, max_size));
  }

  // This operation does not throw, because the space for the new element
  // has already been reserved: hence the new-ed Constraint is safe.
  input_cs.push_back(new Constraint(c));
}

void Parma_Polyhedra_Library::MIP_Problem::add_constraints

(

const Constraint_System &

cs

)

Adds a copy of the constraints in cs to the MIP problem.

Exceptions

std::invalid_argument

Thrown if the constraint system cs contains any strict inequality or if its space dimension is strictly greater than the space dimension of *this.

Definition at line 184 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::Constraint_System::begin(), Parma_Polyhedra_Library::Constraint_System::end(), Parma_Polyhedra_Library::Constraint_System::has_strict_inequalities(), and Parma_Polyhedra_Library::Constraint_System::space_dimension().

Referenced by Parma_Polyhedra_Library::BD_Shape< T >::BD_Shape(), Parma_Polyhedra_Library::Box< ITV >::Box(), Parma_Polyhedra_Library::Octagonal_Shape< T >::Octagonal_Shape(), Parma_Polyhedra_Library::Polyhedron::simplify_using_context_assign(), and Parma_Polyhedra_Library::Polyhedron::strongly_minimize_constraints().

                                                           {
  if (space_dimension() < cs.space_dimension()) {
    std::ostringstream s;
    s << "PPL::MIP_Problem::add_constraints(cs):\n"
      << "cs.space_dimension() == " << cs.space_dimension()
      << " exceeds this->space_dimension() == " << this->space_dimension()
      << ".";
    throw std::invalid_argument(s.str());
  }
  if (cs.has_strict_inequalities()) {
    throw std::invalid_argument("PPL::MIP_Problem::add_constraints(cs):\n"
                                "cs contains strict inequalities.");
  }
  for (Constraint_System::const_iterator
         i = cs.begin(), i_end = cs.end(); i != i_end; ++i) {
    add_constraint_helper(*i);
  }
  if (status != UNSATISFIABLE) {
    status = PARTIALLY_SATISFIABLE;
  }
  PPL_ASSERT(OK());
}

void Parma_Polyhedra_Library::MIP_Problem::add_space_dimensions_and_embed

(

dimension_type

m

)

Adds m new space dimensions and embeds the old MIP problem in the new vector space.

Parameters

m	The number of dimensions to add.

Exceptions

std::length_error

Thrown if adding m new space dimensions would cause the vector space to exceed dimension max_space_dimension().

The new space dimensions will be those having the highest indexes in the new MIP problem; they are initially unconstrained.

Definition at line 374 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::max_space_dimension().

Referenced by Parma_Polyhedra_Library::Polyhedron::simplify_using_context_assign(), and Parma_Polyhedra_Library::Polyhedron::strongly_minimize_constraints().

                                                                     {
  // The space dimension of the resulting MIP problem should not
  // overflow the maximum allowed space dimension.
  if (m > max_space_dimension() - space_dimension()) {
    throw std::length_error("PPL::MIP_Problem::"
                            "add_space_dimensions_and_embed(m):\n"
                            "adding m new space dimensions exceeds "
                            "the maximum allowed space dimension.");
  }
  external_space_dim += m;
  if (status != UNSATISFIABLE) {
    status = PARTIALLY_SATISFIABLE;
  }
  PPL_ASSERT(OK());
}

void Parma_Polyhedra_Library::MIP_Problem::add_to_integer_space_dimensions

(

const Variables_Set &

i_vars

)

Sets the variables whose indexes are in set i_vars to be integer space dimensions.

Exceptions

std::invalid_argument

Thrown if some index in i_vars does not correspond to a space dimension in *this.

Definition at line 392 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::Variables_Set::space_dimension().

                                                             {
  if (i_vars.space_dimension() > external_space_dim) {
    throw std::invalid_argument("PPL::MIP_Problem::"
                                "add_to_integer_space_dimension(i_vars):\n"
                                "*this and i_vars are dimension"
                                "incompatible.");
  }
  const dimension_type original_size = i_variables.size();
  i_variables.insert(i_vars.begin(), i_vars.end());
  // If a new integral variable was inserted, set the internal status to
  // PARTIALLY_SATISFIABLE.
  if (i_variables.size() != original_size && status != UNSATISFIABLE) {
    status = PARTIALLY_SATISFIABLE;
  }
}

void Parma_Polyhedra_Library::MIP_Problem::ascii_dump

(

)

const

Writes to std::cerr an ASCII representation of *this.

void Parma_Polyhedra_Library::MIP_Problem::ascii_dump

(

std::ostream &

s

)

const

Writes to s an ASCII representation of *this.

Definition at line 2545 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::MAXIMIZATION.

                                              {
  using namespace IO_Operators;
  s << "\nexternal_space_dim: " << external_space_dim << " \n";
  s << "\ninternal_space_dim: " << internal_space_dim << " \n";

  const dimension_type input_cs_size = input_cs.size();

  s << "\ninput_cs( " << input_cs_size << " )\n";
  for (dimension_type i = 0; i < input_cs_size; ++i) {
    input_cs[i]->ascii_dump(s);
  }

  s << "\ninherited_constraints: " <<  inherited_constraints
    << std::endl;

  s << "\nfirst_pending_constraint: " <<  first_pending_constraint
    << std::endl;

  s << "\ninput_obj_function\n";
  input_obj_function.ascii_dump(s);
  s << "\nopt_mode "
    << ((opt_mode == MAXIMIZATION) ? "MAXIMIZATION" : "MINIMIZATION") << "\n";

  s << "\ninitialized: " << (initialized ? "YES" : "NO") << "\n";
  s << "\npricing: ";
  switch (pricing) {
  case PRICING_STEEPEST_EDGE_FLOAT:
    s << "PRICING_STEEPEST_EDGE_FLOAT";
    break;
  case PRICING_STEEPEST_EDGE_EXACT:
    s << "PRICING_STEEPEST_EDGE_EXACT";
    break;
  case PRICING_TEXTBOOK:
    s << "PRICING_TEXTBOOK";
    break;
  }
  s << "\n";

  s << "\nstatus: ";
  switch (status) {
  case UNSATISFIABLE:
    s << "UNSATISFIABLE";
    break;
  case SATISFIABLE:
    s << "SATISFIABLE";
    break;
  case UNBOUNDED:
    s << "UNBOUNDED";
    break;
  case OPTIMIZED:
    s << "OPTIMIZED";
    break;
  case PARTIALLY_SATISFIABLE:
    s << "PARTIALLY_SATISFIABLE";
    break;
  }
  s << "\n";

  s << "\ntableau\n";
  tableau.ascii_dump(s);
  s << "\nworking_cost( " << working_cost.size()<< " )\n";
  working_cost.ascii_dump(s);

  const dimension_type base_size = base.size();
  s << "\nbase( " << base_size << " )\n";
  for (dimension_type i = 0; i != base_size; ++i) {
    s << base[i] << ' ';
  }

  s << "\nlast_generator\n";
  last_generator.ascii_dump(s);

  const dimension_type mapping_size = mapping.size();
  s << "\nmapping( " << mapping_size << " )\n";
  for (dimension_type i = 1; i < mapping_size; ++i) {
    s << "\n"<< i << " -> " << mapping[i].first << " -> " << mapping[i].second
      << ' ';
  }

  s << "\n\ninteger_variables";
  i_variables.ascii_dump(s);
}

bool Parma_Polyhedra_Library::MIP_Problem::ascii_load

(

std::istream &

s

)

Loads from s an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets *this accordingly. Returns true if successful, false otherwise.

Definition at line 2631 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::Constraint::ascii_load(), c, Parma_Polyhedra_Library::MAXIMIZATION, Parma_Polyhedra_Library::MINIMIZATION, and Parma_Polyhedra_Library::Constraint::zero_dim_positivity().

                                        {
  std::string str;
  if (!(s >> str) || str != "external_space_dim:") {
    return false;
  }

  if (!(s >> external_space_dim)) {
    return false;
  }

  if (!(s >> str) || str != "internal_space_dim:") {
    return false;
  }

  if (!(s >> internal_space_dim)) {
    return false;
  }

  if (!(s >> str) || str != "input_cs(") {
    return false;
  }

  dimension_type input_cs_size;

  if (!(s >> input_cs_size)) {
    return false;
  }

  if (!(s >> str) || str != ")") {
    return false;
  }

  Constraint c(Constraint::zero_dim_positivity());
  input_cs.reserve(input_cs_size);
  for (dimension_type i = 0; i < input_cs_size; ++i) {
    if (!c.ascii_load(s)) {
      return false;
    }
    add_constraint_helper(c);
  }

  if (!(s >> str) || str != "inherited_constraints:") {
    return false;
  }

  if (!(s >> inherited_constraints)) {
    return false;
  }
  // NOTE: we loaded the number of inherited constraints, but we nonetheless
  // reset to zero the corresponding data member, since we do not support
  // constraint inheritance via ascii_load.
  inherited_constraints = 0;

  if (!(s >> str) || str != "first_pending_constraint:") {
    return false;
  }
  if (!(s >> first_pending_constraint)) {
    return false;
  }
  if (!(s >> str) || str != "input_obj_function") {
    return false;
  }
  if (!input_obj_function.ascii_load(s)) {
    return false;
  }
  if (!(s >> str) || str != "opt_mode") {
    return false;
  }
  if (!(s >> str)) {
    return false;
  }
  if (str == "MAXIMIZATION") {
    set_optimization_mode(MAXIMIZATION);
  }
  else {
    if (str != "MINIMIZATION") {
      return false;
    }
    set_optimization_mode(MINIMIZATION);
  }

  if (!(s >> str) || str != "initialized:") {
    return false;
  }
  if (!(s >> str)) {
    return false;
  }
  if (str == "YES") {
    initialized = true;
  }
  else if (str == "NO") {
    initialized = false;
  }
  else {
    return false;
  }

  if (!(s >> str) || str != "pricing:") {
    return false;
  }
  if (!(s >> str)) {
    return false;
  }
  if (str == "PRICING_STEEPEST_EDGE_FLOAT") {
    pricing = PRICING_STEEPEST_EDGE_FLOAT;
  }
  else if (str == "PRICING_STEEPEST_EDGE_EXACT") {
    pricing = PRICING_STEEPEST_EDGE_EXACT;
  }
  else if (str == "PRICING_TEXTBOOK") {
    pricing = PRICING_TEXTBOOK;
  }
  else {
    return false;
  }

  if (!(s >> str) || str != "status:") {
    return false;
  }

  if (!(s >> str)) {
    return false;
  }

  if (str == "UNSATISFIABLE") {
    status = UNSATISFIABLE;
  }
  else if (str == "SATISFIABLE") {
    status = SATISFIABLE;
  }
  else if (str == "UNBOUNDED") {
    status = UNBOUNDED;
  }
  else if (str == "OPTIMIZED") {
    status = OPTIMIZED;
  }
  else if (str == "PARTIALLY_SATISFIABLE") {
    status = PARTIALLY_SATISFIABLE;
  }
  else {
    return false;
  }

  if (!(s >> str) || str != "tableau") {
    return false;
  }

  if (!tableau.ascii_load(s)) {
    return false;
  }

  if (!(s >> str) || str != "working_cost(") {
    return false;
  }

  dimension_type working_cost_dim;

  if (!(s >> working_cost_dim)) {
    return false;
  }

  if (!(s >> str) || str != ")") {
    return false;
  }

  if (!working_cost.ascii_load(s)) {
    return false;
  }

  if (!(s >> str) || str != "base(") {
    return false;
  }

  dimension_type base_size;
  if (!(s >> base_size)) {
    return false;
  }

  if (!(s >> str) || str != ")") {
    return false;
  }

  for (dimension_type i = 0; i != base_size; ++i) {
    dimension_type base_value;
    if (!(s >> base_value)) {
      return false;
    }
    base.push_back(base_value);
  }

  if (!(s >> str) || str != "last_generator") {
    return false;
  }

  if (!last_generator.ascii_load(s)) {
    return false;
  }

  if (!(s >> str) || str != "mapping(") {
    return false;
  }

  dimension_type mapping_size;
  if (!(s >> mapping_size)) {
    return false;
  }
  if (!(s >> str) || str != ")") {
    return false;
  }

  // The first `mapping' index is never used, so we initialize
  // it pushing back a dummy value.
  if (tableau.num_columns() != 0) {
    mapping.push_back(std::make_pair(0, 0));
  }

  for (dimension_type i = 1; i < mapping_size; ++i) {
    dimension_type index;
    if (!(s >> index)) {
      return false;
    }

    if (!(s >> str) || str != "->") {
      return false;
    }

    dimension_type first_value;
    if (!(s >> first_value)) {
      return false;
    }

    if (!(s >> str) || str != "->") {
      return false;
    }

    dimension_type second_value;
    if (!(s >> second_value)) {
      return false;
    }

    mapping.push_back(std::make_pair(first_value, second_value));
  }

  if (!(s >> str) || str != "integer_variables") {
    return false;
  }

  if (!i_variables.ascii_load(s)) {
    return false;
  }

  PPL_ASSERT(OK());
  return true;
}

bool Parma_Polyhedra_Library::MIP_Problem::choose_branching_variable ( const MIP_Problem &  mip, const Variables_Set &  i_vars, dimension_type &  branching_index  )

staticprivate

Returns true if and if only mip.last_generator satisfies all the integrality conditions implicitly stated using by i_vars.

Parameters

mip	The MIP problem. This is assumed to have no integral space dimension (so that it is a pure LP problem).
i_vars	The variables that are constrained to take an integer value.
branching_index	If false is returned, this will encode the non-integral variable index on which the `branch and bound' algorithm should be applied.

Definition at line 2137 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::Generator::coefficient(), Parma_Polyhedra_Library::Generator::divisor(), Parma_Polyhedra_Library::gcd_assign(), input_cs, Parma_Polyhedra_Library::Variables_Set::insert(), last_generator, PPL_DIRTY_TEMP_COEFFICIENT, and Parma_Polyhedra_Library::Variables_Set::space_dimension().

                                                                             {
  // Insert here the variables that do not satisfy the integrality
  // condition.
  const std::vector<Constraint*>& input_cs = mip.input_cs;
  const Generator& last_generator = mip.last_generator;
  Coefficient_traits::const_reference last_generator_divisor
    = last_generator.divisor();
  Variables_Set candidate_variables;

  // TODO: This can be optimized more, exploiting the (possible)
  // sparseness of last_generator, if the size of i_vars is expected to be
  // greater than the number of nonzeroes in last_generator in most cases.
  PPL_DIRTY_TEMP_COEFFICIENT(gcd);
  for (Variables_Set::const_iterator v_it = i_vars.begin(),
         v_end = i_vars.end(); v_it != v_end; ++v_it) {
    gcd_assign(gcd,
               last_generator.coefficient(Variable(*v_it)),
               last_generator_divisor);
    if (gcd != last_generator_divisor) {
      candidate_variables.insert(*v_it);
    }
  }
  // If this set is empty, we have finished.
  if (candidate_variables.empty()) {
    return true;
  }

  // Check how many `active constraints' we have and track them.
  const dimension_type input_cs_num_rows = input_cs.size();
  std::deque<bool> satisfiable_constraints(input_cs_num_rows, false);
  for (dimension_type i = input_cs_num_rows; i-- > 0; ) {
    // An equality is an `active constraint' by definition.
    // If we have an inequality, check if it is an `active constraint'.
    if (input_cs[i]->is_equality()
        || is_saturated(*(input_cs[i]), last_generator)) {
      satisfiable_constraints[i] = true;
    }
  }

  dimension_type winning_num_appearances = 0;

  std::vector<dimension_type>
    num_appearances(candidate_variables.space_dimension(), 0);

  // For every candidate variable, check how many times this appear in the
  // active constraints.
  for (dimension_type i = input_cs_num_rows; i-- > 0; ) {
    if (!satisfiable_constraints[i]) {
      continue;
    }
    // TODO: This can be optimized more, exploiting the (possible)
    // sparseness of input_cs, if the size of candidate_variables is expected
    // to be greater than the number of nonzeroes of most rows.
    for (Variables_Set::const_iterator v_it = candidate_variables.begin(),
            v_end = candidate_variables.end(); v_it != v_end; ++v_it) {
      if (*v_it >= input_cs[i]->space_dimension()) {
        break;
      }
      if (input_cs[i]->coefficient(Variable(*v_it)) != 0) {
        ++num_appearances[*v_it];
      }
    }
  }
  for (Variables_Set::const_iterator v_it = candidate_variables.begin(),
         v_end = candidate_variables.end(); v_it != v_end; ++v_it) {
    const dimension_type n = num_appearances[*v_it];
    if (n >= winning_num_appearances) {
      winning_num_appearances = n;
      branching_index = *v_it;
    }
  }
  return false;
}

void Parma_Polyhedra_Library::MIP_Problem::clear ( )

inline

Resets *this to be equal to the trivial MIP problem.

The space dimension is reset to .

Definition at line 205 of file MIP_Problem_inlines.hh.

References m_swap().

                   {
  MIP_Problem tmp;
  m_swap(tmp);
}

void Parma_Polyhedra_Library::MIP_Problem::compute_generator ( ) const

private

Computes a valid generator that satisfies all the constraints of the Linear Programming problem associated to *this.

Definition at line 1760 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::add_mul_assign(), Parma_Polyhedra_Library::exact_div_assign(), Parma_Polyhedra_Library::Sparse_Row::get(), last_generator, Parma_Polyhedra_Library::lcm_assign(), Parma_Polyhedra_Library::neg_assign(), PPL_DIRTY_TEMP_COEFFICIENT, and Parma_Polyhedra_Library::sub_mul_assign().

                                        {
  // Early exit for 0-dimensional problems.
  if (external_space_dim == 0) {
    MIP_Problem& x = const_cast<MIP_Problem&>(*this);
    x.last_generator = point();
    return;
  }

  // We will store in numer[] and in denom[] the numerators and
  // the denominators of every variable of the original problem.
  std::vector<Coefficient> numer(external_space_dim);
  std::vector<Coefficient> denom(external_space_dim);
  dimension_type row = 0;

  PPL_DIRTY_TEMP_COEFFICIENT(lcm);
  // Speculatively allocate temporaries out of loop.
  PPL_DIRTY_TEMP_COEFFICIENT(split_numer);
  PPL_DIRTY_TEMP_COEFFICIENT(split_denom);

  // We start to compute numer[] and denom[].
  for (dimension_type i = external_space_dim; i-- > 0; ) {
    Coefficient& numer_i = numer[i];
    Coefficient& denom_i = denom[i];
    // Get the value of the variable from the tableau
    // (if it is not a basic variable, the value is 0).
    const dimension_type original_var = mapping[i+1].first;
    if (is_in_base(original_var, row)) {
      const Row& t_row = tableau[row];
      Coefficient_traits::const_reference t_row_original_var
        = t_row.get(original_var);
      if (t_row_original_var > 0) {
        neg_assign(numer_i, t_row.get(0));
        denom_i = t_row_original_var;
      }
      else {
        numer_i = t_row.get(0);
        neg_assign(denom_i, t_row_original_var);
      }
    }
    else {
      numer_i = 0;
      denom_i = 1;
    }
    // Check whether the variable was split.
    const dimension_type split_var = mapping[i+1].second;
    if (split_var != 0) {
      // The variable was split: get the value for the negative component,
      // having index mapping[i+1].second .
      // Like before, we he have to check if the variable is in base.
      if (is_in_base(split_var, row)) {
        const Row& t_row = tableau[row];
        Coefficient_traits::const_reference t_row_split_var
          = t_row.get(split_var);
        if (t_row_split_var > 0) {
          neg_assign(split_numer, t_row.get(0));
          split_denom = t_row_split_var;
        }
        else {
          split_numer = t_row.get(0);
          neg_assign(split_denom, t_row_split_var);
        }
        // We compute the lcm to compute subsequently the difference
        // between the 2 variables.
        lcm_assign(lcm, denom_i, split_denom);
        exact_div_assign(denom_i, lcm, denom_i);
        exact_div_assign(split_denom, lcm, split_denom);
        numer_i *= denom_i;
        sub_mul_assign(numer_i, split_numer, split_denom);
        if (numer_i == 0) {
          denom_i = 1;
        }
        else {
          denom_i = lcm;
        }
      }
      // Note: if the negative component was not in base, then
      // it has value zero and there is nothing left to do.
    }
  }

  // Compute the lcm of all denominators.
  PPL_ASSERT(external_space_dim > 0);
  lcm = denom[0];
  for (dimension_type i = 1; i < external_space_dim; ++i) {
    lcm_assign(lcm, lcm, denom[i]);
  }
  // Use the denominators to store the numerators' multipliers
  // and then compute the normalized numerators.
  for (dimension_type i = external_space_dim; i-- > 0; ) {
    exact_div_assign(denom[i], lcm, denom[i]);
    numer[i] *= denom[i];
  }

  // Finally, build the generator.
  Linear_Expression expr;
  for (dimension_type i = external_space_dim; i-- > 0; ) {
    add_mul_assign(expr, numer[i], Variable(i));
  }

  MIP_Problem& x = const_cast<MIP_Problem&>(*this);
  x.last_generator = point(expr, lcm);
}

bool Parma_Polyhedra_Library::MIP_Problem::compute_simplex_using_exact_pricing ( )

private

Returns true if and if only the algorithm successfully computed a feasible solution.

Note

Uses an exact pricing method (either textbook or exact steepest edge), so that the result is deterministic across different architectures.

Definition at line 1629 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::maybe_abandon().

                                                    {
  PPL_ASSERT(tableau.num_columns() == working_cost.size());
  PPL_ASSERT(get_control_parameter(PRICING) == PRICING_STEEPEST_EDGE_EXACT
         || get_control_parameter(PRICING) == PRICING_TEXTBOOK);

  const dimension_type tableau_num_rows = tableau.num_rows();
  const bool textbook_pricing
    = (PRICING_TEXTBOOK == get_control_parameter(PRICING));

  while (true) {
    // Choose the index of the variable entering the base, if any.
    const dimension_type entering_var_index
      = textbook_pricing
      ? textbook_entering_index()
      : steepest_edge_exact_entering_index();
    // If no entering index was computed, the problem is solved.
    if (entering_var_index == 0) {
      return true;
    }

    // Choose the index of the row exiting the base.
    const dimension_type exiting_base_index
      = get_exiting_base_index(entering_var_index);
    // If no exiting index was computed, the problem is unbounded.
    if (exiting_base_index == tableau_num_rows) {
      return false;
    }

    // Check if the client has requested abandoning all expensive
    // computations. If so, the exception specified by the client
    // is thrown now.
    maybe_abandon();

    // We have not reached the optimality or unbounded condition:
    // compute the new base and the corresponding vertex of the
    // feasible region.
    pivot(entering_var_index, exiting_base_index);
#if PPL_NOISY_SIMPLEX
    ++num_iterations;
    if (num_iterations % 200 == 0) {
      std::cout << "Primal simplex: iteration " << num_iterations
                << "." << std::endl;
    }
#endif // PPL_NOISY_SIMPLEX
  }
}

bool Parma_Polyhedra_Library::MIP_Problem::compute_simplex_using_steepest_edge_float ( )

private

Returns true if and if only the algorithm successfully computed a feasible solution.

Note

Uses a floating point implementation of the steepest edge pricing method, so that the result is correct, but not deterministic across different architectures.

Definition at line 1531 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::abs_assign(), Parma_Polyhedra_Library::maybe_abandon(), Parma_Polyhedra_Library::neg_assign(), PPL_DIRTY_TEMP_COEFFICIENT, WEIGHT_ADD, and WEIGHT_BEGIN.

                                                          {
  // We may need to temporarily switch to the textbook pricing.
  const unsigned long allowed_non_increasing_loops = 200;
  unsigned long non_increased_times = 0;
  bool textbook_pricing = false;

  PPL_DIRTY_TEMP_COEFFICIENT(cost_sgn_coeff);
  PPL_DIRTY_TEMP_COEFFICIENT(current_numer);
  PPL_DIRTY_TEMP_COEFFICIENT(current_denom);
  PPL_DIRTY_TEMP_COEFFICIENT(challenger);
  PPL_DIRTY_TEMP_COEFFICIENT(current);

  cost_sgn_coeff = working_cost.get(working_cost.size() - 1);
  current_numer = working_cost.get(0);
  if (cost_sgn_coeff < 0) {
    neg_assign(current_numer);
  }
  abs_assign(current_denom, cost_sgn_coeff);
  PPL_ASSERT(tableau.num_columns() == working_cost.size());
  const dimension_type tableau_num_rows = tableau.num_rows();

  while (true) {
    // Choose the index of the variable entering the base, if any.
    const dimension_type entering_var_index
      = textbook_pricing
      ? textbook_entering_index()
      : steepest_edge_float_entering_index();

    // If no entering index was computed, the problem is solved.
    if (entering_var_index == 0) {
      return true;
    }

    // Choose the index of the row exiting the base.
    const dimension_type exiting_base_index
      = get_exiting_base_index(entering_var_index);
    // If no exiting index was computed, the problem is unbounded.
    if (exiting_base_index == tableau_num_rows) {
      return false;
    }

    // Check if the client has requested abandoning all expensive
    // computations. If so, the exception specified by the client
    // is thrown now.
    maybe_abandon();

    // We have not reached the optimality or unbounded condition:
    // compute the new base and the corresponding vertex of the
    // feasible region.
    pivot(entering_var_index, exiting_base_index);

    WEIGHT_BEGIN();
    // Now begins the objective function's value check to choose between
    // the `textbook' and the float `steepest-edge' technique.
    cost_sgn_coeff = working_cost.get(working_cost.size() - 1);

    challenger = working_cost.get(0);
    if (cost_sgn_coeff < 0) {
      neg_assign(challenger);
    }
    challenger *= current_denom;
    abs_assign(current, cost_sgn_coeff);
    current *= current_numer;
#if PPL_NOISY_SIMPLEX
    ++num_iterations;
    if (num_iterations % 200 == 0) {
      std::cout << "Primal simplex: iteration " << num_iterations
                << "." << std::endl;
    }
#endif // PPL_NOISY_SIMPLEX
    // If the following condition fails, probably there's a bug.
    PPL_ASSERT(challenger >= current);
    // If the value of the objective function does not improve,
    // keep track of that.
    if (challenger == current) {
      ++non_increased_times;
      // In the following case we will proceed using the `textbook'
      // technique, until the objective function is not improved.
      if (non_increased_times > allowed_non_increasing_loops) {
        textbook_pricing = true;
      }
    }
    // The objective function has an improvement:
    // reset `non_increased_times' and `textbook_pricing'.
    else {
      non_increased_times = 0;
      textbook_pricing = false;
    }
    current_numer = working_cost.get(0);
    if (cost_sgn_coeff < 0) {
      neg_assign(current_numer);
    }
    abs_assign(current_denom, cost_sgn_coeff);
    WEIGHT_ADD(433);
  }
}

MIP_Problem_Status Parma_Polyhedra_Library::MIP_Problem::compute_tableau ( std::vector< dimension_type > &  worked_out_row )

private

Assigns to this->tableau a simplex tableau representing the MIP problem, inserting into this->mapping the information that is required to recover the original MIP problem.

Returns

UNFEASIBLE_MIP_PROBLEM if the constraint system contains any trivially unfeasible constraint (tableau was not computed); UNBOUNDED_MIP_PROBLEM if the problem is trivially unbounded (the computed tableau contains no constraints); OPTIMIZED_MIP_PROBLEM> if the problem is neither trivially unfeasible nor trivially unbounded (the tableau was computed successfully).

MIP_Problem::const_iterator Parma_Polyhedra_Library::MIP_Problem::constraints_begin ( ) const

inline

Returns a read-only iterator to the first constraint defining the feasible region.

Definition at line 150 of file MIP_Problem_inlines.hh.

References input_cs.

Referenced by operator<<().

                                     {
  return const_iterator(input_cs.begin());
}

MIP_Problem::const_iterator Parma_Polyhedra_Library::MIP_Problem::constraints_end ( ) const

inline

Returns a past-the-end read-only iterator to the sequence of constraints defining the feasible region.

Definition at line 155 of file MIP_Problem_inlines.hh.

References input_cs.

Referenced by operator<<().

                                   {
  return const_iterator(input_cs.end());
}

void Parma_Polyhedra_Library::MIP_Problem::erase_artificials ( dimension_type  begin_artificials, dimension_type  end_artificials  )

private

Drop unnecessary artificial variables from the tableau and get ready for the second phase of the simplex algorithm.

Note

The two parameters denote a STL-like half-open range. It is assumed that begin_artificials is strictly greater than 0 and smaller than end_artificials.

Parameters

begin_artificials	The start of the tableau column index range for artificial variables.
end_artificials	The end of the tableau column index range for artificial variables. Note that column index end_artificial is excluded from the range.

Definition at line 1679 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::Sparse_Row::begin(), Parma_Polyhedra_Library::Sparse_Row::end(), Parma_Polyhedra_Library::CO_Tree::const_iterator::index(), and Parma_Polyhedra_Library::Sparse_Row::m_swap().

                                                                          {
  PPL_ASSERT(0 < begin_artificials && begin_artificials < end_artificials);

  const dimension_type old_last_column = tableau.num_columns() - 1;
  dimension_type tableau_n_rows = tableau.num_rows();
  // Step 1: try to remove from the base all the remaining slack variables.
  for (dimension_type i = 0; i < tableau_n_rows; ++i) {
    if (begin_artificials <= base[i] && base[i] < end_artificials) {
      // Search for a non-zero element to enter the base.
      Row& tableau_i = tableau[i];
      bool redundant = true;
      Row::const_iterator j = tableau_i.begin();
      Row::const_iterator j_end = tableau_i.end();
      // Skip the first element
      if (j != j_end && j.index() == 0) {
        ++j;
      }
      for ( ; (j != j_end) && (j.index() < begin_artificials); ++j) {
        if (*j != 0) {
          pivot(j.index(), i);
          redundant = false;
          break;
        }
      }
      if (redundant) {
        // No original variable entered the base:
        // the constraint is redundant and should be deleted.
        --tableau_n_rows;
        if (i < tableau_n_rows) {
          // Replace the redundant row with the last one,
          // taking care of adjusting the iteration index.
          tableau_i.m_swap(tableau[tableau_n_rows]);
          base[i] = base[tableau_n_rows];
          --i;
        }
        tableau.remove_trailing_rows(1);
        base.pop_back();
      }
    }
  }
  // Step 2: Adjust data structures so as to enter phase 2 of the simplex.

  // Resize the tableau.
  const dimension_type num_artificials = end_artificials - begin_artificials;
  tableau.remove_trailing_columns(num_artificials);

  // Zero the last column of the tableau.
  const dimension_type new_last_column = tableau.num_columns() - 1;
  for (dimension_type i = tableau_n_rows; i-- > 0; ) {
    tableau[i].reset(new_last_column);
  }

  // ... then properly set the element in the (new) last column,
  // encoding the kind of optimization; ...
  {
    // This block is equivalent to
    //
    // <CODE>
    //   working_cost[new_last_column] = working_cost.get(old_last_column);
    // </CODE>
    //
    // but it avoids storing zeroes.
    Coefficient_traits::const_reference old_cost
      = working_cost.get(old_last_column);
    if (old_cost == 0) {
      working_cost.reset(new_last_column);
    }
    else {
      working_cost.insert(new_last_column, old_cost);
    }
  }

  // ... and finally remove redundant columns.
  const dimension_type working_cost_new_size
    = working_cost.size() - num_artificials;
  working_cost.shrink(working_cost_new_size);
}

void Parma_Polyhedra_Library::MIP_Problem::evaluate_objective_function	(	const Generator &	evaluating_point,
		Coefficient &	numer,
		Coefficient &	denom
	)		const

Sets num and denom so that is the result of evaluating the objective function on evaluating_point.

Parameters

evaluating_point	The point on which the objective function will be evaluated.
numer	On exit will contain the numerator of the evaluated value.
denom	On exit will contain the denominator of the evaluated value.

Exceptions

std::invalid_argument

Thrown if *this and evaluating_point are dimension-incompatible or if the generator evaluating_point is not a point.

Definition at line 1942 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::Generator::divisor(), Parma_Polyhedra_Library::Generator::expr, Parma_Polyhedra_Library::Generator::is_point(), Parma_Polyhedra_Library::normalize2(), and Parma_Polyhedra_Library::Generator::space_dimension().

Referenced by Parma_Polyhedra_Library::BD_Shape< T >::BD_Shape(), Parma_Polyhedra_Library::Box< ITV >::Box(), Parma_Polyhedra_Library::BD_Shape< T >::max_min(), Parma_Polyhedra_Library::Octagonal_Shape< T >::max_min(), Parma_Polyhedra_Library::Octagonal_Shape< T >::Octagonal_Shape(), optimal_value(), and solve_mip().

                                                        {
  const dimension_type ep_space_dim = evaluating_point.space_dimension();
  if (space_dimension() < ep_space_dim) {
    throw std::invalid_argument("PPL::MIP_Problem::"
                                "evaluate_objective_function(p, n, d):\n"
                                "*this and p are dimension incompatible.");
  }
  if (!evaluating_point.is_point()) {
    throw std::invalid_argument("PPL::MIP_Problem::"
                                "evaluate_objective_function(p, n, d):\n"
                                "p is not a point.");
  }
  // Compute the smallest space dimension  between `input_obj_function'
  // and `evaluating_point'.
  const dimension_type working_space_dim
    = std::min(ep_space_dim, input_obj_function.space_dimension());
  input_obj_function.scalar_product_assign(numer,
                                           evaluating_point.expr,
                                           0, working_space_dim + 1);

  // Numerator and denominator should be coprime.
  normalize2(numer, evaluating_point.divisor(), numer, denom);
}

memory_size_type Parma_Polyhedra_Library::MIP_Problem::external_memory_in_bytes ( ) const

inline

Returns the size in bytes of the memory managed by *this.

Definition at line 212 of file MIP_Problem_inlines.hh.

References base, Parma_Polyhedra_Library::Generator::external_memory_in_bytes(), Parma_Polyhedra_Library::Linear_Expression::external_memory_in_bytes(), Parma_Polyhedra_Library::Sparse_Row::external_memory_in_bytes(), inherited_constraints, input_cs, input_obj_function, last_generator, mapping, Parma_Polyhedra_Library::nth_iter(), tableau, and working_cost.

Referenced by total_memory_in_bytes().

                                            {
  memory_size_type n
    = working_cost.external_memory_in_bytes()
    + tableau.external_memory_in_bytes()
    + input_obj_function.external_memory_in_bytes()
    + last_generator.external_memory_in_bytes();

  // Adding the external memory for `input_cs'.
  // NOTE: disregard inherited constraints, as they are owned by ancestors.
  n += input_cs.capacity() * sizeof(Constraint*);
  for (Constraint_Sequence::const_iterator
         i = nth_iter(input_cs, inherited_constraints),
         i_end = input_cs.end(); i != i_end; ++i) {
    n += ((*i)->total_memory_in_bytes());
  }

  // Adding the external memory for `base'.
  n += base.capacity() * sizeof(dimension_type);
  // Adding the external memory for `mapping'.
  n += mapping.capacity() * sizeof(std::pair<dimension_type, dimension_type>);
  return n;
}

const PPL::Generator & Parma_Polyhedra_Library::MIP_Problem::feasible_point

(

)

const

Returns a feasible point for *this, if it exists.

Exceptions

std::domain_error

Thrown if the MIP problem is not satisfiable.

Definition at line 225 of file MIP_Problem.cc.

Referenced by Parma_Polyhedra_Library::Implementation::Termination::one_affine_ranking_function_MS(), and Parma_Polyhedra_Library::Termination_Helpers::one_affine_ranking_function_PR_original().

                                     {
  if (is_satisfiable()) {
    return last_generator;
  }
  else {
    throw std::domain_error("PPL::MIP_Problem::feasible_point():\n"
                            "*this is not satisfiable.");
  }
}

MIP_Problem::Control_Parameter_Value Parma_Polyhedra_Library::MIP_Problem::get_control_parameter ( Control_Parameter_Name  name ) const

inline

Returns the value of the control parameter name.

Definition at line 165 of file MIP_Problem_inlines.hh.

References PPL_USED, PRICING, and pricing.

                                                                    {
  PPL_USED(name);
  PPL_ASSERT(name == PRICING);
  return pricing;
}

PPL::dimension_type Parma_Polyhedra_Library::MIP_Problem::get_exiting_base_index ( dimension_type  entering_var_index ) const

private

Computes the row index of the variable exiting the base of the MIP problem. Implemented with anti-cycling rule.

Returns

The row index of the variable exiting the base.

Parameters

entering_var_index

The column index of the variable entering the base.

Definition at line 1472 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::abs_assign(), Parma_Polyhedra_Library::exact_div_assign(), Parma_Polyhedra_Library::Sparse_Row::get(), Parma_Polyhedra_Library::lcm_assign(), PPL_DIRTY_TEMP_COEFFICIENT, Parma_Polyhedra_Library::Boundary_NS::sgn(), WEIGHT_ADD, and WEIGHT_BEGIN.

                                                                      {
  // The variable exiting the base should be associated to a tableau
  // constraint such that the ratio
  // tableau[i][entering_var_index] / tableau[i][base[i]]
  // is strictly positive and minimal.

  // Find the first tableau constraint `c' having a positive value for
  // tableau[i][entering_var_index] / tableau[i][base[i]]
  const dimension_type tableau_num_rows = tableau.num_rows();
  dimension_type exiting_base_index = tableau_num_rows;
  for (dimension_type i = 0; i < tableau_num_rows; ++i) {
    const Row& t_i = tableau[i];
    const int num_sign = sgn(t_i.get(entering_var_index));
    if (num_sign != 0 && num_sign == sgn(t_i.get(base[i]))) {
      exiting_base_index = i;
      break;
    }
  }
  // Check for unboundedness.
  if (exiting_base_index == tableau_num_rows) {
    return tableau_num_rows;
  }

  // Reaching this point means that a variable will definitely exit the base.
  PPL_DIRTY_TEMP_COEFFICIENT(lcm);
  PPL_DIRTY_TEMP_COEFFICIENT(current_min);
  PPL_DIRTY_TEMP_COEFFICIENT(challenger);
  Coefficient t_e0 = tableau[exiting_base_index].get(0);
  Coefficient t_ee = tableau[exiting_base_index].get(entering_var_index);
  for (dimension_type i = exiting_base_index + 1; i < tableau_num_rows; ++i) {
    const Row& t_i = tableau[i];
    Coefficient_traits::const_reference t_ie = t_i.get(entering_var_index);
    const int t_ie_sign = sgn(t_ie);
    if (t_ie_sign != 0 && t_ie_sign == sgn(t_i.get(base[i]))) {
      WEIGHT_BEGIN();
      Coefficient_traits::const_reference t_i0 = t_i.get(0);
      lcm_assign(lcm, t_ee, t_ie);
      exact_div_assign(current_min, lcm, t_ee);
      current_min *= t_e0;
      abs_assign(current_min);
      exact_div_assign(challenger, lcm, t_ie);
      challenger *= t_i0;
      abs_assign(challenger);
      current_min -= challenger;
      const int sign = sgn(current_min);
      if (sign > 0
          || (sign == 0 && base[i] < base[exiting_base_index])) {
        exiting_base_index = i;
        t_e0 = t_i0;
        t_ee = t_ie;
      }
      WEIGHT_ADD(642);
    }
  }
  return exiting_base_index;
}

const Variables_Set & Parma_Polyhedra_Library::MIP_Problem::integer_space_dimensions ( ) const

inline

Returns a set containing all the variables' indexes constrained to be integral.

Definition at line 160 of file MIP_Problem_inlines.hh.

References i_variables.

Referenced by is_mip_satisfiable(), operator<<(), and solve().

                                            {
  return i_variables;
}

bool Parma_Polyhedra_Library::MIP_Problem::is_in_base ( dimension_type  var_index, dimension_type &  row_index  ) const

private

Definition at line 409 of file MIP_Problem.cc.

                                                              {
  for (row_index = base.size(); row_index-- > 0; ) {
    if (base[row_index] == var_index) {
      return true;
    }
  }
  return false;
}

bool Parma_Polyhedra_Library::MIP_Problem::is_lp_satisfiable ( ) const

private

Returns true if and if only the LP problem is satisfiable.

Definition at line 1969 of file MIP_Problem.cc.

References external_space_dim, first_pending_constraint, initialized, internal_space_dim, mapping, process_pending_constraints(), and tableau.

Referenced by is_mip_satisfiable(), is_satisfiable(), solve(), and solve_mip().

                                        {
#if PPL_NOISY_SIMPLEX
  num_iterations = 0;
#endif // PPL_NOISY_SIMPLEX
  switch (status) {
  case UNSATISFIABLE:
    return false;
  case SATISFIABLE:
    // Intentionally fall through.
  case UNBOUNDED:
    // Intentionally fall through.
  case OPTIMIZED:
    // Intentionally fall through.
    return true;
  case PARTIALLY_SATISFIABLE:
    {
      MIP_Problem& x = const_cast<MIP_Problem&>(*this);
      // This code tries to handle the case that happens if the tableau is
      // empty, so it must be initialized.
      if (tableau.num_columns() == 0) {
        // Add two columns, the first that handles the inhomogeneous term and
        // the second that represent the `sign'.
        x.tableau.add_zero_columns(2);
        // Sync `mapping' for the inhomogeneous term.
        x.mapping.push_back(std::make_pair(0, 0));
        // The internal data structures are ready, so prepare for more
        // assertion to be checked.
        x.initialized = true;
      }

      // Apply incrementality to the pending constraint system.
      x.process_pending_constraints();
      // Update `first_pending_constraint': no more pending.
      x.first_pending_constraint = input_cs.size();
      // Update also `internal_space_dim'.
      x.internal_space_dim = x.external_space_dim;
      PPL_ASSERT(OK());
      return status != UNSATISFIABLE;
    }
  }
  // We should not be here!
  PPL_UNREACHABLE;
  return false;
}

bool Parma_Polyhedra_Library::MIP_Problem::is_mip_satisfiable ( MIP_Problem &  mip, const Variables_Set &  i_vars, Generator &  p  )

staticprivate

Returns true if and if only the MIP problem mip is satisfiable when variables in i_vars can only take integral values.

Parameters

mip	The MIP problem. This is assumed to have no integral space dimension (so that it is a pure LP problem).
i_vars	The variables that are constrained to take integral values.
p	If true is returned, it will encode a feasible point.

Definition at line 2214 of file MIP_Problem.cc.

References add_constraint(), Parma_Polyhedra_Library::assign_r(), Parma_Polyhedra_Library::Generator::coefficient(), Parma_Polyhedra_Library::Generator::divisor(), Parma_Polyhedra_Library::gcd_assign(), integer_space_dimensions(), is_lp_satisfiable(), last_generator, PPL_DIRTY_TEMP, PPL_DIRTY_TEMP_COEFFICIENT, Parma_Polyhedra_Library::ROUND_DOWN, Parma_Polyhedra_Library::ROUND_NOT_NEEDED, Parma_Polyhedra_Library::ROUND_UP, and space_dimension().

                                                   {
#if PPL_NOISY_SIMPLEX
  ++mip_recursion_level;
  std::cout << "MIP_Problem::is_mip_satisfiable(): "
            << "entering recursion level " << mip_recursion_level
            << "." << std::endl;
#endif // PPL_NOISY_SIMPLEX
  PPL_ASSERT(mip.integer_space_dimensions().empty());

  // Solve the MIP problem.
  if (!mip.is_lp_satisfiable()) {
#if PPL_NOISY_SIMPLEX
    std::cout << "MIP_Problem::is_mip_satisfiable(): "
              << "exiting from recursion level " << mip_recursion_level
              << "." << std::endl;
    --mip_recursion_level;
#endif // PPL_NOISY_SIMPLEX
    return false;
  }

  PPL_DIRTY_TEMP(mpq_class, tmp_rational);
  PPL_DIRTY_TEMP_COEFFICIENT(tmp_coeff1);
  PPL_DIRTY_TEMP_COEFFICIENT(tmp_coeff2);
  bool found_satisfiable_generator = true;
  dimension_type non_int_dim;
  p = mip.last_generator;
  Coefficient_traits::const_reference p_divisor = p.divisor();

#if PPL_SIMPLEX_USE_MIP_HEURISTIC
  found_satisfiable_generator
    = choose_branching_variable(mip, i_vars, non_int_dim);
#else
  PPL_DIRTY_TEMP_COEFFICIENT(gcd);
  // TODO: This can be optimized more, exploiting the (possible)
  // sparseness of p, if the size of i_vars is expected to be greater than
  // the number of nonzeroes in p in most cases.
  for (Variables_Set::const_iterator v_begin = i_vars.begin(),
         v_end = i_vars.end(); v_begin != v_end; ++v_begin) {
    gcd_assign(gcd, p.coefficient(Variable(*v_begin)), p_divisor);
    if (gcd != p_divisor) {
      non_int_dim = *v_begin;
      found_satisfiable_generator = false;
      break;
    }
  }
#endif

  if (found_satisfiable_generator) {
    return true;
  }

  PPL_ASSERT(non_int_dim < mip.space_dimension());

  assign_r(tmp_rational.get_num(), p.coefficient(Variable(non_int_dim)),
           ROUND_NOT_NEEDED);
  assign_r(tmp_rational.get_den(), p_divisor, ROUND_NOT_NEEDED);
  tmp_rational.canonicalize();
  assign_r(tmp_coeff1, tmp_rational, ROUND_DOWN);
  assign_r(tmp_coeff2, tmp_rational, ROUND_UP);
  {
    MIP_Problem mip_aux(mip, Inherit_Constraints());
    mip_aux.add_constraint(Variable(non_int_dim) <= tmp_coeff1);
#if PPL_NOISY_SIMPLEX
    using namespace IO_Operators;
    std::cout << "MIP_Problem::is_mip_satisfiable(): "
              << "descending with: "
              << (Variable(non_int_dim) <= tmp_coeff1)
              << "." << std::endl;
#endif // PPL_NOISY_SIMPLEX
    if (is_mip_satisfiable(mip_aux, i_vars, p)) {
#if PPL_NOISY_SIMPLEX
      std::cout << "MIP_Problem::is_mip_satisfiable(): "
                << "exiting from recursion level " << mip_recursion_level
                << "." << std::endl;
      --mip_recursion_level;
#endif // PPL_NOISY_SIMPLEX
      return true;
    }
  }
  mip.add_constraint(Variable(non_int_dim) >= tmp_coeff2);
#if PPL_NOISY_SIMPLEX
  using namespace IO_Operators;
  std::cout << "MIP_Problem::is_mip_satisfiable(): "
            << "descending with: "
            << (Variable(non_int_dim) >= tmp_coeff2)
            << "." << std::endl;
#endif // PPL_NOISY_SIMPLEX
  const bool satisfiable = is_mip_satisfiable(mip, i_vars, p);
#if PPL_NOISY_SIMPLEX
  std::cout << "MIP_Problem::is_mip_satisfiable(): "
            << "exiting from recursion level " << mip_recursion_level
            << "." << std::endl;
  --mip_recursion_level;
#endif // PPL_NOISY_SIMPLEX
  return satisfiable;
}

bool Parma_Polyhedra_Library::MIP_Problem::is_satisfiable

(

)

const

Checks satisfiability of *this.

Returns

true if and only if the MIP problem is satisfiable.

Definition at line 247 of file MIP_Problem.cc.

References i_variables, Parma_Polyhedra_Library::MIP_Problem::RAII_Temporary_Real_Relaxation::i_vars, is_lp_satisfiable(), last_generator, Parma_Polyhedra_Library::MIP_Problem::RAII_Temporary_Real_Relaxation::lp, and status.

Referenced by Parma_Polyhedra_Library::BD_Shape< T >::BD_Shape(), Parma_Polyhedra_Library::Box< ITV >::Box(), Parma_Polyhedra_Library::Octagonal_Shape< T >::Octagonal_Shape(), Parma_Polyhedra_Library::Implementation::Termination::one_affine_ranking_function_MS(), Parma_Polyhedra_Library::Termination_Helpers::one_affine_ranking_function_PR_original(), Parma_Polyhedra_Library::Implementation::Termination::termination_test_MS(), Parma_Polyhedra_Library::Implementation::Termination::termination_test_PR(), and Parma_Polyhedra_Library::Implementation::Termination::termination_test_PR_original().

                                     {
  // Check `status' to filter out trivial cases.
  switch (status) {
  case UNSATISFIABLE:
    PPL_ASSERT(OK());
    return false;
  case SATISFIABLE:
    // Intentionally fall through
  case UNBOUNDED:
    // Intentionally fall through.
  case OPTIMIZED:
    PPL_ASSERT(OK());
    return true;
  case PARTIALLY_SATISFIABLE:
    {
      MIP_Problem& x = const_cast<MIP_Problem&>(*this);
      // LP case.
      if (x.i_variables.empty()) {
        return x.is_lp_satisfiable();
      }
      // MIP case.
      {
        // Temporarily relax the MIP into an LP problem.
        RAII_Temporary_Real_Relaxation relaxed(x);
        Generator p = point();
        relaxed.lp.is_lp_satisfiable();
#if PPL_NOISY_SIMPLEX
        mip_recursion_level = 0;
#endif // PPL_NOISY_SIMPLEX
        if (is_mip_satisfiable(relaxed.lp, relaxed.i_vars, p)) {
          x.last_generator = p;
          x.status = SATISFIABLE;
        }
        else {
          x.status = UNSATISFIABLE;
        }
      } // `relaxed' destroyed here: relaxation automatically reset.
      return (x.status == SATISFIABLE);
    }
  }
  // We should not be here!
  PPL_UNREACHABLE;
  return false;
}

bool Parma_Polyhedra_Library::MIP_Problem::is_satisfied ( const Constraint &  c, const Generator &  g  )

staticprivate

Returns true if and only if c is satisfied by g.

Definition at line 467 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::Constraint::is_inequality(), Parma_Polyhedra_Library::Scalar_Products::sign(), Parma_Polyhedra_Library::Constraint::space_dimension(), and Parma_Polyhedra_Library::Generator::space_dimension().

                                                                    {
  // Scalar_Products::sign() requires the second argument to be at least
  // as large as the first one.
  const int sp_sign
    = (g.space_dimension() <= c.space_dimension())
    ? Scalar_Products::sign(g, c)
    : Scalar_Products::sign(c, g);
  return c.is_inequality() ? (sp_sign >= 0) : (sp_sign == 0);
}

bool Parma_Polyhedra_Library::MIP_Problem::is_saturated ( const Constraint &  c, const Generator &  g  )

staticprivate

Returns true if and only if c is saturated by g.

Definition at line 478 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::Scalar_Products::sign(), Parma_Polyhedra_Library::Constraint::space_dimension(), and Parma_Polyhedra_Library::Generator::space_dimension().

                                                                    {
  // Scalar_Products::sign() requires the space dimension of the second
  // argument to be at least as large as the one of the first one.
  const int sp_sign
    = (g.space_dimension() <= c.space_dimension())
    ? Scalar_Products::sign(g, c)
    : Scalar_Products::sign(c, g);
  return sp_sign == 0;
}

bool Parma_Polyhedra_Library::MIP_Problem::is_unbounded_obj_function ( const Linear_Expression &  obj_function, const std::vector< std::pair< dimension_type, dimension_type > > &  mapping, Optimization_Mode  optimization_mode  )

staticprivate

Definition at line 1420 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::Linear_Expression::begin(), Parma_Polyhedra_Library::Linear_Expression::end(), Parma_Polyhedra_Library::MAXIMIZATION, and Parma_Polyhedra_Library::MINIMIZATION.

                                       {

  for (Linear_Expression::const_iterator i = x.begin(),
         i_end = x.end(); i != i_end; ++i) {
    // If a the value of a variable in the objective function is
    // different from zero, the final status is unbounded.
    // In the first part the variable is constrained to be greater or equal
    // than zero.
    if (mapping[i.variable().space_dimension()].second != 0) {
      return true;
    }
    if (optimization_mode == MAXIMIZATION) {
      if (*i > 0) {
        return true;
      }
    }
    else {
      PPL_ASSERT(optimization_mode == MINIMIZATION);
      if (*i < 0) {
        return true;
      }
    }
  }
  return false;
}

void Parma_Polyhedra_Library::MIP_Problem::linear_combine ( Row &  x, const Row &  y, const dimension_type  k  )

staticprivate

Linearly combines x with y so that *this[k] is 0.

Parameters

x	The row that will be combined with y object.
y	The row that will be combined with x object.
k	The position of *this that have to be .

Computes a linear combination of x and y having the element of index k equal to . Then it assigns the resulting Row to x and normalizes it.

Definition at line 1360 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::Sparse_Row::end(), Parma_Polyhedra_Library::Sparse_Row::find(), Parma_Polyhedra_Library::Sparse_Row::get(), Parma_Polyhedra_Library::Sparse_Row::linear_combine(), Parma_Polyhedra_Library::neg_assign(), Parma_Polyhedra_Library::Sparse_Row::normalize(), Parma_Polyhedra_Library::normalize2(), PPL_DIRTY_TEMP_COEFFICIENT, Parma_Polyhedra_Library::Sparse_Row::size(), WEIGHT_ADD_MUL, and WEIGHT_BEGIN.

                                                         {
  PPL_ASSERT(x.size() == y.size());
  WEIGHT_BEGIN();
  const dimension_type x_size = x.size();
  Coefficient_traits::const_reference x_k = x.get(k);
  Coefficient_traits::const_reference y_k = y.get(k);
  PPL_ASSERT(y_k != 0 && x_k != 0);
  // Let g be the GCD between `x[k]' and `y[k]'.
  // For each i the following computes
  //   x[i] = x[i]*y[k]/g - y[i]*x[k]/g.
  PPL_DIRTY_TEMP_COEFFICIENT(normalized_x_k);
  PPL_DIRTY_TEMP_COEFFICIENT(normalized_y_k);
  normalize2(x_k, y_k, normalized_x_k, normalized_y_k);

  neg_assign(normalized_y_k);
  x.linear_combine(y, normalized_y_k, normalized_x_k);

  PPL_ASSERT(x.get(k) == 0);

#if PPL_USE_SPARSE_MATRIX
  PPL_ASSERT(x.find(k) == x.end());
#endif

  x.normalize();
  WEIGHT_ADD_MUL(31, x_size);
}

void Parma_Polyhedra_Library::MIP_Problem::linear_combine ( Dense_Row &  x, const Sparse_Row &  y, const dimension_type  k  )

staticprivate

Linearly combines x with y so that *this[k] is 0.

Parameters

x	The row that will be combined with y object.
y	The row that will be combined with x object.
k	The position of *this that have to be .

Computes a linear combination of x and y having the element of index k equal to . Then it assigns the resulting Dense_Row to x and normalizes it.

Definition at line 1392 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::Dense_Row::get(), Parma_Polyhedra_Library::Sparse_Row::get(), Parma_Polyhedra_Library::linear_combine(), Parma_Polyhedra_Library::neg_assign(), Parma_Polyhedra_Library::Dense_Row::normalize(), Parma_Polyhedra_Library::normalize2(), PPL_DIRTY_TEMP_COEFFICIENT, Parma_Polyhedra_Library::Sparse_Row::size(), Parma_Polyhedra_Library::Dense_Row::size(), WEIGHT_ADD_MUL, and WEIGHT_BEGIN.

                                                         {
  PPL_ASSERT(x.size() == y.size());
  WEIGHT_BEGIN();
  const dimension_type x_size = x.size();
  Coefficient_traits::const_reference x_k = x.get(k);
  Coefficient_traits::const_reference y_k = y.get(k);
  PPL_ASSERT(y_k != 0 && x_k != 0);
  // Let g be the GCD between `x[k]' and `y[k]'.
  // For each i the following computes
  //   x[i] = x[i]*y[k]/g - y[i]*x[k]/g.
  PPL_DIRTY_TEMP_COEFFICIENT(normalized_x_k);
  PPL_DIRTY_TEMP_COEFFICIENT(normalized_y_k);
  normalize2(x_k, y_k, normalized_x_k, normalized_y_k);

  neg_assign(normalized_y_k);
  Parma_Polyhedra_Library::linear_combine(x, y, normalized_y_k, normalized_x_k);

  PPL_ASSERT(x[k] == 0);

  x.normalize();
  WEIGHT_ADD_MUL(83, x_size);
}

void Parma_Polyhedra_Library::MIP_Problem::m_swap ( MIP_Problem &  y )

inline

Swaps *this with y.

Definition at line 177 of file MIP_Problem_inlines.hh.

References base, external_space_dim, first_pending_constraint, i_variables, inherited_constraints, initialized, input_cs, input_obj_function, internal_space_dim, last_generator, mapping, opt_mode, pricing, status, swap(), Parma_Polyhedra_Library::swap(), tableau, and working_cost.

Referenced by clear(), operator=(), and swap().

                                  {
  using std::swap;
  swap(external_space_dim, y.external_space_dim);
  swap(internal_space_dim, y.internal_space_dim);
  swap(tableau, y.tableau);
  swap(working_cost, y.working_cost);
  swap(mapping, y.mapping);
  swap(initialized, y.initialized);
  swap(base, y.base);
  swap(status, y.status);
  swap(pricing, y.pricing);
  swap(input_cs, y.input_cs);
  swap(inherited_constraints, y.inherited_constraints);
  swap(first_pending_constraint, y.first_pending_constraint);
  swap(input_obj_function, y.input_obj_function);
  swap(opt_mode, y.opt_mode);
  swap(last_generator, y.last_generator);
  swap(i_variables, y.i_variables);
}

dimension_type Parma_Polyhedra_Library::MIP_Problem::max_space_dimension ( )

inlinestatic

Returns the maximum space dimension an MIP_Problem can handle.

Definition at line 33 of file MIP_Problem_inlines.hh.

References Parma_Polyhedra_Library::Constraint::max_space_dimension().

Referenced by MIP_Problem().

                                 {
  return Constraint::max_space_dimension();
}

PPL::dimension_type Parma_Polyhedra_Library::MIP_Problem::merge_split_variable ( dimension_type  var_index )

private

Merges back the positive and negative part of a (previously split) variable after detecting a corresponding nonnegativity constraint.

Returns

If the negative part of var_index was in base, the index of the corresponding tableau row (which has become non-feasible); otherwise not_a_dimension().

Parameters

var_index

The index of the variable that has to be merged.

Definition at line 420 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::not_a_dimension().

                                                             {
  // Initialize the return value to a dummy index.
  dimension_type unfeasible_tableau_row = not_a_dimension();

  const dimension_type removing_column = mapping[1+var_index].second;

  // Check if the negative part of the split variable is in base:
  // if so, the corresponding row of the tableau becomes non-feasible.
  {
    dimension_type base_index;
    if (is_in_base(removing_column, base_index)) {
      // Set the return value.
      unfeasible_tableau_row = base_index;
      // Reset base[base_index] to zero to remember non-feasibility.
      base[base_index] = 0;
      // Since the negative part of the variable is in base,
      // the positive part can not be in base too.
      PPL_ASSERT(!is_in_base(mapping[1+var_index].first, base_index));
    }
  }

  tableau.remove_column(removing_column);

  // var_index is no longer split.
  mapping[1+var_index].second = 0;

  // Adjust data structures, `shifting' the proper columns to the left by 1.
  const dimension_type base_size = base.size();
  for (dimension_type i = base_size; i-- > 0; ) {
    if (base[i] > removing_column) {
      --base[i];
    }
  }
  const dimension_type mapping_size = mapping.size();
  for (dimension_type i = mapping_size; i-- > 0; ) {
    if (mapping[i].first > removing_column) {
      --mapping[i].first;
    }
    if (mapping[i].second > removing_column) {
      --mapping[i].second;
    }
  }

  return unfeasible_tableau_row;
}

const Linear_Expression & Parma_Polyhedra_Library::MIP_Problem::objective_function ( ) const

inline

Returns the objective function.

Definition at line 134 of file MIP_Problem_inlines.hh.

References input_obj_function.

Referenced by operator<<().

                                      {
  return input_obj_function;
}

bool Parma_Polyhedra_Library::MIP_Problem::OK

(

)

const

Checks if all the invariants are satisfied.

Definition at line 2314 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::ascii_dump(), Parma_Polyhedra_Library::Sparse_Row::begin(), Parma_Polyhedra_Library::Sparse_Row::end(), Parma_Polyhedra_Library::gcd_assign(), Parma_Polyhedra_Library::CO_Tree::const_iterator::index(), Parma_Polyhedra_Library::Sparse_Row::lower_bound(), and PPL_DIRTY_TEMP_COEFFICIENT.

Referenced by MIP_Problem(), and set_optimization_mode().

                         {
#ifndef NDEBUG
  using std::endl;
  using std::cerr;
#endif
  const dimension_type input_cs_num_rows = input_cs.size();

  // Check that every member used is OK.

  if (inherited_constraints > input_cs_num_rows) {
#ifndef NDEBUG
    cerr << "The MIP_Problem claims to have inherited from its ancestors "
         << "more constraints than are recorded in this->input_cs."
         << endl;
    ascii_dump(cerr);
#endif
    return false;
  }

  if (first_pending_constraint > input_cs_num_rows) {
#ifndef NDEBUG
    cerr << "The MIP_Problem claims to have pending constraints "
         << "that are not recorded in this->input_cs."
         << endl;
    ascii_dump(cerr);
#endif
    return false;
  }

  if (!tableau.OK() || !last_generator.OK()) {
    return false;
  }

  // Constraint system should contain no strict inequalities.
  for (dimension_type i = input_cs_num_rows; i-- > 0; ) {
    if (input_cs[i]->is_strict_inequality()) {
#ifndef NDEBUG
      cerr << "The feasible region of the MIP_Problem is defined by "
           << "a constraint system containing strict inequalities."
           << endl;
      ascii_dump(cerr);
#endif
      return false;
    }

  }

  if (external_space_dim < internal_space_dim) {
#ifndef NDEBUG
    cerr << "The MIP_Problem claims to have an internal space dimension "
         << "greater than its external space dimension."
         << endl;
    ascii_dump(cerr);
#endif
    return false;
  }

  if (external_space_dim > internal_space_dim
      && status != UNSATISFIABLE
      && status != PARTIALLY_SATISFIABLE) {
#ifndef NDEBUG
    cerr << "The MIP_Problem claims to have a pending space dimension "
         << "addition, but the status is incompatible."
         << endl;
    ascii_dump(cerr);
#endif
    return false;
  }

  // Constraint system and objective function should be dimension compatible.
  if (external_space_dim < input_obj_function.space_dimension()) {
#ifndef NDEBUG
    cerr << "The MIP_Problem and the objective function have "
         << "incompatible space dimensions ("
         << external_space_dim << " < "
         << input_obj_function.space_dimension() << ")."
         << endl;
    ascii_dump(cerr);
#endif
    return false;
  }

  if (status != UNSATISFIABLE && initialized) {
    // Here `last_generator' has to be meaningful.
    // Check for dimension compatibility and actual feasibility.
    if (internal_space_dim != last_generator.space_dimension()) {
#ifndef NDEBUG
      cerr << "The MIP_Problem and the cached feasible point have "
           << "incompatible space dimensions ("
           << internal_space_dim << " != "
           << last_generator.space_dimension() << ")."
           << endl;
      ascii_dump(cerr);
#endif
      return false;
    }

    for (dimension_type i = 0; i < first_pending_constraint; ++i) {
      if (!is_satisfied(*(input_cs[i]), last_generator)) {
#ifndef NDEBUG
        cerr << "The cached feasible point does not belong to "
             << "the feasible region of the MIP_Problem."
             << endl;
        ascii_dump(cerr);
#endif
        return false;
      }
    }

    // Check that every integer declared variable is really integer.
    // in the solution found.
    if (!i_variables.empty()) {
      PPL_DIRTY_TEMP_COEFFICIENT(gcd);
      // TODO: This can be optimized more, exploiting the (possible)
      // sparseness of last_generator, if the size of i_variables is expected
      // to be greater than the number of nonzeroes in last_generator in most
      // cases.
      for (Variables_Set::const_iterator v_it = i_variables.begin(),
             v_end = i_variables.end(); v_it != v_end; ++v_it) {
        gcd_assign(gcd, last_generator.coefficient(Variable(*v_it)),
                   last_generator.divisor());
        if (gcd != last_generator.divisor()) {
          return false;
        }
      }
    }

    const dimension_type tableau_num_rows = tableau.num_rows();
    const dimension_type tableau_num_columns = tableau.num_columns();

    // The number of rows in the tableau and base should be equal.
    if (tableau_num_rows != base.size()) {
#ifndef NDEBUG
      cerr << "tableau and base have incompatible sizes" << endl;
      ascii_dump(cerr);
#endif
      return false;
    }
    // The size of `mapping' should be equal to the internal
    // space dimension plus one.
    if (mapping.size() != internal_space_dim + 1) {
#ifndef NDEBUG
      cerr << "The internal space dimension and `mapping' "
           << "have incompatible sizes" << endl;
      ascii_dump(cerr);
#endif
      return false;
    }

    // The number of columns in the tableau and working_cost should be equal.
    if (tableau_num_columns != working_cost.size()) {
#ifndef NDEBUG
      cerr << "tableau and working_cost have incompatible sizes" << endl;
      ascii_dump(cerr);
#endif
      return false;
    }

    // The vector base should contain indices of tableau's columns.
    for (dimension_type i = base.size(); i-- > 0; ) {
      if (base[i] > tableau_num_columns) {
#ifndef NDEBUG
        cerr << "base contains an invalid column index" << endl;
        ascii_dump(cerr);
#endif
        return false;
      }
    }

    {
      // Needed to sort accesses to tableau_j, improving performance.
      typedef std::vector<std::pair<dimension_type, dimension_type> >
        pair_vector_t;
      pair_vector_t vars_in_base;
      for (dimension_type i = base.size(); i-- > 0; ) {
        vars_in_base.push_back(std::make_pair(base[i], i));
      }

      std::sort(vars_in_base.begin(), vars_in_base.end());

      for (dimension_type j = tableau_num_rows; j-- > 0; ) {
        const Row& tableau_j = tableau[j];
        pair_vector_t::iterator i = vars_in_base.begin();
        pair_vector_t::iterator i_end = vars_in_base.end();
        Row::const_iterator itr = tableau_j.begin();
        Row::const_iterator itr_end = tableau_j.end();
        for ( ; i != i_end && itr != itr_end; ++i) {
          // tableau[i][base[j]], with i different from j, must be zero.
          if (itr.index() < i->first) {
            itr = tableau_j.lower_bound(itr, itr.index());
          }
          if (i->second != j && itr.index() == i->first && *itr != 0) {
#ifndef NDEBUG
            cerr << "tableau[i][base[j]], with i different from j, must be "
                 << "zero" << endl;
            ascii_dump(cerr);
#endif
            return false;
          }
        }
      }
    }
    // tableau[i][base[i]] must not be a zero.
    for (dimension_type i = base.size(); i-- > 0; ) {
      if (tableau[i].get(base[i]) == 0) {
#ifndef NDEBUG
        cerr << "tableau[i][base[i]] must not be a zero" << endl;
        ascii_dump(cerr);
#endif
        return false;
      }
    }

    // The last column of the tableau must contain only zeroes.
    for (dimension_type i = tableau_num_rows; i-- > 0; ) {
      if (tableau[i].get(tableau_num_columns - 1) != 0) {
#ifndef NDEBUG
        cerr << "the last column of the tableau must contain only"
          "zeroes"<< endl;
        ascii_dump(cerr);
#endif
        return false;
      }
    }
  }

  // All checks passed.
  return true;
}

MIP_Problem & Parma_Polyhedra_Library::MIP_Problem::operator= ( const MIP_Problem &  y )

inline

Assignment operator.

Definition at line 198 of file MIP_Problem_inlines.hh.

References m_swap().

                                           {
  MIP_Problem tmp(y);
  m_swap(tmp);
  return *this;
}

void Parma_Polyhedra_Library::MIP_Problem::optimal_value ( Coefficient &  numer, Coefficient &  denom  ) const

inline

Sets numer and denom so that is the solution of the optimization problem.

Exceptions

std::domain_error

Thrown if *this does not not have an optimizing point, i.e., if the MIP problem is unbounded or not satisfiable.

Definition at line 144 of file MIP_Problem_inlines.hh.

References evaluate_objective_function(), and optimizing_point().

Referenced by Parma_Polyhedra_Library::BD_Shape< T >::BFT00_upper_bound_assign_if_exact(), Parma_Polyhedra_Library::BD_Shape< T >::max_min(), Parma_Polyhedra_Library::Octagonal_Shape< T >::max_min(), and Parma_Polyhedra_Library::Polyhedron::simplify_using_context_assign().

                                                                       {
  const Generator& g = optimizing_point();
  evaluate_objective_function(g, numer, denom);
}

Optimization_Mode Parma_Polyhedra_Library::MIP_Problem::optimization_mode ( ) const

inline

Returns the optimization mode.

Definition at line 139 of file MIP_Problem_inlines.hh.

References opt_mode.

Referenced by operator<<(), and solve_mip().

                                     {
  return opt_mode;
}

const PPL::Generator & Parma_Polyhedra_Library::MIP_Problem::optimizing_point

(

)

const

Returns an optimal point for *this, if it exists.

Exceptions

std::domain_error

Thrown if *this does not not have an optimizing point, i.e., if the MIP problem is unbounded or not satisfiable.

Definition at line 236 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::OPTIMIZED_MIP_PROBLEM.

Referenced by Parma_Polyhedra_Library::BD_Shape< T >::BD_Shape(), Parma_Polyhedra_Library::Box< ITV >::Box(), Parma_Polyhedra_Library::BD_Shape< T >::max_min(), Parma_Polyhedra_Library::Octagonal_Shape< T >::max_min(), Parma_Polyhedra_Library::Octagonal_Shape< T >::Octagonal_Shape(), and optimal_value().

                                       {
  if (solve() == OPTIMIZED_MIP_PROBLEM) {
    return last_generator;
  }
  else {
    throw std::domain_error("PPL::MIP_Problem::optimizing_point():\n"
                            "*this does not have an optimizing point.");
  }
}

bool Parma_Polyhedra_Library::MIP_Problem::parse_constraints ( dimension_type &  additional_tableau_rows, dimension_type &  additional_slack_variables, std::deque< bool > &  is_tableau_constraint, std::deque< bool > &  is_satisfied_inequality, std::deque< bool > &  is_nonnegative_variable, std::deque< bool > &  is_remergeable_variable  ) const

private

Parses the pending constraints to gather information on how to resize the tableau.

Note

All of the method parameters are output parameters; their value is only meaningful when the function exit returning value true.

Returns

false if a trivially false constraint is detected, true otherwise.

Parameters

additional_tableau_rows	On exit, this will store the number of rows that have to be added to the original tableau.
additional_slack_variables	This will store the number of slack variables that have to be added to the original tableau.
is_tableau_constraint	This container of Boolean flags is initially empty. On exit, it size will be equal to the number of pending constraints in input_cs. For each pending constraint index i, the corresponding element of this container (having index i - first_pending_constraint) will be set to true if and only if the constraint has to be included in the tableau.
is_satisfied_inequality	This container of Boolean flags is initially empty. On exit, its size will be equal to the number of pending constraints in input_cs. For each pending constraint index i, the corresponding element of this container (having index i - first_pending_constraint) will be set to true if and only if it is an inequality and it is already satisfied by last_generator (hence it does not require the introduction of an artificial variable).
is_nonnegative_variable	This container of Boolean flags is initially empty. On exit, it size is equal to external_space_dim. For each variable (index), the corresponding element of this container is true if the variable is known to be nonnegative (and hence should not be split into a positive and a negative part).
is_remergeable_variable	This container of Boolean flags is initially empty. On exit, it size is equal to internal_space_dim. For each variable (index), the corresponding element of this container is true if the variable was previously split into positive and negative parts that can now be merged back, since it is known that the variable is nonnegative.

Definition at line 490 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::Expression_Hide_Last< T >::all_zeroes(), Parma_Polyhedra_Library::Constraint::coefficient(), Parma_Polyhedra_Library::Constraint::expression(), Parma_Polyhedra_Library::Expression_Hide_Last< T >::first_nonzero(), Parma_Polyhedra_Library::Constraint::inhomogeneous_term(), Parma_Polyhedra_Library::Constraint::is_equality(), Parma_Polyhedra_Library::Constraint::is_inequality(), Parma_Polyhedra_Library::Boundary_NS::sgn(), Parma_Polyhedra_Library::Boundary_NS::sgn_b(), and Parma_Polyhedra_Library::Constraint::space_dimension().

                                                                   {
  // Initially all containers are empty.
  PPL_ASSERT(is_tableau_constraint.empty()
             && is_satisfied_inequality.empty()
             && is_nonnegative_variable.empty()
             && is_remergeable_variable.empty());

  const dimension_type cs_space_dim = external_space_dim;
  const dimension_type cs_num_rows = input_cs.size();
  const dimension_type cs_num_pending
    = cs_num_rows - first_pending_constraint;

  // Counters determining the change in dimensions of the tableau:
  // initialized here, they will be updated while examining `input_cs'.
  additional_tableau_rows = cs_num_pending;
  additional_slack_variables = 0;

  // Resize containers appropriately.

  // On exit, `is_tableau_constraint[i]' will be true if and only if
  // `input_cs[first_pending_constraint + i]' is neither a tautology
  // (e.g., 1 >= 0) nor a non-negativity constraint (e.g., X >= 0).
  is_tableau_constraint.insert(is_tableau_constraint.end(),
                               cs_num_pending, true);

  // On exit, `is_satisfied_inequality[i]' will be true if and only if
  // `input_cs[first_pending_constraint + i]' is an inequality and it is
  // satisfied by `last_generator'.
  is_satisfied_inequality.insert(is_satisfied_inequality.end(),
                                 cs_num_pending, false);

  // On exit, `is_nonnegative_variable[j]' will be true if and only if
  // Variable(j) is bound to be nonnegative in `input_cs'.
  is_nonnegative_variable.insert(is_nonnegative_variable.end(),
                                 cs_space_dim, false);

  // On exit, `is_remergeable_variable[j]' will be true if and only if
  // Variable(j) was initially split and is now remergeable.
  is_remergeable_variable.insert(is_remergeable_variable.end(),
                                 internal_space_dim, false);

  // Check for variables that are already known to be nonnegative
  // due to non-pending constraints.
  const dimension_type mapping_size = mapping.size();
  if (mapping_size > 0) {
    // Note: mapping[0] is associated to the cost function.
    for (dimension_type i = std::min(mapping_size - 1, cs_space_dim);
         i-- > 0; ) {
      if (mapping[i + 1].second == 0) {
        is_nonnegative_variable[i] = true;
      }
    }
  }

  // Process each pending constraint in `input_cs' and
  //  - detect variables that are constrained to be nonnegative;
  //  - detect (non-negativity or tautology) pending constraints that
  //    will not be part of the tableau;
  //  - count the number of new slack variables.
  for (dimension_type i = cs_num_rows; i-- > first_pending_constraint; ) {
    const Constraint& cs_i = *(input_cs[i]);
    const dimension_type cs_i_end = cs_i.space_dimension() + 1;

    const dimension_type nonzero_coeff_column_index
      = cs_i.expression().first_nonzero(1, cs_i_end);
    const bool found_a_nonzero_coeff = (nonzero_coeff_column_index != cs_i_end);
    const bool found_many_nonzero_coeffs
      = (found_a_nonzero_coeff
         && !cs_i.expression().all_zeroes(nonzero_coeff_column_index + 1,
                                               cs_i_end));

    // If more than one coefficient is nonzero,
    // continue with next constraint.
    if (found_many_nonzero_coeffs) {
      if (cs_i.is_inequality()) {
        ++additional_slack_variables;
      // CHECKME: Is it true that in the first phase we can apply
      // `is_satisfied()' with the generator `point()'?  If so, the following
      // code works even if we do not have a feasible point.
      // Check for satisfiability of the inequality. This can be done if we
      // have a feasible point of *this.
      }
      if (cs_i.is_inequality() && is_satisfied(cs_i, last_generator)) {
        is_satisfied_inequality[i - first_pending_constraint] = true;
      }
      continue;
    }

    if (!found_a_nonzero_coeff) {
      // All coefficients are 0.
      // The constraint is either trivially true or trivially false.
      if (cs_i.is_inequality()) {
        if (cs_i.inhomogeneous_term() < 0) {
          // A constraint such as -1 >= 0 is trivially false.
          return false;
        }
      }
      else {
        // The constraint is an equality.
        if (cs_i.inhomogeneous_term() != 0) {
          // A constraint such as 1 == 0 is trivially false.
          return false;
        }
      }
      // Here the constraint is trivially true.
      is_tableau_constraint[i - first_pending_constraint] = false;
      --additional_tableau_rows;
      continue;
    }
    else {
      // Here we have only one nonzero coefficient.
      /*

      We have the following methods:
      A) Do split the variable and do add the constraint
         in the tableau.
      B) Do not split the variable and do add the constraint
         in the tableau.
      C) Do not split the variable and do not add the constraint
         in the tableau.

      Let the constraint be (a*v + b relsym 0).
      These are the 12 possible combinations we can have:
                a |  b | relsym | method
      ----------------------------------
      1)       >0 | >0 |   >=   |   A
      2)       >0 | >0 |   ==   |   A
      3)       <0 | <0 |   >=   |   A
      4)       >0 | =0 |   ==   |   B
      5)       >0 | <0 |   ==   |   B
      Note:    <0 | >0 |   ==   | impossible by strong normalization
      Note:    <0 | =0 |   ==   | impossible by strong normalization
      Note:    <0 | <0 |   ==   | impossible by strong normalization
      6)       >0 | <0 |   >=   |   B
      7)       >0 | =0 |   >=   |   C
      8)       <0 | >0 |   >=   |   A
      9)       <0 | =0 |   >=   |   A

      The next lines will apply the correct method to each case.
      */

      // The variable index is not equal to the column index.
      const dimension_type nonzero_var_index = nonzero_coeff_column_index - 1;

      const int sgn_a = sgn(cs_i.coefficient(Variable(nonzero_var_index)));
      const int sgn_b = sgn(cs_i.inhomogeneous_term());

      // Cases 1-3: apply method A.
      if (sgn_a == sgn_b) {
        if (cs_i.is_inequality()) {
          ++additional_slack_variables;
        }
      }
      // Cases 4-5: apply method B.
      else if (cs_i.is_equality()) {
        is_nonnegative_variable[nonzero_var_index] = true;
      // Case 6: apply method B.
      }
      else if (sgn_b < 0) {
        is_nonnegative_variable[nonzero_var_index] = true;
        ++additional_slack_variables;
      }
      // Case 7: apply method C.
      else if (sgn_a > 0) {
        if (!is_nonnegative_variable[nonzero_var_index]) {
          is_nonnegative_variable[nonzero_var_index] = true;
          if (nonzero_coeff_column_index < mapping_size) {
            // Remember to merge back the positive and negative parts.
            PPL_ASSERT(nonzero_var_index < internal_space_dim);
            is_remergeable_variable[nonzero_var_index] = true;
          }
        }
        is_tableau_constraint[i - first_pending_constraint] = false;
        --additional_tableau_rows;
      }
      // Cases 8-9: apply method A.
      else {
        PPL_ASSERT(cs_i.is_inequality());
        ++additional_slack_variables;
      }
    }
  }
  return true;
}

void Parma_Polyhedra_Library::MIP_Problem::pivot ( dimension_type  entering_var_index, dimension_type  exiting_base_index  )

private

Performs the pivoting operation on the tableau.

Parameters

entering_var_index	The index of the variable entering the base.
exiting_base_index	The index of the row exiting the base.

Definition at line 1451 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::Sparse_Row::get(), and Parma_Polyhedra_Library::linear_combine().

                                                                 {
  const Row& tableau_out = tableau[exiting_base_index];
  // Linearly combine the constraints.
  for (dimension_type i = tableau.num_rows(); i-- > 0; ) {
    Row& tableau_i = tableau[i];
    if (i != exiting_base_index && tableau_i.get(entering_var_index) != 0) {
      linear_combine(tableau_i, tableau_out, entering_var_index);
    }
  }
  // Linearly combine the cost function.
  if (working_cost.get(entering_var_index) != 0) {
    linear_combine(working_cost, tableau_out, entering_var_index);
  }
  // Adjust the base.
  base[exiting_base_index] = entering_var_index;
}

void Parma_Polyhedra_Library::MIP_Problem::print

(

)

const

Prints *this to std::cerr using operator<<.

void Parma_Polyhedra_Library::MIP_Problem::process_pending_constraints ( )

private

Processes the pending constraints of *this.

Definition at line 681 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::Expression_Adapter< T >::begin(), Parma_Polyhedra_Library::Sparse_Row::begin(), c, Parma_Polyhedra_Library::Coefficient_one(), Parma_Polyhedra_Library::Expression_Hide_Last< T >::end(), Parma_Polyhedra_Library::Sparse_Row::end(), Parma_Polyhedra_Library::Constraint::expression(), Parma_Polyhedra_Library::Sparse_Row::get(), Parma_Polyhedra_Library::CO_Tree::const_iterator::index(), Parma_Polyhedra_Library::Constraint::inhomogeneous_term(), Parma_Polyhedra_Library::Sparse_Row::insert(), Parma_Polyhedra_Library::Constraint::is_inequality(), Parma_Polyhedra_Library::linear_combine(), Parma_Polyhedra_Library::neg_assign(), and Parma_Polyhedra_Library::not_a_dimension().

Referenced by is_lp_satisfiable().

                                            {
  // Check the pending constraints to adjust the data structures.
  // If `false' is returned, they are trivially unfeasible.
  dimension_type additional_tableau_rows = 0;
  dimension_type additional_slack_vars = 0;
  std::deque<bool> is_tableau_constraint;
  std::deque<bool> is_satisfied_inequality;
  std::deque<bool> is_nonnegative_variable;
  std::deque<bool> is_remergeable_variable;
  if (!parse_constraints(additional_tableau_rows,
                         additional_slack_vars,
                         is_tableau_constraint,
                         is_satisfied_inequality,
                         is_nonnegative_variable,
                         is_remergeable_variable)) {
    status = UNSATISFIABLE;
    return;
  }

  // Merge back any variable that was previously split into a positive
  // and a negative part and is now known to be nonnegative.
  std::vector<dimension_type> unfeasible_tableau_rows;
  for (dimension_type i = internal_space_dim; i-- > 0; ) {
    if (!is_remergeable_variable[i]) {
      continue;
    }
    // TODO: merging all rows in a single shot may be more efficient
    // as it would require a single call to permute_columns().
    const dimension_type unfeasible_row = merge_split_variable(i);
    if (unfeasible_row != not_a_dimension()) {
      unfeasible_tableau_rows.push_back(unfeasible_row);
    }
  }

  const dimension_type old_tableau_num_rows = tableau.num_rows();
  const dimension_type old_tableau_num_cols = tableau.num_columns();
  const dimension_type first_free_tableau_index = old_tableau_num_cols - 1;

  // Update mapping for the new problem variables (if any).
  dimension_type additional_problem_vars = 0;
  if (external_space_dim > internal_space_dim) {
    const dimension_type space_diff = external_space_dim - internal_space_dim;
    for (dimension_type i = 0, j = 0; i < space_diff; ++i) {
      // Let `mapping' associate the variable index with the corresponding
      // tableau column: split the variable into positive and negative
      // parts if it is not known to be nonnegative.
      const dimension_type positive = first_free_tableau_index + j;
      if (is_nonnegative_variable[internal_space_dim + i]) {
        // Do not split.
        mapping.push_back(std::make_pair(positive, 0));
        ++j;
        ++additional_problem_vars;
      }
      else {
        // Split: negative index is positive + 1.
        mapping.push_back(std::make_pair(positive, positive + 1));
        j += 2;
        additional_problem_vars += 2;
      }
    }
  }

  // Resize the tableau: first add additional rows ...
  if (additional_tableau_rows > 0) {
    tableau.add_zero_rows(additional_tableau_rows);
  }

  // ... then add additional columns.
  // We need columns for additional (split) problem variables, additional
  // slack variables and additional artificials.
  // The number of artificials to be added is computed as:
  // * number of pending constraints entering the tableau
  //     minus
  // * pending constraints that are inequalities and are already satisfied
  //   by `last_generator'
  //     plus
  // * number of non-pending constraints that are no longer satisfied
  //   due to re-merging of split variables.

  const dimension_type num_satisfied_inequalities
    = static_cast<dimension_type>(std::count(is_satisfied_inequality.begin(),
                                             is_satisfied_inequality.end(),
                                             true));
  const dimension_type unfeasible_tableau_rows_size
    = unfeasible_tableau_rows.size();

  PPL_ASSERT(additional_tableau_rows >= num_satisfied_inequalities);
  const dimension_type additional_artificial_vars
    = (additional_tableau_rows - num_satisfied_inequalities)
    + unfeasible_tableau_rows_size;

  const dimension_type additional_tableau_columns
    = additional_problem_vars
    + additional_slack_vars
    + additional_artificial_vars;

  if (additional_tableau_columns > 0) {
    tableau.add_zero_columns(additional_tableau_columns);
  }

  // Dimensions of the tableau after resizing.
  const dimension_type tableau_num_rows = tableau.num_rows();
  const dimension_type tableau_num_cols = tableau.num_columns();

  // The following vector will be useful know if a constraint is feasible
  // and does not require an additional artificial variable.
  std::deque<bool> worked_out_row(tableau_num_rows, false);

  // Sync the `base' vector size to the new tableau: fill with zeros
  // to encode that these rows are not OK and must be adjusted.
  base.insert(base.end(), additional_tableau_rows, 0);
  const dimension_type base_size = base.size();

  // These indexes will be used to insert slack and artificial variables
  // in the appropriate position.
  dimension_type slack_index
    = tableau_num_cols - additional_artificial_vars - 1;
  dimension_type artificial_index = slack_index;

  // The first column index of the tableau that contains an
  // artificial variable. Encode with 0 the fact the there are not
  // artificial variables.
  const dimension_type begin_artificials
    = (additional_artificial_vars > 0)
    ? artificial_index
    : 0;

  // Proceed with the insertion of the constraints.
  for (dimension_type k = tableau_num_rows,
       i = input_cs.size() - first_pending_constraint; i-- > 0; ) {
    if (!is_tableau_constraint[i]) {
      continue;
    }
    // Copy the original constraint in the tableau.
    Row& tableau_k = tableau[--k];
    Row::iterator itr = tableau_k.end();

    const Constraint& c = *(input_cs[i + first_pending_constraint]);
    const Constraint::expr_type c_e = c.expression();
    for (Constraint::expr_type::const_iterator j = c_e.begin(),
           j_end = c_e.end(); j != j_end; ++j) {
      Coefficient_traits::const_reference coeff_sd = *j;
      const std::pair<dimension_type, dimension_type> mapped
        = mapping[j.variable().space_dimension()];
      itr = tableau_k.insert(itr, mapped.first, coeff_sd);
      // Split if needed.
      if (mapped.second != 0) {
        itr = tableau_k.insert(itr, mapped.second);
        neg_assign(*itr, coeff_sd);
      }
    }
    Coefficient_traits::const_reference inhomo = c.inhomogeneous_term();
    if (inhomo != 0) {
      tableau_k.insert(itr, mapping[0].first, inhomo);
      // Split if needed.
      if (mapping[0].second != 0) {
        itr = tableau_k.insert(itr, mapping[0].second);
        neg_assign(*itr, inhomo);
      }
    }

    // Add the slack variable, if needed.
    if (c.is_inequality()) {
      neg_assign(tableau_k[--slack_index], Coefficient_one());
      // If the constraint is already satisfied, we will not use artificial
      // variables to compute a feasible base: this to speed up
      // the algorithm.
      if (is_satisfied_inequality[i]) {
        base[k] = slack_index;
        worked_out_row[k] = true;
      }
    }
    for (dimension_type j = base_size; j-- > 0; ) {
      if (k != j && base[j] != 0 && tableau_k.get(base[j]) != 0) {
        linear_combine(tableau_k, tableau[j], base[j]);
      }
    }
  }

  // Let all inhomogeneous terms in the tableau be nonpositive,
  // so as to simplify the insertion of artificial variables
  // (the coefficient of each artificial variable will be 1).
  for (dimension_type i = tableau_num_rows; i-- > 0 ; ) {
    Row& tableau_i = tableau[i];
    if (tableau_i.get(0) > 0) {
      for (Row::iterator
           j = tableau_i.begin(), j_end = tableau_i.end();
           j != j_end; ++j) {
        neg_assign(*j);
      }
    }
  }

  // Reset the working cost function to have the right size.
  working_cost = working_cost_type(tableau_num_cols);

  // Set up artificial variables: these will have coefficient 1 in the
  // constraint, will enter the base and will have coefficient -1 in
  // the cost function.

  // This is used as a hint for insertions in working_cost.
  working_cost_type::iterator cost_itr = working_cost.end();

  // First go through non-pending constraints that became unfeasible
  // due to re-merging of split variables.
  for (dimension_type i = 0; i < unfeasible_tableau_rows_size; ++i) {
    tableau[unfeasible_tableau_rows[i]].insert(artificial_index,
                                               Coefficient_one());
    cost_itr = working_cost.insert(cost_itr, artificial_index);
    *cost_itr = -1;
    base[unfeasible_tableau_rows[i]] = artificial_index;
    ++artificial_index;
  }
  // Then go through newly added tableau rows, disregarding inequalities
  // that are already satisfied by `last_generator' (this information
  // is encoded in `worked_out_row').
  for (dimension_type i = old_tableau_num_rows; i < tableau_num_rows; ++i) {
    if (worked_out_row[i]) {
      continue;
    }
    tableau[i].insert(artificial_index, Coefficient_one());
    cost_itr = working_cost.insert(cost_itr, artificial_index);
    *cost_itr = -1;
    base[i] = artificial_index;
    ++artificial_index;
  }
  // One past the last tableau column index containing an artificial variable.
  const dimension_type end_artificials = artificial_index;

  // Set the extra-coefficient of the cost functions to record its sign.
  // This is done to keep track of the possible sign's inversion.
  const dimension_type last_obj_index = working_cost.size() - 1;
  working_cost.insert(cost_itr, last_obj_index, Coefficient_one());

  // Express the problem in terms of the variables in base.
  {
    working_cost_type::const_iterator itr = working_cost.end();
    for (dimension_type i = tableau_num_rows; i-- > 0; ) {
      itr = working_cost.lower_bound(itr, base[i]);
      if (itr != working_cost.end() && itr.index() == base[i] && *itr != 0) {
        linear_combine(working_cost, tableau[i], base[i]);
        // itr has been invalidated by the call to linear_combine().
        itr = working_cost.end();
      }
    }
  }

  // Deal with zero dimensional problems.
  if (space_dimension() == 0) {
    status = OPTIMIZED;
    last_generator = point();
    return;
  }
  // Deal with trivial cases.
  // If there is no constraint in the tableau, then the feasible region
  // is only delimited by non-negativity constraints. Therefore,
  // the problem is unbounded as soon as the cost function has
  // a variable with a positive coefficient.
  if (tableau_num_rows == 0) {
    if (is_unbounded_obj_function(input_obj_function, mapping, opt_mode)) {
      // Ensure the right space dimension is obtained.
      last_generator = point();
      last_generator.set_space_dimension(space_dimension());
      status = UNBOUNDED;
      return;
    }

    // The problem is neither trivially unfeasible nor trivially unbounded.
    // The tableau was successful computed and the caller has to figure
    // out which case applies.
    status = OPTIMIZED;
    // Ensure the right space dimension is obtained.
    last_generator = point();
    last_generator.set_space_dimension(space_dimension());
    return;
  }

  // Now we are ready to solve the first phase.
  const bool first_phase_successful
    = (get_control_parameter(PRICING) == PRICING_STEEPEST_EDGE_FLOAT)
    ? compute_simplex_using_steepest_edge_float()
    : compute_simplex_using_exact_pricing();

#if PPL_NOISY_SIMPLEX
  std::cout << "MIP_Problem::process_pending_constraints(): "
            << "1st phase ended at iteration " << num_iterations
            << "." << std::endl;
#endif // PPL_NOISY_SIMPLEX

  if (!first_phase_successful || working_cost.get(0) != 0) {
    // The feasible region is empty.
    status = UNSATISFIABLE;
    return;
  }

  // Prepare *this for a possible second phase.
  if (begin_artificials != 0) {
    erase_artificials(begin_artificials, end_artificials);
  }
  compute_generator();
  status = SATISFIABLE;
}

void Parma_Polyhedra_Library::MIP_Problem::second_phase ( )

private

Optimizes the MIP problem using the second phase of the primal simplex algorithm.

Definition at line 1864 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::Sparse_Row::begin(), Parma_Polyhedra_Library::Coefficient_one(), Parma_Polyhedra_Library::Sparse_Row::end(), Parma_Polyhedra_Library::CO_Tree::iterator::index(), Parma_Polyhedra_Library::linear_combine(), Parma_Polyhedra_Library::Sparse_Row::lower_bound(), Parma_Polyhedra_Library::MINIMIZATION, Parma_Polyhedra_Library::neg_assign(), and Parma_Polyhedra_Library::swap().

Referenced by solve(), and solve_mip().

                             {
  // Second_phase requires that *this is satisfiable.
  PPL_ASSERT(status == SATISFIABLE
             || status == UNBOUNDED
             || status == OPTIMIZED);
  // In the following cases the problem is already solved.
  if (status == UNBOUNDED || status == OPTIMIZED) {
    return;
  }
  // Build the objective function for the second phase.
  Row new_cost;
  input_obj_function.get_row(new_cost);

  // Negate the cost function if we are minimizing.
  if (opt_mode == MINIMIZATION) {
    for (Row::iterator i = new_cost.begin(),
           i_end = new_cost.end(); i != i_end; ++i) {
      neg_assign(*i);
    }
  }

  const dimension_type cost_zero_size = working_cost.size();

  // Substitute properly the cost function in the `costs' matrix.
  {
    working_cost_type tmp_cost(cost_zero_size, cost_zero_size);
    swap(tmp_cost, working_cost);
  }

  {
    working_cost_type::iterator itr
      = working_cost.insert(cost_zero_size - 1, Coefficient_one());

    // Split the variables in the cost function.
    for (Row::const_iterator i = new_cost.lower_bound(1),
           i_end = new_cost.end(); i != i_end; ++i) {
      const dimension_type index = i.index();
      const dimension_type original_var = mapping[index].first;
      const dimension_type split_var = mapping[index].second;
      itr = working_cost.insert(itr, original_var, *i);
      if (mapping[index].second != 0) {
        itr = working_cost.insert(itr, split_var);
        neg_assign(*itr, *i);
      }
    }
  }

  // Here the first phase problem succeeded with optimum value zero.
  // Express the old cost function in terms of the computed base.
  {
    working_cost_type::iterator itr = working_cost.end();
    for (dimension_type i = tableau.num_rows(); i-- > 0; ) {
      const dimension_type base_i = base[i];
      itr = working_cost.lower_bound(itr, base_i);
      if (itr != working_cost.end() && itr.index() == base_i && *itr != 0) {
        linear_combine(working_cost, tableau[i], base_i);
        itr = working_cost.end();
      }
    }
  }

  // Solve the second phase problem.
  const bool second_phase_successful
    = (get_control_parameter(PRICING) == PRICING_STEEPEST_EDGE_FLOAT)
    ? compute_simplex_using_steepest_edge_float()
    : compute_simplex_using_exact_pricing();
  compute_generator();
#if PPL_NOISY_SIMPLEX
  std::cout << "MIP_Problem::second_phase(): 2nd phase ended at iteration "
            << num_iterations
            << "." << std::endl;
#endif // PPL_NOISY_SIMPLEX
  status = second_phase_successful ? OPTIMIZED : UNBOUNDED;
  PPL_ASSERT(OK());
}

void Parma_Polyhedra_Library::MIP_Problem::set_control_parameter ( Control_Parameter_Value  value )

inline

Sets control parameter value.

Definition at line 172 of file MIP_Problem_inlines.hh.

References pricing, and value.

                                                                {
  pricing = value;
}

void Parma_Polyhedra_Library::MIP_Problem::set_objective_function

(

const Linear_Expression &

obj

)

Sets the objective function to obj.

Exceptions

std::invalid_argument

Thrown if the space dimension of obj is strictly greater than the space dimension of *this.

Definition at line 208 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::Linear_Expression::space_dimension().

Referenced by Parma_Polyhedra_Library::BD_Shape< T >::BD_Shape(), Parma_Polyhedra_Library::Box< ITV >::Box(), Parma_Polyhedra_Library::Octagonal_Shape< T >::Octagonal_Shape(), Parma_Polyhedra_Library::Polyhedron::simplify_using_context_assign(), and Parma_Polyhedra_Library::Polyhedron::strongly_minimize_constraints().

                                                                   {
  if (space_dimension() < obj.space_dimension()) {
    std::ostringstream s;
    s << "PPL::MIP_Problem::set_objective_function(obj):\n"
      << "obj.space_dimension() == " << obj.space_dimension()
      << " exceeds this->space_dimension == " << space_dimension()
      << ".";
    throw std::invalid_argument(s.str());
  }
  input_obj_function = obj;
  if (status == UNBOUNDED || status == OPTIMIZED) {
    status = SATISFIABLE;
  }
  PPL_ASSERT(OK());
}

void Parma_Polyhedra_Library::MIP_Problem::set_optimization_mode ( Optimization_Mode  mode )

inline

Sets the optimization mode to mode.

Definition at line 123 of file MIP_Problem_inlines.hh.

References OK(), opt_mode, OPTIMIZED, SATISFIABLE, status, and UNBOUNDED.

Referenced by Parma_Polyhedra_Library::BD_Shape< T >::BD_Shape(), Parma_Polyhedra_Library::Box< ITV >::Box(), Parma_Polyhedra_Library::Octagonal_Shape< T >::Octagonal_Shape(), and Parma_Polyhedra_Library::Polyhedron::strongly_minimize_constraints().

                                                               {
  if (opt_mode != mode) {
    opt_mode = mode;
    if (status == UNBOUNDED || status == OPTIMIZED) {
      status = SATISFIABLE;
    }
    PPL_ASSERT(OK());
  }
}

PPL::MIP_Problem_Status Parma_Polyhedra_Library::MIP_Problem::solve

(

)

const

Optimizes the MIP problem.

Returns

An MIP_Problem_Status flag indicating the outcome of the optimization attempt (unfeasible, unbounded or optimized problem).

Definition at line 293 of file MIP_Problem.cc.

References i_variables, Parma_Polyhedra_Library::MIP_Problem::RAII_Temporary_Real_Relaxation::i_vars, integer_space_dimensions(), is_lp_satisfiable(), last_generator, Parma_Polyhedra_Library::MIP_Problem::RAII_Temporary_Real_Relaxation::lp, Parma_Polyhedra_Library::OPTIMIZED_MIP_PROBLEM, PPL_DIRTY_TEMP, second_phase(), status, Parma_Polyhedra_Library::UNBOUNDED_MIP_PROBLEM, and Parma_Polyhedra_Library::UNFEASIBLE_MIP_PROBLEM.

Referenced by Parma_Polyhedra_Library::BD_Shape< T >::BD_Shape(), Parma_Polyhedra_Library::BD_Shape< T >::BFT00_upper_bound_assign_if_exact(), Parma_Polyhedra_Library::BD_Shape< T >::bounds(), Parma_Polyhedra_Library::Octagonal_Shape< T >::bounds(), Parma_Polyhedra_Library::Box< ITV >::Box(), Parma_Polyhedra_Library::BD_Shape< T >::max_min(), Parma_Polyhedra_Library::Octagonal_Shape< T >::max_min(), Parma_Polyhedra_Library::Octagonal_Shape< T >::Octagonal_Shape(), Parma_Polyhedra_Library::Polyhedron::simplify_using_context_assign(), and Parma_Polyhedra_Library::Polyhedron::strongly_minimize_constraints().

                           {
  switch (status) {
  case UNSATISFIABLE:
    PPL_ASSERT(OK());
    return UNFEASIBLE_MIP_PROBLEM;
  case UNBOUNDED:
    PPL_ASSERT(OK());
    return UNBOUNDED_MIP_PROBLEM;
  case OPTIMIZED:
    PPL_ASSERT(OK());
    return OPTIMIZED_MIP_PROBLEM;
  case SATISFIABLE:
    // Intentionally fall through
  case PARTIALLY_SATISFIABLE:
    {
      MIP_Problem& x = const_cast<MIP_Problem&>(*this);
      if (x.i_variables.empty()) {
        // LP case.
        if (x.is_lp_satisfiable()) {
          x.second_phase();
          if (x.status == UNBOUNDED) {
            return UNBOUNDED_MIP_PROBLEM;
          }
          else {
            PPL_ASSERT(x.status == OPTIMIZED);
            return OPTIMIZED_MIP_PROBLEM;
          }
        }
        return UNFEASIBLE_MIP_PROBLEM;
      }

      // MIP case.
      MIP_Problem_Status return_value;
      Generator g = point();
      {
        // Temporarily relax the MIP into an LP problem.
        RAII_Temporary_Real_Relaxation relaxed(x);
        if (relaxed.lp.is_lp_satisfiable()) {
          relaxed.lp.second_phase();
        }
        else {
          x.status = UNSATISFIABLE;
          // NOTE: `relaxed' destroyed: relaxation automatically reset.
          return UNFEASIBLE_MIP_PROBLEM;
        }
        PPL_DIRTY_TEMP(mpq_class, incumbent_solution);
        bool have_incumbent_solution = false;

        MIP_Problem lp_copy(relaxed.lp, Inherit_Constraints());
        PPL_ASSERT(lp_copy.integer_space_dimensions().empty());
        return_value = solve_mip(have_incumbent_solution,
                                 incumbent_solution, g,
                                 lp_copy, relaxed.i_vars);
      } // `relaxed' destroyed here: relaxation automatically reset.

      switch (return_value) {
      case UNFEASIBLE_MIP_PROBLEM:
        x.status = UNSATISFIABLE;
        break;
      case UNBOUNDED_MIP_PROBLEM:
        x.status = UNBOUNDED;
        // A feasible point has been set in `solve_mip()', so that
        // a call to `feasible_point' will be successful.
        x.last_generator = g;
        break;
      case OPTIMIZED_MIP_PROBLEM:
        x.status = OPTIMIZED;
        // Set the internal generator.
        x.last_generator = g;
        break;
      }
      PPL_ASSERT(OK());
      return return_value;
    }
  }
  // We should not be here!
  PPL_UNREACHABLE;
  return UNFEASIBLE_MIP_PROBLEM;
}

PPL::MIP_Problem_Status Parma_Polyhedra_Library::MIP_Problem::solve_mip ( bool &  have_incumbent_solution, mpq_class &  incumbent_solution_value, Generator &  incumbent_solution_point, MIP_Problem &  mip, const Variables_Set &  i_vars  )

staticprivate

Returns a status that encodes the solution of the MIP problem.

Parameters

have_incumbent_solution	It is used to store if the solving process has found a provisional optimum point.
incumbent_solution_value	Encodes the evaluated value of the provisional optimum point found.
incumbent_solution_point	If the method returns `OPTIMIZED', this will contain the optimality point.
mip	The problem that has to be solved.
i_vars	The variables that are constrained to take an integer value.

Definition at line 2015 of file MIP_Problem.cc.

References add_constraint(), Parma_Polyhedra_Library::assign_r(), Parma_Polyhedra_Library::Generator::coefficient(), Parma_Polyhedra_Library::Generator::divisor(), evaluate_objective_function(), Parma_Polyhedra_Library::gcd_assign(), Parma_Polyhedra_Library::is_canonical(), is_lp_satisfiable(), last_generator, Parma_Polyhedra_Library::MAXIMIZATION, Parma_Polyhedra_Library::MINIMIZATION, optimization_mode(), Parma_Polyhedra_Library::OPTIMIZED_MIP_PROBLEM, PPL_DIRTY_TEMP, PPL_DIRTY_TEMP_COEFFICIENT, Parma_Polyhedra_Library::ROUND_DOWN, Parma_Polyhedra_Library::ROUND_NOT_NEEDED, Parma_Polyhedra_Library::ROUND_UP, second_phase(), space_dimension(), status, Parma_Polyhedra_Library::UNBOUNDED_MIP_PROBLEM, and Parma_Polyhedra_Library::UNFEASIBLE_MIP_PROBLEM.

                                                         {
  // Solve the problem as a non MIP one, it must be done internally.
  PPL::MIP_Problem_Status mip_status;
  if (mip.is_lp_satisfiable()) {
    mip.second_phase();
    mip_status = (mip.status == OPTIMIZED) ? OPTIMIZED_MIP_PROBLEM
      : UNBOUNDED_MIP_PROBLEM;
  }
  else {
    return UNFEASIBLE_MIP_PROBLEM;
  }
  PPL_DIRTY_TEMP(mpq_class, tmp_rational);

  Generator p = point();
  PPL_DIRTY_TEMP_COEFFICIENT(tmp_coeff1);
  PPL_DIRTY_TEMP_COEFFICIENT(tmp_coeff2);

  if (mip_status == UNBOUNDED_MIP_PROBLEM) {
    p = mip.last_generator;
  }
  else {
    PPL_ASSERT(mip_status == OPTIMIZED_MIP_PROBLEM);
    // Do not call optimizing_point().
    p = mip.last_generator;
    mip.evaluate_objective_function(p, tmp_coeff1, tmp_coeff2);
    assign_r(tmp_rational.get_num(), tmp_coeff1, ROUND_NOT_NEEDED);
    assign_r(tmp_rational.get_den(), tmp_coeff2, ROUND_NOT_NEEDED);
    PPL_ASSERT(is_canonical(tmp_rational));
    if (have_incumbent_solution
        && ((mip.optimization_mode() == MAXIMIZATION
              && tmp_rational <= incumbent_solution_value)
            || (mip.optimization_mode() == MINIMIZATION
                && tmp_rational >= incumbent_solution_value))) {
      // Abandon this path.
      return mip_status;
    }
  }

  bool found_satisfiable_generator = true;
  PPL_DIRTY_TEMP_COEFFICIENT(gcd);
  Coefficient_traits::const_reference p_divisor = p.divisor();
  dimension_type non_int_dim = mip.space_dimension();
  // TODO: This can be optimized more, exploiting the (possible)
  // sparseness of p, if the size of i_vars is expected to be greater than
  // the number of nonzeroes in p in most cases.
  for (Variables_Set::const_iterator v_begin = i_vars.begin(),
         v_end = i_vars.end(); v_begin != v_end; ++v_begin) {
    gcd_assign(gcd, p.coefficient(Variable(*v_begin)), p_divisor);
    if (gcd != p_divisor) {
      non_int_dim = *v_begin;
      found_satisfiable_generator = false;
      break;
    }
  }
  if (found_satisfiable_generator) {
    // All the coordinates of `point' are satisfiable.
    if (mip_status == UNBOUNDED_MIP_PROBLEM) {
      // This is a point that belongs to the MIP_Problem.
      // In this way we are sure that we will return every time
      // a feasible point if requested by the user.
      incumbent_solution_point = p;
      return mip_status;
    }
    if (!have_incumbent_solution
        || (mip.optimization_mode() == MAXIMIZATION
            && tmp_rational > incumbent_solution_value)
        || tmp_rational < incumbent_solution_value) {
      incumbent_solution_value = tmp_rational;
      incumbent_solution_point = p;
      have_incumbent_solution = true;
#if PPL_NOISY_SIMPLEX
      PPL_DIRTY_TEMP_COEFFICIENT(numer);
      PPL_DIRTY_TEMP_COEFFICIENT(denom);
      mip.evaluate_objective_function(p, numer, denom);
      std::cout << "MIP_Problem::solve_mip(): "
                << "new value found: " << numer << "/" << denom
                << "." << std::endl;
#endif // PPL_NOISY_SIMPLEX
    }
    return mip_status;
  }

  PPL_ASSERT(non_int_dim < mip.space_dimension());

  assign_r(tmp_rational.get_num(), p.coefficient(Variable(non_int_dim)),
           ROUND_NOT_NEEDED);
  assign_r(tmp_rational.get_den(), p_divisor, ROUND_NOT_NEEDED);
  tmp_rational.canonicalize();
  assign_r(tmp_coeff1, tmp_rational, ROUND_DOWN);
  assign_r(tmp_coeff2, tmp_rational, ROUND_UP);
  {
    MIP_Problem mip_aux(mip, Inherit_Constraints());
    mip_aux.add_constraint(Variable(non_int_dim) <= tmp_coeff1);
#if PPL_NOISY_SIMPLEX
    using namespace IO_Operators;
    std::cout << "MIP_Problem::solve_mip(): "
              << "descending with: "
              << (Variable(non_int_dim) <= tmp_coeff1)
              << "." << std::endl;
#endif // PPL_NOISY_SIMPLEX
    solve_mip(have_incumbent_solution, incumbent_solution_value,
              incumbent_solution_point, mip_aux, i_vars);
  }
  // TODO: change this when we will be able to remove constraints.
  mip.add_constraint(Variable(non_int_dim) >= tmp_coeff2);
#if PPL_NOISY_SIMPLEX
  using namespace IO_Operators;
  std::cout << "MIP_Problem::solve_mip(): "
            << "descending with: "
            << (Variable(non_int_dim) >= tmp_coeff2)
            << "." << std::endl;
#endif // PPL_NOISY_SIMPLEX
  solve_mip(have_incumbent_solution, incumbent_solution_value,
            incumbent_solution_point, mip, i_vars);
  return have_incumbent_solution ? mip_status : UNFEASIBLE_MIP_PROBLEM;
}

dimension_type Parma_Polyhedra_Library::MIP_Problem::space_dimension ( ) const

inline

Returns the space dimension of the MIP problem.

Definition at line 38 of file MIP_Problem_inlines.hh.

References external_space_dim.

Referenced by is_mip_satisfiable(), and solve_mip().

                                   {
  return external_space_dim;
}

PPL::dimension_type Parma_Polyhedra_Library::MIP_Problem::steepest_edge_exact_entering_index ( ) const

private

Computes the column index of the variable entering the base, using an exact steepest-edge algorithm with anti-cycling rule.

Returns

The column index of the variable that enters the base. If no such variable exists, optimality was achieved and 0 is returned.

To compute the entering_index, the steepest edge algorithm chooses the index `j' such that 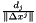is the largest in absolute value, where

Recall that, due to the exact integer implementation of the algorithm, our tableau does not contain the ``real'' 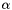values, but these can be computed dividing the value of the coefficient by the value of the variable in base. Obviously the result may not be an integer, so we will proceed in another way: we compute the lcm of all the variables in base to get the good ``weight'' of each Coefficient of the tableau.

Definition at line 1134 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::add_mul_assign(), Parma_Polyhedra_Library::Sparse_Row::begin(), Parma_Polyhedra_Library::Sparse_Row::end(), Parma_Polyhedra_Library::exact_div_assign(), Parma_Polyhedra_Library::CO_Tree::const_iterator::index(), Parma_Polyhedra_Library::lcm_assign(), Parma_Polyhedra_Library::Sparse_Row::lower_bound(), PPL_DIRTY_TEMP_COEFFICIENT, Parma_Polyhedra_Library::Boundary_NS::sgn(), Parma_Polyhedra_Library::swap(), WEIGHT_ADD_MUL, and WEIGHT_BEGIN.

                                                         {
  using std::swap;
  const dimension_type tableau_num_rows = tableau.num_rows();
  PPL_ASSERT(tableau_num_rows == base.size());
  // The square of the lcm of all the coefficients of variables in base.
  PPL_DIRTY_TEMP_COEFFICIENT(squared_lcm_basis);
  // The normalization factor for each coefficient in the tableau.
  std::vector<Coefficient> norm_factor(tableau_num_rows);
  {
    WEIGHT_BEGIN();
    // Compute the lcm of all the coefficients of variables in base.
    PPL_DIRTY_TEMP_COEFFICIENT(lcm_basis);
    lcm_basis = 1;
    for (dimension_type i = tableau_num_rows; i-- > 0; ) {
      lcm_assign(lcm_basis, lcm_basis, tableau[i].get(base[i]));
    }
    // Compute normalization factors.
    for (dimension_type i = tableau_num_rows; i-- > 0; ) {
      exact_div_assign(norm_factor[i], lcm_basis, tableau[i].get(base[i]));
    }
    // Compute the square of `lcm_basis', exploiting the fact that
    // `lcm_basis' will no longer be needed.
    lcm_basis *= lcm_basis;
    swap(squared_lcm_basis, lcm_basis);
    WEIGHT_ADD_MUL(444, tableau_num_rows);
  }

  PPL_DIRTY_TEMP_COEFFICIENT(challenger_numer);
  PPL_DIRTY_TEMP_COEFFICIENT(scalar_value);
  PPL_DIRTY_TEMP_COEFFICIENT(challenger_value);
  PPL_DIRTY_TEMP_COEFFICIENT(current_value);

  PPL_DIRTY_TEMP_COEFFICIENT(current_numer);
  PPL_DIRTY_TEMP_COEFFICIENT(current_denom);
  dimension_type entering_index = 0;
  const int cost_sign = sgn(working_cost.get(working_cost.size() - 1));

  // These two implementation work for both sparse and dense matrices.
  // However, when using sparse matrices the first one is fast and the second
  // one is slow, and when using dense matrices the first one is slow and
  // the second one is fast.
#if PPL_USE_SPARSE_MATRIX

  const dimension_type tableau_num_columns = tableau.num_columns();
  const dimension_type tableau_num_columns_minus_1 = tableau_num_columns - 1;
  // This is static to improve performance.
  // A pair (i, x) means that sgn(working_cost[i]) == cost_sign and x
  // is the denominator of the challenger, for the column i.
  static std::vector<std::pair<dimension_type, Coefficient> > columns;
  columns.clear();
  // tableau_num_columns - 2 is only an upper bound on the required elements.
  // This helps to reduce the number of calls to new [] and delete [] and
  // the construction/destruction of Coefficient objects.
  columns.reserve(tableau_num_columns - 2);
  {
    working_cost_type::const_iterator i = working_cost.lower_bound(1);
    // Note that find() is used instead of lower_bound.
    working_cost_type::const_iterator i_end
      = working_cost.find(tableau_num_columns_minus_1);
    for ( ; i != i_end; ++i) {
      if (sgn(*i) == cost_sign) {
        columns.push_back(std::pair<dimension_type, Coefficient>
                          (i.index(), squared_lcm_basis));
      }
    }
  }
  for (dimension_type i = tableau_num_rows; i-- > 0; ) {
    const Row& tableau_i = tableau[i];
    Row::const_iterator j = tableau_i.begin();
    Row::const_iterator j_end = tableau_i.end();
    std::vector<std::pair<dimension_type, Coefficient> >::iterator
      k = columns.begin();
    std::vector<std::pair<dimension_type, Coefficient> >::iterator
      k_end = columns.end();
    while (j != j_end) {
      while (k != k_end && j.index() > k->first) {
        ++k;
      }
      if (k == k_end) {
        break;
      }
      PPL_ASSERT(j.index() <= k->first);
      if (j.index() < k->first) {
        j = tableau_i.lower_bound(j, k->first);
      }
      else {
        Coefficient_traits::const_reference tableau_ij = *j;
        WEIGHT_BEGIN();
#if PPL_USE_SPARSE_MATRIX
        scalar_value = tableau_ij * norm_factor[i];
        add_mul_assign(k->second, scalar_value, scalar_value);
#else
        // The test against 0 gives rise to a consistent speed up in the dense
        // implementation: see
        // http://www.cs.unipr.it/pipermail/ppl-devel/2009-February/
        // 014000.html
        if (tableau_ij != 0) {
          scalar_value = tableau_ij * norm_factor[i];
          add_mul_assign(k->second, scalar_value, scalar_value);
        }
#endif
        WEIGHT_ADD_MUL(47, tableau_num_rows);
        ++k;
        ++j;
      }
    }
  }
  working_cost_type::const_iterator itr = working_cost.end();
  for (std::vector<std::pair<dimension_type, Coefficient> >::reverse_iterator
       k = columns.rbegin(), k_end = columns.rend(); k != k_end; ++k) {
    itr = working_cost.lower_bound(itr, k->first);
    if (itr != working_cost.end() && itr.index() == k->first) {
      // We cannot compute the (exact) square root of abs(\Delta x_j).
      // The workaround is to compute the square of `cost[j]'.
      challenger_numer = (*itr) * (*itr);
      // Initialization during the first loop.
      if (entering_index == 0) {
        swap(current_numer, challenger_numer);
        swap(current_denom, k->second);
        entering_index = k->first;
        continue;
      }
      challenger_value = challenger_numer * current_denom;
      current_value = current_numer * k->second;
      // Update the values, if the challenger wins.
      if (challenger_value > current_value) {
        swap(current_numer, challenger_numer);
        swap(current_denom, k->second);
        entering_index = k->first;
      }
    }
    else {
      PPL_ASSERT(working_cost.get(k->first) == 0);
      // Initialization during the first loop.
      if (entering_index == 0) {
        current_numer = 0;
        swap(current_denom, k->second);
        entering_index = k->first;
        continue;
      }
      // Update the values, if the challenger wins.
      if (0 > sgn(current_numer) * sgn(k->second)) {
        current_numer = 0;
        swap(current_denom, k->second);
        entering_index = k->first;
      }
    }
  }

#else // !PPL_USE_SPARSE_MATRIX

  PPL_DIRTY_TEMP_COEFFICIENT(challenger_denom);
  for (dimension_type j = tableau.num_columns() - 1; j-- > 1; ) {
    Coefficient_traits::const_reference cost_j = working_cost[j];
    if (sgn(cost_j) == cost_sign) {
      WEIGHT_BEGIN();
      // We cannot compute the (exact) square root of abs(\Delta x_j).
      // The workaround is to compute the square of `cost[j]'.
      challenger_numer = cost_j * cost_j;
      // Due to our integer implementation, the `1' term in the denominator
      // of the original formula has to be replaced by `squared_lcm_basis'.
      challenger_denom = squared_lcm_basis;
      for (dimension_type i = tableau_num_rows; i-- > 0; ) {
        Coefficient_traits::const_reference tableau_ij = tableau[i][j];
        // The test against 0 gives rise to a consistent speed up: see
        // http://www.cs.unipr.it/pipermail/ppl-devel/2009-February/
        // 014000.html
        if (tableau_ij != 0) {
          scalar_value = tableau_ij * norm_factor[i];
          add_mul_assign(challenger_denom, scalar_value, scalar_value);
        }
      }
      // Initialization during the first loop.
      if (entering_index == 0) {
        swap(current_numer, challenger_numer);
        swap(current_denom, challenger_denom);
        entering_index = j;
        continue;
      }
      challenger_value = challenger_numer * current_denom;
      current_value = current_numer * challenger_denom;
      // Update the values, if the challenger wins.
      if (challenger_value > current_value) {
        swap(current_numer, challenger_numer);
        swap(current_denom, challenger_denom);
        entering_index = j;
      }
      WEIGHT_ADD_MUL(47, tableau_num_rows);
    }
  }

#endif // !PPL_USE_SPARSE_MATRIX

  return entering_index;
}

PPL::dimension_type Parma_Polyhedra_Library::MIP_Problem::steepest_edge_float_entering_index ( ) const

private

Same as steepest_edge_exact_entering_index, but using floating points.

Note

Due to rounding errors, the index of the variable entering the base of the MIP problem is not predictable across different architectures. Hence, the overall simplex computation may differ in the path taken to reach the optimum. Anyway, the exact final result will be computed for the MIP_Problem.

Definition at line 1009 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::Boundary_NS::assign(), Parma_Polyhedra_Library::Sparse_Row::begin(), Parma_Polyhedra_Library::Sparse_Row::end(), Parma_Polyhedra_Library::Sparse_Row::get(), Parma_Polyhedra_Library::CO_Tree::const_iterator::index(), Parma_Polyhedra_Library::CO_Tree::iterator::index(), Parma_Polyhedra_Library::Sparse_Row::lower_bound(), Parma_Polyhedra_Library::Boundary_NS::sgn(), WEIGHT_ADD, WEIGHT_ADD_MUL, and WEIGHT_BEGIN.

                                                         {
  const dimension_type tableau_num_rows = tableau.num_rows();
  const dimension_type tableau_num_columns = tableau.num_columns();
  PPL_ASSERT(tableau_num_rows == base.size());
  double current_value = 0.0;
  // Due to our integer implementation, the `1' term in the denominator
  // of the original formula has to be replaced by `squared_lcm_basis'.
  double float_tableau_value;
  double float_tableau_denom;
  dimension_type entering_index = 0;
  const int cost_sign = sgn(working_cost.get(working_cost.size() - 1));

  // These two implementation work for both sparse and dense matrices.
  // However, when using sparse matrices the first one is fast and the second
  // one is slow, and when using dense matrices the first one is slow and
  // the second one is fast.
#if PPL_USE_SPARSE_MATRIX

  const dimension_type tableau_num_columns_minus_1 = tableau_num_columns - 1;
  // This is static to improve performance.
  // A vector of <column_index, challenger_denom> pairs, ordered by
  // column_index.
  static std::vector<std::pair<dimension_type, double> > columns;
  columns.clear();
  // (working_cost.size() - 2) is an upper bound only.
  columns.reserve(working_cost.size() - 2);
  {
    working_cost_type::const_iterator i = working_cost.lower_bound(1);
    // Note that find() is used instead of lower_bound().
    working_cost_type::const_iterator i_end
      = working_cost.find(tableau_num_columns_minus_1);
    for ( ; i != i_end; ++i) {
      if (sgn(*i) == cost_sign) {
        columns.push_back(std::make_pair(i.index(), 1.0));
      }
    }
  }
  for (dimension_type i = tableau_num_rows; i-- > 0; ) {
    const Row& tableau_i = tableau[i];
    assign(float_tableau_denom, tableau_i.get(base[i]));
    Row::const_iterator j = tableau_i.begin();
    Row::const_iterator j_end = tableau_i.end();
    std::vector<std::pair<dimension_type, double> >::iterator k
      = columns.begin();
    std::vector<std::pair<dimension_type, double> >::iterator k_end
      = columns.end();
    while (j != j_end && k != k_end) {
      const dimension_type column = j.index();
      while (k != k_end && column > k->first) {
        ++k;
      }
      if (k == k_end) {
        break;
      }
      if (k->first > column) {
        j = tableau_i.lower_bound(j, k->first);
      }
      else {
        PPL_ASSERT(k->first == column);
        PPL_ASSERT(tableau_i.get(base[i]) != 0);
        WEIGHT_BEGIN();
        assign(float_tableau_value, *j);
        float_tableau_value /= float_tableau_denom;
        float_tableau_value *= float_tableau_value;
        k->second += float_tableau_value;
        WEIGHT_ADD(22);
        ++j;
        ++k;
      }
    }
  }
  // The candidates are processed backwards to get the same result in both
  // this implementation and the dense implementation below.
  for (std::vector<std::pair<dimension_type, double> >::const_reverse_iterator
       i = columns.rbegin(), i_end = columns.rend(); i != i_end; ++i) {
    const double challenger_value = sqrt(i->second);
    if (entering_index == 0 || challenger_value > current_value) {
      current_value = challenger_value;
      entering_index = i->first;
    }
  }

#else // !PPL_USE_SPARSE_MATRIX

  double challenger_numer = 0.0;
  double challenger_denom = 0.0;
  for (dimension_type j = tableau_num_columns - 1; j-- > 1; ) {
    Coefficient_traits::const_reference cost_j = working_cost.get(j);
    if (sgn(cost_j) == cost_sign) {
      WEIGHT_BEGIN();
      // We cannot compute the (exact) square root of abs(\Delta x_j).
      // The workaround is to compute the square of `cost[j]'.
      assign(challenger_numer, cost_j);
      challenger_numer = std::abs(challenger_numer);
      // Due to our integer implementation, the `1' term in the denominator
      // of the original formula has to be replaced by `squared_lcm_basis'.
      challenger_denom = 1.0;
      for (dimension_type i = tableau_num_rows; i-- > 0; ) {
        const Row& tableau_i = tableau[i];
        Coefficient_traits::const_reference tableau_ij = tableau_i[j];
        if (tableau_ij != 0) {
          PPL_ASSERT(tableau_i[base[i]] != 0);
          assign(float_tableau_value, tableau_ij);
          assign(float_tableau_denom, tableau_i[base[i]]);
          float_tableau_value /= float_tableau_denom;
          challenger_denom += float_tableau_value * float_tableau_value;
        }
      }
      double challenger_value = sqrt(challenger_denom);
      // Initialize `current_value' during the first iteration.
      // Otherwise update if the challenger wins.
      if (entering_index == 0 || challenger_value > current_value) {
        current_value = challenger_value;
        entering_index = j;
      }
      WEIGHT_ADD_MUL(10, tableau_num_rows);
    }
  }

#endif // !PPL_USE_SPARSE_MATRIX

  return entering_index;
}

PPL::dimension_type Parma_Polyhedra_Library::MIP_Problem::textbook_entering_index ( ) const

private

Computes the column index of the variable entering the base, using the textbook algorithm with anti-cycling rule.

Returns

The column index of the variable that enters the base. If no such variable exists, optimality was achieved and 0 is returned.

Definition at line 1333 of file MIP_Problem.cc.

References Parma_Polyhedra_Library::CO_Tree::const_iterator::index(), and Parma_Polyhedra_Library::Boundary_NS::sgn().

                                              {
  // The variable entering the base is the first one whose coefficient
  // in the cost function has the same sign the cost function itself.
  // If no such variable exists, then we met the optimality condition
  // (and return 0 to the caller).

  // Get the "sign" of the cost function.
  const dimension_type cost_sign_index = working_cost.size() - 1;
  const int cost_sign = sgn(working_cost.get(cost_sign_index));
  PPL_ASSERT(cost_sign != 0);

  working_cost_type::const_iterator i = working_cost.lower_bound(1);
  // Note that find() is used instead of lower_bound() because they are
  // equivalent when searching the last element in the row.
  working_cost_type::const_iterator i_end
    = working_cost.find(cost_sign_index);
  for ( ; i != i_end; ++i) {
    if (sgn(*i) == cost_sign) {
      return i.index();
    }
  }
  // No variable has to enter the base:
  // the cost function was optimized.
  return 0;
}

memory_size_type Parma_Polyhedra_Library::MIP_Problem::total_memory_in_bytes ( ) const

inline

Returns the total size in bytes of the memory occupied by *this.

Definition at line 236 of file MIP_Problem_inlines.hh.

References external_memory_in_bytes().

                                         {
  return sizeof(*this) + external_memory_in_bytes();
}

Friends And Related Function Documentation

std::ostream & operator<< ( std::ostream &  s, const MIP_Problem &  mip  )

related

Output operator.

std::ostream & operator<< ( std::ostream &  s, const MIP_Problem &  mip  )

related

Definition at line 2888 of file MIP_Problem.cc.

References constraints_begin(), constraints_end(), integer_space_dimensions(), Parma_Polyhedra_Library::MAXIMIZATION, objective_function(), and optimization_mode().

                                                                 {
  s << "Constraints:";
  for (MIP_Problem::const_iterator i = mip.constraints_begin(),
         i_end = mip.constraints_end(); i != i_end; ++i) {
    s << "\n" << *i;
  }
  s << "\nObjective function: "
    << mip.objective_function()
    << "\nOptimization mode: "
    << ((mip.optimization_mode() == MAXIMIZATION)
        ? "MAXIMIZATION"
        : "MINIMIZATION");
  s << "\nInteger variables: " << mip.integer_space_dimensions();
  return s;
}

friend struct RAII_Temporary_Real_Relaxation

friend

Definition at line 620 of file MIP_Problem_defs.hh.

void swap ( MIP_Problem &  x, MIP_Problem &  y  )

related

Swaps x with y.

Referenced by m_swap(), Parma_Polyhedra_Library::MIP_Problem::RAII_Temporary_Real_Relaxation::RAII_Temporary_Real_Relaxation(), and Parma_Polyhedra_Library::MIP_Problem::RAII_Temporary_Real_Relaxation::~RAII_Temporary_Real_Relaxation().

void swap ( MIP_Problem &  x, MIP_Problem &  y  )

related

Definition at line 320 of file MIP_Problem_inlines.hh.

References m_swap().

                                     {
  x.m_swap(y);
}

Member Data Documentation

std::vector<dimension_type> Parma_Polyhedra_Library::MIP_Problem::base

private

The current basic solution.

Definition at line 533 of file MIP_Problem_defs.hh.

Referenced by external_memory_in_bytes(), and m_swap().

dimension_type Parma_Polyhedra_Library::MIP_Problem::external_space_dim

private

The dimension of the vector space.

Definition at line 499 of file MIP_Problem_defs.hh.

Referenced by is_lp_satisfiable(), m_swap(), MIP_Problem(), and space_dimension().

dimension_type Parma_Polyhedra_Library::MIP_Problem::first_pending_constraint

private

The first index of `input_cs' containing a pending constraint.

Definition at line 585 of file MIP_Problem_defs.hh.

Referenced by is_lp_satisfiable(), and m_swap().

Variables_Set Parma_Polyhedra_Library::MIP_Problem::i_variables

private

A set containing all the indexes of variables that are constrained to have an integer value.

Definition at line 600 of file MIP_Problem_defs.hh.

Referenced by integer_space_dimensions(), is_satisfiable(), m_swap(), MIP_Problem(), Parma_Polyhedra_Library::MIP_Problem::RAII_Temporary_Real_Relaxation::RAII_Temporary_Real_Relaxation(), solve(), and Parma_Polyhedra_Library::MIP_Problem::RAII_Temporary_Real_Relaxation::~RAII_Temporary_Real_Relaxation().

dimension_type Parma_Polyhedra_Library::MIP_Problem::inherited_constraints

private

The number of constraints that are inherited from our parent in the recursion tree built when solving via branch-and-bound.

The first inherited_constraints elements in input_cs point to the inherited constraints, whose resources are owned by our ancestors. The resources of the other elements in input_cs are owned by *this and should be appropriately released on destruction.

Definition at line 582 of file MIP_Problem_defs.hh.

Referenced by external_memory_in_bytes(), m_swap(), and ~MIP_Problem().

bool Parma_Polyhedra_Library::MIP_Problem::initialized

private

A Boolean encoding whether or not internal data structures have already been properly sized and populated: useful to allow for deeper checks in method OK().

Definition at line 568 of file MIP_Problem_defs.hh.

Referenced by is_lp_satisfiable(), and m_swap().

std::vector<Constraint*> Parma_Polyhedra_Library::MIP_Problem::input_cs

private

The sequence of constraints describing the feasible region.

Definition at line 571 of file MIP_Problem_defs.hh.

Referenced by add_constraint_helper(), choose_branching_variable(), constraints_begin(), constraints_end(), external_memory_in_bytes(), m_swap(), MIP_Problem(), and ~MIP_Problem().

Linear_Expression Parma_Polyhedra_Library::MIP_Problem::input_obj_function

private

The objective function to be optimized.

Definition at line 588 of file MIP_Problem_defs.hh.

Referenced by external_memory_in_bytes(), m_swap(), and objective_function().

dimension_type Parma_Polyhedra_Library::MIP_Problem::internal_space_dim

private

The space dimension of the current (partial) solution of the MIP problem; it may be smaller than external_space_dim.

Definition at line 505 of file MIP_Problem_defs.hh.

Referenced by is_lp_satisfiable(), and m_swap().

Generator Parma_Polyhedra_Library::MIP_Problem::last_generator

private

The last successfully computed feasible or optimizing point.

Definition at line 594 of file MIP_Problem_defs.hh.

Referenced by choose_branching_variable(), compute_generator(), external_memory_in_bytes(), is_mip_satisfiable(), is_satisfiable(), m_swap(), solve(), and solve_mip().

std::vector<std::pair<dimension_type, dimension_type> > Parma_Polyhedra_Library::MIP_Problem::mapping

private

A map between the variables of `input_cs' and `tableau'.

Contains all the pairs (i, j) such that mapping[i].first encodes the index of the column in the tableau where input_cs[i] is stored; if mapping[i].second is not a zero, it encodes the split part of the tableau of input_cs[i]. The "positive" one is represented by mapping[i].first and the "negative" one is represented by mapping[i].second.

Definition at line 530 of file MIP_Problem_defs.hh.

Referenced by external_memory_in_bytes(), is_lp_satisfiable(), and m_swap().

Optimization_Mode Parma_Polyhedra_Library::MIP_Problem::opt_mode

private

The optimization mode requested.

Definition at line 591 of file MIP_Problem_defs.hh.

Referenced by m_swap(), optimization_mode(), and set_optimization_mode().

Control_Parameter_Value Parma_Polyhedra_Library::MIP_Problem::pricing

private

The pricing method in use.

Definition at line 561 of file MIP_Problem_defs.hh.

Referenced by get_control_parameter(), m_swap(), and set_control_parameter().

Status Parma_Polyhedra_Library::MIP_Problem::status

private

The internal state of the MIP problem.

Definition at line 554 of file MIP_Problem_defs.hh.

Referenced by is_satisfiable(), m_swap(), set_optimization_mode(), solve(), and solve_mip().

Matrix<Row> Parma_Polyhedra_Library::MIP_Problem::tableau

private

The matrix encoding the current feasible region in tableau form.

Definition at line 514 of file MIP_Problem_defs.hh.

Referenced by external_memory_in_bytes(), is_lp_satisfiable(), and m_swap().

working_cost_type Parma_Polyhedra_Library::MIP_Problem::working_cost

private

The working cost function.

Definition at line 519 of file MIP_Problem_defs.hh.

Referenced by external_memory_in_bytes(), and m_swap().

---

The documentation for this class was generated from the following files:

• MIP_Problem_defs.hh
• MIP_Problem.cc
• MIP_Problem_inlines.hh
• MIP_Problem_templates.hh