A finite sparse sequence of coefficients. More...

#include <Sparse_Row_defs.hh>

Collaboration diagram for Parma_Polyhedra_Library::Sparse_Row:

Public Types
typedef CO_Tree::iterator	iterator
	An iterator on the row elements. More...

typedef CO_Tree::const_iterator	const_iterator
	A const iterator on the row elements. More...

Public Member Functions
	Sparse_Row (dimension_type n=0)
	Constructs a row with the specified size. More...

	Sparse_Row (dimension_type n, dimension_type capacity)
	Constructs a row with the specified size. More...

	Sparse_Row (const Sparse_Row &y, dimension_type capacity)
	Copy constructor with specified capacity. More...

	Sparse_Row (const Sparse_Row &y, dimension_type sz, dimension_type capacity)
	Copy constructor with specified size and capacity. More...

	Sparse_Row (const Dense_Row &row)
	Constructor from a Dense_Row. More...

	Sparse_Row (const Dense_Row &y, dimension_type sz, dimension_type capacity)
	Copy constructor from a Dense_Row with specified size and capacity. More...

Sparse_Row &	operator= (const Dense_Row &row)

void	m_swap (Sparse_Row &x)
	Swaps *this and x. More...

dimension_type	size () const
	Returns the size of the row. More...

dimension_type	num_stored_elements () const
	Returns the number of elements explicitly stored in the row. More...

void	resize (dimension_type n)
	Resizes the row to the specified size. More...

void	expand_within_capacity (dimension_type n)
	Resizes the row to size `n`. More...

void	shrink (dimension_type n)
	Resizes the row to size `n`. More...

void	delete_element_and_shift (dimension_type i)
	Deletes the i-th element from the row, shifting the next elements to the left. More...

void	add_zeroes_and_shift (dimension_type n, dimension_type i)
	Adds `n` zeroes before index `i`. More...

iterator	begin ()
	Returns an iterator that points at the first stored element. More...

const iterator &	end ()
	Returns an iterator that points after the last stored element. More...

const_iterator	begin () const
	Equivalent to `cbegin()`. More...

const const_iterator &	end () const
	Equivalent to `cend()`. More...

const_iterator	cbegin () const
	Returns an iterator that points at the first element. More...

const const_iterator &	cend () const
	Returns an iterator that points after the last element. More...

void	clear ()
	Resets all the elements of this row. More...

Coefficient &	operator[] (dimension_type i)
	Gets a reference to the i-th element. More...

Coefficient_traits::const_reference	operator[] (dimension_type i) const
	Equivalent to `get(i)`, provided for convenience. More...

Coefficient_traits::const_reference	get (dimension_type i) const
	Gets the i-th element in the sequence. More...

iterator	find (dimension_type i)
	Looks for an element with index i. More...

iterator	find (iterator itr, dimension_type i)
	Looks for an element with index i. More...

const_iterator	find (dimension_type i) const
	Looks for an element with index i. More...

const_iterator	find (const_iterator itr, dimension_type i) const
	Looks for an element with index i. More...

iterator	lower_bound (dimension_type i)
	Lower bound of index i. More...

iterator	lower_bound (iterator itr, dimension_type i)
	Lower bound of index i. More...

const_iterator	lower_bound (dimension_type i) const
	Lower bound of index i. More...

const_iterator	lower_bound (const_iterator itr, dimension_type i) const
	Lower bound of index i. More...

iterator	insert (dimension_type i, Coefficient_traits::const_reference x)
	Equivalent to `(*this)[i] = x; find(i)`, but faster. More...

iterator	insert (iterator itr, dimension_type i, Coefficient_traits::const_reference x)
	Equivalent to `(*this)[i] = x; find(i)`, but faster. More...

iterator	insert (dimension_type i)
	Equivalent to `(*this)[i]; find(i)`, but faster. More...

iterator	insert (iterator itr, dimension_type i)
	Equivalent to `(*this)[i]; find(i)`, but faster. More...

void	swap_coefficients (dimension_type i, dimension_type j)
	Swaps the i-th element with the j-th element. More...

void	fast_swap (dimension_type i, iterator itr)

void	swap_coefficients (iterator i, iterator j)
	Swaps the element pointed to by i with the element pointed to by j. More...

iterator	reset (iterator i)
	Resets to zero the value pointed to by i. More...

iterator	reset (iterator first, iterator last)
	Resets to zero the values in the range [first,last). More...

void	reset (dimension_type i)
	Resets to zero the i-th element. More...

void	reset_after (dimension_type i)
	Resets to zero the elements with index greater than or equal to i. More...

void	normalize ()
	Normalizes the modulo of coefficients so that they are mutually prime. More...

template<typename Func1 , typename Func2 >
void	combine_needs_first (const Sparse_Row &y, const Func1 &f, const Func2 &g)
	Calls g(x[i],y[i]), for each i. More...

template<typename Func1 , typename Func2 >
void	combine_needs_second (const Sparse_Row &y, const Func1 &g, const Func2 &h)
	Calls g(x[i],y[i]), for each i. More...

template<typename Func1 , typename Func2 , typename Func3 >
void	combine (const Sparse_Row &y, const Func1 &f, const Func2 &g, const Func3 &h)
	Calls g(x[i],y[i]), for each i. More...

void	linear_combine (const Sparse_Row &y, Coefficient_traits::const_reference coeff1, Coefficient_traits::const_reference coeff2)

void	linear_combine (const Sparse_Row &y, Coefficient_traits::const_reference c1, Coefficient_traits::const_reference c2, dimension_type start, dimension_type end)

void	ascii_dump () const
	Writes to `std::cerr` an ASCII representation of `*this`. More...

void	ascii_dump (std::ostream &s) const
	Writes to `s` an ASCII representation of `*this`. More...

void	print () const
	Prints `*this` to `std::cerr` using `operator<<`. More...

bool	ascii_load (std::istream &s)
	Loads the row from an ASCII representation generated using ascii_dump(). More...

memory_size_type	external_memory_in_bytes () const
	Returns the size in bytes of the memory managed by `*this`. More...

memory_size_type	external_memory_in_bytes (dimension_type capacity) const
	Returns the size in bytes of the memory managed by `*this`. More...

memory_size_type	total_memory_in_bytes () const
	Returns the size in bytes of the memory managed by `*this`. More...

memory_size_type	total_memory_in_bytes (dimension_type capacity) const
	Returns the size in bytes of the memory managed by `*this`. More...

bool	OK () const
	Checks the invariant. More...

bool	OK (dimension_type capacity) const
	Checks the invariant. More...

Static Public Member Functions
static dimension_type	max_size ()
	Returns the size() of the largest possible Sparse_Row. More...

Private Attributes
CO_Tree	tree
	The tree used to store the elements. More...

dimension_type	size_
	The size of the row. More...

Related Functions
(Note that these are not member functions.)
bool	operator== (const Sparse_Row &x, const Sparse_Row &y)

bool	operator!= (const Sparse_Row &x, const Sparse_Row &y)

void	swap (Parma_Polyhedra_Library::Sparse_Row &x, Parma_Polyhedra_Library::Sparse_Row &y)
	Swaps `x` with `y`. More...

bool	operator== (const Sparse_Row &x, const Sparse_Row &y)
	Returns `true` if and only if `x` and `y` are equal. More...

bool	operator!= (const Sparse_Row &x, const Sparse_Row &y)
	Returns `true` if and only if `x` and `y` are different. More...

void	linear_combine (Sparse_Row &x, const Dense_Row &y, Coefficient_traits::const_reference coeff1, Coefficient_traits::const_reference coeff2)

void	linear_combine (Sparse_Row &x, const Dense_Row &y, Coefficient_traits::const_reference c1, Coefficient_traits::const_reference c2, dimension_type start, dimension_type end)

void	linear_combine (Dense_Row &x, const Sparse_Row &y, Coefficient_traits::const_reference coeff1, Coefficient_traits::const_reference coeff2)

void	linear_combine (Dense_Row &x, const Sparse_Row &y, Coefficient_traits::const_reference c1, Coefficient_traits::const_reference c2, dimension_type start, dimension_type end)

void	linear_combine (Sparse_Row &x, const Sparse_Row &y, Coefficient_traits::const_reference coeff1, Coefficient_traits::const_reference coeff2)

void	linear_combine (Sparse_Row &x, const Sparse_Row &y, Coefficient_traits::const_reference c1, Coefficient_traits::const_reference c2, dimension_type start, dimension_type end)

void	swap (Sparse_Row &x, Sparse_Row &y)

Detailed Description

A finite sparse sequence of coefficients.

This class is implemented using a CO_Tree. See the documentation of CO_Tree for details on the implementation and the performance.

This class is a drop-in replacement of Dense_Row, meaning that code using Dense_Row can be ported to Sparse_Row changing only the type. The resulting code will work, but probably needs more CPU and memory (it does not exploit the sparse representation yet).

To take advantage of the sparse representation, the client code must then be modified to use methods which can have a faster implementation on sparse data structures.

The main changes are the replacement of calls to operator[] with calls to find(), lower_bound() or insert(), using hint iterators when possible. Sequential scanning of rows should probably be implemented using iterators rather than indexes, to improve performance. reset() should be called to zero elements.

See also: Sparse_Matrix; CO_Tree

Definition at line 58 of file Sparse_Row_defs.hh.

Member Typedef Documentation

typedef CO_Tree::const_iterator Parma_Polyhedra_Library::Sparse_Row::const_iterator

A const iterator on the row elements.

This iterator skips non-stored zeroes.

See also: CO_Tree::const_iterator

Definition at line 74 of file Sparse_Row_defs.hh.

typedef CO_Tree::iterator Parma_Polyhedra_Library::Sparse_Row::iterator

An iterator on the row elements.

This iterator skips non-stored zeroes.

See also: CO_Tree::iterator

Definition at line 67 of file Sparse_Row_defs.hh.

Constructor & Destructor Documentation

Parma_Polyhedra_Library::Sparse_Row::Sparse_Row ( dimension_type n = 0 )

inlineexplicit

Constructs a row with the specified size.

Parameters

n	The size for the new row.

The row will contain only non-stored zeroes.

This constructor takes $O(1)$ time.

Definition at line 32 of file Sparse_Row_inlines.hh.

References OK().

   : size_(n) {
   PPL_ASSERT(OK());
 }

Parma_Polyhedra_Library::Sparse_Row::Sparse_Row	(	dimension_type	n,
		dimension_type	capacity
	)

inline

Constructs a row with the specified size.

Parameters

n	The size for the new row.
capacity	It is ignored. This parameter is needed for compatibility with Dense_Row.

The row will contain only non-stored zeroes.

This constructor takes $O(1)$ time.

Definition at line 38 of file Sparse_Row_inlines.hh.

References OK().

   : size_(n) {
   PPL_ASSERT(OK());
 }

Parma_Polyhedra_Library::Sparse_Row::Sparse_Row	(	const Sparse_Row &	y,
		dimension_type	capacity
	)

inline

Copy constructor with specified capacity.

It is assumed that capacity is greater than or equal to the size of y.

Definition at line 44 of file Sparse_Row_inlines.hh.

45 : tree(y.tree), size_(y.size_) {

46 }

Parma_Polyhedra_Library::Sparse_Row::tree

CO_Tree tree

The tree used to store the elements.

Definition: Sparse_Row_defs.hh:816

Parma_Polyhedra_Library::Sparse_Row::size_

dimension_type size_

The size of the row.

Definition: Sparse_Row_defs.hh:822

Parma_Polyhedra_Library::Sparse_Row::Sparse_Row	(	const Sparse_Row &	y,
		dimension_type	sz,
		dimension_type	capacity
	)

inline

Copy constructor with specified size and capacity.

It is assumed that sz is less than or equal to capacity.

Definition at line 49 of file Sparse_Row_inlines.hh.

References OK().

   : tree(y.begin(),
          std::distance(y.begin(), y.lower_bound(std::min(y.size(), sz)))),
     size_(sz) {
   PPL_ASSERT(OK());
 }

Parma_Polyhedra_Library::Sparse_Row::Sparse_Row ( const Dense_Row & row )

explicit

Constructor from a Dense_Row.

Parameters

row	The row that will be copied into *this.

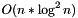This constructor takes $O(n)$ time. Note that constructing of a row of zeroes and then inserting n elements costs $O(n*\log^2 n)$ time.

Definition at line 101 of file Sparse_Row.cc.

References OK().

   : tree(Sparse_Row_from_Dense_Row_helper_iterator(row, row.size()),
          Sparse_Row_from_Dense_Row_helper_function(row, row.size())),
     size_(row.size()) {
   PPL_ASSERT(OK());
 }

Parma_Polyhedra_Library::Sparse_Row::Sparse_Row	(	const Dense_Row &	y,
		dimension_type	sz,
		dimension_type	capacity
	)

Copy constructor from a Dense_Row with specified size and capacity.

It is assumed that sz is less than or equal to capacity.

Definition at line 108 of file Sparse_Row.cc.

References OK().

   : tree(Sparse_Row_from_Dense_Row_helper_iterator(row, row.size()),
          Sparse_Row_from_Dense_Row_helper_function(row, row.size())),
     size_(sz) {
   (void)capacity;
   PPL_ASSERT(OK());
 }

Member Function Documentation

void Parma_Polyhedra_Library::Sparse_Row::add_zeroes_and_shift	(	dimension_type	n,
		dimension_type	i
	)

inline

Adds n zeroes before index i.

Parameters

n	The number of non-stored zeroes that will be added to the row.
i	The index of the element before which the zeroes will be added.

Existing elements with index greater than or equal to i are shifted to the right by n positions. The size is increased by n.

Existing iterators are not invalidated, but are shifted to the right by n if they pointed at or after index i (i.e., they point to the same, possibly shifted, values as before).

This method takes 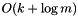$O(k + \log m)$ expected time, where $k$ is the number of elements with index greater than or equal to i and 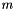$m$ the number of stored elements.

Definition at line 105 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::increase_keys_from(), OK(), size_, and tree.

                                                                    {
   PPL_ASSERT(i <= size_);
   tree.increase_keys_from(i, n);
   size_ += n;
   PPL_ASSERT(OK());
 }

void Parma_Polyhedra_Library::Sparse_Row::ascii_dump ( ) const

Writes to std::cerr an ASCII representation of *this.

void Parma_Polyhedra_Library::Sparse_Row::ascii_dump ( std::ostream & s ) const

Writes to s an ASCII representation of *this.

Definition at line 685 of file Sparse_Row.cc.

                                              {
   s << "size " << size_ << ' ';
   dimension_type n_elements = 0;
   for (const_iterator i = begin(), i_end = end(); i != i_end; ++i) {
     ++n_elements;
   }
   s << "elements " << n_elements << ' ';
   for (const_iterator i = begin(), i_end = end(); i != i_end; ++i) {
     s << "[ " << i.index() << " ]= " << *i << ' ';
   }
   s << "\n";
 }

bool Parma_Polyhedra_Library::Sparse_Row::ascii_load ( std::istream & s )

Loads the row from an ASCII representation generated using ascii_dump().

Parameters

s	The stream from which the ASCII representation will be loaded.

Definition at line 701 of file Sparse_Row.cc.

References PPL_DIRTY_TEMP_COEFFICIENT.

                                        {
   std::string str;
   if (!(s >> str) || str != "size") {
     return false;
   }
   if (!(s >> size_)) {
     return false;
   }
   clear();
 
   if (!(s >> str) || str != "elements") {
     return false;
   }
 
   dimension_type n_elements;
   if (!(s >> n_elements)) {
     return false;
   }
 
   PPL_DIRTY_TEMP_COEFFICIENT(current_data);
   for (dimension_type i = 0; i < n_elements; ++i) {
     dimension_type current_key;
     if (!(s >> str) || str != "[") {
       return false;
     }
     if (!(s >> current_key)) {
       return false;
     }
     if (!(s >> str) || str != "]=") {
       return false;
     }
     if (!(s >> current_data)) {
       return false;
     }
     tree.insert(current_key, current_data);
   }
   PPL_ASSERT(OK());
   return true;
 }

Sparse_Row::iterator Parma_Polyhedra_Library::Sparse_Row::begin ( )

inline

Returns an iterator that points at the first stored element.

This method takes $O(1)$ time.

Definition at line 113 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::begin(), and tree.

                   {
   return tree.begin();
 }

Sparse_Row::const_iterator Parma_Polyhedra_Library::Sparse_Row::begin ( ) const

inline

Equivalent to cbegin().

Definition at line 123 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::cbegin(), and tree.

                         {
   return tree.cbegin();
 }

Sparse_Row::const_iterator Parma_Polyhedra_Library::Sparse_Row::cbegin ( ) const

inline

Returns an iterator that points at the first element.

This method takes $O(1)$ time.

Definition at line 133 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::cbegin(), and tree.

                          {
   return tree.cbegin();
 }

const Sparse_Row::const_iterator & Parma_Polyhedra_Library::Sparse_Row::cend ( ) const

inline

Returns an iterator that points after the last element.

This method always returns a reference to the same internal iterator, that is updated at each operation that modifies the structure. Client code can keep a const reference to that iterator instead of keep updating a local iterator.

This method takes $O(1)$ time.

Definition at line 138 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::cend(), and tree.

                        {
   return tree.cend();
 }

void Parma_Polyhedra_Library::Sparse_Row::clear ( )

inline

Resets all the elements of this row.

This method takes $O(n)$ time.

Definition at line 148 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::clear(), and tree.

                   {
   tree.clear();
 }

template<typename Func1 , typename Func2 , typename Func3 >

void Parma_Polyhedra_Library::Sparse_Row::combine	(	const Sparse_Row &	y,
		const Func1 &	f,
		const Func2 &	g,
		const Func3 &	h
	)

Calls g(x[i],y[i]), for each i.

Parameters

y	The row that will be combined with *this.
f	A functor that should take a Coefficient&. f(c1) must be equivalent to g(c1, 0).
g	A functor that should take a Coefficient& and a Coefficient_traits::const_reference. g(c1, c2) must do nothing when both c1 and c2 are zero.
h	A functor that should take a Coefficient& and a Coefficient_traits::const_reference. h(c1, c2) must be equivalent to g(c1, c2) when c1 is zero.

This method takes 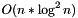$O(n*\log^2 n)$ time.

Note: The functors will only be called when necessary, assuming the requested properties hold.

See also: combine_needs_first; combine_needs_second

Definition at line 101 of file Sparse_Row_templates.hh.

References begin(), end(), Parma_Polyhedra_Library::CO_Tree::const_iterator::index(), Parma_Polyhedra_Library::CO_Tree::iterator::index(), insert(), and reset().

                                                     {
   if (this == &y) {
     for (iterator i = begin(), i_end = end(); i != i_end; ++i) {
       g(*i, *i);
     }
   }
   else {
     iterator i = begin();
     // This is a const reference to an internal iterator, that is kept valid.
     // If we just stored a copy, that would be invalidated by the calls to
     // reset() and insert().
     const iterator& i_end = end();
     const_iterator j = y.begin();
     const_iterator j_end = y.end();
     while (i != i_end && j != j_end) {
       if (i.index() == j.index()) {
         g(*i, *j);
         if (*i == 0) {
           i = reset(i);
         }
         else {
           ++i;
         }
         ++j;
       }
       else
         if (i.index() < j.index()) {
           f(*i);
           if (*i == 0) {
             i = reset(i);
           }
           else {
             ++i;
           }
         }
         else {
           PPL_ASSERT(i.index() > j.index());
           i = insert(i, j.index());
           h(*i, *j);
           if (*i == 0) {
             i = reset(i);
           }
           else {
             ++i;
           }
           ++j;
         }
     }
     PPL_ASSERT(i == i_end || j == j_end);
     while (i != i_end) {
       f(*i);
       if (*i == 0) {
         i = reset(i);
       }
       else {
         ++i;
       }
     }
     while (j != j_end) {
       i = insert(i, j.index());
       h(*i, *j);
       if (*i == 0) {
         i = reset(i);
       }
       ++j;
     }
   }
 }

template<typename Func1 , typename Func2 >

void Parma_Polyhedra_Library::Sparse_Row::combine_needs_first	(	const Sparse_Row &	y,
		const Func1 &	f,
		const Func2 &	g
	)

Calls g(x[i],y[i]), for each i.

Parameters

y	The row that will be combined with *this.
f	A functor that should take a Coefficient&. f(c1) must be equivalent to g(c1, 0).
g	A functor that should take a Coefficient& and a Coefficient_traits::const_reference. g(c1, c2) must do nothing when c1 is zero.

This method takes 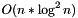$O(n*\log^2 n)$ time.

Note: The functors will only be called when necessary, assuming the requested properties hold.

See also: combine_needs_second; combine

Definition at line 32 of file Sparse_Row_templates.hh.

References begin(), end(), Parma_Polyhedra_Library::CO_Tree::const_iterator::index(), Parma_Polyhedra_Library::CO_Tree::iterator::index(), lower_bound(), and reset().

                                                                 {
   if (this == &y) {
     for (iterator i = begin(), i_end = end(); i != i_end; ++i) {
       g(*i, *i);
     }
   }
   else {
     iterator i = begin();
     // This is a const reference to an internal iterator, that is kept valid.
     // If we just stored a copy, that would be invalidated by the calls to
     // reset().
     const iterator& i_end = end();
     const_iterator j = y.begin();
     const_iterator j_end = y.end();
     while (i != i_end && j != j_end) {
       if (i.index() == j.index()) {
         g(*i, *j);
         if (*i == 0) {
           i = reset(i);
         }
         else {
           ++i;
         }
         ++j;
       }
       else
         if (i.index() < j.index()) {
           f(*i);
           if (*i == 0) {
             i = reset(i);
           }
           else {
             ++i;
           }
         }
         else {
           j = y.lower_bound(j, i.index());
         }
     }
     while (i != i_end) {
       f(*i);
       if (*i == 0) {
         i = reset(i);
       }
       else {
         ++i;
       }
     }
   }
 }

template<typename Func1 , typename Func2 >

void Parma_Polyhedra_Library::Sparse_Row::combine_needs_second	(	const Sparse_Row &	y,
		const Func1 &	g,
		const Func2 &	h
	)

Calls g(x[i],y[i]), for each i.

Parameters

y	The row that will be combined with *this.
g	A functor that should take a Coefficient& and a Coefficient_traits::const_reference. g(c1, 0) must do nothing, for every c1.
h	A functor that should take a Coefficient& and a Coefficient_traits::const_reference. h(c1, c2) must be equivalent to g(c1, c2) when c1 is zero.

This method takes 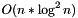$O(n*\log^2 n)$ time.

Note: The functors will only be called when necessary, assuming the requested properties hold.

See also: combine_needs_first; combine

Definition at line 86 of file Sparse_Row_templates.hh.

References begin(), end(), Parma_Polyhedra_Library::CO_Tree::iterator::index(), insert(), and reset().

                                                  {
   iterator i = begin();
   for (const_iterator j = y.begin(), j_end = y.end(); j != j_end; ++j) {
     i = insert(i, j.index());
     g(*i, *j);
     if (*i == 0) {
       i = reset(i);
     }
   }
 }

void Parma_Polyhedra_Library::Sparse_Row::delete_element_and_shift ( dimension_type i )

inline

Deletes the i-th element from the row, shifting the next elements to the left.

Parameters

i	The index of the element that will be deleted.

The size of the row is decreased by 1.

This operation invalidates existing iterators.

This method takes 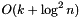$O(k+\log^2 n)$ amortized time, where k is the number of elements with index greater than i.

Definition at line 97 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::erase_element_and_shift_left(), OK(), size_, and tree.

                                                      {
   PPL_ASSERT(i < size_);
   tree.erase_element_and_shift_left(i);
   --size_;
   PPL_ASSERT(OK());
 }

const Sparse_Row::iterator & Parma_Polyhedra_Library::Sparse_Row::end ( )

inline

Returns an iterator that points after the last stored element.

This method always returns a reference to the same internal iterator, that is kept valid. Client code can keep a const reference to that iterator instead of keep updating a local iterator.

This method takes $O(1)$ time.

Definition at line 118 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::end(), and tree.

                 {
   return tree.end();
 }

const Sparse_Row::const_iterator & Parma_Polyhedra_Library::Sparse_Row::end ( ) const

inline

Equivalent to cend().

Definition at line 128 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::cend(), and tree.

                       {
   return tree.cend();
 }

void Parma_Polyhedra_Library::Sparse_Row::expand_within_capacity ( dimension_type n )

inline

Resizes the row to size n.

Parameters

n	The new size for the row.

This method, with this signature, is needed for compatibility with Dense_Row.

This method takes $O(1)$ time.

Definition at line 91 of file Sparse_Row_inlines.hh.

References resize(), and size().

                                                    {
   PPL_ASSERT(size() <= n);
   resize(n);
 }

memory_size_type Parma_Polyhedra_Library::Sparse_Row::external_memory_in_bytes ( ) const

inline

Returns the size in bytes of the memory managed by *this.

This method takes $O(n)$ time.

Definition at line 362 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::external_memory_in_bytes(), and tree.

Referenced by Parma_Polyhedra_Library::MIP_Problem::external_memory_in_bytes(), external_memory_in_bytes(), and total_memory_in_bytes().

                                            {
   return tree.external_memory_in_bytes();
 }

memory_size_type Parma_Polyhedra_Library::Sparse_Row::external_memory_in_bytes ( dimension_type capacity ) const

inline

Returns the size in bytes of the memory managed by *this.

This method is provided for compatibility with Dense_Row.

This method takes $O(n)$ time.

Parameters

capacity This parameter is ignored.

Definition at line 367 of file Sparse_Row_inlines.hh.

References external_memory_in_bytes().

                                                            {
   return external_memory_in_bytes();
 }

void Parma_Polyhedra_Library::Sparse_Row::fast_swap	(	dimension_type	i,
		iterator	itr
	)

inline

Equivalent to swap(i,itr.index()), but it assumes that lower_bound(i)==itr.

Iterators that pointed to the itr.index()-th element remain valid but now point to the i-th element. Other iterators are unaffected.

This method takes $O(1)$ time.

Definition at line 339 of file Sparse_Row_inlines.hh.

References end(), Parma_Polyhedra_Library::CO_Tree::fast_shift(), lower_bound(), OK(), and tree.

                                                     {
   PPL_ASSERT(lower_bound(i) == itr);
   PPL_ASSERT(itr != end());
   tree.fast_shift(i, itr);
   PPL_ASSERT(OK());
 }

Sparse_Row::iterator Parma_Polyhedra_Library::Sparse_Row::find ( dimension_type i )

inline

Looks for an element with index i.

Parameters

i	The index of the desired element.

If possible, use the find() method that takes a hint iterator, to improve performance.

This method takes $O(\log n)$ time.

Definition at line 180 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::bisect(), end(), Parma_Polyhedra_Library::CO_Tree::iterator::index(), size(), and tree.

Referenced by get(), Parma_Polyhedra_Library::MIP_Problem::linear_combine(), and Parma_Polyhedra_Library::PIP_Solution_Node::solve().

                                  {
   PPL_ASSERT(i < size());
 
   iterator itr = tree.bisect(i);
 
   if (itr != end() && itr.index() == i) {
     return itr;
   }
   return end();
 }

Sparse_Row::iterator Parma_Polyhedra_Library::Sparse_Row::find	(	iterator	itr,
		dimension_type	i
	)

inline

Looks for an element with index i.

Parameters

i	The index of the desired element.
itr	It is used as a hint. This method will be faster if the searched element is near to `itr`.

The value of itr does not affect the result of this method, as long it is a valid iterator for this row. itr may even be end().

This method takes $O(\log n)$ time. If the distance between itr and the searched position is $O(1)$ , this method takes $O(1)$ time.

Definition at line 192 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::bisect_near(), end(), Parma_Polyhedra_Library::CO_Tree::iterator::index(), size(), and tree.

                                                 {
   PPL_ASSERT(i < size());
 
   iterator itr = tree.bisect_near(hint, i);
 
   if (itr != end() && itr.index() == i) {
     return itr;
   }
   return end();
 }

Sparse_Row::const_iterator Parma_Polyhedra_Library::Sparse_Row::find ( dimension_type i ) const

inline

Looks for an element with index i.

Parameters

i	The index of the desired element.

If possible, use the find() method that takes a hint iterator, to improve performance.

This method takes $O(\log n)$ time.

Definition at line 204 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::bisect(), end(), Parma_Polyhedra_Library::CO_Tree::const_iterator::index(), size(), and tree.

                                        {
   PPL_ASSERT(i < size());
 
   const_iterator itr = tree.bisect(i);
 
   if (itr != end() && itr.index() == i) {
     return itr;
   }
 
   return end();
 }

Sparse_Row::const_iterator Parma_Polyhedra_Library::Sparse_Row::find	(	const_iterator	itr,
		dimension_type	i
	)		const

inline

Looks for an element with index i.

Parameters

i	The index of the desired element.
itr	It is used as a hint. This method will be faster if the searched element is near to `itr`.

The value of itr does not affect the result of this method, as long it is a valid iterator for this row. itr may even be end().

This method takes $O(\log n)$ time. If the distance between itr and the searched position is $O(1)$ , this method takes $O(1)$ time.

Definition at line 217 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::bisect_near(), end(), Parma_Polyhedra_Library::CO_Tree::const_iterator::index(), size(), and tree.

                                                             {
   PPL_ASSERT(i < size());
 
   const_iterator itr = tree.bisect_near(hint, i);
 
   if (itr != end() && itr.index() == i) {
     return itr;
   }
   return end();
 }

Coefficient_traits::const_reference Parma_Polyhedra_Library::Sparse_Row::get ( dimension_type i ) const

inline

Gets the i-th element in the sequence.

Parameters

i	The index of the desired element.

If possible, use the insert(), find() or lower_bound() methods with a hint instead of this, to improve performance.

This method takes $O(\log n)$ time.

Definition at line 165 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::Coefficient_zero(), Parma_Polyhedra_Library::CO_Tree::empty(), end(), find(), size_, and tree.

                                       {
   PPL_ASSERT(i < size_);
   if (tree.empty()) {
     return Coefficient_zero();
   }
   const_iterator itr = find(i);
   if (itr != end()) {
     return *itr;
   }
   else {
     return Coefficient_zero();
   }
 }

Sparse_Row::iterator Parma_Polyhedra_Library::Sparse_Row::insert	(	dimension_type	i,
		Coefficient_traits::const_reference	x
	)

inline

Equivalent to (*this)[i] = x; find(i), but faster.

Parameters

i	The index of the desired element.
x	The value that will be associated to the element.

If possible, use versions of this method that take a hint, to improve performance.

This operation invalidates existing iterators.

This method takes 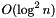$O(\log^2 n)$ amortized time.

Definition at line 305 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::insert(), size_, and tree.

Referenced by combine(), combine_needs_second(), Parma_Polyhedra_Library::PIP_Solution_Node::generate_cut(), operator[](), Parma_Polyhedra_Library::MIP_Problem::process_pending_constraints(), Parma_Polyhedra_Library::PIP_Problem::solve(), Parma_Polyhedra_Library::PIP_Solution_Node::solve(), and Parma_Polyhedra_Library::PIP_Solution_Node::update_tableau().

                                                                         {
   PPL_ASSERT(i < size_);
   return tree.insert(i, x);
 }

Sparse_Row::iterator Parma_Polyhedra_Library::Sparse_Row::insert	(	iterator	itr,
		dimension_type	i,
		Coefficient_traits::const_reference	x
	)

inline

Equivalent to (*this)[i] = x; find(i), but faster.

Parameters

i	The index of the desired element.
x	The value that will be associated to the element.
itr	It is used as a hint. This method will be faster if the searched element is near to `itr`, even faster than `(*this)[i] = x`.

The value of itr does not affect the result of this method, as long it is a valid iterator for this row. itr may even be end().

This operation invalidates existing iterators.

This method takes 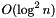$O(\log^2 n)$ amortized time. If the distance between itr and the searched position is $O(1)$ and the row already contains an element with this index, this method takes $O(1)$ time.

Definition at line 311 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::insert(), size_, and tree.

                                                         {
   PPL_ASSERT(i < size_);
   return tree.insert(itr, i, x);
 }

Sparse_Row::iterator Parma_Polyhedra_Library::Sparse_Row::insert ( dimension_type i )

inline

Equivalent to (*this)[i]; find(i), but faster.

Parameters

i	The index of the desired element.

If possible, use versions of this method that take a hint, to improve performance.

This operation invalidates existing iterators.

This method takes 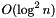$O(\log^2 n)$ amortized time.

Definition at line 318 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::insert(), size_, and tree.

                                    {
   PPL_ASSERT(i < size_);
   return tree.insert(i);
 }

Sparse_Row::iterator Parma_Polyhedra_Library::Sparse_Row::insert	(	iterator	itr,
		dimension_type	i
	)

inline

Equivalent to (*this)[i]; find(i), but faster.

Parameters

i	The index of the desired element.
itr	It is used as a hint. This method will be faster if the searched element is near to `itr`, even faster than `(*this)[i]`.

The value of itr does not affect the result of this method, as long it is a valid iterator for this row. itr may even be end().

This operation invalidates existing iterators.

This method takes 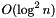$O(\log^2 n)$ amortized time. If the distance between itr and the searched position is $O(1)$ and the row already contains an element with this index, this method takes $O(1)$ time.

Definition at line 324 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::insert(), size_, and tree.

                                                  {
   PPL_ASSERT(i < size_);
   return tree.insert(itr, i);
 }

void Parma_Polyhedra_Library::Sparse_Row::linear_combine	(	const Sparse_Row &	y,
		Coefficient_traits::const_reference	coeff1,
		Coefficient_traits::const_reference	coeff2
	)

Executes (*this)[i] = (*this)[i]*coeff1 + y[i]*coeff2, for each i.

Parameters

y	The row that will be combined with *this.
coeff1	The coefficient used for elements of *this. This must not be 0.
coeff2	The coefficient used for elements of y. This must not be 0.

This method takes 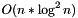$O(n*\log^2 n)$ time.

Note: The functors will only be called when necessary. This method can be implemented in user code, too. It is provided for convenience only.

See also: combine_needs_first; combine_needs_second; combine

Definition at line 370 of file Sparse_Row.cc.

References Parma_Polyhedra_Library::add_mul_assign(), begin(), end(), Parma_Polyhedra_Library::CO_Tree::const_iterator::index(), Parma_Polyhedra_Library::CO_Tree::iterator::index(), and Parma_Polyhedra_Library::CO_Tree::m_swap().

Referenced by Parma_Polyhedra_Library::MIP_Problem::linear_combine().

                                                                           {
   PPL_ASSERT(coeff1 != 0);
   PPL_ASSERT(coeff2 != 0);
   PPL_ASSERT(this != &y);
 
   if (coeff1 == 1) {
     // Optimize for this special case.
     iterator i = end();
     for (const_iterator j = y.begin(), j_end = y.end(); j != j_end; ++j) {
       i = insert(i, j.index());
       add_mul_assign(*i, *j, coeff2);
       if (*i == 0) {
         i = reset(i);
       }
     }
     return;
   }
 
   dimension_type counter = 0;
   // Count the number of elements that are stored in y but not in *this.
   {
     iterator i = begin();
     iterator i_end = end();
     const_iterator j = y.begin();
     const_iterator j_end = y.end();
     if (i != i_end) {
       while (j != j_end) {
         PPL_ASSERT(i != i_end);
         if (i.index() == j.index()) {
           ++i;
           ++j;
           if (i == i_end) {
             break;
           }
         }
         else {
           if (i.index() < j.index()) {
             i = lower_bound(i, j.index());
             if (i == i_end) {
               break;
             }
           }
           else {
             PPL_ASSERT(i.index() > j.index());
             ++counter;
             ++j;
           }
         }
       }
     }
     PPL_ASSERT(i == i_end || j == j_end);
     for ( ; j != j_end; ++j) {
       ++counter;
     }
   }
   // This condition is arbitrary. Changing it affects performance but not
   // correctness. The values have been tuned using some ppl_lpsol benchmarks
   // on 2 October 2010.
   if (counter == 0 || counter < (7 * size()) / 64) {
     // Few insertions needed, do them directly.
     iterator i = begin();
     // This is a const reference to an internal iterator, that is kept valid.
     // If we just stored a copy, that would be invalidated by the calls to
     // reset() and insert().
     const iterator& i_end = end();
     const_iterator j = y.begin();
     const_iterator j_end = y.end();
     while (i != i_end && j != j_end) {
       if (i.index() == j.index()) {
         (*i) *= coeff1;
         add_mul_assign(*i, *j, coeff2);
         if (*i == 0) {
           i = reset(i);
         }
         else {
           ++i;
         }
         ++j;
       }
       else {
         if (i.index() < j.index()) {
           (*i) *= coeff1;
           ++i;
         }
         else {
           PPL_ASSERT(i.index() > j.index());
           i = insert(i, j.index(), *j);
           (*i) *= coeff2;
           ++i;
           ++j;
         }
       }
     }
     PPL_ASSERT(i == i_end || j == j_end);
     for ( ; i != i_end; ++i) {
       (*i) *= coeff1;
     }
     for ( ; j != j_end; ++j) {
       i = insert(i, j.index(), *j);
       (*i) *= coeff2;
     }
   }
   else {
     // Too many insertions needed, a full copy is probably faster than
     // inserting all those new elements into *this.
     CO_Tree new_tree(sparse_row_linear_combine_helper_iterator(*this, y,
                                                                 coeff1,
                                                                 coeff2),
                      counter + tree.size());
     tree.m_swap(new_tree);
 
     // Now remove stored zeroes.
     iterator i = begin();
     // Note that end() can not be called only once, because reset()
     // invalidates all iterators.
     while (i != end()) {
       if (*i == 0) {
 #ifndef NDEBUG
         const dimension_type old_index = i.index();
 #endif
         i = reset(i);
         PPL_ASSERT(find(old_index) == end());
       }
       else {
         ++i;
       }
     }
   }
 }

void Parma_Polyhedra_Library::Sparse_Row::linear_combine	(	const Sparse_Row &	y,
		Coefficient_traits::const_reference	c1,
		Coefficient_traits::const_reference	c2,
		dimension_type	start,
		dimension_type	end
	)

Equivalent to (*this)[i] = (*this)[i] * c1 + y[i] * c2, for each i in [start, end).

This method, unlike the other linear_combine() method, detects when coeff1==1 and/or coeff2==1 or coeff2==-1 in order to save some work.

Definition at line 503 of file Sparse_Row.cc.

References Parma_Polyhedra_Library::add_mul_assign(), Parma_Polyhedra_Library::CO_Tree::const_iterator::index(), Parma_Polyhedra_Library::CO_Tree::iterator::index(), lower_bound(), and Parma_Polyhedra_Library::neg_assign().

                                                                           {
   PPL_ASSERT(coeff1 != 0);
   PPL_ASSERT(coeff2 != 0);
   PPL_ASSERT(this != &y);
 
   if (coeff1 == 1) {
     if (coeff2 == 1) {
       // Optimized implementation for coeff1==1, coeff2==1.
       iterator i = this->end();
       for (const_iterator j = y.lower_bound(start),
              j_end = y.lower_bound(end); j != j_end; ++j) {
         i = insert(i, j.index());
         *i += *j;
         if (*i == 0) {
           i = reset(i);
         }
       }
       return;
     }
     if (coeff2 == -1) {
       // Optimized implementation for coeff1==1, coeff2==-1.
       iterator i = this->end();
       for (const_iterator j = y.lower_bound(start),
              j_end = y.lower_bound(end); j != j_end; ++j) {
         i = insert(i, j.index());
         *i -= *j;
         if (*i == 0) {
           i = reset(i);
         }
       }
       return;
     }
     // Optimized implementation for coeff1==1.
     iterator i = this->end();
     for (const_iterator j = y.lower_bound(start),
            j_end = y.lower_bound(end); j != j_end; ++j) {
       i = insert(i, j.index());
       add_mul_assign(*i, *j, coeff2);
       if (*i == 0) {
         i = reset(i);
       }
     }
     return;
   }
 
   if (coeff2 == 1) {
     // Optimized implementation for coeff2==1.
     iterator i = lower_bound(start);
     // This is a const reference to an internal iterator, that is kept valid.
     // If we just stored a copy, that would be invalidated by the calls to
     // reset() and insert().
     const iterator& i_end = this->end();
     const_iterator j = y.lower_bound(start);
     const_iterator j_end = y.lower_bound(end);
     while (i != i_end && i.index() < end && j != j_end) {
       if (i.index() == j.index()) {
         (*i) *= coeff1;
         *i += *j;
         if (*i == 0) {
           i = reset(i);
         }
         else {
           ++i;
         }
         ++j;
       }
       else {
         if (i.index() < j.index()) {
           (*i) *= coeff1;
           ++i;
         }
         else {
           PPL_ASSERT(i.index() > j.index());
           i = insert(i, j.index(), *j);
           ++i;
           ++j;
         }
       }
     }
     PPL_ASSERT(i == i_end || j == j_end);
     for ( ; i != i_end && i.index() < end; ++i) {
       (*i) *= coeff1;
     }
     for ( ; j != j_end; ++j) {
       i = insert(i, j.index(), *j);
     }
     return;
   }
 
   if (coeff2 == -1) {
     // Optimized implementation for coeff2==-1.
     iterator i = lower_bound(start);
     // This is a const reference to an internal iterator, that is kept valid.
     // If we just stored a copy, that would be invalidated by the calls to
     // reset() and insert().
     const iterator& i_end = this->end();
     const_iterator j = y.lower_bound(start);
     const_iterator j_end = y.lower_bound(end);
     while (i != i_end && i.index() < end && j != j_end) {
       if (i.index() == j.index()) {
         (*i) *= coeff1;
         *i -= *j;
         if (*i == 0) {
           i = reset(i);
         }
         else {
           ++i;
         }
         ++j;
       }
       else {
         if (i.index() < j.index()) {
           (*i) *= coeff1;
           ++i;
         }
         else {
           PPL_ASSERT(i.index() > j.index());
           i = insert(i, j.index(), *j);
           neg_assign(*i);
           ++i;
           ++j;
         }
       }
     }
     PPL_ASSERT(i == i_end || j == j_end);
     for ( ; i != i_end && i.index() < end; ++i) {
       (*i) *= coeff1;
     }
     for ( ; j != j_end; ++j) {
       i = insert(i, j.index(), *j);
       neg_assign(*i);
     }
     return;
   }
 
   iterator i = lower_bound(start);
   // This is a const reference to an internal iterator, that is kept valid.
   // If we just stored a copy, that would be invalidated by the calls to
   // reset() and insert().
   const iterator& i_end = this->end();
   const_iterator j = y.lower_bound(start);
   const_iterator j_end = y.lower_bound(end);
   while (i != i_end && i.index() < end && j != j_end) {
     if (i.index() == j.index()) {
       (*i) *= coeff1;
       add_mul_assign(*i, *j, coeff2);
       if (*i == 0) {
         i = reset(i);
       }
       else {
         ++i;
       }
       ++j;
     }
     else {
       if (i.index() < j.index()) {
         (*i) *= coeff1;
         ++i;
       }
       else {
         PPL_ASSERT(i.index() > j.index());
         i = insert(i, j.index(), *j);
         (*i) *= coeff2;
         ++i;
         ++j;
       }
     }
   }
   PPL_ASSERT(i == i_end || j == j_end);
   for ( ; i != i_end && i.index() < end; ++i) {
     (*i) *= coeff1;
   }
   for ( ; j != j_end; ++j) {
     i = insert(i, j.index(), *j);
     (*i) *= coeff2;
   }
 }

Sparse_Row::iterator Parma_Polyhedra_Library::Sparse_Row::lower_bound ( dimension_type i )

inline

Lower bound of index i.

Parameters

i	The index of the desired element.

Returns: an iterator to the first element with index greater than or equal to i. If there are no such elements, returns end().

If possible, use the find() method that takes a hint iterator, to improve performance.

This method takes $O(\log n)$ time.

Definition at line 229 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::bisect(), end(), Parma_Polyhedra_Library::CO_Tree::iterator::index(), size(), and tree.

Referenced by combine_needs_first(), Parma_Polyhedra_Library::Dense_Row::Dense_Row(), fast_swap(), Parma_Polyhedra_Library::Linear_Expression_Impl< Row >::have_a_common_variable(), linear_combine(), Parma_Polyhedra_Library::MIP_Problem::OK(), Parma_Polyhedra_Library::operator==(), Parma_Polyhedra_Library::MIP_Problem::second_phase(), Parma_Polyhedra_Library::MIP_Problem::steepest_edge_exact_entering_index(), and Parma_Polyhedra_Library::MIP_Problem::steepest_edge_float_entering_index().

                                         {
   PPL_ASSERT(i <= size());
 
   iterator itr = tree.bisect(i);
 
   if (itr == end()) {
     return end();
   }
 
   if (itr.index() < i) {
     ++itr;
   }
 
   PPL_ASSERT(itr == end() || itr.index() >= i);
 
   return itr;
 }

Sparse_Row::iterator Parma_Polyhedra_Library::Sparse_Row::lower_bound	(	iterator	itr,
		dimension_type	i
	)

inline

Lower bound of index i.

Parameters

i	The index of the desired element.
itr	It is used as a hint. This method will be faster if the searched element is near to `itr`.

Returns: an iterator to the first element with index greater than or equal to i. If there are no such elements, returns end().

The value of itr does not affect the result of this method, as long it is a valid iterator for this row. itr may even be end().

This method takes $O(\log n)$ time. If the distance between itr and the searched position is $O(1)$ , this method takes $O(1)$ time.

Definition at line 248 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::bisect_near(), end(), Parma_Polyhedra_Library::CO_Tree::iterator::index(), size(), and tree.

                                                        {
   PPL_ASSERT(i <= size());
 
   iterator itr = tree.bisect_near(hint, i);
 
   if (itr == end()) {
     return end();
   }
 
   if (itr.index() < i) {
     ++itr;
   }
 
   PPL_ASSERT(itr == end() || itr.index() >= i);
 
   return itr;
 }

Sparse_Row::const_iterator Parma_Polyhedra_Library::Sparse_Row::lower_bound ( dimension_type i ) const

inline

Lower bound of index i.

Parameters

i	The index of the desired element.

Returns: an iterator to the first element with index greater than or equal to i. If there are no such elements, returns end().

If possible, use the find() method that takes a hint iterator, to improve performance.

This method takes $O(\log n)$ time.

Definition at line 267 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::bisect(), end(), Parma_Polyhedra_Library::CO_Tree::const_iterator::index(), size(), and tree.

                                               {
   PPL_ASSERT(i <= size());
 
   const_iterator itr = tree.bisect(i);
 
   if (itr == end()) {
     return end();
   }
 
   if (itr.index() < i) {
     ++itr;
   }
 
   PPL_ASSERT(itr == end() || itr.index() >= i);
 
   return itr;
 }

Sparse_Row::const_iterator Parma_Polyhedra_Library::Sparse_Row::lower_bound	(	const_iterator	itr,
		dimension_type	i
	)		const

inline

Lower bound of index i.

Parameters

i	The index of the desired element.
itr	It is used as a hint. This method will be faster if the searched element is near to `itr`.

Returns: an iterator to the first element with index greater than or equal to i. If there are no such elements, returns end().

The value of itr does not affect the result of this method, as long it is a valid iterator for this row. itr may even be end().

This method takes $O(\log n)$ time. If the distance between itr and the searched position is $O(1)$ , this method takes $O(1)$ time.

Definition at line 286 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::bisect_near(), end(), Parma_Polyhedra_Library::CO_Tree::const_iterator::index(), size(), and tree.

                                                                    {
   PPL_ASSERT(i <= size());
 
   const_iterator itr = tree.bisect_near(hint, i);
 
   if (itr == end()) {
     return end();
   }
 
   if (itr.index() < i) {
     ++itr;
   }
 
   PPL_ASSERT(itr == end() || itr.index() >= i);
 
   return itr;
 }

void Parma_Polyhedra_Library::Sparse_Row::m_swap ( Sparse_Row & x )

inline

Swaps *this and x.

Parameters

x	The row that will be swapped with *this.

This method takes $O(1)$ time.

Definition at line 57 of file Sparse_Row_inlines.hh.

References OK(), size_, swap(), Parma_Polyhedra_Library::swap(), and tree.

Referenced by Parma_Polyhedra_Library::MIP_Problem::erase_artificials(), Parma_Polyhedra_Library::PIP_Solution_Node::solve(), and swap().

                                 {
   using std::swap;
   swap(tree, x.tree);
   swap(size_, x.size_);
   PPL_ASSERT(OK());
   PPL_ASSERT(x.OK());
 }

dimension_type Parma_Polyhedra_Library::Sparse_Row::max_size ( )

inlinestatic

Returns the size() of the largest possible Sparse_Row.

Definition at line 143 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::max_size().

                      {
   return CO_Tree::max_size();
 }

void Parma_Polyhedra_Library::Sparse_Row::normalize ( )

Normalizes the modulo of coefficients so that they are mutually prime.

Computes the Greatest Common Divisor (GCD) among the elements of the row and normalizes them by the GCD itself.

This method takes $O(n)$ time.

Definition at line 210 of file Sparse_Row.cc.

References Parma_Polyhedra_Library::exact_div_assign(), Parma_Polyhedra_Library::gcd_assign(), Parma_Polyhedra_Library::neg_assign(), PPL_DIRTY_TEMP_COEFFICIENT, and Parma_Polyhedra_Library::Boundary_NS::sgn().

Referenced by Parma_Polyhedra_Library::MIP_Problem::linear_combine().

                          {
   // Compute the GCD of all the coefficients.
   PPL_DIRTY_TEMP_COEFFICIENT(gcd);
   const_iterator i = begin();
   const_iterator i_end = end();
   for ( ; i != i_end; ++i) {
     Coefficient_traits::const_reference x_i = *i;
     if (const int x_i_sign = sgn(x_i)) {
       gcd = x_i;
       if (x_i_sign < 0) {
         neg_assign(gcd);
       }
       goto compute_gcd;
     }
   }
   // We reach this point only if all the coefficients were zero.
   return;
 
  compute_gcd:
   if (gcd == 1) {
     return;
   }
   for (++i; i != i_end; ++i) {
     Coefficient_traits::const_reference x_i = *i;
     if (x_i != 0) {
       // Note: we use the ternary version instead of a more concise
       // gcd_assign(gcd, x_i) to take advantage of the fact that
       // `gcd' will decrease very rapidly (see D. Knuth, The Art of
       // Computer Programming, second edition, Section 4.5.2,
       // Algorithm C, and the discussion following it).  Our
       // implementation of gcd_assign(x, y, z) for checked numbers is
       // optimized for the case where `z' is smaller than `y', so that
       // on checked numbers we gain.  On the other hand, for the
       // implementation of gcd_assign(x, y, z) on GMP's unbounded
       // integers we cannot make any assumption, so here we draw.
       // Overall, we win.
       gcd_assign(gcd, x_i, gcd);
       if (gcd == 1) {
         return;
       }
     }
   }
   // Divide the coefficients by the GCD.
   for (iterator j = begin(), j_end = end(); j != j_end; ++j) {
     Coefficient& x_j = *j;
     exact_div_assign(x_j, x_j, gcd);
   }
 
   PPL_ASSERT(OK());
 }

dimension_type Parma_Polyhedra_Library::Sparse_Row::num_stored_elements ( ) const

inline

Returns the number of elements explicitly stored in the row.

This is equivalent to std::distance(begin(), end()), but it's much faster.

This method takes $O(1)$ time.

Definition at line 71 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::size(), and tree.

                                       {
   return tree.size();
 }

bool Parma_Polyhedra_Library::Sparse_Row::OK ( ) const

Checks the invariant.

Definition at line 742 of file Sparse_Row.cc.

References Parma_Polyhedra_Library::CO_Tree::const_iterator::index().

Referenced by add_zeroes_and_shift(), delete_element_and_shift(), fast_swap(), m_swap(), reset(), resize(), Sparse_Row(), and swap_coefficients().

                         {
   if (begin() == end()) {
     return true;
   }
   const_iterator last = end();
   --last;
   return (last.index() < size_);
 }

bool Parma_Polyhedra_Library::Sparse_Row::OK ( dimension_type capacity ) const

Checks the invariant.

This method is provided for compatibility with Dense_Row.

Parameters

capacity This parameter is ignored.

Definition at line 752 of file Sparse_Row.cc.

                                         {
   return OK();
 }

PPL::Sparse_Row & Parma_Polyhedra_Library::Sparse_Row::operator= ( const Dense_Row & row )

Definition at line 118 of file Sparse_Row.cc.

References Parma_Polyhedra_Library::swap().

                                                 {
   Sparse_Row tmp(row);
   swap(*this, tmp);
   PPL_ASSERT(OK());
 
   return *this;
 }

Coefficient & Parma_Polyhedra_Library::Sparse_Row::operator[] ( dimension_type i )

inline

Gets a reference to the i-th element.

Parameters

i	The index of the desired element.

For read-only access it's better to use get(), that avoids allocating space for zeroes.

If possible, use the insert(), find() or lower_bound() methods with a hint instead of this, to improve performance.

This operation invalidates existing iterators.

This method takes $O(\log n)$ amortized time when there is already an element with index i, and 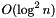$O(\log^2 n)$ otherwise.

Definition at line 153 of file Sparse_Row_inlines.hh.

References insert(), and size_.

                                        {
   PPL_ASSERT(i < size_);
   iterator itr = insert(i);
   return *itr;
 }

Coefficient_traits::const_reference Parma_Polyhedra_Library::Sparse_Row::operator[] ( dimension_type i ) const

inline

Equivalent to get(i), provided for convenience.

This method takes $O(\log n)$ time.

Definition at line 160 of file Sparse_Row_inlines.hh.

                                              {
   return get(i);
 }

void Parma_Polyhedra_Library::Sparse_Row::print ( ) const

Prints *this to std::cerr using operator<<.

Sparse_Row::iterator Parma_Polyhedra_Library::Sparse_Row::reset ( iterator i )

inline

Resets to zero the value pointed to by i.

Parameters

i	An iterator pointing to the element that will be reset (not stored anymore).

By calling this method instead of getting a reference to the value and setting it to zero, the element will no longer be stored.

This operation invalidates existing iterators.

This method takes 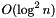$O(\log^2 n)$ amortized time.

Definition at line 347 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::erase(), OK(), and tree.

Referenced by combine(), combine_needs_first(), combine_needs_second(), and Parma_Polyhedra_Library::Expression_Hide_Inhomo< T >::get_row().

                             {
   iterator res = tree.erase(i);
   PPL_ASSERT(OK());
   return res;
 }

PPL::Sparse_Row::iterator Parma_Polyhedra_Library::Sparse_Row::reset	(	iterator	first,
		iterator	last
	)

Resets to zero the values in the range [first,last).

Parameters

first	An iterator pointing to the first element to reset.
last	An iterator pointing after the last element to reset.

By calling this method instead of getting a reference to the values and setting them to zero, the elements will no longer be stored.

This operation invalidates existing iterators.

This method takes 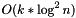$O(k*\log^2 n)$ amortized time, where k is the number of elements in [first,last).

Definition at line 171 of file Sparse_Row.cc.

References Parma_Polyhedra_Library::CO_Tree::iterator::index().

                                                   {
   if (first == last) {
     return first;
   }
 
   PPL_ASSERT(last != end());
   --last;
   const dimension_type j = last.index();
   PPL_ASSERT(first.index() <= j);
   // We can't just compare first and last at each iteration, because last will
   // be invalidated by the first erase.
   while (first.index() < j) {
     first = reset(first);
   }
 
   first = reset(first);
 
   PPL_ASSERT(OK());
   return first;
 }

void Parma_Polyhedra_Library::Sparse_Row::reset ( dimension_type i )

inline

Resets to zero the i-th element.

Parameters

i	The index of the element to reset.

By calling this method instead of getting a reference to the value and setting it to zero, the element will no longer be stored.

This operation invalidates existing iterators.

This method takes 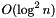$O(\log^2 n)$ amortized time.

Definition at line 354 of file Sparse_Row_inlines.hh.

References Parma_Polyhedra_Library::CO_Tree::erase(), OK(), size(), and tree.

                                   {
   PPL_ASSERT(i < size());
 
   tree.erase(i);
   PPL_ASSERT(OK());
 }

void Parma_Polyhedra_Library::Sparse_Row::reset_after ( dimension_type i )

Resets to zero the elements with index greater than or equal to i.

Parameters

i	The index of the first element to reset.

By calling this method instead of getting a reference to the values and setting them to zero, the elements will no longer be stored.

This operation invalidates existing iterators.

This method takes 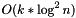$O(k*\log^2 n)$ amortized time, where k is the number of elements with index greater than or equal to i.

Definition at line 193 of file Sparse_Row.cc.

Referenced by resize().

                                            {
   PPL_ASSERT(i < size_);
 
   iterator itr = lower_bound(i);
   // This is a const reference to an internal iterator, that is kept valid.
   // If we just stored a copy, that would be invalidated by the calls to
   // reset().
   const iterator& itr_end = end();
 
   while (itr != itr_end) {
     itr = reset(itr);
   }
 
   PPL_ASSERT(OK());
 }

void Parma_Polyhedra_Library::Sparse_Row::resize ( dimension_type n )

inline

Resizes the row to the specified size.

Parameters

n	The new size for the row.

This method takes 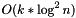$O(k*\log^2 n)$ amortized time when shrinking the row and removing the trailing k elements. It takes $O(1)$ time when enlarging the row.

Definition at line 76 of file Sparse_Row_inlines.hh.

References OK(), reset_after(), and size_.

Referenced by expand_within_capacity(), Parma_Polyhedra_Library::Expression_Hide_Last< T >::get_row(), and shrink().

                                    {
   if (n < size_) {
     reset_after(n);
   }
   size_ = n;
   PPL_ASSERT(OK());
 }

void Parma_Polyhedra_Library::Sparse_Row::shrink ( dimension_type n )

inline

Resizes the row to size n.

Parameters

n	The new size for the row.

This method, with this signature, is needed for compatibility with Dense_Row.

This method takes 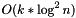$O(k*\log^2 n)$ amortized time where k is the number of removed elements.

Definition at line 85 of file Sparse_Row_inlines.hh.

References resize(), and size().

                                    {
   PPL_ASSERT(size() >= n);
   resize(n);
 }

dimension_type Parma_Polyhedra_Library::Sparse_Row::size ( ) const

inline

Returns the size of the row.

This method takes $O(1)$ time.

Definition at line 66 of file Sparse_Row_inlines.hh.

References size_.

                        {
   return size_;
 }

void Parma_Polyhedra_Library::Sparse_Row::swap_coefficients	(	dimension_type	i,
		dimension_type	j
	)

Swaps the i-th element with the j-th element.

Parameters

i	The index of an element.
j	The index of another element.

This operation invalidates existing iterators.

This method takes 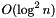$O(\log^2 n)$ amortized time.

Definition at line 127 of file Sparse_Row.cc.

References Parma_Polyhedra_Library::CO_Tree::iterator::index(), PPL_DIRTY_TEMP_COEFFICIENT, and Parma_Polyhedra_Library::swap().

                                                                    {
   PPL_ASSERT(i < size_);
   PPL_ASSERT(j < size_);
 
   if (tree.empty()) {
     return;
   }
 
   using std::swap;
 
   iterator itr_i = tree.bisect(i);
   iterator itr_j = tree.bisect(j);
   if (itr_i.index() == i) {
     if (itr_j.index() == j) {
       // Both elements are in the tree.
       swap(*itr_i, *itr_j);
     }
     else {
       // i is in the tree, j is not.
       PPL_DIRTY_TEMP_COEFFICIENT(tmp);
       swap(*itr_i, tmp);
       tree.erase(itr_i);
       // Now both iterators have been invalidated.
       itr_j = tree.insert(j);
       swap(*itr_j, tmp);
     }
   }
   else {
     if (itr_j.index() == j) {
       // j is in the tree, i is not.
       PPL_DIRTY_TEMP_COEFFICIENT(tmp);
       swap(*itr_j, tmp);
       // Now both iterators have been invalidated.
       tree.erase(itr_j);
       itr_i = tree.insert(i);
       swap(*itr_i, tmp);
     }
     else {
       // Do nothing, elements are both non-stored zeroes.
     }
   }
 }

void Parma_Polyhedra_Library::Sparse_Row::swap_coefficients	(	iterator	i,
		iterator	j
	)

inline

Swaps the element pointed to by i with the element pointed to by j.

Parameters

i	An iterator pointing to an element.
j	An iterator pointing to another element.

This method takes $O(1)$ time.

Definition at line 330 of file Sparse_Row_inlines.hh.

References end(), OK(), swap(), and Parma_Polyhedra_Library::swap().

                                                     {
   PPL_ASSERT(i != end());
   PPL_ASSERT(j != end());
   using std::swap;
   swap(*i, *j);
   PPL_ASSERT(OK());
 }

memory_size_type Parma_Polyhedra_Library::Sparse_Row::total_memory_in_bytes ( ) const

inline

Returns the size in bytes of the memory managed by *this.

This method takes $O(n)$ time.

Definition at line 372 of file Sparse_Row_inlines.hh.

References external_memory_in_bytes().

Referenced by total_memory_in_bytes().

                                         {
   return external_memory_in_bytes() + sizeof(*this);
 }

memory_size_type Parma_Polyhedra_Library::Sparse_Row::total_memory_in_bytes ( dimension_type capacity ) const

inline

Returns the size in bytes of the memory managed by *this.

This method is provided for compatibility with Dense_Row.

This method takes $O(n)$ time.

Parameters

capacity This parameter is ignored.

Definition at line 377 of file Sparse_Row_inlines.hh.

References total_memory_in_bytes().

                                                         {
   return total_memory_in_bytes();
 }

Friends And Related Function Documentation

void linear_combine	(	Sparse_Row &	x,
		const Dense_Row &	y,
		Coefficient_traits::const_reference	coeff1,
		Coefficient_traits::const_reference	coeff2
	)

void linear_combine	(	Sparse_Row &	x,
		const Dense_Row &	y,
		Coefficient_traits::const_reference	c1,
		Coefficient_traits::const_reference	c2,
		dimension_type	start,
		dimension_type	end
	)

This function detects when coeff1==1 and/or coeff2==1 or coeff2==-1 in order to save some work.

void linear_combine	(	Dense_Row &	x,
		const Sparse_Row &	y,
		Coefficient_traits::const_reference	coeff1,
		Coefficient_traits::const_reference	coeff2
	)

void linear_combine	(	Dense_Row &	x,
		const Sparse_Row &	y,
		Coefficient_traits::const_reference	c1,
		Coefficient_traits::const_reference	c2,
		dimension_type	start,
		dimension_type	end
	)

This function detects when coeff1==1 and/or coeff2==1 or coeff2==-1 in order to save some work.

void linear_combine	(	Sparse_Row &	x,
		const Sparse_Row &	y,
		Coefficient_traits::const_reference	coeff1,
		Coefficient_traits::const_reference	coeff2
	)

void linear_combine	(	Sparse_Row &	x,
		const Sparse_Row &	y,
		Coefficient_traits::const_reference	c1,
		Coefficient_traits::const_reference	c2,
		dimension_type	start,
		dimension_type	end
	)

This function detects when coeff1==1 and/or coeff2==1 or coeff2==-1 in order to save some work.

bool operator!=	(	const Sparse_Row &	x,
		const Sparse_Row &	y
	)

                                                         {
   return !(x == y);
 }

bool operator!=	(	const Sparse_Row &	x,
		const Sparse_Row &	y
	)

bool operator==	(	const Sparse_Row &	x,
		const Sparse_Row &	y
	)

References begin(), end(), Parma_Polyhedra_Library::CO_Tree::const_iterator::index(), and size().

                                                         {
   if (x.size() != y.size()) {
     return false;
   }
   Sparse_Row::const_iterator i = x.begin();
   Sparse_Row::const_iterator i_end = x.end();
   Sparse_Row::const_iterator j = y.begin();
   Sparse_Row::const_iterator j_end = y.end();
   while (i != i_end && j != j_end) {
     if (i.index() == j.index()) {
       if (*i != *j) {
         return false;
       }
       ++i;
       ++j;
     }
     else {
       if (i.index() < j.index()) {
         if (*i != 0) {
           return false;
         }
         ++i;
       }
       else {
         PPL_ASSERT(i.index() > j.index());
         if (*j != 0) {
           return false;
         }
         ++j;
       }
     }
   }
   for ( ; i != i_end; ++i) {
     if (*i != 0) {
       return false;
     }
   }
   for ( ; j != j_end; ++j) {
     if (*j != 0) {
       return false;
     }
   }
   return true;
 }

bool operator==	(	const Sparse_Row &	x,
		const Sparse_Row &	y
	)

void swap	(	Sparse_Row &	x,
		Sparse_Row &	y
	)

References m_swap().

                                    {
   x.m_swap(y);
 }

void swap	(	Parma_Polyhedra_Library::Sparse_Row &	x,
		Parma_Polyhedra_Library::Sparse_Row &	y
	)

Referenced by m_swap(), and swap_coefficients().

Member Data Documentation

dimension_type Parma_Polyhedra_Library::Sparse_Row::size_

private

The size of the row.

The elements contained in this row have indexes that are less than size_.

Definition at line 822 of file Sparse_Row_defs.hh.

Referenced by add_zeroes_and_shift(), delete_element_and_shift(), get(), insert(), m_swap(), operator[](), resize(), and size().

CO_Tree Parma_Polyhedra_Library::Sparse_Row::tree

private

The tree used to store the elements.

Definition at line 816 of file Sparse_Row_defs.hh.

Referenced by add_zeroes_and_shift(), begin(), cbegin(), cend(), clear(), delete_element_and_shift(), end(), external_memory_in_bytes(), fast_swap(), find(), get(), insert(), lower_bound(), m_swap(), num_stored_elements(), and reset().

The documentation for this class was generated from the following files:

Public Types

Public Member Functions

Static Public Member Functions

Private Attributes

Related Functions

Detailed Description

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation

Friends And Related Function Documentation

Member Data Documentation