A linear equality or inequality. More...
#include <Constraint_defs.hh>
Public Types | |
| enum | Type { EQUALITY, NONSTRICT_INEQUALITY, STRICT_INEQUALITY } |
| The constraint type. More... | |
| typedef Expression_Hide_Last< Linear_Expression > | expr_type |
| The type of the (adapted) internal expression. More... | |
Public Member Functions | |
| Constraint (Representation r=default_representation) | |
Constructs the 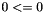 constraint. More... constraint. More... | |
| Constraint (const Constraint &c) | |
| Ordinary copy constructor. More... | |
| Constraint (const Constraint &c, dimension_type space_dim) | |
| Copy constructor with given size. More... | |
| Constraint (const Constraint &c, Representation r) | |
| Copy constructor with given representation. More... | |
| Constraint (const Constraint &c, dimension_type space_dim, Representation r) | |
| Copy constructor with given size and representation. More... | |
| Constraint (const Congruence &cg, Representation r=default_representation) | |
Copy-constructs from equality congruence cg. More... | |
| ~Constraint () | |
| Destructor. More... | |
| Representation | representation () const |
| Returns the current representation of *this. More... | |
| void | set_representation (Representation r) |
| Converts *this to the specified representation. More... | |
| Constraint & | operator= (const Constraint &c) |
| Assignment operator. More... | |
| dimension_type | space_dimension () const |
Returns the dimension of the vector space enclosing *this. More... | |
| void | set_space_dimension (dimension_type space_dim) |
| void | swap_space_dimensions (Variable v1, Variable v2) |
Swaps the coefficients of the variables v1 and v2 . More... | |
| bool | remove_space_dimensions (const Variables_Set &vars) |
| Removes all the specified dimensions from the constraint. More... | |
| void | permute_space_dimensions (const std::vector< Variable > &cycle) |
| Permutes the space dimensions of the constraint. More... | |
| void | shift_space_dimensions (Variable v, dimension_type n) |
| Type | type () const |
Returns the constraint type of *this. More... | |
| bool | is_equality () const |
Returns true if and only if *this is an equality constraint. More... | |
| bool | is_inequality () const |
Returns true if and only if *this is an inequality constraint (either strict or non-strict). More... | |
| bool | is_nonstrict_inequality () const |
Returns true if and only if *this is a non-strict inequality constraint. More... | |
| bool | is_strict_inequality () const |
Returns true if and only if *this is a strict inequality constraint. More... | |
| Coefficient_traits::const_reference | coefficient (Variable v) const |
Returns the coefficient of v in *this. More... | |
| Coefficient_traits::const_reference | inhomogeneous_term () const |
Returns the inhomogeneous term of *this. More... | |
| memory_size_type | total_memory_in_bytes () const |
Returns a lower bound to the total size in bytes of the memory occupied by *this. More... | |
| memory_size_type | external_memory_in_bytes () const |
Returns the size in bytes of the memory managed by *this. More... | |
| bool | is_tautological () const |
Returns true if and only if *this is a tautology (i.e., an always true constraint). More... | |
| bool | is_inconsistent () const |
Returns true if and only if *this is inconsistent (i.e., an always false constraint). More... | |
| bool | is_equivalent_to (const Constraint &y) const |
Returns true if and only if *this and y are equivalent constraints. More... | |
| bool | is_equal_to (const Constraint &y) const |
Returns true if *this is identical to y. More... | |
| bool | OK () const |
| Checks if all the invariants are satisfied. More... | |
| void | ascii_dump () const |
Writes to std::cerr an ASCII representation of *this. More... | |
| void | ascii_dump (std::ostream &s) const |
Writes to s an ASCII representation of *this. More... | |
| void | print () const |
Prints *this to std::cerr using operator<<. More... | |
| bool | ascii_load (std::istream &s) |
Loads from s an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets *this accordingly. Returns true if successful, false otherwise. More... | |
| void | m_swap (Constraint &y) |
Swaps *this with y. More... | |
| expr_type | expression () const |
| Partial read access to the (adapted) internal expression. More... | |
Static Public Member Functions | |
| static dimension_type | max_space_dimension () |
| Returns the maximum space dimension a Constraint can handle. More... | |
| static void | initialize () |
| Initializes the class. More... | |
| static void | finalize () |
| Finalizes the class. More... | |
| static const Constraint & | zero_dim_false () |
The unsatisfiable (zero-dimension space) constraint 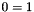 . More... . More... | |
| static const Constraint & | zero_dim_positivity () |
The true (zero-dimension space) constraint 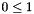 , also known as positivity constraint. More... , also known as positivity constraint. More... | |
| static const Constraint & | epsilon_geq_zero () |
Returns the zero-dimension space constraint 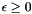 . More... . More... | |
| static const Constraint & | epsilon_leq_one () |
The zero-dimension space constraint 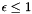 (used to implement NNC polyhedra). More... (used to implement NNC polyhedra). More... | |
Static Public Attributes | |
| static const Representation | default_representation = SPARSE |
| The representation used for new Constraints. More... | |
Private Types | |
| enum | Kind { LINE_OR_EQUALITY = 0, RAY_OR_POINT_OR_INEQUALITY = 1 } |
| The possible kinds of Constraint objects. More... | |
Private Member Functions | |
| Constraint (dimension_type space_dim, Kind kind, Topology topology, Representation r=default_representation) | |
Constructs the 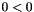 constraint. More... constraint. More... | |
| Constraint (Linear_Expression &e, Kind kind, Topology topology) | |
Builds a constraint of kind kind and topology topology, stealing the coefficients from e. More... | |
| Constraint (Linear_Expression &e, Type type, Topology topology) | |
Builds a constraint of type type and topology topology, stealing the coefficients from e. More... | |
| bool | is_line_or_equality () const |
Returns true if and only if *this row represents a line or an equality. More... | |
| bool | is_ray_or_point_or_inequality () const |
Returns true if and only if *this row represents a ray, a point or an inequality. More... | |
| void | set_is_line_or_equality () |
Sets to LINE_OR_EQUALITY the kind of *this row. More... | |
| void | set_is_ray_or_point_or_inequality () |
Sets to RAY_OR_POINT_OR_INEQUALITY the kind of *this row. More... | |
| void | set_space_dimension_no_ok (dimension_type space_dim) |
| void | throw_invalid_argument (const char *method, const char *message) const |
Throws a std::invalid_argument exception containing error message message. More... | |
| void | throw_dimension_incompatible (const char *method, const char *name_var, Variable v) const |
Throws a std::invalid_argument exception containing the appropriate error message. More... | |
| Coefficient_traits::const_reference | epsilon_coefficient () const |
| Returns the epsilon coefficient. The constraint must be NNC. More... | |
| void | set_epsilon_coefficient (Coefficient_traits::const_reference n) |
Sets the epsilon coefficient to n. The constraint must be NNC. More... | |
| void | mark_as_necessarily_closed () |
| Marks the epsilon dimension as a standard dimension. More... | |
| void | mark_as_not_necessarily_closed () |
| Marks the last dimension as the epsilon dimension. More... | |
| void | set_is_equality () |
Sets the constraint type to EQUALITY. More... | |
| void | set_is_inequality () |
| Sets the constraint to be an inequality. More... | |
| void | linear_combine (const Constraint &y, dimension_type i) |
Linearly combines *this with y so that i-th coefficient is 0. More... | |
| void | sign_normalize () |
| Normalizes the sign of the coefficients so that the first non-zero (homogeneous) coefficient of a line-or-equality is positive. More... | |
| void | strong_normalize () |
| Strong normalization: ensures that different Constraint objects represent different hyperplanes or hyperspaces. More... | |
| bool | check_strong_normalized () const |
Returns true if and only if the coefficients are strongly normalized. More... | |
Flags inspection methods | |
| Topology | topology () const |
Returns the topological kind of *this. More... | |
| bool | is_not_necessarily_closed () const |
Returns true if and only if the topology of *this row is not necessarily closed. More... | |
| bool | is_necessarily_closed () const |
Returns true if and only if the topology of *this row is necessarily closed. More... | |
Flags coercion methods | |
| void | set_topology (Topology x) |
Sets to x the topological kind of *this row. More... | |
| void | set_necessarily_closed () |
Sets to NECESSARILY_CLOSED the topological kind of *this row. More... | |
| void | set_not_necessarily_closed () |
Sets to NOT_NECESSARILY_CLOSED the topological kind of *this row. More... | |
Static Private Member Functions | |
| static Constraint | construct_epsilon_geq_zero () |
Builds a new copy of the zero-dimension space constraint 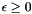 (used to implement NNC polyhedra). More... (used to implement NNC polyhedra). More... | |
Private Attributes | |
| Linear_Expression | expr |
| Kind | kind_ |
| Topology | topology_ |
Static Private Attributes | |
| static const Constraint * | zero_dim_false_p = 0 |
Holds (between class initialization and finalization) a pointer to the unsatisfiable (zero-dimension space) constraint 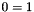 . More... . More... | |
| static const Constraint * | zero_dim_positivity_p = 0 |
Holds (between class initialization and finalization) a pointer to the true (zero-dimension space) constraint 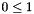 , also known as positivity constraint. More... , also known as positivity constraint. More... | |
| static const Constraint * | epsilon_geq_zero_p = 0 |
Holds (between class initialization and finalization) a pointer to the zero-dimension space constraint 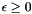 . More... . More... | |
| static const Constraint * | epsilon_leq_one_p = 0 |
Holds (between class initialization and finalization) a pointer to the zero-dimension space constraint 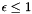 (used to implement NNC polyhedra). More... (used to implement NNC polyhedra). More... | |
Related Functions | |
(Note that these are not member functions.) | |
| int | compare (const Constraint &x, const Constraint &y) |
| std::ostream & | operator<< (std::ostream &s, const Constraint &c) |
| std::ostream & | operator<< (std::ostream &s, const Constraint::Type &t) |
| Constraint | operator< (const Linear_Expression &e1, const Linear_Expression &e2) |
Returns the constraint e1 < e2. More... | |
| Constraint | operator< (Variable v1, Variable v2) |
Returns the constraint v1 < v2. More... | |
| Constraint | operator< (const Linear_Expression &e, Coefficient_traits::const_reference n) |
Returns the constraint e < n. More... | |
| Constraint | operator< (Coefficient_traits::const_reference n, const Linear_Expression &e) |
Returns the constraint n < e. More... | |
| Constraint | operator> (const Linear_Expression &e1, const Linear_Expression &e2) |
Returns the constraint e1 > e2. More... | |
| Constraint | operator> (Variable v1, Variable v2) |
Returns the constraint v1 > v2. More... | |
| Constraint | operator> (const Linear_Expression &e, Coefficient_traits::const_reference n) |
Returns the constraint e > n. More... | |
| Constraint | operator> (Coefficient_traits::const_reference n, const Linear_Expression &e) |
Returns the constraint n > e. More... | |
| Constraint | operator== (const Linear_Expression &e1, const Linear_Expression &e2) |
Returns the constraint e1 = e2. More... | |
| Constraint | operator== (Variable v1, Variable v2) |
Returns the constraint v1 = v2. More... | |
| Constraint | operator== (const Linear_Expression &e, Coefficient_traits::const_reference n) |
Returns the constraint e = n. More... | |
| Constraint | operator== (Coefficient_traits::const_reference n, const Linear_Expression &e) |
Returns the constraint n = e. More... | |
| Constraint | operator<= (const Linear_Expression &e1, const Linear_Expression &e2) |
Returns the constraint e1 <= e2. More... | |
| Constraint | operator<= (Variable v1, Variable v2) |
Returns the constraint v1 <= v2. More... | |
| Constraint | operator<= (const Linear_Expression &e, Coefficient_traits::const_reference n) |
Returns the constraint e <= n. More... | |
| Constraint | operator<= (Coefficient_traits::const_reference n, const Linear_Expression &e) |
Returns the constraint n <= e. More... | |
| Constraint | operator>= (const Linear_Expression &e1, const Linear_Expression &e2) |
Returns the constraint e1 >= e2. More... | |
| Constraint | operator>= (Variable v1, Variable v2) |
Returns the constraint v1 >= v2. More... | |
| Constraint | operator>= (const Linear_Expression &e, Coefficient_traits::const_reference n) |
Returns the constraint e >= n. More... | |
| Constraint | operator>= (Coefficient_traits::const_reference n, const Linear_Expression &e) |
Returns the constraint n >= e. More... | |
| int | compare (const Constraint &x, const Constraint &y) |
| The basic comparison function. More... | |
| std::ostream & | operator<< (std::ostream &s, const Constraint &c) |
| Output operator. More... | |
| std::ostream & | operator<< (std::ostream &s, const Constraint::Type &t) |
| Output operator. More... | |
| bool | operator== (const Constraint &x, const Constraint &y) |
Returns true if and only if x is equivalent to y. More... | |
| bool | operator!= (const Constraint &x, const Constraint &y) |
Returns true if and only if x is not equivalent to y. More... | |
| void | swap (Constraint &x, Constraint &y) |
| bool | operator== (const Constraint &x, const Constraint &y) |
| bool | operator!= (const Constraint &x, const Constraint &y) |
| Constraint | operator== (const Linear_Expression &e1, const Linear_Expression &e2) |
| Constraint | operator== (Variable v1, Variable v2) |
| Constraint | operator>= (const Linear_Expression &e1, const Linear_Expression &e2) |
| Constraint | operator>= (const Variable v1, const Variable v2) |
| Constraint | operator> (const Linear_Expression &e1, const Linear_Expression &e2) |
| Constraint | operator> (const Variable v1, const Variable v2) |
| Constraint | operator== (Coefficient_traits::const_reference n, const Linear_Expression &e) |
| Constraint | operator>= (Coefficient_traits::const_reference n, const Linear_Expression &e) |
| Constraint | operator> (Coefficient_traits::const_reference n, const Linear_Expression &e) |
| Constraint | operator== (const Linear_Expression &e, Coefficient_traits::const_reference n) |
| Constraint | operator>= (const Linear_Expression &e, Coefficient_traits::const_reference n) |
| Constraint | operator> (const Linear_Expression &e, Coefficient_traits::const_reference n) |
| Constraint | operator<= (const Linear_Expression &e1, const Linear_Expression &e2) |
| Constraint | operator<= (const Variable v1, const Variable v2) |
| Constraint | operator<= (Coefficient_traits::const_reference n, const Linear_Expression &e) |
| Constraint | operator<= (const Linear_Expression &e, Coefficient_traits::const_reference n) |
| Constraint | operator< (const Linear_Expression &e1, const Linear_Expression &e2) |
| Constraint | operator< (const Variable v1, const Variable v2) |
| Constraint | operator< (Coefficient_traits::const_reference n, const Linear_Expression &e) |
| Constraint | operator< (const Linear_Expression &e, Coefficient_traits::const_reference n) |
| void | swap (Constraint &x, Constraint &y) |
Detailed Description
A linear equality or inequality.
An object of the class Constraint is either:
- an equality:
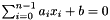 ;
; - a non-strict inequality:
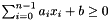 ; or
; or - a strict inequality:
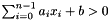 ;
;
where  is the dimension of the space,
is the dimension of the space, 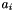 is the integer coefficient of variable
is the integer coefficient of variable 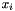 and
and 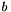 is the integer inhomogeneous term.
is the integer inhomogeneous term.
- How to build a constraint
- Constraints are typically built by applying a relation symbol to a pair of linear expressions. Available relation symbols are equality (
==), non-strict inequalities (>=and<=) and strict inequalities (<and>). The space dimension of a constraint is defined as the maximum space dimension of the arguments of its constructor.
- In the following examples it is assumed that variables
x,yandzare defined as follows:Variable x(0);Variable y(1);Variable z(2);
- Example 1
- The following code builds the equality constraint
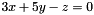 , having space dimension
, having space dimension 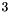 : The following code builds the (non-strict) inequality constraintConstraint eq_c(3*x + 5*y - z == 0);
: The following code builds the (non-strict) inequality constraintConstraint eq_c(3*x + 5*y - z == 0);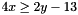 , having space dimension
, having space dimension 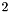 : The corresponding strict inequality constraintConstraint ineq_c(4*x >= 2*y - 13);
: The corresponding strict inequality constraintConstraint ineq_c(4*x >= 2*y - 13);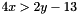 is obtained as follows: An unsatisfiable constraint on the zero-dimension spaceConstraint strict_ineq_c(4*x > 2*y - 13);
is obtained as follows: An unsatisfiable constraint on the zero-dimension spaceConstraint strict_ineq_c(4*x > 2*y - 13); can be specified as follows: Equivalent, but more involved ways are the following:Constraint false_c = Constraint::zero_dim_false();In contrast, the following code defines an unsatisfiable constraint having space dimensionConstraint false_c1(Linear_Expression::zero() == 1);Constraint false_c2(Linear_Expression::zero() >= 1);Constraint false_c3(Linear_Expression::zero() > 0);
can be specified as follows: Equivalent, but more involved ways are the following:Constraint false_c = Constraint::zero_dim_false();In contrast, the following code defines an unsatisfiable constraint having space dimensionConstraint false_c1(Linear_Expression::zero() == 1);Constraint false_c2(Linear_Expression::zero() >= 1);Constraint false_c3(Linear_Expression::zero() > 0);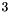 : Constraint false_c(0*z == 1);
: Constraint false_c(0*z == 1);
- How to inspect a constraint
- Several methods are provided to examine a constraint and extract all the encoded information: its space dimension, its type (equality, non-strict inequality, strict inequality) and the value of its integer coefficients.
- Example 2
- The following code shows how it is possible to access each single coefficient of a constraint. Given an inequality constraint (in this case
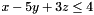 ), we construct a new constraint corresponding to its complement (thus, in this case we want to obtain the strict inequality constraint
), we construct a new constraint corresponding to its complement (thus, in this case we want to obtain the strict inequality constraint 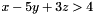 ). The actual output is the following:Constraint c1(x - 5*y + 3*z <= 4);cout << "Constraint c1: " << c1 << endl;if (c1.is_equality())cout << "Constraint c1 is not an inequality." << endl;else {Linear_Expression e;for (dimension_type i = c1.space_dimension(); i-- > 0; )e += c1.coefficient(Variable(i)) * Variable(i);e += c1.inhomogeneous_term();Constraint c2 = c1.is_strict_inequality() ? (e <= 0) : (e < 0);cout << "Complement c2: " << c2 << endl;}Note that, in general, the particular output obtained can be syntactically different from the (semantically equivalent) constraint considered.Constraint c1: -A + 5*B - 3*C >= -4Complement c2: A - 5*B + 3*C > 4
). The actual output is the following:Constraint c1(x - 5*y + 3*z <= 4);cout << "Constraint c1: " << c1 << endl;if (c1.is_equality())cout << "Constraint c1 is not an inequality." << endl;else {Linear_Expression e;for (dimension_type i = c1.space_dimension(); i-- > 0; )e += c1.coefficient(Variable(i)) * Variable(i);e += c1.inhomogeneous_term();Constraint c2 = c1.is_strict_inequality() ? (e <= 0) : (e < 0);cout << "Complement c2: " << c2 << endl;}Note that, in general, the particular output obtained can be syntactically different from the (semantically equivalent) constraint considered.Constraint c1: -A + 5*B - 3*C >= -4Complement c2: A - 5*B + 3*C > 4
Definition at line 284 of file Constraint_defs.hh.
Member Typedef Documentation
The type of the (adapted) internal expression.
Definition at line 521 of file Constraint_defs.hh.
Constructor & Destructor Documentation
|
inlineexplicit |
Constructs the 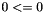 constraint.
constraint.
Definition at line 120 of file Constraint_inlines.hh.
References OK().
|
inline |
Ordinary copy constructor.
- Note
- The new Constraint will have the same representation as `c', not default_representation, so that they are indistinguishable.
Definition at line 171 of file Constraint_inlines.hh.
|
inline |
Copy constructor with given size.
- Note
- The new Constraint will have the same representation as `c', not default_representation, so that they are indistinguishable.
Definition at line 187 of file Constraint_inlines.hh.
References OK(), and space_dimension().
|
inline |
Copy constructor with given representation.
Definition at line 179 of file Constraint_inlines.hh.
References OK().
|
inline |
Copy constructor with given size and representation.
Definition at line 195 of file Constraint_inlines.hh.
References OK(), and space_dimension().
|
explicit |
Copy-constructs from equality congruence cg.
- Exceptions
-
std::invalid_argument Thrown if cgis a proper congruence.
Definition at line 66 of file Constraint.cc.
References Parma_Polyhedra_Library::Congruence::is_equality(), OK(), strong_normalize(), and throw_invalid_argument().
|
inline |
|
inlineprivate |
Constructs the 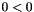 constraint.
constraint.
Definition at line 128 of file Constraint_inlines.hh.
References expr, OK(), Parma_Polyhedra_Library::Linear_Expression::set_space_dimension(), and space_dimension().
|
inlineprivate |
Builds a constraint of kind kind and topology topology, stealing the coefficients from e.
- Note
- The new Constraint will have the same representation as `e'.
Definition at line 139 of file Constraint_inlines.hh.
References expr, Parma_Polyhedra_Library::NOT_NECESSARILY_CLOSED, OK(), RAY_OR_POINT_OR_INEQUALITY, Parma_Polyhedra_Library::Linear_Expression::set_space_dimension(), Parma_Polyhedra_Library::Linear_Expression::space_dimension(), strong_normalize(), and swap().
|
inlineprivate |
Builds a constraint of type type and topology topology, stealing the coefficients from e.
- Note
- The new Constraint will have the same representation as `e'.
Definition at line 153 of file Constraint_inlines.hh.
References EQUALITY, expr, kind_, LINE_OR_EQUALITY, Parma_Polyhedra_Library::NOT_NECESSARILY_CLOSED, OK(), RAY_OR_POINT_OR_INEQUALITY, Parma_Polyhedra_Library::Linear_Expression::set_space_dimension(), Parma_Polyhedra_Library::Linear_Expression::space_dimension(), STRICT_INEQUALITY, strong_normalize(), and swap().
Member Function Documentation
| void Parma_Polyhedra_Library::Constraint::ascii_dump | ( | ) | const |
Writes to std::cerr an ASCII representation of *this.
| void Parma_Polyhedra_Library::Constraint::ascii_dump | ( | std::ostream & | s | ) | const |
Writes to s an ASCII representation of *this.
Definition at line 309 of file Constraint.cc.
References EQUALITY, Parma_Polyhedra_Library::NECESSARILY_CLOSED, NONSTRICT_INEQUALITY, and STRICT_INEQUALITY.
| bool Parma_Polyhedra_Library::Constraint::ascii_load | ( | std::istream & | s | ) |
Loads from s an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets *this accordingly. Returns true if successful, false otherwise.
Definition at line 336 of file Constraint.cc.
References Parma_Polyhedra_Library::NECESSARILY_CLOSED, and Parma_Polyhedra_Library::NOT_NECESSARILY_CLOSED.
Referenced by Parma_Polyhedra_Library::MIP_Problem::ascii_load(), and Parma_Polyhedra_Library::PIP_Problem::ascii_load().
|
private |
Returns true if and only if the coefficients are strongly normalized.
Definition at line 259 of file Constraint.cc.
References Parma_Polyhedra_Library::compare(), and strong_normalize().
|
inline |
Returns the coefficient of v in *this.
- Exceptions
-
std::invalid_argument thrown if the index of vis greater than or equal to the space dimension of*this.
Definition at line 312 of file Constraint_inlines.hh.
References Parma_Polyhedra_Library::Linear_Expression::coefficient(), expr, Parma_Polyhedra_Library::Variable::space_dimension(), space_dimension(), and throw_dimension_incompatible().
Referenced by Parma_Polyhedra_Library::Box< ITV >::add_constraint_no_check(), Parma_Polyhedra_Library::Constraint_System::affine_preimage(), Parma_Polyhedra_Library::Polyhedron::expand_space_dimension(), Parma_Polyhedra_Library::Octagonal_Shape< T >::extract_octagonal_difference(), Parma_Polyhedra_Library::Box< ITV >::get_limiting_box(), Parma_Polyhedra_Library::MIP_Problem::parse_constraints(), Parma_Polyhedra_Library::Box< ITV >::refine_no_check(), Parma_Polyhedra_Library::Box< ITV >::relation_with(), Parma_Polyhedra_Library::PIP_Problem::solve(), Parma_Polyhedra_Library::Implementation::wrap_assign(), and Parma_Polyhedra_Library::Box< ITV >::wrap_assign().
|
staticprivate |
Builds a new copy of the zero-dimension space constraint 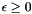 (used to implement NNC polyhedra).
(used to implement NNC polyhedra).
Definition at line 58 of file Constraint.cc.
References c, Parma_Polyhedra_Library::Coefficient_one(), Parma_Polyhedra_Library::NOT_NECESSARILY_CLOSED, OK(), and set_epsilon_coefficient().
|
inlineprivate |
Returns the epsilon coefficient. The constraint must be NNC.
Definition at line 570 of file Constraint_inlines.hh.
References Parma_Polyhedra_Library::Linear_Expression::coefficient(), expr, is_not_necessarily_closed(), and Parma_Polyhedra_Library::Linear_Expression::space_dimension().
Referenced by Parma_Polyhedra_Library::Polyhedron::drop_some_non_integer_points(), Parma_Polyhedra_Library::Constraint_System::has_strict_inequalities(), Parma_Polyhedra_Library::Polyhedron::is_universe(), Parma_Polyhedra_Library::Polyhedron::strongly_minimize_constraints(), Parma_Polyhedra_Library::Polyhedron::topological_closure_assign(), and type().
|
inlinestatic |
Returns the zero-dimension space constraint 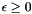 .
.
Definition at line 550 of file Constraint_inlines.hh.
References epsilon_geq_zero_p.
Referenced by Parma_Polyhedra_Library::Constraint_System::add_low_level_constraints().
|
inlinestatic |
The zero-dimension space constraint 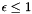 (used to implement NNC polyhedra).
(used to implement NNC polyhedra).
Definition at line 556 of file Constraint_inlines.hh.
References epsilon_leq_one_p.
Referenced by Parma_Polyhedra_Library::Constraint_System::add_low_level_constraints(), Parma_Polyhedra_Library::Polyhedron::drop_some_non_integer_points(), Parma_Polyhedra_Library::Polyhedron::strongly_minimize_constraints(), and Parma_Polyhedra_Library::Polyhedron::topological_closure_assign().
|
inline |
Partial read access to the (adapted) internal expression.
Definition at line 42 of file Constraint_inlines.hh.
References expr, and is_not_necessarily_closed().
Referenced by Parma_Polyhedra_Library::Implementation::Termination::assign_all_inequalities_approximation(), Parma_Polyhedra_Library::BD_Shape< T >::BD_Shape(), Parma_Polyhedra_Library::Polyhedron::BHZ09_NNC_poly_hull_assign_if_exact(), Parma_Polyhedra_Library::Box< ITV >::Box(), Parma_Polyhedra_Library::C_Polyhedron::C_Polyhedron(), Parma_Polyhedra_Library::Polyhedron::contains_integer_point(), Parma_Polyhedra_Library::Octagonal_Shape< T >::difference_assign(), Parma_Polyhedra_Library::BD_Shape< T >::difference_assign(), Parma_Polyhedra_Library::Polyhedron::drop_some_non_integer_points(), Parma_Polyhedra_Library::BD_Shape< T >::extract_bounded_difference(), Parma_Polyhedra_Library::Box_Helpers::extract_interval_constraint(), Parma_Polyhedra_Library::Octagonal_Shape< T >::extract_octagonal_difference(), Parma_Polyhedra_Library::Implementation::Termination::fill_constraint_systems_MS(), is_equivalent_to(), Parma_Polyhedra_Library::Polyhedron::is_universe(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::linear_partition(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::linear_partition_aux(), Parma_Polyhedra_Library::Octagonal_Shape< T >::Octagonal_Shape(), operator<<(), Parma_Polyhedra_Library::MIP_Problem::parse_constraints(), Parma_Polyhedra_Library::Polyhedron::poly_difference_assign(), Parma_Polyhedra_Library::MIP_Problem::process_pending_constraints(), Parma_Polyhedra_Library::Shape_Preserving_Reduction< D1, D2 >::product_reduce(), Parma_Polyhedra_Library::Box< ITV >::propagate_constraint_no_check(), Parma_Polyhedra_Library::Polyhedron::refine_no_check(), Parma_Polyhedra_Library::Polyhedron::refine_with_constraints(), Parma_Polyhedra_Library::Box< ITV >::relation_with(), Parma_Polyhedra_Library::BD_Shape< T >::relation_with(), Parma_Polyhedra_Library::Polyhedron::simplify_using_context_assign(), Parma_Polyhedra_Library::PIP_Problem::solve(), space_dimension(), Parma_Polyhedra_Library::Polyhedron::strongly_minimize_constraints(), and Parma_Polyhedra_Library::PIP_Solution_Node::update_tableau().
|
inline |
Returns the size in bytes of the memory managed by *this.
Definition at line 325 of file Constraint_inlines.hh.
References expr, and Parma_Polyhedra_Library::Linear_Expression::external_memory_in_bytes().
Referenced by total_memory_in_bytes().
|
static |
Finalizes the class.
Definition at line 290 of file Constraint.cc.
Referenced by Parma_Polyhedra_Library::Init::~Init().
|
inline |
Returns the inhomogeneous term of *this.
Definition at line 320 of file Constraint_inlines.hh.
References expr, and Parma_Polyhedra_Library::Linear_Expression::inhomogeneous_term().
Referenced by Parma_Polyhedra_Library::BD_Shape< T >::add_constraint(), Parma_Polyhedra_Library::Octagonal_Shape< T >::add_constraint(), Parma_Polyhedra_Library::Box< ITV >::add_constraint_no_check(), Parma_Polyhedra_Library::Polyhedron::contains_integer_point(), Parma_Polyhedra_Library::Octagonal_Shape< T >::extract_octagonal_difference(), Parma_Polyhedra_Library::Implementation::Termination::fill_constraint_systems_MS(), Parma_Polyhedra_Library::Box< ITV >::get_limiting_box(), Parma_Polyhedra_Library::BD_Shape< T >::get_limiting_shape(), Parma_Polyhedra_Library::Polyhedron::is_universe(), operator<<(), Parma_Polyhedra_Library::MIP_Problem::parse_constraints(), Parma_Polyhedra_Library::MIP_Problem::process_pending_constraints(), Parma_Polyhedra_Library::Box< ITV >::propagate_constraint_no_check(), Parma_Polyhedra_Library::Box< ITV >::refine_no_check(), Parma_Polyhedra_Library::Octagonal_Shape< T >::refine_no_check(), Parma_Polyhedra_Library::BD_Shape< T >::refine_no_check(), Parma_Polyhedra_Library::Box< ITV >::relation_with(), Parma_Polyhedra_Library::Polyhedron::relation_with(), Parma_Polyhedra_Library::Octagonal_Shape< T >::relation_with(), Parma_Polyhedra_Library::Grid::relation_with(), Parma_Polyhedra_Library::BD_Shape< T >::relation_with(), Parma_Polyhedra_Library::PIP_Problem::solve(), Parma_Polyhedra_Library::PIP_Solution_Node::update_tableau(), and Parma_Polyhedra_Library::Box< ITV >::wrap_assign().
|
static |
Initializes the class.
Definition at line 271 of file Constraint.cc.
References Parma_Polyhedra_Library::Coefficient_one(), and Parma_Polyhedra_Library::Linear_Expression::zero().
Referenced by Parma_Polyhedra_Library::Init::Init().
| bool Parma_Polyhedra_Library::Constraint::is_equal_to | ( | const Constraint & | y | ) | const |
Returns true if *this is identical to y.
This is faster than is_equivalent_to(), but it may return `false' even for equivalent constraints.
Definition at line 247 of file Constraint.cc.
References expr, kind_, and topology().
|
inline |
Returns true if and only if *this is an equality constraint.
Definition at line 266 of file Constraint_inlines.hh.
References is_line_or_equality().
Referenced by Parma_Polyhedra_Library::BD_Shape< T >::add_constraint(), Parma_Polyhedra_Library::Octagonal_Shape< T >::add_constraint(), Parma_Polyhedra_Library::Box< ITV >::add_constraint_no_check(), Parma_Polyhedra_Library::Grid::add_constraint_no_check(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::affine_dimension(), Parma_Polyhedra_Library::Implementation::Termination::assign_all_inequalities_approximation(), Parma_Polyhedra_Library::Polyhedron::BFT00_poly_hull_assign_if_exact(), Parma_Polyhedra_Library::Polyhedron::BHZ09_NNC_poly_hull_assign_if_exact(), Parma_Polyhedra_Library::Congruence::Congruence(), Parma_Polyhedra_Library::Octagonal_Shape< T >::difference_assign(), Parma_Polyhedra_Library::BD_Shape< T >::difference_assign(), Parma_Polyhedra_Library::Polyhedron::drop_some_non_integer_points(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::linear_partition(), Parma_Polyhedra_Library::MIP_Problem::parse_constraints(), Parma_Polyhedra_Library::Shape_Preserving_Reduction< D1, D2 >::product_reduce(), Parma_Polyhedra_Library::Box< ITV >::refine_no_check(), Parma_Polyhedra_Library::Octagonal_Shape< T >::refine_no_check(), Parma_Polyhedra_Library::Polyhedron::refine_no_check(), Parma_Polyhedra_Library::BD_Shape< T >::refine_no_check(), Parma_Polyhedra_Library::Grid::refine_no_check(), Parma_Polyhedra_Library::Polyhedron::refine_with_constraints(), Parma_Polyhedra_Library::Box< ITV >::relation_with(), Parma_Polyhedra_Library::Polyhedron::relation_with(), Parma_Polyhedra_Library::Octagonal_Shape< T >::relation_with(), Parma_Polyhedra_Library::Grid::relation_with(), Parma_Polyhedra_Library::BD_Shape< T >::relation_with(), Parma_Polyhedra_Library::PIP_Problem::solve(), type(), and Parma_Polyhedra_Library::PIP_Solution_Node::update_tableau().
| bool Parma_Polyhedra_Library::Constraint::is_equivalent_to | ( | const Constraint & | y | ) | const |
Returns true if and only if *this and y are equivalent constraints.
Constraints having different space dimensions are not equivalent. Note that constraints having different types may nonetheless be equivalent, if they both are tautologies or inconsistent.
Definition at line 208 of file Constraint.cc.
References expr, expression(), Parma_Polyhedra_Library::Linear_Expression::is_equal_to(), is_inconsistent(), is_tautological(), Parma_Polyhedra_Library::Linear_Expression::normalize(), space_dimension(), and type().
Referenced by operator!=(), and operator==().
| bool Parma_Polyhedra_Library::Constraint::is_inconsistent | ( | ) | const |
Returns true if and only if *this is inconsistent (i.e., an always false constraint).
An inconsistent constraint can have either one of the following forms:
- an equality:
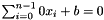 , where
, where 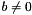 ; or
; or - a non-strict inequality:
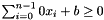 , where
, where 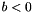 ; or
; or - a strict inequality:
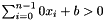 , where
, where 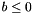 .
.
Definition at line 148 of file Constraint.cc.
Referenced by Parma_Polyhedra_Library::Polyhedron::add_constraint(), Parma_Polyhedra_Library::BD_Shape< T >::add_constraint(), Parma_Polyhedra_Library::Octagonal_Shape< T >::add_constraint(), Parma_Polyhedra_Library::Grid::add_constraint_no_check(), Parma_Polyhedra_Library::Polyhedron::contains_integer_point(), is_equivalent_to(), Parma_Polyhedra_Library::Polyhedron::poly_difference_assign(), Parma_Polyhedra_Library::Polyhedron::refine_no_check(), Parma_Polyhedra_Library::Grid::refine_no_check(), Parma_Polyhedra_Library::Polyhedron::relation_with(), Parma_Polyhedra_Library::Grid::relation_with(), and Parma_Polyhedra_Library::Box< ITV >::wrap_assign().
|
inline |
Returns true if and only if *this is an inequality constraint (either strict or non-strict).
Definition at line 271 of file Constraint_inlines.hh.
References is_ray_or_point_or_inequality().
Referenced by Parma_Polyhedra_Library::Grid::add_constraint_no_check(), Parma_Polyhedra_Library::Polyhedron::BHRZ03_combining_constraints(), Parma_Polyhedra_Library::Octagonal_Shape< T >::get_limiting_octagon(), Parma_Polyhedra_Library::BD_Shape< T >::get_limiting_shape(), Parma_Polyhedra_Library::Polyhedron::is_included_in(), Parma_Polyhedra_Library::MIP_Problem::is_satisfied(), Parma_Polyhedra_Library::MIP_Problem::parse_constraints(), Parma_Polyhedra_Library::MIP_Problem::process_pending_constraints(), Parma_Polyhedra_Library::Box< ITV >::relation_with(), Parma_Polyhedra_Library::Octagonal_Shape< T >::relation_with(), Parma_Polyhedra_Library::BD_Shape< T >::relation_with(), Parma_Polyhedra_Library::Constraint_System::satisfies_all_constraints(), and Parma_Polyhedra_Library::Polyhedron::simplify_using_context_assign().
|
inlineprivate |
Returns true if and only if *this row represents a line or an equality.
Definition at line 57 of file Constraint_inlines.hh.
References kind_, and LINE_OR_EQUALITY.
Referenced by compare(), and is_equality().
|
inlineprivate |
Returns true if and only if the topology of *this row is necessarily closed.
Definition at line 32 of file Constraint_inlines.hh.
References Parma_Polyhedra_Library::NECESSARILY_CLOSED, and topology_.
Referenced by is_not_necessarily_closed(), mark_as_not_necessarily_closed(), Parma_Polyhedra_Library::Topology_Adjusted_Scalar_Product_Sign::operator()(), Parma_Polyhedra_Library::Scalar_Products::reduced_sign(), Parma_Polyhedra_Library::Polyhedron::refine_no_check(), Parma_Polyhedra_Library::Polyhedron::refine_with_constraints(), and type().
|
inline |
Returns true if and only if *this is a non-strict inequality constraint.
Definition at line 292 of file Constraint_inlines.hh.
References NONSTRICT_INEQUALITY, and type().
Referenced by Parma_Polyhedra_Library::Octagonal_Shape< T >::relation_with(), and Parma_Polyhedra_Library::BD_Shape< T >::relation_with().
|
inlineprivate |
Returns true if and only if the topology of *this row is not necessarily closed.
Definition at line 37 of file Constraint_inlines.hh.
References is_necessarily_closed().
Referenced by epsilon_coefficient(), expression(), mark_as_necessarily_closed(), and set_epsilon_coefficient().
|
inlineprivate |
Returns true if and only if *this row represents a ray, a point or an inequality.
Definition at line 62 of file Constraint_inlines.hh.
References kind_, and RAY_OR_POINT_OR_INEQUALITY.
Referenced by is_inequality().
|
inline |
Returns true if and only if *this is a strict inequality constraint.
Definition at line 297 of file Constraint_inlines.hh.
References STRICT_INEQUALITY, and type().
Referenced by Parma_Polyhedra_Library::MIP_Problem::add_constraint(), Parma_Polyhedra_Library::Polyhedron::add_constraint(), Parma_Polyhedra_Library::BD_Shape< T >::add_constraint(), Parma_Polyhedra_Library::Octagonal_Shape< T >::add_constraint(), Parma_Polyhedra_Library::Box< ITV >::add_constraint_no_check(), Parma_Polyhedra_Library::Implementation::Termination::assign_all_inequalities_approximation(), Parma_Polyhedra_Library::BD_Shape< T >::BD_Shape(), Parma_Polyhedra_Library::Polyhedron::BHZ09_NNC_poly_hull_assign_if_exact(), Parma_Polyhedra_Library::Box< ITV >::Box(), Parma_Polyhedra_Library::C_Polyhedron::C_Polyhedron(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::linear_partition_aux(), Parma_Polyhedra_Library::Octagonal_Shape< T >::Octagonal_Shape(), Parma_Polyhedra_Library::Box< ITV >::refine_no_check(), Parma_Polyhedra_Library::Octagonal_Shape< T >::refine_no_check(), Parma_Polyhedra_Library::BD_Shape< T >::refine_no_check(), Parma_Polyhedra_Library::Box< ITV >::relation_with(), Parma_Polyhedra_Library::Polyhedron::relation_with(), Parma_Polyhedra_Library::Octagonal_Shape< T >::relation_with(), Parma_Polyhedra_Library::Grid::relation_with(), Parma_Polyhedra_Library::BD_Shape< T >::relation_with(), Parma_Polyhedra_Library::Polyhedron::select_H79_constraints(), Parma_Polyhedra_Library::PIP_Problem::solve(), and Parma_Polyhedra_Library::PIP_Solution_Node::update_tableau().
| bool Parma_Polyhedra_Library::Constraint::is_tautological | ( | ) | const |
Returns true if and only if *this is a tautology (i.e., an always true constraint).
A tautology can have either one of the following forms:
- an equality:
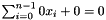 ; or
; or - a non-strict inequality:
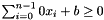 , where
, where 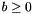 ; or
; or - a strict inequality:
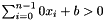 , where
, where 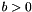 .
.
Definition at line 105 of file Constraint.cc.
References Parma_Polyhedra_Library::Boundary_NS::sgn().
Referenced by Parma_Polyhedra_Library::Polyhedron::add_constraint(), Parma_Polyhedra_Library::BD_Shape< T >::add_constraint(), Parma_Polyhedra_Library::Octagonal_Shape< T >::add_constraint(), Parma_Polyhedra_Library::Grid::add_constraint_no_check(), Parma_Polyhedra_Library::Polyhedron::drop_some_non_integer_points(), Parma_Polyhedra_Library::Constraint_System::has_strict_inequalities(), is_equivalent_to(), Parma_Polyhedra_Library::Polyhedron::poly_difference_assign(), Parma_Polyhedra_Library::Polyhedron::simplify_using_context_assign(), and Parma_Polyhedra_Library::Polyhedron::topological_closure_assign().
|
private |
Linearly combines *this with y so that i-th coefficient is 0.
- Parameters
-
y The Constraint that will be combined with *thisobject;i The index of the coefficient that has to become  .
.
Computes a linear combination of *this and y having the i-th coefficient equal to  . Then it assigns the resulting Constraint to
. Then it assigns the resulting Constraint to *this and normalizes it.
Definition at line 189 of file Constraint.cc.
References expr.
|
inline |
Swaps *this with y.
Definition at line 562 of file Constraint_inlines.hh.
References expr, kind_, swap(), Parma_Polyhedra_Library::swap(), and topology_.
Referenced by swap().
|
inlineprivate |
Marks the epsilon dimension as a standard dimension.
The row topology is changed to NOT_NECESSARILY_CLOSED, and the number of space dimensions is increased by 1.
Definition at line 98 of file Constraint_inlines.hh.
References is_not_necessarily_closed(), Parma_Polyhedra_Library::NECESSARILY_CLOSED, and topology_.
|
inlineprivate |
Marks the last dimension as the epsilon dimension.
The row topology is changed to NECESSARILY_CLOSED, and the number of space dimensions is decreased by 1.
Definition at line 104 of file Constraint_inlines.hh.
References is_necessarily_closed(), Parma_Polyhedra_Library::NOT_NECESSARILY_CLOSED, and topology_.
|
inlinestatic |
Returns the maximum space dimension a Constraint can handle.
Definition at line 226 of file Constraint_inlines.hh.
References Parma_Polyhedra_Library::Linear_Expression::max_space_dimension().
Referenced by Parma_Polyhedra_Library::MIP_Problem::max_space_dimension(), and Parma_Polyhedra_Library::PIP_Problem::max_space_dimension().
| bool Parma_Polyhedra_Library::Constraint::OK | ( | ) | const |
Checks if all the invariants are satisfied.
Definition at line 467 of file Constraint.cc.
References strong_normalize().
Referenced by Parma_Polyhedra_Library::Constraint_System::affine_preimage(), Constraint(), construct_epsilon_geq_zero(), Parma_Polyhedra_Library::Polyhedron::drop_some_non_integer_points(), Parma_Polyhedra_Library::Polyhedron::expand_space_dimension(), operator>(), set_space_dimension(), and Parma_Polyhedra_Library::Polyhedron::topological_closure_assign().
|
inline |
Assignment operator.
Definition at line 208 of file Constraint_inlines.hh.
| void Parma_Polyhedra_Library::Constraint::permute_space_dimensions | ( | const std::vector< Variable > & | cycle | ) |
Permutes the space dimensions of the constraint.
Definition at line 91 of file Constraint.cc.
| void Parma_Polyhedra_Library::Constraint::print | ( | ) | const |
Prints *this to std::cerr using operator<<.
|
inline |
Removes all the specified dimensions from the constraint.
The space dimension of the variable with the highest space dimension in vars must be at most the space dimension of this.
Always returns true. The return value is needed for compatibility with the Generator class.
Definition at line 260 of file Constraint_inlines.hh.
References expr, and Parma_Polyhedra_Library::Linear_Expression::remove_space_dimensions().
|
inline |
Returns the current representation of *this.
Definition at line 216 of file Constraint_inlines.hh.
References expr, and Parma_Polyhedra_Library::Linear_Expression::representation().
|
inlineprivate |
Sets the epsilon coefficient to n. The constraint must be NNC.
Definition at line 576 of file Constraint_inlines.hh.
References expr, is_not_necessarily_closed(), Parma_Polyhedra_Library::Linear_Expression::set_coefficient(), and Parma_Polyhedra_Library::Linear_Expression::space_dimension().
Referenced by construct_epsilon_geq_zero(), Parma_Polyhedra_Library::Polyhedron::drop_some_non_integer_points(), operator>(), and Parma_Polyhedra_Library::Polyhedron::topological_closure_assign().
|
inlineprivate |
Sets the constraint type to EQUALITY.
Definition at line 302 of file Constraint_inlines.hh.
References set_is_line_or_equality().
|
inlineprivate |
Sets the constraint to be an inequality.
Whether the constraint type will become NONSTRICT_INEQUALITY or STRICT_INEQUALITY depends on the topology and the value of the low-level coefficients of the constraint.
Definition at line 307 of file Constraint_inlines.hh.
References set_is_ray_or_point_or_inequality().
|
inlineprivate |
Sets to LINE_OR_EQUALITY the kind of *this row.
Definition at line 72 of file Constraint_inlines.hh.
References kind_, and LINE_OR_EQUALITY.
Referenced by set_is_equality(), and Parma_Polyhedra_Library::Polyhedron::simplify_using_context_assign().
|
inlineprivate |
Sets to RAY_OR_POINT_OR_INEQUALITY the kind of *this row.
Definition at line 77 of file Constraint_inlines.hh.
References kind_, and RAY_OR_POINT_OR_INEQUALITY.
Referenced by set_is_inequality().
|
inlineprivate |
Sets to NECESSARILY_CLOSED the topological kind of *this row.
Definition at line 110 of file Constraint_inlines.hh.
References Parma_Polyhedra_Library::NECESSARILY_CLOSED, and set_topology().
|
inlineprivate |
Sets to NOT_NECESSARILY_CLOSED the topological kind of *this row.
Definition at line 115 of file Constraint_inlines.hh.
References Parma_Polyhedra_Library::NOT_NECESSARILY_CLOSED, and set_topology().
|
inline |
Converts *this to the specified representation.
Definition at line 221 of file Constraint_inlines.hh.
References expr, and Parma_Polyhedra_Library::Linear_Expression::set_representation().
|
inline |
Sets the dimension of the vector space enclosing *this to space_dim .
Definition at line 254 of file Constraint_inlines.hh.
References OK(), and set_space_dimension_no_ok().
|
inlineprivate |
Sets the dimension of the vector space enclosing *this to space_dim . Sets the space dimension of the rows in the system to space_dim .
This method is for internal use, it does *not* assert OK() at the end, so it can be used for invalid objects.
Definition at line 231 of file Constraint_inlines.hh.
References expr, Parma_Polyhedra_Library::NECESSARILY_CLOSED, Parma_Polyhedra_Library::Linear_Expression::set_space_dimension(), space_dimension(), Parma_Polyhedra_Library::Linear_Expression::space_dimension(), strong_normalize(), Parma_Polyhedra_Library::Linear_Expression::swap_space_dimensions(), and topology().
Referenced by set_space_dimension().
|
inlineprivate |
Sets to x the topological kind of *this row.
Definition at line 82 of file Constraint_inlines.hh.
References expr, Parma_Polyhedra_Library::NECESSARILY_CLOSED, Parma_Polyhedra_Library::Linear_Expression::set_space_dimension(), Parma_Polyhedra_Library::Linear_Expression::space_dimension(), topology(), and topology_.
Referenced by Parma_Polyhedra_Library::Constraint_System::insert(), Parma_Polyhedra_Library::Constraint_System::insert_pending(), set_necessarily_closed(), and set_not_necessarily_closed().
|
inline |
Shift by n positions the coefficients of variables, starting from the coefficient of v. This increases the space dimension by n.
Definition at line 52 of file Constraint_inlines.hh.
References expr, and Parma_Polyhedra_Library::Linear_Expression::shift_space_dimensions().
|
private |
Normalizes the sign of the coefficients so that the first non-zero (homogeneous) coefficient of a line-or-equality is positive.
Definition at line 252 of file Constraint.cc.
Referenced by Parma_Polyhedra_Library::Polyhedron::simplify_using_context_assign(), and strong_normalize().
|
inline |
Returns the dimension of the vector space enclosing *this.
Definition at line 47 of file Constraint_inlines.hh.
References expression(), and Parma_Polyhedra_Library::Expression_Hide_Last< T >::space_dimension().
Referenced by Parma_Polyhedra_Library::MIP_Problem::add_constraint(), Parma_Polyhedra_Library::PIP_Problem::add_constraint(), Parma_Polyhedra_Library::Box< ITV >::add_constraint(), Parma_Polyhedra_Library::Polyhedron::add_constraint(), Parma_Polyhedra_Library::BD_Shape< T >::add_constraint(), Parma_Polyhedra_Library::Octagonal_Shape< T >::add_constraint(), Parma_Polyhedra_Library::Grid::add_constraint(), Parma_Polyhedra_Library::Box< ITV >::add_constraint_no_check(), Parma_Polyhedra_Library::Grid::add_constraint_no_check(), Parma_Polyhedra_Library::Octagonal_Shape< T >::bounds(), coefficient(), Constraint(), Parma_Polyhedra_Library::BD_Shape< T >::extract_bounded_difference(), Parma_Polyhedra_Library::Box_Helpers::extract_interval_constraint(), Parma_Polyhedra_Library::Octagonal_Shape< T >::extract_octagonal_difference(), Parma_Polyhedra_Library::Scalar_Products::homogeneous_assign(), Parma_Polyhedra_Library::Congruence_System::insert(), is_equivalent_to(), Parma_Polyhedra_Library::MIP_Problem::is_satisfied(), Parma_Polyhedra_Library::MIP_Problem::is_saturated(), Parma_Polyhedra_Library::Octagonal_Shape< T >::max_min(), Parma_Polyhedra_Library::Topology_Adjusted_Scalar_Product_Sign::operator()(), Parma_Polyhedra_Library::MIP_Problem::parse_constraints(), Parma_Polyhedra_Library::Box< ITV >::propagate_constraint(), Parma_Polyhedra_Library::Box< ITV >::propagate_constraint_no_check(), Parma_Polyhedra_Library::Box< ITV >::refine_no_check(), Parma_Polyhedra_Library::Octagonal_Shape< T >::refine_no_check(), Parma_Polyhedra_Library::Polyhedron::refine_no_check(), Parma_Polyhedra_Library::BD_Shape< T >::refine_no_check(), Parma_Polyhedra_Library::Grid::refine_no_check(), Parma_Polyhedra_Library::Box< ITV >::refine_with_constraint(), Parma_Polyhedra_Library::Polyhedron::refine_with_constraint(), Parma_Polyhedra_Library::BD_Shape< T >::refine_with_constraint(), Parma_Polyhedra_Library::Octagonal_Shape< T >::refine_with_constraint(), Parma_Polyhedra_Library::Grid::refine_with_constraint(), Parma_Polyhedra_Library::Box< ITV >::relation_with(), Parma_Polyhedra_Library::Polyhedron::relation_with(), Parma_Polyhedra_Library::Generator_System::relation_with(), Parma_Polyhedra_Library::Octagonal_Shape< T >::relation_with(), Parma_Polyhedra_Library::Grid::relation_with(), Parma_Polyhedra_Library::BD_Shape< T >::relation_with(), Parma_Polyhedra_Library::Generator_System::satisfied_by_all_generators(), set_space_dimension_no_ok(), Parma_Polyhedra_Library::PIP_Problem::solve(), Parma_Polyhedra_Library::Box< ITV >::throw_dimension_incompatible(), Parma_Polyhedra_Library::Octagonal_Shape< T >::throw_dimension_incompatible(), Parma_Polyhedra_Library::BD_Shape< T >::throw_dimension_incompatible(), Parma_Polyhedra_Library::Grid::throw_dimension_incompatible(), and Parma_Polyhedra_Library::Polyhedron::throw_dimension_incompatible().
|
inlineprivate |
Strong normalization: ensures that different Constraint objects represent different hyperplanes or hyperspaces.
Applies both Constraint::normalize() and Constraint::sign_normalize().
Definition at line 335 of file Constraint_inlines.hh.
References expr, Parma_Polyhedra_Library::Linear_Expression::normalize(), and sign_normalize().
Referenced by Parma_Polyhedra_Library::Constraint_System::affine_preimage(), check_strong_normalized(), Constraint(), OK(), and set_space_dimension_no_ok().
Swaps the coefficients of the variables v1 and v2 .
Definition at line 80 of file Constraint.cc.
References Parma_Polyhedra_Library::Variable::space_dimension().
|
private |
Throws a std::invalid_argument exception containing the appropriate error message.
Definition at line 47 of file Constraint.cc.
References Parma_Polyhedra_Library::Variable::space_dimension().
Referenced by coefficient().
|
private |
Throws a std::invalid_argument exception containing error message message.
Definition at line 38 of file Constraint.cc.
Referenced by Constraint().
|
inlineprivate |
Returns the topological kind of *this.
Definition at line 67 of file Constraint_inlines.hh.
References topology_.
Referenced by Parma_Polyhedra_Library::Constraint_System::insert(), Parma_Polyhedra_Library::Constraint_System::insert_pending(), is_equal_to(), set_space_dimension_no_ok(), and set_topology().
|
inline |
Returns a lower bound to the total size in bytes of the memory occupied by *this.
Definition at line 330 of file Constraint_inlines.hh.
References external_memory_in_bytes().
|
inline |
Returns the constraint type of *this.
Definition at line 276 of file Constraint_inlines.hh.
References epsilon_coefficient(), EQUALITY, is_equality(), is_necessarily_closed(), NONSTRICT_INEQUALITY, and STRICT_INEQUALITY.
Referenced by Parma_Polyhedra_Library::Box< ITV >::add_constraint_no_check(), Parma_Polyhedra_Library::Polyhedron::contains_integer_point(), Parma_Polyhedra_Library::Box< ITV >::get_limiting_box(), is_equivalent_to(), Parma_Polyhedra_Library::Polyhedron::is_included_in(), is_nonstrict_inequality(), is_strict_inequality(), operator<<(), Parma_Polyhedra_Library::Polyhedron::poly_difference_assign(), Parma_Polyhedra_Library::Box< ITV >::propagate_constraint_no_check(), Parma_Polyhedra_Library::Box< ITV >::refine_no_check(), Parma_Polyhedra_Library::Box< ITV >::relation_with(), Parma_Polyhedra_Library::Generator_System::relation_with(), Parma_Polyhedra_Library::Generator_System::satisfied_by_all_generators(), Parma_Polyhedra_Library::Constraint_System::satisfies_all_constraints(), Parma_Polyhedra_Library::Polyhedron::simplify_using_context_assign(), and Parma_Polyhedra_Library::Box< ITV >::wrap_assign().
|
inlinestatic |
The unsatisfiable (zero-dimension space) constraint 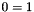 .
.
Definition at line 538 of file Constraint_inlines.hh.
References zero_dim_false_p.
Referenced by Parma_Polyhedra_Library::BD_Shape< T >::constraints(), Parma_Polyhedra_Library::Octagonal_Shape< T >::constraints(), Parma_Polyhedra_Library::Box< ITV >::constraints(), Parma_Polyhedra_Library::Constraint_System::initialize(), Parma_Polyhedra_Library::BD_Shape< T >::minimized_constraints(), and Parma_Polyhedra_Library::Box< ITV >::minimized_constraints().
|
inlinestatic |
The true (zero-dimension space) constraint 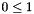 , also known as positivity constraint.
, also known as positivity constraint.
Definition at line 544 of file Constraint_inlines.hh.
References zero_dim_positivity_p.
Referenced by Parma_Polyhedra_Library::Constraint_System::add_low_level_constraints(), Parma_Polyhedra_Library::MIP_Problem::ascii_load(), Parma_Polyhedra_Library::PIP_Problem::ascii_load(), and Parma_Polyhedra_Library::Polyhedron::drop_some_non_integer_points().
Friends And Related Function Documentation
|
related |
The basic comparison function.
- Returns
- The returned absolute value can be
 ,
, 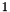 or
or 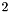 .
.
- Parameters
-
x A row of coefficients; y Another row.
Compares x and y, where x and y may be of different size, in which case the "missing" coefficients are assumed to be zero. The comparison is such that:
- equalities are smaller than inequalities;
- lines are smaller than points and rays;
- the ordering is lexicographic;
- the positions compared are, in decreasing order of significance, 1, 2, ...,
size(), 0; - the result is negative, zero, or positive if x is smaller than, equal to, or greater than y, respectively;
- when
xandyare different, the absolute value of the result is 1 if the difference is due to the coefficient in position 0; it is 2 otherwise.
When x and y represent the hyper-planes associated to two equality or inequality constraints, the coefficient at 0 is the known term. In this case, the return value can be characterized as follows:
- -2, if
xis smaller thanyand they are not parallel; - -1, if
xis smaller thanyand they are parallel; - 0, if
xand y are equal; - +1, if
yis smaller thanxand they are parallel; - +2, if
yis smaller thanxand they are not parallel.
|
related |
Definition at line 196 of file Constraint.cc.
References Parma_Polyhedra_Library::compare(), expr, and is_line_or_equality().
|
friend |
|
friend |
Definition at line 735 of file Constraint_defs.hh.
|
friend |
Definition at line 740 of file Constraint_defs.hh.
|
friend |
Definition at line 734 of file Constraint_defs.hh.
|
friend |
Definition at line 742 of file Constraint_defs.hh.
|
related |
Definition at line 348 of file Constraint_inlines.hh.
References is_equivalent_to().
|
related |
Returns true if and only if x is not equivalent to y.
|
related |
Returns the constraint e1 < e2.
|
related |
Returns the constraint v1 < v2.
|
related |
Returns the constraint e < n.
|
related |
Returns the constraint n < e.
|
related |
Definition at line 515 of file Constraint_inlines.hh.
|
related |
Definition at line 521 of file Constraint_inlines.hh.
|
related |
Definition at line 527 of file Constraint_inlines.hh.
|
related |
Definition at line 533 of file Constraint_inlines.hh.
|
friend |
|
friend |
|
friend |
|
friend |
|
related |
Definition at line 400 of file Constraint.cc.
References Parma_Polyhedra_Library::Expression_Adapter< T >::begin(), Parma_Polyhedra_Library::Coefficient_zero(), Parma_Polyhedra_Library::Expression_Hide_Last< T >::end(), EQUALITY, expression(), inhomogeneous_term(), Parma_Polyhedra_Library::neg_assign(), NONSTRICT_INEQUALITY, PPL_DIRTY_TEMP_COEFFICIENT, STRICT_INEQUALITY, and type().
|
related |
Definition at line 447 of file Constraint.cc.
References EQUALITY, NONSTRICT_INEQUALITY, and STRICT_INEQUALITY.
|
related |
Output operator.
|
related |
Output operator.
|
related |
Returns the constraint e1 <= e2.
|
related |
Returns the constraint v1 <= v2.
|
related |
Returns the constraint e <= n.
|
related |
Returns the constraint n <= e.
|
related |
Definition at line 491 of file Constraint_inlines.hh.
|
related |
Definition at line 497 of file Constraint_inlines.hh.
|
related |
Definition at line 503 of file Constraint_inlines.hh.
|
related |
Definition at line 509 of file Constraint_inlines.hh.
|
friend |
|
friend |
|
friend |
|
friend |
|
related |
Returns the constraint e1 = e2.
|
related |
Returns the constraint v1 = v2.
|
related |
Returns the constraint e = n.
|
related |
Returns the constraint n = e.
|
related |
Definition at line 342 of file Constraint_inlines.hh.
References is_equivalent_to().
|
related |
Definition at line 354 of file Constraint_inlines.hh.
References default_representation, EQUALITY, Parma_Polyhedra_Library::NECESSARILY_CLOSED, and Parma_Polyhedra_Library::Linear_Expression::space_dimension().
|
related |
Definition at line 364 of file Constraint_inlines.hh.
References default_representation, EQUALITY, Parma_Polyhedra_Library::NECESSARILY_CLOSED, Parma_Polyhedra_Library::Variable::space_dimension(), and Parma_Polyhedra_Library::swap().
|
related |
Definition at line 428 of file Constraint_inlines.hh.
References default_representation, EQUALITY, Parma_Polyhedra_Library::NECESSARILY_CLOSED, and Parma_Polyhedra_Library::neg_assign().
|
related |
Definition at line 461 of file Constraint_inlines.hh.
References default_representation, EQUALITY, and Parma_Polyhedra_Library::NECESSARILY_CLOSED.
|
friend |
|
friend |
|
friend |
|
friend |
|
related |
Returns true if and only if x is equivalent to y.
|
related |
Returns the constraint e1 > e2.
|
related |
Returns the constraint v1 > v2.
|
related |
Returns the constraint e > n.
|
related |
Returns the constraint n > e.
|
related |
Definition at line 398 of file Constraint_inlines.hh.
References c, default_representation, Parma_Polyhedra_Library::NOT_NECESSARILY_CLOSED, OK(), set_epsilon_coefficient(), and STRICT_INEQUALITY.
|
related |
Definition at line 412 of file Constraint_inlines.hh.
References c, default_representation, Parma_Polyhedra_Library::NOT_NECESSARILY_CLOSED, OK(), set_epsilon_coefficient(), Parma_Polyhedra_Library::Linear_Expression::set_space_dimension(), Parma_Polyhedra_Library::Variable::space_dimension(), and STRICT_INEQUALITY.
|
related |
Definition at line 446 of file Constraint_inlines.hh.
References c, default_representation, Parma_Polyhedra_Library::neg_assign(), Parma_Polyhedra_Library::NOT_NECESSARILY_CLOSED, OK(), set_epsilon_coefficient(), and STRICT_INEQUALITY.
|
related |
Definition at line 477 of file Constraint_inlines.hh.
References c, default_representation, Parma_Polyhedra_Library::NOT_NECESSARILY_CLOSED, OK(), set_epsilon_coefficient(), and STRICT_INEQUALITY.
|
friend |
|
friend |
|
friend |
|
friend |
|
related |
Returns the constraint e1 >= e2.
|
related |
Returns the constraint v1 >= v2.
|
related |
Returns the constraint e >= n.
|
related |
Returns the constraint n >= e.
|
related |
Definition at line 377 of file Constraint_inlines.hh.
References default_representation, Parma_Polyhedra_Library::NECESSARILY_CLOSED, NONSTRICT_INEQUALITY, and Parma_Polyhedra_Library::Linear_Expression::space_dimension().
|
related |
Definition at line 387 of file Constraint_inlines.hh.
References default_representation, Parma_Polyhedra_Library::NECESSARILY_CLOSED, NONSTRICT_INEQUALITY, Parma_Polyhedra_Library::Linear_Expression::set_space_dimension(), and Parma_Polyhedra_Library::Variable::space_dimension().
|
related |
Definition at line 437 of file Constraint_inlines.hh.
References default_representation, Parma_Polyhedra_Library::NECESSARILY_CLOSED, Parma_Polyhedra_Library::neg_assign(), and NONSTRICT_INEQUALITY.
|
related |
Definition at line 469 of file Constraint_inlines.hh.
References default_representation, Parma_Polyhedra_Library::NECESSARILY_CLOSED, and NONSTRICT_INEQUALITY.
|
friend |
|
friend |
|
friend |
|
friend |
|
friend |
Definition at line 736 of file Constraint_defs.hh.
|
friend |
Definition at line 737 of file Constraint_defs.hh.
|
related |
Definition at line 583 of file Constraint_inlines.hh.
References m_swap().
|
related |
Referenced by Constraint(), m_swap(), and operator=().
|
friend |
Definition at line 739 of file Constraint_defs.hh.
|
friend |
Definition at line 738 of file Constraint_defs.hh.
Member Data Documentation
|
static |
The representation used for new Constraints.
- Note
- The copy constructor and the copy constructor with specified size use the representation of the original object, so that it is indistinguishable from the original object.
Definition at line 303 of file Constraint_defs.hh.
Referenced by operator==(), operator>(), and operator>=().
|
staticprivate |
Holds (between class initialization and finalization) a pointer to the zero-dimension space constraint 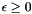 .
.
Definition at line 556 of file Constraint_defs.hh.
Referenced by epsilon_geq_zero().
|
staticprivate |
Holds (between class initialization and finalization) a pointer to the zero-dimension space constraint 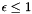 (used to implement NNC polyhedra).
(used to implement NNC polyhedra).
Definition at line 563 of file Constraint_defs.hh.
Referenced by epsilon_leq_one().
|
private |
Definition at line 533 of file Constraint_defs.hh.
Referenced by Parma_Polyhedra_Library::Constraint_System::affine_preimage(), Parma_Polyhedra_Library::Scalar_Products::assign(), coefficient(), compare(), Constraint(), Parma_Polyhedra_Library::Polyhedron::drop_some_non_integer_points(), epsilon_coefficient(), Parma_Polyhedra_Library::Polyhedron::expand_space_dimension(), expression(), external_memory_in_bytes(), Parma_Polyhedra_Library::Scalar_Products::homogeneous_assign(), inhomogeneous_term(), is_equal_to(), is_equivalent_to(), linear_combine(), m_swap(), Parma_Polyhedra_Library::Topology_Adjusted_Scalar_Product_Sign::operator()(), Parma_Polyhedra_Library::Scalar_Products::reduced_sign(), Parma_Polyhedra_Library::Octagonal_Shape< T >::relation_with(), Parma_Polyhedra_Library::Grid::relation_with(), remove_space_dimensions(), representation(), set_epsilon_coefficient(), set_representation(), set_space_dimension_no_ok(), set_topology(), shift_space_dimensions(), Parma_Polyhedra_Library::Scalar_Products::sign(), strong_normalize(), and Parma_Polyhedra_Library::Polyhedron::topological_closure_assign().
|
private |
Definition at line 535 of file Constraint_defs.hh.
Referenced by Constraint(), is_equal_to(), is_line_or_equality(), is_ray_or_point_or_inequality(), m_swap(), set_is_line_or_equality(), and set_is_ray_or_point_or_inequality().
|
private |
Definition at line 537 of file Constraint_defs.hh.
Referenced by is_necessarily_closed(), m_swap(), mark_as_necessarily_closed(), mark_as_not_necessarily_closed(), set_topology(), and topology().
|
staticprivate |
Holds (between class initialization and finalization) a pointer to the unsatisfiable (zero-dimension space) constraint 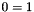 .
.
Definition at line 543 of file Constraint_defs.hh.
Referenced by zero_dim_false().
|
staticprivate |
Holds (between class initialization and finalization) a pointer to the true (zero-dimension space) constraint 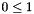 , also known as positivity constraint.
, also known as positivity constraint.
Definition at line 550 of file Constraint_defs.hh.
Referenced by zero_dim_positivity().
The documentation for this class was generated from the following files:
