A system of constraints. More...

#include <Constraint_System_defs.hh>

Collaboration diagram for Parma_Polyhedra_Library::Constraint_System:

[legend]

Public Types
typedef Constraint	row_type

typedef Constraint_System_const_iterator	const_iterator

Public Member Functions
	Constraint_System (Representation r=default_representation)
	Default constructor: builds an empty system of constraints. More...

	Constraint_System (const Constraint &c, Representation r=default_representation)
	Builds the singleton system containing only constraint `c`. More...

	Constraint_System (const Congruence_System &cgs, Representation r=default_representation)
	Builds a system containing copies of any equalities in `cgs`. More...

	Constraint_System (const Constraint_System &cs)
	Ordinary copy constructor. More...

	Constraint_System (const Constraint_System &cs, Representation r)
	Copy constructor with specified representation. More...

	~Constraint_System ()
	Destructor. More...

Constraint_System &	operator= (const Constraint_System &y)
	Assignment operator. More...

Representation	representation () const
	Returns the current representation of *this. More...

void	set_representation (Representation r)
	Converts *this to the specified representation. More...

dimension_type	space_dimension () const
	Returns the dimension of the vector space enclosing `*this`. More...

void	set_space_dimension (dimension_type space_dim)
	Sets the space dimension of the rows in the system to `space_dim` . More...

bool	has_equalities () const
	Returns `true` if and only if `*this` contains one or more equality constraints. More...

bool	has_strict_inequalities () const
	Returns `true` if and only if `*this` contains one or more strict inequality constraints. More...

void	insert (const Constraint &c)
	Inserts in `*this` a copy of the constraint `c`, increasing the number of space dimensions if needed. More...

bool	empty () const
	Returns `true` if and only if `*this` has no constraints. More...

void	clear ()
	Removes all the constraints from the constraint system and sets its space dimension to 0. More...

const_iterator	begin () const
	Returns the const_iterator pointing to the first constraint, if `*this` is not empty; otherwise, returns the past-the-end const_iterator. More...

const_iterator	end () const
	Returns the past-the-end const_iterator. More...

bool	OK () const
	Checks if all the invariants are satisfied. More...

void	ascii_dump () const
	Writes to `std::cerr` an ASCII representation of `*this`. More...

void	ascii_dump (std::ostream &s) const
	Writes to `s` an ASCII representation of `*this`. More...

void	print () const
	Prints `*this` to `std::cerr` using `operator<<`. More...

bool	ascii_load (std::istream &s)
	Loads from `s` an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets `*this` accordingly. Returns `true` if successful, `false` otherwise. More...

memory_size_type	total_memory_in_bytes () const
	Returns the total size in bytes of the memory occupied by `*this`. More...

memory_size_type	external_memory_in_bytes () const
	Returns the size in bytes of the memory managed by `*this`. More...

void	m_swap (Constraint_System &y)
	Swaps `*this` with `y`. More...

Static Public Member Functions
static dimension_type	max_space_dimension ()
	Returns the maximum space dimension a Constraint_System can handle. More...

static void	initialize ()
	Initializes the class. More...

static void	finalize ()
	Finalizes the class. More...

static const Constraint_System &	zero_dim_empty ()
	Returns the singleton system containing only Constraint::zero_dim_false(). More...

Static Public Attributes
static const Representation	default_representation = SPARSE

Private Member Functions
	Constraint_System (Topology topol, Representation r=default_representation)
	Builds an empty system of constraints having the specified topology. More...

	Constraint_System (Topology topol, dimension_type space_dim, Representation r=default_representation)
	Builds a system of constraints on a `space_dim` dimensional space. If `topol` is `NOT_NECESSARILY_CLOSED` the 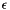$\epsilon$ dimension is added. More...

dimension_type	num_equalities () const
	Returns the number of equality constraints. More...

dimension_type	num_inequalities () const
	Returns the number of inequality constraints. More...

void	simplify ()
	Applies Gaussian elimination and back-substitution so as to provide a partial simplification of the system of constraints. More...

bool	adjust_topology_and_space_dimension (Topology new_topology, dimension_type new_space_dim)
	Adjusts `this` so that it matches `new_topology` and `new_space_dim` (adding or removing columns if needed). Returns `false` if and only if `topol` is equal to `NECESSARILY_CLOSED` and `this` contains strict inequalities. More...

const Constraint &	operator[] (dimension_type k) const
	Returns a constant reference to the `k-` th constraint of the system. More...

bool	satisfies_all_constraints (const Generator &g) const
	Returns `true` if `g` satisfies all the constraints. More...

void	affine_preimage (Variable v, const Linear_Expression &expr, Coefficient_traits::const_reference denominator)
	Substitutes a given column of coefficients by a given affine expression. More...

void	insert_pending (const Constraint &c)
	Inserts in `*this` a copy of the constraint `c`, increasing the number of space dimensions if needed. It is a pending constraint. More...

void	add_low_level_constraints ()
	Adds low-level constraints to the constraint system. More...

Topology	topology () const
	Returns the system topology. More...

dimension_type	num_rows () const

bool	is_necessarily_closed () const
	Returns `true` if and only if the system topology is `NECESSARILY_CLOSED`. More...

dimension_type	num_pending_rows () const
	Returns the number of rows that are in the pending part of the system. More...

dimension_type	first_pending_row () const
	Returns the index of the first pending row. More...

bool	is_sorted () const
	Returns the value of the sortedness flag. More...

void	unset_pending_rows ()
	Sets the index to indicate that the system has no pending rows. More...

void	set_index_first_pending_row (dimension_type i)
	Sets the index of the first pending row to `i`. More...

void	set_sorted (bool b)
	Sets the sortedness flag of the system to `b`. More...

void	remove_row (dimension_type i, bool keep_sorted=false)
	Makes the system shrink by removing its i-th row. More...

void	remove_rows (const std::vector< dimension_type > &indexes)

void	remove_rows (dimension_type first, dimension_type last, bool keep_sorted=false)
	Makes the system shrink by removing the rows in [first,last). More...

void	remove_trailing_rows (dimension_type n)
	Makes the system shrink by removing its `n` trailing rows. More...

void	remove_space_dimensions (const Variables_Set &vars)
	Removes all the specified dimensions from the constraint system. More...

void	shift_space_dimensions (Variable v, dimension_type n)

void	permute_space_dimensions (const std::vector< Variable > &cycle)
	Permutes the space dimensions of the matrix. More...

void	swap_space_dimensions (Variable v1, Variable v2)
	Swaps the coefficients of the variables `v1` and `v2` . More...

bool	has_no_rows () const

void	strong_normalize ()
	Strongly normalizes the system. More...

void	sort_rows ()
	Sorts the non-pending rows (in growing order) and eliminates duplicated ones. More...

void	insert_pending (Constraint &r, Recycle_Input)
	Adds the given row to the pending part of the system, stealing its contents and automatically resizing the system or the row, if needed. More...

void	insert_pending (Constraint_System &r, Recycle_Input)

void	insert (Constraint &r, Recycle_Input)
	Adds `r` to the system, stealing its contents and automatically resizing the system or the row, if needed. More...

void	insert (Constraint_System &r, Recycle_Input)
	Adds to `*this` a the rows of `y', stealing them from `y'. More...

void	insert_pending (const Constraint_System &r)
	Adds a copy of the rows of `y' to the pending part of `*this'. More...

void	merge_rows_assign (const Constraint_System &y)
	Assigns to `*this` the result of merging its rows with those of `y`, obtaining a sorted system. More...

void	insert (const Constraint_System &y)
	Adds to `*this` a copy of the rows of `y`. More...

void	mark_as_necessarily_closed ()
	Marks the epsilon dimension as a standard dimension. More...

void	mark_as_not_necessarily_closed ()
	Marks the last dimension as the epsilon dimension. More...

dimension_type	gauss (dimension_type n_lines_or_equalities)
	Minimizes the subsystem of equations contained in `*this`. More...

void	back_substitute (dimension_type n_lines_or_equalities)
	Back-substitutes the coefficients to reduce the complexity of the system. More...

void	assign_with_pending (const Constraint_System &y)
	Full assignment operator: pending rows are copied as pending. More...

void	sort_pending_and_remove_duplicates ()
	Sorts the pending rows and eliminates those that also occur in the non-pending part of the system. More...

void	sort_and_remove_with_sat (Bit_Matrix &sat)
	Sorts the system, removing duplicates, keeping the saturation matrix consistent. More...

bool	check_sorted () const
	Returns `true` if and only if `*this` is sorted, without checking for duplicates. More...

dimension_type	num_lines_or_equalities () const
	Returns the number of rows in the system that represent either lines or equalities. More...

void	add_universe_rows_and_space_dimensions (dimension_type n)
	Adds `n` rows and space dimensions to the system. More...

Private Attributes
Linear_System< Constraint >	sys

Static Private Attributes
static const Constraint_System *	zero_dim_empty_p = 0
	Holds (between class initialization and finalization) a pointer to the singleton system containing only Constraint::zero_dim_false(). More...

Friends
class	Constraint_System_const_iterator

class	Polyhedron

class	Termination_Helpers

bool	operator== (const Constraint_System &x, const Constraint_System &y)

Related Functions
(Note that these are not member functions.)
std::ostream &	operator<< (std::ostream &s, const Constraint_System &cs)

std::ostream &	operator<< (std::ostream &s, const Constraint_System &cs)
	Output operator. More...

bool	operator== (const Constraint_System &x, const Constraint_System &y)
	Returns `true` if and only if `x` and `y` are identical. More...

bool	operator!= (const Constraint_System &x, const Constraint_System &y)
	Returns `true` if and only if `x` and `y` are different. More...

void	swap (Constraint_System &x, Constraint_System &y)

void	swap (Constraint_System &x, Constraint_System &y)

dimension_type	num_constraints (const Constraint_System &cs)

Detailed Description

A system of constraints.

An object of the class Constraint_System is a system of constraints, i.e., a multiset of objects of the class Constraint. When inserting constraints in a system, space dimensions are automatically adjusted so that all the constraints in the system are defined on the same vector space.

: In all the examples it is assumed that variables x and y are defined as follows:
Variable x(0);

Variable y(1);

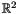Example 1: The following code builds a system of constraints corresponding to a square in $\Rset^2$ :
Constraint_System cs;

cs.insert(x >= 0);

cs.insert(x <= 3);

cs.insert(y >= 0);

cs.insert(y <= 3);

Note that: the constraint system is created with space dimension zero; the first and third constraint insertions increase the space dimension to 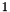and 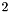, respectively.

Example 2: By adding four strict inequalities to the constraint system of the previous example, we can remove just the four vertices from the square defined above.
cs.insert(x + y > 0);

cs.insert(x + y < 6);

cs.insert(x - y < 3);

cs.insert(y - x < 3);

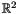Example 3: The following code builds a system of constraints corresponding to a half-strip in $\Rset^2$ :
Constraint_System cs;

cs.insert(x >= 0);

cs.insert(x - y <= 0);

cs.insert(x - y + 1 >= 0);

Note: After inserting a multiset of constraints in a constraint system, there are no guarantees that an exact copy of them can be retrieved: in general, only an equivalent constraint system will be available, where original constraints may have been reordered, removed (if they are trivial, duplicate or implied by other constraints), linearly combined, etc.

Definition at line 137 of file Constraint_System_defs.hh.

Member Typedef Documentation

typedef Constraint_System_const_iterator Parma_Polyhedra_Library::Constraint_System::const_iterator

Definition at line 214 of file Constraint_System_defs.hh.

typedef Constraint Parma_Polyhedra_Library::Constraint_System::row_type

Definition at line 139 of file Constraint_System_defs.hh.

Constructor & Destructor Documentation

Parma_Polyhedra_Library::Constraint_System::Constraint_System ( Representation r = default_representation )

inlineexplicit

Default constructor: builds an empty system of constraints.

Definition at line 32 of file Constraint_System_inlines.hh.

33 : sys(NECESSARILY_CLOSED, r) {

34 }

Parma_Polyhedra_Library::Constraint_System::sys

Linear_System< Constraint > sys

Definition: Constraint_System_defs.hh:257

Parma_Polyhedra_Library::NECESSARILY_CLOSED

Definition: Topology_types.hh:23

Parma_Polyhedra_Library::Constraint_System::Constraint_System	(	const Constraint &	c,
		Representation	r = `default_representation`
	)

inlineexplicit

Builds the singleton system containing only constraint c.

Definition at line 37 of file Constraint_System_inlines.hh.

References sys.

   : sys(c.topology(), r) {
   sys.insert(c);
 }

Parma_Polyhedra_Library::Constraint_System::Constraint_System	(	const Congruence_System &	cgs,
		Representation	r = `default_representation`
	)

explicit

Builds a system containing copies of any equalities in cgs.

Definition at line 40 of file Constraint_System.cc.

References Parma_Polyhedra_Library::Congruence_System::begin(), Parma_Polyhedra_Library::Congruence_System::end(), insert(), and OK().

   : sys(NECESSARILY_CLOSED, cgs.space_dimension(), r) {
   for (Congruence_System::const_iterator i = cgs.begin(),
          cgs_end = cgs.end(); i != cgs_end; ++i) {
     if (i->is_equality()) {
       Constraint tmp(*i);
       insert(tmp, Recycle_Input());
     }
   }
   PPL_ASSERT(OK());
 }

Parma_Polyhedra_Library::Constraint_System::Constraint_System ( const Constraint_System & cs )

inline

Ordinary copy constructor.

Note: The copy will have the same representation as `cs', to make it indistinguishable from `cs'.

Definition at line 43 of file Constraint_System_inlines.hh.

44 : sys(cs.sys) {

45 }

Parma_Polyhedra_Library::Constraint_System::sys

Linear_System< Constraint > sys

Definition: Constraint_System_defs.hh:257

Parma_Polyhedra_Library::Constraint_System::Constraint_System	(	const Constraint_System &	cs,
		Representation	r
	)

inline

Copy constructor with specified representation.

Definition at line 48 of file Constraint_System_inlines.hh.

50 : sys(cs.sys, r) {

51 }

Parma_Polyhedra_Library::Constraint_System::sys

Linear_System< Constraint > sys

Definition: Constraint_System_defs.hh:257

Parma_Polyhedra_Library::Constraint_System::~Constraint_System ( )

inline

Destructor.

Definition at line 66 of file Constraint_System_inlines.hh.

66 {

67 }

Parma_Polyhedra_Library::Constraint_System::Constraint_System	(	Topology	topol,
		Representation	r = `default_representation`
	)

inlineexplicitprivate

Builds an empty system of constraints having the specified topology.

Definition at line 54 of file Constraint_System_inlines.hh.

55 : sys(topol, r) {

56 }

Parma_Polyhedra_Library::Constraint_System::sys

Linear_System< Constraint > sys

Definition: Constraint_System_defs.hh:257

Parma_Polyhedra_Library::Constraint_System::Constraint_System	(	Topology	topol,
		dimension_type	space_dim,
		Representation	r = `default_representation`
	)

inlineprivate

Builds a system of constraints on a space_dim dimensional space. If topol is NOT_NECESSARILY_CLOSED the 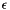$\epsilon$ dimension is added.

Definition at line 59 of file Constraint_System_inlines.hh.

62 : sys(topol, space_dim, r) {

63 }

Parma_Polyhedra_Library::Constraint_System::sys

Linear_System< Constraint > sys

Definition: Constraint_System_defs.hh:257

Member Function Documentation

void Parma_Polyhedra_Library::Constraint_System::add_low_level_constraints ( )

inlineprivate

Adds low-level constraints to the constraint system.

Definition at line 198 of file Constraint_System_inlines.hh.

References Parma_Polyhedra_Library::Constraint::epsilon_geq_zero(), Parma_Polyhedra_Library::Constraint::epsilon_leq_one(), insert(), sys, and Parma_Polyhedra_Library::Constraint::zero_dim_positivity().

Referenced by Parma_Polyhedra_Library::Polyhedron::Polyhedron().

                                              {
   if (sys.is_necessarily_closed()) {
     // The positivity constraint.
     insert(Constraint::zero_dim_positivity());
   }
   else {
     // Add the epsilon constraints.
     insert(Constraint::epsilon_leq_one());
     insert(Constraint::epsilon_geq_zero());
   }
 }

void Parma_Polyhedra_Library::Constraint_System::add_universe_rows_and_space_dimensions ( dimension_type n )

inlineprivate

Adds n rows and space dimensions to the system.

Parameters

n	The number of rows and space dimensions to be added: must be strictly positive.

Turns the system 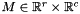$M \in \Rset^r \times \Rset^c$ into the system 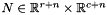$N \in \Rset^{r+n} \times \Rset^{c+n}$ such that 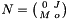$N = \bigl(\genfrac{}{}{0pt}{}{0}{M}\genfrac{}{}{0pt}{}{J}{o}\bigr)$ , where 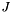$J$ is the specular image of the 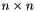$n \times n$ identity matrix.

Definition at line 406 of file Constraint_System_inlines.hh.

References sys.

                                                                           {
   sys.add_universe_rows_and_space_dimensions(n);
 }

bool Parma_Polyhedra_Library::Constraint_System::adjust_topology_and_space_dimension	(	Topology	new_topology,
		dimension_type	new_space_dim
	)

private

Adjusts *this so that it matches new_topology and new_space_dim (adding or removing columns if needed). Returns false if and only if topol is equal to NECESSARILY_CLOSED and *this contains strict inequalities.

Definition at line 55 of file Constraint_System.cc.

References Parma_Polyhedra_Library::NECESSARILY_CLOSED, and Parma_Polyhedra_Library::NOT_NECESSARILY_CLOSED.

Referenced by Parma_Polyhedra_Library::Polyhedron::add_recycled_constraints(), Parma_Polyhedra_Library::Polyhedron::constraints(), and Parma_Polyhedra_Library::Polyhedron::Polyhedron().

                                                                         {
   PPL_ASSERT(space_dimension() <= new_space_dim);
 
   if (sys.topology() == NOT_NECESSARILY_CLOSED
       && new_topology == NECESSARILY_CLOSED) {
     // A NOT_NECESSARILY_CLOSED constraint system
     // can be converted to a NECESSARILY_CLOSED one
     // only if it does not contain strict inequalities.
     if (has_strict_inequalities()) {
       return false;
     }
     // Since there were no strict inequalities,
     // the only constraints that may have a non-zero epsilon coefficient
     // are the eps-leq-one and the eps-geq-zero constraints.
     // If they are present, we erase these rows, so that the
     // epsilon column will only contain zeroes: as a consequence,
     // we just decrement the number of columns to be added.
     const bool was_sorted = sys.is_sorted();
 
     // Note that num_rows() is *not* constant, because it is decreased by
     // remove_row().
     for (dimension_type i = 0; i < num_rows(); ) {
       if (sys[i].epsilon_coefficient() != 0) {
         sys.remove_row(i, false);
       }
       else {
         ++i;
       }
     }
 
     // If `cs' was sorted we sort it again.
     if (was_sorted) {
       sys.sort_rows();
     }
   }
 
   sys.set_topology(new_topology);
   sys.set_space_dimension(new_space_dim);
 
   // We successfully adjusted space dimensions and topology.
   PPL_ASSERT(OK());
   return true;
 }

void Parma_Polyhedra_Library::Constraint_System::affine_preimage	(	Variable	v,
		const Linear_Expression &	expr,
		Coefficient_traits::const_reference	denominator
	)

private

Substitutes a given column of coefficients by a given affine expression.

Parameters

v	The variable to which the affine transformation is substituted.
expr	The numerator of the affine transformation: 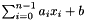$\sum_{i = 0}^{n - 1} a_i x_i + b$ ;
denominator	The denominator of the affine transformation.

We want to allow affine transformations (see Section Images and Preimages of Affine Transfer Relations) having any rational coefficients. Since the coefficients of the constraints are integers we must also provide an integer denominator that will be used as denominator of the affine transformation. The denominator is required to be a positive integer.

The affine transformation substitutes the matrix of constraints by a new matrix whose elements 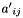${a'}_{ij}$ are built from the old one 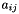$a_{ij}$ as follows:

${a'}_{ij} = \begin{cases} a_{ij} * \mathrm{denominator} + a_{iv} * \mathrm{expr}[j] \quad \text{for } j \neq v; \\ \mathrm{expr}[v] * a_{iv} \quad \text{for } j = v. \end{cases}$

expr is a constant parameter and unaltered by this computation.

Definition at line 327 of file Constraint_System.cc.

                                                                  {
   PPL_ASSERT(v.space_dimension() <= sys.space_dimension());
   PPL_ASSERT(expr.space_dimension() <= sys.space_dimension());
   PPL_ASSERT(denominator > 0);
 
   Coefficient_traits::const_reference expr_v = expr.coefficient(v);
 
   const dimension_type n_rows = sys.num_rows();
   const bool not_invertible = (v.space_dimension() > expr.space_dimension()
                                || expr_v == 0);
 
   for (dimension_type i = n_rows; i-- > 0; ) {
     Constraint& row = sys.rows[i];
     Coefficient_traits::const_reference row_v = row.coefficient(v);
     if (row_v != 0) {
       const Coefficient c = row_v;
       if (denominator != 1) {
         row.expr *= denominator;
       }
       row.expr.linear_combine(expr, 1, c, 0, expr.space_dimension() + 1);
       if (not_invertible) {
         row.expr.set_coefficient(v, Coefficient_zero());
       }
       else {
         row.expr.set_coefficient(v, c * expr_v);
       }
       row.strong_normalize();
       PPL_ASSERT(row.OK());
     }
   }
 
   // Strong normalization also resets the sortedness flag.
   sys.strong_normalize();
 
   PPL_ASSERT(sys.OK());
 }

void Parma_Polyhedra_Library::Constraint_System::ascii_dump ( std::ostream & s ) const

Writes to s an ASCII representation of *this.

Definition at line 367 of file Constraint_System.cc.

                                                     {
   sys.ascii_dump(s);
 }

void Parma_Polyhedra_Library::Constraint_System::ascii_dump ( ) const

Writes to std::cerr an ASCII representation of *this.

Referenced by Parma_Polyhedra_Library::PIP_Tree_Node::ascii_dump(), and Parma_Polyhedra_Library::Polyhedron::OK().

bool Parma_Polyhedra_Library::Constraint_System::ascii_load ( std::istream & s )

Loads from s an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets *this accordingly. Returns true if successful, false otherwise.

Definition at line 374 of file Constraint_System.cc.

Referenced by Parma_Polyhedra_Library::PIP_Tree_Node::ascii_load().

                                               {
   if (!sys.ascii_load(s)) {
     return false;
   }
 
   PPL_ASSERT(OK());
   return true;
 }

void Parma_Polyhedra_Library::Constraint_System::assign_with_pending ( const Constraint_System & y )

inlineprivate

Full assignment operator: pending rows are copied as pending.

Definition at line 381 of file Constraint_System_inlines.hh.

References sys.

Referenced by Parma_Polyhedra_Library::Polyhedron::Polyhedron().

                                                                  {
   sys.assign_with_pending(y.sys);
 }

void Parma_Polyhedra_Library::Constraint_System::back_substitute ( dimension_type n_lines_or_equalities )

inlineprivate

Back-substitutes the coefficients to reduce the complexity of the system.

Takes an upper triangular system having n_lines_or_equalities rows. For each row, starting from the one having the minimum number of coefficients different from zero, computes the expression of an element as a function of the remaining ones and then substitutes this expression in all the other rows.

Definition at line 376 of file Constraint_System_inlines.hh.

References sys.

                                                                        {
   sys.back_substitute(n_lines_or_equalities);
 }

Constraint_System_const_iterator Parma_Polyhedra_Library::Constraint_System::begin ( ) const

inline

Returns the const_iterator pointing to the first constraint, if *this is not empty; otherwise, returns the past-the-end const_iterator.

Definition at line 180 of file Constraint_System_inlines.hh.

References Parma_Polyhedra_Library::Constraint_System_const_iterator::skip_forward(), and sys.

                                {
   const_iterator i(sys.begin(), *this);
   i.skip_forward();
   return i;
 }

bool Parma_Polyhedra_Library::Constraint_System::check_sorted ( ) const

inlineprivate

Returns true if and only if *this is sorted, without checking for duplicates.

Definition at line 396 of file Constraint_System_inlines.hh.

References sys.

                                       {
   return sys.check_sorted();
 }

void Parma_Polyhedra_Library::Constraint_System::clear ( )

inline

Removes all the constraints from the constraint system and sets its space dimension to 0.

Definition at line 107 of file Constraint_System_inlines.hh.

References sys.

Referenced by Parma_Polyhedra_Library::Polyhedron::add_space_dimensions_and_embed(), Parma_Polyhedra_Library::Polyhedron::BHRZ03_combining_constraints(), Parma_Polyhedra_Library::Polyhedron::concatenate_assign(), Parma_Polyhedra_Library::Polyhedron::map_space_dimensions(), and Parma_Polyhedra_Library::Shape_Preserving_Reduction< D1, D2 >::product_reduce().

                          {
   sys.clear();
 }

bool Parma_Polyhedra_Library::Constraint_System::empty ( ) const

inline

Returns true if and only if *this has no constraints.

Definition at line 193 of file Constraint_System_inlines.hh.

References begin(), and end().

Referenced by Parma_Polyhedra_Library::BD_Shape< T >::BFT00_upper_bound_assign_if_exact(), Parma_Polyhedra_Library::PIP_Tree_Node::print_tree(), Parma_Polyhedra_Library::PIP_Solution_Node::print_tree(), Parma_Polyhedra_Library::PIP_Solution_Node::solve(), and Parma_Polyhedra_Library::PIP_Decision_Node::solve().

                                {
   return begin() == end();
 }

Constraint_System_const_iterator Parma_Polyhedra_Library::Constraint_System::end ( ) const

inline

Returns the past-the-end const_iterator.

Definition at line 187 of file Constraint_System_inlines.hh.

References sys.

                              {
   const Constraint_System_const_iterator i(sys.end(), *this);
   return i;
 }

memory_size_type Parma_Polyhedra_Library::Constraint_System::external_memory_in_bytes ( ) const

inline

Returns the size in bytes of the memory managed by *this.

Definition at line 216 of file Constraint_System_inlines.hh.

References sys.

Referenced by Parma_Polyhedra_Library::PIP_Tree_Node::external_memory_in_bytes(), and total_memory_in_bytes().

                                                   {
   return sys.external_memory_in_bytes();
 }

void Parma_Polyhedra_Library::Constraint_System::finalize ( )

static

Finalizes the class.

Definition at line 393 of file Constraint_System.cc.

Referenced by Parma_Polyhedra_Library::Init::~Init().

                                {
   PPL_ASSERT(zero_dim_empty_p != 0);
   delete zero_dim_empty_p;
   zero_dim_empty_p = 0;
 }

dimension_type Parma_Polyhedra_Library::Constraint_System::first_pending_row ( ) const

inlineprivate

Returns the index of the first pending row.

Definition at line 251 of file Constraint_System_inlines.hh.

References sys.

                                            {
   return sys.first_pending_row();
 }

dimension_type Parma_Polyhedra_Library::Constraint_System::gauss ( dimension_type n_lines_or_equalities )

inlineprivate

Minimizes the subsystem of equations contained in *this.

This method works only on the equalities of the system: the system is required to be partially sorted, so that all the equalities are grouped at its top; it is assumed that the number of equalities is exactly n_lines_or_equalities. The method finds a minimal system for the equalities and returns its rank, i.e., the number of linearly independent equalities. The result is an upper triangular subsystem of equalities: for each equality, the pivot is chosen starting from the right-most columns.

Definition at line 371 of file Constraint_System_inlines.hh.

References sys.

                                                              {
   return sys.gauss(n_lines_or_equalities);
 }

bool Parma_Polyhedra_Library::Constraint_System::has_equalities ( ) const

Returns true if and only if *this contains one or more equality constraints.

Definition at line 101 of file Constraint_System.cc.

Referenced by Parma_Polyhedra_Library::Implementation::Termination::assign_all_inequalities_approximation().

                                            {
   // We verify if the system has equalities also in the pending part.
   for (dimension_type i = sys.num_rows(); i-- > 0; ) {
     if (sys[i].is_equality()) {
       return true;
     }
   }
   return false;
 }

bool Parma_Polyhedra_Library::Constraint_System::has_no_rows ( ) const

inlineprivate

Definition at line 321 of file Constraint_System_inlines.hh.

References sys.

Referenced by Parma_Polyhedra_Library::Polyhedron::add_recycled_constraints(), Parma_Polyhedra_Library::Polyhedron::BHRZ03_widening_assign(), Parma_Polyhedra_Library::Polyhedron::H79_widening_assign(), and Parma_Polyhedra_Library::Polyhedron::refine_with_constraints().

                                      {
   return sys.has_no_rows();
 }

bool Parma_Polyhedra_Library::Constraint_System::has_strict_inequalities ( ) const

Returns true if and only if *this contains one or more strict inequality constraints.

Definition at line 112 of file Constraint_System.cc.

References c, Parma_Polyhedra_Library::Constraint::epsilon_coefficient(), and Parma_Polyhedra_Library::Constraint::is_tautological().

                                                     {
   if (sys.is_necessarily_closed()) {
     return false;
   }
   // We verify if the system has strict inequalities
   // also in the pending part.
   for (dimension_type i = sys.num_rows(); i-- > 0; ) {
     const Constraint& c = sys[i];
     // Optimized type checking: we already know the topology;
     // also, equalities have the epsilon coefficient equal to zero.
     // NOTE: the constraint eps_leq_one should not be considered
     //       a strict inequality.
     if (c.epsilon_coefficient() < 0 && !c.is_tautological()) {
       return true;
     }
   }
   return false;
 }

void Parma_Polyhedra_Library::Constraint_System::initialize ( )

static

Initializes the class.

Definition at line 386 of file Constraint_System.cc.

References Parma_Polyhedra_Library::Constraint::zero_dim_false().

Referenced by Parma_Polyhedra_Library::Init::Init().

                                  {
   PPL_ASSERT(zero_dim_empty_p == 0);
   zero_dim_empty_p
     = new Constraint_System(Constraint::zero_dim_false());
 }

void Parma_Polyhedra_Library::Constraint_System::insert ( const Constraint & c )

Inserts in *this a copy of the constraint c, increasing the number of space dimensions if needed.

Definition at line 132 of file Constraint_System.cc.

                                                 {
   Constraint tmp = r;
   insert(tmp, Recycle_Input());
 }

void Parma_Polyhedra_Library::Constraint_System::insert	(	Constraint &	r,
		Recycle_Input
	)

private

Adds r to the system, stealing its contents and automatically resizing the system or the row, if needed.

Definition at line 138 of file Constraint_System.cc.

References Parma_Polyhedra_Library::NECESSARILY_CLOSED, Parma_Polyhedra_Library::NOT_NECESSARILY_CLOSED, Parma_Polyhedra_Library::Constraint::set_topology(), and Parma_Polyhedra_Library::Constraint::topology().

                                                          {
   // We are sure that the matrix has no pending rows
   // and that the new row is not a pending constraint.
   PPL_ASSERT(sys.num_pending_rows() == 0);
 
   if (sys.topology() != c.topology()) {
     if (sys.topology() == NECESSARILY_CLOSED) {
       sys.set_topology(NOT_NECESSARILY_CLOSED);
     }
     else {
       c.set_topology(NOT_NECESSARILY_CLOSED);
     }
   }
 
   sys.insert(c, Recycle_Input());
 
   PPL_ASSERT(OK());
 }

void Parma_Polyhedra_Library::Constraint_System::insert	(	Constraint_System &	r,
		Recycle_Input
	)

inlineprivate

Adds to *this a the rows of `y', stealing them from `y'.

It is assumed that *this has no pending rows.

Definition at line 341 of file Constraint_System_inlines.hh.

References sys.

                                                              {
   sys.insert(r.sys, Recycle_Input());
 }

void Parma_Polyhedra_Library::Constraint_System::insert ( const Constraint_System & y )

inlineprivate

Adds to *this a copy of the rows of y.

It is assumed that *this has no pending rows.

Definition at line 356 of file Constraint_System_inlines.hh.

References sys.

                                                     {
   sys.insert(y.sys);
 }

void Parma_Polyhedra_Library::Constraint_System::insert_pending ( const Constraint & c )

private

Inserts in *this a copy of the constraint c, increasing the number of space dimensions if needed. It is a pending constraint.

Definition at line 158 of file Constraint_System.cc.

Referenced by Parma_Polyhedra_Library::Polyhedron::intersection_assign(), and Parma_Polyhedra_Library::Polyhedron::refine_with_constraints().

                                                         {
   Constraint tmp = r;
   insert_pending(tmp, Recycle_Input());
 }

void Parma_Polyhedra_Library::Constraint_System::insert_pending	(	Constraint &	r,
		Recycle_Input
	)

private

Adds the given row to the pending part of the system, stealing its contents and automatically resizing the system or the row, if needed.

Definition at line 164 of file Constraint_System.cc.

References Parma_Polyhedra_Library::NECESSARILY_CLOSED, Parma_Polyhedra_Library::NOT_NECESSARILY_CLOSED, Parma_Polyhedra_Library::Constraint::set_topology(), and Parma_Polyhedra_Library::Constraint::topology().

                                                                  {
   if (sys.topology() != c.topology()) {
     if (sys.topology() == NECESSARILY_CLOSED) {
       sys.set_topology(NOT_NECESSARILY_CLOSED);
     }
     else {
       c.set_topology(NOT_NECESSARILY_CLOSED);
     }
   }
 
   sys.insert_pending(c, Recycle_Input());
   PPL_ASSERT(OK());
 }

void Parma_Polyhedra_Library::Constraint_System::insert_pending	(	Constraint_System &	r,
		Recycle_Input
	)

inlineprivate

Adds the rows of `y' to the pending part of `*this', stealing them from `y'.

Definition at line 336 of file Constraint_System_inlines.hh.

References sys.

                                                                      {
   sys.insert_pending(r.sys, Recycle_Input());
 }

void Parma_Polyhedra_Library::Constraint_System::insert_pending ( const Constraint_System & r )

inlineprivate

Adds a copy of the rows of `y' to the pending part of `*this'.

Definition at line 346 of file Constraint_System_inlines.hh.

References sys.

                                                             {
   sys.insert_pending(r.sys);
 }

bool Parma_Polyhedra_Library::Constraint_System::is_necessarily_closed ( ) const

inlineprivate

Returns true if and only if the system topology is NECESSARILY_CLOSED.

Definition at line 241 of file Constraint_System_inlines.hh.

References sys.

Referenced by Parma_Polyhedra_Library::Polyhedron::is_necessarily_closed().

                                                {
   return sys.is_necessarily_closed();
 }

bool Parma_Polyhedra_Library::Constraint_System::is_sorted ( ) const

inlineprivate

Returns the value of the sortedness flag.

Definition at line 256 of file Constraint_System_inlines.hh.

References sys.

Referenced by Parma_Polyhedra_Library::Polyhedron::intersection_assign(), Parma_Polyhedra_Library::Polyhedron::obtain_sorted_constraints(), Parma_Polyhedra_Library::Polyhedron::obtain_sorted_constraints_with_sat_c(), and Parma_Polyhedra_Library::Polyhedron::process_pending_constraints().

                                    {
   return sys.is_sorted();
 }

void Parma_Polyhedra_Library::Constraint_System::m_swap ( Constraint_System & y )

inline

Swaps *this with y.

Definition at line 211 of file Constraint_System_inlines.hh.

References swap(), and sys.

Referenced by swap().

                                               {
   swap(sys, y.sys);
 }

void Parma_Polyhedra_Library::Constraint_System::mark_as_necessarily_closed ( )

inlineprivate

Marks the epsilon dimension as a standard dimension.

The system topology is changed to NOT_NECESSARILY_CLOSED, and the number of space dimensions is increased by 1.

Definition at line 361 of file Constraint_System_inlines.hh.

References sys.

Referenced by Parma_Polyhedra_Library::Polyhedron::strongly_minimize_constraints().

                                               {
   sys.mark_as_necessarily_closed();
 }

void Parma_Polyhedra_Library::Constraint_System::mark_as_not_necessarily_closed ( )

inlineprivate

Marks the last dimension as the epsilon dimension.

The system topology is changed to NECESSARILY_CLOSED, and the number of space dimensions is decreased by 1.

Definition at line 366 of file Constraint_System_inlines.hh.

References sys.

Referenced by Parma_Polyhedra_Library::Polyhedron::strongly_minimize_constraints().

                                                   {
   sys.mark_as_not_necessarily_closed();
 }

dimension_type Parma_Polyhedra_Library::Constraint_System::max_space_dimension ( )

inlinestatic

Returns the maximum space dimension a Constraint_System can handle.

Definition at line 92 of file Constraint_System_inlines.hh.

References Parma_Polyhedra_Library::Linear_System< Row >::max_space_dimension().

Referenced by Parma_Polyhedra_Library::Polyhedron::max_space_dimension().

                                        {
   return Linear_System<Constraint>::max_space_dimension();
 }

void Parma_Polyhedra_Library::Constraint_System::merge_rows_assign ( const Constraint_System & y )

inlineprivate

Assigns to *this the result of merging its rows with those of y, obtaining a sorted system.

Duplicated rows will occur only once in the result. On entry, both systems are assumed to be sorted and have no pending rows.

Definition at line 351 of file Constraint_System_inlines.hh.

References sys.

Referenced by Parma_Polyhedra_Library::Polyhedron::intersection_assign().

                                                                {
   sys.merge_rows_assign(y.sys);
 }

PPL::dimension_type Parma_Polyhedra_Library::Constraint_System::num_equalities ( ) const

private

Returns the number of equality constraints.

Definition at line 204 of file Constraint_System.cc.

Referenced by Parma_Polyhedra_Library::Polyhedron::H79_widening_assign(), Parma_Polyhedra_Library::Polyhedron::OK(), and Parma_Polyhedra_Library::Polyhedron::quick_equivalence_test().

                                            {
   // We are sure that we call this method only when
   // the matrix has no pending rows.
   PPL_ASSERT(sys.num_pending_rows() == 0);
   return sys.num_rows() - num_inequalities();
 }

PPL::dimension_type Parma_Polyhedra_Library::Constraint_System::num_inequalities ( ) const

private

Returns the number of inequality constraints.

Definition at line 179 of file Constraint_System.cc.

                                              {
   // We are sure that we call this method only when
   // the matrix has no pending rows.
   PPL_ASSERT(sys.num_pending_rows() == 0);
   const Constraint_System& cs = *this;
   dimension_type n = 0;
   // If the Base happens to be sorted, take advantage of the fact
   // that inequalities are at the bottom of the system.
   if (sys.is_sorted()) {
     for (dimension_type i = sys.num_rows();
          i > 0 && cs[--i].is_inequality(); ) {
       ++n;
     }
   }
   else {
     for (dimension_type i = sys.num_rows(); i-- > 0 ; ) {
       if (cs[i].is_inequality()) {
         ++n;
       }
     }
   }
   return n;
 }

dimension_type Parma_Polyhedra_Library::Constraint_System::num_lines_or_equalities ( ) const

inlineprivate

Returns the number of rows in the system that represent either lines or equalities.

Definition at line 401 of file Constraint_System_inlines.hh.

References sys.

                                                  {
   return sys.num_lines_or_equalities();
 }

dimension_type Parma_Polyhedra_Library::Constraint_System::num_pending_rows ( ) const

inlineprivate

Returns the number of rows that are in the pending part of the system.

Definition at line 246 of file Constraint_System_inlines.hh.

References sys.

Referenced by Parma_Polyhedra_Library::Polyhedron::Polyhedron(), Parma_Polyhedra_Library::Polyhedron::process_pending_constraints(), Parma_Polyhedra_Library::Polyhedron::simplified_constraints(), and Parma_Polyhedra_Library::Polyhedron::strongly_minimize_constraints().

                                           {
   return sys.num_pending_rows();
 }

dimension_type Parma_Polyhedra_Library::Constraint_System::num_rows ( ) const

inlineprivate

Definition at line 236 of file Constraint_System_inlines.hh.

References sys.

                                   {
   return sys.num_rows();
 }

bool Parma_Polyhedra_Library::Constraint_System::OK ( ) const

Checks if all the invariants are satisfied.

Definition at line 400 of file Constraint_System.cc.

Referenced by Constraint_System().

                                {
   return sys.OK();
 }

Constraint_System & Parma_Polyhedra_Library::Constraint_System::operator= ( const Constraint_System & y )

inline

Assignment operator.

Definition at line 70 of file Constraint_System_inlines.hh.

References swap().

                                                        {
   Constraint_System tmp = y;
   swap(*this, tmp);
   return *this;
 }

const Constraint & Parma_Polyhedra_Library::Constraint_System::operator[] ( dimension_type k ) const

inlineprivate

Returns a constant reference to the k- th constraint of the system.

Definition at line 77 of file Constraint_System_inlines.hh.

References sys.

                                                           {
   return sys[k];
 }

void Parma_Polyhedra_Library::Constraint_System::permute_space_dimensions ( const std::vector< Variable > & cycle )

inlineprivate

Permutes the space dimensions of the matrix.

Definition at line 310 of file Constraint_System_inlines.hh.

Referenced by Parma_Polyhedra_Library::Polyhedron::map_space_dimensions().

                                                            {
   sys.permute_space_dimensions(cycle);
 }

void Parma_Polyhedra_Library::Constraint_System::print ( ) const

Prints *this to std::cerr using operator<<.

void Parma_Polyhedra_Library::Constraint_System::remove_row	(	dimension_type	i,
		bool	keep_sorted = `false`
	)

inlineprivate

Makes the system shrink by removing its i-th row.

When keep_sorted is true and the system is sorted, sortedness will be preserved, but this method costs O(n).

Otherwise, this method just swaps the i-th row with the last and then removes it, so it costs O(1).

Definition at line 276 of file Constraint_System_inlines.hh.

References sys.

Referenced by Parma_Polyhedra_Library::Polyhedron::strongly_minimize_constraints().

                                                                 {
   sys.remove_row(i, keep_sorted);
 }

void Parma_Polyhedra_Library::Constraint_System::remove_rows ( const std::vector< dimension_type > & indexes )

inlineprivate

Removes the specified rows. The row ordering of remaining rows is preserved.

Parameters

indexes specifies a list of row indexes. It must be sorted.

Definition at line 287 of file Constraint_System_inlines.hh.

References sys.

                                                                        {
   sys.remove_rows(indexes);
 }

void Parma_Polyhedra_Library::Constraint_System::remove_rows	(	dimension_type	first,
		dimension_type	last,
		bool	keep_sorted = `false`
	)

inlineprivate

Makes the system shrink by removing the rows in [first,last).

When keep_sorted is true and the system is sorted, sortedness will be preserved, but this method costs O(num_rows()).

Otherwise, this method just swaps the rows with the last ones and then removes them, so it costs O(last - first).

Definition at line 281 of file Constraint_System_inlines.hh.

References sys.

                                                  {
   sys.remove_rows(first, last, keep_sorted);
 }

void Parma_Polyhedra_Library::Constraint_System::remove_space_dimensions ( const Variables_Set & vars )

inlineprivate

Removes all the specified dimensions from the constraint system.

The space dimension of the variable with the highest space dimension in vars must be at most the space dimension of this.

Definition at line 298 of file Constraint_System_inlines.hh.

                                                    {
   sys.remove_space_dimensions(vars);
 }

void Parma_Polyhedra_Library::Constraint_System::remove_trailing_rows ( dimension_type n )

inlineprivate

Makes the system shrink by removing its n trailing rows.

Definition at line 292 of file Constraint_System_inlines.hh.

References sys.

Referenced by Parma_Polyhedra_Library::Polyhedron::OK().

                                                         {
   sys.remove_trailing_rows(n);
 }

Representation Parma_Polyhedra_Library::Constraint_System::representation ( ) const

inline

Returns the current representation of *this.

Definition at line 82 of file Constraint_System_inlines.hh.

References sys.

                                         {
   return sys.representation();
 }

bool Parma_Polyhedra_Library::Constraint_System::satisfies_all_constraints ( const Generator & g ) const

private

Returns true if g satisfies all the constraints.

Definition at line 220 of file Constraint_System.cc.

                                                                         {
   PPL_ASSERT(g.space_dimension() <= space_dimension());
 
   // Setting `sps' to the appropriate scalar product sign operator.
   // This also avoids problems when having _legal_ topology mismatches
   // (which could also cause a mismatch in the number of columns).
   const Topology_Adjusted_Scalar_Product_Sign sps(g);
 
   if (sys.is_necessarily_closed()) {
     if (g.is_line()) {
       // Lines must saturate all constraints.
       for (dimension_type i = sys.num_rows(); i-- > 0; ) {
         if (sps(g, sys[i]) != 0) {
           return false;
         }
       }
     }
     else {
       // `g' is either a ray, a point or a closure point.
       for (dimension_type i = sys.num_rows(); i-- > 0; ) {
         const Constraint& c = sys[i];
         const int sp_sign = sps(g, c);
         if (c.is_inequality()) {
           // As `cs' is necessarily closed,
           // `c' is a non-strict inequality.
           if (sp_sign < 0) {
             return false;
           }
         }
         else {
           // `c' is an equality.
           if (sp_sign != 0) {
             return false;
           }
         }
       }
     }
   }
   else {
     // `cs' is not necessarily closed.
     switch (g.type()) {
 
     case Generator::LINE:
       // Lines must saturate all constraints.
       for (dimension_type i = sys.num_rows(); i-- > 0; ) {
         if (sps(g, sys[i]) != 0) {
           return false;
         }
       }
 
       break;
 
     case Generator::POINT:
       // Have to perform the special test
       // when dealing with a strict inequality.
       for (dimension_type i = sys.num_rows(); i-- > 0; ) {
         const Constraint& c = sys[i];
         const int sp_sign = sps(g, c);
         switch (c.type()) {
         case Constraint::EQUALITY:
           if (sp_sign != 0) {
             return false;
           }
           break;
         case Constraint::NONSTRICT_INEQUALITY:
           if (sp_sign < 0) {
             return false;
           }
           break;
         case Constraint::STRICT_INEQUALITY:
           if (sp_sign <= 0) {
             return false;
           }
           break;
         }
       }
       break;
 
     case Generator::RAY:
       // Intentionally fall through.
     case Generator::CLOSURE_POINT:
       for (dimension_type i = sys.num_rows(); i-- > 0; ) {
         const Constraint& c = sys[i];
         const int sp_sign = sps(g, c);
         if (c.is_inequality()) {
           // Constraint `c' is either a strict or a non-strict inequality.
           if (sp_sign < 0) {
             return false;
           }
         }
         else
           // Constraint `c' is an equality.
           if (sp_sign != 0) {
             return false;
           }
       }
       break;
     }
   }
 
   // If we reach this point, `g' satisfies all constraints.
   return true;
 }

void Parma_Polyhedra_Library::Constraint_System::set_index_first_pending_row ( dimension_type i )

inlineprivate

Sets the index of the first pending row to i.

Definition at line 266 of file Constraint_System_inlines.hh.

References sys.

                                                                {
   sys.set_index_first_pending_row(i);
 }

void Parma_Polyhedra_Library::Constraint_System::set_representation ( Representation r )

inline

Converts *this to the specified representation.

Definition at line 87 of file Constraint_System_inlines.hh.

References sys.

                                                       {
   sys.set_representation(r);
 }

void Parma_Polyhedra_Library::Constraint_System::set_sorted ( bool b )

inlineprivate

Sets the sortedness flag of the system to b.

Definition at line 271 of file Constraint_System_inlines.hh.

References sys.

Referenced by Parma_Polyhedra_Library::Polyhedron::obtain_sorted_constraints_with_sat_c(), Parma_Polyhedra_Library::Polyhedron::Polyhedron(), and Parma_Polyhedra_Library::Polyhedron::remove_pending_to_obtain_constraints().

                                     {
   sys.set_sorted(b);
 }

void Parma_Polyhedra_Library::Constraint_System::set_space_dimension ( dimension_type space_dim )

inline

Sets the space dimension of the rows in the system to space_dim .

Definition at line 102 of file Constraint_System_inlines.hh.

References sys.

Referenced by Parma_Polyhedra_Library::Polyhedron::add_space_dimensions_and_embed(), Parma_Polyhedra_Library::BD_Shape< T >::constraints(), Parma_Polyhedra_Library::Octagonal_Shape< T >::constraints(), Parma_Polyhedra_Library::Box< ITV >::constraints(), Parma_Polyhedra_Library::BD_Shape< T >::minimized_constraints(), Parma_Polyhedra_Library::Box< ITV >::minimized_constraints(), and Parma_Polyhedra_Library::Polyhedron::Polyhedron().

                                                                {
   return sys.set_space_dimension(space_dim);
 }

void Parma_Polyhedra_Library::Constraint_System::shift_space_dimensions	(	Variable	v,
		dimension_type	n
	)

inlineprivate

Shift by n positions the coefficients of variables, starting from the coefficient of v. This increases the space dimension by n.

Definition at line 304 of file Constraint_System_inlines.hh.

Referenced by Parma_Polyhedra_Library::Termination_Helpers::assign_all_inequalities_approximation().

                                                      {
   sys.shift_space_dimensions(v, n);
 }

void Parma_Polyhedra_Library::Constraint_System::simplify ( )

inlineprivate

Applies Gaussian elimination and back-substitution so as to provide a partial simplification of the system of constraints.

It is assumed that the system has no pending constraints.

Definition at line 226 of file Constraint_System_inlines.hh.

References sys.

Referenced by Parma_Polyhedra_Library::Polyhedron::OK(), and Parma_Polyhedra_Library::Polyhedron::simplified_constraints().

                             {
   sys.simplify();
 }

void Parma_Polyhedra_Library::Constraint_System::sort_and_remove_with_sat ( Bit_Matrix & sat )

inlineprivate

Sorts the system, removing duplicates, keeping the saturation matrix consistent.

Parameters

sat	Bit matrix with rows corresponding to the rows of `*this`.

Definition at line 391 of file Constraint_System_inlines.hh.

References sys.

Referenced by Parma_Polyhedra_Library::Polyhedron::obtain_sorted_constraints(), and Parma_Polyhedra_Library::Polyhedron::obtain_sorted_constraints_with_sat_c().

                                                            {
   sys.sort_and_remove_with_sat(sat);
 }

void Parma_Polyhedra_Library::Constraint_System::sort_pending_and_remove_duplicates ( )

inlineprivate

Sorts the pending rows and eliminates those that also occur in the non-pending part of the system.

Definition at line 386 of file Constraint_System_inlines.hh.

References sys.

Referenced by Parma_Polyhedra_Library::Polyhedron::process_pending_constraints().

                                                       {
   sys.sort_pending_and_remove_duplicates();
 }

void Parma_Polyhedra_Library::Constraint_System::sort_rows ( )

inlineprivate

Sorts the non-pending rows (in growing order) and eliminates duplicated ones.

Definition at line 331 of file Constraint_System_inlines.hh.

References sys.

Referenced by Parma_Polyhedra_Library::Polyhedron::obtain_sorted_constraints(), and Parma_Polyhedra_Library::Polyhedron::OK().

                              {
   sys.sort_rows();
 }

dimension_type Parma_Polyhedra_Library::Constraint_System::space_dimension ( ) const

inline

Returns the dimension of the vector space enclosing *this.

Definition at line 97 of file Constraint_System_inlines.hh.

References sys.

                                          {
   return sys.space_dimension();
 }

void Parma_Polyhedra_Library::Constraint_System::strong_normalize ( )

inlineprivate

Strongly normalizes the system.

Definition at line 326 of file Constraint_System_inlines.hh.

References sys.

Referenced by Parma_Polyhedra_Library::Polyhedron::OK().

                                     {
   sys.strong_normalize();
 }

void Parma_Polyhedra_Library::Constraint_System::swap_space_dimensions	(	Variable	v1,
		Variable	v2
	)

inlineprivate

Swaps the coefficients of the variables v1 and v2 .

Definition at line 316 of file Constraint_System_inlines.hh.

                                                 {
   sys.swap_space_dimensions(v1, v2);
 }

Topology Parma_Polyhedra_Library::Constraint_System::topology ( ) const

inlineprivate

Returns the system topology.

Definition at line 231 of file Constraint_System_inlines.hh.

References sys.

Referenced by Parma_Polyhedra_Library::Polyhedron::BHRZ03_combining_constraints(), Parma_Polyhedra_Library::Polyhedron::expand_space_dimension(), Parma_Polyhedra_Library::Polyhedron::select_CH78_constraints(), Parma_Polyhedra_Library::Polyhedron::select_H79_constraints(), and Parma_Polyhedra_Library::Polyhedron::topology().

                                   {
   return sys.topology();
 }

memory_size_type Parma_Polyhedra_Library::Constraint_System::total_memory_in_bytes ( ) const

inline

Returns the total size in bytes of the memory occupied by *this.

Definition at line 221 of file Constraint_System_inlines.hh.

References external_memory_in_bytes().

                                                {
   return external_memory_in_bytes() + sizeof(*this);
 }

void Parma_Polyhedra_Library::Constraint_System::unset_pending_rows ( )

inlineprivate

Sets the index to indicate that the system has no pending rows.

Definition at line 261 of file Constraint_System_inlines.hh.

References sys.

Referenced by Parma_Polyhedra_Library::Polyhedron::OK(), Parma_Polyhedra_Library::Polyhedron::Polyhedron(), Parma_Polyhedra_Library::Polyhedron::remove_pending_to_obtain_constraints(), and Parma_Polyhedra_Library::Polyhedron::simplified_constraints().

                                       {
   sys.unset_pending_rows();
 }

const Constraint_System & Parma_Polyhedra_Library::Constraint_System::zero_dim_empty ( )

inlinestatic

Returns the singleton system containing only Constraint::zero_dim_false().

Definition at line 112 of file Constraint_System_inlines.hh.

References zero_dim_empty_p.

Referenced by Parma_Polyhedra_Library::Polyhedron::constraints(), Parma_Polyhedra_Library::BD_Shape< T >::constraints(), Parma_Polyhedra_Library::Octagonal_Shape< T >::constraints(), Parma_Polyhedra_Library::Box< ITV >::constraints(), Parma_Polyhedra_Library::BD_Shape< T >::minimized_constraints(), and Parma_Polyhedra_Library::Box< ITV >::minimized_constraints().

                                   {
   PPL_ASSERT(zero_dim_empty_p != 0);
   return *zero_dim_empty_p;
 }

Friends And Related Function Documentation

friend class Constraint_System_const_iterator

friend

Definition at line 265 of file Constraint_System_defs.hh.

dimension_type num_constraints ( const Constraint_System & cs )

References begin(), and end().

                                              {
   return static_cast<dimension_type>(std::distance(cs.begin(), cs.end()));
 }

bool operator!=	(	const Constraint_System &	x,
		const Constraint_System &	y
	)

Definition at line 416 of file Constraint_System_inlines.hh.

                                                                    {
   return !(x == y);
 }

std::ostream & operator<<	(	std::ostream &	s,
		const Constraint_System &	cs
	)

Writes true if cs is empty. Otherwise, writes on s the constraints of cs, all in one row and separated by ", ".

std::ostream & operator<<	(	std::ostream &	s,
		const Constraint_System &	cs
	)

References begin(), and end().

                                                                       {
   Constraint_System_const_iterator i = cs.begin();
   const Constraint_System_const_iterator cs_end = cs.end();
   if (i == cs_end) {
     s << "true";
   }
   else {
     while (i != cs_end) {
       s << *i;
       ++i;
       if (i != cs_end) {
         s << ", ";
       }
     }
   }
   return s;
 }

bool operator==	(	const Constraint_System &	x,
		const Constraint_System &	y
	)

Definition at line 411 of file Constraint_System_inlines.hh.

                                                                    {
   return x.sys == y.sys;
 }

bool operator==	(	const Constraint_System &	x,
		const Constraint_System &	y
	)

friend

Definition at line 411 of file Constraint_System_inlines.hh.

                                                                    {
   return x.sys == y.sys;
 }

friend class Polyhedron

friend

Definition at line 588 of file Constraint_System_defs.hh.

void swap	(	Constraint_System &	x,
		Constraint_System &	y
	)

void swap	(	Constraint_System &	x,
		Constraint_System &	y
	)

References m_swap().

                                                  {
   x.m_swap(y);
 }

friend class Termination_Helpers

friend

Definition at line 589 of file Constraint_System_defs.hh.

Member Data Documentation

const Representation Parma_Polyhedra_Library::Constraint_System::default_representation = SPARSE

static

Definition at line 141 of file Constraint_System_defs.hh.

Linear_System<Constraint> Parma_Polyhedra_Library::Constraint_System::sys

private

Definition at line 257 of file Constraint_System_defs.hh.

Referenced by add_low_level_constraints(), add_universe_rows_and_space_dimensions(), assign_with_pending(), back_substitute(), begin(), check_sorted(), clear(), Parma_Polyhedra_Library::Polyhedron::concatenate_assign(), Constraint_System(), end(), external_memory_in_bytes(), first_pending_row(), gauss(), has_no_rows(), insert(), insert_pending(), is_necessarily_closed(), is_sorted(), m_swap(), mark_as_necessarily_closed(), mark_as_not_necessarily_closed(), merge_rows_assign(), num_lines_or_equalities(), num_pending_rows(), num_rows(), Parma_Polyhedra_Library::operator==(), operator[](), remove_row(), remove_rows(), remove_trailing_rows(), representation(), set_index_first_pending_row(), set_representation(), set_sorted(), set_space_dimension(), simplify(), sort_and_remove_with_sat(), sort_pending_and_remove_duplicates(), sort_rows(), space_dimension(), strong_normalize(), topology(), and unset_pending_rows().

const PPL::Constraint_System * Parma_Polyhedra_Library::Constraint_System::zero_dim_empty_p = 0

staticprivate

Holds (between class initialization and finalization) a pointer to the singleton system containing only Constraint::zero_dim_false().

Definition at line 263 of file Constraint_System_defs.hh.

Referenced by zero_dim_empty().

The documentation for this class was generated from the following files:

Public Types

Public Member Functions

Static Public Member Functions

Static Public Attributes

Private Member Functions

Private Attributes

Static Private Attributes

Friends

Related Functions

Detailed Description

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation

Friends And Related Function Documentation

Member Data Documentation