Parma_Polyhedra_Library::Linear_System< Row > Class Template Reference

The base class for systems of constraints and generators. More...

#include <Linear_System_defs.hh>

Inheritance diagram for Parma_Polyhedra_Library::Linear_System< Row >:

Collaboration diagram for Parma_Polyhedra_Library::Linear_System< Row >:

Classes
struct	Row_Less_Than
	Ordering predicate (used when implementing the sort algorithm). More...
struct	Unique_Compare
	Comparison predicate (used when implementing the unique algorithm). More...
struct	With_Pending
	A tag class. More...

Public Types
typedef Swapping_Vector< Row >::const_iterator	iterator
typedef Swapping_Vector< Row >::const_iterator	const_iterator

Public Member Functions
	Linear_System (Topology topol, Representation r)
	Builds an empty linear system with specified topology. More...
	Linear_System (Topology topol, dimension_type space_dim, Representation r)
	Builds a system with specified topology and dimensions. More...
	Linear_System (const Linear_System &y)
	Copy constructor: pending rows are transformed into non-pending ones. More...
	Linear_System (const Linear_System &y, Representation r)
	Linear_System (const Linear_System &y, With_Pending)
	Full copy constructor: pending rows are copied as pending. More...
	Linear_System (const Linear_System &y, Representation r, With_Pending)
	Full copy constructor: pending rows are copied as pending. More...
Linear_System &	operator= (const Linear_System &y)
	Assignment operator: pending rows are transformed into non-pending ones. More...
void	assign_with_pending (const Linear_System &y)
	Full assignment operator: pending rows are copied as pending. More...
void	m_swap (Linear_System &y)
	Swaps *this with y. More...
Representation	representation () const
	Returns the current representation of *this. More...
void	set_representation (Representation r)
	Converts *this to the specified representation. More...
dimension_type	space_dimension () const
	Returns the space dimension of the rows in the system. More...
void	set_space_dimension (dimension_type space_dim)
	Sets the space dimension of the rows in the system to space_dim . More...
void	remove_trailing_rows (dimension_type n)
	Makes the system shrink by removing its n trailing rows. More...
void	remove_row (dimension_type i, bool keep_sorted=false)
	Makes the system shrink by removing its i-th row. More...
void	remove_rows (dimension_type first, dimension_type last, bool keep_sorted=false)
	Makes the system shrink by removing the rows in [first,last). More...
void	remove_rows (const std::vector< dimension_type > &indexes)
void	remove_space_dimensions (const Variables_Set &vars)
	Removes all the specified dimensions from the system. More...
void	shift_space_dimensions (Variable v, dimension_type n)
void	permute_space_dimensions (const std::vector< Variable > &cycle)
	Permutes the space dimensions of the matrix. More...
void	swap_space_dimensions (Variable v1, Variable v2)
	Swaps the coefficients of the variables v1 and v2 . More...
iterator	begin ()
iterator	end ()
const_iterator	begin () const
const_iterator	end () const
bool	has_no_rows () const
dimension_type	num_rows () const
void	strong_normalize ()
	Strongly normalizes the system. More...
void	sign_normalize ()
	Sign-normalizes the system. More...
bool	check_sorted () const
	Returns true if and only if *this is sorted, without checking for duplicates. More...
void	set_topology (Topology t)
	Sets the system topology to t . More...
void	set_necessarily_closed ()
	Sets the system topology to NECESSARILY_CLOSED. More...
void	set_not_necessarily_closed ()
	Sets the system topology to NOT_NECESSARILY_CLOSED. More...
void	mark_as_necessarily_closed ()
	Marks the epsilon dimension as a standard dimension. More...
void	mark_as_not_necessarily_closed ()
	Marks the last dimension as the epsilon dimension. More...
void	unset_pending_rows ()
	Sets the index to indicate that the system has no pending rows. More...
void	set_index_first_pending_row (dimension_type i)
	Sets the index of the first pending row to i. More...
void	set_sorted (bool b)
	Sets the sortedness flag of the system to b. More...
void	add_universe_rows_and_space_dimensions (dimension_type n)
	Adds n rows and space dimensions to the system. More...
void	insert (const Row &r)
	Adds a copy of r to the system, automatically resizing the system or the row's copy, if needed. More...
void	insert_pending (const Row &r)
	Adds a copy of the given row to the pending part of the system, automatically resizing the system or the row, if needed. More...
void	insert (Row &r, Recycle_Input)
	Adds r to the system, stealing its contents and automatically resizing the system or the row, if needed. More...
void	insert_pending (Row &r, Recycle_Input)
	Adds the given row to the pending part of the system, stealing its contents and automatically resizing the system or the row, if needed. More...
void	insert (const Linear_System &y)
	Adds to *this a copy of the rows of y. More...
void	insert_pending (const Linear_System &r)
	Adds a copy of the rows of `y' to the pending part of `*this'. More...
void	insert (Linear_System &r, Recycle_Input)
	Adds to *this a the rows of `y', stealing them from `y'. More...
void	insert_pending (Linear_System &r, Recycle_Input)
void	sort_rows ()
	Sorts the non-pending rows (in growing order) and eliminates duplicated ones. More...
void	sort_rows (dimension_type first_row, dimension_type last_row)
	Sorts the rows (in growing order) form first_row to last_row and eliminates duplicated ones. More...
void	merge_rows_assign (const Linear_System &y)
	Assigns to *this the result of merging its rows with those of y, obtaining a sorted system. More...
void	sort_pending_and_remove_duplicates ()
	Sorts the pending rows and eliminates those that also occur in the non-pending part of the system. More...
void	sort_and_remove_with_sat (Bit_Matrix &sat)
	Sorts the system, removing duplicates, keeping the saturation matrix consistent. More...
dimension_type	gauss (dimension_type n_lines_or_equalities)
	Minimizes the subsystem of equations contained in *this. More...
void	back_substitute (dimension_type n_lines_or_equalities)
	Back-substitutes the coefficients to reduce the complexity of the system. More...
void	simplify ()
	Applies Gaussian elimination and back-substitution so as to simplify the linear system. More...
void	clear ()
	Clears the system deallocating all its rows. More...
void	ascii_dump () const
	Writes to std::cerr an ASCII representation of *this. More...
void	ascii_dump (std::ostream &s) const
	Writes to s an ASCII representation of *this. More...
void	print () const
	Prints *this to std::cerr using operator<<. More...
bool	ascii_load (std::istream &s)
	Loads from s an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets *this accordingly. Returns true if successful, false otherwise. More...
memory_size_type	total_memory_in_bytes () const
	Returns the total size in bytes of the memory occupied by *this. More...
memory_size_type	external_memory_in_bytes () const
	Returns the size in bytes of the memory managed by *this. More...
bool	OK () const
	Checks if all the invariants are satisfied. More...
Subscript operators
const Row &	operator[] (dimension_type k) const
	Returns a const reference to the k-th row of the system. More...
Accessors
Topology	topology () const
	Returns the system topology. More...
bool	is_sorted () const
	Returns the value of the sortedness flag. More...
bool	is_necessarily_closed () const
	Returns true if and only if the system topology is NECESSARILY_CLOSED. More...
dimension_type	num_lines_or_equalities () const
	Returns the number of rows in the system that represent either lines or equalities. More...
dimension_type	first_pending_row () const
	Returns the index of the first pending row. More...
dimension_type	num_pending_rows () const
	Returns the number of rows that are in the pending part of the system. More...

Static Public Member Functions
static dimension_type	max_space_dimension ()
	Returns the maximum space dimension a Linear_System can handle. More...

Public Attributes
Swapping_Vector< Row >	rows
	The vector that contains the rows. More...

Private Member Functions
void	remove_row_no_ok (dimension_type i, bool keep_sorted=false)
	Makes the system shrink by removing its i-th row. More...
void	insert_pending_no_ok (Row &r, Recycle_Input)
	Adds r to the pending part of the system, stealing its contents and automatically resizing the system or the row, if needed. More...
void	insert_no_ok (Row &r, Recycle_Input)
	Adds r to the system, stealing its contents and automatically resizing the system or the row, if needed. More...
void	set_space_dimension_no_ok (dimension_type space_dim)
	Sets the space dimension of the rows in the system to space_dim . More...
void	swap_row_intervals (dimension_type first, dimension_type last, dimension_type offset)

Private Attributes
dimension_type	space_dimension_
Topology	row_topology
dimension_type	index_first_pending
	The index of the first pending row. More...
bool	sorted
	true if rows are sorted in the ascending order as defined by bool compare(const Row&, const Row&). If false may not be sorted. More...
Representation	representation_

Friends
class	Polyhedron
class	Generator_System

Related Functions
(Note that these are not member functions.)
template<typename Row >
void	swap (Parma_Polyhedra_Library::Linear_System< Row > &x, Parma_Polyhedra_Library::Linear_System< Row > &y)
	Swaps x with y. More...
template<typename Row >
bool	operator== (const Linear_System< Row > &x, const Linear_System< Row > &y)
	Returns true if and only if x and y are identical. More...
template<typename Row >
bool	operator!= (const Linear_System< Row > &x, const Linear_System< Row > &y)
	Returns true if and only if x and y are different. More...
template<typename Row >
bool	operator!= (const Linear_System< Row > &x, const Linear_System< Row > &y)
template<typename Row >
void	swap (Linear_System< Row > &x, Linear_System< Row > &y)
template<typename Row >
bool	operator== (const Linear_System< Row > &x, const Linear_System< Row > &y)

Detailed Description

template<typename Row>
class Parma_Polyhedra_Library::Linear_System< Row >

The base class for systems of constraints and generators.

An object of this class represents either a constraint system or a generator system. Each Linear_System object can be viewed as a finite sequence of strong-normalized Row objects, where each Row implements a constraint or a generator. Linear systems are characterized by the matrix of coefficients, also encoding the number, size and capacity of Row objects, as well as a few additional information, including:

• the topological kind of (all) the rows;
• an indication of whether or not some of the rows in the Linear_System are pending, meaning that they still have to undergo an (unspecified) elaboration; if there are pending rows, then these form a proper suffix of the overall sequence of rows;
• a Boolean flag that, when true, ensures that the non-pending prefix of the sequence of rows is sorted.

Definition at line 61 of file Linear_System_defs.hh.

Member Typedef Documentation

template<typename Row>

typedef Swapping_Vector<Row>::const_iterator Parma_Polyhedra_Library::Linear_System< Row >::const_iterator

Definition at line 66 of file Linear_System_defs.hh.

template<typename Row>

typedef Swapping_Vector<Row>::const_iterator Parma_Polyhedra_Library::Linear_System< Row >::iterator

Definition at line 65 of file Linear_System_defs.hh.

Constructor & Destructor Documentation

template<typename Row >

Parma_Polyhedra_Library::Linear_System< Row >::Linear_System ( Topology  topol, Representation  r  )

inline

Builds an empty linear system with specified topology.

Rows size and capacity are initialized to .

Definition at line 66 of file Linear_System_inlines.hh.

References Parma_Polyhedra_Library::Linear_System< Row >::OK().

  : rows(),
    space_dimension_(0),
    row_topology(topol),
    index_first_pending(0),
    sorted(true),
    representation_(r) {

  PPL_ASSERT(OK());
}

template<typename Row >

Parma_Polyhedra_Library::Linear_System< Row >::Linear_System ( Topology  topol, dimension_type  space_dim, Representation  r  )

inline

Builds a system with specified topology and dimensions.

Parameters

topol	The topology of the system that will be created;
space_dim	The number of space dimensions of the system that will be created.
r	The representation for system's rows.

Creates a n_rows space_dim system whose coefficients are all zero and with the given topology.

Definition at line 79 of file Linear_System_inlines.hh.

References Parma_Polyhedra_Library::Linear_System< Row >::OK(), and Parma_Polyhedra_Library::Linear_System< Row >::set_space_dimension().

  : rows(),
    space_dimension_(0),
    row_topology(topol),
    index_first_pending(0),
    sorted(true),
    representation_(r) {
  set_space_dimension(space_dim);
  PPL_ASSERT(OK());
}

template<typename Row >

Parma_Polyhedra_Library::Linear_System< Row >::Linear_System ( const Linear_System< Row > &  y )

inline

Copy constructor: pending rows are transformed into non-pending ones.

Definition at line 121 of file Linear_System_inlines.hh.

References Parma_Polyhedra_Library::Linear_System< Row >::num_pending_rows(), Parma_Polyhedra_Library::Linear_System< Row >::OK(), Parma_Polyhedra_Library::Linear_System< Row >::sorted, and Parma_Polyhedra_Library::Linear_System< Row >::unset_pending_rows().

  : rows(y.rows),
    space_dimension_(y.space_dimension_),
    row_topology(y.row_topology),
    representation_(y.representation_) {
  // Previously pending rows may violate sortedness.
  sorted = (y.num_pending_rows() > 0) ? false : y.sorted;
  unset_pending_rows();
  PPL_ASSERT(OK());
}

template<typename Row >

Parma_Polyhedra_Library::Linear_System< Row >::Linear_System ( const Linear_System< Row > &  y, Representation  r  )

inline

Copy constructor with specified representation. Pending rows are transformed into non-pending ones.

Definition at line 134 of file Linear_System_inlines.hh.

References Parma_Polyhedra_Library::Linear_System< Row >::num_pending_rows(), Parma_Polyhedra_Library::Linear_System< Row >::num_rows(), Parma_Polyhedra_Library::Linear_System< Row >::OK(), Parma_Polyhedra_Library::Swapping_Vector< T >::resize(), Parma_Polyhedra_Library::Linear_System< Row >::rows, Parma_Polyhedra_Library::Linear_System< Row >::sorted, Parma_Polyhedra_Library::Linear_System< Row >::swap(), and Parma_Polyhedra_Library::Linear_System< Row >::unset_pending_rows().

  : rows(),
    space_dimension_(y.space_dimension_),
    row_topology(y.row_topology),
    representation_(r) {
  rows.resize(y.num_rows());
  for (dimension_type i = 0; i < y.num_rows(); ++i) {
    // Create the copies with the right representation.
    Row row(y.rows[i], r);
    swap(rows[i], row);
  }
  // Previously pending rows may violate sortedness.
  sorted = (y.num_pending_rows() > 0) ? false : y.sorted;
  unset_pending_rows();
  PPL_ASSERT(OK());
}

template<typename Row >

Parma_Polyhedra_Library::Linear_System< Row >::Linear_System ( const Linear_System< Row > &  y, With_Pending    )

inline

Full copy constructor: pending rows are copied as pending.

Definition at line 153 of file Linear_System_inlines.hh.

References Parma_Polyhedra_Library::Linear_System< Row >::OK().

  : rows(y.rows),
    space_dimension_(y.space_dimension_),
    row_topology(y.row_topology),
    index_first_pending(y.index_first_pending),
    sorted(y.sorted),
    representation_(y.representation_) {
  PPL_ASSERT(OK());
}

template<typename Row >

Parma_Polyhedra_Library::Linear_System< Row >::Linear_System ( const Linear_System< Row > &  y, Representation  r, With_Pending    )

inline

Full copy constructor: pending rows are copied as pending.

Definition at line 165 of file Linear_System_inlines.hh.

References Parma_Polyhedra_Library::Linear_System< Row >::num_rows(), Parma_Polyhedra_Library::Linear_System< Row >::OK(), Parma_Polyhedra_Library::Swapping_Vector< T >::resize(), Parma_Polyhedra_Library::Linear_System< Row >::rows, and Parma_Polyhedra_Library::Linear_System< Row >::swap().

  : rows(),
    space_dimension_(y.space_dimension_),
    row_topology(y.row_topology),
    index_first_pending(y.index_first_pending),
    sorted(y.sorted),
    representation_(r) {
  rows.resize(y.num_rows());
  for (dimension_type i = 0; i < y.num_rows(); ++i) {
    // Create the copies with the right representation.
    Row row(y.rows[i], r);
    swap(rows[i], row);
  }
  PPL_ASSERT(OK());
}

Member Function Documentation

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::add_universe_rows_and_space_dimensions

(

dimension_type

n

)

Adds n rows and space dimensions to the system.

Parameters

n	The number of rows and space dimensions to be added: must be strictly positive.

Turns the system 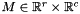into the system 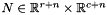such that 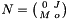, where 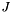is the specular image of the 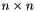identity matrix.

Definition at line 779 of file Linear_System_templates.hh.

References c, Parma_Polyhedra_Library::compare(), Parma_Polyhedra_Library::Boundary_NS::le(), Parma_Polyhedra_Library::NECESSARILY_CLOSED, Parma_Polyhedra_Library::NOT_NECESSARILY_CLOSED, Parma_Polyhedra_Library::Linear_Expression::set_space_dimension(), and Parma_Polyhedra_Library::swap().

                                                               {
  PPL_ASSERT(n > 0);
  const bool was_sorted = is_sorted();
  const dimension_type old_n_rows = num_rows();
  const dimension_type old_space_dim
    = is_necessarily_closed() ? space_dimension() : space_dimension() + 1;
  set_space_dimension(space_dimension() + n);
  rows.resize(rows.size() + n);
  // The old system is moved to the bottom.
  for (dimension_type i = old_n_rows; i-- > 0; ) {
    swap(rows[i], rows[i + n]);
  }
  for (dimension_type i = n, c = old_space_dim; i-- > 0; ) {
    // The top right-hand sub-system (i.e., the system made of new
    // rows and columns) is set to the specular image of the identity
    // matrix.
    if (Variable(c).space_dimension() <= space_dimension()) {
      // Variable(c) is a user variable.
      Linear_Expression le(representation());
      le.set_space_dimension(space_dimension());
      le += Variable(c);
      Row r(le, Row::LINE_OR_EQUALITY, row_topology);
      swap(r, rows[i]);
    }
    else {
      // Variable(c) is the epsilon dimension.
      PPL_ASSERT(row_topology == NOT_NECESSARILY_CLOSED);
      Linear_Expression le(Variable(c), representation());
      Row r(le, Row::LINE_OR_EQUALITY, NECESSARILY_CLOSED);
      r.mark_as_not_necessarily_closed();
      swap(r, rows[i]);
      // Note: `r' is strongly normalized.
    }
    ++c;
  }
  // If the old system was empty, the last row added is either
  // a positivity constraint or a point.
  if (was_sorted) {
    sorted = (compare(rows[n-1], rows[n]) <= 0);
  }

  // If the system is not necessarily closed, move the epsilon coefficients to
  // the last column.
  if (!is_necessarily_closed()) {
    // Try to preserve sortedness of `gen_sys'.
    PPL_ASSERT(old_space_dim != 0);
    if (!is_sorted()) {
      for (dimension_type i = n; i-- > 0; ) {
        rows[i].expr.swap_space_dimensions(Variable(old_space_dim - 1),
                                           Variable(old_space_dim - 1 + n));
        PPL_ASSERT(rows[i].OK());
      }
    }
    else {
      dimension_type old_eps_index = old_space_dim - 1;
      // The upper-right corner of `rows' contains the J matrix:
      // swap coefficients to preserve sortedness.
      for (dimension_type i = n; i-- > 0; ++old_eps_index) {
        rows[i].expr.swap_space_dimensions(Variable(old_eps_index),
                                           Variable(old_eps_index + 1));
        PPL_ASSERT(rows[i].OK());
      }

      sorted = true;
    }
  }
  // NOTE: this already checks for OK().
  set_index_first_pending_row(index_first_pending + n);
}

template<typename Row>

void Parma_Polyhedra_Library::Linear_System< Row >::ascii_dump

(

)

const

Writes to std::cerr an ASCII representation of *this.

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::ascii_dump

(

std::ostream &

s

)

const

Writes to s an ASCII representation of *this.

Definition at line 119 of file Linear_System_templates.hh.

References Parma_Polyhedra_Library::ascii_dump().

                                                  {
  // Prints the topology, the number of rows, the number of columns
  // and the sorted flag.  The specialized methods provided by
  // Constraint_System and Generator_System take care of properly
  // printing the contents of the system.
  s << "topology " << (is_necessarily_closed()
                       ? "NECESSARILY_CLOSED"
                       : "NOT_NECESSARILY_CLOSED")
    << "\n"
    << num_rows() << " x " << space_dimension() << " ";
  Parma_Polyhedra_Library::ascii_dump(s, representation());
  s << " " << (sorted ? "(sorted)" : "(not_sorted)")
    << "\n"
    << "index_first_pending " << first_pending_row()
    << "\n";
  for (dimension_type i = 0; i < rows.size(); ++i) {
    rows[i].ascii_dump(s);
  }
}

template<typename Row >

bool Parma_Polyhedra_Library::Linear_System< Row >::ascii_load

(

std::istream &

s

)

Loads from s an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets *this accordingly. Returns true if successful, false otherwise.

Reads into a Linear_System object the information produced by the output of ascii_dump(std::ostream&) const. The specialized methods provided by Constraint_System and Generator_System take care of properly reading the contents of the system.

Definition at line 143 of file Linear_System_templates.hh.

References Parma_Polyhedra_Library::ascii_load(), Parma_Polyhedra_Library::NECESSARILY_CLOSED, and Parma_Polyhedra_Library::NOT_NECESSARILY_CLOSED.

                                            {
  std::string str;
  if (!(s >> str) || str != "topology") {
    return false;
  }
  if (!(s >> str)) {
    return false;
  }

  clear();

  Topology t;
  if (str == "NECESSARILY_CLOSED") {
    t = NECESSARILY_CLOSED;
  }
  else {
    if (str != "NOT_NECESSARILY_CLOSED") {
      return false;
    }
    t = NOT_NECESSARILY_CLOSED;
  }

  set_topology(t);

  dimension_type nrows;
  dimension_type space_dims;
  if (!(s >> nrows)) {
    return false;
  }
  if (!(s >> str) || str != "x") {
    return false;
  }
  if (!(s >> space_dims)) {
    return false;
  }

  space_dimension_ = space_dims;

  if (!Parma_Polyhedra_Library::ascii_load(s, representation_)) {
    return false;
  }

  if (!(s >> str) || (str != "(sorted)" && str != "(not_sorted)")) {
    return false;
  }
  const bool sortedness = (str == "(sorted)");
  dimension_type index;
  if (!(s >> str) || str != "index_first_pending") {
    return false;
  }
  if (!(s >> index)) {
    return false;
  }

  Row row;
  for (dimension_type i = 0; i < nrows; ++i) {
    if (!row.ascii_load(s)) {
      return false;
    }
    insert(row, Recycle_Input());
  }
  index_first_pending = index;
  sorted = sortedness;

  // Check invariants.
  PPL_ASSERT(OK());
  return true;
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::assign_with_pending ( const Linear_System< Row > &  y )

inline

Full assignment operator: pending rows are copied as pending.

Definition at line 193 of file Linear_System_inlines.hh.

References Parma_Polyhedra_Library::swap().

                                                              {
  Linear_System<Row> tmp(y, With_Pending());
  swap(*this, tmp);
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::back_substitute

(

dimension_type

n_lines_or_equalities

)

Back-substitutes the coefficients to reduce the complexity of the system.

Takes an upper triangular system having n_lines_or_equalities rows. For each row, starting from the one having the minimum number of coefficients different from zero, computes the expression of an element as a function of the remaining ones and then substitutes this expression in all the other rows.

Definition at line 628 of file Linear_System_templates.hh.

References Parma_Polyhedra_Library::compare(), and Parma_Polyhedra_Library::neg_assign().

                                                            {
  // This method is only applied to a system having no pending rows and
  // exactly `n_lines_or_equalities' lines or equalities, all of which occur
  // before the first ray or point or inequality.
  PPL_ASSERT(num_pending_rows() == 0);
  PPL_ASSERT(n_lines_or_equalities <= num_lines_or_equalities());
#ifndef NDEBUG
  for (dimension_type i = n_lines_or_equalities; i-- > 0; ) {
    PPL_ASSERT((*this)[i].is_line_or_equality());
  }
#endif

  const dimension_type nrows = num_rows();
  // Trying to keep sortedness.
  bool still_sorted = is_sorted();
  // This deque of Booleans will be used to flag those rows that,
  // before exiting, need to be re-checked for sortedness.
  std::deque<bool> check_for_sortedness;
  if (still_sorted) {
    check_for_sortedness.insert(check_for_sortedness.end(), nrows, false);
  }

  for (dimension_type k = n_lines_or_equalities; k-- > 0; ) {
    // For each line or equality, starting from the last one,
    // looks for the last non-zero element.
    // `j' will be the index of such a element.
    Row& row_k = rows[k];
    const dimension_type j = row_k.expr.last_nonzero();
    // TODO: Check this.
    PPL_ASSERT(j != 0);

    // Go through the equalities above `row_k'.
    for (dimension_type i = k; i-- > 0; ) {
      Row& row_i = rows[i];
      if (row_i.expr.get(Variable(j - 1)) != 0) {
        // Combine linearly `row_i' with `row_k'
        // so that `row_i[j]' becomes zero.
        row_i.linear_combine(row_k, j);
        if (still_sorted) {
          // Trying to keep sortedness: remember which rows
          // have to be re-checked for sortedness at the end.
          if (i > 0) {
            check_for_sortedness[i-1] = true;
          }
          check_for_sortedness[i] = true;
        }
      }
    }

    // Due to strong normalization during previous iterations,
    // the pivot coefficient `row_k[j]' may now be negative.
    // Since an inequality (or ray or point) cannot be multiplied
    // by a negative factor, the coefficient of the pivot must be
    // forced to be positive.
    const bool have_to_negate = (row_k.expr.get(Variable(j - 1)) < 0);
    if (have_to_negate) {
      neg_assign(row_k.expr);
    }

    // NOTE: Here row_k will *not* be ok if we have negated it.

    // Note: we do not mark index `k' in `check_for_sortedness',
    // because we will later negate back the row.

    // Go through all the other rows of the system.
    for (dimension_type i = n_lines_or_equalities; i < nrows; ++i) {
      Row& row_i = rows[i];
      if (row_i.expr.get(Variable(j - 1)) != 0) {
        // Combine linearly the `row_i' with `row_k'
        // so that `row_i[j]' becomes zero.
        row_i.linear_combine(row_k, j);
        if (still_sorted) {
          // Trying to keep sortedness: remember which rows
          // have to be re-checked for sortedness at the end.
          if (i > n_lines_or_equalities) {
            check_for_sortedness[i-1] = true;
          }
          check_for_sortedness[i] = true;
        }
      }
    }
    if (have_to_negate) {
      // Negate `row_k' to restore strong-normalization.
      neg_assign(row_k.expr);
    }

    PPL_ASSERT(row_k.OK());
  }

  // Trying to keep sortedness.
  for (dimension_type i = 0; still_sorted && i+1 < nrows; ++i) {
    if (check_for_sortedness[i]) {
      // Have to check sortedness of `(*this)[i]' with respect to `(*this)[i+1]'.
      still_sorted = (compare((*this)[i], (*this)[i+1]) <= 0);
    }
  }

  // Set the sortedness flag.
  sorted = still_sorted;

  PPL_ASSERT(OK());
}

template<typename Row >

Linear_System< Row >::iterator Parma_Polyhedra_Library::Linear_System< Row >::begin ( )

inline

Definition at line 286 of file Linear_System_inlines.hh.

                          {
  return rows.begin();
}

template<typename Row >

Linear_System< Row >::const_iterator Parma_Polyhedra_Library::Linear_System< Row >::begin ( ) const

inline

Definition at line 298 of file Linear_System_inlines.hh.

                                {
  return rows.begin();
}

template<typename Row >

bool Parma_Polyhedra_Library::Linear_System< Row >::check_sorted

(

)

const

Returns true if and only if *this is sorted, without checking for duplicates.

Definition at line 912 of file Linear_System_templates.hh.

References Parma_Polyhedra_Library::compare().

Referenced by Parma_Polyhedra_Library::Linear_System< Row >::merge_rows_assign().

                                       {
  for (dimension_type i = first_pending_row(); i-- > 1; ) {
    if (compare(rows[i], rows[i-1]) < 0) {
      return false;
    }
  }
  return true;
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::clear ( )

inline

Clears the system deallocating all its rows.

Definition at line 214 of file Linear_System_inlines.hh.

Referenced by Parma_Polyhedra_Library::Linear_System< Row >::insert_pending().

                          {
  // Note: do NOT modify the value of `row_topology' and `representation'.
  rows.clear();
  index_first_pending = 0;
  sorted = true;
  space_dimension_ = 0;

  PPL_ASSERT(OK());
}

template<typename Row >

Linear_System< Row >::iterator Parma_Polyhedra_Library::Linear_System< Row >::end ( )

inline

Definition at line 292 of file Linear_System_inlines.hh.

                        {
  return rows.end();
}

template<typename Row >

Linear_System< Row >::const_iterator Parma_Polyhedra_Library::Linear_System< Row >::end ( ) const

inline

Definition at line 304 of file Linear_System_inlines.hh.

                              {
  return rows.end();
}

template<typename Row >

memory_size_type Parma_Polyhedra_Library::Linear_System< Row >::external_memory_in_bytes ( ) const

inline

Returns the size in bytes of the memory managed by *this.

Definition at line 36 of file Linear_System_inlines.hh.

                                                   {
  return rows.external_memory_in_bytes();
}

template<typename Row >

dimension_type Parma_Polyhedra_Library::Linear_System< Row >::first_pending_row ( ) const

inline

Returns the index of the first pending row.

Definition at line 94 of file Linear_System_inlines.hh.

Referenced by Parma_Polyhedra_Library::Linear_System< Row >::operator==().

                                            {
  return index_first_pending;
}

template<typename Row >

dimension_type Parma_Polyhedra_Library::Linear_System< Row >::gauss

(

dimension_type

n_lines_or_equalities

)

Minimizes the subsystem of equations contained in *this.

This method works only on the equalities of the system: the system is required to be partially sorted, so that all the equalities are grouped at its top; it is assumed that the number of equalities is exactly n_lines_or_equalities. The method finds a minimal system for the equalities and returns its rank, i.e., the number of linearly independent equalities. The result is an upper triangular subsystem of equalities: for each equality, the pivot is chosen starting from the right-most space dimensions.

Definition at line 567 of file Linear_System_templates.hh.

References Parma_Polyhedra_Library::swap().

                                                                    {
  // This method is only applied to a linear system having no pending rows and
  // exactly `n_lines_or_equalities' lines or equalities, all of which occur
  // before the rays or points or inequalities.
  PPL_ASSERT(num_pending_rows() == 0);
  PPL_ASSERT(n_lines_or_equalities == num_lines_or_equalities());
#ifndef NDEBUG
  for (dimension_type i = n_lines_or_equalities; i-- > 0; ) {
    PPL_ASSERT((*this)[i].is_line_or_equality());
  }
#endif

  dimension_type rank = 0;
  // Will keep track of the variations on the system of equalities.
  bool changed = false;
  // TODO: Don't use the number of columns.
  const dimension_type num_cols
    = is_necessarily_closed() ? space_dimension() + 1 : space_dimension() + 2;
  // TODO: Consider exploiting the row (possible) sparseness of rows in the
  // following loop, if needed. It would probably make it more cache-efficient
  // for dense rows, too.
  for (dimension_type j = num_cols; j-- > 0; ) {
    for (dimension_type i = rank; i < n_lines_or_equalities; ++i) {
      // Search for the first row having a non-zero coefficient
      // (the pivot) in the j-th column.
      if ((*this)[i].expr.get(j) == 0) {
        continue;
      }
      // Pivot found: if needed, swap rows so that this one becomes
      // the rank-th row in the linear system.
      if (i > rank) {
        swap(rows[i], rows[rank]);
        // After swapping the system is no longer sorted.
        changed = true;
      }
      // Combine the row containing the pivot with all the lines or
      // equalities following it, so that all the elements on the j-th
      // column in these rows become 0.
      for (dimension_type k = i + 1; k < n_lines_or_equalities; ++k) {
        if (rows[k].expr.get(Variable(j - 1)) != 0) {
          rows[k].linear_combine(rows[rank], j);
          changed = true;
        }
      }
      // Already dealt with the rank-th row.
      ++rank;
      // Consider another column index `j'.
      break;
    }
  }
  if (changed) {
    sorted = false;
  }

  PPL_ASSERT(OK());
  return rank;
}

template<typename Row >

bool Parma_Polyhedra_Library::Linear_System< Row >::has_no_rows ( ) const

inline

Definition at line 310 of file Linear_System_inlines.hh.

Referenced by Parma_Polyhedra_Library::Linear_System< Row >::insert().

                                      {
  return rows.empty();
}

template<typename Row>

void Parma_Polyhedra_Library::Linear_System< Row >::insert

(

const Row &

r

)

Adds a copy of r to the system, automatically resizing the system or the row's copy, if needed.

Definition at line 214 of file Linear_System_templates.hh.

                                       {
  Row tmp(r, representation());
  insert(tmp, Recycle_Input());
}

template<typename Row>

void Parma_Polyhedra_Library::Linear_System< Row >::insert	(	Row &	r,
		Recycle_Input
	)

Adds r to the system, stealing its contents and automatically resizing the system or the row, if needed.

Definition at line 221 of file Linear_System_templates.hh.

                                                {
  insert_no_ok(r, Recycle_Input());
  PPL_ASSERT(OK());
}

template<typename Row>

void Parma_Polyhedra_Library::Linear_System< Row >::insert

(

const Linear_System< Row > &

y

)

Adds to *this a copy of the rows of y.

It is assumed that *this has no pending rows.

Definition at line 323 of file Linear_System_templates.hh.

                                                 {
  Linear_System tmp(y, representation(), With_Pending());
  insert(tmp, Recycle_Input());
}

template<typename Row>

void Parma_Polyhedra_Library::Linear_System< Row >::insert	(	Linear_System< Row > &	r,
		Recycle_Input
	)

Adds to *this a the rows of `y', stealing them from `y'.

It is assumed that *this has no pending rows.

Definition at line 330 of file Linear_System_templates.hh.

References Parma_Polyhedra_Library::compare(), Parma_Polyhedra_Library::Linear_System< Row >::has_no_rows(), Parma_Polyhedra_Library::Linear_System< Row >::is_sorted(), and Parma_Polyhedra_Library::Linear_System< Row >::num_pending_rows().

                                                          {
  PPL_ASSERT(num_pending_rows() == 0);

  // Adding no rows is a no-op.
  if (y.has_no_rows()) {
    return;
  }

  // Check if sortedness is preserved.
  if (is_sorted()) {
    if (!y.is_sorted() || y.num_pending_rows() > 0) {
      sorted = false;
    }
    else {
      // `y' is sorted and has no pending rows.
      const dimension_type n_rows = num_rows();
      if (n_rows > 0) {
        sorted = (compare(rows[n_rows-1], y[0]) <= 0);
      }
    }
  }

  // Add the rows of `y' as if they were pending.
  insert_pending(y, Recycle_Input());

  // TODO: May y have pending rows? Should they remain pending?

  // There are no pending_rows.
  unset_pending_rows();

  PPL_ASSERT(OK());
}

template<typename Row>

void Parma_Polyhedra_Library::Linear_System< Row >::insert_no_ok ( Row &  r, Recycle_Input    )

private

Adds r to the system, stealing its contents and automatically resizing the system or the row, if needed.

This method is for internal use, it does *not* assert OK() at the end, so it can be used for invalid systems.

Definition at line 228 of file Linear_System_templates.hh.

References Parma_Polyhedra_Library::compare().

                                                      {
  PPL_ASSERT(topology() == r.topology());
  // This method is only used when the system has no pending rows.
  PPL_ASSERT(num_pending_rows() == 0);

  const bool was_sorted = is_sorted();

  insert_pending_no_ok(r, Recycle_Input());

  if (was_sorted) {
    const dimension_type nrows = num_rows();
    // The added row may have caused the system to be not sorted anymore.
    if (nrows > 1) {
      // If the system is not empty and the inserted row is the
      // greatest one, the system is set to be sorted.
      // If it is not the greatest one then the system is no longer sorted.
      sorted = (compare(rows[nrows-2], rows[nrows-1]) <= 0);
    }
    else {
      // A system having only one row is sorted.
      sorted = true;
    }
  }

  unset_pending_rows();
}

template<typename Row>

void Parma_Polyhedra_Library::Linear_System< Row >::insert_pending

(

const Row &

r

)

Adds a copy of the given row to the pending part of the system, automatically resizing the system or the row, if needed.

Definition at line 284 of file Linear_System_templates.hh.

Referenced by Parma_Polyhedra_Library::Linear_System< Row >::insert_pending().

                                               {
  Row tmp(r, representation());
  insert_pending(tmp, Recycle_Input());
}

template<typename Row>

void Parma_Polyhedra_Library::Linear_System< Row >::insert_pending	(	Row &	r,
		Recycle_Input
	)

Adds the given row to the pending part of the system, stealing its contents and automatically resizing the system or the row, if needed.

Definition at line 291 of file Linear_System_templates.hh.

                                                        {
  insert_pending_no_ok(r, Recycle_Input());
  PPL_ASSERT(OK());
}

template<typename Row>

void Parma_Polyhedra_Library::Linear_System< Row >::insert_pending

(

const Linear_System< Row > &

r

)

Adds a copy of the rows of `y' to the pending part of `*this'.

Definition at line 298 of file Linear_System_templates.hh.

                                                         {
  Linear_System tmp(y, representation(), With_Pending());
  insert_pending(tmp, Recycle_Input());
}

template<typename Row>

void Parma_Polyhedra_Library::Linear_System< Row >::insert_pending	(	Linear_System< Row > &	r,
		Recycle_Input
	)

Adds the rows of `y' to the pending part of `*this', stealing them from `y'.

Definition at line 305 of file Linear_System_templates.hh.

References Parma_Polyhedra_Library::Linear_System< Row >::clear(), Parma_Polyhedra_Library::Linear_System< Row >::insert_pending(), Parma_Polyhedra_Library::Linear_System< Row >::num_rows(), Parma_Polyhedra_Library::Linear_System< Row >::OK(), Parma_Polyhedra_Library::Linear_System< Row >::rows, and Parma_Polyhedra_Library::Linear_System< Row >::space_dimension().

                                                                  {
  Linear_System& x = *this;
  PPL_ASSERT(x.space_dimension() == y.space_dimension());

  // Steal the rows of `y'.
  // This loop must use an increasing index (instead of a decreasing one) to
  // preserve the row ordering.
  for (dimension_type i = 0; i < y.num_rows(); ++i) {
    x.insert_pending(y.rows[i], Recycle_Input());
  }

  y.clear();

  PPL_ASSERT(x.OK());
}

template<typename Row>

void Parma_Polyhedra_Library::Linear_System< Row >::insert_pending_no_ok ( Row &  r, Recycle_Input    )

private

Adds r to the pending part of the system, stealing its contents and automatically resizing the system or the row, if needed.

This method is for internal use, it does *not* assert OK() at the end, so it can be used for invalid systems.

Definition at line 257 of file Linear_System_templates.hh.

References Parma_Polyhedra_Library::swap().

                                                              {
  // TODO: A Grid_Generator_System may contain non-normalized lines that
  // represent parameters, so this check is disabled. Consider re-enabling it
  // when it's possibile.
#if 0
  // The added row must be strongly normalized and have the same
  // number of elements as the existing rows of the system.
  PPL_ASSERT(r.check_strong_normalized());
#endif

  PPL_ASSERT(r.topology() == topology());

  r.set_representation(representation());

  if (space_dimension() < r.space_dimension()) {
    set_space_dimension_no_ok(r.space_dimension());
  }
  else {
    r.set_space_dimension_no_ok(space_dimension());
  }

  rows.resize(rows.size() + 1);
  swap(rows.back(), r);
}

template<typename Row >

bool Parma_Polyhedra_Library::Linear_System< Row >::is_necessarily_closed ( ) const

inline

Returns true if and only if the system topology is NECESSARILY_CLOSED.

Definition at line 274 of file Linear_System_inlines.hh.

References Parma_Polyhedra_Library::NECESSARILY_CLOSED.

                                                {
  return row_topology == NECESSARILY_CLOSED;
}

template<typename Row >

bool Parma_Polyhedra_Library::Linear_System< Row >::is_sorted ( ) const

inline

Returns the value of the sortedness flag.

Definition at line 48 of file Linear_System_inlines.hh.

Referenced by Parma_Polyhedra_Library::Linear_System< Row >::insert().

                                    {
  // The flag `sorted' does not really reflect the sortedness status
  // of a system (if `sorted' evaluates to `false' nothing is known).
  // This assertion is used to ensure that the system
  // is actually sorted when `sorted' value is 'true'.
  PPL_ASSERT(!sorted || check_sorted());
  return sorted;
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::m_swap ( Linear_System< Row > &  y )

inline

Swaps *this with y.

Definition at line 200 of file Linear_System_inlines.hh.

References Parma_Polyhedra_Library::Linear_System< Row >::index_first_pending, Parma_Polyhedra_Library::Linear_System< Row >::OK(), Parma_Polyhedra_Library::Linear_System< Row >::representation_, Parma_Polyhedra_Library::Linear_System< Row >::row_topology, Parma_Polyhedra_Library::Linear_System< Row >::rows, Parma_Polyhedra_Library::Linear_System< Row >::sorted, Parma_Polyhedra_Library::Linear_System< Row >::space_dimension_, and Parma_Polyhedra_Library::swap().

Referenced by Parma_Polyhedra_Library::Linear_System< Row >::swap().

                                           {
  using std::swap;
  swap(rows, y.rows);
  swap(space_dimension_, y.space_dimension_);
  swap(row_topology, y.row_topology);
  swap(index_first_pending, y.index_first_pending);
  swap(sorted, y.sorted);
  swap(representation_, y.representation_);
  PPL_ASSERT(OK());
  PPL_ASSERT(y.OK());
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::mark_as_necessarily_closed ( )

inline

Marks the epsilon dimension as a standard dimension.

The system topology is changed to NOT_NECESSARILY_CLOSED, and the number of space dimensions is increased by 1.

Definition at line 226 of file Linear_System_inlines.hh.

References Parma_Polyhedra_Library::NECESSARILY_CLOSED, and Parma_Polyhedra_Library::NOT_NECESSARILY_CLOSED.

                                               {
  PPL_ASSERT(topology() == NOT_NECESSARILY_CLOSED);
  row_topology = NECESSARILY_CLOSED;
  ++space_dimension_;
  for (dimension_type i = num_rows(); i-- > 0; ) {
    rows[i].mark_as_necessarily_closed();
  }
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::mark_as_not_necessarily_closed ( )

inline

Marks the last dimension as the epsilon dimension.

The system topology is changed to NECESSARILY_CLOSED, and the number of space dimensions is decreased by 1.

Definition at line 237 of file Linear_System_inlines.hh.

References Parma_Polyhedra_Library::NECESSARILY_CLOSED, and Parma_Polyhedra_Library::NOT_NECESSARILY_CLOSED.

                                                   {
  PPL_ASSERT(topology() == NECESSARILY_CLOSED);
  PPL_ASSERT(space_dimension() > 0);
  row_topology = NOT_NECESSARILY_CLOSED;
  --space_dimension_;
  for (dimension_type i = num_rows(); i-- > 0; ) {
    rows[i].mark_as_not_necessarily_closed();
  }
}

template<typename Row >

dimension_type Parma_Polyhedra_Library::Linear_System< Row >::max_space_dimension ( )

inlinestatic

Returns the maximum space dimension a Linear_System can handle.

Definition at line 344 of file Linear_System_inlines.hh.

References Parma_Polyhedra_Library::max_space_dimension().

Referenced by Parma_Polyhedra_Library::Constraint_System::max_space_dimension(), Parma_Polyhedra_Library::Grid_Generator_System::max_space_dimension(), and Parma_Polyhedra_Library::Generator_System::max_space_dimension().

                                        {
  return Row::max_space_dimension();
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::merge_rows_assign

(

const Linear_System< Row > &

y

)

Assigns to *this the result of merging its rows with those of y, obtaining a sorted system.

Duplicated rows will occur only once in the result. On entry, both systems are assumed to be sorted and have no pending rows.

Definition at line 55 of file Linear_System_templates.hh.

References Parma_Polyhedra_Library::Swapping_Vector< T >::back(), Parma_Polyhedra_Library::Linear_System< Row >::check_sorted(), Parma_Polyhedra_Library::compare(), Parma_Polyhedra_Library::compute_capacity(), Parma_Polyhedra_Library::Swapping_Vector< T >::max_num_rows(), Parma_Polyhedra_Library::Linear_System< Row >::num_pending_rows(), Parma_Polyhedra_Library::Linear_System< Row >::num_rows(), Parma_Polyhedra_Library::Swapping_Vector< T >::reserve(), Parma_Polyhedra_Library::Swapping_Vector< T >::resize(), Parma_Polyhedra_Library::Linear_System< Row >::rows, Parma_Polyhedra_Library::Swapping_Vector< T >::size(), Parma_Polyhedra_Library::Linear_System< Row >::space_dimension(), and Parma_Polyhedra_Library::swap().

                                                            {
  PPL_ASSERT(space_dimension() >= y.space_dimension());
  // Both systems have to be sorted and have no pending rows.
  PPL_ASSERT(check_sorted() && y.check_sorted());
  PPL_ASSERT(num_pending_rows() == 0 && y.num_pending_rows() == 0);

  Linear_System& x = *this;

  // A temporary vector...
  Swapping_Vector<Row> tmp;
  // ... with enough capacity not to require any reallocations.
  tmp.reserve(compute_capacity(x.rows.size() + y.rows.size(),
                               tmp.max_num_rows()));

  dimension_type xi = 0;
  const dimension_type x_num_rows = x.num_rows();
  dimension_type yi = 0;
  const dimension_type y_num_rows = y.num_rows();

  while (xi < x_num_rows && yi < y_num_rows) {
    const int comp = compare(x[xi], y[yi]);
    if (comp <= 0) {
      // Elements that can be taken from `x' are actually _stolen_ from `x'
      tmp.resize(tmp.size() + 1);
      swap(tmp.back(), x.rows[xi++]);
      tmp.back().set_representation(representation());
      if (comp == 0) {
        // A duplicate element.
        ++yi;
      }
    }
    else {
      // (comp > 0)
      tmp.resize(tmp.size() + 1);
      Row copy(y[yi++], space_dimension(), representation());
      swap(tmp.back(), copy);
    }
  }
  // Insert what is left.
  if (xi < x_num_rows) {
    while (xi < x_num_rows) {
      tmp.resize(tmp.size() + 1);
      swap(tmp.back(), x.rows[xi++]);
      tmp.back().set_representation(representation());
    }
  }
  else {
    while (yi < y_num_rows) {
      tmp.resize(tmp.size() + 1);
      Row copy(y[yi++], space_dimension(), representation());
      swap(tmp.back(), copy);
    }
  }

  // We get the result matrix and let the old one be destroyed.
  swap(tmp, rows);
  // There are no pending rows.
  unset_pending_rows();
  PPL_ASSERT(check_sorted());
  PPL_ASSERT(OK());
}

template<typename Row >

dimension_type Parma_Polyhedra_Library::Linear_System< Row >::num_lines_or_equalities

(

)

const

Returns the number of rows in the system that represent either lines or equalities.

Definition at line 41 of file Linear_System_templates.hh.

                                                  {
  PPL_ASSERT(num_pending_rows() == 0);
  const Linear_System& x = *this;
  dimension_type n = 0;
  for (dimension_type i = num_rows(); i-- > 0; ) {
    if (x[i].is_line_or_equality()) {
      ++n;
    }
  }
  return n;
}

template<typename Row >

dimension_type Parma_Polyhedra_Library::Linear_System< Row >::num_pending_rows ( ) const

inline

Returns the number of rows that are in the pending part of the system.

Definition at line 100 of file Linear_System_inlines.hh.

Referenced by Parma_Polyhedra_Library::Linear_System< Row >::insert(), Parma_Polyhedra_Library::Linear_System< Row >::Linear_System(), and Parma_Polyhedra_Library::Linear_System< Row >::merge_rows_assign().

                                           {
  PPL_ASSERT(num_rows() >= first_pending_row());
  return num_rows() - first_pending_row();
}

template<typename Row >

dimension_type Parma_Polyhedra_Library::Linear_System< Row >::num_rows ( ) const

inline

Definition at line 316 of file Linear_System_inlines.hh.

Referenced by Parma_Polyhedra_Library::Linear_System< Row >::insert_pending(), Parma_Polyhedra_Library::Linear_System< Row >::Linear_System(), Parma_Polyhedra_Library::Linear_System< Row >::merge_rows_assign(), and Parma_Polyhedra_Library::Linear_System< Row >::operator==().

                                   {
  return rows.size();
}

template<typename Row >

bool Parma_Polyhedra_Library::Linear_System< Row >::OK

(

)

const

Checks if all the invariants are satisfied.

Definition at line 923 of file Linear_System_templates.hh.

Referenced by Parma_Polyhedra_Library::Linear_System< Row >::insert_pending(), Parma_Polyhedra_Library::Linear_System< Row >::Linear_System(), and Parma_Polyhedra_Library::Linear_System< Row >::m_swap().

                             {
#ifndef NDEBUG
  using std::endl;
  using std::cerr;
#endif

  for (dimension_type i = rows.size(); i-- > 0; ) {
    if (rows[i].representation() != representation()) {
#ifndef NDEBUG
      cerr << "Linear_System has a row with the wrong representation!"
           << endl;
#endif
      return false;
    }
    if (rows[i].space_dimension() != space_dimension()) {
#ifndef NDEBUG
      cerr << "Linear_System has a row with the wrong number of space dimensions!"
           << endl;
#endif
      return false;
    }
  }

  for (dimension_type i = rows.size(); i-- > 0; ) {
    if (rows[i].topology() != topology()) {
#ifndef NDEBUG
      cerr << "Linear_System has a row with the wrong topology!"
           << endl;
#endif
      return false;
    }

  }
  // `index_first_pending' must be less than or equal to `num_rows()'.
  if (first_pending_row() > num_rows()) {
#ifndef NDEBUG
    cerr << "Linear_System has a negative number of pending rows!"
         << endl;
#endif
    return false;
  }

  // Check for topology mismatches.
  const dimension_type n_rows = num_rows();
  for (dimension_type i = 0; i < n_rows; ++i) {
    if (topology() != rows[i].topology()) {
#ifndef NDEBUG
      cerr << "Topology mismatch between the system "
           << "and one of its rows!"
           << endl;
#endif
      return false;
    }

  }
  if (sorted && !check_sorted()) {
#ifndef NDEBUG
    cerr << "The system declares itself to be sorted but it is not!"
         << endl;
#endif
    return false;
  }

  // All checks passed.
  return true;
}

template<typename Row >

Linear_System< Row > & Parma_Polyhedra_Library::Linear_System< Row >::operator= ( const Linear_System< Row > &  y )

inline

Assignment operator: pending rows are transformed into non-pending ones.

Definition at line 184 of file Linear_System_inlines.hh.

References Parma_Polyhedra_Library::swap().

                                                    {
  // NOTE: Pending rows are transformed into non-pending ones.
  Linear_System<Row> tmp = y;
  swap(*this, tmp);
  return *this;
}

template<typename Row >

const Row & Parma_Polyhedra_Library::Linear_System< Row >::operator[] ( dimension_type  k ) const

inline

Returns a const reference to the k-th row of the system.

Definition at line 280 of file Linear_System_inlines.hh.

                                                           {
  return rows[k];
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::permute_space_dimensions ( const std::vector< Variable > &  cycle )

inline

Permutes the space dimensions of the matrix.

Definition at line 659 of file Linear_System_inlines.hh.

                                                           {
  for (dimension_type i = num_rows(); i-- > 0; ) {
    rows[i].permute_space_dimensions(cycle);
  }
  sorted = false;
  PPL_ASSERT(OK());
}

template<typename Row>

void Parma_Polyhedra_Library::Linear_System< Row >::print

(

)

const

Prints *this to std::cerr using operator<<.

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::remove_row ( dimension_type  i, bool  keep_sorted = false  )

inline

Makes the system shrink by removing its i-th row.

When keep_sorted is true and the system is sorted, sortedness will be preserved, but this method costs O(n).

Otherwise, this method just swaps the i-th row with the last and then removes it, so it costs O(1).

Definition at line 414 of file Linear_System_inlines.hh.

                                                                       {
  remove_row_no_ok(i, keep_sorted);
  PPL_ASSERT(OK());
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::remove_row_no_ok ( dimension_type  i, bool  keep_sorted = false  )

inlineprivate

Makes the system shrink by removing its i-th row.

When keep_sorted is true and the system is sorted, sortedness will be preserved, but this method costs O(n).

Otherwise, this method just swaps the i-th row with the last and then removes it, so it costs O(1).

This method is for internal use, it does *not* assert OK() at the end, so it can be used for invalid systems.

Definition at line 372 of file Linear_System_inlines.hh.

References Parma_Polyhedra_Library::swap().

                                                             {
  PPL_ASSERT(i < num_rows());
  const bool was_pending = (i >= index_first_pending);

  if (sorted && keep_sorted && !was_pending) {
    for (dimension_type j = i + 1; j < rows.size(); ++j) {
      swap(rows[j], rows[j-1]);
    }
    rows.pop_back();
  }
  else {
    if (!was_pending) {
      sorted = false;
    }
    const bool last_row_is_pending = (num_rows() - 1 >= index_first_pending);
    if (was_pending == last_row_is_pending) {
      // Either both rows are pending or both rows are not pending.
      swap(rows[i], rows.back());
    }
    else {
      // Pending rows are stored after the non-pending ones.
      PPL_ASSERT(!was_pending);
      PPL_ASSERT(last_row_is_pending);

      // Swap the row with the last non-pending row.
      swap(rows[i], rows[index_first_pending - 1]);

      // Now the (non-pending) row that has to be deleted is between the
      // non-pending and the pending rows.
      swap(rows[i], rows.back());
    }
    rows.pop_back();
  }
  if (!was_pending) {
    // A non-pending row has been removed.
    --index_first_pending;
  }
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::remove_rows ( dimension_type  first, dimension_type  last, bool  keep_sorted = false  )

inline

Makes the system shrink by removing the rows in [first,last).

When keep_sorted is true and the system is sorted, sortedness will be preserved, but this method costs O(num_rows()).

Otherwise, this method just swaps the rows with the last ones and then removes them, so it costs O(last - first).

Definition at line 422 of file Linear_System_inlines.hh.

References Parma_Polyhedra_Library::swap().

                                                  {
  PPL_ASSERT(first <= last);
  PPL_ASSERT(last <= num_rows());
  const dimension_type n = last - first;

  if (n == 0) {
    return;
  }

  // All the rows that have to be removed must have the same (pending or
  // non-pending) status.
  PPL_ASSERT(first >= index_first_pending || last <= index_first_pending);

  const bool were_pending = (first >= index_first_pending);

  // Move the rows in [first,last) at the end of the system.
  if (sorted && keep_sorted && !were_pending) {
    // Preserve the row ordering.
    for (dimension_type i = last; i < rows.size(); ++i) {
      swap(rows[i], rows[i - n]);
    }

    rows.resize(rows.size() - n);

    // `n' non-pending rows have been removed.
    index_first_pending -= n;

    PPL_ASSERT(OK());
    return;
  }

  // We can ignore the row ordering, but we must not mix pending and
  // non-pending rows.

  const dimension_type offset = rows.size() - n - first;
  // We want to swap the rows in [first, last) and
  // [first + offset, last + offset) (note that these intervals may not be
  // disjunct).

  if (index_first_pending == num_rows()) {
    // There are no pending rows.
    PPL_ASSERT(!were_pending);

    swap_row_intervals(first, last, offset);

    rows.resize(rows.size() - n);

    // `n' non-pending rows have been removed.
    index_first_pending -= n;
  }
  else {
    // There are some pending rows in [first + offset, last + offset).
    if (were_pending) {
      // Both intervals contain only pending rows, because the second
      // interval is after the first.

      swap_row_intervals(first, last, offset);

      rows.resize(rows.size() - n);

      // `n' non-pending rows have been removed.
      index_first_pending -= n;
    }
    else {
      PPL_ASSERT(rows.size() - n < index_first_pending);
      PPL_ASSERT(rows.size() > index_first_pending);
      PPL_ASSERT(!were_pending);
      // In the [size() - n, size()) interval there are some non-pending
      // rows and some pending ones. Be careful not to mix them.

      PPL_ASSERT(index_first_pending >= last);
      swap_row_intervals(first, last, index_first_pending - last);

      // Mark the rows that must be deleted as pending.
      index_first_pending -= n;
      first = index_first_pending;
      last = first + n;

      // Move them at the end of the system.
      swap_row_intervals(first, last, num_rows() - last);

      // Actually remove the rows.
      rows.resize(rows.size() - n);
    }
  }

  PPL_ASSERT(OK());
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::remove_rows ( const std::vector< dimension_type > &  indexes )

inline

Removes the specified rows. The row ordering of remaining rows is preserved.

Parameters

indexes

specifies a list of row indexes. It must be sorted.

Definition at line 560 of file Linear_System_inlines.hh.

References Parma_Polyhedra_Library::swap().

                                                                        {
#ifndef NDEBUG
  {
    // Check that `indexes' is sorted.
    std::vector<dimension_type> sorted_indexes = indexes;
    std::sort(sorted_indexes.begin(), sorted_indexes.end());
    PPL_ASSERT(indexes == sorted_indexes);

    // Check that the last index (if any) is lower than num_rows().
    // This guarantees that all indexes are in [0, num_rows()).
    if (!indexes.empty()) {
      PPL_ASSERT(indexes.back() < num_rows());
    }
  }
#endif

  if (indexes.empty()) {
    return;
  }

  const dimension_type rows_size = rows.size();
  typedef std::vector<dimension_type>::const_iterator itr_t;

  // `i' and last_unused_row' start with the value `indexes[0]' instead
  // of `0', because the loop would just increment `last_unused_row' in the
  // preceding iterations.
  dimension_type last_unused_row = indexes[0];
  dimension_type i = indexes[0];
  itr_t itr = indexes.begin();
  itr_t itr_end = indexes.end();
  while (itr != itr_end) {
    // i <= *itr < rows_size
    PPL_ASSERT(i < rows_size);
    if (*itr == i) {
      // The current row has to be removed, don't increment last_unused_row.
      ++itr;
    }
    else {
      // The current row must not be removed, swap it after the last used row.
      swap(rows[last_unused_row], rows[i]);
      ++last_unused_row;
    }
    ++i;
  }

  // Move up the remaining rows, if any.
  for ( ; i < rows_size; ++i) {
    swap(rows[last_unused_row], rows[i]);
    ++last_unused_row;
  }

  PPL_ASSERT(last_unused_row == num_rows() - indexes.size());

  // The rows that have to be removed are now at the end of the system, just
  // remove them.
  rows.resize(last_unused_row);

  // Adjust index_first_pending.
  if (indexes[0] >= index_first_pending) {
    // Removing pending rows only.
  }
  else {
    if (indexes.back() < index_first_pending) {
      // Removing non-pending rows only.
      index_first_pending -= indexes.size();
    }
    else {
      // Removing some pending and some non-pending rows, count the
      // non-pending rows that must be removed.
      // This exploits the fact that `indexes' is sorted by using binary
      // search.
      itr_t j = std::lower_bound(indexes.begin(), indexes.end(),
                                 index_first_pending);
      std::iterator_traits<itr_t>::difference_type
        non_pending = j - indexes.begin();
      index_first_pending -= static_cast<dimension_type>(non_pending);
    }
  }

  // NOTE: This method does *not* call set_sorted(false), because it preserves
  // the relative row ordering.

  PPL_ASSERT(OK());
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::remove_space_dimensions

(

const Variables_Set &

vars

)

Removes all the specified dimensions from the system.

The space dimension of the variable with the highest space dimension in vars must be at most the space dimension of this.

Definition at line 365 of file Linear_System_templates.hh.

References Parma_Polyhedra_Library::Variables_Set::space_dimension().

                                                                     {
  // Dimension-compatibility assertion.
  PPL_ASSERT(space_dimension() >= vars.space_dimension());

  // The removal of no dimensions from any system is a no-op.  This
  // case also captures the only legal removal of dimensions from a
  // 0-dim system.
  if (vars.empty()) {
    return;
  }

  // NOTE: num_rows() is *not* constant, because it may be decreased by
  // remove_row_no_ok().
  for (dimension_type i = 0; i < num_rows(); ) {
    const bool valid = rows[i].remove_space_dimensions(vars);
    if (!valid) {
      // Remove the current row.
      // We can't call remove_row(i) here, because the system is not OK as
      // some rows already have the new space dimension and others still have
      // the old one.
      remove_row_no_ok(i, false);
    }
    else {
      ++i;
    }
  }

  space_dimension_ -= vars.size();

  PPL_ASSERT(OK());
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::remove_trailing_rows ( dimension_type  n )

inline

Makes the system shrink by removing its n trailing rows.

Definition at line 647 of file Linear_System_inlines.hh.

                                                               {
  PPL_ASSERT(rows.size() >= n);
  rows.resize(rows.size() - n);
  if (first_pending_row() > rows.size()) {
    index_first_pending = rows.size();
  }
  PPL_ASSERT(OK());
}

template<typename Row >

Representation Parma_Polyhedra_Library::Linear_System< Row >::representation ( ) const

inline

Returns the current representation of *this.

Definition at line 328 of file Linear_System_inlines.hh.

                                         {
  return representation_;
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::set_index_first_pending_row ( dimension_type  i )

inline

Sets the index of the first pending row to i.

Definition at line 114 of file Linear_System_inlines.hh.

                                                                      {
  index_first_pending = i;
  PPL_ASSERT(OK());
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::set_necessarily_closed ( )

inline

Sets the system topology to NECESSARILY_CLOSED.

Definition at line 262 of file Linear_System_inlines.hh.

References Parma_Polyhedra_Library::NECESSARILY_CLOSED.

                                           {
  set_topology(NECESSARILY_CLOSED);
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::set_not_necessarily_closed ( )

inline

Sets the system topology to NOT_NECESSARILY_CLOSED.

Definition at line 268 of file Linear_System_inlines.hh.

References Parma_Polyhedra_Library::NOT_NECESSARILY_CLOSED.

                                               {
  set_topology(NOT_NECESSARILY_CLOSED);
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::set_representation ( Representation  r )

inline

Converts *this to the specified representation.

Definition at line 334 of file Linear_System_inlines.hh.

                                                       {
  representation_ = r;
  for (dimension_type i = 0; i < rows.size(); ++i) {
    rows[i].set_representation(r);
  }
  PPL_ASSERT(OK());
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::set_sorted ( bool  b )

inline

Sets the sortedness flag of the system to b.

Definition at line 59 of file Linear_System_inlines.hh.

                                           {
  sorted = b;
  PPL_ASSERT(OK());
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::set_space_dimension ( dimension_type  space_dim )

inline

Sets the space dimension of the rows in the system to space_dim .

Definition at line 365 of file Linear_System_inlines.hh.

Referenced by Parma_Polyhedra_Library::Linear_System< Row >::Linear_System().

                                                                {
  set_space_dimension_no_ok(space_dim);
  PPL_ASSERT(OK());
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::set_space_dimension_no_ok ( dimension_type  space_dim )

inlineprivate

Sets the space dimension of the rows in the system to space_dim .

This method is for internal use, it does *not* assert OK() at the end, so it can be used for invalid systems.

Definition at line 356 of file Linear_System_inlines.hh.

                                                                      {
  for (dimension_type i = rows.size(); i-- > 0; ) {
    rows[i].set_space_dimension_no_ok(space_dim);
  }
  space_dimension_ = space_dim;
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::set_topology ( Topology  t )

inline

Sets the system topology to t .

Definition at line 249 of file Linear_System_inlines.hh.

                                           {
  if (topology() == t) {
    return;
  }
  for (dimension_type i = num_rows(); i-- > 0; ) {
    rows[i].set_topology(t);
  }
  row_topology = t;
  PPL_ASSERT(OK());
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::shift_space_dimensions	(	Variable	v,
		dimension_type	n
	)

Shift by n positions the coefficients of variables, starting from the coefficient of v. This increases the space dimension by n.

Definition at line 399 of file Linear_System_templates.hh.

References Parma_Polyhedra_Library::Variable::id().

                                                                       {
  // NOTE: v.id() may be equal to the space dimension of the system
  // (when no space dimension need to be shifted).
  PPL_ASSERT(v.id() <= space_dimension());
  for (dimension_type i = rows.size(); i-- > 0; ) {
    rows[i].shift_space_dimensions(v, n);
  }
  space_dimension_ += n;
  PPL_ASSERT(OK());
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::sign_normalize

(

)

Sign-normalizes the system.

Definition at line 481 of file Linear_System_templates.hh.

                                   {
  const dimension_type nrows = rows.size();
  // We sign-normalize also the pending rows.
  for (dimension_type i = nrows; i-- > 0; ) {
    rows[i].sign_normalize();
  }
  sorted = (nrows <= 1);
  PPL_ASSERT(OK());
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::simplify

(

)

Applies Gaussian elimination and back-substitution so as to simplify the linear system.

Definition at line 733 of file Linear_System_templates.hh.

References Parma_Polyhedra_Library::swap().

                             {
  // This method is only applied to a system having no pending rows.
  PPL_ASSERT(num_pending_rows() == 0);

  // Partially sort the linear system so that all lines/equalities come first.
  const dimension_type old_nrows = num_rows();
  dimension_type nrows = old_nrows;
  dimension_type n_lines_or_equalities = 0;
  for (dimension_type i = 0; i < nrows; ++i) {
    if ((*this)[i].is_line_or_equality()) {
      if (n_lines_or_equalities < i) {
        swap(rows[i], rows[n_lines_or_equalities]);
        // The system was not sorted.
        PPL_ASSERT(!sorted);
      }
      ++n_lines_or_equalities;
    }
  }
  // Apply Gaussian elimination to the subsystem of lines/equalities.
  const dimension_type rank = gauss(n_lines_or_equalities);
  // Eliminate any redundant line/equality that has been detected.
  if (rank < n_lines_or_equalities) {
    const dimension_type
      n_rays_or_points_or_inequalities = nrows - n_lines_or_equalities;
    const dimension_type
      num_swaps = std::min(n_lines_or_equalities - rank,
                           n_rays_or_points_or_inequalities);
    for (dimension_type i = num_swaps; i-- > 0; ) {
      swap(rows[--nrows], rows[rank + i]);
    }
    remove_trailing_rows(old_nrows - nrows);
    if (n_rays_or_points_or_inequalities > num_swaps) {
      set_sorted(false);
    }
    unset_pending_rows();
    n_lines_or_equalities = rank;
  }
  // Apply back-substitution to the system of rays/points/inequalities.
  back_substitute(n_lines_or_equalities);

  PPL_ASSERT(OK());
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::sort_and_remove_with_sat

(

Bit_Matrix &

sat

)

Sorts the system, removing duplicates, keeping the saturation matrix consistent.

Parameters

sat	Bit matrix with rows corresponding to the rows of *this.

Definition at line 521 of file Linear_System_templates.hh.

References Parma_Polyhedra_Library::Implementation::indirect_sort_and_unique(), Parma_Polyhedra_Library::Bit_Matrix::num_rows(), Parma_Polyhedra_Library::Bit_Matrix::remove_trailing_rows(), and Parma_Polyhedra_Library::swap().

                                                            {
  // We can only sort the non-pending part of the system.
  PPL_ASSERT(first_pending_row() == sat.num_rows());
  if (first_pending_row() <= 1) {
    set_sorted(true);
    return;
  }

  const dimension_type num_elems = sat.num_rows();
  // Build the function objects implementing indirect sort comparison,
  // indirect unique comparison and indirect swap operation.
  typedef Swapping_Vector<Row> Cont;
  const Implementation::Indirect_Sort_Compare<Cont, Row_Less_Than>
    sort_cmp(rows);
  const Unique_Compare unique_cmp(rows);
  const Implementation::Indirect_Swapper2<Cont, Bit_Matrix> swapper(rows, sat);

  const dimension_type num_duplicates
    = Implementation::indirect_sort_and_unique(num_elems, sort_cmp,
                                               unique_cmp, swapper);

  const dimension_type new_first_pending_row
    = first_pending_row() - num_duplicates;

  if (num_pending_rows() > 0) {
    // In this case, we must put the duplicates after the pending rows.
    const dimension_type n_rows = num_rows() - 1;
    for (dimension_type i = 0; i < num_duplicates; ++i) {
      swap(rows[new_first_pending_row + i], rows[n_rows - i]);
    }
  }

  // Erasing the duplicated rows...
  rows.resize(rows.size() - num_duplicates);
  index_first_pending = new_first_pending_row;
  // ... and the corresponding rows of the saturation matrix.
  sat.remove_trailing_rows(num_duplicates);

  // Now the system is sorted.
  sorted = true;

  PPL_ASSERT(OK());
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::sort_pending_and_remove_duplicates

(

)

Sorts the pending rows and eliminates those that also occur in the non-pending part of the system.

Definition at line 851 of file Linear_System_templates.hh.

References Parma_Polyhedra_Library::cmp(), Parma_Polyhedra_Library::compare(), and Parma_Polyhedra_Library::swap().

                                                       {
  PPL_ASSERT(num_pending_rows() > 0);
  PPL_ASSERT(is_sorted());

  // The non-pending part of the system is already sorted.
  // Now sorting the pending part..
  const dimension_type first_pending = first_pending_row();
  sort_rows(first_pending, num_rows());
  // Recompute the number of rows, because we may have removed
  // some rows occurring more than once in the pending part.
  const dimension_type old_num_rows = num_rows();
  dimension_type num_rows = old_num_rows;

  dimension_type k1 = 0;
  dimension_type k2 = first_pending;
  dimension_type num_duplicates = 0;
  // In order to erase them, put at the end of the system
  // those pending rows that also occur in the non-pending part.
  while (k1 < first_pending && k2 < num_rows) {
    const int cmp = compare(rows[k1], rows[k2]);
    if (cmp == 0) {
      // We found the same row.
      ++num_duplicates;
      --num_rows;
      // By initial sortedness, we can increment index `k1'.
      ++k1;
      // Do not increment `k2'; instead, swap there the next pending row.
      if (k2 < num_rows) {
        swap(rows[k2], rows[k2 + num_duplicates]);
      }
    }
    else if (cmp < 0) {
      // By initial sortedness, we can increment `k1'.
      ++k1;
    }
    else {
      // Here `cmp > 0'.
      // Increment `k2' and, if we already found any duplicate,
      // swap the next pending row in position `k2'.
      ++k2;
      if (num_duplicates > 0 && k2 < num_rows) {
        swap(rows[k2], rows[k2 + num_duplicates]);
      }
    }
  }
  // If needed, swap any duplicates found past the pending rows
  // that has not been considered yet; then erase the duplicates.
  if (num_duplicates > 0) {
    if (k2 < num_rows) {
      for (++k2; k2 < num_rows; ++k2)  {
        swap(rows[k2], rows[k2 + num_duplicates]);
      }
    }
    rows.resize(num_rows);
  }
  sorted = true;
  PPL_ASSERT(OK());
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::sort_rows

(

)

Sorts the non-pending rows (in growing order) and eliminates duplicated ones.

Definition at line 412 of file Linear_System_templates.hh.

                              {
  // We sort the non-pending rows only.
  sort_rows(0, first_pending_row());
  sorted = true;
  PPL_ASSERT(OK());
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::sort_rows	(	dimension_type	first_row,
		dimension_type	last_row
	)

Sorts the rows (in growing order) form first_row to last_row and eliminates duplicated ones.

Definition at line 421 of file Linear_System_templates.hh.

References Parma_Polyhedra_Library::Implementation::indirect_sort_and_unique().

                                                             {
  PPL_ASSERT(first_row <= last_row && last_row <= num_rows());
  // We cannot mix pending and non-pending rows.
  PPL_ASSERT(first_row >= first_pending_row()
             || last_row <= first_pending_row());

  const bool sorting_pending = (first_row >= first_pending_row());
  const dimension_type old_num_pending = num_pending_rows();

  const dimension_type num_elems = last_row - first_row;
  if (num_elems < 2) {
    return;
  }

  // Build the function objects implementing indirect sort comparison,
  // indirect unique comparison and indirect swap operation.
  using namespace Implementation;
  typedef Swapping_Vector<Row> Cont;
  typedef Indirect_Sort_Compare<Cont, Row_Less_Than> Sort_Compare;
  typedef Indirect_Swapper<Cont> Swapper;
  const dimension_type num_duplicates
    = indirect_sort_and_unique(num_elems,
                               Sort_Compare(rows, first_row),
                               Unique_Compare(rows, first_row),
                               Swapper(rows, first_row));

  if (num_duplicates > 0) {
    typedef typename Cont::iterator Iter;
    typedef typename std::iterator_traits<Iter>::difference_type diff_t;
    Iter last = rows.begin() + static_cast<diff_t>(last_row);
    Iter first = last - + static_cast<diff_t>(num_duplicates);
    rows.erase(first, last);
  }

  if (sorting_pending) {
    PPL_ASSERT(old_num_pending >= num_duplicates);
    index_first_pending = num_rows() - (old_num_pending - num_duplicates);
  }
  else {
    index_first_pending = num_rows() - old_num_pending;
  }

  PPL_ASSERT(OK());
}

template<typename Row >

dimension_type Parma_Polyhedra_Library::Linear_System< Row >::space_dimension ( ) const

inline

Returns the space dimension of the rows in the system.

The computation of the space dimension correctly ignores the column encoding the inhomogeneous terms of constraint (resp., the divisors of generators); if the system topology is NOT_NECESSARILY_CLOSED, also the column of the 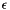-dimension coefficients will be ignored.

Definition at line 350 of file Linear_System_inlines.hh.

Referenced by Parma_Polyhedra_Library::Linear_System< Row >::insert_pending(), Parma_Polyhedra_Library::Linear_System< Row >::merge_rows_assign(), and Parma_Polyhedra_Library::Linear_System< Row >::operator==().

                                          {
  return space_dimension_;
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::strong_normalize

(

)

Strongly normalizes the system.

Definition at line 469 of file Linear_System_templates.hh.

                                     {
  const dimension_type nrows = rows.size();
  // We strongly normalize also the pending rows.
  for (dimension_type i = nrows; i-- > 0; ) {
    rows[i].strong_normalize();
  }
  sorted = (nrows <= 1);
  PPL_ASSERT(OK());
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::swap_row_intervals ( dimension_type  first, dimension_type  last, dimension_type  offset  )

inlineprivate

Swaps the [first,last) row interval with the [first + offset, last + offset) interval.

These intervals may not be disjunct.

Sorting of these intervals is *not* preserved.

Either both intervals contain only not-pending rows, or they both contain pending rows.

Definition at line 515 of file Linear_System_inlines.hh.

References Parma_Polyhedra_Library::swap().

                                                              {
  PPL_ASSERT(first <= last);
  PPL_ASSERT(last + offset <= num_rows());
#ifndef NDEBUG
  if (first < last) {
    bool first_interval_has_pending_rows = (last > index_first_pending);
    bool second_interval_has_pending_rows = (last + offset > index_first_pending);
    bool first_interval_has_not_pending_rows = (first < index_first_pending);
    bool second_interval_has_not_pending_rows = (first + offset < index_first_pending);
    PPL_ASSERT(first_interval_has_not_pending_rows
               == !first_interval_has_pending_rows);
    PPL_ASSERT(second_interval_has_not_pending_rows
               == !second_interval_has_pending_rows);
    PPL_ASSERT(first_interval_has_pending_rows
               == second_interval_has_pending_rows);
  }
#endif
  if (first + offset < last) {
    // The intervals are not disjunct, make them so.
    const dimension_type k = last - first - offset;
    last -= k;
    offset += k;
  }

  if (first == last) {
    // Nothing to do.
    return;
  }

  for (dimension_type i = first; i < last; ++i) {
    swap(rows[i], rows[i + offset]);
  }

  if (first < index_first_pending) {
    // The swaps involved not pending rows, so they may not be sorted anymore.
    set_sorted(false);
  }

  PPL_ASSERT(OK());
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::swap_space_dimensions ( Variable  v1, Variable  v2  )

inline

Swaps the coefficients of the variables v1 and v2 .

Definition at line 670 of file Linear_System_inlines.hh.

References Parma_Polyhedra_Library::Variable::space_dimension().

                                                {
  PPL_ASSERT(v1.space_dimension() <= space_dimension());
  PPL_ASSERT(v2.space_dimension() <= space_dimension());
  for (dimension_type k = num_rows(); k-- > 0; ) {
    rows[k].swap_space_dimensions(v1, v2);
  }
  sorted = false;
  PPL_ASSERT(OK());
}

template<typename Row >

Topology Parma_Polyhedra_Library::Linear_System< Row >::topology ( ) const

inline

Returns the system topology.

Definition at line 322 of file Linear_System_inlines.hh.

                                   {
  return row_topology;
}

template<typename Row >

memory_size_type Parma_Polyhedra_Library::Linear_System< Row >::total_memory_in_bytes ( ) const

inline

Returns the total size in bytes of the memory occupied by *this.

Definition at line 42 of file Linear_System_inlines.hh.

References Parma_Polyhedra_Library::external_memory_in_bytes().

                                                {
  return sizeof(*this) + external_memory_in_bytes();
}

template<typename Row >

void Parma_Polyhedra_Library::Linear_System< Row >::unset_pending_rows ( )

inline

Sets the index to indicate that the system has no pending rows.

Definition at line 107 of file Linear_System_inlines.hh.

Referenced by Parma_Polyhedra_Library::Linear_System< Row >::Linear_System().

                                       {
  index_first_pending = num_rows();
  PPL_ASSERT(OK());
}

Friends And Related Function Documentation

template<typename Row>

friend class Generator_System

friend

Definition at line 546 of file Linear_System_defs.hh.

template<typename Row >

bool operator!= ( const Linear_System< Row > &  x, const Linear_System< Row > &  y  )

related

Returns true if and only if x and y are different.

template<typename Row >

bool operator!= ( const Linear_System< Row > &  x, const Linear_System< Row > &  y  )

related

Definition at line 683 of file Linear_System_inlines.hh.

                                                                     {
  return !(x == y);
}

template<typename Row >

bool operator== ( const Linear_System< Row > &  x, const Linear_System< Row > &  y  )

related

Definition at line 494 of file Linear_System_templates.hh.

References Parma_Polyhedra_Library::Linear_System< Row >::first_pending_row(), Parma_Polyhedra_Library::Linear_System< Row >::num_rows(), and Parma_Polyhedra_Library::Linear_System< Row >::space_dimension().

                                                                     {
  if (x.space_dimension() != y.space_dimension()) {
    return false;
  }
  const dimension_type x_num_rows = x.num_rows();
  const dimension_type y_num_rows = y.num_rows();
  if (x_num_rows != y_num_rows) {
    return false;
  }
  if (x.first_pending_row() != y.first_pending_row()) {
    return false;
  }
  // TODO: Check if the following comment is up to date.
  // Notice that calling operator==(const Swapping_Vector<Row>&,
  //                                const Swapping_Vector<Row>&)
  // would be wrong here, as equality of the type fields would
  // not be checked.
  for (dimension_type i = x_num_rows; i-- > 0; ) {
    if (x[i] != y[i]) {
      return false;
    }
  }
  return true;
}

template<typename Row >

bool operator== ( const Linear_System< Row > &  x, const Linear_System< Row > &  y  )

related

Returns true if and only if x and y are identical.

template<typename Row>

friend class Polyhedron

friend

Definition at line 545 of file Linear_System_defs.hh.

template<typename Row >

void swap ( Parma_Polyhedra_Library::Linear_System< Row > &  x, Parma_Polyhedra_Library::Linear_System< Row > &  y  )

related

Swaps x with y.

Referenced by Parma_Polyhedra_Library::Linear_System< Row >::Linear_System().

template<typename Row >

void swap ( Linear_System< Row > &  x, Linear_System< Row > &  y  )

related

Definition at line 712 of file Linear_System_inlines.hh.

References Parma_Polyhedra_Library::Linear_System< Row >::m_swap().

                                                   {
  x.m_swap(y);
}

Member Data Documentation

template<typename Row>

dimension_type Parma_Polyhedra_Library::Linear_System< Row >::index_first_pending

private

The index of the first pending row.

Definition at line 518 of file Linear_System_defs.hh.

Referenced by Parma_Polyhedra_Library::Linear_System< Row >::m_swap().

template<typename Row>

Representation Parma_Polyhedra_Library::Linear_System< Row >::representation_

private

Definition at line 527 of file Linear_System_defs.hh.

Referenced by Parma_Polyhedra_Library::Linear_System< Row >::m_swap().

template<typename Row>

Topology Parma_Polyhedra_Library::Linear_System< Row >::row_topology

private

The topological kind of the rows in the system. All rows must have this topology.

Definition at line 515 of file Linear_System_defs.hh.

Referenced by Parma_Polyhedra_Library::Linear_System< Row >::m_swap().

template<typename Row>

Swapping_Vector<Row> Parma_Polyhedra_Library::Linear_System< Row >::rows

The vector that contains the rows.

Note

This is public for convenience. Clients that modify if must preserve the class invariant.

Definition at line 452 of file Linear_System_defs.hh.

Referenced by Parma_Polyhedra_Library::Linear_System< Row >::insert_pending(), Parma_Polyhedra_Library::Linear_System< Row >::Linear_System(), Parma_Polyhedra_Library::Linear_System< Row >::m_swap(), and Parma_Polyhedra_Library::Linear_System< Row >::merge_rows_assign().

template<typename Row>

bool Parma_Polyhedra_Library::Linear_System< Row >::sorted

private

true if rows are sorted in the ascending order as defined by bool compare(const Row&, const Row&). If false may not be sorted.

Definition at line 525 of file Linear_System_defs.hh.

Referenced by Parma_Polyhedra_Library::Linear_System< Row >::Linear_System(), and Parma_Polyhedra_Library::Linear_System< Row >::m_swap().

template<typename Row>

dimension_type Parma_Polyhedra_Library::Linear_System< Row >::space_dimension_

private

The space dimension of each row. All rows must have this number of space dimensions.

Definition at line 511 of file Linear_System_defs.hh.

Referenced by Parma_Polyhedra_Library::Linear_System< Row >::m_swap().

---

The documentation for this class was generated from the following files:

• Linear_System_defs.hh
• Linear_System_inlines.hh
• Linear_System_templates.hh