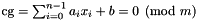A linear congruence. More...
#include <Congruence_defs.hh>
Public Types | |
| typedef Expression_Adapter_Transparent< Linear_Expression > | expr_type |
| The type of the (adapted) internal expression. More... | |
Public Member Functions | |
| Congruence (Representation r=default_representation) | |
Constructs the 0 = 0 congruence with space dimension 0 . More... | |
| Congruence (const Congruence &cg) | |
| Ordinary copy constructor. More... | |
| Congruence (const Congruence &cg, Representation r) | |
| Copy constructor with specified representation. More... | |
| Congruence (const Constraint &c, Representation r=default_representation) | |
Copy-constructs (modulo 0) from equality constraint c. More... | |
| ~Congruence () | |
| Destructor. More... | |
| Congruence & | operator= (const Congruence &y) |
| Assignment operator. More... | |
| Representation | representation () const |
| Returns the current representation of *this. More... | |
| void | set_representation (Representation r) |
| Converts *this to the specified representation. More... | |
| dimension_type | space_dimension () const |
Returns the dimension of the vector space enclosing *this. More... | |
| void | permute_space_dimensions (const std::vector< Variable > &cycles) |
| expr_type | expression () const |
| Partial read access to the (adapted) internal expression. More... | |
| Coefficient_traits::const_reference | coefficient (Variable v) const |
Returns the coefficient of v in *this. More... | |
| Coefficient_traits::const_reference | inhomogeneous_term () const |
Returns the inhomogeneous term of *this. More... | |
| Coefficient_traits::const_reference | modulus () const |
Returns a const reference to the modulus of *this. More... | |
| void | set_modulus (Coefficient_traits::const_reference m) |
| void | scale (Coefficient_traits::const_reference factor) |
Multiplies all the coefficients, including the modulus, by factor . More... | |
| void | affine_preimage (Variable v, const Linear_Expression &expr, Coefficient_traits::const_reference denominator) |
| Congruence & | operator/= (Coefficient_traits::const_reference k) |
Multiplies k into the modulus of *this. More... | |
| bool | is_tautological () const |
Returns true if and only if *this is a tautology (i.e., an always true congruence). More... | |
| bool | is_inconsistent () const |
Returns true if and only if *this is inconsistent (i.e., an always false congruence). More... | |
| bool | is_proper_congruence () const |
Returns true if the modulus is greater than zero. More... | |
| bool | is_equality () const |
Returns true if *this is an equality. More... | |
| memory_size_type | total_memory_in_bytes () const |
Returns a lower bound to the total size in bytes of the memory occupied by *this. More... | |
| memory_size_type | external_memory_in_bytes () const |
Returns the size in bytes of the memory managed by *this. More... | |
| bool | OK () const |
| Checks if all the invariants are satisfied. More... | |
| void | ascii_dump () const |
Writes to std::cerr an ASCII representation of *this. More... | |
| void | ascii_dump (std::ostream &s) const |
Writes to s an ASCII representation of *this. More... | |
| void | print () const |
Prints *this to std::cerr using operator<<. More... | |
| bool | ascii_load (std::istream &s) |
Loads from s an ASCII representation of the internal representation of *this. More... | |
| void | m_swap (Congruence &y) |
Swaps *this with y. More... | |
| Congruence (const Congruence &cg, dimension_type new_space_dimension) | |
| Copy-constructs with the specified space dimension. More... | |
| Congruence (const Congruence &cg, dimension_type new_space_dimension, Representation r) | |
| Copy-constructs with the specified space dimension and representation. More... | |
| Congruence (const Constraint &cg, dimension_type new_space_dimension, Representation r=default_representation) | |
| Congruence (Linear_Expression &le, Coefficient_traits::const_reference m, Recycle_Input) | |
Constructs from Linear_Expression le, using modulus m. More... | |
| void | swap_space_dimensions (Variable v1, Variable v2) |
Swaps the coefficients of the variables v1 and v2 . More... | |
| void | set_space_dimension (dimension_type n) |
| void | shift_space_dimensions (Variable v, dimension_type n) |
| void | sign_normalize () |
| Normalizes the signs. More... | |
| void | normalize () |
| Normalizes signs and the inhomogeneous term. More... | |
| void | strong_normalize () |
| Calls normalize, then divides out common factors. More... | |
Static Public Member Functions | |
| static dimension_type | max_space_dimension () |
| Returns the maximum space dimension a Congruence can handle. More... | |
| static void | initialize () |
| Initializes the class. More... | |
| static void | finalize () |
| Finalizes the class. More... | |
| static const Congruence & | zero_dim_integrality () |
Returns a reference to the true (zero-dimension space) congruence 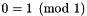 , also known as the integrality congruence. More... , also known as the integrality congruence. More... | |
| static const Congruence & | zero_dim_false () |
Returns a reference to the false (zero-dimension space) congruence 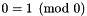 . More... . More... | |
| static Congruence | create (const Linear_Expression &e1, const Linear_Expression &e2, Representation r=default_representation) |
Returns the congruence 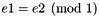 . More... . More... | |
| static Congruence | create (const Linear_Expression &e, Coefficient_traits::const_reference n, Representation r=default_representation) |
Returns the congruence 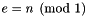 . More... . More... | |
| static Congruence | create (Coefficient_traits::const_reference n, const Linear_Expression &e, Representation r=default_representation) |
Returns the congruence 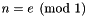 . More... . More... | |
Static Public Attributes | |
| static const Representation | default_representation = SPARSE |
| The representation used for new Congruences. More... | |
Private Member Functions | |
| bool | is_equal_at_dimension (Variable v, const Congruence &cg) const |
Returns true if *this is equal to cg in dimension v. More... | |
| void | throw_invalid_argument (const char *method, const char *message) const |
Throws a std::invalid_argument exception containing error message message. More... | |
| void | throw_dimension_incompatible (const char *method, const char *v_name, Variable v) const |
Throws a std::invalid_argument exception containing the appropriate error message. More... | |
Private Attributes | |
| Linear_Expression | expr |
| Coefficient | modulus_ |
Static Private Attributes | |
| static const Congruence * | zero_dim_false_p = 0 |
Holds (between class initialization and finalization) a pointer to the false (zero-dimension space) congruence 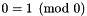 . More... . More... | |
| static const Congruence * | zero_dim_integrality_p = 0 |
Holds (between class initialization and finalization) a pointer to the true (zero-dimension space) congruence 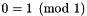 , also known as the integrality congruence. More... , also known as the integrality congruence. More... | |
Friends | |
| class | Scalar_Products |
| class | Grid |
| bool | operator== (const Congruence &x, const Congruence &y) |
| bool | operator!= (const Congruence &x, const Congruence &y) |
Related Functions | |
(Note that these are not member functions.) | |
| std::ostream & | operator<< (std::ostream &s, const Congruence &c) |
| bool | operator== (const Congruence &x, const Congruence &y) |
Returns true if and only if x and y are equivalent. More... | |
| bool | operator!= (const Congruence &x, const Congruence &y) |
Returns false if and only if x and y are equivalent. More... | |
| std::ostream & | operator<< (std::ostream &s, const Congruence &c) |
| Output operators. More... | |
| Congruence | operator%= (const Linear_Expression &e1, const Linear_Expression &e2) |
Returns the congruence 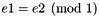 . More... . More... | |
| Congruence | operator%= (const Linear_Expression &e, Coefficient_traits::const_reference n) |
Returns the congruence 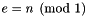 . More... . More... | |
| Congruence | operator/ (const Congruence &cg, Coefficient_traits::const_reference k) |
Returns a copy of cg, multiplying k into the copy's modulus. More... | |
| Congruence | operator/ (const Constraint &c, Coefficient_traits::const_reference m) |
Creates a congruence from c, with m as the modulus. More... | |
| void | swap (Congruence &x, Congruence &y) |
| Congruence | operator%= (const Linear_Expression &e1, const Linear_Expression &e2) |
| Congruence | operator%= (const Linear_Expression &e, Coefficient_traits::const_reference n) |
| Congruence | operator/ (const Congruence &cg, Coefficient_traits::const_reference k) |
| Congruence | operator/ (const Constraint &c, Coefficient_traits::const_reference m) |
| bool | operator== (const Congruence &x, const Congruence &y) |
| bool | operator!= (const Congruence &x, const Congruence &y) |
| void | swap (Congruence &x, Congruence &y) |
Detailed Description
A linear congruence.
An object of the class Congruence is a congruence:
where  is the dimension of the space,
is the dimension of the space, 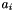 is the integer coefficient of variable
is the integer coefficient of variable 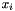 ,
, 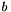 is the integer inhomogeneous term and
is the integer inhomogeneous term and 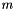 is the integer modulus; if
is the integer modulus; if 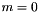 , then
, then 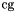 represents the equality congruence
represents the equality congruence 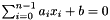 and, if
and, if 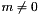 , then the congruence
, then the congruence 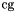 is said to be a proper congruence.
is said to be a proper congruence.
- How to build a congruence
- Congruences
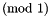 are typically built by applying the congruence symbol `
are typically built by applying the congruence symbol `%=' to a pair of linear expressions. Congruences with modulusmare typically constructed by building a congruence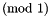 using the given pair of linear expressions and then adding the modulus
using the given pair of linear expressions and then adding the modulus musing the modulus symbol is `/'.
The space dimension of a congruence is defined as the maximum space dimension of the arguments of its constructor.
- In the following examples it is assumed that variables
x,yandzare defined as follows:Variable x(0);Variable y(1);Variable z(2);
- Example 1
- The following code builds the equality congruence
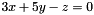 , having space dimension
, having space dimension 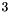 : The following code builds the congruenceCongruence eq_cg((3*x + 5*y - z %= 0) / 0);
: The following code builds the congruenceCongruence eq_cg((3*x + 5*y - z %= 0) / 0);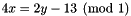 , having space dimension
, having space dimension 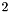 : The following code builds the congruenceCongruence mod1_cg(4*x %= 2*y - 13);
: The following code builds the congruenceCongruence mod1_cg(4*x %= 2*y - 13);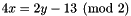 , having space dimension
, having space dimension 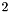 : An unsatisfiable congruence on the zero-dimension spaceCongruence mod2_cg((4*x %= 2*y - 13) / 2);
: An unsatisfiable congruence on the zero-dimension spaceCongruence mod2_cg((4*x %= 2*y - 13) / 2);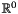 can be specified as follows: Equivalent, but more involved ways are the following:Congruence false_cg = Congruence::zero_dim_false();In contrast, the following code defines an unsatisfiable congruence having space dimensionCongruence false_cg1((Linear_Expression::zero() %= 1) / 0);Congruence false_cg2((Linear_Expression::zero() %= 1) / 2);
can be specified as follows: Equivalent, but more involved ways are the following:Congruence false_cg = Congruence::zero_dim_false();In contrast, the following code defines an unsatisfiable congruence having space dimensionCongruence false_cg1((Linear_Expression::zero() %= 1) / 0);Congruence false_cg2((Linear_Expression::zero() %= 1) / 2);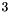 : Congruence false_cg3((0*z %= 1) / 0);
: Congruence false_cg3((0*z %= 1) / 0);
- How to inspect a congruence
- Several methods are provided to examine a congruence and extract all the encoded information: its space dimension, its modulus and the value of its integer coefficients.
- Example 2
- The following code shows how it is possible to access the modulus as well as each of the coefficients. Given a congruence with linear expression
eand modulusm(in this case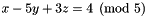 ), we construct a new congruence with the same modulus
), we construct a new congruence with the same modulus mbut where the linear expression is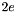 (
( 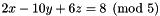 ). The actual output could be the following:Congruence cg1((x - 5*y + 3*z %= 4) / 5);cout << "Congruence cg1: " << cg1 << endl;const Coefficient& m = cg1.modulus();if (m == 0)cout << "Congruence cg1 is an equality." << endl;else {Linear_Expression e;for (dimension_type i = cg1.space_dimension(); i-- > 0; )e += 2 * cg1.coefficient(Variable(i)) * Variable(i);e += 2 * cg1.inhomogeneous_term();Congruence cg2((e %= 0) / m);cout << "Congruence cg2: " << cg2 << endl;}Note that, in general, the particular output obtained can be syntactically different from the (semantically equivalent) congruence considered.Congruence cg1: A - 5*B + 3*C %= 4 / 5Congruence cg2: 2*A - 10*B + 6*C %= 8 / 5
). The actual output could be the following:Congruence cg1((x - 5*y + 3*z %= 4) / 5);cout << "Congruence cg1: " << cg1 << endl;const Coefficient& m = cg1.modulus();if (m == 0)cout << "Congruence cg1 is an equality." << endl;else {Linear_Expression e;for (dimension_type i = cg1.space_dimension(); i-- > 0; )e += 2 * cg1.coefficient(Variable(i)) * Variable(i);e += 2 * cg1.inhomogeneous_term();Congruence cg2((e %= 0) / m);cout << "Congruence cg2: " << cg2 << endl;}Note that, in general, the particular output obtained can be syntactically different from the (semantically equivalent) congruence considered.Congruence cg1: A - 5*B + 3*C %= 4 / 5Congruence cg2: 2*A - 10*B + 6*C %= 8 / 5
Definition at line 161 of file Congruence_defs.hh.
Member Typedef Documentation
| typedef Expression_Adapter_Transparent<Linear_Expression> Parma_Polyhedra_Library::Congruence::expr_type |
The type of the (adapted) internal expression.
Definition at line 214 of file Congruence_defs.hh.
Constructor & Destructor Documentation
|
inlineexplicit |
Constructs the 0 = 0 congruence with space dimension 0 .
Definition at line 32 of file Congruence_inlines.hh.
References OK().
|
inline |
Ordinary copy constructor.
- Note
- The new Congruence will have the same representation as `cg', not default_representation, so that they are indistinguishable.
Definition at line 38 of file Congruence_inlines.hh.
|
inline |
Copy constructor with specified representation.
Definition at line 43 of file Congruence_inlines.hh.
|
explicit |
Copy-constructs (modulo 0) from equality constraint c.
- Exceptions
-
std::invalid_argument Thrown if cis an inequality.
Definition at line 36 of file Congruence.cc.
References Parma_Polyhedra_Library::Constraint::is_equality(), and throw_invalid_argument().
|
inline |
|
inline |
Copy-constructs with the specified space dimension.
- Note
- The new Congruence will have the same representation as `cg', not default_representation, for consistency with the copy constructor.
Definition at line 48 of file Congruence_inlines.hh.
References OK().
|
inline |
Copy-constructs with the specified space dimension and representation.
Definition at line 55 of file Congruence_inlines.hh.
References OK().
| Parma_Polyhedra_Library::Congruence::Congruence | ( | const Constraint & | cg, |
| dimension_type | new_space_dimension, | ||
| Representation | r = default_representation |
||
| ) |
Copy-constructs from a constraint, with the specified space dimension and (optional) representation.
Definition at line 45 of file Congruence.cc.
References Parma_Polyhedra_Library::Constraint::is_equality(), and throw_invalid_argument().
|
inline |
Constructs from Linear_Expression le, using modulus m.
Builds a congruence with modulus m, stealing the coefficients from le.
- Note
- The new Congruence will have the same representation as `le'.
- Parameters
-
le The Linear_Expression holding the coefficients. m The modulus for the congruence, which must be zero or greater.
Definition at line 93 of file Congruence_inlines.hh.
References expr, OK(), and swap().
Member Function Documentation
| void Parma_Polyhedra_Library::Congruence::affine_preimage | ( | Variable | v, |
| const Linear_Expression & | expr, | ||
| Coefficient_traits::const_reference | denominator | ||
| ) |
Definition at line 115 of file Congruence.cc.
References c, Parma_Polyhedra_Library::Coefficient_zero(), Parma_Polyhedra_Library::Linear_Expression::get(), PPL_DIRTY_TEMP_COEFFICIENT, Parma_Polyhedra_Library::Variable::space_dimension(), and Parma_Polyhedra_Library::Linear_Expression::space_dimension().
| void Parma_Polyhedra_Library::Congruence::ascii_dump | ( | ) | const |
Writes to std::cerr an ASCII representation of *this.
| void Parma_Polyhedra_Library::Congruence::ascii_dump | ( | std::ostream & | s | ) | const |
Writes to s an ASCII representation of *this.
Definition at line 227 of file Congruence.cc.
| bool Parma_Polyhedra_Library::Congruence::ascii_load | ( | std::istream & | s | ) |
Loads from s an ASCII representation of the internal representation of *this.
Definition at line 235 of file Congruence.cc.
Referenced by Parma_Polyhedra_Library::Congruence_System::ascii_load().
|
inline |
Returns the coefficient of v in *this.
- Exceptions
-
std::invalid_argument thrown if the index of vis greater than or equal to the space dimension of*this.
Definition at line 210 of file Congruence_inlines.hh.
References Parma_Polyhedra_Library::Linear_Expression::coefficient(), expr, Parma_Polyhedra_Library::Variable::space_dimension(), space_dimension(), and throw_dimension_incompatible().
Referenced by Parma_Polyhedra_Library::Box< ITV >::add_congruence_no_check(), Parma_Polyhedra_Library::Grid::expand_space_dimension(), and is_equal_at_dimension().
|
static |
Returns the congruence 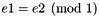 .
.
Definition at line 139 of file Congruence.cc.
References Parma_Polyhedra_Library::Linear_Expression::space_dimension().
Referenced by operator%=().
|
inlinestatic |
Returns the congruence 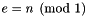 .
.
Definition at line 104 of file Congruence_inlines.hh.
|
inlinestatic |
Returns the congruence 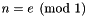 .
.
Definition at line 114 of file Congruence_inlines.hh.
|
inline |
Partial read access to the (adapted) internal expression.
Definition at line 73 of file Congruence_inlines.hh.
References expr.
Referenced by Parma_Polyhedra_Library::Polyhedron::add_congruence(), Parma_Polyhedra_Library::Polyhedron::add_congruences(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::approximate_partition_aux(), Parma_Polyhedra_Library::Grid::conversion(), Parma_Polyhedra_Library::Grid::difference_assign(), Parma_Polyhedra_Library::Box_Helpers::extract_interval_congruence(), operator<<(), Parma_Polyhedra_Library::Polyhedron::refine_with_congruence(), Parma_Polyhedra_Library::Box< ITV >::relation_with(), Parma_Polyhedra_Library::Polyhedron::relation_with(), Parma_Polyhedra_Library::Octagonal_Shape< T >::relation_with(), Parma_Polyhedra_Library::BD_Shape< T >::relation_with(), Parma_Polyhedra_Library::shrink_to_congruence_no_check(), and Parma_Polyhedra_Library::Grid::simplify_using_context_assign().
|
inline |
Returns the size in bytes of the memory managed by *this.
Definition at line 255 of file Congruence_inlines.hh.
References expr, Parma_Polyhedra_Library::external_memory_in_bytes(), Parma_Polyhedra_Library::Linear_Expression::external_memory_in_bytes(), and modulus_.
Referenced by total_memory_in_bytes().
|
static |
Finalizes the class.
Definition at line 281 of file Congruence.cc.
Referenced by Parma_Polyhedra_Library::Init::~Init().
|
inline |
Returns the inhomogeneous term of *this.
Definition at line 223 of file Congruence_inlines.hh.
References expr, and Parma_Polyhedra_Library::Linear_Expression::inhomogeneous_term().
Referenced by Parma_Polyhedra_Library::Box< ITV >::add_congruence_no_check(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::approximate_partition_aux(), operator<<(), Parma_Polyhedra_Library::Box< ITV >::relation_with(), Parma_Polyhedra_Library::Grid::relation_with(), and Parma_Polyhedra_Library::Grid::simplify().
|
static |
Initializes the class.
Definition at line 270 of file Congruence.cc.
References Parma_Polyhedra_Library::Linear_Expression::zero().
Referenced by Parma_Polyhedra_Library::Init::Init().
|
inlineprivate |
Returns true if *this is equal to cg in dimension v.
Definition at line 249 of file Congruence_inlines.hh.
References coefficient(), and modulus().
Referenced by Parma_Polyhedra_Library::Grid::select_wider_congruences().
|
inline |
Returns true if *this is an equality.
A modulus of zero denotes a linear equality.
Definition at line 244 of file Congruence_inlines.hh.
References modulus().
Referenced by Parma_Polyhedra_Library::Polyhedron::add_congruence(), Parma_Polyhedra_Library::BD_Shape< T >::add_congruence(), Parma_Polyhedra_Library::Octagonal_Shape< T >::add_congruence(), Parma_Polyhedra_Library::Box< ITV >::add_congruence_no_check(), Parma_Polyhedra_Library::Polyhedron::add_congruences(), Parma_Polyhedra_Library::Constraint::Constraint(), Parma_Polyhedra_Library::Box_Helpers::extract_interval_congruence(), Parma_Polyhedra_Library::Grid::multiply_grid(), Parma_Polyhedra_Library::Congruences_Reduction< D1, D2 >::product_reduce(), Parma_Polyhedra_Library::Box< ITV >::refine_no_check(), Parma_Polyhedra_Library::Octagonal_Shape< T >::refine_no_check(), Parma_Polyhedra_Library::BD_Shape< T >::refine_no_check(), Parma_Polyhedra_Library::Polyhedron::refine_with_congruence(), Parma_Polyhedra_Library::Box< ITV >::relation_with(), Parma_Polyhedra_Library::Polyhedron::relation_with(), Parma_Polyhedra_Library::Grid::relation_with(), Parma_Polyhedra_Library::Octagonal_Shape< T >::relation_with(), Parma_Polyhedra_Library::BD_Shape< T >::relation_with(), Parma_Polyhedra_Library::Congruence_System::satisfies_all_congruences(), Parma_Polyhedra_Library::Grid::simplify(), and Parma_Polyhedra_Library::Grid::simplify_using_context_assign().
| bool Parma_Polyhedra_Library::Congruence::is_inconsistent | ( | ) | const |
Returns true if and only if *this is inconsistent (i.e., an always false congruence).
An inconsistent congruence has one of the following two forms:
- an equality:
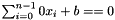 where
where 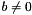 ; or
; or - a proper congruence:
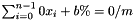 , where
, where 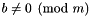 .
.
Definition at line 218 of file Congruence.cc.
Referenced by Parma_Polyhedra_Library::Polyhedron::add_congruence(), Parma_Polyhedra_Library::BD_Shape< T >::add_congruence(), Parma_Polyhedra_Library::Octagonal_Shape< T >::add_congruence(), Parma_Polyhedra_Library::Box< ITV >::add_congruence_no_check(), Parma_Polyhedra_Library::Grid::add_congruence_no_check(), Parma_Polyhedra_Library::Polyhedron::add_congruences(), Parma_Polyhedra_Library::Box< ITV >::refine_no_check(), Parma_Polyhedra_Library::Octagonal_Shape< T >::refine_no_check(), Parma_Polyhedra_Library::BD_Shape< T >::refine_no_check(), Parma_Polyhedra_Library::Box< ITV >::relation_with(), Parma_Polyhedra_Library::Polyhedron::relation_with(), Parma_Polyhedra_Library::Grid::relation_with(), Parma_Polyhedra_Library::Octagonal_Shape< T >::relation_with(), and Parma_Polyhedra_Library::BD_Shape< T >::relation_with().
|
inline |
Returns true if the modulus is greater than zero.
A congruence with a modulus of 0 is a linear equality.
Definition at line 239 of file Congruence_inlines.hh.
References modulus().
Referenced by Parma_Polyhedra_Library::Polyhedron::add_congruence(), Parma_Polyhedra_Library::BD_Shape< T >::add_congruence(), Parma_Polyhedra_Library::Octagonal_Shape< T >::add_congruence(), Parma_Polyhedra_Library::Box< ITV >::add_congruence_no_check(), Parma_Polyhedra_Library::Polyhedron::add_congruences(), Parma_Polyhedra_Library::Grid::conversion(), Parma_Polyhedra_Library::Grid::difference_assign(), Parma_Polyhedra_Library::Grid::multiply_grid(), Parma_Polyhedra_Library::Congruence_System::num_proper_congruences(), operator<<(), Parma_Polyhedra_Library::Grid::reduce_congruence_with_equality(), Parma_Polyhedra_Library::Box< ITV >::refine_no_check(), Parma_Polyhedra_Library::Octagonal_Shape< T >::refine_no_check(), Parma_Polyhedra_Library::BD_Shape< T >::refine_no_check(), Parma_Polyhedra_Library::Grid::relation_with(), Parma_Polyhedra_Library::Grid::simplify(), and Parma_Polyhedra_Library::Grid::simplify_using_context_assign().
| bool Parma_Polyhedra_Library::Congruence::is_tautological | ( | ) | const |
Returns true if and only if *this is a tautology (i.e., an always true congruence).
A tautological congruence has one the following two forms:
- an equality:
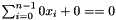 ; or
; or - a proper congruence:
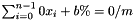 , where
, where 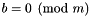 .
.
Definition at line 210 of file Congruence.cc.
Referenced by Parma_Polyhedra_Library::Polyhedron::add_congruence(), Parma_Polyhedra_Library::BD_Shape< T >::add_congruence(), Parma_Polyhedra_Library::Octagonal_Shape< T >::add_congruence(), Parma_Polyhedra_Library::Box< ITV >::add_congruence_no_check(), Parma_Polyhedra_Library::Polyhedron::add_congruences(), Parma_Polyhedra_Library::Polyhedron::refine_with_congruence(), and Parma_Polyhedra_Library::Grid::simplify_using_context_assign().
|
inline |
Swaps *this with y.
Definition at line 266 of file Congruence_inlines.hh.
References expr, modulus_, swap(), and Parma_Polyhedra_Library::swap().
Referenced by swap().
|
inlinestatic |
Returns the maximum space dimension a Congruence can handle.
Definition at line 200 of file Congruence_inlines.hh.
References Parma_Polyhedra_Library::Linear_Expression::max_space_dimension().
Referenced by Parma_Polyhedra_Library::Congruence_System::max_space_dimension().
|
inline |
Returns a const reference to the modulus of *this.
Definition at line 228 of file Congruence_inlines.hh.
References modulus_.
Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::approximate_partition_aux(), Parma_Polyhedra_Library::Grid::difference_assign(), is_equal_at_dimension(), is_equality(), is_proper_congruence(), operator<<(), operator==(), Parma_Polyhedra_Library::Grid::reduce_congruence_with_equality(), Parma_Polyhedra_Library::Grid::reduce_equality_with_equality(), Parma_Polyhedra_Library::Box< ITV >::relation_with(), Parma_Polyhedra_Library::Polyhedron::relation_with(), Parma_Polyhedra_Library::Grid::relation_with(), Parma_Polyhedra_Library::Octagonal_Shape< T >::relation_with(), Parma_Polyhedra_Library::BD_Shape< T >::relation_with(), Parma_Polyhedra_Library::Congruence_System::satisfies_all_congruences(), Parma_Polyhedra_Library::shrink_to_congruence_no_check(), Parma_Polyhedra_Library::Grid::simplify(), and Parma_Polyhedra_Library::Grid::simplify_using_context_assign().
| void Parma_Polyhedra_Library::Congruence::normalize | ( | ) |
Normalizes signs and the inhomogeneous term.
Applies sign_normalize, then reduces the inhomogeneous term to the smallest possible positive number.
Definition at line 62 of file Congruence.cc.
References c, and PPL_DIRTY_TEMP_COEFFICIENT.
| bool Parma_Polyhedra_Library::Congruence::OK | ( | ) | const |
Checks if all the invariants are satisfied.
Definition at line 252 of file Congruence.cc.
Referenced by Congruence(), Parma_Polyhedra_Library::Congruence_System::insert(), Parma_Polyhedra_Library::Congruence_System::insert_verbatim(), Parma_Polyhedra_Library::Congruence_System::OK(), Parma_Polyhedra_Library::Grid::reduce_equality_with_equality(), set_modulus(), and set_space_dimension().
|
inline |
Multiplies k into the modulus of *this.
If called with *this representing the congruence 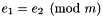 , then it returns with *this representing the congruence
, then it returns with *this representing the congruence 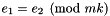 .
.
Definition at line 169 of file Congruence_inlines.hh.
References modulus_.
|
inline |
Assignment operator.
Definition at line 154 of file Congruence_inlines.hh.
References swap().
|
inline |
Definition at line 218 of file Congruence_inlines.hh.
References expr, and Parma_Polyhedra_Library::Linear_Expression::permute_space_dimensions().
Referenced by Parma_Polyhedra_Library::Congruence_System::permute_space_dimensions().
| void Parma_Polyhedra_Library::Congruence::print | ( | ) | const |
Prints *this to std::cerr using operator<<.
|
inline |
Returns the current representation of *this.
Definition at line 63 of file Congruence_inlines.hh.
References expr, and Parma_Polyhedra_Library::Linear_Expression::representation().
Referenced by Parma_Polyhedra_Library::Congruence_System::OK().
| void Parma_Polyhedra_Library::Congruence::scale | ( | Coefficient_traits::const_reference | factor | ) |
Multiplies all the coefficients, including the modulus, by factor .
Definition at line 103 of file Congruence.cc.
Referenced by Parma_Polyhedra_Library::Grid::multiply_grid(), and Parma_Polyhedra_Library::Grid::reduce_congruence_with_equality().
|
inline |
Sets the modulus of *this to m . If m is 0, the congruence becomes an equality.
Definition at line 233 of file Congruence_inlines.hh.
References modulus_, and OK().
Referenced by Parma_Polyhedra_Library::Grid::conversion(), and Parma_Polyhedra_Library::Grid::simplify().
|
inline |
Converts *this to the specified representation.
Definition at line 68 of file Congruence_inlines.hh.
References expr, and Parma_Polyhedra_Library::Linear_Expression::set_representation().
Referenced by Parma_Polyhedra_Library::Congruence_System::concatenate(), and Parma_Polyhedra_Library::Congruence_System::insert_verbatim().
|
inline |
Sets the space dimension by n , adding or removing coefficients as needed.
Definition at line 78 of file Congruence_inlines.hh.
References expr, OK(), and Parma_Polyhedra_Library::Linear_Expression::set_space_dimension().
Referenced by Parma_Polyhedra_Library::Congruence_System::insert_verbatim(), and Parma_Polyhedra_Library::Grid::simplify().
|
inline |
Shift by n positions the coefficients of variables, starting from the coefficient of v. This increases the space dimension by n.
Definition at line 84 of file Congruence_inlines.hh.
References expr, and Parma_Polyhedra_Library::Linear_Expression::shift_space_dimensions().
Referenced by Parma_Polyhedra_Library::Congruence_System::concatenate().
| void Parma_Polyhedra_Library::Congruence::sign_normalize | ( | ) |
Normalizes the signs.
The signs of the coefficients and the inhomogeneous term are normalized, leaving the first non-zero homogeneous coefficient positive.
Definition at line 57 of file Congruence.cc.
|
inline |
Returns the dimension of the vector space enclosing *this.
Definition at line 205 of file Congruence_inlines.hh.
References expr, and Parma_Polyhedra_Library::Linear_Expression::space_dimension().
Referenced by Parma_Polyhedra_Library::Box< ITV >::add_congruence(), Parma_Polyhedra_Library::Polyhedron::add_congruence(), Parma_Polyhedra_Library::BD_Shape< T >::add_congruence(), Parma_Polyhedra_Library::Grid::add_congruence(), Parma_Polyhedra_Library::Octagonal_Shape< T >::add_congruence(), Parma_Polyhedra_Library::Box< ITV >::add_congruence_no_check(), Parma_Polyhedra_Library::Grid::add_congruence_no_check(), Parma_Polyhedra_Library::Scalar_Products::assign(), coefficient(), Parma_Polyhedra_Library::Box_Helpers::extract_interval_congruence(), Parma_Polyhedra_Library::Scalar_Products::homogeneous_assign(), Parma_Polyhedra_Library::Congruence_System::insert_verbatim(), Parma_Polyhedra_Library::Congruence_System::OK(), operator<<(), operator==(), Parma_Polyhedra_Library::Scalar_Products::reduced_assign(), Parma_Polyhedra_Library::Box< ITV >::refine_no_check(), Parma_Polyhedra_Library::Octagonal_Shape< T >::refine_no_check(), Parma_Polyhedra_Library::BD_Shape< T >::refine_no_check(), Parma_Polyhedra_Library::Box< ITV >::refine_with_congruence(), Parma_Polyhedra_Library::Polyhedron::refine_with_congruence(), Parma_Polyhedra_Library::BD_Shape< T >::refine_with_congruence(), Parma_Polyhedra_Library::Octagonal_Shape< T >::refine_with_congruence(), Parma_Polyhedra_Library::Box< ITV >::relation_with(), Parma_Polyhedra_Library::Polyhedron::relation_with(), Parma_Polyhedra_Library::Grid::relation_with(), Parma_Polyhedra_Library::Octagonal_Shape< T >::relation_with(), Parma_Polyhedra_Library::BD_Shape< T >::relation_with(), Parma_Polyhedra_Library::Box< ITV >::throw_dimension_incompatible(), Parma_Polyhedra_Library::Octagonal_Shape< T >::throw_dimension_incompatible(), Parma_Polyhedra_Library::BD_Shape< T >::throw_dimension_incompatible(), Parma_Polyhedra_Library::Grid::throw_dimension_incompatible(), and Parma_Polyhedra_Library::Polyhedron::throw_dimension_incompatible().
| void Parma_Polyhedra_Library::Congruence::strong_normalize | ( | ) |
Calls normalize, then divides out common factors.
Strongly normalized Congruences have equivalent semantics if and only if they have the same syntax (as output by operator<<).
Definition at line 84 of file Congruence.cc.
References Parma_Polyhedra_Library::gcd_assign().
Referenced by Parma_Polyhedra_Library::Congruence_System::insert(), Parma_Polyhedra_Library::Congruence_System::operator<<(), and operator==().
Swaps the coefficients of the variables v1 and v2 .
Definition at line 273 of file Congruence_inlines.hh.
References expr, and Parma_Polyhedra_Library::Linear_Expression::swap_space_dimensions().
|
private |
Throws a std::invalid_argument exception containing the appropriate error message.
Definition at line 159 of file Congruence.cc.
References Parma_Polyhedra_Library::Variable::space_dimension().
Referenced by coefficient().
|
private |
Throws a std::invalid_argument exception containing error message message.
Definition at line 150 of file Congruence.cc.
Referenced by Congruence().
|
inline |
Returns a lower bound to the total size in bytes of the memory occupied by *this.
Definition at line 261 of file Congruence_inlines.hh.
References external_memory_in_bytes().
|
inlinestatic |
Returns a reference to the false (zero-dimension space) congruence 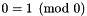 .
.
Definition at line 149 of file Congruence_inlines.hh.
References zero_dim_false_p.
Referenced by Parma_Polyhedra_Library::Box< ITV >::congruences(), Parma_Polyhedra_Library::Grid::construct(), Parma_Polyhedra_Library::Grid::Grid(), Parma_Polyhedra_Library::Congruence_System::initialize(), Parma_Polyhedra_Library::BD_Shape< T >::minimized_congruences(), Parma_Polyhedra_Library::Octagonal_Shape< T >::minimized_congruences(), Parma_Polyhedra_Library::Grid::remove_higher_space_dimensions(), and Parma_Polyhedra_Library::Grid::set_empty().
|
inlinestatic |
Returns a reference to the true (zero-dimension space) congruence 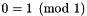 , also known as the integrality congruence.
, also known as the integrality congruence.
Definition at line 144 of file Congruence_inlines.hh.
References zero_dim_integrality_p.
Referenced by Parma_Polyhedra_Library::Grid::construct().
Friends And Related Function Documentation
|
friend |
Definition at line 458 of file Congruence_defs.hh.
|
related |
Returns false if and only if x and y are equivalent.
|
related |
Definition at line 195 of file Congruence_inlines.hh.
|
friend |
|
related |
Definition at line 125 of file Congruence_inlines.hh.
References create().
|
related |
Definition at line 131 of file Congruence_inlines.hh.
References create().
|
related |
Returns the congruence 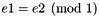 .
.
|
related |
Returns the congruence 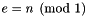 .
.
|
related |
Definition at line 137 of file Congruence_inlines.hh.
|
related |
Definition at line 162 of file Congruence_inlines.hh.
|
related |
Returns a copy of cg, multiplying k into the copy's modulus.
If cg represents the congruence 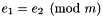 , then the result represents the congruence
, then the result represents the congruence 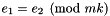 .
.
|
related |
Creates a congruence from c, with m as the modulus.
|
related |
Definition at line 171 of file Congruence.cc.
References Parma_Polyhedra_Library::Expression_Adapter< T >::begin(), Parma_Polyhedra_Library::Coefficient_zero(), expression(), inhomogeneous_term(), is_proper_congruence(), Parma_Polyhedra_Library::Expression_Adapter< T >::lower_bound(), modulus(), Parma_Polyhedra_Library::neg_assign(), PPL_DIRTY_TEMP_COEFFICIENT, and space_dimension().
|
related |
Output operators.
|
related |
Returns true if and only if x and y are equivalent.
|
related |
Definition at line 181 of file Congruence_inlines.hh.
References expr, Parma_Polyhedra_Library::Linear_Expression::is_equal_to(), modulus(), space_dimension(), and strong_normalize().
|
friend |
|
friend |
Definition at line 457 of file Congruence_defs.hh.
|
related |
Definition at line 279 of file Congruence_inlines.hh.
References m_swap().
|
related |
Referenced by Congruence(), m_swap(), and operator=().
Member Data Documentation
|
static |
The representation used for new Congruences.
- Note
- The copy constructor and the copy constructor with specified size use the representation of the original object, so that it is indistinguishable from the original object.
Definition at line 170 of file Congruence_defs.hh.
|
private |
Definition at line 424 of file Congruence_defs.hh.
Referenced by Parma_Polyhedra_Library::Scalar_Products::assign(), coefficient(), Congruence(), Parma_Polyhedra_Library::Grid::conversion(), Parma_Polyhedra_Library::Grid::expand_space_dimension(), expression(), external_memory_in_bytes(), Parma_Polyhedra_Library::Scalar_Products::homogeneous_assign(), inhomogeneous_term(), Parma_Polyhedra_Library::Grid::lower_triangular(), m_swap(), operator==(), permute_space_dimensions(), Parma_Polyhedra_Library::Grid::reduce_congruence_with_equality(), Parma_Polyhedra_Library::Grid::reduce_equality_with_equality(), Parma_Polyhedra_Library::Scalar_Products::reduced_assign(), representation(), set_representation(), set_space_dimension(), shift_space_dimensions(), Parma_Polyhedra_Library::Grid::simplify(), space_dimension(), and swap_space_dimensions().
|
private |
Definition at line 426 of file Congruence_defs.hh.
Referenced by external_memory_in_bytes(), m_swap(), modulus(), operator/=(), and set_modulus().
|
staticprivate |
Holds (between class initialization and finalization) a pointer to the false (zero-dimension space) congruence 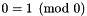 .
.
Definition at line 415 of file Congruence_defs.hh.
Referenced by zero_dim_false().
|
staticprivate |
Holds (between class initialization and finalization) a pointer to the true (zero-dimension space) congruence 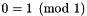 , also known as the integrality congruence.
, also known as the integrality congruence.
Definition at line 422 of file Congruence_defs.hh.
Referenced by zero_dim_integrality().
The documentation for this class was generated from the following files: