A sparse matrix of Coefficient. More...

#include <Matrix_defs.hh>

Inheritance diagram for Parma_Polyhedra_Library::Matrix< Row >:

Collaboration diagram for Parma_Polyhedra_Library::Matrix< Row >:

Public Types
typedef Swapping_Vector< Row >::iterator	iterator

typedef Swapping_Vector< Row >::const_iterator	const_iterator

Public Member Functions
	Matrix (dimension_type n=0)
	Constructs a square matrix with the given size, filled with unstored zeroes. More...

	Matrix (dimension_type num_rows, dimension_type num_columns)
	Constructs a matrix with the given dimensions, filled with unstored zeroes. More...

void	m_swap (Matrix &x)
	Swaps (*this) with x. More...

dimension_type	num_rows () const
	Returns the number of rows in the matrix. More...

dimension_type	num_columns () const
	Returns the number of columns in the matrix. More...

dimension_type	capacity () const
	Returns the capacity of the row vector. More...

bool	has_no_rows () const
	Returns `true` if and only if `*this` has no rows. More...

void	resize (dimension_type n)
	Equivalent to resize(n, n). More...

void	reserve_rows (dimension_type n)
	Reserves space for at least `n` rows. More...

void	resize (dimension_type num_rows, dimension_type num_columns)
	Resizes this matrix to the specified dimensions. More...

void	add_zero_rows_and_columns (dimension_type n, dimension_type m)
	Adds `n` rows and `m` columns of zeroes to the matrix. More...

void	add_zero_rows (dimension_type n)
	Adds to the matrix `n` rows of zeroes. More...

void	add_row (const Row &x)
	Adds a copy of the row `x` at the end of the matrix. More...

void	add_recycled_row (Row &y)
	Adds the row `y` to the matrix. More...

void	remove_trailing_rows (dimension_type n)
	Removes from the matrix the last `n` rows. More...

void	remove_rows (iterator first, iterator last)

void	permute_columns (const std::vector< dimension_type > &cycles)
	Permutes the columns of the matrix. More...

void	swap_columns (dimension_type i, dimension_type j)
	Swaps the columns having indexes `i` and `j`. More...

void	add_zero_columns (dimension_type n)
	Adds `n` columns of zeroes to the matrix. More...

void	add_zero_columns (dimension_type n, dimension_type i)
	Adds `n` columns of non-stored zeroes to the matrix before column i. More...

void	remove_column (dimension_type i)
	Removes the i-th from the matrix, shifting other columns to the left. More...

void	remove_trailing_columns (dimension_type n)
	Shrinks the matrix by removing its `n` trailing columns. More...

void	clear ()
	Equivalent to resize(0,0). More...

iterator	begin ()
	Returns an iterator pointing to the first row. More...

iterator	end ()
	Returns an iterator pointing after the last row. More...

const_iterator	begin () const
	Returns an iterator pointing to the first row. More...

const_iterator	end () const
	Returns an iterator pointing after the last row. More...

Row &	operator[] (dimension_type i)
	Returns a reference to the i-th row. More...

const Row &	operator[] (dimension_type i) const
	Returns a const reference to the i-th row. More...

bool	ascii_load (std::istream &s)
	Loads the row from an ASCII representation generated using ascii_dump(). More...

void	ascii_dump () const
	Writes to `std::cerr` an ASCII representation of `*this`. More...

void	ascii_dump (std::ostream &s) const
	Writes to `s` an ASCII representation of `*this`. More...

void	print () const
	Prints `*this` to `std::cerr` using `operator<<`. More...

memory_size_type	total_memory_in_bytes () const
	Returns the total size in bytes of the memory occupied by `*this`. More...

memory_size_type	external_memory_in_bytes () const
	Returns the size in bytes of the memory managed by `*this`. More...

bool	OK () const
	Checks if all the invariants are satisfied. More...

Static Public Member Functions
static dimension_type	max_num_rows ()
	Returns the maximum number of rows of a Sparse_Matrix. More...

static dimension_type	max_num_columns ()
	Returns the maximum number of columns of a Sparse_Matrix. More...

Private Attributes
Swapping_Vector< Row >	rows
	The vector that stores the matrix's elements. More...

dimension_type	num_columns_
	The number of columns in this matrix. More...

Related Functions
(Note that these are not member functions.)
template<typename Row >
void	swap (Matrix< Row > &x, Matrix< Row > &y)

template<typename Row >
bool	operator== (const Matrix< Row > &x, const Matrix< Row > &y)
	Returns `true` if and only if `x` and `y` are identical. More...

template<typename Row >
bool	operator!= (const Matrix< Row > &x, const Matrix< Row > &y)
	Returns `true` if and only if `x` and `y` are different. More...

template<typename Row >
bool	operator== (const Matrix< Row > &x, const Matrix< Row > &y)

template<typename Row >
bool	operator!= (const Matrix< Row > &x, const Matrix< Row > &y)

Detailed Description

template<typename Row>
class Parma_Polyhedra_Library::Matrix< Row >

A sparse matrix of Coefficient.

Definition at line 37 of file Matrix_defs.hh.

Member Typedef Documentation

template<typename Row>

typedef Swapping_Vector<Row>::const_iterator Parma_Polyhedra_Library::Matrix< Row >::const_iterator

Definition at line 41 of file Matrix_defs.hh.

template<typename Row>

typedef Swapping_Vector<Row>::iterator Parma_Polyhedra_Library::Matrix< Row >::iterator

Definition at line 40 of file Matrix_defs.hh.

Constructor & Destructor Documentation

template<typename Row >

Parma_Polyhedra_Library::Matrix< Row >::Matrix ( dimension_type n = 0 )

explicit

Constructs a square matrix with the given size, filled with unstored zeroes.

Parameters

n	The size of the new square matrix.

This method takes $O(n)$ time.

Definition at line 30 of file Matrix_templates.hh.

References Parma_Polyhedra_Library::Matrix< Row >::num_columns_, Parma_Polyhedra_Library::Matrix< Row >::OK(), Parma_Polyhedra_Library::Swapping_Vector< T >::resize(), Parma_Polyhedra_Library::Matrix< Row >::rows, and Parma_Polyhedra_Library::Swapping_Vector< T >::size().

   : rows(n), num_columns_(n) {
   for (dimension_type i = 0; i < rows.size(); ++i) {
     rows[i].resize(num_columns_);
   }
   PPL_ASSERT(OK());
 }

template<typename Row >

Parma_Polyhedra_Library::Matrix< Row >::Matrix	(	dimension_type	num_rows,
		dimension_type	num_columns
	)

Constructs a matrix with the given dimensions, filled with unstored zeroes.

Parameters

num_rows	The number of rows in the new matrix.
num_columns	The number of columns in the new matrix.

This method takes $O(n)$ time, where n is num_rows.

Definition at line 39 of file Matrix_templates.hh.

References Parma_Polyhedra_Library::Matrix< Row >::num_columns_, Parma_Polyhedra_Library::Matrix< Row >::OK(), Parma_Polyhedra_Library::Swapping_Vector< T >::resize(), Parma_Polyhedra_Library::Matrix< Row >::rows, and Parma_Polyhedra_Library::Swapping_Vector< T >::size().

   : rows(num_rows), num_columns_(num_columns) {
   for (dimension_type i = 0; i < rows.size(); ++i) {
     rows[i].resize(num_columns_);
   }
   PPL_ASSERT(OK());
 }

Member Function Documentation

template<typename Row>

void Parma_Polyhedra_Library::Matrix< Row >::add_recycled_row ( Row & y )

inline

Adds the row y to the matrix.

Parameters

y	The row to be added: it must have the same size and capacity as `*this`. It is not declared `const` because its data-structures will recycled to build the new matrix row.

Turns the 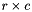$r \times c$ matrix 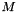$M$ into the 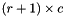$(r+1) \times c$ matrix 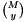$\genfrac{(}{)}{0pt}{}{M}{y}$ . The matrix is expanded avoiding reallocation whenever possible.

Definition at line 111 of file Matrix_inlines.hh.

References Parma_Polyhedra_Library::swap().

                                     {
   add_zero_rows(1);
   swap(rows.back(), x);
   PPL_ASSERT(OK());
 }

template<typename Row>

void Parma_Polyhedra_Library::Matrix< Row >::add_row ( const Row & x )

inline

Adds a copy of the row x at the end of the matrix.

Parameters

x	The row that will be appended to the matrix.

This operation invalidates existing iterators.

This method takes $O(n)$ amortized time, where n is the numer of elements stored in x.

Definition at line 100 of file Matrix_inlines.hh.

References Parma_Polyhedra_Library::swap().

Referenced by Parma_Polyhedra_Library::PIP_Tree_Node::compatibility_check(), and Parma_Polyhedra_Library::PIP_Solution_Node::solve().

                                  {
   // TODO: Optimize this.
   Row row(x);
   add_zero_rows(1);
   // Now x may have been invalidated, if it was a row of this matrix.
   swap(rows.back(), row);
   PPL_ASSERT(OK());
 }

template<typename Row >

void Parma_Polyhedra_Library::Matrix< Row >::add_zero_columns ( dimension_type n )

inline

Adds n columns of zeroes to the matrix.

Parameters

n	The number of columns to be added: must be strictly positive.

Turns the 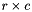$r \times c$ matrix 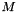$M$ into the 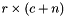$r \times (c+n)$ matrix $(M \, 0)$ .

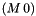This method takes 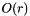$O(r)$ amortized time, where r is the numer of the matrix's rows.

Definition at line 131 of file Matrix_inlines.hh.

Referenced by Parma_Polyhedra_Library::PIP_Solution_Node::generate_cut().

                                               {
   resize(num_rows(), num_columns() + n);
 }

template<typename Row >

void Parma_Polyhedra_Library::Matrix< Row >::add_zero_columns	(	dimension_type	n,
		dimension_type	i
	)

Adds n columns of non-stored zeroes to the matrix before column i.

Parameters

n	The numer of columns that will be added.
i	The index of the column before which the new columns will be added.

This operation invalidates existing iterators.

This method takes 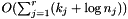$O(\sum_{j=1}^{r} (k_j+\log n_j))$ time, where r is the number of rows, 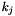$k_j$ is the number of elements stored in the columns of the j-th row that must be shifted and 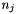$n_j$ is the number of elements stored in the j-th row. A weaker (but simpler) bound is 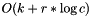$O(k+r*\log c)$ time, where k is the number of elements that must be shifted, r is the number of the rows and c is the number of the columns.

Definition at line 120 of file Matrix_templates.hh.

                                                                 {
   for (dimension_type j = rows.size(); j-- > 0; ) {
     rows[j].add_zeroes_and_shift(n, i);
   }
   num_columns_ += n;
   PPL_ASSERT(OK());
 }

template<typename Row >

void Parma_Polyhedra_Library::Matrix< Row >::add_zero_rows ( dimension_type n )

inline

Adds to the matrix n rows of zeroes.

Parameters

n	The number of rows to be added: must be strictly positive.

Turns the 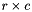$r \times c$ matrix 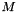$M$ into the 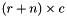$(r+n) \times c$ matrix 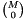$\genfrac{(}{)}{0pt}{}{M}{0}$ . The matrix is expanded avoiding reallocation whenever possible.

This method takes 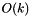$O(k)$ amortized time, where k is the number of the new rows.

Definition at line 94 of file Matrix_inlines.hh.

Referenced by Parma_Polyhedra_Library::PIP_Tree_Node::compatibility_check(), and Parma_Polyhedra_Library::PIP_Solution_Node::generate_cut().

                                            {
   resize(num_rows() + n, num_columns());
 }

template<typename Row >

void Parma_Polyhedra_Library::Matrix< Row >::add_zero_rows_and_columns	(	dimension_type	n,
		dimension_type	m
	)

inline

Adds n rows and m columns of zeroes to the matrix.

Parameters

n	The number of rows to be added: must be strictly positive.
m	The number of columns to be added: must be strictly positive.

Turns the 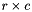$r \times c$ matrix 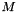$M$ into the 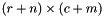$(r+n) \times (c+m)$ matrix 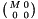$\bigl(\genfrac{}{}{0pt}{}{M}{0} \genfrac{}{}{0pt}{}{0}{0}\bigr)$ . The matrix is expanded avoiding reallocation whenever possible.

This method takes 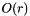$O(r)$ time, where r is the number of the matrix's rows after the operation.

Definition at line 88 of file Matrix_inlines.hh.

                                                                          {
   resize(num_rows() + n, num_columns() + m);
 }

template<typename Row >

void Parma_Polyhedra_Library::Matrix< Row >::ascii_dump ( std::ostream & s ) const

Writes to s an ASCII representation of *this.

Definition at line 140 of file Matrix_templates.hh.

                                            {
   s << num_rows() << " x ";
   s << num_columns() << "\n";
   for (const_iterator i = begin(), i_end = end(); i !=i_end; ++i) {
     i->ascii_dump(s);
   }
 }

template<typename Row>

void Parma_Polyhedra_Library::Matrix< Row >::ascii_dump ( ) const

Writes to std::cerr an ASCII representation of *this.

Referenced by Parma_Polyhedra_Library::PIP_Solution_Node::solve().

template<typename Row >

bool Parma_Polyhedra_Library::Matrix< Row >::ascii_load ( std::istream & s )

Loads the row from an ASCII representation generated using ascii_dump().

Parameters

s	The stream from which read the ASCII representation.

This method takes 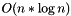$O(n*\log n)$ time.

Definition at line 152 of file Matrix_templates.hh.

References Parma_Polyhedra_Library::ascii_load().

                                      {
   std::string str;
   dimension_type new_num_rows;
   dimension_type new_num_cols;
   if (!(s >> new_num_rows)) {
     return false;
   }
   if (!(s >> str) || str != "x") {
     return false;
   }
   if (!(s >> new_num_cols)) {
     return false;
   }
 
   for (iterator i = rows.begin(), i_end = rows.end();
        i != i_end; ++i) {
     i->clear();
   }
 
   resize(new_num_rows, new_num_cols);
 
   for (dimension_type row = 0; row < new_num_rows; ++row) {
     if (!rows[row].ascii_load(s)) {
       return false;
     }
   }
 
   // Check invariants.
   PPL_ASSERT(OK());
   return true;
 }

template<typename Row >

Matrix< Row >::iterator Parma_Polyhedra_Library::Matrix< Row >::begin ( )

inline

Returns an iterator pointing to the first row.

This method takes $O(1)$ time.

Definition at line 150 of file Matrix_inlines.hh.

                    {
   return rows.begin();
 }

template<typename Row >

Matrix< Row >::const_iterator Parma_Polyhedra_Library::Matrix< Row >::begin ( ) const

inline

Returns an iterator pointing to the first row.

This method takes $O(1)$ time.

Definition at line 162 of file Matrix_inlines.hh.

                          {
   return rows.begin();
 }

template<typename Row >

dimension_type Parma_Polyhedra_Library::Matrix< Row >::capacity ( ) const

inline

Returns the capacity of the row vector.

Definition at line 63 of file Matrix_inlines.hh.

                             {
   return rows.capacity();
 }

template<typename Row >

void Parma_Polyhedra_Library::Matrix< Row >::clear ( )

inline

Equivalent to resize(0,0).

Definition at line 144 of file Matrix_inlines.hh.

                    {
   resize(0, 0);
 }

template<typename Row >

Matrix< Row >::iterator Parma_Polyhedra_Library::Matrix< Row >::end ( )

inline

Returns an iterator pointing after the last row.

This method takes $O(1)$ time.

Definition at line 156 of file Matrix_inlines.hh.

                  {
   return rows.end();
 }

template<typename Row >

Matrix< Row >::const_iterator Parma_Polyhedra_Library::Matrix< Row >::end ( ) const

inline

Returns an iterator pointing after the last row.

This method takes $O(1)$ time.

Definition at line 168 of file Matrix_inlines.hh.

                        {
   return rows.end();
 }

template<typename Row >

memory_size_type Parma_Polyhedra_Library::Matrix< Row >::external_memory_in_bytes ( ) const

Returns the size in bytes of the memory managed by *this.

This method is 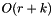$O(r+k)$ , where r is the number of rows and k is the number of elements stored in the matrix.

Definition at line 186 of file Matrix_templates.hh.

                                             {
   return rows.external_memory_in_bytes();
 }

template<typename Row >

bool Parma_Polyhedra_Library::Matrix< Row >::has_no_rows ( ) const

inline

Returns true if and only if *this has no rows.

Note: The unusual naming for this method is intentional: we do not want it to be named empty because this would cause an error prone name clash with the corresponding methods in derived classes Constraint_System and Congruence_System (which have a different semantics).

Definition at line 69 of file Matrix_inlines.hh.

                                {
   return num_rows() == 0;
 }

template<typename Row >

void Parma_Polyhedra_Library::Matrix< Row >::m_swap ( Matrix< Row > & x )

inline

Swaps (*this) with x.

Parameters

x	The matrix that will be swapped with *this.

This method takes $O(1)$ time.

Definition at line 43 of file Matrix_inlines.hh.

References Parma_Polyhedra_Library::Matrix< Row >::num_columns_, Parma_Polyhedra_Library::Matrix< Row >::rows, and Parma_Polyhedra_Library::swap().

Referenced by Parma_Polyhedra_Library::swap().

                              {
   using std::swap;
   swap(rows, x.rows);
   swap(num_columns_, x.num_columns_);
 }

template<typename Row >

dimension_type Parma_Polyhedra_Library::Matrix< Row >::max_num_columns ( )

inlinestatic

Returns the maximum number of columns of a Sparse_Matrix.

Definition at line 37 of file Matrix_inlines.hh.

                              {
   return Row::max_size();
 }

template<typename Row >

dimension_type Parma_Polyhedra_Library::Matrix< Row >::max_num_rows ( )

inlinestatic

Returns the maximum number of rows of a Sparse_Matrix.

Definition at line 31 of file Matrix_inlines.hh.

                           {
   return std::vector<Row>().max_size();
 }

template<typename Row >

dimension_type Parma_Polyhedra_Library::Matrix< Row >::num_columns ( ) const

inline

Returns the number of columns in the matrix.

This method takes $O(1)$ time.

Definition at line 57 of file Matrix_inlines.hh.

Referenced by Parma_Polyhedra_Library::PIP_Tree_Node::compatibility_check(), and Parma_Polyhedra_Library::Matrix< Row >::operator==().

                                {
   return num_columns_;
 }

template<typename Row >

dimension_type Parma_Polyhedra_Library::Matrix< Row >::num_rows ( ) const

inline

Returns the number of rows in the matrix.

This method takes $O(1)$ time.

Definition at line 51 of file Matrix_inlines.hh.

Referenced by Parma_Polyhedra_Library::PIP_Tree_Node::compatibility_check(), Parma_Polyhedra_Library::PIP_Solution_Node::generate_cut(), Parma_Polyhedra_Library::Matrix< Row >::operator==(), Parma_Polyhedra_Library::PIP_Solution_Node::solve(), and Parma_Polyhedra_Library::PIP_Decision_Node::solve().

                             {
   return rows.size();
 }

template<typename Row >

bool Parma_Polyhedra_Library::Matrix< Row >::OK ( ) const

Checks if all the invariants are satisfied.

Definition at line 192 of file Matrix_templates.hh.

Referenced by Parma_Polyhedra_Library::PIP_Tree_Node::compatibility_check(), and Parma_Polyhedra_Library::Matrix< Row >::Matrix().

                       {
   for (const_iterator i = begin(), i_end = end(); i != i_end; ++i) {
     if (i->size() != num_columns_) {
       return false;
     }
   }
   return true;
 }

template<typename Row >

Row & Parma_Polyhedra_Library::Matrix< Row >::operator[] ( dimension_type i )

inline

Returns a reference to the i-th row.

Parameters

i	The index of the desired row.

This method takes $O(1)$ time.

Definition at line 174 of file Matrix_inlines.hh.

                                         {
   PPL_ASSERT(i < rows.size());
   return rows[i];
 }

template<typename Row >

const Row & Parma_Polyhedra_Library::Matrix< Row >::operator[] ( dimension_type i ) const

inline

Returns a const reference to the i-th row.

Parameters

i	The index of the desired row.

This method takes $O(1)$ time.

Definition at line 181 of file Matrix_inlines.hh.

                                               {
   PPL_ASSERT(i < rows.size());
   return rows[i];
 }

template<typename Row >

void Parma_Polyhedra_Library::Matrix< Row >::permute_columns ( const std::vector< dimension_type > & cycles )

Permutes the columns of the matrix.

This method may be slow for some Row types, and should be avoided if possible.

Parameters

cycles A vector representing the non-trivial cycles of the permutation according to which the columns must be rearranged.

The cycles vector contains, one after the other, the non-trivial cycles (i.e., the cycles of length greater than one) of a permutation of non-zero column indexes. Each cycle is terminated by zero. For example, assuming the matrix has 7 columns, the permutation 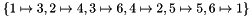$\{ 1 \mapsto 3, 2 \mapsto 4, 3 \mapsto 6, 4 \mapsto 2, 5 \mapsto 5, 6 \mapsto 1 \}$ can be represented by the non-trivial cycles 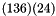$(1 3 6)(2 4)$ that, in turn can be represented by a vector of 6 elements containing 1, 3, 6, 0, 2, 4, 0.

This method takes 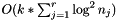$O(k*\sum_{j=1}^{r} \log^2 n_j)$ expected time, where k is the size of the cycles vector, r the number of rows and 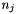$n_j$ the number of elements stored in row j. A weaker (but simpler) bound is 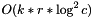$O(k*r*\log^2 c)$ , where k is the size of the cycles vector, r is the number of rows and c is the number of columns.

Note: The first column of the matrix, having index zero, is never involved in a permutation.

Definition at line 75 of file Matrix_templates.hh.

References PPL_DIRTY_TEMP_COEFFICIENT, and Parma_Polyhedra_Library::swap().

                                                                     {
   PPL_DIRTY_TEMP_COEFFICIENT(tmp);
   const dimension_type n = cycles.size();
   PPL_ASSERT(cycles[n - 1] == 0);
   for (dimension_type k = num_rows(); k-- > 0; ) {
     Row& rows_k = (*this)[k];
     for (dimension_type i = 0, j = 0; i < n; i = ++j) {
       // Make `j' be the index of the next cycle terminator.
       while (cycles[j] != 0) {
         ++j;
       }
       // Cycles of length less than 2 are not allowed.
       PPL_ASSERT(j - i >= 2);
       if (j - i == 2) {
         // For cycles of length 2 no temporary is needed, just a swap.
         rows_k.swap_coefficients(cycles[i], cycles[i + 1]);
       }
       else {
         // Longer cycles need a temporary.
         tmp = rows_k.get(cycles[j - 1]);
         for (dimension_type l = (j - 1); l > i; --l) {
           rows_k.swap_coefficients(cycles[l-1], cycles[l]);
         }
         if (tmp == 0) {
           rows_k.reset(cycles[i]);
         }
         else {
           using std::swap;
           swap(tmp, rows_k[cycles[i]]);
         }
       }
     }
   }
 }

template<typename Row>

void Parma_Polyhedra_Library::Matrix< Row >::print ( ) const

Prints *this to std::cerr using operator<<.

template<typename Row >

void Parma_Polyhedra_Library::Matrix< Row >::remove_column ( dimension_type i )

Removes the i-th from the matrix, shifting other columns to the left.

Parameters

i	The index of the column that will be removed.

This operation invalidates existing iterators on rows' elements.

This method takes 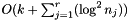$O(k + \sum_{j=1}^{r} (\log^2 n_j))$ amortized time, where k is the number of elements stored with column index greater than i, r the number of rows in this matrix and 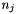$n_j$ the number of elements stored in row j. A weaker (but simpler) bound is 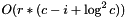$O(r*(c-i+\log^2 c))$ , where r is the number of rows, c is the number of columns and i is the parameter passed to this method.

Definition at line 130 of file Matrix_templates.hh.

                                            {
   for (dimension_type j = rows.size(); j-- > 0; ) {
     rows[j].delete_element_and_shift(i);
   }
   --num_columns_;
   PPL_ASSERT(OK());
 }

template<typename Row >

void Parma_Polyhedra_Library::Matrix< Row >::remove_rows	(	iterator	first,
		iterator	last
	)

inline

Definition at line 125 of file Matrix_inlines.hh.

                                                       {
   rows.erase(first, last);
 }

template<typename Row >

void Parma_Polyhedra_Library::Matrix< Row >::remove_trailing_columns ( dimension_type n )

inline

Shrinks the matrix by removing its n trailing columns.

Parameters

n	The number of trailing columns that will be removed.

This operation invalidates existing iterators.

This method takes 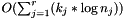$O(\sum_{j=1}^r (k_j*\log n_j))$ amortized time, where r is the number of rows, 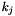$k_j$ is the number of elements that have to be removed from row j and 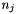$n_j$ is the total number of elements stored in row j. A weaker (but simpler) bound is 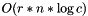$O(r*n*\log c)$ , where r is the number of rows, c the number of columns and n the parameter passed to this method.

Definition at line 137 of file Matrix_inlines.hh.

                                                      {
   PPL_ASSERT(n <= num_columns());
   resize(num_rows(), num_columns() - n);
 }

template<typename Row >

void Parma_Polyhedra_Library::Matrix< Row >::remove_trailing_rows ( dimension_type n )

inline

Removes from the matrix the last n rows.

Parameters

n	The number of row that will be removed.

It is equivalent to num_rows() - n, num_columns()).

This method takes 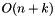$O(n+k)$ amortized time, where k is the total number of elements stored in the removed rows and n is the number of removed rows.

Definition at line 119 of file Matrix_inlines.hh.

Referenced by Parma_Polyhedra_Library::PIP_Tree_Node::compatibility_check().

                                                   {
   resize(num_rows() - n, num_columns());
 }

template<typename Row >

void Parma_Polyhedra_Library::Matrix< Row >::reserve_rows ( dimension_type n )

inline

Reserves space for at least n rows.

Definition at line 81 of file Matrix_inlines.hh.

                                                            {
 
   rows.reserve(requested_capacity);
 }

template<typename Row >

void Parma_Polyhedra_Library::Matrix< Row >::resize ( dimension_type n )

inline

Equivalent to resize(n, n).

Definition at line 75 of file Matrix_inlines.hh.

                                     {
   resize(n, n);
 }

template<typename Row >

void Parma_Polyhedra_Library::Matrix< Row >::resize	(	dimension_type	num_rows,
		dimension_type	num_columns
	)

Resizes this matrix to the specified dimensions.

Parameters

num_rows	The desired numer of rows.
num_columns	The desired numer of columns.

New rows and columns will contain non-stored zeroes.

This operation invalidates existing iterators.

Adding n rows takes $O(n)$ amortized time.

Adding n columns takes 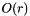$O(r)$ time, where r is num_rows.

Removing n rows takes 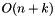$O(n+k)$ amortized time, where k is the total number of elements stored in the removed rows.

Removing n columns takes 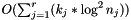$O(\sum_{j=1}^{r} (k_j*\log^2 n_j))$ time, where r is the number of rows, 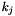$k_j$ is the number of elements stored in the columns of the j-th row that must be removed and 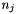$n_j$ is the total number of elements stored in the j-th row. A weaker (but simpler) bound is 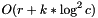$O(r+k*\log^2 c)$ , where r is the number of rows, k is the number of elements that have to be removed and c is the number of columns.

Definition at line 49 of file Matrix_templates.hh.

                                                                        {
   const dimension_type old_num_rows = rows.size();
   rows.resize(num_rows);
   if (old_num_rows < num_rows) {
     for (dimension_type i = old_num_rows; i < num_rows; ++i) {
       rows[i].resize(num_columns);
     }
     if (num_columns_ != num_columns) {
       num_columns_ = num_columns;
       for (dimension_type i = 0; i < old_num_rows; ++i) {
         rows[i].resize(num_columns);
       }
     }
   }
   else
     if (num_columns_ != num_columns) {
       num_columns_ = num_columns;
       for (dimension_type i = 0; i < num_rows; ++i) {
         rows[i].resize(num_columns);
       }
     }
   PPL_ASSERT(OK());
 }

template<typename Row >

void Parma_Polyhedra_Library::Matrix< Row >::swap_columns	(	dimension_type	i,
		dimension_type	j
	)

Swaps the columns having indexes i and j.

Definition at line 112 of file Matrix_templates.hh.

                                                             {
   for (dimension_type k = num_rows(); k-- > 0; ) {
     (*this)[k].swap_coefficients(i, j);
   }
 }

template<typename Row >

memory_size_type Parma_Polyhedra_Library::Matrix< Row >::total_memory_in_bytes ( ) const

inline

Returns the total size in bytes of the memory occupied by *this.

This method is 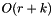$O(r+k)$ , where r is the number of rows and k is the number of elements stored in the matrix.

Definition at line 188 of file Matrix_inlines.hh.

References Parma_Polyhedra_Library::external_memory_in_bytes().

                                          {
   return sizeof(*this) + external_memory_in_bytes();
 }

Friends And Related Function Documentation

template<typename Row >

bool operator!=	(	const Matrix< Row > &	x,
		const Matrix< Row > &	y
	)

                                                        {
   return !(x == y);
 }

template<typename Row >

bool operator!=	(	const Matrix< Row > &	x,
		const Matrix< Row > &	y
	)

template<typename Row >

bool operator==	(	const Matrix< Row > &	x,
		const Matrix< Row > &	y
	)

References Parma_Polyhedra_Library::Matrix< Row >::num_columns(), and Parma_Polyhedra_Library::Matrix< Row >::num_rows().

                                                        {
   if (x.num_rows() != y.num_rows()) {
     return false;
   }
   if (x.num_columns() != y.num_columns()) {
     return false;
   }
   for (dimension_type i = x.num_rows(); i-- > 0; ) {
     if (x[i] != y[i]) {
       return false;
     }
   }
   return true;
 }

template<typename Row >

bool operator==	(	const Matrix< Row > &	x,
		const Matrix< Row > &	y
	)

template<typename Row >

void swap	(	Matrix< Row > &	x,
		Matrix< Row > &	y
	)

                                      {
   x.m_swap(y);
 }

Member Data Documentation

template<typename Row>

dimension_type Parma_Polyhedra_Library::Matrix< Row >::num_columns_

private

The number of columns in this matrix.

Definition at line 406 of file Matrix_defs.hh.

Referenced by Parma_Polyhedra_Library::Matrix< Row >::m_swap(), and Parma_Polyhedra_Library::Matrix< Row >::Matrix().

template<typename Row>

Swapping_Vector<Row> Parma_Polyhedra_Library::Matrix< Row >::rows

private

The vector that stores the matrix's elements.

Definition at line 403 of file Matrix_defs.hh.

Referenced by Parma_Polyhedra_Library::Matrix< Row >::m_swap(), and Parma_Polyhedra_Library::Matrix< Row >::Matrix().

The documentation for this class was generated from the following files:

Public Types

Public Member Functions

Static Public Member Functions

Private Attributes

Related Functions

Detailed Description

template<typename Row> class Parma_Polyhedra_Library::Matrix< Row >

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation

Friends And Related Function Documentation

Member Data Documentation

template<typename Row>
class Parma_Polyhedra_Library::Matrix< Row >