Parma_Polyhedra_Library::BHRZ03_Certificate Class Reference

The convergence certificate for the BHRZ03 widening operator. More...

#include <BHRZ03_Certificate_defs.hh>

Classes
struct	Compare
	A total ordering on BHRZ03 certificates. More...

Public Member Functions
	BHRZ03_Certificate ()
	Default constructor. More...
	BHRZ03_Certificate (const Polyhedron &ph)
	Constructor: computes the certificate for ph. More...
	BHRZ03_Certificate (const BHRZ03_Certificate &y)
	Copy constructor. More...
	~BHRZ03_Certificate ()
	Destructor. More...
int	compare (const BHRZ03_Certificate &y) const
	The comparison function for certificates. More...
int	compare (const Polyhedron &ph) const
	Compares *this with the certificate for polyhedron ph. More...
bool	is_stabilizing (const Polyhedron &ph) const
	Returns true if and only if the certificate for polyhedron ph is strictly smaller than *this. More...
bool	OK () const
	Check if gathered information is meaningful. More...

Private Attributes
dimension_type	affine_dim
	Affine dimension of the polyhedron. More...
dimension_type	lin_space_dim
	Dimension of the lineality space of the polyhedron. More...
dimension_type	num_constraints
	Cardinality of a non-redundant constraint system for the polyhedron. More...
dimension_type	num_points
	Number of non-redundant points in a generator system for the polyhedron. More...
std::vector< dimension_type >	num_rays_null_coord
	A vector containing, for each index `0 <= i < space_dim', the number of non-redundant rays in a generator system of the polyhedron having exactly `i' null coordinates. More...

Detailed Description

The convergence certificate for the BHRZ03 widening operator.

Convergence certificates are used to instantiate the BHZ03 framework so as to define widening operators for the finite powerset domain.

Note

Each convergence certificate has to be used together with a compatible widening operator. In particular, BHRZ03_Certificate can certify the convergence of both the BHRZ03 and the H79 widenings.

Definition at line 42 of file BHRZ03_Certificate_defs.hh.

Constructor & Destructor Documentation

Parma_Polyhedra_Library::BHRZ03_Certificate::BHRZ03_Certificate ( )

inline

Default constructor.

Definition at line 32 of file BHRZ03_Certificate_inlines.hh.

References OK().

  : affine_dim(0), lin_space_dim(0), num_constraints(0), num_points(1),
    num_rays_null_coord() {
  // This is the certificate for a zero-dim universe polyhedron.
  PPL_ASSERT(OK());
}

Parma_Polyhedra_Library::BHRZ03_Certificate::BHRZ03_Certificate

(

const Polyhedron &

ph

)

Constructor: computes the certificate for ph.

Definition at line 32 of file BHRZ03_Certificate.cc.

References affine_dim, Parma_Polyhedra_Library::Constraint_System::begin(), Parma_Polyhedra_Library::Generator_System::begin(), Parma_Polyhedra_Library::Generator::CLOSURE_POINT, Parma_Polyhedra_Library::Constraint_System::end(), Parma_Polyhedra_Library::Generator_System::end(), Parma_Polyhedra_Library::Polyhedron::is_necessarily_closed(), lin_space_dim, Parma_Polyhedra_Library::Generator::LINE, Parma_Polyhedra_Library::Polyhedron::marked_empty(), Parma_Polyhedra_Library::Polyhedron::minimize(), Parma_Polyhedra_Library::Polyhedron::minimized_constraints(), Parma_Polyhedra_Library::Polyhedron::minimized_generators(), num_constraints, num_points, num_rays_null_coord, OK(), Parma_Polyhedra_Library::Generator::POINT, Parma_Polyhedra_Library::Generator::RAY, and Parma_Polyhedra_Library::Polyhedron::space_dimension().

  : affine_dim(0), lin_space_dim(0), num_constraints(0), num_points(0),
    num_rays_null_coord(ph.space_dimension(), 0) {
  // TODO: provide a correct and reasonably efficient
  // implementation for NNC polyhedra.

  // The computation of the certificate requires both the
  // constraint and the generator systems in minimal form.
  ph.minimize();
  // It is assumed that `ph' is not an empty polyhedron.
  PPL_ASSERT(!ph.marked_empty());

  // The dimension of the polyhedron is obtained by subtracting
  // the number of equalities from the space dimension.
  // When counting constraints, for a correct reasoning, we have
  // to disregard the low-level constraints (i.e., the positivity
  // constraint and epsilon bounds).
  const dimension_type space_dim = ph.space_dimension();
  affine_dim = space_dim;
  PPL_ASSERT(num_constraints == 0);
  const Constraint_System& cs = ph.minimized_constraints();
  for (Constraint_System::const_iterator i = cs.begin(),
         cs_end = cs.end(); i != cs_end; ++i) {
    ++num_constraints;
    if (i->is_equality()) {
      --affine_dim;
    }
  }

  PPL_ASSERT(lin_space_dim == 0);
  PPL_ASSERT(num_points == 0);
  const Generator_System& gs = ph.minimized_generators();
  for (Generator_System::const_iterator i = gs.begin(),
         gs_end = gs.end(); i != gs_end; ++i) {
    switch (i->type()) {
    case Generator::POINT:
      // Intentionally fall through.
    case Generator::CLOSURE_POINT:
      ++num_points;
      break;
    case Generator::RAY:
      // For each i such that 0 <= j < space_dim,
      // `num_rays_null_coord[j]' will be the number of rays
      // having exactly `j' coordinates equal to 0.
      ++num_rays_null_coord[i->expression().num_zeroes(1, space_dim + 1)];
      break;
    case Generator::LINE:
      // Since the generator systems is minimized, the dimension of
      // the lineality space is equal to the number of lines.
      ++lin_space_dim;
      break;
    }
  }
  PPL_ASSERT(OK());

  // TODO: this is an inefficient workaround.
  // For NNC polyhedra, constraints might be no longer up-to-date
  // (and hence, neither minimized) due to the strong minimization
  // process applied to generators when constructing the certificate.
  // We have to reinforce the (normal) minimization of the constraint
  // system. The future, lazy implementation of the strong minimization
  // process will solve this problem.
  if (!ph.is_necessarily_closed()) {
    ph.minimize();
  }
}

Parma_Polyhedra_Library::BHRZ03_Certificate::BHRZ03_Certificate ( const BHRZ03_Certificate &  y )

inline

Copy constructor.

Definition at line 40 of file BHRZ03_Certificate_inlines.hh.

  : affine_dim(y.affine_dim), lin_space_dim(y.lin_space_dim),
    num_constraints(y.num_constraints), num_points(y.num_points),
    num_rays_null_coord(y.num_rays_null_coord) {
}

Parma_Polyhedra_Library::BHRZ03_Certificate::~BHRZ03_Certificate ( )

inline

Destructor.

Definition at line 47 of file BHRZ03_Certificate_inlines.hh.

                                        {
}

Member Function Documentation

int Parma_Polyhedra_Library::BHRZ03_Certificate::compare

(

const BHRZ03_Certificate &

y

)

const

The comparison function for certificates.

Returns

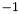, or 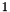depending on whether *this is smaller than, equal to, or greater than y, respectively.

Compares *this with y, using a total ordering which is a refinement of the limited growth ordering relation for the BHRZ03 widening.

Definition at line 100 of file BHRZ03_Certificate.cc.

References affine_dim, lin_space_dim, num_constraints, Parma_Polyhedra_Library::Implementation::num_constraints(), num_points, num_rays_null_coord, and OK().

Referenced by is_stabilizing(), and Parma_Polyhedra_Library::BHRZ03_Certificate::Compare::operator()().

                                                                {
  PPL_ASSERT(OK() && y.OK());
  if (affine_dim != y.affine_dim) {
    return (affine_dim > y.affine_dim) ? 1 : -1;
  }
  if (lin_space_dim != y.lin_space_dim) {
    return (lin_space_dim > y.lin_space_dim) ? 1 : -1;
  }
  if (num_constraints != y.num_constraints) {
    return (num_constraints > y.num_constraints) ? 1 : -1;
  }
  if (num_points != y.num_points) {
    return (num_points > y.num_points) ? 1 : -1;
  }
  const dimension_type space_dim = num_rays_null_coord.size();
  PPL_ASSERT(num_rays_null_coord.size() == y.num_rays_null_coord.size());
  // Note: iterating upwards, because we have to check first
  // the number of rays having more NON-zero coordinates.
  for (dimension_type i = 0; i < space_dim; ++i) {
    if (num_rays_null_coord[i] != y.num_rays_null_coord[i]) {
      return (num_rays_null_coord[i] > y.num_rays_null_coord[i]) ? 1 : -1;
    }
  }
  // All components are equal.
  return 0;
}

int Parma_Polyhedra_Library::BHRZ03_Certificate::compare

(

const Polyhedron &

ph

)

const

Compares *this with the certificate for polyhedron ph.

Definition at line 128 of file BHRZ03_Certificate.cc.

References Parma_Polyhedra_Library::Constraint_System::begin(), Parma_Polyhedra_Library::Generator_System::begin(), Parma_Polyhedra_Library::Generator::CLOSURE_POINT, Parma_Polyhedra_Library::Constraint_System::end(), Parma_Polyhedra_Library::Generator_System::end(), Parma_Polyhedra_Library::Polyhedron::is_necessarily_closed(), Parma_Polyhedra_Library::Generator::LINE, Parma_Polyhedra_Library::Polyhedron::marked_empty(), Parma_Polyhedra_Library::Polyhedron::minimize(), Parma_Polyhedra_Library::Polyhedron::minimized_constraints(), Parma_Polyhedra_Library::Polyhedron::minimized_generators(), Parma_Polyhedra_Library::Implementation::num_constraints(), Parma_Polyhedra_Library::Generator::POINT, Parma_Polyhedra_Library::Generator::RAY, Parma_Polyhedra_Library::Polyhedron::space_dim, and Parma_Polyhedra_Library::Polyhedron::space_dimension().

                                                         {
  PPL_ASSERT(ph.space_dimension() == num_rays_null_coord.size());

  // TODO: provide a correct and reasonably efficient
  // implementation for NNC polyhedra.

  // The computation of the certificate requires both the
  // constraint and the generator systems in minimal form.
  ph.minimize();
  // It is assumed that `ph' is a polyhedron containing the
  // polyhedron described by `*this': hence, it cannot be empty.
  PPL_ASSERT(!ph.marked_empty());

  // The dimension of the polyhedron is obtained by subtracting
  // the number of equalities from the space dimension.
  // When counting constraints, for a correct reasoning, we have
  // to disregard the low-level constraints (i.e., the positivity
  // constraint and epsilon bounds).
  const dimension_type space_dim = ph.space_dimension();
  dimension_type ph_affine_dim = space_dim;
  dimension_type ph_num_constraints = 0;
  const Constraint_System& cs = ph.minimized_constraints();
  for (Constraint_System::const_iterator i = cs.begin(),
         cs_end = cs.end(); i != cs_end; ++i) {
    ++ph_num_constraints;
    if (i->is_equality()) {
      --ph_affine_dim;
    }
  }
  // TODO: this is an inefficient workaround.
  // For NNC polyhedra, constraints might be no longer up-to-date
  // (and hence, neither minimized) due to the strong minimization
  // process applied to generators when constructing the certificate.
  // We have to reinforce the (normal) minimization of the constraint
  // system. The future, lazy implementation of the strong minimization
  // process will solve this problem.
  if (!ph.is_necessarily_closed()) {
    ph.minimize();
  }
  // If the dimension of `ph' is increasing, the chain is stabilizing.
  if (ph_affine_dim > affine_dim) {
    return 1;
  }
  // At this point the two polyhedra must have the same dimension.
  PPL_ASSERT(ph_affine_dim == affine_dim);

  // Speculative optimization: in order to better exploit the incrementality
  // of the comparison, we do not compute information about rays here,
  // hoping that the other components will be enough.
  dimension_type ph_lin_space_dim = 0;
  dimension_type ph_num_points = 0;
  const Generator_System& gs = ph.minimized_generators();
  for (Generator_System::const_iterator i = gs.begin(),
         gs_end = gs.end(); i != gs_end; ++i) {
    switch (i->type()) {
    case Generator::POINT:
      // Intentionally fall through.
    case Generator::CLOSURE_POINT:
      ++ph_num_points;
      break;
    case Generator::RAY:
      break;
    case Generator::LINE:
      // Since the generator systems is minimized, the dimension of
      // the lineality space is equal to the number of lines.
      ++ph_lin_space_dim;
      break;
    }
  }
  // TODO: this is an inefficient workaround.
  // For NNC polyhedra, constraints might be no longer up-to-date
  // (and hence, neither minimized) due to the strong minimization
  // process applied to generators when constructing the certificate.
  // We have to reinforce the (normal) minimization of the constraint
  // system. The future, lazy implementation of the strong minimization
  // process will solve this problem.
  if (!ph.is_necessarily_closed()) {
    ph.minimize();
  }
  // If the dimension of the lineality space is increasing,
  // then the chain is stabilizing.
  if (ph_lin_space_dim > lin_space_dim) {
    return 1;
  }
  // At this point the lineality space of the two polyhedra must have
  // the same dimension.
  PPL_ASSERT(ph_lin_space_dim == lin_space_dim);

  // If the number of constraints of `ph' is decreasing, then the chain
  // is stabilizing. If it is increasing, the chain is not stabilizing.
  // If they are equal, further investigation is needed.
  if (ph_num_constraints != num_constraints) {
    return (ph_num_constraints < num_constraints) ? 1 : -1;
  }
  // If the number of points of `ph' is decreasing, then the chain
  // is stabilizing. If it is increasing, the chain is not stabilizing.
  // If they are equal, further investigation is needed.
  if (ph_num_points != num_points) {
    return (ph_num_points < num_points) ? 1 : -1;
  }
  // The speculative optimization was not worth:
  // compute information about rays.
  std::vector<dimension_type> ph_num_rays_null_coord(ph.space_dim, 0);
  for (Generator_System::const_iterator i = gs.begin(),
         gs_end = gs.end(); i != gs_end; ++i) {
    if (i->is_ray()) {
      ++ph_num_rays_null_coord[i->expression().num_zeroes(1, space_dim + 1)];
    }
  }
  // Compare (lexicographically) the two vectors:
  // if ph_num_rays_null_coord < num_rays_null_coord the chain is stabilizing.
  for (dimension_type i = 0; i < space_dim; ++i) {
    if (ph_num_rays_null_coord[i] != num_rays_null_coord[i]) {
      return (ph_num_rays_null_coord[i] < num_rays_null_coord[i]) ? 1 : -1;
    }
  }
  // All components are equal.
  return 0;
}

bool Parma_Polyhedra_Library::BHRZ03_Certificate::is_stabilizing ( const Polyhedron &  ph ) const

inline

Returns true if and only if the certificate for polyhedron ph is strictly smaller than *this.

Definition at line 51 of file BHRZ03_Certificate_inlines.hh.

References compare().

Referenced by Parma_Polyhedra_Library::Polyhedron::BHRZ03_combining_constraints(), Parma_Polyhedra_Library::Polyhedron::BHRZ03_evolving_points(), Parma_Polyhedra_Library::Polyhedron::BHRZ03_evolving_rays(), and Parma_Polyhedra_Library::Polyhedron::BHRZ03_widening_assign().

                                                             {
  return compare(ph) == 1;
}

bool Parma_Polyhedra_Library::BHRZ03_Certificate::OK

(

)

const

Check if gathered information is meaningful.

Definition at line 249 of file BHRZ03_Certificate.cc.

References Parma_Polyhedra_Library::Implementation::num_constraints().

Referenced by BHRZ03_Certificate(), and compare().

                                {
#ifndef NDEBUG
  using std::endl;
  using std::cerr;
#endif

  // The dimension of the vector space.
  const dimension_type space_dim = num_rays_null_coord.size();

  if (affine_dim > space_dim) {
#ifndef NDEBUG
    cerr << "In the BHRZ03 certificate about a non-empty polyhedron:"
         << endl
         << "the affine dimension is greater than the space dimension!"
         << endl;
#endif
    return false;
  }

  if (lin_space_dim > affine_dim) {
#ifndef NDEBUG
    cerr << "In the BHRZ03 certificate about a non-empty polyhedron:"
         << endl
         << "the lineality space dimension is greater than "
         << "the affine dimension!"
         << endl;
#endif
    return false;
  }

  if (num_constraints < space_dim - affine_dim) {
#ifndef NDEBUG
    cerr << "In the BHRZ03 certificate about a non-empty polyhedron:"
         << endl
         << "in a vector space of dimension `n',"
         << "any polyhedron of affine dimension `k'" << endl
         << "should have `n-k' non-redundant constraints at least."
         << endl
         << "Here space_dim = " << space_dim << ", "
         << "affine_dim = " << affine_dim << ", "
         << "but num_constraints = " << num_constraints << "!"
         << endl;
#endif
    return false;
  }

  if (num_points == 0) {
#ifndef NDEBUG
    cerr << "In the BHRZ03 certificate about a non-empty polyhedron:"
         << endl
         << "the generator system has no points!"
         << endl;
#endif
    return false;
  }

  if (lin_space_dim == space_dim) {
    // This was a universe polyhedron.
    if (num_constraints > 0) {
#ifndef NDEBUG
      cerr << "In the BHRZ03 certificate about a non-empty polyhedron:"
           << endl
           << "a universe polyhedron has non-redundant constraints!"
           << endl;
#endif
      return false;
    }

    if (num_points != 1) {
#ifndef NDEBUG
      cerr << "In the BHRZ03 certificate about a non-empty polyhedron:"
           << endl
           << "a universe polyhedron has more than one non-redundant point!"
           << endl;
#endif
      return false;
    }
  }

  // All tests passed.
  return true;
}

Member Data Documentation

dimension_type Parma_Polyhedra_Library::BHRZ03_Certificate::affine_dim

private

Affine dimension of the polyhedron.

Definition at line 97 of file BHRZ03_Certificate_defs.hh.

Referenced by BHRZ03_Certificate(), and compare().

dimension_type Parma_Polyhedra_Library::BHRZ03_Certificate::lin_space_dim

private

Dimension of the lineality space of the polyhedron.

Definition at line 99 of file BHRZ03_Certificate_defs.hh.

Referenced by BHRZ03_Certificate(), and compare().

dimension_type Parma_Polyhedra_Library::BHRZ03_Certificate::num_constraints

private

Cardinality of a non-redundant constraint system for the polyhedron.

Definition at line 101 of file BHRZ03_Certificate_defs.hh.

Referenced by BHRZ03_Certificate(), and compare().

dimension_type Parma_Polyhedra_Library::BHRZ03_Certificate::num_points

private

Number of non-redundant points in a generator system for the polyhedron.

Definition at line 106 of file BHRZ03_Certificate_defs.hh.

Referenced by BHRZ03_Certificate(), and compare().

std::vector<dimension_type> Parma_Polyhedra_Library::BHRZ03_Certificate::num_rays_null_coord

private

A vector containing, for each index `0 <= i < space_dim', the number of non-redundant rays in a generator system of the polyhedron having exactly `i' null coordinates.

Definition at line 112 of file BHRZ03_Certificate_defs.hh.

Referenced by BHRZ03_Certificate(), and compare().

---

The documentation for this class was generated from the following files:

• BHRZ03_Certificate_defs.hh
• BHRZ03_Certificate.cc
• BHRZ03_Certificate_inlines.hh