An affine space. More...
#include <Affine_Space_defs.hh>

Public Types | |
| typedef Coefficient | coefficient_type |
| The numeric type of coefficients. More... | |
Public Member Functions | |
| Affine_Space (dimension_type num_dimensions=0, Degenerate_Element kind=UNIVERSE) | |
| Builds an affine space having the specified properties. More... | |
| Affine_Space (const Constraint_System &cs) | |
| Builds an affine space, copying a system of constraints. More... | |
| Affine_Space (Constraint_System &cs, Recycle_Input dummy) | |
| Builds an affine space, recycling a system of constraints. More... | |
| Affine_Space (const Generator_System &gs) | |
| Builds an affine space, copying a system of affine space generators. More... | |
| Affine_Space (Generator_System &gs, Recycle_Input dummy) | |
| Builds an affine space, recycling a system of generators. More... | |
| template<typename Interval > | |
| Affine_Space (const Box< Interval > &box, Complexity_Class complexity=ANY_COMPLEXITY) | |
| Builds an affine space out of a box. More... | |
| template<typename U > | |
| Affine_Space (const BD_Shape< U > &bd, Complexity_Class complexity=ANY_COMPLEXITY) | |
| Builds an affine space out of a bounded-difference shape. More... | |
| template<typename U > | |
| Affine_Space (const Octagonal_Shape< U > &os, Complexity_Class complexity=ANY_COMPLEXITY) | |
| Builds an affine space out of an octagonal shape. More... | |
| Affine_Space (const Polyhedron &ph, Complexity_Class complexity=ANY_COMPLEXITY) | |
Builds an affine space from a polyhedron using algorithms whose complexity does not exceed the one specified by complexity. If complexity is ANY_COMPLEXITY, then the affine space built is the smallest one containing ph. More... | |
| Affine_Space (const Affine_Space &y, Complexity_Class complexity=ANY_COMPLEXITY) | |
| Ordinary copy constructor. More... | |
| Affine_Space & | operator= (const Affine_Space &y) |
The assignment operator. (*this and y can be dimension-incompatible.) More... | |
Member Functions that Do Not Modify the Affine_Space | |
| dimension_type | space_dimension () const |
Returns the dimension of the vector space enclosing *this. More... | |
| dimension_type | affine_dimension () const |
Returns  , if , if *this is empty; otherwise, returns affine dimension of *this. More... | |
| Constraint_System | constraints () const |
Returns a system of equality constraints satisfied by *this with the same affine dimension as *this. More... | |
| Constraint_System | minimized_constraints () const |
Returns a minimal system of equality constraints satisfied by *this with the same affine dimension as *this. More... | |
| const Congruence_System & | congruences () const |
Returns the system of equality congruences satisfied by *this. More... | |
| const Congruence_System & | minimized_congruences () const |
Returns the system of equality congruences satisfied by *this, with no redundant congruences and having the same affine dimension as *this. More... | |
| Generator_System | generators () const |
Returns a system of generators defining *this. More... | |
| Generator_System | minimized_generators () const |
Returns a minimized system of generators defining *this. More... | |
| Poly_Con_Relation | relation_with (const Congruence &cg) const |
Returns the relations holding between *this and cg. More... | |
| Poly_Gen_Relation | relation_with (const Generator &g) const |
Returns the relations holding between *this and g. More... | |
| Poly_Con_Relation | relation_with (const Constraint &c) const |
Returns the relations holding between *this and c. More... | |
| bool | is_empty () const |
Returns true if and only if *this is an empty affine space. More... | |
| bool | is_universe () const |
Returns true if and only if *this is a universe affine space. More... | |
| bool | is_topologically_closed () const |
Returns true if and only if *this is a topologically closed subset of the vector space. More... | |
| bool | is_disjoint_from (const Affine_Space &y) const |
Returns true if and only if *this and y are disjoint. More... | |
| bool | is_discrete () const |
Returns true if and only if *this is discrete. More... | |
| bool | is_bounded () const |
Returns true if and only if *this is bounded. More... | |
| bool | contains_integer_point () const |
Returns true if and only if *this contains at least one integer point. More... | |
| bool | constrains (Variable var) const |
Returns true if and only if var is constrained in *this. More... | |
| bool | bounds_from_above (const Linear_Expression &expr) const |
Returns true if and only if expr is bounded in *this. More... | |
| bool | bounds_from_below (const Linear_Expression &expr) const |
Returns true if and only if expr is bounded in *this. More... | |
| bool | maximize (const Linear_Expression &expr, Coefficient &sup_n, Coefficient &sup_d, bool &maximum) const |
Returns true if and only if *this is not empty and expr is bounded from above in *this, in which case the supremum value is computed. More... | |
| bool | maximize (const Linear_Expression &expr, Coefficient &sup_n, Coefficient &sup_d, bool &maximum, Generator &point) const |
Returns true if and only if *this is not empty and expr is bounded from above in *this, in which case the supremum value and a point where expr reaches it are computed. More... | |
| bool | minimize (const Linear_Expression &expr, Coefficient &inf_n, Coefficient &inf_d, bool &minimum) const |
Returns true if and only if *this is not empty and expr is bounded from below in *this, in which case the infimum value is computed. More... | |
| bool | minimize (const Linear_Expression &expr, Coefficient &inf_n, Coefficient &inf_d, bool &minimum, Generator &point) const |
Returns true if and only if *this is not empty and expr is bounded from below in *this, in which case the infimum value and a point where expr reaches it are computed. More... | |
| bool | frequency (const Linear_Expression &expr, Coefficient &freq_n, Coefficient &freq_d, Coefficient &val_n, Coefficient &val_d) const |
Returns true if and only if *this is not empty and expr is discrete in *this, in which case the maximum frequency and the value for expr that is closest to zero are computed. More... | |
| bool | contains (const Affine_Space &y) const |
Returns true if and only if *this contains y. More... | |
| bool | strictly_contains (const Affine_Space &y) const |
Returns true if and only if *this strictly contains y. More... | |
| bool | OK (bool check_not_empty=false) const |
| Checks if all the invariants are satisfied. More... | |
Space Dimension Preserving Member Functions that May Modify the Affine_Space | |
| void | add_congruence (const Congruence &cg) |
Adds a copy of congruence cg to *this. More... | |
| void | add_generator (const Generator &g) |
Adds a copy of affine space generator g to the system of generators of *this. More... | |
| void | add_congruences (const Congruence_System &cgs) |
Adds a copy of each congruence in cgs to *this. More... | |
| void | add_recycled_congruences (Congruence_System &cgs) |
Adds the congruences in cgs to *this. More... | |
| void | add_constraint (const Constraint &c) |
Adds to *this a congruence equivalent to constraint c. More... | |
| void | add_constraints (const Constraint_System &cs) |
Adds to *this congruences equivalent to the constraints in cs. More... | |
| void | add_recycled_constraints (Constraint_System &cs) |
Adds to *this congruences equivalent to the constraints in cs. More... | |
| void | refine_with_congruence (const Congruence &cg) |
Uses a copy of the congruence cg to refine *this. More... | |
| void | refine_with_congruences (const Congruence_System &cgs) |
Uses a copy of the congruences in cgs to refine *this. More... | |
| void | refine_with_constraint (const Constraint &c) |
Uses a copy of the constraint c to refine *this. More... | |
| void | refine_with_constraints (const Constraint_System &cs) |
Uses a copy of the constraints in cs to refine *this. More... | |
| void | add_generators (const Generator_System &gs) |
Adds a copy of the generators in gs to the system of generators of *this. More... | |
| void | add_recycled_generators (Generator_System &gs) |
Adds the generators in gs to the system of generators of this. More... | |
| void | unconstrain (Variable var) |
Computes the cylindrification of *this with respect to space dimension var, assigning the result to *this. More... | |
| void | unconstrain (const Variables_Set &vars) |
Computes the cylindrification of *this with respect to the set of space dimensions vars, assigning the result to *this. More... | |
| void | intersection_assign (const Affine_Space &y) |
Assigns to *this the intersection of *this and y. More... | |
| void | upper_bound_assign (const Affine_Space &y) |
Assigns to *this the least upper bound of *this and y. More... | |
| bool | upper_bound_assign_if_exact (const Affine_Space &y) |
If the upper bound of *this and y is exact it is assigned to this and true is returned, otherwise false is returned. More... | |
| void | difference_assign (const Affine_Space &y) |
Assigns to *this the poly-difference of *this and y. More... | |
| bool | simplify_using_context_assign (const Affine_Space &y) |
Assigns to *this a meet-preserving simplification of *this with respect to y. If false is returned, then the intersection is empty. More... | |
| void | affine_image (Variable var, const Linear_Expression &expr, Coefficient_traits::const_reference denominator=Coefficient_one()) |
Assigns to *this the affine image of *this under the function mapping variable var to the affine expression specified by expr and denominator. More... | |
| void | affine_preimage (Variable var, const Linear_Expression &expr, Coefficient_traits::const_reference denominator=Coefficient_one()) |
Assigns to *this the affine preimage of *this under the function mapping variable var to the affine expression specified by expr and denominator. More... | |
| void | generalized_affine_image (Variable var, Relation_Symbol relsym, const Linear_Expression &expr, Coefficient_traits::const_reference denominator=Coefficient_one()) |
Assigns to *this the image of *this with respect to the generalized affine relation 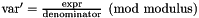 . More... . More... | |
| void | generalized_affine_preimage (Variable var, Relation_Symbol relsym, const Linear_Expression &expr, Coefficient_traits::const_reference denominator=Coefficient_one()) |
Assigns to *this the preimage of *this with respect to the generalized affine relation 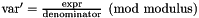 . More... . More... | |
| void | generalized_affine_image (const Linear_Expression &lhs, Relation_Symbol relsym, const Linear_Expression &rhs) |
Assigns to *this the image of *this with respect to the generalized affine relation 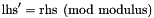 . More... . More... | |
| void | generalized_affine_preimage (const Linear_Expression &lhs, Relation_Symbol relsym, const Linear_Expression &rhs) |
Assigns to *this the preimage of *this with respect to the generalized affine relation 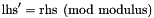 . More... . More... | |
| void | bounded_affine_image (Variable var, const Linear_Expression &lb_expr, const Linear_Expression &ub_expr, Coefficient_traits::const_reference denominator=Coefficient_one()) |
Assigns to *this the image of *this with respect to the bounded affine relation  . More... . More... | |
| void | bounded_affine_preimage (Variable var, const Linear_Expression &lb_expr, const Linear_Expression &ub_expr, Coefficient_traits::const_reference denominator=Coefficient_one()) |
Assigns to *this the preimage of *this with respect to the bounded affine relation  . More... . More... | |
| void | time_elapse_assign (const Affine_Space &y) |
Assigns to *this the result of computing the time-elapse between *this and y. More... | |
| void | topological_closure_assign () |
Assigns to *this its topological closure. More... | |
| void | widening_assign (const Affine_Space &y, unsigned *tp=NULL) |
| Does nothing, as the domain of affine spaces has finite height. More... | |
| void | limited_extrapolation_assign (const Affine_Space &y, const Constraint_System &cs, unsigned *tp=NULL) |
| Does nothing, as the domain of affine spaces has finite height. More... | |
Member Functions that May Modify the Dimension of the Vector Space | |
| void | add_space_dimensions_and_embed (dimension_type m) |
Adds m new space dimensions and embeds the old affine space in the new vector space. More... | |
| void | add_space_dimensions_and_project (dimension_type m) |
Adds m new space dimensions to the affine space and does not embed it in the new vector space. More... | |
| void | concatenate_assign (const Affine_Space &y) |
Assigns to *this the concatenation of *this and y, taken in this order. More... | |
| void | remove_space_dimensions (const Variables_Set &vars) |
| Removes all the specified dimensions from the vector space. More... | |
| void | remove_higher_space_dimensions (dimension_type new_dimension) |
Removes the higher dimensions of the vector space so that the resulting space will have dimension new_dimension. More... | |
| template<typename Partial_Function > | |
| void | map_space_dimensions (const Partial_Function &pfunc) |
| Remaps the dimensions of the vector space according to a partial function. More... | |
| void | expand_space_dimension (Variable var, dimension_type m) |
Creates m copies of the space dimension corresponding to var. More... | |
| void | fold_space_dimensions (const Variables_Set &to_be_folded, Variable var) |
Folds the space dimensions in to_be_folded into var. More... | |
Miscellaneous Member Functions | |
| ~Affine_Space () | |
| Destructor. More... | |
| void | m_swap (Affine_Space &y) |
Swaps *this with affine space y. (*this and y can be dimension-incompatible.) More... | |
| void | ascii_dump () const |
Writes to std::cerr an ASCII representation of *this. More... | |
| void | ascii_dump (std::ostream &s) const |
Writes to s an ASCII representation of *this. More... | |
| void | print () const |
Prints *this to std::cerr using operator<<. More... | |
| bool | ascii_load (std::istream &s) |
Loads from s an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets *this accordingly. Returns true if successful, false otherwise. More... | |
| memory_size_type | total_memory_in_bytes () const |
Returns the total size in bytes of the memory occupied by *this. More... | |
| memory_size_type | external_memory_in_bytes () const |
Returns the size in bytes of the memory managed by *this. More... | |
| int32_t | hash_code () const |
Returns a 32-bit hash code for *this. More... | |
Static Public Member Functions | |
| static dimension_type | max_space_dimension () |
| Returns the maximum space dimension all kinds of Affine_Space can handle. More... | |
| static bool | can_recycle_constraint_systems () |
| Returns true indicating that this domain has methods that can recycle constraints. More... | |
| static bool | can_recycle_congruence_systems () |
| Returns true indicating that this domain has methods that can recycle congruences. More... | |
Private Attributes | |
| Grid | gr |
The rational grid implementing *this. More... | |
Friends | |
| bool | operator== (const Affine_Space &x, const Affine_Space &y) |
Related Functions | |
(Note that these are not member functions.) | |
| bool | operator== (const Affine_Space &x, const Affine_Space &y) |
| std::ostream & | operator<< (std::ostream &s, const Affine_Space &gr) |
| std::ostream & | operator<< (std::ostream &s, const Affine_Space &gr) |
| Output operator. More... | |
| void | swap (Affine_Space &x, Affine_Space &y) |
Swaps x with y. More... | |
| bool | operator== (const Affine_Space &x, const Affine_Space &y) |
Returns true if and only if x and y are the same affine space. More... | |
| bool | operator!= (const Affine_Space &x, const Affine_Space &y) |
Returns true if and only if x and y are different affine spaces. More... | |
| bool | operator!= (const Affine_Space &x, const Affine_Space &y) |
| void | swap (Affine_Space &x, Affine_Space &y) |
Exception Throwers | |
| void | throw_dimension_incompatible (const char *method, const char *other_name, dimension_type other_dim) const |
| void | throw_dimension_incompatible (const char *method, const char *as_name, const Affine_Space &as) const |
| void | throw_invalid_constraint (const char *method, const char *c_name) const |
| void | throw_invalid_constraints (const char *method, const char *cs_name) const |
| void | throw_invalid_generator (const char *method, const char *g_name) const |
| void | throw_invalid_generators (const char *method, const char *gs_name) const |
| static void | throw_space_dimension_overflow (const char *method, const char *reason) |
Detailed Description
An affine space.
An object of the class Affine_Space represents an affine space in the vector space 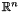 .
.
The domain of affine spaces linear equality constraints. Depending on the method, using a constraint that is not optimally supported by the domain will either raise an exception or result in a (possibly non-optimal) upward approximation.
The domain of affine spaces support a concept of double description similar to the one developed for polyhedra: hence, an affine space can be specified as either a finite system of equalities or a finite system of generators (see Section Representations of Convex Polyhedra) and it is always possible to obtain either representation. That is, if we know the system of equalities, we can obtain from this a system of generators that define the same affine space and vice versa. These systems can contain redundant members, or they can be in the minimal form.
A key attribute of any affine space is its space dimension (the dimension 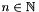 of the enclosing vector space):
of the enclosing vector space):
- all affine spaces, the empty ones included, are endowed with a space dimension;
- most operations working on an affine space and another object (another affine space, a congruence, a generator, a set of variables, etc.) will throw an exception if the affine space and the object are not dimension-compatible (see Section Representations of Convex Polyhedra);
- the only ways in which the space dimension of an affine space can be changed are with explicit calls to operators provided for that purpose, and with standard copy, assignment and swap operators.
Note that two different affine spaces can be defined on the zero-dimension space: the empty affine space and the universe affine space 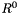 .
.
- In all the examples it is assumed that variables
xandyare defined (where they are used) as follows:Variable x(0);Variable y(1);
FIXME: revise the contents below this point of this comment block.
- Example 1
- The following code builds an affine space corresponding to the even integer pairs in
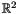 , given as a system of congruences: The following code builds the same affine space as above, but starting from a system of generators specifying three of the points: Affine_Space_Generator_System gs;gs.insert(affine space_point(0*x + 0*y));gs.insert(affine space_point(0*x + 2*y));gs.insert(affine space_point(2*x + 0*y));Affine_Space gr(gs);
, given as a system of congruences: The following code builds the same affine space as above, but starting from a system of generators specifying three of the points: Affine_Space_Generator_System gs;gs.insert(affine space_point(0*x + 0*y));gs.insert(affine space_point(0*x + 2*y));gs.insert(affine space_point(2*x + 0*y));Affine_Space gr(gs);
- Example 2
- The following code builds an affine space corresponding to a line in
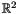 by adding a single congruence to the universe affine space: The following code builds the same affine space as above, but starting from a system of generators specifying a point and a line: Affine_Space_Generator_System gs;gs.insert(affine space_point(0*x + 0*y));gs.insert(affine space_line(x + y));Affine_Space gr(gs);
by adding a single congruence to the universe affine space: The following code builds the same affine space as above, but starting from a system of generators specifying a point and a line: Affine_Space_Generator_System gs;gs.insert(affine space_point(0*x + 0*y));gs.insert(affine space_line(x + y));Affine_Space gr(gs);
- Example 3
- The following code builds an affine space corresponding to the integral points on the line
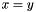 in
in 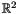 constructed by adding an equality and congruence to the universe affine space: The following code builds the same affine space as above, but starting from a system of generators specifying a point and a parameter: Affine_Space_Generator_System gs;gs.insert(affine space_point(0*x + 0*y));gs.insert(parameter(x + y));Affine_Space gr(gs);
constructed by adding an equality and congruence to the universe affine space: The following code builds the same affine space as above, but starting from a system of generators specifying a point and a parameter: Affine_Space_Generator_System gs;gs.insert(affine space_point(0*x + 0*y));gs.insert(parameter(x + y));Affine_Space gr(gs);
- Example 4
- The following code builds the affine space corresponding to a plane by creating the universe affine space in
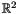 : The following code builds the same affine space as above, but starting from the empty affine space inAffine_Space gr(2);
: The following code builds the same affine space as above, but starting from the empty affine space inAffine_Space gr(2);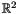 and inserting the appropriate generators (a point, and two lines). Note that a generator system must contain a point when describing an affine space. To ensure that this is always the case it is required that the first generator inserted in an empty affine space is a point (otherwise, an exception is thrown).gr.add_grid_generator(affine space_point(0*x + 0*y));gr.add_grid_generator(affine space_line(x));gr.add_grid_generator(affine space_line(y));
and inserting the appropriate generators (a point, and two lines). Note that a generator system must contain a point when describing an affine space. To ensure that this is always the case it is required that the first generator inserted in an empty affine space is a point (otherwise, an exception is thrown).gr.add_grid_generator(affine space_point(0*x + 0*y));gr.add_grid_generator(affine space_line(x));gr.add_grid_generator(affine space_line(y));
- Example 5
- The following code shows the use of the function
add_space_dimensions_and_embed: We build the universe affine space in the 1-dimension space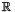 . Then we add a single equality congruence, thus obtaining the affine space corresponding to the singleton set
. Then we add a single equality congruence, thus obtaining the affine space corresponding to the singleton set 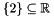 . After the last line of code, the resulting affine space is
. After the last line of code, the resulting affine space is ![\[ \bigl\{\, (2, y)^\transpose \in \Rset^2 \bigm| y \in \Rset \,\bigr\}. \]](form_695.png)
- Example 6
- The following code shows the use of the function
add_space_dimensions_and_project: The first two lines of code are the same as in Example 4 foradd_space_dimensions_and_embed. After the last line of code, the resulting affine space is the singleton set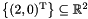 .
.
- Example 7
- The following code shows the use of the function
affine_image:In this example the starting affine space is all the pairs ofgr.add_grid_generator(affine space_point(0*x + 0*y));gr.add_grid_generator(affine space_point(4*x + 0*y));gr.add_grid_generator(affine space_point(0*x + 2*y));Linear_Expression expr = x + 3;gr.affine_image(x, expr);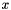 and
and 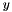 in
in 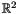 where
where 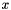 is an integer multiple of 4 and
is an integer multiple of 4 and 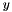 is an integer multiple of 2. The considered variable is
is an integer multiple of 2. The considered variable is 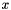 and the affine expression is
and the affine expression is 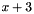 . The resulting affine space is the given affine space translated 3 integers to the right (all the pairs
. The resulting affine space is the given affine space translated 3 integers to the right (all the pairs 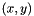 where
where 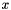 is -1 plus an integer multiple of 4 and
is -1 plus an integer multiple of 4 and 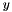 is an integer multiple of 2). Moreover, if the affine transformation for the same variable
is an integer multiple of 2). Moreover, if the affine transformation for the same variable xis instead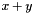 : the resulting affine space is every second integral point along theLinear_Expression expr = x + y;
: the resulting affine space is every second integral point along theLinear_Expression expr = x + y;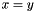 line, with this line of points repeated at every fourth integral value along the
line, with this line of points repeated at every fourth integral value along the 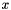 axis. Instead, if we do not use an invertible transformation for the same variable; for example, the affine expression
axis. Instead, if we do not use an invertible transformation for the same variable; for example, the affine expression 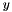 : the resulting affine space is every second point along theLinear_Expression expr = y;
: the resulting affine space is every second point along theLinear_Expression expr = y;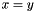 line.
line.
- Example 8
- The following code shows the use of the function
affine_preimage:In this example the starting affine space,gr.add_grid_generator(affine space_point(0*x + 0*y));gr.add_grid_generator(affine space_point(4*x + 0*y));gr.add_grid_generator(affine space_point(0*x + 2*y));Linear_Expression expr = x + 3;gr.affine_preimage(x, expr);varand the affine expression and the denominator are the same as in Example 6, while the resulting affine space is similar but translated 3 integers to the left (all the pairs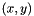 where
where 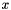 is -3 plus an integer multiple of 4 and
is -3 plus an integer multiple of 4 and 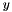 is an integer multiple of 2).. Moreover, if the affine transformation for
is an integer multiple of 2).. Moreover, if the affine transformation for xis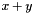 the resulting affine space is a similar affine space to the result in Example 6, only the affine space is slanted alongLinear_Expression expr = x + y;
the resulting affine space is a similar affine space to the result in Example 6, only the affine space is slanted alongLinear_Expression expr = x + y;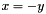 . Instead, if we do not use an invertible transformation for the same variable
. Instead, if we do not use an invertible transformation for the same variable x, for example, the affine expression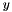 : the resulting affine space is every fourth line parallel to theLinear_Expression expr = y;
: the resulting affine space is every fourth line parallel to theLinear_Expression expr = y;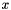 axis.
axis.
- Example 9
- For this example we also use the variables: The following code shows the use of the functionVariable z(2);Variable w(3);
remove_space_dimensions:The starting affine space is the singleton setAffine_Space_Generator_System gs;gs.insert(affine space_point(3*x + y +0*z + 2*w));Affine_Space gr(gs);Variables_Set vars;vars.insert(y);vars.insert(z);gr.remove_space_dimensions(vars);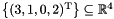 , while the resulting affine space is
, while the resulting affine space is 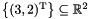 . Be careful when removing space dimensions incrementally: since dimensions are automatically renamed after each application of the
. Be careful when removing space dimensions incrementally: since dimensions are automatically renamed after each application of the remove_space_dimensionsoperator, unexpected results can be obtained. For instance, by using the following code we would obtain a different result:In this case, the result is the affine spaceset<Variable> vars1;vars1.insert(y);gr.remove_space_dimensions(vars1);set<Variable> vars2;vars2.insert(z);gr.remove_space_dimensions(vars2);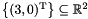 : when removing the set of dimensions
: when removing the set of dimensions vars2we are actually removing variable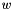 of the original affine space. For the same reason, the operator
of the original affine space. For the same reason, the operator remove_space_dimensionsis not idempotent: removing twice the same non-empty set of dimensions is never the same as removing them just once.
Definition at line 357 of file Affine_Space_defs.hh.
Member Typedef Documentation
The numeric type of coefficients.
Definition at line 360 of file Affine_Space_defs.hh.
Constructor & Destructor Documentation
|
inlineexplicit |
Builds an affine space having the specified properties.
- Parameters
-
num_dimensions The number of dimensions of the vector space enclosing the affine space; kind Specifies whether the universe or the empty affine space has to be built.
- Exceptions
-
std::length_error Thrown if num_dimensionsexceeds the maximum allowed space dimension.
Definition at line 35 of file Affine_Space_inlines.hh.
Referenced by Affine_Space().
|
inlineexplicit |
Builds an affine space, copying a system of constraints.
The affine space inherits the space dimension of the constraint system.
- Parameters
-
cs The system of constraints defining the affine space.
- Exceptions
-
std::invalid_argument Thrown if the constraint system cscontains inequality constraints.std::length_error Thrown if num_dimensionsexceeds the maximum allowed space dimension.
Definition at line 47 of file Affine_Space_inlines.hh.
|
inline |
Builds an affine space, recycling a system of constraints.
The affine space inherits the space dimension of the constraint system.
- Parameters
-
cs The system of constraints defining the affine space. Its data-structures may be recycled to build the affine space. dummy A dummy tag to syntactically differentiate this one from the other constructors.
- Exceptions
-
std::invalid_argument Thrown if the constraint system cscontains inequality constraints.std::length_error Thrown if num_dimensionsexceeds the maximum allowed space dimension.
Definition at line 52 of file Affine_Space_inlines.hh.
|
explicit |
Builds an affine space, copying a system of affine space generators.
The affine space inherits the space dimension of the generator system.
- Parameters
-
gs The system of generators defining the affine space.
- Exceptions
-
std::invalid_argument Thrown if the system of generators contains rays or is not empty but has no points. std::length_error Thrown if num_dimensionsexceeds the maximum allowed space dimension.
Definition at line 30 of file Affine_Space.cc.
References Parma_Polyhedra_Library::Linear_Expression::all_homogeneous_terms_are_zero(), Parma_Polyhedra_Library::Generator_System::begin(), Parma_Polyhedra_Library::EMPTY, Parma_Polyhedra_Library::Generator_System::end(), gr, Parma_Polyhedra_Library::Grid_Generator_System::insert(), Parma_Polyhedra_Library::Linear_Expression::linear_combine(), Parma_Polyhedra_Library::Grid::m_swap(), OK(), PPL_DIRTY_TEMP_COEFFICIENT, and Parma_Polyhedra_Library::Generator_System::space_dimension().
|
inline |
Builds an affine space, recycling a system of generators.
The affine space inherits the space dimension of the generator system.
- Parameters
-
gs The system of generators defining the affine space. Its data-structures may be recycled to build the affine space. dummy A dummy tag to syntactically differentiate this one from the other constructors.
- Exceptions
-
std::invalid_argument Thrown if the system of generators contains rays or is not empty but has no points. std::length_error Thrown if num_dimensionsexceeds the maximum allowed space dimension.
Definition at line 63 of file Affine_Space_inlines.hh.
References Affine_Space().
|
explicit |
Builds an affine space out of a box.
The affine space inherits the space dimension of the box. The built affine space is the most precise affine space that includes the box.
- Parameters
-
box The box representing the affine space to be built. complexity This argument is ignored as the algorithm used has polynomial complexity.
- Exceptions
-
std::length_error Thrown if the space dimension of boxexceeds the maximum allowed space dimension.
|
inlineexplicit |
Builds an affine space out of a bounded-difference shape.
The affine space inherits the space dimension of the BDS. The built affine space is the most precise affine space that includes the BDS.
- Parameters
-
bd The BDS representing the affine space to be built. complexity This argument is ignored as the algorithm used has polynomial complexity.
- Exceptions
-
std::length_error Thrown if the space dimension of bdexceeds the maximum allowed space dimension.
Definition at line 70 of file Affine_Space_inlines.hh.
|
inlineexplicit |
Builds an affine space out of an octagonal shape.
The affine space inherits the space dimension of the octagonal shape. The built affine space is the most precise affine space that includes the octagonal shape.
- Parameters
-
os The octagonal shape representing the affine space to be built. complexity This argument is ignored as the algorithm used has polynomial complexity.
- Exceptions
-
std::length_error Thrown if the space dimension of osexceeds the maximum allowed space dimension.
Definition at line 77 of file Affine_Space_inlines.hh.
|
inlineexplicit |
Builds an affine space from a polyhedron using algorithms whose complexity does not exceed the one specified by complexity. If complexity is ANY_COMPLEXITY, then the affine space built is the smallest one containing ph.
The affine space inherits the space dimension of ph.
- Parameters
-
ph The polyhedron. complexity The complexity class.
- Exceptions
-
std::length_error Thrown if num_dimensionsexceeds the maximum allowed space dimension.
Definition at line 57 of file Affine_Space_inlines.hh.
|
inline |
Ordinary copy constructor.
The complexity argument is ignored.
Definition at line 41 of file Affine_Space_inlines.hh.
|
inline |
Member Function Documentation
|
inline |
Adds a copy of congruence cg to *this.
- Exceptions
-
std::invalid_argument Thrown if *thisand congruencecgare dimension-incompatible.
Definition at line 117 of file Affine_Space_inlines.hh.
References Parma_Polyhedra_Library::Grid::add_congruence(), and gr.
|
inline |
Adds a copy of each congruence in cgs to *this.
- Parameters
-
cgs Contains the congruences that will be added to the system of congruences of *this.
- Exceptions
-
std::invalid_argument Thrown if *thisandcgsare dimension-incompatible.
Definition at line 122 of file Affine_Space_inlines.hh.
References Parma_Polyhedra_Library::Grid::add_congruences(), and gr.
|
inline |
Adds to *this a congruence equivalent to constraint c.
- Parameters
-
c The constraint to be added.
- Exceptions
-
std::invalid_argument Thrown if *thisandcare dimension-incompatible or if constraintcis not optimally supported by the affine space domain.
Definition at line 147 of file Affine_Space_inlines.hh.
References Parma_Polyhedra_Library::Grid::add_constraint(), and gr.
| void Parma_Polyhedra_Library::Affine_Space::add_constraints | ( | const Constraint_System & | cs | ) |
Adds to *this congruences equivalent to the constraints in cs.
- Parameters
-
cs The constraints to be added.
- Exceptions
-
std::invalid_argument Thrown if *thisandcsare dimension-incompatible or ifcscontains a constraint whcih is not optimally supported by the affine space domain.
Definition at line 167 of file Affine_Space.cc.
| void Parma_Polyhedra_Library::Affine_Space::add_generator | ( | const Generator & | g | ) |
Adds a copy of affine space generator g to the system of generators of *this.
- Exceptions
-
std::invalid_argument Thrown if *thisand generatorgare dimension-incompatible, or if*thisis an empty affine space andgis not a point.
Definition at line 172 of file Affine_Space.cc.
| void Parma_Polyhedra_Library::Affine_Space::add_generators | ( | const Generator_System & | gs | ) |
Adds a copy of the generators in gs to the system of generators of *this.
- Parameters
-
gs Contains the generators that will be added to the system of generators of *this.
- Exceptions
-
std::invalid_argument Thrown if *thisandgsare dimension-incompatible, or if*thisis empty and the system of generatorsgsis not empty, but has no points.
Definition at line 190 of file Affine_Space.cc.
| void Parma_Polyhedra_Library::Affine_Space::add_recycled_congruences | ( | Congruence_System & | cgs | ) |
Adds the congruences in cgs to *this.
- Parameters
-
cgs The congruence system to be added to *this. The congruences incgsmay be recycled.
- Exceptions
-
std::invalid_argument Thrown if *thisandcsare dimension-incompatible.
- Warning
- The only assumption that can be made about
cgsupon successful or exceptional return is that it can be safely destroyed.
Definition at line 178 of file Affine_Space.cc.
|
inline |
Adds to *this congruences equivalent to the constraints in cs.
- Parameters
-
cs The constraints to be added. They may be recycled.
- Exceptions
-
std::invalid_argument Thrown if *thisandcsare dimension-incompatible or ifcscontains a constraint whcih is not optimally supported by the affine space domain.
- Warning
- The only assumption that can be made about
csupon successful or exceptional return is that it can be safely destroyed.
Definition at line 152 of file Affine_Space_inlines.hh.
References Parma_Polyhedra_Library::Grid::add_recycled_constraints(), and gr.
| void Parma_Polyhedra_Library::Affine_Space::add_recycled_generators | ( | Generator_System & | gs | ) |
Adds the generators in gs to the system of generators of this.
- Parameters
-
gs The generator system to be added to *this. The generators ingsmay be recycled.
- Exceptions
-
std::invalid_argument Thrown if *thisandgsare dimension-incompatible.
- Warning
- The only assumption that can be made about
gsupon successful or exceptional return is that it can be safely destroyed.
Definition at line 184 of file Affine_Space.cc.
| void Parma_Polyhedra_Library::Affine_Space::add_space_dimensions_and_embed | ( | dimension_type | m | ) |
Adds m new space dimensions and embeds the old affine space in the new vector space.
- Parameters
-
m The number of dimensions to add.
- Exceptions
-
std::length_error Thrown if adding mnew space dimensions would cause the vector space to exceed dimensionmax_space_dimension().
The new space dimensions will be those having the highest indexes in the new affine space, which is characterized by a system of congruences in which the variables which are the new dimensions can have any value. For instance, when starting from the affine space 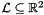 and adding a third space dimension, the result will be the affine space
and adding a third space dimension, the result will be the affine space
![\[ \bigl\{\, (x, y, z)^\transpose \in \Rset^3 \bigm| (x, y)^\transpose \in \cL \,\bigr\}. \]](form_713.png)
Definition at line 351 of file Affine_Space.cc.
| void Parma_Polyhedra_Library::Affine_Space::add_space_dimensions_and_project | ( | dimension_type | m | ) |
Adds m new space dimensions to the affine space and does not embed it in the new vector space.
- Parameters
-
m The number of space dimensions to add.
- Exceptions
-
std::length_error Thrown if adding mnew space dimensions would cause the vector space to exceed dimensionmax_space_dimension().
The new space dimensions will be those having the highest indexes in the new affine space, which is characterized by a system of congruences in which the variables running through the new dimensions are all constrained to be equal to 0. For instance, when starting from the affine space 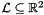 and adding a third space dimension, the result will be the affine space
and adding a third space dimension, the result will be the affine space
![\[ \bigl\{\, (x, y, 0)^\transpose \in \Rset^3 \bigm| (x, y)^\transpose \in \cL \,\bigr\}. \]](form_714.png)
Definition at line 356 of file Affine_Space.cc.
| PPL::dimension_type Parma_Polyhedra_Library::Affine_Space::affine_dimension | ( | ) | const |
Returns  , if
, if *this is empty; otherwise, returns affine dimension of *this.
Definition at line 85 of file Affine_Space.cc.
| void Parma_Polyhedra_Library::Affine_Space::affine_image | ( | Variable | var, |
| const Linear_Expression & | expr, | ||
| Coefficient_traits::const_reference | denominator = Coefficient_one() |
||
| ) |
Assigns to *this the affine image of *this under the function mapping variable var to the affine expression specified by expr and denominator.
- Parameters
-
var The variable to which the affine expression is assigned; expr The numerator of the affine expression; denominator The denominator of the affine expression (optional argument with default value 1).
- Exceptions
-
std::invalid_argument Thrown if denominatoris zero or ifexprand*thisare dimension-incompatible or ifvaris not a space dimension of*this.
When considering the generators of an affine space, the affine transformation
![\[ \frac{\sum_{i=0}^{n-1} a_i x_i + b}{\mathrm{denominator}} \]](form_704.png)
is assigned to var where expr is 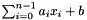 (
( 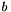 is the inhomogeneous term).
is the inhomogeneous term).
If congruences are up-to-date, it uses the specialized function affine_preimage() (for the system of congruences) and inverse transformation to reach the same result. To obtain the inverse transformation we use the following observation.
Observation:
- The affine transformation is invertible if the coefficient of
varin this transformation (i.e.,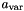 ) is different from zero.
) is different from zero. - If the transformation is invertible, then we can write
so that the inverse transformation is![\[ \mathrm{denominator} * {x'}_\mathrm{var} = \sum_{i = 0}^{n - 1} a_i x_i + b = a_\mathrm{var} x_\mathrm{var} + \sum_{i \neq var} a_i x_i + b, \]](form_707.png)
![\[ a_\mathrm{var} x_\mathrm{var} = \mathrm{denominator} * {x'}_\mathrm{var} - \sum_{i \neq j} a_i x_i - b. \]](form_708.png)
Then, if the transformation is invertible, all the entities that were up-to-date remain up-to-date. Otherwise only generators remain up-to-date.
Definition at line 244 of file Affine_Space.cc.
| void Parma_Polyhedra_Library::Affine_Space::affine_preimage | ( | Variable | var, |
| const Linear_Expression & | expr, | ||
| Coefficient_traits::const_reference | denominator = Coefficient_one() |
||
| ) |
Assigns to *this the affine preimage of *this under the function mapping variable var to the affine expression specified by expr and denominator.
- Parameters
-
var The variable to which the affine expression is substituted; expr The numerator of the affine expression; denominator The denominator of the affine expression (optional argument with default value 1).
- Exceptions
-
std::invalid_argument Thrown if denominatoris zero or ifexprand*thisare dimension-incompatible or ifvaris not a space dimension of*this.
Definition at line 253 of file Affine_Space.cc.
| void Parma_Polyhedra_Library::Affine_Space::ascii_dump | ( | ) | const |
Writes to std::cerr an ASCII representation of *this.
| void Parma_Polyhedra_Library::Affine_Space::ascii_dump | ( | std::ostream & | s | ) | const |
Writes to s an ASCII representation of *this.
Definition at line 334 of file Affine_Space.cc.
| bool Parma_Polyhedra_Library::Affine_Space::ascii_load | ( | std::istream & | s | ) |
Loads from s an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets *this accordingly. Returns true if successful, false otherwise.
Definition at line 341 of file Affine_Space.cc.
| void Parma_Polyhedra_Library::Affine_Space::bounded_affine_image | ( | Variable | var, |
| const Linear_Expression & | lb_expr, | ||
| const Linear_Expression & | ub_expr, | ||
| Coefficient_traits::const_reference | denominator = Coefficient_one() |
||
| ) |
Assigns to *this the image of *this with respect to the bounded affine relation  .
.
- Parameters
-
var The variable updated by the affine relation; lb_expr The numerator of the lower bounding affine expression; ub_expr The numerator of the upper bounding affine expression; denominator The (common) denominator for the lower and upper bounding affine expressions (optional argument with default value 1).
- Exceptions
-
std::invalid_argument Thrown if denominatoris zero or iflb_expr(resp.,ub_expr) and*thisare dimension-incompatible or ifvaris not a space dimension of*this.
Definition at line 295 of file Affine_Space.cc.
| void Parma_Polyhedra_Library::Affine_Space::bounded_affine_preimage | ( | Variable | var, |
| const Linear_Expression & | lb_expr, | ||
| const Linear_Expression & | ub_expr, | ||
| Coefficient_traits::const_reference | denominator = Coefficient_one() |
||
| ) |
Assigns to *this the preimage of *this with respect to the bounded affine relation  .
.
- Parameters
-
var The variable updated by the affine relation; lb_expr The numerator of the lower bounding affine expression; ub_expr The numerator of the upper bounding affine expression; denominator The (common) denominator for the lower and upper bounding affine expressions (optional argument with default value 1).
- Exceptions
-
std::invalid_argument Thrown if denominatoris zero or iflb_expr(resp.,ub_expr) and*thisare dimension-incompatible or ifvaris not a space dimension of*this.
Definition at line 305 of file Affine_Space.cc.
|
inline |
Returns true if and only if expr is bounded in *this.
This method is the same as bounds_from_below.
- Exceptions
-
std::invalid_argument Thrown if exprand*thisare dimension-incompatible.
Definition at line 157 of file Affine_Space_inlines.hh.
References Parma_Polyhedra_Library::Grid::bounds_from_above(), and gr.
|
inline |
Returns true if and only if expr is bounded in *this.
This method is the same as bounds_from_above.
- Exceptions
-
std::invalid_argument Thrown if exprand*thisare dimension-incompatible.
Definition at line 162 of file Affine_Space_inlines.hh.
References Parma_Polyhedra_Library::Grid::bounds_from_below(), and gr.
|
inlinestatic |
Returns true indicating that this domain has methods that can recycle congruences.
Definition at line 142 of file Affine_Space_inlines.hh.
References Parma_Polyhedra_Library::Grid::can_recycle_congruence_systems().
|
inlinestatic |
Returns true indicating that this domain has methods that can recycle constraints.
Definition at line 137 of file Affine_Space_inlines.hh.
References Parma_Polyhedra_Library::Grid::can_recycle_constraint_systems().
| void Parma_Polyhedra_Library::Affine_Space::concatenate_assign | ( | const Affine_Space & | y | ) |
Assigns to *this the concatenation of *this and y, taken in this order.
- Exceptions
-
std::length_error Thrown if the concatenation would cause the vector space to exceed dimension max_space_dimension().
Definition at line 361 of file Affine_Space.cc.
References gr.
| const PPL::Congruence_System & Parma_Polyhedra_Library::Affine_Space::congruences | ( | ) | const |
Returns the system of equality congruences satisfied by *this.
Definition at line 90 of file Affine_Space.cc.
| bool Parma_Polyhedra_Library::Affine_Space::constrains | ( | Variable | var | ) | const |
Returns true if and only if var is constrained in *this.
- Exceptions
-
std::invalid_argument Thrown if varis not a space dimension of*this.
Definition at line 157 of file Affine_Space.cc.
|
inline |
Returns a system of equality constraints satisfied by *this with the same affine dimension as *this.
Definition at line 102 of file Affine_Space_inlines.hh.
References Parma_Polyhedra_Library::Grid::constraints(), and gr.
| bool Parma_Polyhedra_Library::Affine_Space::contains | ( | const Affine_Space & | y | ) | const |
Returns true if and only if *this contains y.
- Exceptions
-
std::invalid_argument Thrown if *thisandyare dimension-incompatible.
Definition at line 324 of file Affine_Space.cc.
References gr.
| bool Parma_Polyhedra_Library::Affine_Space::contains_integer_point | ( | ) | const |
Returns true if and only if *this contains at least one integer point.
Definition at line 152 of file Affine_Space.cc.
| void Parma_Polyhedra_Library::Affine_Space::difference_assign | ( | const Affine_Space & | y | ) |
Assigns to *this the poly-difference of *this and y.
- Exceptions
-
std::invalid_argument Thrown if *thisandyare dimension-incompatible.
Definition at line 234 of file Affine_Space.cc.
References gr.
| void Parma_Polyhedra_Library::Affine_Space::expand_space_dimension | ( | Variable | var, |
| dimension_type | m | ||
| ) |
Creates m copies of the space dimension corresponding to var.
- Parameters
-
var The variable corresponding to the space dimension to be replicated; m The number of replicas to be created.
- Exceptions
-
std::invalid_argument Thrown if vardoes not correspond to a dimension of the vector space.std::length_error Thrown if adding mnew space dimensions would cause the vector space to exceed dimensionmax_space_dimension().
If *this has space dimension  , with
, with 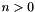 , and
, and var has space dimension 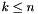 , then the
, then the  -th space dimension is expanded to
-th space dimension is expanded to m new space dimensions  ,
, 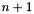 ,
,  ,
, 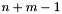 .
.
Definition at line 377 of file Affine_Space.cc.
| PPL::memory_size_type Parma_Polyhedra_Library::Affine_Space::external_memory_in_bytes | ( | ) | const |
Returns the size in bytes of the memory managed by *this.
Definition at line 346 of file Affine_Space.cc.
| void Parma_Polyhedra_Library::Affine_Space::fold_space_dimensions | ( | const Variables_Set & | to_be_folded, |
| Variable | var | ||
| ) |
Folds the space dimensions in to_be_folded into var.
- Parameters
-
to_be_folded The set of Variable objects corresponding to the space dimensions to be folded; var The variable corresponding to the space dimension that is the destination of the folding operation.
- Exceptions
-
std::invalid_argument Thrown if *thisis dimension-incompatible withvaror with one of the Variable objects contained into_be_folded. Also thrown ifvaris contained into_be_folded.
If *this has space dimension  , with
, with 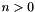 ,
, var has space dimension 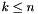 ,
, to_be_folded is a set of variables whose maximum space dimension is also less than or equal to  , and
, and var is not a member of to_be_folded, then the space dimensions corresponding to variables in to_be_folded are folded into the  -th space dimension.
-th space dimension.
Definition at line 382 of file Affine_Space.cc.
|
inline |
Returns true if and only if *this is not empty and expr is discrete in *this, in which case the maximum frequency and the value for expr that is closest to zero are computed.
- Parameters
-
expr The linear expression for which the frequency is needed; freq_n The numerator of the maximum frequency of expr;freq_d The denominator of the maximum frequency of expr;val_n The numerator of a value of exprat a point in the grid that is closest to zero;val_d The denominator of a value of exprat a point in the grid that is closest to zero;
- Exceptions
-
std::invalid_argument Thrown if exprand*thisare dimension-incompatible.
If *this is empty or expr can take any real number in *this, false is returned and freq_n, freq_d, val_n and val_d are left untouched.
Definition at line 195 of file Affine_Space_inlines.hh.
References Parma_Polyhedra_Library::Grid::frequency(), and gr.
| void Parma_Polyhedra_Library::Affine_Space::generalized_affine_image | ( | Variable | var, |
| Relation_Symbol | relsym, | ||
| const Linear_Expression & | expr, | ||
| Coefficient_traits::const_reference | denominator = Coefficient_one() |
||
| ) |
Assigns to *this the image of *this with respect to the generalized affine relation 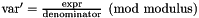 .
.
- Parameters
-
var The left hand side variable of the generalized affine relation; relsym The relation symbol where EQUAL is the symbol for a congruence relation; expr The numerator of the right hand side affine expression; denominator The denominator of the right hand side affine expression. Optional argument with an automatic value of one;
- Exceptions
-
std::invalid_argument Thrown if denominatoris zero or ifexprand*thisare dimension-incompatible or ifvaris not a space dimension ofthis.
Definition at line 261 of file Affine_Space.cc.
| void Parma_Polyhedra_Library::Affine_Space::generalized_affine_image | ( | const Linear_Expression & | lhs, |
| Relation_Symbol | relsym, | ||
| const Linear_Expression & | rhs | ||
| ) |
Assigns to *this the image of *this with respect to the generalized affine relation 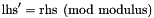 .
.
- Parameters
-
lhs The left hand side affine expression. relsym The relation symbol where EQUAL is the symbol for a congruence relation; rhs The right hand side affine expression.
- Exceptions
-
std::invalid_argument Thrown if *thisis dimension-incompatible withlhsorrhs.
Definition at line 279 of file Affine_Space.cc.
| void Parma_Polyhedra_Library::Affine_Space::generalized_affine_preimage | ( | Variable | var, |
| Relation_Symbol | relsym, | ||
| const Linear_Expression & | expr, | ||
| Coefficient_traits::const_reference | denominator = Coefficient_one() |
||
| ) |
Assigns to *this the preimage of *this with respect to the generalized affine relation 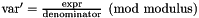 .
.
- Parameters
-
var The left hand side variable of the generalized affine relation; relsym The relation symbol where EQUAL is the symbol for a congruence relation; expr The numerator of the right hand side affine expression; denominator The denominator of the right hand side affine expression. Optional argument with an automatic value of one;
- Exceptions
-
std::invalid_argument Thrown if denominatoris zero or ifexprand*thisare dimension-incompatible or ifvaris not a space dimension ofthis.
Definition at line 270 of file Affine_Space.cc.
| void Parma_Polyhedra_Library::Affine_Space::generalized_affine_preimage | ( | const Linear_Expression & | lhs, |
| Relation_Symbol | relsym, | ||
| const Linear_Expression & | rhs | ||
| ) |
Assigns to *this the preimage of *this with respect to the generalized affine relation 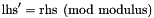 .
.
- Parameters
-
lhs The left hand side affine expression; relsym The relation symbol where EQUAL is the symbol for a congruence relation; rhs The right hand side affine expression;
- Exceptions
-
std::invalid_argument Thrown if *thisis dimension-incompatible withlhsorrhs.
Definition at line 287 of file Affine_Space.cc.
| PPL::Generator_System Parma_Polyhedra_Library::Affine_Space::generators | ( | ) | const |
Returns a system of generators defining *this.
Definition at line 100 of file Affine_Space.cc.
|
inline |
Returns a 32-bit hash code for *this.
If x and y are such that x == y, then x.hash_code() == y.hash_code().
Definition at line 97 of file Affine_Space_inlines.hh.
References gr, and Parma_Polyhedra_Library::Grid::hash_code().
| void Parma_Polyhedra_Library::Affine_Space::intersection_assign | ( | const Affine_Space & | y | ) |
Assigns to *this the intersection of *this and y.
- Exceptions
-
std::invalid_argument Thrown if *thisandyare dimension-incompatible.
Definition at line 216 of file Affine_Space.cc.
References gr.
| bool Parma_Polyhedra_Library::Affine_Space::is_bounded | ( | ) | const |
Returns true if and only if *this is bounded.
Definition at line 137 of file Affine_Space.cc.
| bool Parma_Polyhedra_Library::Affine_Space::is_discrete | ( | ) | const |
Returns true if and only if *this is discrete.
An affine space is discrete if it can be defined by a generator system that contains at most one point. This includes the empty affine space and any affine space in dimension zero.
Definition at line 142 of file Affine_Space.cc.
| bool Parma_Polyhedra_Library::Affine_Space::is_disjoint_from | ( | const Affine_Space & | y | ) | const |
Returns true if and only if *this and y are disjoint.
- Exceptions
-
std::invalid_argument Thrown if xandyare dimension-incompatible.
Definition at line 329 of file Affine_Space.cc.
References gr.
| bool Parma_Polyhedra_Library::Affine_Space::is_empty | ( | ) | const |
Returns true if and only if *this is an empty affine space.
Definition at line 127 of file Affine_Space.cc.
| bool Parma_Polyhedra_Library::Affine_Space::is_topologically_closed | ( | ) | const |
Returns true if and only if *this is a topologically closed subset of the vector space.
An affine space is always topologically closed.
Definition at line 147 of file Affine_Space.cc.
| bool Parma_Polyhedra_Library::Affine_Space::is_universe | ( | ) | const |
Returns true if and only if *this is a universe affine space.
Definition at line 132 of file Affine_Space.cc.
| void Parma_Polyhedra_Library::Affine_Space::limited_extrapolation_assign | ( | const Affine_Space & | y, |
| const Constraint_System & | cs, | ||
| unsigned * | tp = NULL |
||
| ) |
Does nothing, as the domain of affine spaces has finite height.
- Parameters
-
y An affine space that must be contained in *this;cs A system of constraints, which is ignored. tp An optional pointer, which is ignored.
- Exceptions
-
std::invalid_argument Thrown if *this,yandcsare dimension-incompatible.
Definition at line 400 of file Affine_Space.cc.
References space_dimension().
|
inline |
Swaps *this with affine space y. (*this and y can be dimension-incompatible.)
Definition at line 112 of file Affine_Space_inlines.hh.
Referenced by swap().
| void Parma_Polyhedra_Library::Affine_Space::map_space_dimensions | ( | const Partial_Function & | pfunc | ) |
Remaps the dimensions of the vector space according to a partial function.
If pfunc maps only some of the dimensions of *this then the rest will be projected away.
If the highest dimension mapped to by pfunc is higher than the highest dimension in *this then the number of dimensions in this will be increased to the highest dimension mapped to by pfunc.
- Parameters
-
pfunc The partial function specifying the destiny of each space dimension.
The template type parameter Partial_Function must provide the following methods.
returns true if and only if the represented partial function has an empty codomain (i.e., it is always undefined). The has_empty_codomain() method will always be called before the methods below. However, if has_empty_codomain() returns true, none of the functions below will be called.
returns the maximum value that belongs to the codomain of the partial function. The max_in_codomain() method is called at most once.
Let 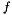 be the represented function and
be the represented function and  be the value of
be the value of i. If 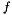 is defined in
is defined in  , then
, then 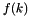 is assigned to
is assigned to j and true is returned. If 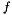 is undefined in
is undefined in  , then
, then false is returned. This method is called at most  times, where
times, where  is the dimension of the vector space enclosing the affine space.
is the dimension of the vector space enclosing the affine space.
The result is undefined if pfunc does not encode a partial function with the properties described in the specification of the mapping operator.
|
inlinestatic |
Returns the maximum space dimension all kinds of Affine_Space can handle.
Definition at line 30 of file Affine_Space_inlines.hh.
References Parma_Polyhedra_Library::Grid::max_space_dimension().
|
inline |
Returns true if and only if *this is not empty and expr is bounded from above in *this, in which case the supremum value is computed.
- Parameters
-
expr The linear expression to be maximized subject to *this;sup_n The numerator of the supremum value; sup_d The denominator of the supremum value; maximum trueif the supremum value can be reached inthis. Alwaystruewhenthisboundsexpr. Present for interface compatibility with class Polyhedron, where closure points can result in a value of false.
- Exceptions
-
std::invalid_argument Thrown if exprand*thisare dimension-incompatible.
If *this is empty or expr is not bounded by *this, false is returned and sup_n, sup_d and maximum are left untouched.
Definition at line 167 of file Affine_Space_inlines.hh.
References gr, and Parma_Polyhedra_Library::Grid::maximize().
|
inline |
Returns true if and only if *this is not empty and expr is bounded from above in *this, in which case the supremum value and a point where expr reaches it are computed.
- Parameters
-
expr The linear expression to be maximized subject to *this;sup_n The numerator of the supremum value; sup_d The denominator of the supremum value; maximum trueif the supremum value can be reached inthis. Alwaystruewhenthisboundsexpr. Present for interface compatibility with class Polyhedron, where closure points can result in a value of false;point When maximization succeeds, will be assigned a point where exprreaches its supremum value.
- Exceptions
-
std::invalid_argument Thrown if exprand*thisare dimension-incompatible.
If *this is empty or expr is not bounded by *this, false is returned and sup_n, sup_d, maximum and point are left untouched.
Definition at line 174 of file Affine_Space_inlines.hh.
References gr, and Parma_Polyhedra_Library::Grid::maximize().
|
inline |
Returns true if and only if *this is not empty and expr is bounded from below in *this, in which case the infimum value is computed.
- Parameters
-
expr The linear expression to be minimized subject to *this;inf_n The numerator of the infimum value; inf_d The denominator of the infimum value; minimum trueif the is the infimum value can be reached inthis. Alwaystruewhenthisboundsexpr. Present for interface compatibility with class Polyhedron, where closure points can result in a value of false.
- Exceptions
-
std::invalid_argument Thrown if exprand*thisare dimension-incompatible.
If *this is empty or expr is not bounded from below, false is returned and inf_n, inf_d and minimum are left untouched.
Definition at line 181 of file Affine_Space_inlines.hh.
References gr, and Parma_Polyhedra_Library::Grid::minimize().
|
inline |
Returns true if and only if *this is not empty and expr is bounded from below in *this, in which case the infimum value and a point where expr reaches it are computed.
- Parameters
-
expr The linear expression to be minimized subject to *this;inf_n The numerator of the infimum value; inf_d The denominator of the infimum value; minimum trueif the is the infimum value can be reached inthis. Alwaystruewhenthisboundsexpr. Present for interface compatibility with class Polyhedron, where closure points can result in a value of false;point When minimization succeeds, will be assigned a point where exprreaches its infimum value.
- Exceptions
-
std::invalid_argument Thrown if exprand*thisare dimension-incompatible.
If *this is empty or expr is not bounded from below, false is returned and inf_n, inf_d, minimum and point are left untouched.
Definition at line 188 of file Affine_Space_inlines.hh.
References gr, and Parma_Polyhedra_Library::Grid::minimize().
| const PPL::Congruence_System & Parma_Polyhedra_Library::Affine_Space::minimized_congruences | ( | ) | const |
Returns the system of equality congruences satisfied by *this, with no redundant congruences and having the same affine dimension as *this.
Definition at line 95 of file Affine_Space.cc.
|
inline |
Returns a minimal system of equality constraints satisfied by *this with the same affine dimension as *this.
Definition at line 107 of file Affine_Space_inlines.hh.
References gr, and Parma_Polyhedra_Library::Grid::minimized_constraints().
| PPL::Generator_System Parma_Polyhedra_Library::Affine_Space::minimized_generators | ( | ) | const |
Returns a minimized system of generators defining *this.
Definition at line 106 of file Affine_Space.cc.
| bool Parma_Polyhedra_Library::Affine_Space::OK | ( | bool | check_not_empty = false | ) | const |
Checks if all the invariants are satisfied.
- Returns
trueif and only if*thissatisfies all the invariants and eithercheck_not_emptyisfalseor*thisis not empty.
- Parameters
-
check_not_empty trueif and only if, in addition to checking the invariants,*thismust be checked to be not empty.
The check is performed so as to intrude as little as possible. If the library has been compiled with run-time assertions enabled, error messages are written on std::cerr in case invariants are violated. This is useful for the purpose of debugging the library.
Definition at line 162 of file Affine_Space.cc.
Referenced by Affine_Space().
| PPL::Affine_Space & Parma_Polyhedra_Library::Affine_Space::operator= | ( | const Affine_Space & | y | ) |
The assignment operator. (*this and y can be dimension-incompatible.)
Definition at line 79 of file Affine_Space.cc.
References gr.
| void Parma_Polyhedra_Library::Affine_Space::print | ( | ) | const |
Prints *this to std::cerr using operator<<.
|
inline |
Uses a copy of the congruence cg to refine *this.
- Parameters
-
cg The congruence used.
- Exceptions
-
std::invalid_argument Thrown if *thisand congruencecgare dimension-incompatible.
Definition at line 127 of file Affine_Space_inlines.hh.
References gr, and Parma_Polyhedra_Library::Grid::refine_with_congruence().
|
inline |
Uses a copy of the congruences in cgs to refine *this.
- Parameters
-
cgs The congruences used.
- Exceptions
-
std::invalid_argument Thrown if *thisandcgsare dimension-incompatible.
Definition at line 132 of file Affine_Space_inlines.hh.
References gr, and Parma_Polyhedra_Library::Grid::refine_with_congruences().
| void Parma_Polyhedra_Library::Affine_Space::refine_with_constraint | ( | const Constraint & | c | ) |
Uses a copy of the constraint c to refine *this.
- Parameters
-
c The constraint used. If it is not an equality, it will be ignored
- Exceptions
-
std::invalid_argument Thrown if *thisandcare dimension-incompatible.
Definition at line 196 of file Affine_Space.cc.
| void Parma_Polyhedra_Library::Affine_Space::refine_with_constraints | ( | const Constraint_System & | cs | ) |
Uses a copy of the constraints in cs to refine *this.
- Parameters
-
cs The constraints used. Constraints that are not equalities are ignored.
- Exceptions
-
std::invalid_argument Thrown if *thisandcsare dimension-incompatible.
Definition at line 201 of file Affine_Space.cc.
| PPL::Poly_Con_Relation Parma_Polyhedra_Library::Affine_Space::relation_with | ( | const Congruence & | cg | ) | const |
Returns the relations holding between *this and cg.
Definition at line 112 of file Affine_Space.cc.
| PPL::Poly_Gen_Relation Parma_Polyhedra_Library::Affine_Space::relation_with | ( | const Generator & | g | ) | const |
Returns the relations holding between *this and g.
Definition at line 117 of file Affine_Space.cc.
| PPL::Poly_Con_Relation Parma_Polyhedra_Library::Affine_Space::relation_with | ( | const Constraint & | c | ) | const |
Returns the relations holding between *this and c.
Definition at line 122 of file Affine_Space.cc.
| void Parma_Polyhedra_Library::Affine_Space::remove_higher_space_dimensions | ( | dimension_type | new_dimension | ) |
Removes the higher dimensions of the vector space so that the resulting space will have dimension new_dimension.
- Exceptions
-
std::invalid_argument Thrown if new_dimensionsis greater than the space dimension of*this.
Definition at line 371 of file Affine_Space.cc.
| void Parma_Polyhedra_Library::Affine_Space::remove_space_dimensions | ( | const Variables_Set & | vars | ) |
Removes all the specified dimensions from the vector space.
- Parameters
-
vars The set of Variable objects corresponding to the space dimensions to be removed.
- Exceptions
-
std::invalid_argument Thrown if *thisis dimension-incompatible with one of the Variable objects contained invars.
Definition at line 366 of file Affine_Space.cc.
| bool Parma_Polyhedra_Library::Affine_Space::simplify_using_context_assign | ( | const Affine_Space & | y | ) |
Assigns to *this a meet-preserving simplification of *this with respect to y. If false is returned, then the intersection is empty.
- Exceptions
-
std::invalid_argument Thrown if *thisandyare topology-incompatible or dimension-incompatible.
Definition at line 239 of file Affine_Space.cc.
References gr.
|
inline |
Returns the dimension of the vector space enclosing *this.
Definition at line 87 of file Affine_Space_inlines.hh.
References gr, and Parma_Polyhedra_Library::Grid::space_dimension().
Referenced by limited_extrapolation_assign(), throw_dimension_incompatible(), and widening_assign().
|
inline |
Returns true if and only if *this strictly contains y.
- Exceptions
-
std::invalid_argument Thrown if *thisandyare dimension-incompatible.
Definition at line 208 of file Affine_Space_inlines.hh.
References gr, and Parma_Polyhedra_Library::Grid::strictly_contains().
|
protected |
Definition at line 423 of file Affine_Space.cc.
|
protected |
Definition at line 435 of file Affine_Space.cc.
References space_dimension().
|
protected |
|
protected |
|
protected |
|
protected |
|
staticprotected |
| void Parma_Polyhedra_Library::Affine_Space::time_elapse_assign | ( | const Affine_Space & | y | ) |
Assigns to *this the result of computing the time-elapse between *this and y.
- Exceptions
-
std::invalid_argument Thrown if *thisandyare dimension-incompatible.
Definition at line 313 of file Affine_Space.cc.
References gr.
|
inline |
Assigns to *this its topological closure.
Definition at line 213 of file Affine_Space_inlines.hh.
|
inline |
Returns the total size in bytes of the memory occupied by *this.
Definition at line 92 of file Affine_Space_inlines.hh.
References gr, and Parma_Polyhedra_Library::Grid::total_memory_in_bytes().
| void Parma_Polyhedra_Library::Affine_Space::unconstrain | ( | Variable | var | ) |
Computes the cylindrification of *this with respect to space dimension var, assigning the result to *this.
- Parameters
-
var The space dimension that will be unconstrained.
- Exceptions
-
std::invalid_argument Thrown if varis not a space dimension of*this.
Definition at line 206 of file Affine_Space.cc.
| void Parma_Polyhedra_Library::Affine_Space::unconstrain | ( | const Variables_Set & | vars | ) |
Computes the cylindrification of *this with respect to the set of space dimensions vars, assigning the result to *this.
- Parameters
-
vars The set of space dimension that will be unconstrained.
- Exceptions
-
std::invalid_argument Thrown if *thisis dimension-incompatible with one of the Variable objects contained invars.
Definition at line 211 of file Affine_Space.cc.
| void Parma_Polyhedra_Library::Affine_Space::upper_bound_assign | ( | const Affine_Space & | y | ) |
Assigns to *this the least upper bound of *this and y.
- Exceptions
-
std::invalid_argument Thrown if *thisandyare dimension-incompatible.
Definition at line 221 of file Affine_Space.cc.
References gr.
| bool Parma_Polyhedra_Library::Affine_Space::upper_bound_assign_if_exact | ( | const Affine_Space & | y | ) |
If the upper bound of *this and y is exact it is assigned to this and true is returned, otherwise false is returned.
- Exceptions
-
std::invalid_argument Thrown if *thisandyare dimension-incompatible.
Definition at line 229 of file Affine_Space.cc.
References gr.
| void Parma_Polyhedra_Library::Affine_Space::widening_assign | ( | const Affine_Space & | y, |
| unsigned * | tp = NULL |
||
| ) |
Does nothing, as the domain of affine spaces has finite height.
- Parameters
-
y An affine space that must be contained in *this;tp An optional pointer, which is ignored.
- Exceptions
-
std::invalid_argument Thrown if *thisandyare dimension-incompatible.
Definition at line 388 of file Affine_Space.cc.
References space_dimension().
Friends And Related Function Documentation
|
related |
Returns true if and only if x and y are different affine spaces.
Note that x and y may be dimension-incompatible affine spaces: in those cases, the value true is returned.
|
related |
Definition at line 203 of file Affine_Space_inlines.hh.
|
related |
Output operator.
Writes a textual representation of a on s: false is written if a is an empty affine space; true is written if a is a universe affine space; a minimized system of equalitiy constraints defining a is written otherwise, all equalities in one row separated by ", "s.
|
related |
Definition at line 416 of file Affine_Space.cc.
|
related |
Returns true if and only if x and y are the same affine space.
Note that x and y may be dimension-incompatible affine spaces: in those cases, the value false is returned.
|
related |
|
friend |
|
related |
|
related |
Definition at line 218 of file Affine_Space_inlines.hh.
References m_swap().
Member Data Documentation
|
private |
The rational grid implementing *this.
Definition at line 1677 of file Affine_Space_defs.hh.
Referenced by add_congruence(), add_congruences(), add_constraint(), add_recycled_constraints(), Affine_Space(), bounds_from_above(), bounds_from_below(), concatenate_assign(), constraints(), contains(), difference_assign(), frequency(), hash_code(), intersection_assign(), is_disjoint_from(), m_swap(), maximize(), minimize(), minimized_constraints(), operator=(), operator==(), refine_with_congruence(), refine_with_congruences(), simplify_using_context_assign(), space_dimension(), strictly_contains(), time_elapse_assign(), total_memory_in_bytes(), upper_bound_assign(), and upper_bound_assign_if_exact().
The documentation for this class was generated from the following files:
