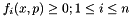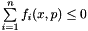A tree node representing part of the space of solutions. More...

#include <PIP_Tree_defs.hh>

Inheritance diagram for Parma_Polyhedra_Library::PIP_Solution_Node:

Collaboration diagram for Parma_Polyhedra_Library::PIP_Solution_Node:

[legend]

Classes
struct	No_Constraints
	A tag type to select the alternative copy constructor. More...

struct	Tableau
	The type for parametric simplex tableau. More...

Public Member Functions
	PIP_Solution_Node (const PIP_Problem *owner)
	Constructor: builds a solution node owned by `*owner`. More...

virtual PIP_Tree_Node *	clone () const
	Returns a pointer to a dynamically-allocated copy of `*this`. More...

virtual	~PIP_Solution_Node ()
	Destructor. More...

virtual bool	OK () const
	Returns `true` if and only if `*this` is well formed. More...

virtual const PIP_Solution_Node *	as_solution () const
	Returns `this`. More...

virtual const PIP_Decision_Node *	as_decision () const
	Returns 0, since `this` is not a decision node. More...

const Linear_Expression &	parametric_values (Variable var) const
	Returns a parametric expression for the values of problem variable `var`. More...

void	ascii_dump (std::ostream &os) const
	Dumps to `os` an ASCII representation of `*this`. More...

bool	ascii_load (std::istream &is)
	Loads from `is` an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets `*this` accordingly. Returns `true` if successful, `false` otherwise. More...

virtual memory_size_type	total_memory_in_bytes () const
	Returns the total size in bytes of the memory occupied by `*this`. More...

virtual memory_size_type	external_memory_in_bytes () const
	Returns the size in bytes of the memory managed by `*this`. More...

Public Member Functions inherited from Parma_Polyhedra_Library::PIP_Tree_Node
virtual	~PIP_Tree_Node ()
	Destructor. More...

const Constraint_System &	constraints () const
	Returns the system of parameter constraints controlling `*this`. More...

Artificial_Parameter_Sequence::const_iterator	art_parameter_begin () const
	Returns a const_iterator to the beginning of local artificial parameters. More...

Artificial_Parameter_Sequence::const_iterator	art_parameter_end () const
	Returns a const_iterator to the end of local artificial parameters. More...

dimension_type	art_parameter_count () const
	Returns the number of local artificial parameters. More...

void	print (std::ostream &s, int indent=0) const
	Prints on `s` the tree rooted in `*this`. More...

void	ascii_dump (std::ostream &s) const
	Dumps to `s` an ASCII representation of `*this`. More...

bool	ascii_load (std::istream &s)
	Loads from `s` an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets `*this` accordingly. Returns `true` if successful, `false` otherwise. More...

Protected Member Functions
	PIP_Solution_Node (const PIP_Solution_Node &y)
	Copy constructor. More...

	PIP_Solution_Node (const PIP_Solution_Node &y, No_Constraints)
	Alternative copy constructor. More...

virtual void	set_owner (const PIP_Problem *owner)
	Sets the pointer to the PIP_Problem owning object. More...

virtual bool	check_ownership (const PIP_Problem *owner) const
	Returns `true` if and only if all the nodes in the subtree rooted in `this` is owned by `pip`. More...

virtual void	update_tableau (const PIP_Problem &pip, dimension_type external_space_dim, dimension_type first_pending_constraint, const Constraint_Sequence &input_cs, const Variables_Set &parameters)
	Implements pure virtual method PIP_Tree_Node::update_tableau. More...

void	update_solution (const std::vector< bool > &pip_dim_is_param) const
	Update the solution values. More...

void	update_solution () const
	Helper method. More...

virtual PIP_Tree_Node *	solve (const PIP_Problem &pip, bool check_feasible_context, const Matrix< Row > &context, const Variables_Set &params, dimension_type space_dim, int indent_level)
	Implements pure virtual method PIP_Tree_Node::solve. More...

void	generate_cut (dimension_type index, Variables_Set &parameters, Matrix< Row > &context, dimension_type &space_dimension, int indent_level)
	Generate a Gomory cut using non-integer tableau row `index`. More...

virtual void	print_tree (std::ostream &s, int indent, const std::vector< bool > &pip_dim_is_param, dimension_type first_art_dim) const
	Prints on `s` the tree rooted in `*this`. More...

Protected Member Functions inherited from Parma_Polyhedra_Library::PIP_Tree_Node
	PIP_Tree_Node (const PIP_Problem *owner)
	Constructor: builds a node owned by `*owner`. More...

	PIP_Tree_Node (const PIP_Tree_Node &y)
	Copy constructor. More...

const PIP_Problem *	get_owner () const
	Returns a pointer to the PIP_Problem owning object. More...

const PIP_Decision_Node *	parent () const
	Returns a pointer to this node's parent. More...

void	set_parent (const PIP_Decision_Node *p)
	Set this node's parent to `*p`. More...

void	add_constraint (const Row &row, const Variables_Set &parameters)
	Inserts a new parametric constraint in internal row format. More...

void	parent_merge ()
	Merges parent's artificial parameters into `*this`. More...

Private Types
enum	Row_Sign { UNKNOWN, ZERO, POSITIVE, NEGATIVE, MIXED }
	The possible values for the sign of a parametric linear expression. More...

Static Private Member Functions
static Row_Sign	row_sign (const Row &x, dimension_type big_dimension)
	Returns the sign of row `x`. More...

Private Attributes
Tableau	tableau
	The parametric simplex tableau. More...

std::vector< bool >	basis
	A boolean vector for identifying the basic variables. More...

std::vector< dimension_type >	mapping
	A mapping between the tableau rows/columns and the original variables. More...

std::vector< dimension_type >	var_row
	The variable identifiers associated to the rows of the simplex tableau. More...

std::vector< dimension_type >	var_column
	The variable identifiers associated to the columns of the simplex tableau. More...

dimension_type	special_equality_row
	The variable number of the special inequality used for modeling equality constraints. More...

dimension_type	big_dimension
	The column index in the parametric part of the simplex tableau corresponding to the big parameter; `not_a_dimension()` if not set. More...

std::vector< Row_Sign >	sign
	A cache for computed sign values of constraint parametric RHS. More...

std::vector< Linear_Expression >	solution
	Parametric values for the solution. More...

bool	solution_valid
	An indicator for solution validity. More...

Friends
bool	PIP_Problem::ascii_load (std::istream &s)

Additional Inherited Members
Public Types inherited from Parma_Polyhedra_Library::PIP_Tree_Node
typedef Sparse_Row	Row

typedef std::vector< Artificial_Parameter >	Artificial_Parameter_Sequence
	A type alias for a sequence of Artificial_Parameter's. More...

Protected Types inherited from Parma_Polyhedra_Library::PIP_Tree_Node
typedef std::vector< Constraint >	Constraint_Sequence
	A type alias for a sequence of constraints. More...

Static Protected Member Functions inherited from Parma_Polyhedra_Library::PIP_Tree_Node
static void	indent_and_print (std::ostream &s, int indent, const char *str)
	A helper function used when printing PIP trees. More...

static bool	compatibility_check (Matrix< Row > &s)
	Checks whether a context matrix is satisfiable. More...

static bool	compatibility_check (const Matrix< Row > &context, const Row &row)
	Helper method: checks for satisfiability of the restricted context obtained by adding `row` to `context`. More...

Protected Attributes inherited from Parma_Polyhedra_Library::PIP_Tree_Node
const PIP_Problem *	owner_
	A pointer to the PIP_Problem object owning this node. More...

const PIP_Decision_Node *	parent_
	A pointer to the parent of `this`, null if `this` is the root. More...

Constraint_System	constraints_
	The local system of parameter constraints. More...

Artificial_Parameter_Sequence	artificial_parameters
	The local sequence of expressions for local artificial parameters. More...

Related Functions inherited from Parma_Polyhedra_Library::PIP_Tree_Node
std::ostream &	operator<< (std::ostream &os, const PIP_Tree_Node &x)
	Output operator: prints the solution tree rooted in `x`. More...

Detailed Description

A tree node representing part of the space of solutions.

Definition at line 360 of file PIP_Tree_defs.hh.

Member Enumeration Documentation

enum Parma_Polyhedra_Library::PIP_Solution_Node::Row_Sign

private

The possible values for the sign of a parametric linear expression.

Enumerator
UNKNOWN	Not computed yet (default).
ZERO	All row coefficients are zero.
POSITIVE	All nonzero row coefficients are positive.
NEGATIVE	All nonzero row coefficients are negative.
MIXED	The row contains both positive and negative coefficients.

Definition at line 593 of file PIP_Tree_defs.hh.

                 {
     UNKNOWN,
     ZERO,
     POSITIVE,
     NEGATIVE,
     MIXED
   };

Constructor & Destructor Documentation

Parma_Polyhedra_Library::PIP_Solution_Node::PIP_Solution_Node ( const PIP_Problem * owner )

explicit

Constructor: builds a solution node owned by *owner.

Definition at line 1036 of file PIP_Tree.cc.

Referenced by Parma_Polyhedra_Library::PIP_Decision_Node::ascii_load(), clone(), and solve().

   : PIP_Tree_Node(owner),
     tableau(),
     basis(),
     mapping(),
     var_row(),
     var_column(),
     special_equality_row(0),
     big_dimension(not_a_dimension()),
     sign(),
     solution(),
     solution_valid(false) {
 }

Parma_Polyhedra_Library::PIP_Solution_Node::~PIP_Solution_Node ( )

virtual

Destructor.

Definition at line 1079 of file PIP_Tree.cc.

1079 {

1080 }

Parma_Polyhedra_Library::PIP_Solution_Node::PIP_Solution_Node ( const PIP_Solution_Node & y )

protected

Copy constructor.

Definition at line 1050 of file PIP_Tree.cc.

   : PIP_Tree_Node(y),
     tableau(y.tableau),
     basis(y.basis),
     mapping(y.mapping),
     var_row(y.var_row),
     var_column(y.var_column),
     special_equality_row(y.special_equality_row),
     big_dimension(y.big_dimension),
     sign(y.sign),
     solution(y.solution),
     solution_valid(y.solution_valid) {
 }

Parma_Polyhedra_Library::PIP_Solution_Node::PIP_Solution_Node	(	const PIP_Solution_Node &	y,
		No_Constraints
	)

protected

Alternative copy constructor.

This constructor differs from the default copy constructor in that it will not copy the constraint system, nor the artificial parameters.

Definition at line 1064 of file PIP_Tree.cc.

   : PIP_Tree_Node(y.owner_), // NOTE: only copy owner.
     tableau(y.tableau),
     basis(y.basis),
     mapping(y.mapping),
     var_row(y.var_row),
     var_column(y.var_column),
     special_equality_row(y.special_equality_row),
     big_dimension(y.big_dimension),
     sign(y.sign),
     solution(y.solution),
     solution_valid(y.solution_valid) {
 }

Member Function Documentation

const PIP_Decision_Node * Parma_Polyhedra_Library::PIP_Solution_Node::as_decision ( ) const

virtual

Returns 0, since this is not a decision node.

Implements Parma_Polyhedra_Library::PIP_Tree_Node.

Definition at line 1153 of file PIP_Tree.cc.

                                      {
   return 0;
 }

const PIP_Solution_Node * Parma_Polyhedra_Library::PIP_Solution_Node::as_solution ( ) const

virtual

Returns this.

Implements Parma_Polyhedra_Library::PIP_Tree_Node.

Definition at line 1163 of file PIP_Tree.cc.

Referenced by Parma_Polyhedra_Library::PIP_Problem::ascii_dump(), and Parma_Polyhedra_Library::PIP_Decision_Node::ascii_dump().

                                      {
   return this;
 }

void Parma_Polyhedra_Library::PIP_Solution_Node::ascii_dump ( std::ostream & os ) const

Dumps to os an ASCII representation of *this.

Definition at line 1909 of file PIP_Tree.cc.

References Parma_Polyhedra_Library::PIP_Tree_Node::ascii_dump(), big_dimension, MIXED, NEGATIVE, POSITIVE, sign, solution, solution_valid, special_equality_row, UNKNOWN, var_column, var_row, and ZERO.

Referenced by Parma_Polyhedra_Library::PIP_Problem::ascii_dump(), Parma_Polyhedra_Library::PIP_Decision_Node::ascii_dump(), and Parma_Polyhedra_Library::PIP_Tree_Node::OK().

                                                   {
   PIP_Tree_Node::ascii_dump(os);
 
   os << "\ntableau\n";
   tableau.ascii_dump(os);
 
   os << "\nbasis ";
   const dimension_type basis_size = basis.size();
   os << basis_size;
   for (dimension_type i = 0; i < basis_size; ++i) {
     os << (basis[i] ? " true" : " false");
   }
 
   os << "\nmapping ";
   const dimension_type mapping_size = mapping.size();
   os << mapping_size;
   for (dimension_type i = 0; i < mapping_size; ++i) {
     os << " " << mapping[i];
   }
 
   os << "\nvar_row ";
   const dimension_type var_row_size = var_row.size();
   os << var_row_size;
   for (dimension_type i = 0; i < var_row_size; ++i) {
     os << " " << var_row[i];
   }
 
   os << "\nvar_column ";
   const dimension_type var_column_size = var_column.size();
   os << var_column_size;
   for (dimension_type i = 0; i < var_column_size; ++i) {
     os << " " << var_column[i];
   }
 
   os << "\n";
 
   os << "special_equality_row " << special_equality_row << "\n";
   os << "big_dimension " << big_dimension << "\n";
 
   os << "sign ";
   const dimension_type sign_size = sign.size();
   os << sign_size;
   for (dimension_type i = 0; i < sign_size; ++i) {
     os << " ";
     switch (sign[i]) {
     case UNKNOWN:
       os << "UNKNOWN";
       break;
     case ZERO:
       os << "ZERO";
       break;
     case POSITIVE:
       os << "POSITIVE";
       break;
     case NEGATIVE:
       os << "NEGATIVE";
       break;
     case MIXED:
       os << "MIXED";
       break;
     }
   }
   os << "\n";
 
   const dimension_type solution_size = solution.size();
   os << "solution " << solution_size << "\n";
   for (dimension_type i = 0; i < solution_size; ++i) {
     solution[i].ascii_dump(os);
   }
   os << "\n";
 
   os << "solution_valid " << (solution_valid ? "true" : "false") << "\n";
 }

bool Parma_Polyhedra_Library::PIP_Solution_Node::ascii_load ( std::istream & is )

Loads from is an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets *this accordingly. Returns true if successful, false otherwise.

Definition at line 1984 of file PIP_Tree.cc.

References Parma_Polyhedra_Library::PIP_Tree_Node::ascii_load(), Parma_Polyhedra_Library::Linear_Expression::ascii_load(), big_dimension, MIXED, NEGATIVE, OK(), POSITIVE, sign, solution, solution_valid, special_equality_row, UNKNOWN, var_column, var_row, and ZERO.

Referenced by Parma_Polyhedra_Library::PIP_Problem::ascii_load(), and Parma_Polyhedra_Library::PIP_Decision_Node::ascii_load().

                                             {
   if (!PIP_Tree_Node::ascii_load(is)) {
     return false;
   }
 
   std::string str;
   if (!(is >> str) || str != "tableau") {
     return false;
   }
   if (!tableau.ascii_load(is)) {
     return false;
   }
   if (!(is >> str) || str != "basis") {
     return false;
   }
   dimension_type basis_size;
   if (!(is >> basis_size)) {
     return false;
   }
   basis.clear();
   for (dimension_type i = 0; i < basis_size; ++i) {
     if (!(is >> str)) {
       return false;
     }
     bool val = false;
     if (str == "true") {
       val = true;
     }
     else if (str != "false") {
       return false;
     }
     basis.push_back(val);
   }
 
   if (!(is >> str) || str != "mapping") {
     return false;
   }
   dimension_type mapping_size;
   if (!(is >> mapping_size)) {
     return false;
   }
   mapping.clear();
   for (dimension_type i = 0; i < mapping_size; ++i) {
     dimension_type val;
     if (!(is >> val)) {
       return false;
     }
     mapping.push_back(val);
   }
 
   if (!(is >> str) || str != "var_row") {
     return false;
   }
   dimension_type var_row_size;
   if (!(is >> var_row_size)) {
     return false;
   }
   var_row.clear();
   for (dimension_type i = 0; i < var_row_size; ++i) {
     dimension_type val;
     if (!(is >> val)) {
       return false;
     }
     var_row.push_back(val);
   }
 
   if (!(is >> str) || str != "var_column") {
     return false;
   }
   dimension_type var_column_size;
   if (!(is >> var_column_size)) {
     return false;
   }
   var_column.clear();
   for (dimension_type i = 0; i < var_column_size; ++i) {
     dimension_type val;
     if (!(is >> val)) {
       return false;
     }
     var_column.push_back(val);
   }
 
   if (!(is >> str) || str != "special_equality_row") {
     return false;
   }
   if (!(is >> special_equality_row)) {
     return false;
   }
 
   if (!(is >> str) || str != "big_dimension") {
     return false;
   }
   if (!(is >> big_dimension)) {
     return false;
   }
 
   if (!(is >> str) || str != "sign") {
     return false;
   }
   dimension_type sign_size;
   if (!(is >> sign_size)) {
     return false;
   }
 
   sign.clear();
   for (dimension_type i = 0; i < sign_size; ++i) {
     if (!(is >> str)) {
       return false;
     }
     Row_Sign val;
     if (str == "UNKNOWN") {
       val = UNKNOWN;
     }
     else if (str == "ZERO") {
       val = ZERO;
     }
     else if (str == "POSITIVE") {
       val = POSITIVE;
     }
     else if (str == "NEGATIVE") {
       val = NEGATIVE;
     }
     else if (str == "MIXED") {
       val = MIXED;
     }
     else {
       return false;
     }
     sign.push_back(val);
   }
 
   if (!(is >> str) || str != "solution") {
     return false;
   }
   dimension_type solution_size;
   if (!(is >> solution_size)) {
     return false;
   }
   solution.clear();
   for (dimension_type i = 0; i < solution_size; ++i) {
     Linear_Expression val;
     if (!val.ascii_load(is)) {
       return false;
     }
     solution.push_back(val);
   }
 
   if (!(is >> str) || str != "solution_valid") {
     return false;
   }
   if (!(is >> str)) {
     return false;
   }
   if (str == "true") {
     solution_valid = true;
   }
   else if (str == "false") {
     solution_valid = false;
   }
   else {
     return false;
   }
 
   PPL_ASSERT(OK());
   return true;
 }

bool Parma_Polyhedra_Library::PIP_Solution_Node::check_ownership ( const PIP_Problem * owner ) const

protectedvirtual

Returns true if and only if all the nodes in the subtree rooted in *this is owned by *pip.

Implements Parma_Polyhedra_Library::PIP_Tree_Node.

Definition at line 1136 of file PIP_Tree.cc.

References Parma_Polyhedra_Library::PIP_Tree_Node::get_owner().

                                                                  {
   return get_owner() == owner;
 }

PIP_Tree_Node * Parma_Polyhedra_Library::PIP_Solution_Node::clone ( ) const

virtual

Returns a pointer to a dynamically-allocated copy of *this.

Implements Parma_Polyhedra_Library::PIP_Tree_Node.

Definition at line 1863 of file PIP_Tree.cc.

References PIP_Solution_Node().

                                {
   return new PIP_Solution_Node(*this);
 }

memory_size_type Parma_Polyhedra_Library::PIP_Solution_Node::external_memory_in_bytes ( ) const

virtual

Returns the size in bytes of the memory managed by *this.

Implements Parma_Polyhedra_Library::PIP_Tree_Node.

Definition at line 3778 of file PIP_Tree.cc.

References Parma_Polyhedra_Library::Checked::bool, Parma_Polyhedra_Library::PIP_Tree_Node::external_memory_in_bytes(), sign, solution, var_column, and var_row.

Referenced by Parma_Polyhedra_Library::PIP_Tree_Node::Artificial_Parameter::total_memory_in_bytes(), total_memory_in_bytes(), and Parma_Polyhedra_Library::PIP_Decision_Node::total_memory_in_bytes().

                                                   {
   memory_size_type n = PIP_Tree_Node::external_memory_in_bytes();
   n += tableau.external_memory_in_bytes();
   // FIXME: size of std::vector<bool> ?
   n += basis.capacity() * sizeof(bool);
   n += sizeof(dimension_type)
     * (mapping.capacity() + var_row.capacity() + var_column.capacity());
   n += sign.capacity() * sizeof(Row_Sign);
   // FIXME: Adding the external memory for `solution'.
   n += solution.capacity() * sizeof(Linear_Expression);
   for (std::vector<Linear_Expression>::const_iterator
          i = solution.begin(), i_end = solution.end();
          i != i_end; ++i) {
     n += (i->external_memory_in_bytes());
   }
 
   return n;
 }

void Parma_Polyhedra_Library::PIP_Solution_Node::generate_cut	(	dimension_type	index,
		Variables_Set &	parameters,
		Matrix< Row > &	context,
		dimension_type &	space_dimension,
		int	indent_level
	)

protected

Generate a Gomory cut using non-integer tableau row index.

Parameters

index	Row index in simplex tableau from which the cut is generated.
parameters	A std::set of the current parameter dimensions (including artificials); to be updated if a new artificial parameter is to be created.
context	A set of linear inequalities on the parameters, in matrix form; to be updated if a new artificial parameter is to be created.
space_dimension	The current space dimension, including variables and all parameters; to be updated if an extra parameter is to be created.
indent_level	The indentation level (for debugging output only).

Definition at line 3463 of file PIP_Tree.cc.

Referenced by solve().

                                                         {
   PPL_ASSERT(indent_level >= 0);
 #ifdef NOISY_PIP
   std::cerr << std::setw(2 * indent_level) << ""
             << "Row " << index << " requires cut generation.\n";
 #else
   PPL_USED(indent_level);
 #endif // #ifdef NOISY_PIP
 
   const dimension_type num_rows = tableau.t.num_rows();
   PPL_ASSERT(index < num_rows);
   const dimension_type num_vars = tableau.s.num_columns();
   const dimension_type num_params = tableau.t.num_columns();
   PPL_ASSERT(num_params == 1 + parameters.size());
   Coefficient_traits::const_reference denom = tableau.denominator();
 
   PPL_DIRTY_TEMP_COEFFICIENT(mod);
   PPL_DIRTY_TEMP_COEFFICIENT(coeff);
 
   // Test if cut to be generated must be parametric or not.
   bool generate_parametric_cut = false;
   {
     // Limiting the scope of reference row_t (may be later invalidated).
     const Row& row_t = tableau.t[index];
     Row::const_iterator j = row_t.begin();
     Row::const_iterator j_end = row_t.end();
     // Skip the element with index 0.
     if (j != j_end && j.index() == 0) {
       ++j;
     }
     WEIGHT_BEGIN();
     for ( ; j != j_end; ++j) {
       WEIGHT_ADD(7);
       if (*j % denom != 0) {
         generate_parametric_cut = true;
         break;
       }
     }
   }
 
   // Column index of already existing Artificial_Parameter.
   dimension_type ap_column = not_a_dimension();
 
   if (generate_parametric_cut) {
     // Fractional parameter coefficient found: generate parametric cut.
     bool reuse_ap = false;
     Linear_Expression expr;
 
     // Limiting the scope of reference row_t (may be later invalidated).
     {
       const Row& row_t = tableau.t[index];
       Row::const_iterator j = row_t.begin();
       Row::const_iterator j_end = row_t.end();
       if (j != j_end && j.index() == 0) {
         pos_rem_assign(mod, *j, denom);
         ++j;
         if (mod != 0) {
           // Optimizing computation: expr += (denom - mod);
           expr += denom;
           expr -= mod;
         }
       }
       if (!parameters.empty()) {
         // To avoid reallocations of expr.
         add_mul_assign(expr, 0, Variable(*(parameters.rbegin())));
         Variables_Set::const_iterator p_j = parameters.begin();
         dimension_type last_index = 1;
         WEIGHT_BEGIN();
         for ( ; j != j_end; ++j) {
           WEIGHT_ADD(69);
           pos_rem_assign(mod, *j, denom);
           if (mod != 0) {
             // Optimizing computation: expr += (denom - mod) * Variable(*p_j);
             WEIGHT_ADD(164);
             coeff = denom - mod;
             PPL_ASSERT(last_index <= j.index());
             std::advance(p_j, j.index() - last_index);
             last_index = j.index();
             add_mul_assign(expr, coeff, Variable(*p_j));
           }
         }
       }
     }
     // Generate new artificial parameter.
     const Artificial_Parameter ap(expr, denom);
 
     // Search if the Artificial_Parameter has already been generated.
     ap_column = space_dimension;
     const PIP_Tree_Node* node = this;
     do {
       for (dimension_type j = node->artificial_parameters.size(); j-- > 0; ) {
         --ap_column;
         if (node->artificial_parameters[j] == ap) {
           reuse_ap = true;
           break;
         }
       }
       node = node->parent();
     } while (!reuse_ap && node != 0);
 
     if (reuse_ap) {
       // We can re-use an existing Artificial_Parameter.
 #ifdef NOISY_PIP
       using namespace IO_Operators;
       std::cerr << std::setw(2 * indent_level) << ""
                 << "Re-using parameter " << Variable(ap_column)
                 << " = " << ap << std::endl;
 #endif // #ifdef NOISY_PIP
       ap_column = ap_column - num_vars + 1;
     }
     else {
       // Here reuse_ap == false: the Artificial_Parameter does not exist yet.
       // Beware: possible reallocation invalidates row references.
       tableau.t.add_zero_columns(1);
       context.add_zero_columns(1);
       artificial_parameters.push_back(ap);
       parameters.insert(space_dimension);
 #ifdef NOISY_PIP
       using namespace IO_Operators;
       std::cerr << std::setw(2 * indent_level) << ""
                 << "New parameter " << Variable(space_dimension)
                 << " = " << ap << std::endl;
 #endif // #ifdef NOISY_PIP
       ++space_dimension;
       ap_column = num_params;
 
       // Update current context with constraints on the new parameter.
       const dimension_type ctx_num_rows = context.num_rows();
       context.add_zero_rows(2);
       Row& ctx1 = context[ctx_num_rows];
       Row& ctx2 = context[ctx_num_rows+1];
       // Recompute row reference after possible reallocation.
       const Row& row_t = tableau.t[index];
       {
         Row::const_iterator j = row_t.begin();
         Row::const_iterator j_end = row_t.end();
         Row::iterator itr1 = ctx1.end();
         Row::iterator itr2 = ctx2.end();
         if (j != j_end && j.index() == 0) {
           pos_rem_assign(mod, *j, denom);
           if (mod != 0) {
             itr1 = ctx1.insert(0, denom);
             *itr1 -= mod;
             itr2 = ctx2.insert(0, *itr1);
             neg_assign(*itr2);
             // Compute <CODE> ctx2[0] += denom-1; </CODE>
             *itr2 += denom;
             --(*itr2);
           }
           else {
             // Compute <CODE> ctx2[0] += denom-1; </CODE>
             itr2 = ctx2.insert(0, denom);
             --(*itr2);
           }
           ++j;
         }
         else {
           // Compute <CODE> ctx2[0] += denom-1; </CODE>
           itr2 = ctx2.insert(0, denom);
           --(*itr2);
         }
         WEIGHT_BEGIN();
         for ( ; j != j_end; ++j) {
           pos_rem_assign(mod, *j, denom);
           if (mod != 0) {
             const dimension_type j_index = j.index();
             itr1 = ctx1.insert(itr1, j_index, denom);
             *itr1 -= mod;
             itr2 = ctx2.insert(itr2, j_index, *itr1);
             neg_assign(*itr2);
             WEIGHT_ADD(294);
           }
         }
         itr1 = ctx1.insert(itr1, num_params, denom);
         neg_assign(*itr1);
         itr2 = ctx2.insert(itr2, num_params, denom);
         WEIGHT_ADD(122);
       }
 
 #ifdef NOISY_PIP
       {
         using namespace IO_Operators;
         Variables_Set::const_iterator p = parameters.begin();
         Linear_Expression expr1(ctx1.get(0));
         Linear_Expression expr2(ctx2.get(0));
         for (dimension_type j = 1; j <= num_params; ++j, ++p) {
           add_mul_assign(expr1, ctx1.get(j), Variable(*p));
           add_mul_assign(expr2, ctx2.get(j), Variable(*p));
         }
         std::cerr << std::setw(2 * indent_level) << ""
                   << "Adding to context: "
                   << Constraint(expr1 >= 0) << " ; "
                   << Constraint(expr2 >= 0) << std::endl;
       }
 #endif // #ifdef NOISY_PIP
     }
   }
 
   // Generate new cut.
   tableau.s.add_zero_rows(1);
   tableau.t.add_zero_rows(1);
   Row& cut_s = tableau.s[num_rows];
   Row& cut_t = tableau.t[num_rows];
   // Recompute references after possible reallocation.
   const Row& row_s = tableau.s[index];
   const Row& row_t = tableau.t[index];
   WEIGHT_BEGIN();
   {
     Row::iterator itr = cut_s.end();
     for (Row::const_iterator
            j = row_s.begin(), j_end = row_s.end(); j != j_end; ++j) {
       WEIGHT_ADD(55);
       itr = cut_s.insert(itr, j.index(), *j);
       pos_rem_assign(*itr, *itr, denom);
     }
   }
   {
     Row::iterator cut_t_itr = cut_t.end();
     for (Row::const_iterator
            j = row_t.begin(), j_end = row_t.end(); j!=j_end; ++j) {
       WEIGHT_ADD(37);
       pos_rem_assign(mod, *j, denom);
       if (mod != 0) {
         WEIGHT_ADD(108);
         cut_t_itr = cut_t.insert(cut_t_itr, j.index(), mod);
         *cut_t_itr -= denom;
       }
     }
   }
   if (ap_column != not_a_dimension()) {
     // If we re-use an existing Artificial_Parameter
     cut_t[ap_column] = denom;
   }
 #ifdef NOISY_PIP
   {
     using namespace IO_Operators;
     Linear_Expression expr;
     dimension_type ti = 1;
     dimension_type si = 0;
     for (dimension_type j = 0; j < space_dimension; ++j) {
       if (parameters.count(j) == 1) {
         add_mul_assign(expr, cut_t.get(ti), Variable(j));
         ++ti;
       }
       else {
         add_mul_assign(expr, cut_s.get(si), Variable(j));
         ++si;
       }
     }
     std::cerr << std::setw(2 * indent_level) << ""
               << "Adding cut: "
               << Constraint(expr + cut_t.get(0) >= 0)
               << std::endl;
   }
 #endif // #ifdef NOISY_PIP
   var_row.push_back(num_rows + num_vars);
   basis.push_back(false);
   mapping.push_back(num_rows);
   sign.push_back(NEGATIVE);
 }

bool Parma_Polyhedra_Library::PIP_Solution_Node::OK ( ) const

virtual

Returns true if and only if *this is well formed.

Implements Parma_Polyhedra_Library::PIP_Tree_Node.

Definition at line 1263 of file PIP_Tree.cc.

References Parma_Polyhedra_Library::PIP_Tree_Node::OK(), var_column, and var_row.

Referenced by ascii_load(), Parma_Polyhedra_Library::PIP_Solution_Node::Tableau::ascii_load(), Parma_Polyhedra_Library::PIP_Decision_Node::ascii_load(), Parma_Polyhedra_Library::PIP_Tree_Node::parent_merge(), solve(), Parma_Polyhedra_Library::PIP_Decision_Node::solve(), update_tableau(), and Parma_Polyhedra_Library::PIP_Decision_Node::update_tableau().

                             {
 #ifndef NDEBUG
   using std::cerr;
 #endif
   if (!PIP_Tree_Node::OK()) {
     return false;
   }
 
   // Check that every member used is OK.
 
   if (!tableau.OK()) {
     return false;
   }
 
   // Check coherency of basis, mapping, var_row and var_column
   if (basis.size() != mapping.size()) {
 #ifndef NDEBUG
     cerr << "The PIP_Solution_Node::basis and PIP_Solution_Node::mapping "
          << "vectors do not have the same number of elements.\n";
 #endif
     return false;
   }
   if (basis.size() != var_row.size() + var_column.size()) {
 #ifndef NDEBUG
     cerr << "The sum of number of elements in the PIP_Solution_Node::var_row "
          << "and PIP_Solution_Node::var_column vectors is different from the "
          << "number of elements in the PIP_Solution_Node::basis vector.\n";
 #endif
     return false;
   }
   if (var_column.size() != tableau.s.num_columns()) {
 #ifndef NDEBUG
     cerr << "The number of elements in the PIP_Solution_Node::var_column "
          << "vector is different from the number of columns in the "
          << "PIP_Solution_Node::tableau.s matrix.\n";
 #endif
     return false;
   }
   if (var_row.size() != tableau.s.num_rows()) {
 #ifndef NDEBUG
     cerr << "The number of elements in the PIP_Solution_Node::var_row "
          << "vector is different from the number of rows in the "
          << "PIP_Solution_Node::tableau.s matrix.\n";
 #endif
     return false;
   }
   for (dimension_type i = mapping.size(); i-- > 0; ) {
     const dimension_type row_column = mapping[i];
     if (basis[i] && var_column[row_column] != i) {
 #ifndef NDEBUG
       cerr << "Variable " << i << " is basic and corresponds to column "
            << row_column << " but PIP_Solution_Node::var_column["
            << row_column << "] does not correspond to variable " << i
            << ".\n";
 #endif
       return false;
     }
     if (!basis[i] && var_row[row_column] != i) {
 #ifndef NDEBUG
       cerr << "Variable " << i << " is nonbasic and corresponds to row "
            << row_column << " but PIP_Solution_Node::var_row["
            << row_column << "] does not correspond to variable " << i
            << ".\n";
 #endif
       return false;
     }
   }
   // All checks passed.
   return true;
 }

const Linear_Expression & Parma_Polyhedra_Library::PIP_Solution_Node::parametric_values ( Variable var ) const

Returns a parametric expression for the values of problem variable var.

The returned linear expression may involve problem parameters as well as artificial parameters.

Parameters

var	The problem variable which is queried about.

Exceptions

std::invalid_argument Thrown if var is dimension-incompatible with the PIP_Problem owning this solution node, or if var is a problem parameter.

Definition at line 3920 of file PIP_Tree.cc.

References Parma_Polyhedra_Library::PIP_Tree_Node::get_owner(), Parma_Polyhedra_Library::Variable::id(), Parma_Polyhedra_Library::PIP_Problem::parameter_space_dimensions(), solution, Parma_Polyhedra_Library::Variable::space_dimension(), Parma_Polyhedra_Library::PIP_Problem::space_dimension(), and update_solution().

                                                              {
   const PIP_Problem* const pip = get_owner();
   PPL_ASSERT(pip != 0);
 
   const dimension_type space_dim = pip->space_dimension();
   if (var.space_dimension() > space_dim) {
     std::ostringstream s;
     s << "PPL::PIP_Solution_Node::parametric_values(v):\n"
       << "v.space_dimension() == " << var.space_dimension()
       << " is incompatible with the owning PIP_Problem "
       << " (space dim == " << space_dim << ").";
     throw std::invalid_argument(s.str());
   }
 
   dimension_type solution_index = var.id();
   const Variables_Set& params = pip->parameter_space_dimensions();
   for (Variables_Set::const_iterator p = params.begin(),
          p_end = params.end(); p != p_end; ++p) {
     const dimension_type param_index = *p;
     if (param_index < var.id()) {
       --solution_index;
     }
     else if (param_index == var.id()) {
       throw std::invalid_argument("PPL::PIP_Solution_Node"
                                   "::parametric_values(v):\n"
                                   "v is a problem parameter.");
     }
     else {
       break;
     }
   }
 
   update_solution();
   return solution[solution_index];
 }

void Parma_Polyhedra_Library::PIP_Solution_Node::print_tree	(	std::ostream &	s,
		int	indent,
		const std::vector< bool > &	pip_dim_is_param,
		dimension_type	first_art_dim
	)		const

protectedvirtual

Prints on s the tree rooted in *this.

Implements Parma_Polyhedra_Library::PIP_Tree_Node.

Definition at line 3887 of file PIP_Tree.cc.

References Parma_Polyhedra_Library::PIP_Tree_Node::constraints_, Parma_Polyhedra_Library::Constraint_System::empty(), Parma_Polyhedra_Library::PIP_Tree_Node::indent_and_print(), Parma_Polyhedra_Library::PIP_Tree_Node::print_tree(), solution, and update_solution().

Referenced by Parma_Polyhedra_Library::PIP_Tree_Node::print().

                                                                         {
   // Print info common to decision and solution nodes.
   PIP_Tree_Node::print_tree(s, indent, pip_dim_is_param, first_art_dim);
 
   // Print info specific of solution nodes:
   // first update solution if needed ...
   update_solution(pip_dim_is_param);
   // ... and then actually print it.
   const bool no_constraints = constraints_.empty();
   indent_and_print(s, indent + (no_constraints ? 0 : 1), "{");
   const dimension_type pip_space_dim = pip_dim_is_param.size();
   for (dimension_type i = 0, num_var = 0; i < pip_space_dim; ++i) {
     if (pip_dim_is_param[i]) {
       continue;
     }
     if (num_var > 0) {
       s << " ; ";
     }
     using namespace IO_Operators;
     s << solution[num_var];
     ++num_var;
   }
   s << "}\n";
 
   if (!no_constraints) {
     indent_and_print(s, indent, "else\n");
     indent_and_print(s, indent+1, "_|_\n");
   }
 }

PIP_Solution_Node::Row_Sign Parma_Polyhedra_Library::PIP_Solution_Node::row_sign	(	const Row &	x,
		dimension_type	big_dimension
	)

staticprivate

Returns the sign of row x.

Definition at line 2152 of file PIP_Tree.cc.

References Parma_Polyhedra_Library::Sparse_Row::begin(), Parma_Polyhedra_Library::Sparse_Row::end(), Parma_Polyhedra_Library::Sparse_Row::get(), MIXED, NEGATIVE, Parma_Polyhedra_Library::not_a_dimension(), POSITIVE, sign, and ZERO.

Referenced by solve(), and update_tableau().

                                                                 {
   if (big_dimension != not_a_dimension()) {
     // If a big parameter has been set and its coefficient is not zero,
     // then return the sign of the coefficient.
     Coefficient_traits::const_reference x_big = x.get(big_dimension);
     if (x_big > 0) {
       return POSITIVE;
     }
     if (x_big < 0) {
       return NEGATIVE;
     }
     // Otherwise x_big == 0, then no big parameter involved.
   }
 
   PIP_Solution_Node::Row_Sign sign = ZERO;
   for (Row::const_iterator i = x.begin(), i_end = x.end(); i != i_end; ++i) {
     Coefficient_traits::const_reference x_i = *i;
     if (x_i > 0) {
       if (sign == NEGATIVE) {
         return MIXED;
       }
       sign = POSITIVE;
     }
     else if (x_i < 0) {
       if (sign == POSITIVE) {
         return MIXED;
       }
       sign = NEGATIVE;
     }
   }
   return sign;
 }

void Parma_Polyhedra_Library::PIP_Solution_Node::set_owner ( const PIP_Problem * owner )

protectedvirtual

Sets the pointer to the PIP_Problem owning object.

Implements Parma_Polyhedra_Library::PIP_Tree_Node.

Definition at line 1120 of file PIP_Tree.cc.

References Parma_Polyhedra_Library::PIP_Tree_Node::owner_.

Referenced by Parma_Polyhedra_Library::PIP_Problem::ascii_load().

                                                      {
   owner_ = owner;
 }

PIP_Tree_Node * Parma_Polyhedra_Library::PIP_Solution_Node::solve	(	const PIP_Problem &	pip,
		bool	check_feasible_context,
		const Matrix< Row > &	context,
		const Variables_Set &	params,
		dimension_type	space_dim,
		int	indent_level
	)

protectedvirtual

Implements pure virtual method PIP_Tree_Node::solve.

Implements Parma_Polyhedra_Library::PIP_Tree_Node.

Definition at line 2605 of file PIP_Tree.cc.

                                                  {
   PPL_ASSERT(indent_level >= 0);
 #ifdef NOISY_PIP_TREE_STRUCTURE
   indent_and_print(std::cerr, indent_level, "=== SOLVING NODE\n");
 #else
   PPL_USED(indent_level);
 #endif
   // Reset current solution as invalid.
   solution_valid = false;
 
   Matrix<Row> ctx(context);
   Variables_Set all_params(params);
   const dimension_type num_art_params = artificial_parameters.size();
   add_artificial_parameters(ctx, all_params, space_dim, num_art_params);
   merge_assign(ctx, constraints_, all_params);
 
   // If needed, (re-)check feasibility of context.
   if (check_feasible_context) {
     Matrix<Row> ctx_copy(ctx);
     if (!compatibility_check(ctx_copy)) {
       delete this;
       return 0;
     }
   }
 
   const dimension_type not_a_dim = not_a_dimension();
 
   // Main loop of the simplex algorithm.
   while (true) {
     // Check if the client has requested abandoning all expensive
     // computations. If so, the exception specified by the client
     // is thrown now.
     maybe_abandon();
 
     PPL_ASSERT(OK());
 
     const dimension_type num_rows = tableau.t.num_rows();
     const dimension_type num_vars = tableau.s.num_columns();
     const dimension_type num_params = tableau.t.num_columns();
     Coefficient_traits::const_reference tableau_denom = tableau.denominator();
 
 #ifdef VERY_NOISY_PIP
     tableau.ascii_dump(std::cerr);
     std::cerr << "context ";
     ctx.ascii_dump(std::cerr);
 #endif // #ifdef VERY_NOISY_PIP
 
     // (Re-) Compute parameter row signs.
     // While at it, keep track of the first parameter rows
     // having negative and mixed sign.
     dimension_type first_negative = not_a_dim;
     dimension_type first_mixed = not_a_dim;
     for (dimension_type i = 0; i < num_rows; ++i) {
       Row_Sign& sign_i = sign[i];
       if (sign_i == UNKNOWN || sign_i == MIXED) {
         sign_i = row_sign(tableau.t[i], big_dimension);
       }
 
       if (sign_i == NEGATIVE && first_negative == not_a_dim) {
         first_negative = i;
       }
       else if (sign_i == MIXED && first_mixed == not_a_dim) {
         first_mixed = i;
       }
     }
 
     // If no negative parameter row was found, try to refine the sign of
     // mixed rows using compatibility checks with the current context.
     if (first_negative == not_a_dim && first_mixed != not_a_dim) {
       for (dimension_type i = first_mixed; i < num_rows; ++i) {
         // Consider mixed sign parameter rows only.
         if (sign[i] != MIXED) {
           continue;
         }
         const Row& t_i = tableau.t[i];
         Row_Sign new_sign = ZERO;
         // Check compatibility for constraint t_i(z) >= 0.
         if (compatibility_check(ctx, t_i)) {
           new_sign = POSITIVE;
         }
         // Check compatibility for constraint t_i(z) < 0,
         // i.e., -t_i(z) - 1 >= 0.
         Row t_i_complement(num_params);
         complement_assign(t_i_complement, t_i, tableau_denom);
         if (compatibility_check(ctx, t_i_complement)) {
           new_sign = (new_sign == POSITIVE) ? MIXED : NEGATIVE;
         }
         // Update sign for parameter row i.
         sign[i] = new_sign;
         // Maybe update first_negative and first_mixed.
         if (new_sign == NEGATIVE && first_negative == not_a_dim) {
           first_negative = i;
           if (i == first_mixed) {
             first_mixed = not_a_dim;
           }
         }
         else if (new_sign == MIXED) {
           if (first_mixed == not_a_dim) {
             first_mixed = i;
           }
         }
         else if (i == first_mixed) {
           first_mixed = not_a_dim;
         }
       }
     }
 
     // If there still is no negative parameter row and a mixed sign
     // parameter row (first_mixed) such that:
     //  - it has at least one positive variable coefficient;
     //  - constraint t_i(z) > 0 is not compatible with the context;
     // then this parameter row can be considered negative.
     if (first_negative == not_a_dim && first_mixed != not_a_dim) {
       WEIGHT_BEGIN();
       for (dimension_type i = first_mixed; i < num_rows; ++i) {
         // Consider mixed sign parameter rows only.
         if (sign[i] != MIXED) {
           continue;
         }
         // Check for a positive variable coefficient.
         const Row& s_i = tableau.s[i];
         bool has_positive = false;
         {
           for (Row::const_iterator
                  j = s_i.begin(), j_end = s_i.end(); j != j_end; ++j) {
             if (*j > 0) {
               has_positive = true;
               break;
             }
           }
         }
         if (!has_positive) {
           continue;
         }
         // Check compatibility of constraint t_i(z) > 0.
         Row row(tableau.t[i]);
         PPL_DIRTY_TEMP_COEFFICIENT(mod);
         Coefficient& row0 = row[0];
         pos_rem_assign(mod, row0, tableau_denom);
         row0 -= (mod == 0) ? tableau_denom : mod;
         WEIGHT_ADD(210);
         const bool compatible = compatibility_check(ctx, row);
         // Maybe update sign (and first_* indices).
         if (compatible) {
           // Sign is still mixed.
           if (first_mixed == not_a_dim) {
             first_mixed = i;
           }
         }
         else {
           // Sign becomes negative (i.e., no longer mixed).
           sign[i] = NEGATIVE;
           if (first_negative == not_a_dim) {
             first_negative = i;
           }
           if (first_mixed == i) {
             first_mixed = not_a_dim;
           }
         }
       }
     }
 
 #ifdef VERY_NOISY_PIP
     std::cerr << "sign =";
     for (dimension_type i = 0; i < sign.size(); ++i)
       std::cerr << " " << "?0+-*"[sign[i]];
     std::cerr << std::endl;
 #endif // #ifdef VERY_NOISY_PIP
 
     // If we have found a negative parameter row, then
     // either the problem is unfeasible, or a pivoting step is required.
     if (first_negative != not_a_dim) {
 
       // Search for the best pivot row.
       dimension_type pi = not_a_dim;
       dimension_type pj = not_a_dim;
       for (dimension_type i = first_negative; i < num_rows; ++i) {
         if (sign[i] != NEGATIVE) {
           continue;
         }
         dimension_type j;
         if (!find_lexico_minimal_column(tableau.s, mapping, basis,
                                         tableau.s[i], 0, j)) {
           // No positive s_ij was found: problem is unfeasible.
 #ifdef NOISY_PIP_TREE_STRUCTURE
           indent_and_print(std::cerr, indent_level,
                            "No positive pivot: Solution = _|_\n");
 #endif // #ifdef NOISY_PIP_TREE_STRUCTURE
           delete this;
           return 0;
         }
         if (pj == not_a_dim
             || tableau.is_better_pivot(mapping, basis, i, j, pi, pj)) {
           // Update pivot indices.
           pi = i;
           pj = j;
           if (pip.control_parameters[PIP_Problem::PIVOT_ROW_STRATEGY]
               == PIP_Problem::PIVOT_ROW_STRATEGY_FIRST) {
             // Stop at first valid row.
             break;
           }
         }
       }
 
 #ifdef VERY_NOISY_PIP
       std::cerr << "Pivot (pi, pj) = (" << pi << ", " << pj << ")\n";
 #endif // #ifdef VERY_NOISY_PIP
 
       // Normalize the tableau before pivoting.
       tableau.normalize();
 
       // Perform pivot operation.
 
       // Update basis.
       {
         const dimension_type var_pi = var_row[pi];
         const dimension_type var_pj = var_column[pj];
         var_row[pi] = var_pj;
         var_column[pj] = var_pi;
         basis[var_pi] = true;
         basis[var_pj] = false;
         mapping[var_pi] = pj;
         mapping[var_pj] = pi;
       }
 
       PPL_DIRTY_TEMP_COEFFICIENT(product);
       PPL_DIRTY_TEMP_COEFFICIENT(gcd);
       PPL_DIRTY_TEMP_COEFFICIENT(scale_factor);
 
       // Creating identity rows corresponding to basic variable pj:
       // 1. add them to tableau so as to have proper size and capacity;
       tableau.s.add_zero_rows(1);
       tableau.t.add_zero_rows(1);
       // 2. swap the rows just added with empty ones.
       Row s_pivot(0);
       Row t_pivot(0);
       swap(s_pivot, tableau.s[num_rows]);
       swap(t_pivot, tableau.t[num_rows]);
       // 3. drop rows previously added at end of tableau.
       tableau.s.remove_trailing_rows(1);
       tableau.t.remove_trailing_rows(1);
 
       // Save current pivot denominator.
       PPL_DIRTY_TEMP_COEFFICIENT(pivot_denom);
       pivot_denom = tableau.denominator();
       // Let the (scaled) pivot coordinate be 1.
       s_pivot[pj] = pivot_denom;
 
       // Swap identity row with the pivot row previously found.
       s_pivot.m_swap(tableau.s[pi]);
       t_pivot.m_swap(tableau.t[pi]);
       sign[pi] = ZERO;
 
       PPL_DIRTY_TEMP_COEFFICIENT(s_pivot_pj);
       s_pivot_pj = s_pivot.get(pj);
 
       // Compute columns s[*][j]:
       //
       // <CODE>
       //   s[i][j] -= s[i][pj] * s_pivot[j] / s_pivot_pj;
       // </CODE>
       for (dimension_type i = num_rows; i-- > 0; ) {
         Row& s_i = tableau.s[i];
         PPL_DIRTY_TEMP_COEFFICIENT(s_i_pj);
         s_i_pj = s_i.get(pj);
 
         if (s_i_pj == 0) {
           continue;
         }
 
         WEIGHT_BEGIN();
         Row::iterator itr = s_i.end();
         for (Row::const_iterator
                j = s_pivot.begin(), j_end = s_pivot.end(); j != j_end; ++j) {
           if (j.index() != pj) {
             Coefficient_traits::const_reference s_pivot_j = *j;
             // Do nothing if the j-th pivot element is zero.
             if (s_pivot_j != 0) {
               product = s_pivot_j * s_i_pj;
               if (product % s_pivot_pj != 0) {
                 // Must scale matrix to stay in integer case.
                 gcd_assign(gcd, product, s_pivot_pj);
                 exact_div_assign(scale_factor, s_pivot_pj, gcd);
                 tableau.scale(scale_factor);
                 s_i_pj *= scale_factor;
                 product *= scale_factor;
                 WEIGHT_ADD(102);
               }
               PPL_ASSERT(product % s_pivot_pj == 0);
               exact_div_assign(product, product, s_pivot_pj);
               WEIGHT_ADD(130);
               if (product != 0) {
                 itr = s_i.insert(itr, j.index());
                 *itr -= product;
                 WEIGHT_ADD(34);
               }
             }
           }
         }
       }
 
       // Compute columns t[*][j]:
       //
       // <CODE>
       //   t[i][j] -= s[i][pj] * t_pivot[j] / s_pivot_pj;
       // </CODE>
       for (dimension_type i = num_rows; i-- > 0; ) {
         Row& s_i = tableau.s[i];
         Row& t_i = tableau.t[i];
 
         Row::iterator s_i_pj_itr = s_i.find(pj);
 
         if (s_i_pj_itr == s_i.end()) {
           continue;
         }
 
         // FIXME: the following comment does not make sense.
         // NOTE: This is a Coefficient& instead of a
         // Coefficient_traits::const_reference, because scale() may silently
         // modify it.
         const Coefficient& s_i_pj = *s_i_pj_itr;
 
         if (s_i_pj == 0) {
           continue;
         }
 
         WEIGHT_BEGIN();
         Row::iterator k = t_i.end();
         for (Row::const_iterator
                j = t_pivot.begin(), j_end = t_pivot.end(); j != j_end; ++j) {
           Coefficient_traits::const_reference t_pivot_j = *j;
           // Do nothing if the j-th pivot element is zero.
           if (t_pivot_j != 0) {
             product = t_pivot_j * s_i_pj;
             if (product % s_pivot_pj != 0) {
               // Must scale matrix to stay in integer case.
               gcd_assign(gcd, product, s_pivot_pj);
               exact_div_assign(scale_factor, s_pivot_pj, gcd);
               tableau.scale(scale_factor);
               product *= scale_factor;
               WEIGHT_ADD(261);
             }
             PPL_ASSERT(product % s_pivot_pj == 0);
             exact_div_assign(product, product, s_pivot_pj);
             WEIGHT_ADD(115);
             if (product != 0) {
               k = t_i.insert(k, j.index());
               *k -= product;
               WEIGHT_ADD(41);
             }
 
             // Update row sign.
             Row_Sign& sign_i = sign[i];
             switch (sign_i) {
             case ZERO:
               if (product > 0) {
                 sign_i = NEGATIVE;
               }
               else if (product < 0) {
                 sign_i = POSITIVE;
               }
               break;
             case POSITIVE:
               if (product > 0) {
                 sign_i = MIXED;
               }
               break;
             case NEGATIVE:
               if (product < 0) {
                 sign_i = MIXED;
               }
               break;
             default:
               break;
             }
           }
         }
       }
 
       // Compute column s[*][pj]: s[i][pj] /= s_pivot_pj;
       // Update column only if pivot coordinate != 1.
       if (s_pivot_pj != pivot_denom) {
         WEIGHT_BEGIN();
         Row::iterator itr;
         for (dimension_type i = num_rows; i-- > 0; ) {
           Row& s_i = tableau.s[i];
           itr = s_i.find(pj);
           if (itr == s_i.end()) {
             continue;
           }
           WEIGHT_ADD(43);
           product = *itr * pivot_denom;
           if (product % s_pivot_pj != 0) {
             // As above, perform matrix scaling.
             gcd_assign(gcd, product, s_pivot_pj);
             exact_div_assign(scale_factor, s_pivot_pj, gcd);
             tableau.scale(scale_factor);
             product *= scale_factor;
             WEIGHT_ADD(177);
           }
           PPL_ASSERT(product % s_pivot_pj == 0);
           if (product != 0 || *itr != 0) {
             WEIGHT_ADD(106);
             exact_div_assign(*itr, product, s_pivot_pj);
           }
         }
       }
 
       // Pivoting process ended: jump to next iteration.
       continue;
     } // if (first_negative != not_a_dim)
 
 
     PPL_ASSERT(first_negative == not_a_dim);
     // If no negative parameter row was found,
     // but a mixed parameter row was found ...
     if (first_mixed != not_a_dim) {
       // Look for a constraint (i_neg):
       //  - having mixed parameter sign;
       //  - having no positive variable coefficient;
       //  - minimizing the score (sum of parameter coefficients).
       dimension_type i_neg = not_a_dim;
       PPL_DIRTY_TEMP_COEFFICIENT(best_score);
       PPL_DIRTY_TEMP_COEFFICIENT(score);
       for (dimension_type i = first_mixed; i < num_rows; ++i) {
         // Mixed parameter sign.
         if (sign[i] != MIXED) {
           continue;
         }
         // No positive variable coefficient.
         bool has_positive = false;
         {
           const Row& s_i = tableau.s[i];
           for (Row::const_iterator
                  j = s_i.begin(), j_end = s_i.end(); j != j_end; ++j) {
             if (*j > 0) {
               has_positive = true;
               break;
             }
           }
         }
         if (has_positive) {
           continue;
         }
         // Minimize parameter coefficient score,
         // eliminating implicated tautologies (if any).
         score = 0;
         {
           WEIGHT_BEGIN();
           const Row& t_i = tableau.t[i];
           for (Row::const_iterator
                  j = t_i.begin(), j_end = t_i.end(); j != j_end; ++j) {
             WEIGHT_ADD(55);
             score += *j;
           }
         }
         if (i_neg == not_a_dim || score < best_score) {
           i_neg = i;
           best_score = score;
         }
       }
 
       if (i_neg != not_a_dim) {
         Row tautology = tableau.t[i_neg];
         /* Simplify tautology by exploiting integrality. */
         integral_simplification(tautology);
         ctx.add_row(tautology);
         add_constraint(tautology, all_params);
         sign[i_neg] = POSITIVE;
 #ifdef NOISY_PIP
         {
           Linear_Expression expr = Linear_Expression(tautology.get(0));
           dimension_type j = 1;
           for (Variables_Set::const_iterator p = all_params.begin(),
                  p_end = all_params.end(); p != p_end; ++p, ++j)
             add_mul_assign(expr, tautology.get(j), Variable(*p));
           using namespace IO_Operators;
           std::cerr << std::setw(2 * indent_level) << ""
                     << "Row " << i_neg
                     << ": mixed param sign, negative var coeffs\n";
           std::cerr << std::setw(2 * indent_level) << ""
                     << "==> adding tautology: "
                     << Constraint(expr >= 0) << ".\n";
         }
 #endif // #ifdef NOISY_PIP
         // Jump to next iteration.
         continue;
       }
 
       PPL_ASSERT(i_neg == not_a_dim);
       // Heuristically choose "best" (mixed) pivoting row.
       dimension_type best_i = not_a_dim;
       for (dimension_type i = first_mixed; i < num_rows; ++i) {
         if (sign[i] != MIXED) {
           continue;
         }
         score = 0;
         {
           WEIGHT_BEGIN();
           const Row& t_i = tableau.t[i];
           for (Row::const_iterator
                  j = t_i.begin(), j_end = t_i.end(); j != j_end; ++j) {
             WEIGHT_ADD(51);
             score += *j;
           }
         }
         if (best_i == not_a_dim || score < best_score) {
           best_score = score;
           best_i = i;
         }
       }
 
       Row t_test(tableau.t[best_i]);
       /* Simplify t_test by exploiting integrality. */
       integral_simplification(t_test);
 
 #ifdef NOISY_PIP
       {
         Linear_Expression expr = Linear_Expression(t_test.get(0));
         dimension_type j = 1;
         for (Variables_Set::const_iterator p = all_params.begin(),
                p_end = all_params.end(); p != p_end; ++p, ++j)
           add_mul_assign(expr, t_test.get(j), Variable(*p));
         using namespace IO_Operators;
         std::cerr << std::setw(2 * indent_level) << ""
                   << "Row " << best_i << ": mixed param sign\n";
         std::cerr << std::setw(2 * indent_level) << ""
                   << "==> depends on sign of " << expr << ".\n";
       }
 #endif // #ifdef NOISY_PIP
 
       // Create a solution node for the "true" version of current node.
       PIP_Tree_Node* t_node = new PIP_Solution_Node(*this, No_Constraints());
       // Protect it from exception safety issues via std::auto_ptr.
       std::auto_ptr<PIP_Tree_Node> wrapped_node(t_node);
 
       // Add parametric constraint to context.
       ctx.add_row(t_test);
       // Recursively solve true node with respect to updated context.
 #ifdef NOISY_PIP_TREE_STRUCTURE
       indent_and_print(std::cerr, indent_level, "=== SOLVING THEN CHILD\n");
 #endif
       t_node = t_node->solve(pip, check_feasible_context,
                              ctx, all_params, space_dim,
                              indent_level + 1);
       // Resolution may have changed t_node: in case, re-wrap it.
       if (t_node != wrapped_node.get()) {
         wrapped_node.release();
         wrapped_node.reset(t_node);
       }
 
       // Modify *this in place to become the "false" version of current node.
       PIP_Tree_Node* f_node = this;
       // Swap aside constraints and artificial parameters
       // (these will be later restored if needed).
       Constraint_System cs;
       Artificial_Parameter_Sequence aps;
       swap(cs, f_node->constraints_);
       swap(aps, f_node->artificial_parameters);
       // Compute the complement of the constraint used for the "true" node.
       Row& f_test = ctx[ctx.num_rows() - 1];
       complement_assign(f_test, t_test, 1);
 
       // Recursively solve false node with respect to updated context.
 #ifdef NOISY_PIP_TREE_STRUCTURE
       indent_and_print(std::cerr, indent_level, "=== SOLVING ELSE CHILD\n");
 #endif
       f_node = f_node->solve(pip, check_feasible_context,
                              ctx, all_params, space_dim,
                              indent_level + 1);
 
       // Case analysis on recursive resolution calls outcome.
       if (t_node == 0) {
         if (f_node == 0) {
           // Both t_node and f_node unfeasible.
 #ifdef NOISY_PIP_TREE_STRUCTURE
           indent_and_print(std::cerr, indent_level,
                            "=== EXIT: BOTH BRANCHES UNFEASIBLE: _|_\n");
 #endif
           return 0;
         }
         else {
           // t_node unfeasible, f_node feasible:
           // restore cs and aps into f_node (i.e., this).
           PPL_ASSERT(f_node == this);
           swap(f_node->constraints_, cs);
           swap(f_node->artificial_parameters, aps);
           // Add f_test to constraints.
           f_node->add_constraint(f_test, all_params);
 #ifdef NOISY_PIP_TREE_STRUCTURE
           indent_and_print(std::cerr, indent_level,
                            "=== EXIT: THEN BRANCH UNFEASIBLE: SWAP BRANCHES\n");
 #endif
           return f_node;
         }
       }
       else if (f_node == 0) {
         // t_node feasible, f_node unfeasible.
 #ifdef NOISY_PIP_TREE_STRUCTURE
         indent_and_print(std::cerr, indent_level,
                          "=== EXIT: THEN BRANCH FEASIBLE\n");
 #endif
         // NOTE: in principle, we could merge t_node into its parent.
         // However, if t_node is a decision node having both children,
         // then we would obtain a node violating the PIP_Decision_Node
         // invariant saying that t_node should have a single constraint:
         // it will have, at least, the two splitting constraints.
         const PIP_Decision_Node* const decision_node_p
           = dynamic_cast<PIP_Decision_Node*>(t_node);
         if (decision_node_p != 0 && decision_node_p->false_child != 0) {
           // Do NOT merge: create a new decision node.
           PIP_Tree_Node* const parent
             = new PIP_Decision_Node(t_node->get_owner(), 0, t_node);
           // Previously wrapped 't_node' is now safe: release it
           // and protect new 'parent' node from exception safety issues.
           wrapped_node.release();
           wrapped_node.reset(parent);
           // Restore into parent `cs' and `aps'.
           swap(parent->constraints_, cs);
           swap(parent->artificial_parameters, aps);
           // Add t_test to parent's constraints.
           parent->add_constraint(t_test, all_params);
           // It is now safe to release previously wrapped parent pointer
           // and return it to caller.
           return wrapped_node.release();
         }
         else {
           // Merge t_node with its parent:
           // a) append into `cs' the constraints of t_node;
           for (Constraint_System::const_iterator
                  i = t_node->constraints_.begin(),
                  i_end = t_node->constraints_.end(); i != i_end; ++i) {
             cs.insert(*i);
           }
           // b) append into `aps' the parameters of t_node;
           aps.insert(aps.end(),
                      t_node->artificial_parameters.begin(),
                      t_node->artificial_parameters.end());
           // c) swap the updated `cs' and `aps' into t_node.
           swap(cs, t_node->constraints_);
           swap(aps, t_node->artificial_parameters);
           // d) add t_test to t_nodes's constraints.
           t_node->add_constraint(t_test, all_params);
           // It is now safe to release previously wrapped t_node pointer
           // and return it to caller.
           return wrapped_node.release();
         }
       }
 
       // Here both t_node and f_node are feasible:
       // create a new decision node.
 #ifdef NOISY_PIP_TREE_STRUCTURE
       indent_and_print(std::cerr, indent_level,
                        "=== EXIT: BOTH BRANCHES FEASIBLE: NEW DECISION NODE\n");
 #endif
       PIP_Tree_Node* parent
         = new PIP_Decision_Node(f_node->get_owner(), f_node, t_node);
       // Previously wrapped 't_node' is now safe: release it
       // and protect new 'parent' node from exception safety issues.
       wrapped_node.release();
       wrapped_node.reset(parent);
 
       // Add t_test to the constraints of the new decision node.
       parent->add_constraint(t_test, all_params);
 
       if (!cs.empty()) {
 #ifdef NOISY_PIP_TREE_STRUCTURE
         indent_and_print(std::cerr, indent_level,
                          "=== NODE HAS BOTH BRANCHES AND TAUTOLOGIES:\n");
         indent_and_print(std::cerr, indent_level,
                          "=== CREATE NEW PARENT FOR TAUTOLOGIES\n");
 #endif
         // If node to be solved had tautologies,
         // store them in a new decision node.
         parent = new PIP_Decision_Node(parent->get_owner(), 0, parent);
         // Previously wrapped 'parent' node is now safe: release it
         // and protect new 'parent' node from exception safety issues.
         wrapped_node.release();
         wrapped_node.reset(parent);
         swap(parent->constraints_, cs);
       }
       swap(parent->artificial_parameters, aps);
       // It is now safe to release previously wrapped decision node
       // and return it to the caller.
       return wrapped_node.release();
     } // if (first_mixed != not_a_dim)
 
 
     PPL_ASSERT(first_negative == not_a_dim);
     PPL_ASSERT(first_mixed == not_a_dim);
     // Here all parameters are positive: we have found a continuous
     // solution. If the solution happens to be integer, then it is the
     // solution of the  integer problem. Otherwise, we may need to generate
     // a new cut to try and get back into the integer case.
 #ifdef NOISY_PIP
     indent_and_print(std::cerr, indent_level,
                      "All parameters are positive.\n");
 #endif // #ifdef NOISY_PIP
     tableau.normalize();
 
     // Look for any row having non integer parameter coefficients.
     Coefficient_traits::const_reference denom = tableau.denominator();
     for (dimension_type k = 0; k < num_vars; ++k) {
       if (basis[k]) {
         // Basic variable = 0, hence integer.
         continue;
       }
       const dimension_type i = mapping[k];
       const Row& t_i = tableau.t[i];
       WEIGHT_BEGIN();
       for (Row::const_iterator
              j = t_i.begin(), j_end = t_i.end(); j != j_end; ++j) {
         WEIGHT_ADD(27);
         if (*j % denom != 0) {
           goto non_integer;
         }
       }
     }
     // The goto was not taken, the solution is integer.
 #ifdef NOISY_PIP_TREE_STRUCTURE
     indent_and_print(std::cerr, indent_level,
                      "EXIT: solution found.\n");
 #endif // #ifdef NOISY_PIP
     return this;
 
   non_integer:
     // The solution is non-integer: generate a cut.
     PPL_DIRTY_TEMP_COEFFICIENT(mod);
     dimension_type best_i = not_a_dim;
     dimension_type best_pcount = not_a_dim;
 
     const PIP_Problem::Control_Parameter_Value cutting_strategy
       = pip.control_parameters[PIP_Problem::CUTTING_STRATEGY];
 
     if (cutting_strategy == PIP_Problem::CUTTING_STRATEGY_FIRST) {
       // Find the first row with simplest parametric part.
       for (dimension_type k = 0; k < num_vars; ++k) {
         if (basis[k]) {
           continue;
         }
         const dimension_type i = mapping[k];
         // Count the number of non-integer parameter coefficients.
         WEIGHT_BEGIN();
         dimension_type pcount = 0;
         const Row& t_i = tableau.t[i];
         for (Row::const_iterator
                j = t_i.begin(), j_end = t_i.end(); j != j_end; ++j) {
           WEIGHT_ADD(18);
           pos_rem_assign(mod, *j, denom);
           if (mod != 0) {
             ++pcount;
           }
         }
         if (pcount > 0 && (best_i == not_a_dim || pcount < best_pcount)) {
           best_pcount = pcount;
           best_i = i;
         }
       }
       // Generate cut using 'best_i'.
       generate_cut(best_i, all_params, ctx, space_dim, indent_level);
     }
     else {
       PPL_ASSERT(cutting_strategy == PIP_Problem::CUTTING_STRATEGY_DEEPEST
                  || cutting_strategy == PIP_Problem::CUTTING_STRATEGY_ALL);
       // Find the row with simplest parametric part
       // which will generate the "deepest" cut.
       PPL_DIRTY_TEMP_COEFFICIENT(best_score);
       best_score = 0;
       PPL_DIRTY_TEMP_COEFFICIENT(score);
       PPL_DIRTY_TEMP_COEFFICIENT(s_score);
       std::vector<dimension_type> all_best_is;
 
       for (dimension_type k = 0; k < num_vars; ++k) {
         if (basis[k]) {
           continue;
         }
         const dimension_type i = mapping[k];
         // Compute score and pcount.
         score = 0;
         dimension_type pcount = 0;
         {
           WEIGHT_BEGIN();
           const Row& t_i = tableau.t[i];
           for (Row::const_iterator
                  j = t_i.begin(), j_end = t_i.end(); j != j_end; ++j) {
             WEIGHT_ADD(46);
             pos_rem_assign(mod, *j, denom);
             if (mod != 0) {
               WEIGHT_ADD(94);
               score += denom;
               score -= mod;
               ++pcount;
             }
           }
         }
 
         // Compute s_score.
         s_score = 0;
         {
           WEIGHT_BEGIN();
           const Row& s_i = tableau.s[i];
           for (Row::const_iterator
                  j = s_i.begin(), j_end = s_i.end(); j != j_end; ++j) {
             WEIGHT_ADD(94);
             pos_rem_assign(mod, *j, denom);
             s_score += denom;
             s_score -= mod;
           }
         }
         // Combine 'score' and 's_score'.
         score *= s_score;
         /*
           Select row i if it is non integer AND
             - no row has been chosen yet; OR
             - it has fewer non-integer parameter coefficients; OR
             - it has the same number of non-integer parameter coefficients,
               but its score is greater.
         */
         if (pcount != 0
             && (best_i == not_a_dim
                 || pcount < best_pcount
                 || (pcount == best_pcount && score > best_score))) {
           if (pcount < best_pcount) {
             all_best_is.clear();
           }
           best_i = i;
           best_pcount = pcount;
           best_score = score;
         }
         if (pcount > 0) {
           all_best_is.push_back(i);
         }
       }
       if (cutting_strategy == PIP_Problem::CUTTING_STRATEGY_DEEPEST) {
         generate_cut(best_i, all_params, ctx, space_dim, indent_level);
       }
       else {
         PPL_ASSERT(cutting_strategy == PIP_Problem::CUTTING_STRATEGY_ALL);
         for (dimension_type k = all_best_is.size(); k-- > 0; ) {
           generate_cut(all_best_is[k], all_params, ctx,
                        space_dim, indent_level);
         }
       }
     } // End of processing for non-integer solutions.
 
   } // Main loop of the simplex algorithm
 
   // This point should be unreachable.
   PPL_UNREACHABLE;
   return 0;
 }

memory_size_type Parma_Polyhedra_Library::PIP_Solution_Node::total_memory_in_bytes ( ) const

virtual

Returns the total size in bytes of the memory occupied by *this.

Implements Parma_Polyhedra_Library::PIP_Tree_Node.

Definition at line 3798 of file PIP_Tree.cc.

References external_memory_in_bytes().

                                                {
   return sizeof(*this) + external_memory_in_bytes();
 }

void Parma_Polyhedra_Library::PIP_Solution_Node::update_solution ( const std::vector< bool > & pip_dim_is_param ) const

protected

Update the solution values.

Parameters

pip_dim_is_param A vector of Boolean flags telling which PIP problem dimensions are problem parameters. The size of the vector is equal to the PIP problem internal space dimension (i.e., no artificial parameters).

Definition at line 3977 of file PIP_Tree.cc.

References Parma_Polyhedra_Library::add_mul_assign(), Parma_Polyhedra_Library::Sparse_Row::begin(), Parma_Polyhedra_Library::Sparse_Row::end(), Parma_Polyhedra_Library::Sparse_Row::get(), Parma_Polyhedra_Library::CO_Tree::const_iterator::index(), PPL_DIRTY_TEMP_COEFFICIENT, solution, and solution_valid.

                                                                {
   // Avoid doing useless work.
   if (solution_valid) {
     return;
   }
 
   // const_cast required so as to refresh the solution cache.
   PIP_Solution_Node& x = const_cast<PIP_Solution_Node&>(*this);
 
   const dimension_type num_pip_dims = pip_dim_is_param.size();
   const dimension_type num_pip_vars = tableau.s.num_columns();
   const dimension_type num_pip_params = num_pip_dims - num_pip_vars;
   const dimension_type num_all_params = tableau.t.num_columns() - 1;
   const dimension_type num_art_params = num_all_params - num_pip_params;
 
   if (solution.size() != num_pip_vars) {
     x.solution.resize(num_pip_vars);
   }
 
   // Compute external "names" (i.e., indices) for all parameters.
   std::vector<dimension_type> all_param_names(num_all_params);
 
   // External indices for problem parameters.
   for (dimension_type i = 0, p_index = 0; i < num_pip_dims; ++i) {
     if (pip_dim_is_param[i]) {
       all_param_names[p_index] = i;
       ++p_index;
     }
   }
   // External indices for artificial parameters.
   for (dimension_type i = 0; i < num_art_params; ++i) {
     all_param_names[num_pip_params + i] = num_pip_dims + i;
   }
 
 
   PPL_DIRTY_TEMP_COEFFICIENT(norm_coeff);
   Coefficient_traits::const_reference denom = tableau.denominator();
   for (dimension_type i = num_pip_vars; i-- > 0; ) {
     Linear_Expression& sol_i = x.solution[i];
     sol_i = Linear_Expression(0);
     if (basis[i]) {
       continue;
     }
     const Row& row = tableau.t[mapping[i]];
 
     // Start from index 1 to skip the inhomogeneous term.
     Row::const_iterator j = row.begin();
     Row::const_iterator j_end = row.end();
     // Skip the element with index 0.
     if (j != j_end && j.index() == 0) {
       ++j;
     }
     for ( ; j != j_end; ++j) {
       Coefficient_traits::const_reference coeff = *j;
       if (coeff == 0) {
         continue;
       }
       norm_coeff = coeff / denom;
       if (norm_coeff != 0) {
         add_mul_assign(sol_i, norm_coeff,
                       Variable(all_param_names[j.index() - 1]));
       }
     }
     norm_coeff = row.get(0) / denom;
     sol_i += norm_coeff;
   }
 
   // Mark solution as valid.
   x.solution_valid = true;
 }

void Parma_Polyhedra_Library::PIP_Solution_Node::update_solution ( ) const

protected

Helper method.

Definition at line 3958 of file PIP_Tree.cc.

References Parma_Polyhedra_Library::PIP_Tree_Node::get_owner(), Parma_Polyhedra_Library::PIP_Problem::parameter_space_dimensions(), solution_valid, and Parma_Polyhedra_Library::PIP_Problem::space_dimension().

Referenced by parametric_values(), and print_tree().

                                          {
   // Avoid doing useless work.
   if (solution_valid) {
     return;
   }
   const PIP_Problem* const pip = get_owner();
   PPL_ASSERT(pip != 0);
   std::vector<bool> pip_dim_is_param(pip->space_dimension());
   const Variables_Set& params = pip->parameter_space_dimensions();
   for (Variables_Set::const_iterator p = params.begin(),
          p_end = params.end(); p != p_end; ++p) {
     pip_dim_is_param[*p] = true;
   }
 
   update_solution(pip_dim_is_param);
 }

void Parma_Polyhedra_Library::PIP_Solution_Node::update_tableau	(	const PIP_Problem &	pip,
		dimension_type	external_space_dim,
		dimension_type	first_pending_constraint,
		const Constraint_Sequence &	input_cs,
		const Variables_Set &	parameters
	)

protectedvirtual

Implements pure virtual method PIP_Tree_Node::update_tableau.

Implements Parma_Polyhedra_Library::PIP_Tree_Node.

Definition at line 2406 of file PIP_Tree.cc.

                                                   {
 
   // Make sure a parameter column exists, for the inhomogeneous term.
   if (tableau.t.num_columns() == 0) {
     tableau.t.add_zero_columns(1);
   }
 
   // NOTE: here 'params' stands for problem (i.e., non artificial) parameters.
   const dimension_type old_num_vars = tableau.s.num_columns();
   const dimension_type old_num_params
     = pip.internal_space_dim - old_num_vars;
   const dimension_type num_added_dims
     = pip.external_space_dim - pip.internal_space_dim;
   const dimension_type new_num_params = parameters.size();
   const dimension_type num_added_params = new_num_params - old_num_params;
   const dimension_type num_added_vars = num_added_dims - num_added_params;
 
   // Resize the two tableau matrices.
   if (num_added_vars > 0) {
     tableau.s.add_zero_columns(num_added_vars);
   }
 
   if (num_added_params > 0) {
     tableau.t.add_zero_columns(num_added_params, old_num_params + 1);
   }
 
   dimension_type new_var_column = old_num_vars;
   const dimension_type initial_space_dim = old_num_vars + old_num_params;
   for (dimension_type i = initial_space_dim; i < external_space_dim; ++i) {
     if (parameters.count(i) == 0) {
       // A new problem variable.
       if (tableau.s.num_rows() == 0) {
         // No rows have been added yet
         basis.push_back(true);
         mapping.push_back(new_var_column);
       }
       else {
         /*
           Need to insert the original variable id
           before the slack variable id's to respect variable ordering.
         */
         basis.insert(nth_iter(basis, new_var_column), true);
         mapping.insert(nth_iter(mapping, new_var_column), new_var_column);
         // Update variable id's of slack variables.
         for (dimension_type j = var_row.size(); j-- > 0; ) {
           if (var_row[j] >= new_var_column) {
             ++var_row[j];
           }
         }
         for (dimension_type j = var_column.size(); j-- > 0; ) {
           if (var_column[j] >= new_var_column) {
             ++var_column[j];
           }
         }
         if (special_equality_row > 0) {
           ++special_equality_row;
         }
       }
       var_column.push_back(new_var_column);
       ++new_var_column;
     }
   }
 
   if (big_dimension == not_a_dimension()
       && pip.big_parameter_dimension != not_a_dimension()) {
     // Compute the column number of big parameter in tableau.t matrix.
     Variables_Set::const_iterator pos
       = parameters.find(pip.big_parameter_dimension);
     big_dimension = 1U
       + static_cast<dimension_type>(std::distance(parameters.begin(), pos));
   }
 
   Coefficient_traits::const_reference denom = tableau.denominator();
 
   for (Constraint_Sequence::const_iterator
          c_iter = nth_iter(input_cs, first_pending_constraint),
          c_end = input_cs.end(); c_iter != c_end; ++c_iter) {
     const Constraint& constraint = *c_iter;
     // (Tentatively) Add new rows to s and t matrices.
     // These will be removed at the end if they turn out to be useless.
     const dimension_type row_id = tableau.s.num_rows();
     tableau.s.add_zero_rows(1);
     tableau.t.add_zero_rows(1);
     Row& v_row = tableau.s[row_id];
     Row& p_row = tableau.t[row_id];
 
     {
       dimension_type p_index = 1;
       dimension_type v_index = 0;
       // Setting the inhomogeneous term.
       if (constraint.inhomogeneous_term() != 0) {
         Coefficient& p_row0 = p_row[0];
         p_row0 = constraint.inhomogeneous_term();
         if (constraint.is_strict_inequality()) {
           // Transform (expr > 0) into (expr - 1 >= 0).
           --p_row0;
         }
         p_row0 *= denom;
       }
       else {
         if (constraint.is_strict_inequality()) {
           // Transform (expr > 0) into (expr - 1 >= 0).
           neg_assign(p_row[0], denom);
         }
       }
       WEIGHT_BEGIN();
       dimension_type last_dim = 0;
       const Constraint::expr_type e = constraint.expression();
       for (Constraint::expr_type::const_iterator
           i = e.begin(), i_end = e.end(); i != i_end; ++i) {
         const dimension_type dim = i.variable().space_dimension();
         if (dim != last_dim + 1) {
           // We have skipped some zero coefficients.
           // Update p_index and v_index accordingly.
           const dimension_type n
             = std::distance(parameters.lower_bound(last_dim),
                             parameters.lower_bound(dim - 1));
           const dimension_type num_skipped = dim - last_dim - 1;
           p_index += n;
           v_index += (num_skipped - n);
         }
         PPL_ASSERT(p_index + v_index == i.variable().id() + 1);
         const bool is_parameter = (1 == parameters.count(dim - 1));
         Coefficient_traits::const_reference coeff_i = *i;
 
         WEIGHT_ADD(140);
         if (is_parameter) {
           p_row.insert(p_index, coeff_i * denom);
           ++p_index;
         }
         else {
           const dimension_type mv = mapping[v_index];
           if (basis[v_index]) {
             // Basic variable: add coeff_i * x_i
             add_mul_assign(v_row[mv], coeff_i, denom);
           }
           else {
             // Non-basic variable: add coeff_i * row_i
             add_mul_assign_row(v_row, coeff_i, tableau.s[mv]);
             add_mul_assign_row(p_row, coeff_i, tableau.t[mv]);
           }
           ++v_index;
         }
 
         last_dim = dim;
       }
     }
 
     if (row_sign(v_row, not_a_dimension()) == ZERO) {
       // Parametric-only constraints have already been inserted in
       // initial context, so no need to insert them in the tableau.
       tableau.s.remove_trailing_rows(1);
       tableau.t.remove_trailing_rows(1);
     }
     else {
       const dimension_type var_id = mapping.size();
       sign.push_back(row_sign(p_row, big_dimension));
       basis.push_back(false);
       mapping.push_back(row_id);
       var_row.push_back(var_id);
       if (constraint.is_equality()) {
         // Handle equality constraints.
         // After having added the f_i(x,p) >= 0 constraint,
         // we must add -f_i(x,p) to the special equality row.
         if (special_equality_row == 0 || basis[special_equality_row]) {
           // The special constraint has not been created yet
           // FIXME: for now, we do not handle the case where the variable
           // is basic, and we just create a new row.
           // This might be faster however.
           tableau.s.add_zero_rows(1);
           tableau.t.add_zero_rows(1);
           // NOTE: addition of rows invalidates references v_row and p_row
           // due to possible matrix reallocations: recompute them.
           neg_assign_row(tableau.s[1 + row_id], tableau.s[row_id]);
           neg_assign_row(tableau.t[1 + row_id], tableau.t[row_id]);
           sign.push_back(row_sign(tableau.t[1 + row_id], big_dimension));
           special_equality_row = mapping.size();
           basis.push_back(false);
           mapping.push_back(1 + row_id);
           var_row.push_back(1 + var_id);
         }
         else {
           // The special constraint already exists and is nonbasic.
           const dimension_type m_eq = mapping[special_equality_row];
           sub_assign(tableau.s[m_eq], v_row);
           sub_assign(tableau.t[m_eq], p_row);
           sign[m_eq] = row_sign(tableau.t[m_eq], big_dimension);
         }
       }
     }
   }
   PPL_ASSERT(OK());
 }

Friends And Related Function Documentation

bool PIP_Problem::ascii_load ( std::istream & s )

friend

Member Data Documentation

std::vector<bool> Parma_Polyhedra_Library::PIP_Solution_Node::basis

private

A boolean vector for identifying the basic variables.

Variable identifiers are numbered from 0 to n+m-1, where n is the number of columns in the simplex tableau corresponding to variables, and m is the number of rows.

Indices from 0 to n-1 correspond to the original variables.

Indices from n to n+m-1 correspond to the slack variables associated to the internal constraints, which do not strictly correspond to original constraints, since these may have been transformed to fit the standard form of the dual simplex.

The value for basis[i] is:

true if variable i is basic,
false if variable i is nonbasic.

Definition at line 543 of file PIP_Tree_defs.hh.

Referenced by Parma_Polyhedra_Library::PIP_Tree_Node::compatibility_check().

dimension_type Parma_Polyhedra_Library::PIP_Solution_Node::big_dimension

private

The column index in the parametric part of the simplex tableau corresponding to the big parameter; not_a_dimension() if not set.

Definition at line 590 of file PIP_Tree_defs.hh.

Referenced by ascii_dump(), ascii_load(), solve(), and update_tableau().

std::vector<dimension_type> Parma_Polyhedra_Library::PIP_Solution_Node::mapping

private

A mapping between the tableau rows/columns and the original variables.

The value of mapping[i] depends of the value of basis[i].

If basis[i] is true, mapping[i] encodes the column index of variable i in the s matrix of the tableau.
If basis[i] is false, mapping[i] encodes the row index of variable i in the tableau.

Definition at line 555 of file PIP_Tree_defs.hh.

Referenced by Parma_Polyhedra_Library::PIP_Tree_Node::compatibility_check().

std::vector<Row_Sign> Parma_Polyhedra_Library::PIP_Solution_Node::sign

private

A cache for computed sign values of constraint parametric RHS.

Definition at line 607 of file PIP_Tree_defs.hh.

Referenced by ascii_dump(), ascii_load(), external_memory_in_bytes(), generate_cut(), row_sign(), solve(), and update_tableau().

std::vector<Linear_Expression> Parma_Polyhedra_Library::PIP_Solution_Node::solution

private

Parametric values for the solution.

Definition at line 610 of file PIP_Tree_defs.hh.

Referenced by ascii_dump(), ascii_load(), external_memory_in_bytes(), parametric_values(), print_tree(), and update_solution().

bool Parma_Polyhedra_Library::PIP_Solution_Node::solution_valid

private

An indicator for solution validity.

Definition at line 613 of file PIP_Tree_defs.hh.

Referenced by ascii_dump(), ascii_load(), solve(), and update_solution().

dimension_type Parma_Polyhedra_Library::PIP_Solution_Node::special_equality_row

private

The variable number of the special inequality used for modeling equality constraints.

The subset of equality constraints in a specific problem can be expressed as: 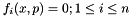$f_i(x,p) = 0 ; 1 \leq i \leq n$ . As the dual simplex standard form requires constraints to be inequalities, the following constraints can be modeled as follows:

$f_i(x,p) \geq 0 ; 1 \leq i \leq n$
$\sum\limits_{i=1}^n f_i(x,p) \leq 0$

The special_equality_row value stores the variable number of the specific constraint which is used to model the latter sum of constraints. If no such constraint exists, the value is set to 0.

Definition at line 584 of file PIP_Tree_defs.hh.

Referenced by ascii_dump(), ascii_load(), and update_tableau().

Tableau Parma_Polyhedra_Library::PIP_Solution_Node::tableau

private

The parametric simplex tableau.

Definition at line 523 of file PIP_Tree_defs.hh.

std::vector<dimension_type> Parma_Polyhedra_Library::PIP_Solution_Node::var_column

private

The variable identifiers associated to the columns of the simplex tableau.

Definition at line 565 of file PIP_Tree_defs.hh.

Referenced by ascii_dump(), ascii_load(), Parma_Polyhedra_Library::PIP_Tree_Node::compatibility_check(), external_memory_in_bytes(), OK(), solve(), and update_tableau().

std::vector<dimension_type> Parma_Polyhedra_Library::PIP_Solution_Node::var_row

private

The variable identifiers associated to the rows of the simplex tableau.

Definition at line 560 of file PIP_Tree_defs.hh.

Referenced by ascii_dump(), ascii_load(), Parma_Polyhedra_Library::PIP_Tree_Node::compatibility_check(), external_memory_in_bytes(), generate_cut(), OK(), solve(), and update_tableau().

The documentation for this class was generated from the following files:

Classes

Public Member Functions

Protected Member Functions

Private Types

Static Private Member Functions

Private Attributes

Friends

Additional Inherited Members

Detailed Description

Member Enumeration Documentation

Constructor & Destructor Documentation

Member Function Documentation

Friends And Related Function Documentation

Member Data Documentation