The type for parametric simplex tableau. More...
Public Member Functions | |
| Tableau () | |
| Default constructor. More... | |
| Tableau (const Tableau &y) | |
| Copy constructor. More... | |
| ~Tableau () | |
| Destructor. More... | |
| bool | is_integer () const |
| Tests whether the matrix is integer, i.e., the denominator is 1. More... | |
| void | scale (Coefficient_traits::const_reference ratio) |
| Multiplies all coefficients and denominator with ratio. More... | |
| void | normalize () |
| Normalizes the modulo of coefficients so that they are mutually prime. More... | |
| bool | is_better_pivot (const std::vector< dimension_type > &mapping, const std::vector< bool > &basis, const dimension_type row_0, const dimension_type col_0, const dimension_type row_1, const dimension_type col_1) const |
| Compares two pivot row and column pairs before pivoting. More... | |
| Coefficient_traits::const_reference | denominator () const |
| Returns the value of the denominator. More... | |
| void | ascii_dump (std::ostream &os) const |
Dumps to os an ASCII representation of *this. More... | |
| bool | ascii_load (std::istream &is) |
Loads from is an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets *this accordingly. Returns true if successful, false otherwise. More... | |
| memory_size_type | external_memory_in_bytes () const |
Returns the size in bytes of the memory managed by *this. More... | |
| bool | OK () const |
Returns true if and only if *this is well formed. More... | |
Public Attributes | |
| Matrix< Row > | s |
| The matrix of simplex coefficients. More... | |
| Matrix< Row > | t |
| The matrix of parameter coefficients. More... | |
| Coefficient | denom |
| A common denominator for all matrix elements. More... | |
Detailed Description
The type for parametric simplex tableau.
Definition at line 413 of file PIP_Tree_defs.hh.
Constructor & Destructor Documentation
|
inline |
Default constructor.
Definition at line 30 of file PIP_Tree_inlines.hh.
References OK().
|
inline |
Copy constructor.
Definition at line 36 of file PIP_Tree_inlines.hh.
References OK().
|
inline |
Member Function Documentation
| void Parma_Polyhedra_Library::PIP_Solution_Node::Tableau::ascii_dump | ( | std::ostream & | os | ) | const |
Dumps to os an ASCII representation of *this.
Definition at line 1873 of file PIP_Tree.cc.
| bool Parma_Polyhedra_Library::PIP_Solution_Node::Tableau::ascii_load | ( | std::istream & | is | ) |
Loads from is an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets *this accordingly. Returns true if successful, false otherwise.
Definition at line 1882 of file PIP_Tree.cc.
References Parma_Polyhedra_Library::PIP_Solution_Node::OK().
|
inline |
Returns the value of the denominator.
Definition at line 51 of file PIP_Tree_inlines.hh.
| memory_size_type Parma_Polyhedra_Library::PIP_Solution_Node::Tableau::external_memory_in_bytes | ( | ) | const |
Returns the size in bytes of the memory managed by *this.
- Note
- No need for a
total_memory_in_bytes()method, since class Tableau is a private inner class of PIP_Solution_Node.
Definition at line 3771 of file PIP_Tree.cc.
References Parma_Polyhedra_Library::external_memory_in_bytes().
| bool Parma_Polyhedra_Library::PIP_Solution_Node::Tableau::is_better_pivot | ( | const std::vector< dimension_type > & | mapping, |
| const std::vector< bool > & | basis, | ||
| const dimension_type | row_0, | ||
| const dimension_type | col_0, | ||
| const dimension_type | row_1, | ||
| const dimension_type | col_1 | ||
| ) | const |
Compares two pivot row and column pairs before pivoting.
The algorithm searches the first (ie, leftmost) column  in parameter matrix for which the
in parameter matrix for which the 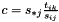 and
and 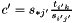 columns are different, where
columns are different, where 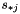 denotes the
denotes the 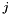 th column from the
th column from the 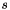 matrix and
matrix and 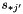 is the
is the 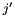 th column of
th column of 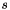 .
.
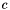 is the computed column that would be subtracted to column
is the computed column that would be subtracted to column  in parameter matrix if pivoting is done using the
in parameter matrix if pivoting is done using the 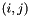 row and column pair.
row and column pair. 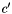 is the computed column that would be subtracted to column
is the computed column that would be subtracted to column  in parameter matrix if pivoting is done using the
in parameter matrix if pivoting is done using the 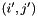 row and column pair.
row and column pair.
The test is true if the computed 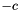 column is lexicographically bigger than the
column is lexicographically bigger than the 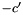 column. Due to the column ordering in the parameter matrix of the tableau, leftmost search will enforce solution increase with respect to the following priority order:
column. Due to the column ordering in the parameter matrix of the tableau, leftmost search will enforce solution increase with respect to the following priority order:
- the constant term
- the coefficients for the original parameters
- the coefficients for the oldest artificial parameters.
- Returns
trueif pivot row and column pair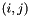 is more suitable for pivoting than the
is more suitable for pivoting than the 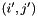 pair
pair
- Parameters
-
mapping The PIP_Solution_Node::mapping vector for the tableau. basis The PIP_Solution_Node::basis vector for the tableau. row_0 The row number for the first pivot row and column pair to be compared. col_0 The column number for the first pivot row and column pair to be compared. row_1 The row number for the second pivot row and column pair to be compared. col_1 The column number for the second pivot row and column pair to be compared.
Definition at line 1733 of file PIP_Tree.cc.
References Parma_Polyhedra_Library::Sparse_Row::begin(), Parma_Polyhedra_Library::Sparse_Row::end(), Parma_Polyhedra_Library::Sparse_Row::get(), Parma_Polyhedra_Library::CO_Tree::const_iterator::index(), PPL_DIRTY_TEMP_COEFFICIENT, WEIGHT_ADD, and WEIGHT_BEGIN.
|
inline |
Tests whether the matrix is integer, i.e., the denominator is 1.
Definition at line 46 of file PIP_Tree_inlines.hh.
| void Parma_Polyhedra_Library::PIP_Solution_Node::Tableau::normalize | ( | ) |
Normalizes the modulo of coefficients so that they are mutually prime.
Computes the Greatest Common Divisor (GCD) among the elements of the matrices and normalizes them and the denominator by the GCD itself.
Definition at line 1654 of file PIP_Tree.cc.
References Parma_Polyhedra_Library::Sparse_Row::begin(), Parma_Polyhedra_Library::Sparse_Row::end(), Parma_Polyhedra_Library::exact_div_assign(), Parma_Polyhedra_Library::gcd_assign(), PPL_DIRTY_TEMP_COEFFICIENT, WEIGHT_ADD, and WEIGHT_BEGIN.
| bool Parma_Polyhedra_Library::PIP_Solution_Node::Tableau::OK | ( | ) | const |
Returns true if and only if *this is well formed.
Definition at line 1168 of file PIP_Tree.cc.
References t.
Referenced by Tableau().
| void Parma_Polyhedra_Library::PIP_Solution_Node::Tableau::scale | ( | Coefficient_traits::const_reference | ratio | ) |
Multiplies all coefficients and denominator with ratio.
Definition at line 1714 of file PIP_Tree.cc.
References Parma_Polyhedra_Library::Sparse_Row::begin(), Parma_Polyhedra_Library::Sparse_Row::end(), WEIGHT_ADD, and WEIGHT_BEGIN.
Member Data Documentation
| Coefficient Parma_Polyhedra_Library::PIP_Solution_Node::Tableau::denom |
A common denominator for all matrix elements.
Definition at line 419 of file PIP_Tree_defs.hh.
The matrix of simplex coefficients.
Definition at line 415 of file PIP_Tree_defs.hh.
The matrix of parameter coefficients.
Definition at line 417 of file PIP_Tree_defs.hh.
Referenced by OK().
The documentation for this struct was generated from the following files:
