Parma_Polyhedra_Library::Float< T > Class Template Reference

#include <Float_defs.hh>

Inheritance diagram for Parma_Polyhedra_Library::Float< T >:

Collaboration diagram for Parma_Polyhedra_Library::Float< T >:

Related Functions
(Note that these are not member functions.)
bool	is_less_precise_than (Floating_Point_Format f1, Floating_Point_Format f2)
template<typename FP_Interval_Type >
const FP_Interval_Type &	compute_absolute_error (Floating_Point_Format analyzed_format)

Additional Inherited Members
Public Types inherited from Parma_Polyhedra_Library::Bool< false >
enum	const_bool_value

Detailed Description

template<typename T>
class Parma_Polyhedra_Library::Float< T >

Definition at line 285 of file Float_defs.hh.

Friends And Related Function Documentation

template<typename FP_Interval_Type >

const FP_Interval_Type & compute_absolute_error ( Floating_Point_Format  analyzed_format )

related

Computes the absolute error of floating point computations.

Template type parameters

• The class template parameter FP_Interval_Type represents the type of the intervals used in the abstract domain. The interval bounds should have a floating point type.

Parameters

analyzed_format

The floating point format used by the analyzed program.

Returns

The interval where 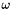is the smallest non-zero positive number in the less precise floating point format between the analyzer format and the analyzed format.

Definition at line 35 of file Float_templates.hh.

                                                                     {
  typedef typename FP_Interval_Type::boundary_type analyzer_format;

  // FIXME: check if initializing caches with EMPTY is better.
  static const FP_Interval_Type ZERO_INTERVAL = FP_Interval_Type(0);
  // Cached results for each different analyzed format.
  static FP_Interval_Type ieee754_half_result = ZERO_INTERVAL;
  static FP_Interval_Type ieee754_single_result = ZERO_INTERVAL;
  static FP_Interval_Type ieee754_double_result = ZERO_INTERVAL;
  static FP_Interval_Type ibm_single_result = ZERO_INTERVAL;
  static FP_Interval_Type ieee754_quad_result = ZERO_INTERVAL;
  static FP_Interval_Type intel_double_extended_result = ZERO_INTERVAL;

  FP_Interval_Type* to_compute = NULL;
  // Get the necessary information on the analyzed's format.
  unsigned int f_base;
  int f_exponent_bias;
  unsigned int f_mantissa_bits;
  switch (analyzed_format) {
    case IEEE754_HALF:
      if (ieee754_half_result != ZERO_INTERVAL) {
        return ieee754_half_result;
      }
      to_compute = &ieee754_half_result;
      f_base = float_ieee754_half::BASE;
      f_exponent_bias = float_ieee754_half::EXPONENT_BIAS;
      f_mantissa_bits = float_ieee754_half::MANTISSA_BITS;
      break;
    case IEEE754_SINGLE:
      if (ieee754_single_result != ZERO_INTERVAL) {
        return ieee754_single_result;
      }

      to_compute = &ieee754_single_result;
      f_base = float_ieee754_single::BASE;
      f_exponent_bias = float_ieee754_single::EXPONENT_BIAS;
      f_mantissa_bits = float_ieee754_single::MANTISSA_BITS;
      break;
    case IEEE754_DOUBLE:
      if (ieee754_double_result != ZERO_INTERVAL) {
        return ieee754_double_result;
      }

      to_compute = &ieee754_double_result;
      f_base = float_ieee754_double::BASE;
      f_exponent_bias = float_ieee754_double::EXPONENT_BIAS;
      f_mantissa_bits = float_ieee754_double::MANTISSA_BITS;
      break;
    case IBM_SINGLE:
      if (ibm_single_result != ZERO_INTERVAL) {
        return ibm_single_result;
      }

      to_compute = &ibm_single_result;
      f_base = float_ibm_single::BASE;
      f_exponent_bias = float_ibm_single::EXPONENT_BIAS;
      f_mantissa_bits = float_ibm_single::MANTISSA_BITS;
      break;
    case IEEE754_QUAD:
      if (ieee754_quad_result != ZERO_INTERVAL) {
        return ieee754_quad_result;
      }

      to_compute = &ieee754_quad_result;
      f_base = float_ieee754_quad::BASE;
      f_exponent_bias = float_ieee754_quad::EXPONENT_BIAS;
      f_mantissa_bits = float_ieee754_quad::MANTISSA_BITS;
      break;
    case INTEL_DOUBLE_EXTENDED:
      if (intel_double_extended_result != ZERO_INTERVAL) {
        return intel_double_extended_result;
      }

      to_compute = &intel_double_extended_result;
      f_base = float_intel_double_extended::BASE;
      f_exponent_bias = float_intel_double_extended::EXPONENT_BIAS;
      f_mantissa_bits = float_intel_double_extended::MANTISSA_BITS;
      break;
    default:
      PPL_UNREACHABLE;
      break;
  }

  PPL_ASSERT(to_compute != NULL);

  // We assume that f_base is a power of 2.
  analyzer_format omega;
  int power = static_cast<int>(msb_position(f_base))
    * ((1 - f_exponent_bias) - static_cast<int>(f_mantissa_bits));
  omega = std::max(static_cast<analyzer_format>(ldexp(1.0, power)),
                   std::numeric_limits<analyzer_format>::denorm_min());

  to_compute->build(i_constraint(GREATER_OR_EQUAL, -omega),
                    i_constraint(LESS_OR_EQUAL, omega));
  return *to_compute;
}

template<typename T>

bool is_less_precise_than ( Floating_Point_Format  f1, Floating_Point_Format  f2  )

related

Returns true if and only if there is some floating point number that is representable by f2 but not by f1.

Definition at line 513 of file Float_inlines.hh.

                                                                         {
  return f1 < f2;
}

---

The documentation for this class was generated from the following file:

• Float_defs.hh