The powerset construction instantiated on PPL pointset domains. More...

#include <Pointset_Powerset_defs.hh>

Inheritance diagram for Parma_Polyhedra_Library::Pointset_Powerset< PSET >:

Collaboration diagram for Parma_Polyhedra_Library::Pointset_Powerset< PSET >:

Public Types
typedef PSET	element_type

typedef Base::size_type	size_type

typedef Base::value_type	value_type

typedef Base::iterator	iterator

typedef Base::const_iterator	const_iterator

typedef Base::reverse_iterator	reverse_iterator

typedef Base::const_reverse_iterator	const_reverse_iterator

Public Types inherited from Parma_Polyhedra_Library::Powerset< Parma_Polyhedra_Library::Determinate< PSET > >
typedef Sequence::size_type	size_type

typedef Sequence::value_type	value_type

typedef iterator_to_const< Sequence >	iterator
	Alias for a read-only bidirectional iterator on the disjuncts of a Powerset element. More...

typedef const_iterator_to_const< Sequence >	const_iterator
	A bidirectional const_iterator on the disjuncts of a Powerset element. More...

typedef std::reverse_iterator< iterator >	reverse_iterator
	The reverse iterator type built from Powerset::iterator. More...

typedef std::reverse_iterator< const_iterator >	const_reverse_iterator
	The reverse iterator type built from Powerset::const_iterator. More...

Public Member Functions
void	ascii_dump () const
	Writes to `std::cerr` an ASCII representation of `*this`. More...

void	ascii_dump (std::ostream &s) const
	Writes to `s` an ASCII representation of `*this`. More...

void	print () const
	Prints `*this` to `std::cerr` using `operator<<`. More...

bool	ascii_load (std::istream &s)
	Loads from `s` an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets `*this` accordingly. Returns `true` if successful, `false` otherwise. More...

template<>
void	difference_assign (const Pointset_Powerset &y)

template<>
bool	geometrically_covers (const Pointset_Powerset &y) const

template<>
void	difference_assign (const Pointset_Powerset &y)

template<>
bool	geometrically_covers (const Pointset_Powerset &y) const

template<>
	Pointset_Powerset (const Pointset_Powerset< C_Polyhedron > &y, Complexity_Class)

template<>
	Pointset_Powerset (const Pointset_Powerset< Grid > &y, Complexity_Class)

template<>
	Pointset_Powerset (const Pointset_Powerset< NNC_Polyhedron > &y, Complexity_Class)

template<>
	Pointset_Powerset (const Pointset_Powerset< QH > &y, Complexity_Class)

template<>
	Pointset_Powerset (const Pointset_Powerset< C_Polyhedron > &y, Complexity_Class)

template<>
	Pointset_Powerset (const Pointset_Powerset< Grid > &y, Complexity_Class)

template<>
	Pointset_Powerset (const Pointset_Powerset< NNC_Polyhedron > &y, Complexity_Class)

template<>
void	difference_assign (const Pointset_Powerset &y)

template<>
void	difference_assign (const Pointset_Powerset &y)

template<>
bool	geometrically_covers (const Pointset_Powerset &y) const

template<>
bool	geometrically_covers (const Pointset_Powerset &y) const

template<typename QH >
Pointset_Powerset< PSET > &	operator= (const Pointset_Powerset< QH > &y)

template<>
bool	geometrically_equals (const Pointset_Powerset &y) const

template<>
bool	geometrically_equals (const Pointset_Powerset &y) const

template<>
	Pointset_Powerset (const Pointset_Powerset< QH > &y, Complexity_Class complexity)

Constructors
	Pointset_Powerset (dimension_type num_dimensions=0, Degenerate_Element kind=UNIVERSE)
	Builds a universe (top) or empty (bottom) Pointset_Powerset. More...

	Pointset_Powerset (const Pointset_Powerset &y, Complexity_Class complexity=ANY_COMPLEXITY)
	Ordinary copy constructor. More...

template<typename QH >
	Pointset_Powerset (const Pointset_Powerset< QH > &y, Complexity_Class complexity=ANY_COMPLEXITY)
	Conversion constructor: the type `QH` of the disjuncts in the source powerset is different from `PSET`. More...

template<typename QH1 , typename QH2 , typename R >
	Pointset_Powerset (const Partially_Reduced_Product< QH1, QH2, R > &prp, Complexity_Class complexity=ANY_COMPLEXITY)
	Creates a Pointset_Powerset from a product This will be created as a single disjunct of type PSET that approximates the product. More...

	Pointset_Powerset (const Constraint_System &cs)
	Creates a Pointset_Powerset with a single disjunct approximating the system of constraints `cs`. More...

	Pointset_Powerset (const Congruence_System &cgs)
	Creates a Pointset_Powerset with a single disjunct approximating the system of congruences `cgs`. More...

	Pointset_Powerset (const C_Polyhedron &ph, Complexity_Class complexity=ANY_COMPLEXITY)
	Builds a pointset_powerset out of a closed polyhedron. More...

	Pointset_Powerset (const NNC_Polyhedron &ph, Complexity_Class complexity=ANY_COMPLEXITY)
	Builds a pointset_powerset out of an nnc polyhedron. More...

	Pointset_Powerset (const Grid &gr, Complexity_Class complexity=ANY_COMPLEXITY)
	Builds a pointset_powerset out of a grid. More...

template<typename T >
	Pointset_Powerset (const Octagonal_Shape< T > &os, Complexity_Class complexity=ANY_COMPLEXITY)
	Builds a pointset_powerset out of an octagonal shape. More...

template<typename T >
	Pointset_Powerset (const BD_Shape< T > &bds, Complexity_Class complexity=ANY_COMPLEXITY)
	Builds a pointset_powerset out of a bd shape. More...

template<typename Interval >
	Pointset_Powerset (const Box< Interval > &box, Complexity_Class complexity=ANY_COMPLEXITY)
	Builds a pointset_powerset out of a box. More...

Member Functions that Do Not Modify the Pointset_Powerset
dimension_type	space_dimension () const
	Returns the dimension of the vector space enclosing `*this`. More...

dimension_type	affine_dimension () const
	Returns the dimension of the vector space enclosing `*this`. More...

bool	is_empty () const
	Returns `true` if and only if `*this` is an empty powerset. More...

bool	is_universe () const
	Returns `true` if and only if `*this` is the top element of the powerset lattice. More...

bool	is_topologically_closed () const
	Returns `true` if and only if all the disjuncts in `*this` are topologically closed. More...

bool	is_bounded () const
	Returns `true` if and only if all elements in `*this` are bounded. More...

bool	is_disjoint_from (const Pointset_Powerset &y) const
	Returns `true` if and only if `*this` and `y` are disjoint. More...

bool	is_discrete () const
	Returns `true` if and only if `*this` is discrete. More...

bool	constrains (Variable var) const
	Returns `true` if and only if `var` is constrained in `*this`. More...

bool	bounds_from_above (const Linear_Expression &expr) const
	Returns `true` if and only if `expr` is bounded from above in `*this`. More...

bool	bounds_from_below (const Linear_Expression &expr) const
	Returns `true` if and only if `expr` is bounded from below in `*this`. More...

bool	maximize (const Linear_Expression &expr, Coefficient &sup_n, Coefficient &sup_d, bool &maximum) const
	Returns `true` if and only if `this` is not empty and `expr` is bounded from above in `this`, in which case the supremum value is computed. More...

bool	maximize (const Linear_Expression &expr, Coefficient &sup_n, Coefficient &sup_d, bool &maximum, Generator &g) const
	Returns `true` if and only if `this` is not empty and `expr` is bounded from above in `this`, in which case the supremum value and a point where `expr` reaches it are computed. More...

bool	minimize (const Linear_Expression &expr, Coefficient &inf_n, Coefficient &inf_d, bool &minimum) const
	Returns `true` if and only if `this` is not empty and `expr` is bounded from below in `this`, in which case the infimum value is computed. More...

bool	minimize (const Linear_Expression &expr, Coefficient &inf_n, Coefficient &inf_d, bool &minimum, Generator &g) const
	Returns `true` if and only if `this` is not empty and `expr` is bounded from below in `this`, in which case the infimum value and a point where `expr` reaches it are computed. More...

bool	geometrically_covers (const Pointset_Powerset &y) const
	Returns `true` if and only if `this` geometrically covers `y`, i.e., if any point (in some element) of `y` is also a point (of some element) of `this`. More...

bool	geometrically_equals (const Pointset_Powerset &y) const
	Returns `true` if and only if `this` is geometrically equal to `y`, i.e., if (the elements of) `this` and `y` contain the same set of points. More...

bool	contains (const Pointset_Powerset &y) const
	Returns `true` if and only if each disjunct of `y` is contained in a disjunct of `*this`. More...

bool	strictly_contains (const Pointset_Powerset &y) const
	Returns `true` if and only if each disjunct of `y` is strictly contained in a disjunct of `*this`. More...

bool	contains_integer_point () const
	Returns `true` if and only if `*this` contains at least one integer point. More...

Poly_Con_Relation	relation_with (const Constraint &c) const
	Returns the relations holding between the powerset `*this` and the constraint `c`. More...

Poly_Gen_Relation	relation_with (const Generator &g) const
	Returns the relations holding between the powerset `*this` and the generator `g`. More...

Poly_Con_Relation	relation_with (const Congruence &cg) const
	Returns the relations holding between the powerset `*this` and the congruence `c`. More...

memory_size_type	total_memory_in_bytes () const
	Returns a lower bound to the total size in bytes of the memory occupied by `*this`. More...

memory_size_type	external_memory_in_bytes () const
	Returns a lower bound to the size in bytes of the memory managed by `*this`. More...

int32_t	hash_code () const
	Returns a 32-bit hash code for `*this`. More...

bool	OK () const
	Checks if all the invariants are satisfied. More...

Space Dimension Preserving Member Functions that May Modify the Pointset_Powerset
void	add_disjunct (const PSET &ph)
	Adds to `*this` the disjunct `ph`. More...

void	add_constraint (const Constraint &c)
	Intersects `*this` with constraint `c`. More...

void	refine_with_constraint (const Constraint &c)
	Use the constraint `c` to refine `*this`. More...

void	add_constraints (const Constraint_System &cs)
	Intersects `*this` with the constraints in `cs`. More...

void	refine_with_constraints (const Constraint_System &cs)
	Use the constraints in `cs` to refine `*this`. More...

void	add_congruence (const Congruence &cg)
	Intersects `*this` with congruence `cg`. More...

void	refine_with_congruence (const Congruence &cg)
	Use the congruence `cg` to refine `*this`. More...

void	add_congruences (const Congruence_System &cgs)
	Intersects `*this` with the congruences in `cgs`. More...

void	refine_with_congruences (const Congruence_System &cgs)
	Use the congruences in `cgs` to refine `*this`. More...

void	unconstrain (Variable var)
	Computes the cylindrification of `this` with respect to space dimension `var`, assigning the result to `this`. More...

void	unconstrain (const Variables_Set &vars)
	Computes the cylindrification of `this` with respect to the set of space dimensions `vars`, assigning the result to `this`. More...

void	drop_some_non_integer_points (Complexity_Class complexity=ANY_COMPLEXITY)
	Possibly tightens `*this` by dropping some points with non-integer coordinates. More...

void	drop_some_non_integer_points (const Variables_Set &vars, Complexity_Class complexity=ANY_COMPLEXITY)
	Possibly tightens `*this` by dropping some points with non-integer coordinates for the space dimensions corresponding to `vars`. More...

void	topological_closure_assign ()
	Assigns to `*this` its topological closure. More...

void	intersection_assign (const Pointset_Powerset &y)
	Assigns to `this` the intersection of `this` and `y`. More...

void	difference_assign (const Pointset_Powerset &y)
	Assigns to `this` an (a smallest) over-approximation as a powerset of the disjunct domain of the set-theoretical difference of `this` and `y`. More...

bool	simplify_using_context_assign (const Pointset_Powerset &y)
	Assigns to `this` a meet-preserving simplification of `this` with respect to `y`. If `false` is returned, then the intersection is empty. More...

void	affine_image (Variable var, const Linear_Expression &expr, Coefficient_traits::const_reference denominator=Coefficient_one())
	Assigns to `this` the affine image of `this` under the function mapping variable `var` to the affine expression specified by `expr` and `denominator`. More...

void	affine_preimage (Variable var, const Linear_Expression &expr, Coefficient_traits::const_reference denominator=Coefficient_one())
	Assigns to `this` the affine preimage of `this` under the function mapping variable `var` to the affine expression specified by `expr` and `denominator`. More...

void	generalized_affine_image (Variable var, Relation_Symbol relsym, const Linear_Expression &expr, Coefficient_traits::const_reference denominator=Coefficient_one())
	Assigns to `this` the image of `this` with respect to the generalized affine relation $\mathrm{var}' \relsym \frac{\mathrm{expr}}{\mathrm{denominator}}$ , where $\mathord{\relsym}$ is the relation symbol encoded by `relsym`. More...

void	generalized_affine_preimage (Variable var, Relation_Symbol relsym, const Linear_Expression &expr, Coefficient_traits::const_reference denominator=Coefficient_one())
	Assigns to `this` the preimage of `this` with respect to the generalized affine relation $\mathrm{var}' \relsym \frac{\mathrm{expr}}{\mathrm{denominator}}$ , where $\mathord{\relsym}$ is the relation symbol encoded by `relsym`. More...

void	generalized_affine_image (const Linear_Expression &lhs, Relation_Symbol relsym, const Linear_Expression &rhs)
	Assigns to `this` the image of `this` with respect to the generalized affine relation $\mathrm{lhs}' \relsym \mathrm{rhs}$ , where $\mathord{\relsym}$ is the relation symbol encoded by `relsym`. More...

void	generalized_affine_preimage (const Linear_Expression &lhs, Relation_Symbol relsym, const Linear_Expression &rhs)
	Assigns to `this` the preimage of `this` with respect to the generalized affine relation $\mathrm{lhs}' \relsym \mathrm{rhs}$ , where $\mathord{\relsym}$ is the relation symbol encoded by `relsym`. More...

void	bounded_affine_image (Variable var, const Linear_Expression &lb_expr, const Linear_Expression &ub_expr, Coefficient_traits::const_reference denominator=Coefficient_one())
	Assigns to `this` the image of `this` with respect to the bounded affine relation $\frac{\mathrm{lb\_expr}}{\mathrm{denominator}} \leq \mathrm{var}' \leq \frac{\mathrm{ub\_expr}}{\mathrm{denominator}}$ . More...

void	bounded_affine_preimage (Variable var, const Linear_Expression &lb_expr, const Linear_Expression &ub_expr, Coefficient_traits::const_reference denominator=Coefficient_one())
	Assigns to `this` the preimage of `this` with respect to the bounded affine relation $\frac{\mathrm{lb\_expr}}{\mathrm{denominator}} \leq \mathrm{var}' \leq \frac{\mathrm{ub\_expr}}{\mathrm{denominator}}$ . More...

void	time_elapse_assign (const Pointset_Powerset &y)
	Assigns to `this` the result of computing the time-elapse between `this` and `y`. More...

void	wrap_assign (const Variables_Set &vars, Bounded_Integer_Type_Width w, Bounded_Integer_Type_Representation r, Bounded_Integer_Type_Overflow o, const Constraint_System *cs_p=0, unsigned complexity_threshold=16, bool wrap_individually=true)
	Wraps the specified dimensions of the vector space. More...

void	pairwise_reduce ()
	Assign to `*this` the result of (recursively) merging together the pairs of disjuncts whose upper-bound is the same as their set-theoretical union. More...

template<typename Widening >
void	BGP99_extrapolation_assign (const Pointset_Powerset &y, Widening widen_fun, unsigned max_disjuncts)
	Assigns to `this` the result of applying the BGP99 extrapolation operator to `this` and `y`, using the widening function `widen_fun` and the cardinality threshold `max_disjuncts`. More...

template<typename Cert , typename Widening >
void	BHZ03_widening_assign (const Pointset_Powerset &y, Widening widen_fun)
	Assigns to `this` the result of computing the BHZ03-widening between `this` and `y`, using the widening function `widen_fun` certified by the convergence certificate `Cert`. More...

Member Functions that May Modify the Dimension of the Vector Space
Pointset_Powerset &	operator= (const Pointset_Powerset &y)
	The assignment operator (`*this` and `y` can be dimension-incompatible). More...

template<typename QH >
Pointset_Powerset &	operator= (const Pointset_Powerset< QH > &y)
	Conversion assignment: the type `QH` of the disjuncts in the source powerset is different from `PSET` (`*this` and `y` can be dimension-incompatible). More...

void	m_swap (Pointset_Powerset &y)
	Swaps `*this` with `y`. More...

void	add_space_dimensions_and_embed (dimension_type m)
	Adds `m` new dimensions to the vector space containing `this` and embeds each disjunct in `this` in the new space. More...

void	add_space_dimensions_and_project (dimension_type m)
	Adds `m` new dimensions to the vector space containing `this` without embedding the disjuncts in `this` in the new space. More...

void	concatenate_assign (const Pointset_Powerset &y)
	Assigns to `this` the concatenation of `this` and `y`. More...

void	remove_space_dimensions (const Variables_Set &vars)
	Removes all the specified space dimensions. More...

void	remove_higher_space_dimensions (dimension_type new_dimension)
	Removes the higher space dimensions so that the resulting space will have dimension `new_dimension`. More...

template<typename Partial_Function >
void	map_space_dimensions (const Partial_Function &pfunc)
	Remaps the dimensions of the vector space according to a partial function. More...

void	expand_space_dimension (Variable var, dimension_type m)
	Creates `m` copies of the space dimension corresponding to `var`. More...

void	fold_space_dimensions (const Variables_Set &vars, Variable dest)
	Folds the space dimensions in `vars` into `dest`. More...

Public Member Functions inherited from Parma_Polyhedra_Library::Powerset< Parma_Polyhedra_Library::Determinate< PSET > >
	Powerset ()
	Default constructor: builds the bottom of the powerset constraint system (i.e., the empty powerset). More...

	Powerset (const Powerset &y)
	Copy constructor. More...

	Powerset (const Parma_Polyhedra_Library::Determinate< PSET > &d)
	If `d` is not bottom, builds a powerset containing only `d`. Builds the empty powerset otherwise. More...

	~Powerset ()
	Destructor. More...

bool	definitely_entails (const Powerset &y) const
	Returns `true` if `this` definitely entails `y`. Returns `false` if `this` may not entail `y` (i.e., if `*this` does not entail `y` or if entailment could not be decided). More...

bool	is_top () const
	Returns `true` if and only if `*this` is the top element of the powerset constraint system (i.e., it represents the universe). More...

bool	is_bottom () const
	Returns `true` if and only if `*this` is the bottom element of the powerset constraint system (i.e., it represents the empty set). More...

memory_size_type	total_memory_in_bytes () const
	Returns a lower bound to the total size in bytes of the memory occupied by `*this`. More...

memory_size_type	external_memory_in_bytes () const
	Returns a lower bound to the size in bytes of the memory managed by `*this`. More...

bool	OK (bool disallow_bottom=false) const
	Checks if all the invariants are satisfied. More...

void	omega_reduce () const
	Drops from the sequence of disjuncts in `this` all the non-maximal elements so that `this` is non-redundant. More...

size_type	size () const
	Returns the number of disjuncts. More...

bool	empty () const
	Returns `true` if and only if there are no disjuncts in `*this`. More...

iterator	begin ()
	Returns an iterator pointing to the first disjunct, if `*this` is not empty; otherwise, returns the past-the-end iterator. More...

const_iterator	begin () const
	Returns a const_iterator pointing to the first disjunct, if `*this` is not empty; otherwise, returns the past-the-end const_iterator. More...

iterator	end ()
	Returns the past-the-end iterator. More...

const_iterator	end () const
	Returns the past-the-end const_iterator. More...

reverse_iterator	rbegin ()
	Returns a reverse_iterator pointing to the last disjunct, if `*this` is not empty; otherwise, returns the before-the-start reverse_iterator. More...

const_reverse_iterator	rbegin () const
	Returns a const_reverse_iterator pointing to the last disjunct, if `*this` is not empty; otherwise, returns the before-the-start const_reverse_iterator. More...

reverse_iterator	rend ()
	Returns the before-the-start reverse_iterator. More...

const_reverse_iterator	rend () const
	Returns the before-the-start const_reverse_iterator. More...

void	add_disjunct (const Parma_Polyhedra_Library::Determinate< PSET > &d)
	Adds to `*this` the disjunct `d`. More...

iterator	drop_disjunct (iterator position)
	Drops the disjunct in `*this` pointed to by `position`, returning an iterator to the disjunct following `position`. More...

void	drop_disjuncts (iterator first, iterator last)
	Drops all the disjuncts from `first` to `last` (excluded). More...

void	clear ()
	Drops all the disjuncts, making `*this` an empty powerset. More...

Powerset &	operator= (const Powerset &y)
	The assignment operator. More...

void	m_swap (Powerset &y)
	Swaps `*this` with `y`. More...

void	least_upper_bound_assign (const Powerset &y)
	Assigns to `this` the least upper bound of `this` and `y`. More...

void	upper_bound_assign (const Powerset &y)
	Assigns to `this` an upper bound of `this` and `y`. More...

bool	upper_bound_assign_if_exact (const Powerset &y)
	Assigns to `this` the least upper bound of `this` and `y` and returns `true`. More...

void	meet_assign (const Powerset &y)
	Assigns to `this` the meet of `this` and `y`. More...

void	collapse ()
	If `*this` is not empty (i.e., it is not the bottom element), it is reduced to a singleton obtained by computing an upper-bound of all the disjuncts. More...

Static Public Member Functions
static dimension_type	max_space_dimension ()
	Returns the maximum space dimension a Pointset_Powerset<PSET> can handle. More...

Private Types
typedef Determinate< PSET >	Det_PSET

typedef Powerset< Det_PSET >	Base

typedef Base::Sequence	Sequence

typedef Base::Sequence_iterator	Sequence_iterator

typedef Base::Sequence_const_iterator	Sequence_const_iterator

Private Member Functions
bool	intersection_preserving_enlarge_element (PSET &dest) const
	Assigns to `dest` a powerset meet-preserving enlargement of itself with respect to `*this`. If `false` is returned, then the intersection is empty. More...

template<typename Widening >
void	BGP99_heuristics_assign (const Pointset_Powerset &y, Widening widen_fun)
	Assigns to `this` the result of applying the BGP99 heuristics to `this` and `y`, using the widening function `widen_fun`. More...

template<typename Cert >
void	collect_certificates (std::map< Cert, size_type, typename Cert::Compare > &cert_ms) const
	Records in `cert_ms` the certificates for this set of disjuncts. More...

template<typename Cert >
bool	is_cert_multiset_stabilizing (const std::map< Cert, size_type, typename Cert::Compare > &y_cert_ms) const
	Returns `true` if and only if the current set of disjuncts is stabilizing with respect to the multiset of certificates `y_cert_ms`. More...

template<typename Cons_or_Congr >
Poly_Con_Relation	relation_with_aux (const Cons_or_Congr &c) const
	Template helper: common implementation for constraints and congruences. More...

Private Attributes
dimension_type	space_dim
	The number of dimensions of the enclosing vector space. More...

Friends
class	Pointset_Powerset< NNC_Polyhedron >

Related Functions
(Note that these are not member functions.)
bool	check_containment (const NNC_Polyhedron &ph, const Pointset_Powerset< NNC_Polyhedron > &ps)

bool	approximate_partition_aux (const PPL::Congruence &c, PPL::Grid &gr, PPL::Pointset_Powerset< PPL::Grid > &r)
	Uses the congruence `c` to approximately partition the grid `gr`. More...

std::pair< PPL::Grid, PPL::Pointset_Powerset< PPL::Grid > >	approximate_partition (const Grid &p, const Grid &q, bool &finite_partition)

bool	check_containment (const Grid &ph, const Pointset_Powerset< Grid > &ps)

template<typename PSET >
void	swap (Pointset_Powerset< PSET > &x, Pointset_Powerset< PSET > &y)
	Swaps `x` with `y`. More...

template<typename PSET >
std::pair< PSET, Pointset_Powerset< NNC_Polyhedron > >	linear_partition (const PSET &p, const PSET &q)
	Partitions `q` with respect to `p`. More...

bool	check_containment (const NNC_Polyhedron &ph, const Pointset_Powerset< NNC_Polyhedron > &ps)
	Returns `true` if and only if the union of the NNC polyhedra in `ps` contains the NNC polyhedron `ph`. More...

std::pair< Grid, Pointset_Powerset< Grid > >	approximate_partition (const Grid &p, const Grid &q, bool &finite_partition)
	Partitions the grid `q` with respect to grid `p` if and only if such a partition is finite. More...

bool	check_containment (const Grid &ph, const Pointset_Powerset< Grid > &ps)
	Returns `true` if and only if the union of the grids `ps` contains the grid `g`. More...

template<typename PSET >
bool	check_containment (const PSET &ph, const Pointset_Powerset< PSET > &ps)
	Returns `true` if and only if the union of the objects in `ps` contains `ph`. More...

template<typename PSET >
bool	check_containment (const PSET &ph, const Pointset_Powerset< PSET > &ps)

template<>
bool	check_containment (const C_Polyhedron &ph, const Pointset_Powerset< C_Polyhedron > &ps)

template<typename PSET >
void	swap (Pointset_Powerset< PSET > &x, Pointset_Powerset< PSET > &y)

template<typename PSET >
void	linear_partition_aux (const Constraint &c, PSET &pset, Pointset_Powerset< NNC_Polyhedron > &r)
	Partitions polyhedron `pset` according to constraint `c`. More...

template<typename PSET >
std::pair< PSET, Pointset_Powerset< NNC_Polyhedron > >	linear_partition (const PSET &p, const PSET &q)

template<typename PSET >
Widening_Function< PSET >	widen_fun_ref (void(PSET::wm)(const PSET &, unsigned ))
	Wraps a widening method into a function object. More...

template<typename PSET , typename CSYS >
Limited_Widening_Function< PSET, CSYS >	widen_fun_ref (void(PSET::lwm)(const PSET &, const CSYS &, unsigned ), const CSYS &cs)
	Wraps a limited widening method into a function object. More...

template<typename PSET >
Widening_Function< PSET >	widen_fun_ref (void(PSET::wm)(const PSET &, unsigned ))

template<typename PSET , typename CSYS >
Limited_Widening_Function< PSET, CSYS >	widen_fun_ref (void(PSET::lwm)(const PSET &, const CSYS &, unsigned ), const CSYS &cs)

Additional Inherited Members
Protected Types inherited from Parma_Polyhedra_Library::Powerset< Parma_Polyhedra_Library::Determinate< PSET > >
typedef std::list< Parma_Polyhedra_Library::Determinate< PSET > >	Sequence
	A powerset is implemented as a sequence of elements. More...

typedef Sequence::iterator	Sequence_iterator
	Alias for the low-level iterator on the disjuncts. More...

typedef Sequence::const_iterator	Sequence_const_iterator
	Alias for the low-level const_iterator on the disjuncts. More...

Protected Member Functions inherited from Parma_Polyhedra_Library::Powerset< Parma_Polyhedra_Library::Determinate< PSET > >
void	collapse (unsigned max_disjuncts)
	Upon return, `*this` will contain at most `max_disjuncts` elements; the set of disjuncts in positions greater than or equal to `max_disjuncts`, will be replaced at that position by their upper-bound. More...

bool	is_omega_reduced () const
	Returns `true` if and only if `*this` does not contain non-maximal elements. More...

iterator	add_non_bottom_disjunct_preserve_reduction (const Parma_Polyhedra_Library::Determinate< PSET > &d, iterator first, iterator last)
	Adds to `*this` the disjunct `d`, assuming `d` is not the bottom element and ensuring partial Omega-reduction. More...

void	add_non_bottom_disjunct_preserve_reduction (const Parma_Polyhedra_Library::Determinate< PSET > &d)
	Adds to `*this` the disjunct `d`, assuming `d` is not the bottom element and preserving Omega-reduction. More...

void	pairwise_apply_assign (const Powerset &y, Binary_Operator_Assign op_assign)
	Assigns to `this` the result of applying `op_assign` pairwise to the elements in `this` and `y`. More...

Protected Attributes inherited from Parma_Polyhedra_Library::Powerset< Parma_Polyhedra_Library::Determinate< PSET > >
Sequence	sequence
	The sequence container holding powerset's elements. More...

bool	reduced
	If `true`, `*this` is Omega-reduced. More...

Detailed Description

template<typename PSET>
class Parma_Polyhedra_Library::Pointset_Powerset< PSET >

The powerset construction instantiated on PPL pointset domains.

Warning: At present, the supported instantiations for the disjunct domain template PSET are the simple pointset domains: C_Polyhedron, NNC_Polyhedron, Grid, Octagonal_Shape<T>, BD_Shape<T>, Box<T>.

Definition at line 61 of file Pointset_Powerset_defs.hh.

Member Typedef Documentation

template<typename PSET>

typedef Powerset<Det_PSET> Parma_Polyhedra_Library::Pointset_Powerset< PSET >::Base

private

Definition at line 69 of file Pointset_Powerset_defs.hh.

template<typename PSET>

typedef Base::const_iterator Parma_Polyhedra_Library::Pointset_Powerset< PSET >::const_iterator

Definition at line 1244 of file Pointset_Powerset_defs.hh.

template<typename PSET>

typedef Base::const_reverse_iterator Parma_Polyhedra_Library::Pointset_Powerset< PSET >::const_reverse_iterator

Definition at line 1246 of file Pointset_Powerset_defs.hh.

template<typename PSET>

typedef Determinate<PSET> Parma_Polyhedra_Library::Pointset_Powerset< PSET >::Det_PSET

private

Definition at line 68 of file Pointset_Powerset_defs.hh.

template<typename PSET>

typedef PSET Parma_Polyhedra_Library::Pointset_Powerset< PSET >::element_type

Definition at line 65 of file Pointset_Powerset_defs.hh.

template<typename PSET>

typedef Base::iterator Parma_Polyhedra_Library::Pointset_Powerset< PSET >::iterator

Definition at line 1243 of file Pointset_Powerset_defs.hh.

template<typename PSET>

typedef Base::reverse_iterator Parma_Polyhedra_Library::Pointset_Powerset< PSET >::reverse_iterator

Definition at line 1245 of file Pointset_Powerset_defs.hh.

template<typename PSET>

typedef Base::Sequence Parma_Polyhedra_Library::Pointset_Powerset< PSET >::Sequence

private

Definition at line 1258 of file Pointset_Powerset_defs.hh.

template<typename PSET>

typedef Base::Sequence_const_iterator Parma_Polyhedra_Library::Pointset_Powerset< PSET >::Sequence_const_iterator

private

Definition at line 1260 of file Pointset_Powerset_defs.hh.

template<typename PSET>

typedef Base::Sequence_iterator Parma_Polyhedra_Library::Pointset_Powerset< PSET >::Sequence_iterator

private

Definition at line 1259 of file Pointset_Powerset_defs.hh.

template<typename PSET>

typedef Base::size_type Parma_Polyhedra_Library::Pointset_Powerset< PSET >::size_type

Definition at line 1241 of file Pointset_Powerset_defs.hh.

template<typename PSET>

typedef Base::value_type Parma_Polyhedra_Library::Pointset_Powerset< PSET >::value_type

Definition at line 1242 of file Pointset_Powerset_defs.hh.

Constructor & Destructor Documentation

template<typename PSET >

Parma_Polyhedra_Library::Pointset_Powerset< PSET >::Pointset_Powerset	(	dimension_type	num_dimensions = `0`,
		Degenerate_Element	kind = `UNIVERSE`
	)

inlineexplicit

Builds a universe (top) or empty (bottom) Pointset_Powerset.

Parameters

num_dimensions	The number of dimensions of the vector space enclosing the powerset;
kind	Specifies whether the universe or the empty powerset has to be built.

Definition at line 54 of file Pointset_Powerset_inlines.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::sequence, and Parma_Polyhedra_Library::UNIVERSE.

   : Base(), space_dim(num_dimensions) {
   Pointset_Powerset& x = *this;
   if (kind == UNIVERSE) {
     x.sequence.push_back(Determinate<PSET>(PSET(num_dimensions, kind)));
   }
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

Parma_Polyhedra_Library::Pointset_Powerset< PSET >::Pointset_Powerset	(	const Pointset_Powerset< PSET > &	y,
		Complexity_Class	complexity = `ANY_COMPLEXITY`
	)

inline

Ordinary copy constructor.

The complexity argument is ignored.

Definition at line 66 of file Pointset_Powerset_inlines.hh.

68 : Base(y), space_dim(y.space_dim) {

69 }

Parma_Polyhedra_Library::Pointset_Powerset::Base

Powerset< Det_PSET > Base

Definition: Pointset_Powerset_defs.hh:69

Parma_Polyhedra_Library::Pointset_Powerset::space_dim

dimension_type space_dim

The number of dimensions of the enclosing vector space.

Definition: Pointset_Powerset_defs.hh:1263

template<typename PSET >

template<typename QH >

Parma_Polyhedra_Library::Pointset_Powerset< PSET >::Pointset_Powerset	(	const Pointset_Powerset< QH > &	y,
		Complexity_Class	complexity = `ANY_COMPLEXITY`
	)

explicit

Conversion constructor: the type QH of the disjuncts in the source powerset is different from PSET.

Parameters

y	The powerset to be used to build the new powerset.
complexity	The maximal complexity of any algorithms used.

Definition at line 88 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Powerset< Parma_Polyhedra_Library::Determinate< PSET > >::begin(), Parma_Polyhedra_Library::Powerset< Parma_Polyhedra_Library::Determinate< PSET > >::end(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, and Parma_Polyhedra_Library::Powerset< D >::sequence.

   : Base(), space_dim(y.space_dimension()) {
   Pointset_Powerset& x = *this;
   for (typename Pointset_Powerset<QH>::const_iterator i = y.begin(),
          y_end = y.end(); i != y_end; ++i) {
     x.sequence.push_back(Determinate<PSET>(PSET(i->pointset(), complexity)));
   }
   // Note: this might be non-reduced even when `y' is known to be
   // omega-reduced, because the constructor of PSET may have made
   // different QH elements to become comparable.
   x.reduced = false;
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

template<typename QH1 , typename QH2 , typename R >

Parma_Polyhedra_Library::Pointset_Powerset< PSET >::Pointset_Powerset	(	const Partially_Reduced_Product< QH1, QH2, R > &	prp,
		Complexity_Class	complexity = `ANY_COMPLEXITY`
	)

inlineexplicit

Creates a Pointset_Powerset from a product This will be created as a single disjunct of type PSET that approximates the product.

Definition at line 124 of file Pointset_Powerset_inlines.hh.

References Parma_Polyhedra_Library::ANY_COMPLEXITY, Parma_Polyhedra_Library::Partially_Reduced_Product< D1, D2, R >::is_empty(), Parma_Polyhedra_Library::Powerset< D >::reduced, and Parma_Polyhedra_Library::Powerset< D >::sequence.

   : Base(), space_dim(prp.space_dimension()) {
   Pointset_Powerset& x = *this;
   if (complexity == ANY_COMPLEXITY) {
     if (prp.is_empty()) {
       return;
     }
   }
   else {
     x.reduced = false;
   }
   x.sequence.push_back(Determinate<PSET>(PSET(prp, complexity)));
   x.reduced = false;
   PPL_ASSERT_HEAVY(OK());
 }

template<typename PSET >

Parma_Polyhedra_Library::Pointset_Powerset< PSET >::Pointset_Powerset ( const Constraint_System & cs )

inlineexplicit

Creates a Pointset_Powerset with a single disjunct approximating the system of constraints cs.

Definition at line 179 of file Pointset_Powerset_inlines.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK().

   : Base(Determinate<PSET>(cs)), space_dim(cs.space_dimension()) {
   PPL_ASSERT_HEAVY(OK());
 }

template<typename PSET >

Parma_Polyhedra_Library::Pointset_Powerset< PSET >::Pointset_Powerset ( const Congruence_System & cgs )

inlineexplicit

Creates a Pointset_Powerset with a single disjunct approximating the system of congruences cgs.

Definition at line 186 of file Pointset_Powerset_inlines.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK().

   : Base(Determinate<PSET>(cgs)), space_dim(cgs.space_dimension()) {
   PPL_ASSERT_HEAVY(OK());
 }

template<typename PSET >

Parma_Polyhedra_Library::Pointset_Powerset< PSET >::Pointset_Powerset	(	const C_Polyhedron &	ph,
		Complexity_Class	complexity = `ANY_COMPLEXITY`
	)

inlineexplicit

Builds a pointset_powerset out of a closed polyhedron.

Builds a powerset that is either empty (if the polyhedron is found to be empty) or contains a single disjunct approximating the polyhedron; this must only use algorithms that do not exceed the specified complexity. The powerset inherits the space dimension of the polyhedron.

Parameters

ph	The closed polyhedron to be used to build the powerset.
complexity	The maximal complexity of any algorithms used.

Exceptions

std::length_error Thrown if the space dimension of ph exceeds the maximum allowed space dimension.

Definition at line 73 of file Pointset_Powerset_inlines.hh.

References Parma_Polyhedra_Library::ANY_COMPLEXITY, Parma_Polyhedra_Library::Polyhedron::is_empty(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, and Parma_Polyhedra_Library::Powerset< D >::sequence.

   : Base(), space_dim(ph.space_dimension()) {
   Pointset_Powerset& x = *this;
   if (complexity == ANY_COMPLEXITY) {
     if (ph.is_empty()) {
       return;
     }
   }
   else {
     x.reduced = false;
   }
   x.sequence.push_back(Determinate<PSET>(PSET(ph, complexity)));
   x.reduced = false;
   PPL_ASSERT_HEAVY(OK());
 }

template<typename PSET >

Parma_Polyhedra_Library::Pointset_Powerset< PSET >::Pointset_Powerset	(	const NNC_Polyhedron &	ph,
		Complexity_Class	complexity = `ANY_COMPLEXITY`
	)

inlineexplicit

Builds a pointset_powerset out of an nnc polyhedron.

Builds a powerset that is either empty (if the polyhedron is found to be empty) or contains a single disjunct approximating the polyhedron; this must only use algorithms that do not exceed the specified complexity. The powerset inherits the space dimension of the polyhedron.

Parameters

ph	The closed polyhedron to be used to build the powerset.
complexity	The maximal complexity of any algorithms used.

Exceptions

std::length_error Thrown if the space dimension of ph exceeds the maximum allowed space dimension.

Definition at line 92 of file Pointset_Powerset_inlines.hh.

References Parma_Polyhedra_Library::ANY_COMPLEXITY, Parma_Polyhedra_Library::Polyhedron::is_empty(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, and Parma_Polyhedra_Library::Powerset< D >::sequence.

   : Base(), space_dim(ph.space_dimension()) {
   Pointset_Powerset& x = *this;
   if (complexity == ANY_COMPLEXITY) {
     if (ph.is_empty()) {
       return;
     }
   }
   else {
     x.reduced = false;
   }
   x.sequence.push_back(Determinate<PSET>(PSET(ph, complexity)));
   PPL_ASSERT_HEAVY(OK());
 }

template<typename PSET >

Parma_Polyhedra_Library::Pointset_Powerset< PSET >::Pointset_Powerset	(	const Grid &	gr,
		Complexity_Class	complexity = `ANY_COMPLEXITY`
	)

inlineexplicit

Builds a pointset_powerset out of a grid.

If the grid is nonempty, builds a powerset containing a single disjunct approximating the grid. Builds the empty powerset otherwise. The powerset inherits the space dimension of the grid.

Parameters

gr	The grid to be used to build the powerset.
complexity	This argument is ignored.

Exceptions

std::length_error Thrown if the space dimension of gr exceeds the maximum allowed space dimension.

Definition at line 110 of file Pointset_Powerset_inlines.hh.

References Parma_Polyhedra_Library::Grid::is_empty(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), and Parma_Polyhedra_Library::Powerset< D >::sequence.

   : Base(), space_dim(gr.space_dimension()) {
   Pointset_Powerset& x = *this;
   if (!gr.is_empty()) {
     x.sequence.push_back(Determinate<PSET>(PSET(gr)));
   }
   PPL_ASSERT_HEAVY(OK());
 }

template<typename PSET >

template<typename T >

Parma_Polyhedra_Library::Pointset_Powerset< PSET >::Pointset_Powerset	(	const Octagonal_Shape< T > &	os,
		Complexity_Class	complexity = `ANY_COMPLEXITY`
	)

explicit

Builds a pointset_powerset out of an octagonal shape.

If the octagonal shape is nonempty, builds a powerset containing a single disjunct approximating the octagonal shape. Builds the empty powerset otherwise. The powerset inherits the space dimension of the octagonal shape.

Parameters

os	The octagonal shape to be used to build the powerset.
complexity	This argument is ignored.

Exceptions

std::length_error Thrown if the space dimension of os exceeds the maximum allowed space dimension.

Definition at line 155 of file Pointset_Powerset_inlines.hh.

References Parma_Polyhedra_Library::Octagonal_Shape< T >::is_empty(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), and Parma_Polyhedra_Library::Powerset< D >::sequence.

   : Base(), space_dim(os.space_dimension()) {
   Pointset_Powerset& x = *this;
   if (!os.is_empty()) {
     x.sequence.push_back(Determinate<PSET>(PSET(os)));
   }
   PPL_ASSERT_HEAVY(OK());
 }

template<typename PSET >

template<typename T >

Parma_Polyhedra_Library::Pointset_Powerset< PSET >::Pointset_Powerset	(	const BD_Shape< T > &	bds,
		Complexity_Class	complexity = `ANY_COMPLEXITY`
	)

explicit

Builds a pointset_powerset out of a bd shape.

If the bd shape is nonempty, builds a powerset containing a single disjunct approximating the bd shape. Builds the empty powerset otherwise. The powerset inherits the space dimension of the bd shape.

Parameters

bds	The bd shape to be used to build the powerset.
complexity	This argument is ignored.

Exceptions

std::length_error Thrown if the space dimension of bds exceeds the maximum allowed space dimension.

Definition at line 167 of file Pointset_Powerset_inlines.hh.

References Parma_Polyhedra_Library::BD_Shape< T >::is_empty(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), and Parma_Polyhedra_Library::Powerset< D >::sequence.

   : Base(), space_dim(bds.space_dimension()) {
   Pointset_Powerset& x = *this;
   if (!bds.is_empty()) {
     x.sequence.push_back(Determinate<PSET>(PSET(bds)));
   }
   PPL_ASSERT_HEAVY(OK());
 }

template<typename PSET >

template<typename Interval >

Parma_Polyhedra_Library::Pointset_Powerset< PSET >::Pointset_Powerset	(	const Box< Interval > &	box,
		Complexity_Class	complexity = `ANY_COMPLEXITY`
	)

explicit

Builds a pointset_powerset out of a box.

If the box is nonempty, builds a powerset containing a single disjunct approximating the box. Builds the empty powerset otherwise. The powerset inherits the space dimension of the box.

Parameters

box	The box to be used to build the powerset.
complexity	This argument is ignored.

Exceptions

std::length_error Thrown if the space dimension of box exceeds the maximum allowed space dimension.

Definition at line 143 of file Pointset_Powerset_inlines.hh.

References Parma_Polyhedra_Library::Box< ITV >::is_empty(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), and Parma_Polyhedra_Library::Powerset< D >::sequence.

   : Base(), space_dim(box.space_dimension()) {
   Pointset_Powerset& x = *this;
   if (!box.is_empty()) {
     x.sequence.push_back(Determinate<PSET>(PSET(box)));
   }
   PPL_ASSERT_HEAVY(OK());
 }

template<>

Parma_Polyhedra_Library::Pointset_Powerset< PPL::NNC_Polyhedron >::Pointset_Powerset	(	const Pointset_Powerset< C_Polyhedron > &	y,
		Complexity_Class
	)

Definition at line 321 of file Pointset_Powerset.cc.

References Parma_Polyhedra_Library::Powerset< Parma_Polyhedra_Library::Determinate< PSET > >::begin(), Parma_Polyhedra_Library::Powerset< Parma_Polyhedra_Library::Determinate< PSET > >::end(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, Parma_Polyhedra_Library::Powerset< Parma_Polyhedra_Library::Determinate< PSET > >::reduced, and Parma_Polyhedra_Library::Powerset< D >::sequence.

   : Base(), space_dim(y.space_dimension()) {
   Pointset_Powerset& x = *this;
   for (Pointset_Powerset<C_Polyhedron>::const_iterator i = y.begin(),
          y_end = y.end(); i != y_end; ++i) {
     x.sequence.push_back(Determinate<NNC_Polyhedron>
                          (NNC_Polyhedron(i->pointset())));
   }
   x.reduced = y.reduced;
   PPL_ASSERT_HEAVY(x.OK());
 }

template<>

Parma_Polyhedra_Library::Pointset_Powerset< PPL::NNC_Polyhedron >::Pointset_Powerset	(	const Pointset_Powerset< Grid > &	y,
		Complexity_Class
	)

Definition at line 337 of file Pointset_Powerset.cc.

References Parma_Polyhedra_Library::Powerset< Parma_Polyhedra_Library::Determinate< PSET > >::begin(), Parma_Polyhedra_Library::Powerset< Parma_Polyhedra_Library::Determinate< PSET > >::end(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, and Parma_Polyhedra_Library::Powerset< D >::sequence.

   : Base(), space_dim(y.space_dimension()) {
   Pointset_Powerset& x = *this;
   for (Pointset_Powerset<Grid>::const_iterator i = y.begin(),
          y_end = y.end(); i != y_end; ++i) {
     x.sequence.push_back(Determinate<NNC_Polyhedron>
                          (NNC_Polyhedron(i->pointset())));
   }
   x.reduced = false;
   PPL_ASSERT_HEAVY(x.OK());
 }

template<>

Parma_Polyhedra_Library::Pointset_Powerset< PPL::C_Polyhedron >::Pointset_Powerset	(	const Pointset_Powerset< NNC_Polyhedron > &	y,
		Complexity_Class
	)

Definition at line 353 of file Pointset_Powerset.cc.

References Parma_Polyhedra_Library::Powerset< Parma_Polyhedra_Library::Determinate< PSET > >::begin(), Parma_Polyhedra_Library::Powerset< Parma_Polyhedra_Library::Determinate< PSET > >::end(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, and Parma_Polyhedra_Library::Powerset< D >::sequence.

   : Base(), space_dim(y.space_dimension()) {
   Pointset_Powerset& x = *this;
   for (Pointset_Powerset<NNC_Polyhedron>::const_iterator i = y.begin(),
          y_end = y.end(); i != y_end; ++i) {
     x.sequence.push_back(Determinate<C_Polyhedron>
                          (C_Polyhedron(i->pointset())));
   }
 
   // Note: this might be non-reduced even when `y' is known to be
   // omega-reduced, because the constructor of C_Polyhedron, by
   // enforcing topological closure, may have made different elements
   // comparable.
   x.reduced = false;
   PPL_ASSERT_HEAVY(x.OK());
 }

template<>

Parma_Polyhedra_Library::Pointset_Powerset< NNC_Polyhedron >::Pointset_Powerset	(	const Pointset_Powerset< QH > &	y,
		Complexity_Class
	)

template<>

Parma_Polyhedra_Library::Pointset_Powerset< NNC_Polyhedron >::Pointset_Powerset	(	const Pointset_Powerset< C_Polyhedron > &	y,
		Complexity_Class
	)

template<>

Parma_Polyhedra_Library::Pointset_Powerset< NNC_Polyhedron >::Pointset_Powerset	(	const Pointset_Powerset< Grid > &	y,
		Complexity_Class
	)

template<>

Parma_Polyhedra_Library::Pointset_Powerset< C_Polyhedron >::Pointset_Powerset	(	const Pointset_Powerset< NNC_Polyhedron > &	y,
		Complexity_Class
	)

template<>

Parma_Polyhedra_Library::Pointset_Powerset< NNC_Polyhedron >::Pointset_Powerset	(	const Pointset_Powerset< QH > &	y,
		Complexity_Class	complexity
	)

Definition at line 61 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Powerset< Parma_Polyhedra_Library::Determinate< PSET > >::begin(), Parma_Polyhedra_Library::Powerset< Parma_Polyhedra_Library::Determinate< PSET > >::end(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, Parma_Polyhedra_Library::Powerset< Parma_Polyhedra_Library::Determinate< PSET > >::reduced, and Parma_Polyhedra_Library::Powerset< D >::sequence.

   : Base(), space_dim(y.space_dimension()) {
   Pointset_Powerset& x = *this;
   for (typename Pointset_Powerset<QH>::const_iterator i = y.begin(),
          y_end = y.end(); i != y_end; ++i) {
     x.sequence.push_back(Determinate<NNC_Polyhedron>
                          (NNC_Polyhedron(i->pointset(), complexity)));
 
   }
   // FIXME: If the domain elements can be represented _exactly_ as NNC
   // polyhedra, then having x.reduced = y.reduced is correct. This is
   // the case if the domains are both linear and convex which holds
   // for all the currently supported instantiations except for
   // Grids; for this reason the Grid specialization has a
   // separate implementation.  For any non-linear or non-convex
   // domains (e.g., a domain of Intervals with restrictions or a
   // domain of circles) that may be supported in the future, the
   // assignment x.reduced = y.reduced will be a bug.
   x.reduced = y.reduced;
 
   PPL_ASSERT_HEAVY(x.OK());
 }

Member Function Documentation

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::add_congruence ( const Congruence & cg )

Intersects *this with congruence cg.

Exceptions

std::invalid_argument Thrown if *this and congruence cg are topology-incompatible or dimension-incompatible.

Definition at line 193 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::add_congruence(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, and Parma_Polyhedra_Library::Powerset< D >::sequence.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::add_congruence().

                                                             {
   Pointset_Powerset& x = *this;
   for (Sequence_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     si->pointset().add_congruence(cg);
   }
   x.reduced = false;
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::add_congruences ( const Congruence_System & cgs )

Intersects *this with the congruences in cgs.

Parameters

cgs	The congruences to intersect with.

Exceptions

std::invalid_argument Thrown if *this and cgs are topology-incompatible or dimension-incompatible.

Definition at line 217 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::add_congruences(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, and Parma_Polyhedra_Library::Powerset< D >::sequence.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::add_congruences().

                                                                      {
   Pointset_Powerset& x = *this;
   for (Sequence_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     si->pointset().add_congruences(cgs);
   }
   x.reduced = false;
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::add_constraint ( const Constraint & c )

Intersects *this with constraint c.

Exceptions

std::invalid_argument Thrown if *this and constraint c are topology-incompatible or dimension-incompatible.

Definition at line 145 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::add_constraint(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, and Parma_Polyhedra_Library::Powerset< D >::sequence.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::add_constraint().

                                                            {
   Pointset_Powerset& x = *this;
   for (Sequence_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     si->pointset().add_constraint(c);
   }
   x.reduced = false;
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::add_constraints ( const Constraint_System & cs )

Intersects *this with the constraints in cs.

Parameters

cs	The constraints to intersect with.

Exceptions

std::invalid_argument Thrown if *this and cs are topology-incompatible or dimension-incompatible.

Definition at line 169 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::add_constraints(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, and Parma_Polyhedra_Library::Powerset< D >::sequence.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::add_constraints().

                                                                     {
   Pointset_Powerset& x = *this;
   for (Sequence_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     si->pointset().add_constraints(cs);
   }
   x.reduced = false;
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::add_disjunct ( const PSET & ph )

Adds to *this the disjunct ph.

Exceptions

std::invalid_argument Thrown if *this and ph are dimension-incompatible.

Definition at line 44 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, Parma_Polyhedra_Library::Powerset< D >::sequence, and Parma_Polyhedra_Library::Pointset_Powerset< PSET >::space_dimension().

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::approximate_partition_aux(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::ascii_load(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::BHZ03_widening_assign(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::check_containment(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::concatenate_assign(), and Parma_Polyhedra_Library::Pointset_Powerset< PSET >::linear_partition_aux().

                                                     {
   Pointset_Powerset& x = *this;
   if (x.space_dimension() != ph.space_dimension()) {
     std::ostringstream s;
     s << "PPL::Pointset_Powerset<PSET>::add_disjunct(ph):\n"
       << "this->space_dimension() == " << x.space_dimension() << ", "
       << "ph.space_dimension() == " << ph.space_dimension() << ".";
     throw std::invalid_argument(s.str());
   }
   x.sequence.push_back(Determinate<PSET>(ph));
   x.reduced = false;
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::add_space_dimensions_and_embed ( dimension_type m )

Adds m new dimensions to the vector space containing *this and embeds each disjunct in *this in the new space.

Definition at line 265 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::add_space_dimensions_and_embed(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::sequence, and Parma_Polyhedra_Library::Pointset_Powerset< PSET >::space_dim.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::add_space_dimensions_and_embed().

                                                                         {
   Pointset_Powerset& x = *this;
   for (Sequence_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     si->pointset().add_space_dimensions_and_embed(m);
   }
   x.space_dim += m;
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::add_space_dimensions_and_project ( dimension_type m )

Adds m new dimensions to the vector space containing *this without embedding the disjuncts in *this in the new space.

Definition at line 277 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::add_space_dimensions_and_project(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::sequence, and Parma_Polyhedra_Library::Pointset_Powerset< PSET >::space_dim.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::add_space_dimensions_and_project().

                                                                           {
   Pointset_Powerset& x = *this;
   for (Sequence_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     si->pointset().add_space_dimensions_and_project(m);
   }
   x.space_dim += m;
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

dimension_type Parma_Polyhedra_Library::Pointset_Powerset< PSET >::affine_dimension ( ) const

Returns the dimension of the vector space enclosing *this.

Definition at line 511 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Polyhedron::add_constraint(), Parma_Polyhedra_Library::Polyhedron::affine_dimension(), Parma_Polyhedra_Library::Constraint_System::begin(), c, Parma_Polyhedra_Library::EMPTY, Parma_Polyhedra_Library::Constraint_System::end(), Parma_Polyhedra_Library::Constraint::is_equality(), Parma_Polyhedra_Library::Polyhedron::poly_hull_assign(), and Parma_Polyhedra_Library::Powerset< D >::sequence.

                                                 {
   // The affine dimension of the powerset is the affine dimension of
   // the smallest vector space in which it can be embedded.
   const Pointset_Powerset& x = *this;
   C_Polyhedron x_ph(space_dim, EMPTY);
 
   for (Sequence_const_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     PSET pi(si->pointset());
     if (!pi.is_empty()) {
       C_Polyhedron phi(space_dim);
       const Constraint_System& cs = pi.minimized_constraints();
       for (Constraint_System::const_iterator i = cs.begin(),
              cs_end = cs.end(); i != cs_end; ++i) {
         const Constraint& c = *i;
         if (c.is_equality()) {
           phi.add_constraint(c);
         }
       }
       x_ph.poly_hull_assign(phi);
     }
   }
 
   return x_ph.affine_dimension();
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::affine_image	(	Variable	var,
		const Linear_Expression &	expr,
		Coefficient_traits::const_reference	denominator = `Coefficient_one()`
	)

Assigns to *this the affine image of *this under the function mapping variable var to the affine expression specified by expr and denominator.

Parameters

var	The variable to which the affine expression is assigned;
expr	The numerator of the affine expression;
denominator	The denominator of the affine expression (optional argument with default value 1).

Exceptions

std::invalid_argument Thrown if denominator is zero or if expr and *this are dimension-incompatible or if var is not a space dimension of *this.

Definition at line 377 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::affine_image(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, and Parma_Polyhedra_Library::Powerset< D >::sequence.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::affine_image().

                                                    {
   Pointset_Powerset& x = *this;
   for (Sequence_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     si->pointset().affine_image(var, expr, denominator);
     // Note that the underlying domain can apply conservative approximation:
     // that is why it would not be correct to make the loss of reduction
     // conditional on `var' and `expr'.
     x.reduced = false;
   }
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::affine_preimage	(	Variable	var,
		const Linear_Expression &	expr,
		Coefficient_traits::const_reference	denominator = `Coefficient_one()`
	)

Assigns to *this the affine preimage of *this under the function mapping variable var to the affine expression specified by expr and denominator.

Parameters

var	The variable to which the affine expression is assigned;
expr	The numerator of the affine expression;
denominator	The denominator of the affine expression (optional argument with default value 1).

Exceptions

std::invalid_argument Thrown if denominator is zero or if expr and *this are dimension-incompatible or if var is not a space dimension of *this.

Definition at line 395 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::affine_preimage(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, and Parma_Polyhedra_Library::Powerset< D >::sequence.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::affine_preimage().

                                                       {
   Pointset_Powerset& x = *this;
   for (Sequence_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     si->pointset().affine_preimage(var, expr, denominator);
     // Note that the underlying domain can apply conservative approximation:
     // that is why it would not be correct to make the loss of reduction
     // conditional on `var' and `expr'.
     x.reduced = false;
   }
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET>

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::ascii_dump ( ) const

Writes to std::cerr an ASCII representation of *this.

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::ascii_dump ( std::ostream & s ) const

Writes to s an ASCII representation of *this.

Definition at line 1545 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Powerset< D >::begin(), Parma_Polyhedra_Library::Powerset< D >::end(), Parma_Polyhedra_Library::Powerset< D >::size(), and Parma_Polyhedra_Library::Pointset_Powerset< PSET >::space_dim.

                                                        {
   const Pointset_Powerset& x = *this;
   s << "size " << x.size()
     << "\nspace_dim " << x.space_dim
     << "\n";
   for (const_iterator xi = x.begin(), x_end = x.end();
        xi != x_end; ++xi) {
     xi->pointset().ascii_dump(s);
   }
 }

template<typename PSET >

bool Parma_Polyhedra_Library::Pointset_Powerset< PSET >::ascii_load ( std::istream & s )

Loads from s an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets *this accordingly. Returns true if successful, false otherwise.

Definition at line 1560 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::add_disjunct(), Parma_Polyhedra_Library::EMPTY, Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::space_dim, and Parma_Polyhedra_Library::swap().

                                                  {
   Pointset_Powerset& x = *this;
   std::string str;
 
   if (!(s >> str) || str != "size") {
     return false;
   }
 
   size_type sz;
 
   if (!(s >> sz)) {
     return false;
   }
 
   if (!(s >> str) || str != "space_dim") {
     return false;
   }
 
   if (!(s >> x.space_dim)) {
     return false;
   }
 
   Pointset_Powerset new_x(x.space_dim, EMPTY);
   while (sz-- > 0) {
     PSET ph;
     if (!ph.ascii_load(s)) {
       return false;
     }
     new_x.add_disjunct(ph);
   }
   swap(x, new_x);
 
   // Check invariants.
   PPL_ASSERT_HEAVY(x.OK());
   return true;
 }

template<typename PSET >

template<typename Widening >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::BGP99_extrapolation_assign	(	const Pointset_Powerset< PSET > &	y,
		Widening	widen_fun,
		unsigned	max_disjuncts
	)

Assigns to *this the result of applying the BGP99 extrapolation operator to *this and y, using the widening function widen_fun and the cardinality threshold max_disjuncts.

Parameters

y	A powerset that must definitely entail `*this`;
widen_fun	The widening function to be used on polyhedra objects. It is obtained from the corresponding widening method by using the helper function Parma_Polyhedra_Library::widen_fun_ref. Legal values are, e.g., `widen_fun_ref(&Polyhedron::H79_widening_assign)` and `widen_fun_ref(&Polyhedron::limited_H79_extrapolation_assign, cs)`;
max_disjuncts	The maximum number of disjuncts occurring in the powerset `this` before* starting the computation. If this number is exceeded, some of the disjuncts in `*this` are collapsed (i.e., joined together).

Exceptions

std::invalid_argument Thrown if *this and y are dimension-incompatible.

For a description of the extrapolation operator, see [BGP99] and [BHZ03b].

Definition at line 1336 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::BGP99_heuristics_assign(), Parma_Polyhedra_Library::Powerset< D >::collapse(), Parma_Polyhedra_Library::Powerset< Parma_Polyhedra_Library::Determinate< PSET > >::definitely_entails(), and Parma_Polyhedra_Library::Pointset_Powerset< PSET >::pairwise_reduce().

                                                    {
   // `x' is the current iteration value.
   Pointset_Powerset& x = *this;
 
 #ifndef NDEBUG
   {
     // We assume that `y' entails `x'.
     const Pointset_Powerset<PSET> x_copy = x;
     const Pointset_Powerset<PSET> y_copy = y;
     PPL_ASSERT_HEAVY(y_copy.definitely_entails(x_copy));
   }
 #endif
 
   x.pairwise_reduce();
   if (max_disjuncts != 0) {
     x.collapse(max_disjuncts);
   }
   x.BGP99_heuristics_assign(y, widen_fun);
 }

template<typename PSET >

template<typename Widening >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::BGP99_heuristics_assign	(	const Pointset_Powerset< PSET > &	y,
		Widening	widen_fun
	)

private

Assigns to *this the result of applying the BGP99 heuristics to *this and y, using the widening function widen_fun.

Definition at line 1282 of file Pointset_Powerset_templates.hh.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::BGP99_extrapolation_assign(), and Parma_Polyhedra_Library::Pointset_Powerset< PSET >::BHZ03_widening_assign().

                                                                         {
   // `x' is the current iteration value.
   Pointset_Powerset& x = *this;
 
 #ifndef NDEBUG
   {
     // We assume that `y' entails `x'.
     const Pointset_Powerset<PSET> x_copy = x;
     const Pointset_Powerset<PSET> y_copy = y;
     PPL_ASSERT_HEAVY(y_copy.definitely_entails(x_copy));
   }
 #endif
 
   size_type n = x.size();
   Pointset_Powerset new_x(x.space_dim, EMPTY);
   std::deque<bool> marked(n, false);
   const_iterator x_begin = x.begin();
   const_iterator x_end = x.end();
   unsigned i_index = 0;
   for (const_iterator i = x_begin,
          y_begin = y.begin(), y_end = y.end();
          i != x_end; ++i, ++i_index) {
     for (const_iterator j = y_begin; j != y_end; ++j) {
       const PSET& pi = i->pointset();
       const PSET& pj = j->pointset();
       if (pi.contains(pj)) {
         PSET pi_copy = pi;
         widen_fun(pi_copy, pj);
         new_x.add_non_bottom_disjunct_preserve_reduction(pi_copy);
         marked[i_index] = true;
       }
     }
   }
   iterator new_x_begin = new_x.begin();
   iterator new_x_end = new_x.end();
   i_index = 0;
   for (const_iterator i = x_begin; i != x_end; ++i, ++i_index) {
     if (!marked[i_index]) {
       new_x_begin
         = new_x.add_non_bottom_disjunct_preserve_reduction(*i,
                                                            new_x_begin,
                                                            new_x_end);
     }
   }
   using std::swap;
   swap(x.sequence, new_x.sequence);
   PPL_ASSERT_HEAVY(x.OK());
   PPL_ASSERT(x.is_omega_reduced());
 }

template<typename PSET >

template<typename Cert , typename Widening >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::BHZ03_widening_assign	(	const Pointset_Powerset< PSET > &	y,
		Widening	widen_fun
	)

Assigns to *this the result of computing the BHZ03-widening between *this and y, using the widening function widen_fun certified by the convergence certificate Cert.

Parameters

y	The finite powerset computed in the previous iteration step. It must definitely entail `*this`;
widen_fun	The widening function to be used on disjuncts. It is obtained from the corresponding widening method by using the helper function widen_fun_ref. Legal values are, e.g., `widen_fun_ref(&Polyhedron::H79_widening_assign)` and `widen_fun_ref(&Polyhedron::limited_H79_extrapolation_assign, cs)`.

Exceptions

std::invalid_argument Thrown if *this and y are dimension-incompatible.

Warning: In order to obtain a proper widening operator, the template parameter Cert should be a finite convergence certificate for the base-level widening function widen_fun; otherwise, an extrapolation operator is obtained. For a description of the methods that should be provided by Cert, see BHRZ03_Certificate or H79_Certificate.

Definition at line 1423 of file Pointset_Powerset_templates.hh.

                                                                    {
   // `x' is the current iteration value.
   Pointset_Powerset& x = *this;
 
 #ifndef NDEBUG
   {
     // We assume that `y' entails `x'.
     const Pointset_Powerset<PSET> x_copy = x;
     const Pointset_Powerset<PSET> y_copy = y;
     PPL_ASSERT_HEAVY(y_copy.definitely_entails(x_copy));
   }
 #endif
 
   // First widening technique: do nothing.
 
   // If `y' is the empty collection, do nothing.
   PPL_ASSERT(x.size() > 0);
   if (y.size() == 0) {
     return;
   }
 
   // Compute the poly-hull of `x'.
   PSET x_hull(x.space_dim, EMPTY);
   for (const_iterator i = x.begin(), x_end = x.end(); i != x_end; ++i) {
     x_hull.upper_bound_assign(i->pointset());
   }
 
   // Compute the poly-hull of `y'.
   PSET y_hull(y.space_dim, EMPTY);
   for (const_iterator i = y.begin(), y_end = y.end(); i != y_end; ++i) {
     y_hull.upper_bound_assign(i->pointset());
   }
   // Compute the certificate for `y_hull'.
   const Cert y_hull_cert(y_hull);
 
   // If the hull is stabilizing, do nothing.
   int hull_stabilization = y_hull_cert.compare(x_hull);
   if (hull_stabilization == 1) {
     return;
   }
 
   // Multiset ordering is only useful when `y' is not a singleton.
   const bool y_is_not_a_singleton = y.size() > 1;
 
   // The multiset certificate for `y':
   // we want to be lazy about its computation.
   typedef std::map<Cert, size_type, typename Cert::Compare> Cert_Multiset;
   Cert_Multiset y_cert_ms;
   bool y_cert_ms_computed = false;
 
   if (hull_stabilization == 0 && y_is_not_a_singleton) {
     // Collect the multiset certificate for `y'.
     y.collect_certificates(y_cert_ms);
     y_cert_ms_computed = true;
     // If multiset ordering is stabilizing, do nothing.
     if (x.is_cert_multiset_stabilizing(y_cert_ms)) {
       return;
     }
   }
 
   // Second widening technique: try the BGP99 powerset heuristics.
   Pointset_Powerset<PSET> bgp99_heuristics = x;
   bgp99_heuristics.BGP99_heuristics_assign(y, widen_fun);
 
   // Compute the poly-hull of `bgp99_heuristics'.
   PSET bgp99_heuristics_hull(x.space_dim, EMPTY);
   for (const_iterator i = bgp99_heuristics.begin(),
          b_h_end = bgp99_heuristics.end(); i != b_h_end; ++i) {
     bgp99_heuristics_hull.upper_bound_assign(i->pointset());
   }
 
   // Check for stabilization and, if successful,
   // commit to the result of the extrapolation.
   hull_stabilization = y_hull_cert.compare(bgp99_heuristics_hull);
   if (hull_stabilization == 1) {
     // The poly-hull is stabilizing.
     swap(x, bgp99_heuristics);
     return;
   }
   else if (hull_stabilization == 0 && y_is_not_a_singleton) {
     // If not already done, compute multiset certificate for `y'.
     if (!y_cert_ms_computed) {
       y.collect_certificates(y_cert_ms);
       y_cert_ms_computed = true;
     }
     if (bgp99_heuristics.is_cert_multiset_stabilizing(y_cert_ms)) {
       swap(x, bgp99_heuristics);
       return;
     }
     // Third widening technique: pairwise-reduction on `bgp99_heuristics'.
     // Note that pairwise-reduction does not affect the computation
     // of the poly-hulls, so that we only have to check the multiset
     // certificate relation.
     Pointset_Powerset<PSET> reduced_bgp99_heuristics(bgp99_heuristics);
     reduced_bgp99_heuristics.pairwise_reduce();
     if (reduced_bgp99_heuristics.is_cert_multiset_stabilizing(y_cert_ms)) {
       swap(x, reduced_bgp99_heuristics);
       return;
     }
   }
 
   // Fourth widening technique: this is applicable only when
   // `y_hull' is a proper subset of `bgp99_heuristics_hull'.
   if (bgp99_heuristics_hull.strictly_contains(y_hull)) {
     // Compute (y_hull \widen bgp99_heuristics_hull).
     PSET ph = bgp99_heuristics_hull;
     widen_fun(ph, y_hull);
     // Compute the difference between `ph' and `bgp99_heuristics_hull'.
     ph.difference_assign(bgp99_heuristics_hull);
     x.add_disjunct(ph);
     return;
   }
 
   // Fall back to the computation of the poly-hull.
   Pointset_Powerset<PSET> x_hull_singleton(x.space_dim, EMPTY);
   x_hull_singleton.add_disjunct(x_hull);
   swap(x, x_hull_singleton);
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::bounded_affine_image	(	Variable	var,
		const Linear_Expression &	lb_expr,
		const Linear_Expression &	ub_expr,
		Coefficient_traits::const_reference	denominator = `Coefficient_one()`
	)

Assigns to *this the image of *this with respect to the bounded affine relation $\frac{\mathrm{lb\_expr}}{\mathrm{denominator}} \leq \mathrm{var}' \leq \frac{\mathrm{ub\_expr}}{\mathrm{denominator}}$ .

Parameters

var	The variable updated by the affine relation;
lb_expr	The numerator of the lower bounding affine expression;
ub_expr	The numerator of the upper bounding affine expression;
denominator	The (common) denominator for the lower and upper bounding affine expressions (optional argument with default value 1).

Exceptions

std::invalid_argument Thrown if denominator is zero or if lb_expr (resp., ub_expr) and *this are dimension-incompatible or if var is not a space dimension of *this.

Definition at line 479 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::bounded_affine_image(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, and Parma_Polyhedra_Library::Powerset< D >::sequence.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::bounded_affine_image().

                                                                       {
   Pointset_Powerset& x = *this;
   for (Sequence_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     si->pointset().bounded_affine_image(var, lb_expr, ub_expr, denominator);
     x.reduced = false;
   }
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::bounded_affine_preimage	(	Variable	var,
		const Linear_Expression &	lb_expr,
		const Linear_Expression &	ub_expr,
		Coefficient_traits::const_reference	denominator = `Coefficient_one()`
	)

Assigns to *this the preimage of *this with respect to the bounded affine relation $\frac{\mathrm{lb\_expr}}{\mathrm{denominator}} \leq \mathrm{var}' \leq \frac{\mathrm{ub\_expr}}{\mathrm{denominator}}$ .

Parameters

var	The variable updated by the affine relation;
lb_expr	The numerator of the lower bounding affine expression;
ub_expr	The numerator of the upper bounding affine expression;
denominator	The (common) denominator for the lower and upper bounding affine expressions (optional argument with default value 1).

Exceptions

std::invalid_argument Thrown if denominator is zero or if lb_expr (resp., ub_expr) and *this are dimension-incompatible or if var is not a space dimension of *this.

Definition at line 495 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::bounded_affine_preimage(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, and Parma_Polyhedra_Library::Powerset< D >::sequence.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::bounded_affine_preimage().

                                                                          {
   Pointset_Powerset& x = *this;
   for (Sequence_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     si->pointset().bounded_affine_preimage(var, lb_expr, ub_expr,
                                           denominator);
     x.reduced = false;
   }
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

bool Parma_Polyhedra_Library::Pointset_Powerset< PSET >::bounds_from_above ( const Linear_Expression & expr ) const

Returns true if and only if expr is bounded from above in *this.

Exceptions

std::invalid_argument Thrown if expr and *this are dimension-incompatible.

Definition at line 910 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Powerset< D >::omega_reduce(), and Parma_Polyhedra_Library::Powerset< D >::sequence.

                                                        {
   const Pointset_Powerset& x = *this;
   x.omega_reduce();
   for (Sequence_const_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     if (!si->pointset().bounds_from_above(expr)) {
       return false;
     }
   }
   return true;
 }

template<typename PSET >

bool Parma_Polyhedra_Library::Pointset_Powerset< PSET >::bounds_from_below ( const Linear_Expression & expr ) const

Returns true if and only if expr is bounded from below in *this.

Exceptions

std::invalid_argument Thrown if expr and *this are dimension-incompatible.

Definition at line 925 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Powerset< D >::omega_reduce(), and Parma_Polyhedra_Library::Powerset< D >::sequence.

                                                        {
   const Pointset_Powerset& x = *this;
   x.omega_reduce();
   for (Sequence_const_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     if (!si->pointset().bounds_from_below(expr)) {
       return false;
     }
   }
   return true;
 }

template<typename PSET >

template<typename Cert >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::collect_certificates ( std::map< Cert, size_type, typename Cert::Compare > & cert_ms ) const

private

Records in cert_ms the certificates for this set of disjuncts.

Definition at line 1362 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Powerset< D >::begin(), Parma_Polyhedra_Library::Powerset< D >::end(), and Parma_Polyhedra_Library::Powerset< D >::is_omega_reduced().

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::BHZ03_widening_assign().

                                                            {
   const Pointset_Powerset& x = *this;
   PPL_ASSERT(x.is_omega_reduced());
   PPL_ASSERT(cert_ms.size() == 0);
   for (const_iterator i = x.begin(), end = x.end(); i != end; ++i) {
     Cert ph_cert(i->pointset());
     ++cert_ms[ph_cert];
   }
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::concatenate_assign ( const Pointset_Powerset< PSET > & y )

Assigns to *this the concatenation of *this and y.

The result is obtained by computing the pairwise concatenation of each disjunct in *this with each disjunct in y.

Definition at line 105 of file Pointset_Powerset_templates.hh.

                                                                       {
   Pointset_Powerset& x = *this;
   // Ensure omega-reduction here, since what follows has quadratic complexity.
   x.omega_reduce();
   y.omega_reduce();
   Pointset_Powerset<PSET> new_x(x.space_dim + y.space_dim, EMPTY);
   for (const_iterator xi = x.begin(), x_end = x.end(),
          y_begin = y.begin(), y_end = y.end(); xi != x_end; ) {
     for (const_iterator yi = y_begin; yi != y_end; ++yi) {
       Det_PSET zi = *xi;
       zi.concatenate_assign(*yi);
       PPL_ASSERT_HEAVY(!zi.is_bottom());
       new_x.sequence.push_back(zi);
     }
     ++xi;
     if ((abandon_expensive_computations != 0)
         && (xi != x_end) && (y_begin != y_end)) {
       // Hurry up!
       PSET x_ph = xi->pointset();
       for (++xi; xi != x_end; ++xi) {
         x_ph.upper_bound_assign(xi->pointset());
       }
       const_iterator yi = y_begin;
       PSET y_ph = yi->pointset();
       for (++yi; yi != y_end; ++yi) {
         y_ph.upper_bound_assign(yi->pointset());
       }
       x_ph.concatenate_assign(y_ph);
       swap(x, new_x);
       x.add_disjunct(x_ph);
       PPL_ASSERT_HEAVY(x.OK());
       return;
     }
   }
   swap(x, new_x);
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

bool Parma_Polyhedra_Library::Pointset_Powerset< PSET >::constrains ( Variable var ) const

Returns true if and only if var is constrained in *this.

Exceptions

std::invalid_argument Thrown if var is not a space dimension of *this.

Note: A variable is constrained if there exists a non-redundant disjunct that is constraining the variable: this definition relies on the powerset lattice structure and may be somewhat different from the geometric intuition. For instance, variable 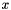is constrained in the powerset
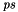$\mathit{ps} = \bigl\{ \{ x \geq 0 \}, \{ x \leq 0 \} \bigr\},$
even though $\mathit{ps}$ is geometrically equal to the whole vector space.

Definition at line 619 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Powerset< D >::begin(), Parma_Polyhedra_Library::Powerset< D >::end(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::is_empty(), Parma_Polyhedra_Library::Powerset< D >::omega_reduce(), Parma_Polyhedra_Library::Variable::space_dimension(), and Parma_Polyhedra_Library::Pointset_Powerset< PSET >::space_dimension().

                                                       {
   const Pointset_Powerset& x = *this;
   // `var' should be one of the dimensions of the powerset.
   const dimension_type var_space_dim = var.space_dimension();
   if (x.space_dimension() < var_space_dim) {
     std::ostringstream s;
     s << "PPL::Pointset_Powerset<PSET>::constrains(v):\n"
       << "this->space_dimension() == " << x.space_dimension() << ", "
       << "v.space_dimension() == " << var_space_dim << ".";
     throw std::invalid_argument(s.str());
   }
   // omega_reduction needed, since a redundant disjunct may constrain var.
   x.omega_reduce();
   // An empty powerset constrains all variables.
   if (x.is_empty()) {
     return true;
   }
   for (const_iterator x_i = x.begin(), x_end = x.end();
        x_i != x_end; ++x_i) {
     if (x_i->pointset().constrains(var)) {
       return true;
     }
   }
   return false;
 }

template<typename PSET >

bool Parma_Polyhedra_Library::Pointset_Powerset< PSET >::contains ( const Pointset_Powerset< PSET > & y ) const

Returns true if and only if each disjunct of y is contained in a disjunct of *this.

Exceptions

std::invalid_argument Thrown if *this and y are topology-incompatible or dimension-incompatible.

Definition at line 782 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Powerset< D >::sequence.

                                                                   {
   const Pointset_Powerset& x = *this;
   for (Sequence_const_iterator si = y.sequence.begin(),
          y_s_end = y.sequence.end(); si != y_s_end; ++si) {
     const PSET& pi = si->pointset();
     bool pi_is_contained = false;
     for (Sequence_const_iterator sj = x.sequence.begin(),
            x_s_end = x.sequence.end();
          (sj != x_s_end && !pi_is_contained);
          ++sj) {
       const PSET& pj = sj->pointset();
       if (pj.contains(pi)) {
         pi_is_contained = true;
       }
     }
     if (!pi_is_contained) {
       return false;
     }
   }
   return true;
 }

template<typename PSET >

bool Parma_Polyhedra_Library::Pointset_Powerset< PSET >::contains_integer_point ( ) const

Returns true if and only if *this contains at least one integer point.

Definition at line 1190 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Powerset< D >::sequence.

                                                       {
   const Pointset_Powerset& x = *this;
   for (Sequence_const_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     if (si->pointset().contains_integer_point()) {
       return true;
     }
   }
   return false;
 }

template<>

void Parma_Polyhedra_Library::Pointset_Powerset< PPL::NNC_Polyhedron >::difference_assign ( const Pointset_Powerset< PSET > & y )

Definition at line 34 of file Pointset_Powerset.cc.

References Parma_Polyhedra_Library::Powerset< D >::begin(), Parma_Polyhedra_Library::Powerset< D >::end(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::linear_partition(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::omega_reduce(), Parma_Polyhedra_Library::Powerset< D >::reduced, Parma_Polyhedra_Library::Powerset< D >::sequence, Parma_Polyhedra_Library::Affine_Space::swap(), and Parma_Polyhedra_Library::swap().

                                               {
   Pointset_Powerset& x = *this;
   using std::swap;
   // Ensure omega-reduction.
   x.omega_reduce();
   y.omega_reduce();
   Sequence new_sequence = x.sequence;
   for (const_iterator yi = y.begin(), y_end = y.end(); yi != y_end; ++yi) {
     const NNC_Polyhedron& ph_yi = yi->pointset();
     Sequence tmp_sequence;
     for (Sequence_const_iterator itr = new_sequence.begin(),
            ns_end = new_sequence.end(); itr != ns_end; ++itr) {
       const std::pair<NNC_Polyhedron, Pointset_Powerset<NNC_Polyhedron> >
         partition = linear_partition(ph_yi, itr->pointset());
       const Pointset_Powerset<NNC_Polyhedron>& residues = partition.second;
       // Append the contents of `residues' to `tmp_sequence'.
       std::copy(residues.begin(), residues.end(), back_inserter(tmp_sequence));
     }
     swap(tmp_sequence, new_sequence);
   }
   swap(x.sequence, new_sequence);
   x.reduced = false;
   PPL_ASSERT_HEAVY(x.OK());
 }

template<>

void Parma_Polyhedra_Library::Pointset_Powerset< PPL::Grid >::difference_assign ( const Pointset_Powerset< PSET > & y )

Definition at line 278 of file Pointset_Powerset.cc.

References Parma_Polyhedra_Library::Powerset< D >::begin(), Parma_Polyhedra_Library::Powerset< D >::end(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::omega_reduce(), Parma_Polyhedra_Library::Powerset< D >::reduced, Parma_Polyhedra_Library::Powerset< D >::sequence, and Parma_Polyhedra_Library::swap().

                                               {
   Pointset_Powerset& x = *this;
   using std::swap;
   // Ensure omega-reduction.
   x.omega_reduce();
   y.omega_reduce();
   Sequence new_sequence = x.sequence;
   for (const_iterator yi = y.begin(), y_end = y.end(); yi != y_end; ++yi) {
     const Grid& gr_yi = yi->pointset();
     Sequence tmp_sequence;
     for (Sequence_const_iterator itr = new_sequence.begin(),
            ns_end = new_sequence.end(); itr != ns_end; ++itr) {
       bool finite_partition;
       const std::pair<Grid, Pointset_Powerset<Grid> > partition
         = approximate_partition(gr_yi, itr->pointset(), finite_partition);
       const Pointset_Powerset<Grid>& residues = partition.second;
       // Append the contents of `residues' to `tmp_sequence'.
       std::copy(residues.begin(), residues.end(), back_inserter(tmp_sequence));
     }
     swap(tmp_sequence, new_sequence);
   }
   swap(x.sequence, new_sequence);
   x.reduced = false;
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::difference_assign ( const Pointset_Powerset< PSET > & y )

inline

Assigns to *this an (a smallest) over-approximation as a powerset of the disjunct domain of the set-theoretical difference of *this and y.

Exceptions

std::invalid_argument Thrown if *this and y are dimension-incompatible.

Definition at line 304 of file Pointset_Powerset_inlines.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::difference_assign().

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::difference_assign().

                                               {
   // This code is only used when PSET is an abstraction of NNC_Polyhedron.
   Pointset_Powerset<NNC_Polyhedron> nnc_this(*this);
   Pointset_Powerset<NNC_Polyhedron> nnc_y(y);
   nnc_this.difference_assign(nnc_y);
   *this = nnc_this;
 }

template<>

void Parma_Polyhedra_Library::Pointset_Powerset< NNC_Polyhedron >::difference_assign ( const Pointset_Powerset< PSET > & y )

template<>

void Parma_Polyhedra_Library::Pointset_Powerset< Grid >::difference_assign ( const Pointset_Powerset< PSET > & y )

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::drop_some_non_integer_points ( Complexity_Class complexity = ANY_COMPLEXITY )

Possibly tightens *this by dropping some points with non-integer coordinates.

Parameters

complexity The maximal complexity of any algorithms used.

Note: Currently there is no optimality guarantee, not even if complexity is ANY_COMPLEXITY.

Definition at line 680 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::drop_some_non_integer_points(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, and Parma_Polyhedra_Library::Powerset< D >::sequence.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::drop_some_non_integer_points().

                                                           {
   Pointset_Powerset& x = *this;
   for (Sequence_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     si->pointset().drop_some_non_integer_points(complexity);
   }
   x.reduced = false;
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::drop_some_non_integer_points	(	const Variables_Set &	vars,
		Complexity_Class	complexity = `ANY_COMPLEXITY`
	)

Possibly tightens *this by dropping some points with non-integer coordinates for the space dimensions corresponding to vars.

Parameters

vars	Points with non-integer coordinates for these variables/space-dimensions can be discarded.
complexity	The maximal complexity of any algorithms used.

Note: Currently there is no optimality guarantee, not even if complexity is ANY_COMPLEXITY.

Definition at line 666 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::drop_some_non_integer_points(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, and Parma_Polyhedra_Library::Powerset< D >::sequence.

                                                             {
   Pointset_Powerset& x = *this;
   for (Sequence_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     si->pointset().drop_some_non_integer_points(vars, complexity);
   }
   x.reduced = false;
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::expand_space_dimension	(	Variable	var,
		dimension_type	m
	)

Creates m copies of the space dimension corresponding to var.

Parameters

var	The variable corresponding to the space dimension to be replicated;
m	The number of replicas to be created.

Exceptions

std::invalid_argument	Thrown if `var` does not correspond to a dimension of the vector space.
std::length_error	Thrown if adding `m` new space dimensions would cause the vector space to exceed dimension `max_space_dimension()`.

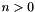If *this has space dimension $n$ , with $n > 0$ , and var has space dimension 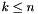$k \leq n$ , then the $k$ -th space dimension is expanded to m new space dimensions $n$ , $n+1$ , $\dots$ , $n+m-1$ .

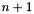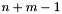Definition at line 348 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::expand_space_dimension(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::sequence, and Parma_Polyhedra_Library::Pointset_Powerset< PSET >::space_dim.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::expand_space_dimension().

                                                                   {
   Pointset_Powerset& x = *this;
   for (Sequence_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     si->pointset().expand_space_dimension(var, m);
   }
   x.space_dim += m;
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

memory_size_type Parma_Polyhedra_Library::Pointset_Powerset< PSET >::external_memory_in_bytes ( ) const

inline

Returns a lower bound to the size in bytes of the memory managed by *this.

Definition at line 285 of file Pointset_Powerset_inlines.hh.

References Parma_Polyhedra_Library::external_memory_in_bytes().

                                                         {
   return Base::external_memory_in_bytes();
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::fold_space_dimensions	(	const Variables_Set &	vars,
		Variable	dest
	)

Folds the space dimensions in vars into dest.

Parameters

vars	The set of Variable objects corresponding to the space dimensions to be folded;
dest	The variable corresponding to the space dimension that is the destination of the folding operation.

Exceptions

std::invalid_argument Thrown if *this is dimension-incompatible with dest or with one of the Variable objects contained in vars. Also thrown if dest is contained in vars.

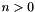If *this has space dimension $n$ , with $n > 0$ , dest has space dimension 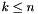$k \leq n$ , vars is a set of variables whose maximum space dimension is also less than or equal to $n$ , and dest is not a member of vars, then the space dimensions corresponding to variables in vars are folded into the $k$ -th space dimension.

Definition at line 361 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::sequence, and Parma_Polyhedra_Library::Pointset_Powerset< PSET >::space_dim.

                                                               {
   Pointset_Powerset& x = *this;
   Variables_Set::size_type num_folded = vars.size();
   if (num_folded > 0) {
     for (Sequence_iterator si = x.sequence.begin(),
            s_end = x.sequence.end(); si != s_end; ++si) {
       si->pointset().fold_space_dimensions(vars, dest);
     }
   }
   x.space_dim -= num_folded;
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::generalized_affine_image	(	Variable	var,
		Relation_Symbol	relsym,
		const Linear_Expression &	expr,
		Coefficient_traits::const_reference	denominator = `Coefficient_one()`
	)

Assigns to *this the image of *this with respect to the generalized affine relation $\mathrm{var}' \relsym \frac{\mathrm{expr}}{\mathrm{denominator}}$ , where $\mathord{\relsym}$ is the relation symbol encoded by relsym.

Parameters

var	The left hand side variable of the generalized affine relation;
relsym	The relation symbol;
expr	The numerator of the right hand side affine expression;
denominator	The denominator of the right hand side affine expression (optional argument with default value 1).

Exceptions

std::invalid_argument Thrown if denominator is zero or if expr and *this are dimension-incompatible or if var is not a space dimension of *this or if *this is a C_Polyhedron and relsym is a strict relation symbol.

Definition at line 445 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::generalized_affine_image(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, and Parma_Polyhedra_Library::Powerset< D >::sequence.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::generalized_affine_image().

                                                                           {
   Pointset_Powerset& x = *this;
   for (Sequence_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     si->pointset().generalized_affine_image(var, relsym, expr, denominator);
     x.reduced = false;
   }
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::generalized_affine_image	(	const Linear_Expression &	lhs,
		Relation_Symbol	relsym,
		const Linear_Expression &	rhs
	)

Assigns to *this the image of *this with respect to the generalized affine relation $\mathrm{lhs}' \relsym \mathrm{rhs}$ , where $\mathord{\relsym}$ is the relation symbol encoded by relsym.

Parameters

lhs	The left hand side affine expression;
relsym	The relation symbol;
rhs	The right hand side affine expression.

Exceptions

std::invalid_argument Thrown if *this is dimension-incompatible with lhs or rhs or if *this is a C_Polyhedron and relsym is a strict relation symbol.

Definition at line 415 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::generalized_affine_image(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, and Parma_Polyhedra_Library::Powerset< D >::sequence.

                                                          {
   Pointset_Powerset& x = *this;
   for (Sequence_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     si->pointset().generalized_affine_image(lhs, relsym, rhs);
     x.reduced = false;
   }
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::generalized_affine_preimage	(	Variable	var,
		Relation_Symbol	relsym,
		const Linear_Expression &	expr,
		Coefficient_traits::const_reference	denominator = `Coefficient_one()`
	)

Assigns to *this the preimage of *this with respect to the generalized affine relation $\mathrm{var}' \relsym \frac{\mathrm{expr}}{\mathrm{denominator}}$ , where $\mathord{\relsym}$ is the relation symbol encoded by relsym.

Parameters

var	The left hand side variable of the generalized affine relation;
relsym	The relation symbol;
expr	The numerator of the right hand side affine expression;
denominator	The denominator of the right hand side affine expression (optional argument with default value 1).

Exceptions

std::invalid_argument Thrown if denominator is zero or if expr and *this are dimension-incompatible or if var is not a space dimension of *this or if *this is a C_Polyhedron and relsym is a strict relation symbol.

Definition at line 461 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::generalized_affine_preimage(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, and Parma_Polyhedra_Library::Powerset< D >::sequence.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::generalized_affine_preimage().

                                            {
   Pointset_Powerset& x = *this;
   for (Sequence_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     si->pointset().generalized_affine_preimage(var, relsym, expr, denominator);
     x.reduced = false;
   }
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::generalized_affine_preimage	(	const Linear_Expression &	lhs,
		Relation_Symbol	relsym,
		const Linear_Expression &	rhs
	)

Assigns to *this the preimage of *this with respect to the generalized affine relation $\mathrm{lhs}' \relsym \mathrm{rhs}$ , where $\mathord{\relsym}$ is the relation symbol encoded by relsym.

Parameters

lhs	The left hand side affine expression;
relsym	The relation symbol;
rhs	The right hand side affine expression.

Exceptions

std::invalid_argument Thrown if *this is dimension-incompatible with lhs or rhs or if *this is a C_Polyhedron and relsym is a strict relation symbol.

Definition at line 430 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::generalized_affine_preimage(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, and Parma_Polyhedra_Library::Powerset< D >::sequence.

                                                             {
   Pointset_Powerset& x = *this;
   for (Sequence_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     si->pointset().generalized_affine_preimage(lhs, relsym, rhs);
     x.reduced = false;
   }
   PPL_ASSERT_HEAVY(x.OK());
 }

template<>

bool Parma_Polyhedra_Library::Pointset_Powerset< PPL::NNC_Polyhedron >::geometrically_covers ( const Pointset_Powerset< PSET > & y ) const

Definition at line 62 of file Pointset_Powerset.cc.

References Parma_Polyhedra_Library::Powerset< D >::begin(), Parma_Polyhedra_Library::Pointset_Ask_Tell< PSET >::check_containment(), and Parma_Polyhedra_Library::Powerset< D >::end().

                                                        {
   const Pointset_Powerset& x = *this;
   for (const_iterator yi = y.begin(), y_end = y.end();
        yi != y_end; ++yi) {
     if (!check_containment(yi->pointset(), x)) {
       return false;
     }
   }
   return true;
 }

template<>

bool Parma_Polyhedra_Library::Pointset_Powerset< PPL::Grid >::geometrically_covers ( const Pointset_Powerset< PSET > & y ) const

Definition at line 307 of file Pointset_Powerset.cc.

References Parma_Polyhedra_Library::Powerset< D >::begin(), and Parma_Polyhedra_Library::Powerset< D >::end().

                                                        {
   const Pointset_Powerset& x = *this;
   for (const_iterator yi = y.begin(), y_end = y.end();
        yi != y_end; ++yi) {
     if (!check_containment(yi->pointset(), x)) {
       return false;
     }
   }
   return true;
 }

template<typename PSET >

bool Parma_Polyhedra_Library::Pointset_Powerset< PSET >::geometrically_covers ( const Pointset_Powerset< PSET > & y ) const

inline

Returns true if and only if *this geometrically covers y, i.e., if any point (in some element) of y is also a point (of some element) of *this.

Exceptions

std::invalid_argument Thrown if *this and y are dimension-incompatible.

Warning: This may be really expensive!

Definition at line 250 of file Pointset_Powerset_inlines.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::geometrically_covers().

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::geometrically_covers(), and Parma_Polyhedra_Library::Pointset_Powerset< PSET >::geometrically_equals().

                                                        {
   // This code is only used when PSET is an abstraction of NNC_Polyhedron.
   const Pointset_Powerset<NNC_Polyhedron> xx(*this);
   const Pointset_Powerset<NNC_Polyhedron> yy(y);
   return xx.geometrically_covers(yy);
 }

template<>

bool Parma_Polyhedra_Library::Pointset_Powerset< NNC_Polyhedron >::geometrically_covers ( const Pointset_Powerset< PSET > & y ) const

template<>

bool Parma_Polyhedra_Library::Pointset_Powerset< Grid >::geometrically_covers ( const Pointset_Powerset< PSET > & y ) const

template<>

bool Parma_Polyhedra_Library::Pointset_Powerset< Grid >::geometrically_equals ( const Pointset_Powerset< PSET > & y ) const

inline

Definition at line 270 of file Pointset_Powerset_inlines.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::geometrically_covers().

                                                        {
   const Pointset_Powerset& x = *this;
   return x.geometrically_covers(y) && y.geometrically_covers(x);
 }

template<>

bool Parma_Polyhedra_Library::Pointset_Powerset< NNC_Polyhedron >::geometrically_equals ( const Pointset_Powerset< PSET > & y ) const

inline

Definition at line 278 of file Pointset_Powerset_inlines.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::geometrically_covers().

                                                        {
   const Pointset_Powerset& x = *this;
   return x.geometrically_covers(y) && y.geometrically_covers(x);
 }

template<typename PSET >

bool Parma_Polyhedra_Library::Pointset_Powerset< PSET >::geometrically_equals ( const Pointset_Powerset< PSET > & y ) const

inline

Returns true if and only if *this is geometrically equal to y, i.e., if (the elements of) *this and y contain the same set of points.

Exceptions

std::invalid_argument Thrown if *this and y are dimension-incompatible.

Warning: This may be really expensive!

Definition at line 260 of file Pointset_Powerset_inlines.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::geometrically_covers().

                                                        {
   // This code is only used when PSET is an abstraction of NNC_Polyhedron.
   const Pointset_Powerset<NNC_Polyhedron> xx(*this);
   const Pointset_Powerset<NNC_Polyhedron> yy(y);
   return xx.geometrically_covers(yy) && yy.geometrically_covers(xx);
 }

template<typename PSET >

int32_t Parma_Polyhedra_Library::Pointset_Powerset< PSET >::hash_code ( ) const

inline

Returns a 32-bit hash code for *this.

If x and y are such that x == y, then x.hash_code() == y.hash_code().

Definition at line 297 of file Pointset_Powerset_inlines.hh.

References Parma_Polyhedra_Library::hash_code_from_dimension().

                                          {
   return hash_code_from_dimension(space_dimension());
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::intersection_assign ( const Pointset_Powerset< PSET > & y )

inline

Assigns to *this the intersection of *this and y.

The result is obtained by intersecting each disjunct in *this with each disjunct in y and collecting all these intersections.

Definition at line 221 of file Pointset_Powerset_inlines.hh.

References Parma_Polyhedra_Library::Powerset< D >::pairwise_apply_assign().

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::intersection_preserving_enlarge_element().

                                                                        {
   Pointset_Powerset& x = *this;
   x.pairwise_apply_assign(y,
                           Det_PSET::lift_op_assign(std::mem_fun_ref(&PSET::intersection_assign)));
 }

template<typename PSET >

bool Parma_Polyhedra_Library::Pointset_Powerset< PSET >::intersection_preserving_enlarge_element ( PSET & dest ) const

private

Assigns to dest a powerset meet-preserving enlargement of itself with respect to *this. If false is returned, then the intersection is empty.

Note: It is assumed that *this and dest are topology-compatible and dimension-compatible.

Definition at line 704 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::intersection_assign(), Parma_Polyhedra_Library::Powerset< D >::sequence, Parma_Polyhedra_Library::Pointset_Powerset< PSET >::space_dimension(), Parma_Polyhedra_Library::swap(), and Parma_Polyhedra_Library::UNIVERSE.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::simplify_using_context_assign().

                                                           {
   // FIXME: this is just an executable specification.
   const Pointset_Powerset& context = *this;
   PPL_ASSERT(context.space_dimension() == dest.space_dimension());
   bool nonempty_intersection = false;
   // TODO: maybe use a *sorted* constraint system?
   PSET enlarged(context.space_dimension(), UNIVERSE);
   for (Sequence_const_iterator si = context.sequence.begin(),
          s_end = context.sequence.end(); si != s_end; ++si) {
     PSET context_i(si->pointset());
     context_i.intersection_assign(enlarged);
     PSET enlarged_i(dest);
     if (enlarged_i.simplify_using_context_assign(context_i)) {
       nonempty_intersection = true;
     }
     // TODO: merge the sorted constraints of `enlarged' and `enlarged_i'?
     enlarged.intersection_assign(enlarged_i);
   }
   swap(dest, enlarged);
   return nonempty_intersection;
 }

template<typename PSET >

bool Parma_Polyhedra_Library::Pointset_Powerset< PSET >::is_bounded ( ) const

Returns true if and only if all elements in *this are bounded.

Definition at line 606 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Powerset< D >::sequence.

                                           {
   const Pointset_Powerset& x = *this;
   for (Sequence_const_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     if (!si->pointset().is_bounded()) {
       return false;
     }
   }
   return true;
 }

template<typename PSET >

template<typename Cert >

bool Parma_Polyhedra_Library::Pointset_Powerset< PSET >::is_cert_multiset_stabilizing ( const std::map< Cert, size_type, typename Cert::Compare > & y_cert_ms ) const

private

Returns true if and only if the current set of disjuncts is stabilizing with respect to the multiset of certificates y_cert_ms.

Definition at line 1377 of file Pointset_Powerset_templates.hh.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::BHZ03_widening_assign().

                                                                      {
   typedef std::map<Cert, size_type, typename Cert::Compare> Cert_Multiset;
   Cert_Multiset x_cert_ms;
   collect_certificates(x_cert_ms);
   typename Cert_Multiset::const_iterator xi = x_cert_ms.begin();
   typename Cert_Multiset::const_iterator x_cert_ms_end = x_cert_ms.end();
   typename Cert_Multiset::const_iterator yi = y_cert_ms.begin();
   typename Cert_Multiset::const_iterator y_cert_ms_end = y_cert_ms.end();
   while (xi != x_cert_ms_end && yi != y_cert_ms_end) {
     const Cert& xi_cert = xi->first;
     const Cert& yi_cert = yi->first;
     switch (xi_cert.compare(yi_cert)) {
     case 0:
       // xi_cert == yi_cert: check the number of multiset occurrences.
       {
         const size_type& xi_count = xi->second;
         const size_type& yi_count = yi->second;
         if (xi_count == yi_count) {
           // Same number of occurrences: compare the next pair.
           ++xi;
           ++yi;
         }
         else {
           // Different number of occurrences: can decide ordering.
           return xi_count < yi_count;
         }
         break;
       }
     case 1:
       // xi_cert > yi_cert: it is not stabilizing.
       return false;
 
     case -1:
       // xi_cert < yi_cert: it is stabilizing.
       return true;
     }
   }
   // Here xi == x_cert_ms_end or yi == y_cert_ms_end.
   // Stabilization is achieved if `y_cert_ms' still has other elements.
   return yi != y_cert_ms_end;
 }

template<typename PSET >

bool Parma_Polyhedra_Library::Pointset_Powerset< PSET >::is_discrete ( ) const

Returns true if and only if *this is discrete.

Definition at line 577 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Powerset< D >::sequence.

                                            {
   const Pointset_Powerset& x = *this;
   for (Sequence_const_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     if (!si->pointset().is_discrete()) {
       return false;
     }
   }
   return true;
 }

template<typename PSET >

bool Parma_Polyhedra_Library::Pointset_Powerset< PSET >::is_disjoint_from ( const Pointset_Powerset< PSET > & y ) const

Returns true if and only if *this and y are disjoint.

Exceptions

std::invalid_argument Thrown if x and y are topology-incompatible or dimension-incompatible.

Definition at line 647 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Powerset< D >::sequence.

                                                                           {
   const Pointset_Powerset& x = *this;
   for (Sequence_const_iterator si = x.sequence.begin(),
          x_s_end = x.sequence.end(); si != x_s_end; ++si) {
     const PSET& pi = si->pointset();
     for (Sequence_const_iterator sj = y.sequence.begin(),
            y_s_end = y.sequence.end(); sj != y_s_end; ++sj) {
       const PSET& pj = sj->pointset();
       if (!pi.is_disjoint_from(pj)) {
         return false;
       }
     }
   }
   return true;
 }

template<typename PSET >

bool Parma_Polyhedra_Library::Pointset_Powerset< PSET >::is_empty ( ) const

Returns true if and only if *this is an empty powerset.

Definition at line 564 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Powerset< D >::sequence.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::constrains(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::maximize(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::minimize(), and Parma_Polyhedra_Library::Pointset_Powerset< PSET >::simplify_using_context_assign().

                                         {
   const Pointset_Powerset& x = *this;
   for (Sequence_const_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     if (!si->pointset().is_empty()) {
       return false;
     }
   }
   return true;
 }

template<typename PSET >

bool Parma_Polyhedra_Library::Pointset_Powerset< PSET >::is_topologically_closed ( ) const

Returns true if and only if all the disjuncts in *this are topologically closed.

Definition at line 590 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Powerset< D >::omega_reduce(), and Parma_Polyhedra_Library::Powerset< D >::sequence.

                                                        {
   const Pointset_Powerset& x = *this;
   // The powerset must be omega-reduced before checking
   // topological closure.
   x.omega_reduce();
   for (Sequence_const_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     if (!si->pointset().is_topologically_closed()) {
       return false;
     }
   }
   return true;
 }

template<typename PSET >

bool Parma_Polyhedra_Library::Pointset_Powerset< PSET >::is_universe ( ) const

Returns true if and only if *this is the top element of the powerset lattice.

Definition at line 539 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Powerset< D >::begin(), Parma_Polyhedra_Library::Powerset< D >::end(), Parma_Polyhedra_Library::Powerset< D >::is_omega_reduced(), Parma_Polyhedra_Library::Powerset< D >::size(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::space_dimension(), Parma_Polyhedra_Library::swap(), Parma_Polyhedra_Library::UNIVERSE, and Parma_Polyhedra_Library::Implementation::Boxes::universe.

                                            {
   const Pointset_Powerset& x = *this;
   // Exploit omega-reduction, if already computed.
   if (x.is_omega_reduced()) {
     return x.size() == 1 && x.begin()->pointset().is_universe();
   }
 
   // A powerset is universe iff one of its disjuncts is.
   for (const_iterator x_i = x.begin(), x_end = x.end();
        x_i != x_end; ++x_i) {
     if (x_i->pointset().is_universe()) {
       // Speculative omega-reduction, if it is worth.
       if (x.size() > 1) {
         Pointset_Powerset<PSET> universe(x.space_dimension(), UNIVERSE);
         Pointset_Powerset& xx = const_cast<Pointset_Powerset&>(x);
         swap(xx, universe);
       }
       return true;
     }
   }
   return false;
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::m_swap ( Pointset_Powerset< PSET > & y )

inline

Swaps *this with y.

Definition at line 202 of file Pointset_Powerset_inlines.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::space_dim, and Parma_Polyhedra_Library::swap().

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::swap().

                                                     {
   Pointset_Powerset& x = *this;
   x.Base::m_swap(y);
   using std::swap;
   swap(x.space_dim, y.space_dim);
 }

template<typename PSET >

template<typename Partial_Function >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::map_space_dimensions ( const Partial_Function & pfunc )

Remaps the dimensions of the vector space according to a partial function.

Definition at line 322 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Powerset< D >::is_bottom(), Parma_Polyhedra_Library::Partial_Function::maps(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, Parma_Polyhedra_Library::Powerset< D >::sequence, and Parma_Polyhedra_Library::Pointset_Powerset< PSET >::space_dim.

                                                                            {
   Pointset_Powerset& x = *this;
   if (x.is_bottom()) {
     dimension_type n = 0;
     for (dimension_type i = x.space_dim; i-- > 0; ) {
       dimension_type new_i;
       if (pfunc.maps(i, new_i)) {
         ++n;
       }
     }
     x.space_dim = n;
   }
   else {
     Sequence_iterator s_begin = x.sequence.begin();
     for (Sequence_iterator si = s_begin,
            s_end = x.sequence.end(); si != s_end; ++si) {
       si->pointset().map_space_dimensions(pfunc);
     }
     x.space_dim = s_begin->pointset().space_dimension();
     x.reduced = false;
   }
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

dimension_type Parma_Polyhedra_Library::Pointset_Powerset< PSET >::max_space_dimension ( )

inlinestatic

Returns the maximum space dimension a Pointset_Powerset<PSET> can handle.

Definition at line 48 of file Pointset_Powerset_inlines.hh.

References Parma_Polyhedra_Library::max_space_dimension().

                                              {
   return PSET::max_space_dimension();
 }

template<typename PSET >

bool Parma_Polyhedra_Library::Pointset_Powerset< PSET >::maximize	(	const Linear_Expression &	expr,
		Coefficient &	sup_n,
		Coefficient &	sup_d,
		bool &	maximum
	)		const

Returns true if and only if *this is not empty and expr is bounded from above in *this, in which case the supremum value is computed.

Parameters

expr	The linear expression to be maximized subject to `*this`;
sup_n	The numerator of the supremum value;
sup_d	The denominator of the supremum value;
maximum	`true` if and only if the supremum is also the maximum value.

Exceptions

std::invalid_argument Thrown if expr and *this are dimension-incompatible.

If *this is empty or expr is not bounded from above, false is returned and sup_n, sup_d and maximum are left untouched.

Definition at line 939 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::is_empty(), Parma_Polyhedra_Library::Powerset< D >::omega_reduce(), PPL_DIRTY_TEMP_COEFFICIENT, and Parma_Polyhedra_Library::Powerset< D >::sequence.

                                                        {
   const Pointset_Powerset& x = *this;
   x.omega_reduce();
   if (x.is_empty()) {
     return false;
   }
 
   bool first = true;
 
   PPL_DIRTY_TEMP_COEFFICIENT(best_sup_n);
   PPL_DIRTY_TEMP_COEFFICIENT(best_sup_d);
   best_sup_n = 0;
   best_sup_d = 1;
   bool best_max = false;
 
   PPL_DIRTY_TEMP_COEFFICIENT(iter_sup_n);
   PPL_DIRTY_TEMP_COEFFICIENT(iter_sup_d);
   iter_sup_n = 0;
   iter_sup_d = 1;
   bool iter_max = false;
 
   PPL_DIRTY_TEMP_COEFFICIENT(tmp);
 
   for (Sequence_const_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     if (!si->pointset().maximize(expr, iter_sup_n, iter_sup_d, iter_max)) {
       return false;
     }
     else
       if (first) {
         first = false;
         best_sup_n = iter_sup_n;
         best_sup_d = iter_sup_d;
         best_max = iter_max;
       }
       else {
         tmp = (best_sup_n * iter_sup_d) - (iter_sup_n * best_sup_d);
         if (tmp < 0) {
           best_sup_n = iter_sup_n;
           best_sup_d = iter_sup_d;
           best_max = iter_max;
         }
         else if (tmp == 0) {
           best_max = (best_max || iter_max);
         }
       }
   }
   sup_n = best_sup_n;
   sup_d = best_sup_d;
   maximum = best_max;
   return true;
 }

template<typename PSET >

bool Parma_Polyhedra_Library::Pointset_Powerset< PSET >::maximize	(	const Linear_Expression &	expr,
		Coefficient &	sup_n,
		Coefficient &	sup_d,
		bool &	maximum,
		Generator &	g
	)		const

Returns true if and only if *this is not empty and expr is bounded from above in *this, in which case the supremum value and a point where expr reaches it are computed.

Parameters

expr	The linear expression to be maximized subject to `*this`;
sup_n	The numerator of the supremum value;
sup_d	The denominator of the supremum value;
maximum	`true` if and only if the supremum is also the maximum value;
g	When maximization succeeds, will be assigned the point or closure point where `expr` reaches its supremum value.

Exceptions

std::invalid_argument Thrown if expr and *this are dimension-incompatible.

If *this is empty or expr is not bounded from above, false is returned and sup_n, sup_d, maximum and g are left untouched.

Definition at line 997 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::is_empty(), Parma_Polyhedra_Library::Powerset< D >::omega_reduce(), PPL_DIRTY_TEMP_COEFFICIENT, and Parma_Polyhedra_Library::Powerset< D >::sequence.

                                                       {
   const Pointset_Powerset& x = *this;
   x.omega_reduce();
   if (x.is_empty()) {
     return false;
   }
 
   bool first = true;
 
   PPL_DIRTY_TEMP_COEFFICIENT(best_sup_n);
   PPL_DIRTY_TEMP_COEFFICIENT(best_sup_d);
   best_sup_n = 0;
   best_sup_d = 1;
   bool best_max = false;
   Generator best_g = point();
 
   PPL_DIRTY_TEMP_COEFFICIENT(iter_sup_n);
   PPL_DIRTY_TEMP_COEFFICIENT(iter_sup_d);
   iter_sup_n = 0;
   iter_sup_d = 1;
   bool iter_max = false;
   Generator iter_g = point();
 
   PPL_DIRTY_TEMP_COEFFICIENT(tmp);
 
   for (Sequence_const_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     if (!si->pointset().maximize(expr,
                                  iter_sup_n, iter_sup_d, iter_max, iter_g)) {
       return false;
     }
     else {
       if (first) {
         first = false;
         best_sup_n = iter_sup_n;
         best_sup_d = iter_sup_d;
         best_max = iter_max;
         best_g = iter_g;
       }
       else {
         tmp = (best_sup_n * iter_sup_d) - (iter_sup_n * best_sup_d);
         if (tmp < 0) {
           best_sup_n = iter_sup_n;
           best_sup_d = iter_sup_d;
           best_max = iter_max;
           best_g = iter_g;
         }
         else if (tmp == 0) {
           best_max = (best_max || iter_max);
           best_g = iter_g;
         }
       }
     }
   }
   sup_n = best_sup_n;
   sup_d = best_sup_d;
   maximum = best_max;
   g = best_g;
   return true;
 }

template<typename PSET >

bool Parma_Polyhedra_Library::Pointset_Powerset< PSET >::minimize	(	const Linear_Expression &	expr,
		Coefficient &	inf_n,
		Coefficient &	inf_d,
		bool &	minimum
	)		const

Returns true if and only if *this is not empty and expr is bounded from below in *this, in which case the infimum value is computed.

Parameters

expr	The linear expression to be minimized subject to `*this`;
inf_n	The numerator of the infimum value;
inf_d	The denominator of the infimum value;
minimum	`true` if and only if the infimum is also the minimum value.

Exceptions

std::invalid_argument Thrown if expr and *this are dimension-incompatible.

If *this is empty or expr is not bounded from below, false is returned and inf_n, inf_d and minimum are left untouched.

Definition at line 1064 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::is_empty(), Parma_Polyhedra_Library::Powerset< D >::omega_reduce(), PPL_DIRTY_TEMP_COEFFICIENT, and Parma_Polyhedra_Library::Powerset< D >::sequence.

                                                        {
   const Pointset_Powerset& x = *this;
   x.omega_reduce();
   if (x.is_empty()) {
     return false;
   }
 
   bool first = true;
 
   PPL_DIRTY_TEMP_COEFFICIENT(best_inf_n);
   PPL_DIRTY_TEMP_COEFFICIENT(best_inf_d);
   best_inf_n = 0;
   best_inf_d = 1;
   bool best_min = false;
 
   PPL_DIRTY_TEMP_COEFFICIENT(iter_inf_n);
   PPL_DIRTY_TEMP_COEFFICIENT(iter_inf_d);
   iter_inf_n = 0;
   iter_inf_d = 1;
   bool iter_min = false;
 
   PPL_DIRTY_TEMP_COEFFICIENT(tmp);
 
   for (Sequence_const_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     if (!si->pointset().minimize(expr, iter_inf_n, iter_inf_d, iter_min)) {
       return false;
     }
     else {
       if (first) {
         first = false;
         best_inf_n = iter_inf_n;
         best_inf_d = iter_inf_d;
         best_min = iter_min;
       }
       else {
         tmp = (best_inf_n * iter_inf_d) - (iter_inf_n * best_inf_d);
         if (tmp > 0) {
           best_inf_n = iter_inf_n;
           best_inf_d = iter_inf_d;
           best_min = iter_min;
         }
         else if (tmp == 0) {
           best_min = (best_min || iter_min);
         }
       }
     }
   }
   inf_n = best_inf_n;
   inf_d = best_inf_d;
   minimum = best_min;
   return true;
 }

template<typename PSET >

bool Parma_Polyhedra_Library::Pointset_Powerset< PSET >::minimize	(	const Linear_Expression &	expr,
		Coefficient &	inf_n,
		Coefficient &	inf_d,
		bool &	minimum,
		Generator &	g
	)		const

Returns true if and only if *this is not empty and expr is bounded from below in *this, in which case the infimum value and a point where expr reaches it are computed.

Parameters

expr	The linear expression to be minimized subject to `*this`;
inf_n	The numerator of the infimum value;
inf_d	The denominator of the infimum value;
minimum	`true` if and only if the infimum is also the minimum value;
g	When minimization succeeds, will be assigned a point or closure point where `expr` reaches its infimum value.

Exceptions

std::invalid_argument Thrown if expr and *this are dimension-incompatible.

If *this is empty or expr is not bounded from below, false is returned and inf_n, inf_d, minimum and g are left untouched.

Definition at line 1123 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::is_empty(), Parma_Polyhedra_Library::Powerset< D >::omega_reduce(), PPL_DIRTY_TEMP_COEFFICIENT, and Parma_Polyhedra_Library::Powerset< D >::sequence.

                                                       {
   const Pointset_Powerset& x = *this;
   x.omega_reduce();
   if (x.is_empty()) {
     return false;
   }
 
   bool first = true;
 
   PPL_DIRTY_TEMP_COEFFICIENT(best_inf_n);
   PPL_DIRTY_TEMP_COEFFICIENT(best_inf_d);
   best_inf_n = 0;
   best_inf_d = 1;
   bool best_min = false;
   Generator best_g = point();
 
   PPL_DIRTY_TEMP_COEFFICIENT(iter_inf_n);
   PPL_DIRTY_TEMP_COEFFICIENT(iter_inf_d);
   iter_inf_n = 0;
   iter_inf_d = 1;
   bool iter_min = false;
   Generator iter_g = point();
 
   PPL_DIRTY_TEMP_COEFFICIENT(tmp);
 
   for (Sequence_const_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     if (!si->pointset().minimize(expr,
                                  iter_inf_n, iter_inf_d, iter_min, iter_g)) {
       return false;
     }
     else {
       if (first) {
         first = false;
         best_inf_n = iter_inf_n;
         best_inf_d = iter_inf_d;
         best_min = iter_min;
         best_g = iter_g;
       }
       else {
         tmp = (best_inf_n * iter_inf_d) - (iter_inf_n * best_inf_d);
         if (tmp > 0) {
           best_inf_n = iter_inf_n;
           best_inf_d = iter_inf_d;
           best_min = iter_min;
           best_g = iter_g;
         }
         else if (tmp == 0) {
           best_min = (best_min || iter_min);
           best_g = iter_g;
         }
       }
     }
   }
   inf_n = best_inf_n;
   inf_d = best_inf_d;
   minimum = best_min;
   g = best_g;
   return true;
 }

template<typename PSET >

bool Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK ( ) const

Checks if all the invariants are satisfied.

Definition at line 1599 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Powerset< D >::begin(), Parma_Polyhedra_Library::Powerset< D >::end(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::space_dim, and Parma_Polyhedra_Library::Pointset_Powerset< PSET >::space_dimension().

                                   {
   const Pointset_Powerset& x = *this;
   for (const_iterator xi = x.begin(), x_end = x.end(); xi != x_end; ++xi) {
     const PSET& pi = xi->pointset();
     if (pi.space_dimension() != x.space_dim) {
 #ifndef NDEBUG
       std::cerr << "Space dimension mismatch: is " << pi.space_dimension()
                 << " in an element of the sequence,\nshould be "
                 << x.space_dim << "."
                 << std::endl;
 #endif
       return false;
     }
   }
   return x.Base::OK();
 }

template<typename PSET>

template<typename QH >

Pointset_Powerset<PSET>& Parma_Polyhedra_Library::Pointset_Powerset< PSET >::operator= ( const Pointset_Powerset< QH > & y )

inline

Definition at line 212 of file Pointset_Powerset_inlines.hh.

References Parma_Polyhedra_Library::swap().

                                                                  {
   Pointset_Powerset& x = *this;
   Pointset_Powerset<PSET> ps(y);
   swap(x, ps);
   return x;
 }

template<typename PSET >

Pointset_Powerset< PSET > & Parma_Polyhedra_Library::Pointset_Powerset< PSET >::operator= ( const Pointset_Powerset< PSET > & y )

inline

The assignment operator (*this and y can be dimension-incompatible).

Definition at line 193 of file Pointset_Powerset_inlines.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::space_dim.

                                                              {
   Pointset_Powerset& x = *this;
   x.Base::operator=(y);
   x.space_dim = y.space_dim;
   return x;
 }

template<typename PSET>

template<typename QH >

Pointset_Powerset& Parma_Polyhedra_Library::Pointset_Powerset< PSET >::operator= ( const Pointset_Powerset< QH > & y )

Conversion assignment: the type QH of the disjuncts in the source powerset is different from PSET (*this and y can be dimension-incompatible).

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::pairwise_reduce ( )

Assign to *this the result of (recursively) merging together the pairs of disjuncts whose upper-bound is the same as their set-theoretical union.

On exit, for all the pairs $\cP$ , $\cQ$ of different disjuncts in *this, we have 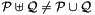$\cP \uplus \cQ \neq \cP \union \cQ$ .

Definition at line 1222 of file Pointset_Powerset_templates.hh.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::BGP99_extrapolation_assign(), and Parma_Polyhedra_Library::Pointset_Powerset< PSET >::BHZ03_widening_assign().

                                          {
   Pointset_Powerset& x = *this;
   // It is wise to omega-reduce before pairwise-reducing.
   x.omega_reduce();
 
   size_type n = x.size();
   size_type deleted;
   do {
     Pointset_Powerset new_x(x.space_dim, EMPTY);
     std::deque<bool> marked(n, false);
     deleted = 0;
     Sequence_iterator s_begin = x.sequence.begin();
     Sequence_iterator s_end = x.sequence.end();
     unsigned si_index = 0;
     for (Sequence_iterator si = s_begin; si != s_end; ++si, ++si_index) {
       if (marked[si_index]) {
         continue;
       }
       PSET& pi = si->pointset();
       Sequence_const_iterator sj = si;
       unsigned sj_index = si_index;
       for (++sj, ++sj_index; sj != s_end; ++sj, ++sj_index) {
         if (marked[sj_index]) {
           continue;
         }
         const PSET& pj = sj->pointset();
         if (pi.upper_bound_assign_if_exact(pj)) {
           marked[si_index] = true;
           marked[sj_index] = true;
           new_x.add_non_bottom_disjunct_preserve_reduction(pi);
           ++deleted;
           goto next;
         }
       }
     next:
       ;
     }
     iterator new_x_begin = new_x.begin();
     iterator new_x_end = new_x.end();
     unsigned xi_index = 0;
     for (const_iterator xi = x.begin(),
            x_end = x.end(); xi != x_end; ++xi, ++xi_index) {
       if (!marked[xi_index]) {
         new_x_begin
           = new_x.add_non_bottom_disjunct_preserve_reduction(*xi,
                                                              new_x_begin,
                                                              new_x_end);
       }
     }
     using std::swap;
     swap(x.sequence, new_x.sequence);
     n -= deleted;
   } while (deleted > 0);
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET>

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::print ( ) const

Prints *this to std::cerr using operator<<.

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::refine_with_congruence ( const Congruence & cg )

Use the congruence cg to refine *this.

Parameters

cg	The congruence to be used for refinement.

Exceptions

std::invalid_argument Thrown if *this and cg are dimension-incompatible.

Definition at line 205 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, Parma_Polyhedra_Library::Pointset_Powerset< PSET >::refine_with_congruence(), and Parma_Polyhedra_Library::Powerset< D >::sequence.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::refine_with_congruence().

                                                                     {
   Pointset_Powerset& x = *this;
   for (Sequence_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     si->pointset().refine_with_congruence(cg);
   }
   x.reduced = false;
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::refine_with_congruences ( const Congruence_System & cgs )

Use the congruences in cgs to refine *this.

Parameters

cgs	The congruences to be used for refinement.

Exceptions

std::invalid_argument Thrown if *this and cgs are dimension-incompatible.

Definition at line 229 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, Parma_Polyhedra_Library::Pointset_Powerset< PSET >::refine_with_congruences(), and Parma_Polyhedra_Library::Powerset< D >::sequence.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::refine_with_congruences().

                                                                              {
   Pointset_Powerset& x = *this;
   for (Sequence_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     si->pointset().refine_with_congruences(cgs);
   }
   x.reduced = false;
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::refine_with_constraint ( const Constraint & c )

Use the constraint c to refine *this.

Parameters

c	The constraint to be used for refinement.

Exceptions

std::invalid_argument Thrown if *this and c are dimension-incompatible.

Definition at line 157 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, Parma_Polyhedra_Library::Pointset_Powerset< PSET >::refine_with_constraint(), and Parma_Polyhedra_Library::Powerset< D >::sequence.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::refine_with_constraint().

                                                                    {
   Pointset_Powerset& x = *this;
   for (Sequence_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     si->pointset().refine_with_constraint(c);
   }
   x.reduced = false;
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::refine_with_constraints ( const Constraint_System & cs )

Use the constraints in cs to refine *this.

Parameters

cs	The constraints to be used for refinement.

Exceptions

std::invalid_argument Thrown if *this and cs are dimension-incompatible.

Definition at line 181 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, Parma_Polyhedra_Library::Pointset_Powerset< PSET >::refine_with_constraints(), and Parma_Polyhedra_Library::Powerset< D >::sequence.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::refine_with_constraints().

                                                                             {
   Pointset_Powerset& x = *this;
   for (Sequence_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     si->pointset().refine_with_constraints(cs);
   }
   x.reduced = false;
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

Poly_Con_Relation Parma_Polyhedra_Library::Pointset_Powerset< PSET >::relation_with ( const Constraint & c ) const

inline

Returns the relations holding between the powerset *this and the constraint c.

Exceptions

std::invalid_argument Thrown if *this and constraint c are dimension-incompatible.

Definition at line 237 of file Pointset_Powerset_inlines.hh.

                                                                 {
   return relation_with_aux(c);
 }

template<typename PSET >

Poly_Gen_Relation Parma_Polyhedra_Library::Pointset_Powerset< PSET >::relation_with ( const Generator & g ) const

Returns the relations holding between the powerset *this and the generator g.

Exceptions

std::invalid_argument Thrown if *this and generator g are dimension-incompatible.

Definition at line 893 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Poly_Gen_Relation::implies(), Parma_Polyhedra_Library::Poly_Gen_Relation::nothing(), Parma_Polyhedra_Library::Powerset< D >::sequence, and Parma_Polyhedra_Library::Poly_Gen_Relation::subsumes().

                                                                {
   const Pointset_Powerset& x = *this;
 
   for (Sequence_const_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     Poly_Gen_Relation relation_i = si->pointset().relation_with(g);
     if (relation_i.implies(Poly_Gen_Relation::subsumes())) {
       return Poly_Gen_Relation::subsumes();
     }
   }
 
   return Poly_Gen_Relation::nothing();
 }

template<typename PSET >

Poly_Con_Relation Parma_Polyhedra_Library::Pointset_Powerset< PSET >::relation_with ( const Congruence & cg ) const

inline

Returns the relations holding between the powerset *this and the congruence c.

Exceptions

std::invalid_argument Thrown if *this and congruence c are dimension-incompatible.

Definition at line 243 of file Pointset_Powerset_inlines.hh.

                                                                  {
   return relation_with_aux(cg);
 }

template<typename PSET >

template<typename Cons_or_Congr >

Poly_Con_Relation Parma_Polyhedra_Library::Pointset_Powerset< PSET >::relation_with_aux ( const Cons_or_Congr & c ) const

private

Template helper: common implementation for constraints and congruences.

Definition at line 834 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Poly_Con_Relation::implies(), Parma_Polyhedra_Library::Poly_Con_Relation::is_disjoint(), Parma_Polyhedra_Library::Poly_Con_Relation::is_included(), Parma_Polyhedra_Library::Poly_Con_Relation::nothing(), Parma_Polyhedra_Library::Poly_Con_Relation::saturates(), Parma_Polyhedra_Library::Powerset< D >::sequence, and Parma_Polyhedra_Library::Poly_Con_Relation::strictly_intersects().

                                                                        {
   const Pointset_Powerset& x = *this;
 
   /* *this is included in c if every disjunct is included in c */
   bool is_included = true;
   /* *this is disjoint with c if every disjunct is disjoint with c */
   bool is_disjoint = true;
   /* *this strictly_intersects with c if:
        - some disjunct strictly intersects with c
      or
        - there exists two disjoints d1 and d2
          such that d1 is included in c and d2 is disjoint with c
   */
   bool is_strictly_intersecting = false;
   bool included_once = false;
   bool disjoint_once = false;
   /* *this saturates c if all disjuncts saturate c */
   bool saturates = true;
   for (Sequence_const_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     Poly_Con_Relation relation_i = si->pointset().relation_with(c);
     if (relation_i.implies(Poly_Con_Relation::is_included())) {
       included_once = true;
     }
     else {
       is_included = false;
     }
     if (relation_i.implies(Poly_Con_Relation::is_disjoint())) {
       disjoint_once = true;
     }
     else {
       is_disjoint = false;
     }
     if (relation_i.implies(Poly_Con_Relation::strictly_intersects())) {
       is_strictly_intersecting = true;
     }
     if (!relation_i.implies(Poly_Con_Relation::saturates())) {
       saturates = false;
     }
   }
 
   Poly_Con_Relation result = Poly_Con_Relation::nothing();
   if (is_included) {
     result = result && Poly_Con_Relation::is_included();
   }
   if (is_disjoint) {
     result = result && Poly_Con_Relation::is_disjoint();
   }
   if (is_strictly_intersecting || (included_once && disjoint_once)) {
     result = result && Poly_Con_Relation::strictly_intersects();
   }
   if (saturates) {
     result = result && Poly_Con_Relation::saturates();
   }
   return result;
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::remove_higher_space_dimensions ( dimension_type new_dimension )

Removes the higher space dimensions so that the resulting space will have dimension new_dimension.

Exceptions

std::invalid_argument Thrown if new_dimensions is greater than the space dimension of *this.

Definition at line 306 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, Parma_Polyhedra_Library::Pointset_Powerset< PSET >::remove_higher_space_dimensions(), Parma_Polyhedra_Library::Powerset< D >::sequence, and Parma_Polyhedra_Library::Pointset_Powerset< PSET >::space_dim.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::remove_higher_space_dimensions().

                                                              {
   Pointset_Powerset& x = *this;
   if (new_dimension < x.space_dim) {
     for (Sequence_iterator si = x.sequence.begin(),
            s_end = x.sequence.end(); si != s_end; ++si) {
       si->pointset().remove_higher_space_dimensions(new_dimension);
       x.reduced = false;
     }
     x.space_dim = new_dimension;
     PPL_ASSERT_HEAVY(x.OK());
   }
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::remove_space_dimensions ( const Variables_Set & vars )

Removes all the specified space dimensions.

Parameters

vars	The set of Variable objects corresponding to the space dimensions to be removed.

Exceptions

std::invalid_argument Thrown if *this is dimension-incompatible with one of the Variable objects contained in vars.

Definition at line 289 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, Parma_Polyhedra_Library::Powerset< D >::sequence, and Parma_Polyhedra_Library::Pointset_Powerset< PSET >::space_dim.

                                                                           {
   Pointset_Powerset& x = *this;
   Variables_Set::size_type num_removed = vars.size();
   if (num_removed > 0) {
     for (Sequence_iterator si = x.sequence.begin(),
            s_end = x.sequence.end(); si != s_end; ++si) {
       si->pointset().remove_space_dimensions(vars);
       x.reduced = false;
     }
     x.space_dim -= num_removed;
     PPL_ASSERT_HEAVY(x.OK());
   }
 }

template<typename PSET >

bool Parma_Polyhedra_Library::Pointset_Powerset< PSET >::simplify_using_context_assign ( const Pointset_Powerset< PSET > & y )

Assigns to *this a meet-preserving simplification of *this with respect to y. If false is returned, then the intersection is empty.

Exceptions

std::invalid_argument Thrown if *this and y are topology-incompatible or dimension-incompatible.

Definition at line 729 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::intersection_preserving_enlarge_element(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::is_empty(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::omega_reduce(), Parma_Polyhedra_Library::Powerset< D >::reduced, Parma_Polyhedra_Library::Powerset< D >::sequence, and Parma_Polyhedra_Library::Powerset< D >::size().

                                                           {
   Pointset_Powerset& x = *this;
 
   // Omega reduction is required.
   // TODO: check whether it would be more efficient to Omega-reduce x
   // during the simplification process: when examining *si, we check
   // if it has been made redundant by any of the elements preceding it
   // (which have been already simplified).
   x.omega_reduce();
   if (x.is_empty()) {
     return false;
   }
   y.omega_reduce();
   if (y.is_empty()) {
     x = y;
     return false;
   }
 
   if (y.size() == 1) {
     // More efficient, special handling of the singleton context case.
     const PSET& y_i = y.sequence.begin()->pointset();
     for (Sequence_iterator si = x.sequence.begin(),
            s_end = x.sequence.end(); si != s_end; ) {
       PSET& x_i = si->pointset();
       if (x_i.simplify_using_context_assign(y_i)) {
         ++si;
       }
       else {
         // Intersection is empty: drop the disjunct.
         si = x.sequence.erase(si);
       }
     }
   }
   else {
     // The context is not a singleton.
     for (Sequence_iterator si = x.sequence.begin(),
            s_end = x.sequence.end(); si != s_end; ) {
       if (y.intersection_preserving_enlarge_element(si->pointset())) {
         ++si;
       }
       else {
         // Intersection with `*si' is empty: drop the disjunct.
         si = x.sequence.erase(si);
       }
     }
   }
   x.reduced = false;
   PPL_ASSERT_HEAVY(x.OK());
   return !x.sequence.empty();
 }

template<typename PSET >

dimension_type Parma_Polyhedra_Library::Pointset_Powerset< PSET >::space_dimension ( ) const

inline

Returns the dimension of the vector space enclosing *this.

Definition at line 42 of file Pointset_Powerset_inlines.hh.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::add_disjunct(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::constrains(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::intersection_preserving_enlarge_element(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::is_universe(), and Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK().

                                                {
   return space_dim;
 }

template<typename PSET >

bool Parma_Polyhedra_Library::Pointset_Powerset< PSET >::strictly_contains ( const Pointset_Powerset< PSET > & y ) const

Returns true if and only if each disjunct of y is strictly contained in a disjunct of *this.

Exceptions

std::invalid_argument Thrown if *this and y are topology-incompatible or dimension-incompatible.

Definition at line 806 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Powerset< D >::omega_reduce(), and Parma_Polyhedra_Library::Powerset< D >::sequence.

                                                                            {
   /* omega reduction ensures that a disjunct of y cannot be strictly
      contained in one disjunct and also contained but not strictly
      contained in another disjunct of *this */
   const Pointset_Powerset& x = *this;
   x.omega_reduce();
   for (Sequence_const_iterator si = y.sequence.begin(),
          y_s_end = y.sequence.end(); si != y_s_end; ++si) {
     const PSET& pi = si->pointset();
     bool pi_is_strictly_contained = false;
     for (Sequence_const_iterator sj = x.sequence.begin(),
            x_s_end = x.sequence.end();
          (sj != x_s_end && !pi_is_strictly_contained); ++sj) {
       const PSET& pj = sj->pointset();
       if (pj.strictly_contains(pi)) {
         pi_is_strictly_contained = true;
       }
     }
     if (!pi_is_strictly_contained) {
       return false;
     }
   }
   return true;
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::time_elapse_assign ( const Pointset_Powerset< PSET > & y )

inline

Assigns to *this the result of computing the time-elapse between *this and y.

The result is obtained by computing the pairwise time elapse of each disjunct in *this with each disjunct in y.

Definition at line 229 of file Pointset_Powerset_inlines.hh.

References Parma_Polyhedra_Library::Powerset< D >::pairwise_apply_assign().

                                                                       {
   Pointset_Powerset& x = *this;
   x.pairwise_apply_assign(y,
                           Det_PSET::lift_op_assign(std::mem_fun_ref(&PSET::time_elapse_assign)));
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::topological_closure_assign ( )

Assigns to *this its topological closure.

Definition at line 692 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::sequence, and Parma_Polyhedra_Library::Pointset_Powerset< PSET >::topological_closure_assign().

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::topological_closure_assign().

                                                     {
   Pointset_Powerset& x = *this;
   for (Sequence_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     si->pointset().topological_closure_assign();
   }
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

memory_size_type Parma_Polyhedra_Library::Pointset_Powerset< PSET >::total_memory_in_bytes ( ) const

inline

Returns a lower bound to the total size in bytes of the memory occupied by *this.

Definition at line 291 of file Pointset_Powerset_inlines.hh.

References Parma_Polyhedra_Library::external_memory_in_bytes().

                                                      {
   return sizeof(*this) + external_memory_in_bytes();
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::unconstrain ( Variable var )

Computes the cylindrification of *this with respect to space dimension var, assigning the result to *this.

Parameters

var	The space dimension that will be unconstrained.

Exceptions

std::invalid_argument Thrown if var is not a space dimension of *this.

Definition at line 241 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, Parma_Polyhedra_Library::Powerset< D >::sequence, and Parma_Polyhedra_Library::Pointset_Powerset< PSET >::unconstrain().

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::unconstrain().

                                                        {
   Pointset_Powerset& x = *this;
   for (Sequence_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     si->pointset().unconstrain(var);
     x.reduced = false;
   }
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::unconstrain ( const Variables_Set & vars )

Computes the cylindrification of *this with respect to the set of space dimensions vars, assigning the result to *this.

Parameters

vars	The set of space dimension that will be unconstrained.

Exceptions

std::invalid_argument Thrown if *this is dimension-incompatible with one of the Variable objects contained in vars.

Definition at line 253 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, Parma_Polyhedra_Library::Powerset< D >::sequence, and Parma_Polyhedra_Library::Pointset_Powerset< PSET >::unconstrain().

                                                               {
   Pointset_Powerset& x = *this;
   for (Sequence_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     si->pointset().unconstrain(vars);
     x.reduced = false;
   }
   PPL_ASSERT_HEAVY(x.OK());
 }

template<typename PSET >

void Parma_Polyhedra_Library::Pointset_Powerset< PSET >::wrap_assign	(	const Variables_Set &	vars,
		Bounded_Integer_Type_Width	w,
		Bounded_Integer_Type_Representation	r,
		Bounded_Integer_Type_Overflow	o,
		const Constraint_System *	cs_p = `0`,
		unsigned	complexity_threshold = `16`,
		bool	wrap_individually = `true`
	)

Wraps the specified dimensions of the vector space.

Parameters

vars	The set of Variable objects corresponding to the space dimensions to be wrapped.
w	The width of the bounded integer type corresponding to all the dimensions to be wrapped.
r	The representation of the bounded integer type corresponding to all the dimensions to be wrapped.
o	The overflow behavior of the bounded integer type corresponding to all the dimensions to be wrapped.
cs_p	Possibly null pointer to a constraint system whose variables are contained in `vars`. If `cs_p` depends on variables not in `vars`, the behavior is undefined. When non-null, the pointed-to constraint system is assumed to represent the conditional or looping construct guard with respect to which wrapping is performed. Since wrapping requires the computation of upper bounds and due to non-distributivity of constraint refinement over upper bounds, passing a constraint system in this way can be more precise than refining the result of the wrapping operation with the constraints in `cs_p`.
complexity_threshold	A precision parameter of the wrapping operator: higher values result in possibly improved precision.
wrap_individually	`true` if the dimensions should be wrapped individually (something that results in much greater efficiency to the detriment of precision).

Exceptions

std::invalid_argument Thrown if *cs_p is dimension-incompatible with vars, or if *this is dimension-incompatible vars or with *cs_p.

Definition at line 1203 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::OK(), Parma_Polyhedra_Library::Powerset< D >::reduced, Parma_Polyhedra_Library::Powerset< D >::sequence, and Parma_Polyhedra_Library::Pointset_Powerset< PSET >::wrap_assign().

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::wrap_assign().

                                                              {
   Pointset_Powerset& x = *this;
   for (Sequence_iterator si = x.sequence.begin(),
          s_end = x.sequence.end(); si != s_end; ++si) {
     si->pointset().wrap_assign(vars, w, r, o, cs_p,
                                complexity_threshold, wrap_individually);
   }
   x.reduced = false;
   PPL_ASSERT_HEAVY(x.OK());
 }

Friends And Related Function Documentation

template<typename PSET>

std::pair< PPL::Grid, PPL::Pointset_Powerset< PPL::Grid > > approximate_partition	(	const Grid &	p,
		const Grid &	q,
		bool &	finite_partition
	)

References Parma_Polyhedra_Library::Congruence_System::begin(), Parma_Polyhedra_Library::Grid::congruences(), Parma_Polyhedra_Library::EMPTY, Parma_Polyhedra_Library::Congruence_System::end(), Parma_Polyhedra_Library::Grid::minimized_congruences(), and Parma_Polyhedra_Library::Grid::space_dimension().

                                                    {
   using namespace PPL;
   finite_partition = true;
   Pointset_Powerset<Grid> r(p.space_dimension(), EMPTY);
   // Ensure that the congruence system of q is minimized
   // before copying and calling approximate_partition_aux().
   (void) q.minimized_congruences();
   Grid gr = q;
   const Congruence_System& p_congruences = p.congruences();
   for (Congruence_System::const_iterator i = p_congruences.begin(),
          p_congruences_end = p_congruences.end();
          i != p_congruences_end; ++i) {
     if (!approximate_partition_aux(*i, gr, r)) {
       finite_partition = false;
       const Pointset_Powerset<Grid> s(q);
       return std::make_pair(gr, s);
     }
   }
   return std::make_pair(gr, r);
 }

template<typename PSET>

std::pair< Grid, Pointset_Powerset< Grid > > approximate_partition	(	const Grid &	p,
		const Grid &	q,
		bool &	finite_partition
	)

Let p and q be two grids. The function returns an object r of type std::pair<PSET, Pointset_Powerset<Grid> > such that

r.first is the intersection of p and q;
If there is a finite partition of q with respect to p the Boolean finite_partition is set to true and r.second has the property that all its elements are pairwise disjoint and disjoint from p and the set-theoretical union of r.first with all the elements of r.second gives q (i.e., r is the representation of a partition of q).
Otherwise the Boolean finite_partition is set to false and the singleton set that contains q is stored in r.secondr.

template<typename PSET>

bool approximate_partition_aux	(	const PPL::Congruence &	c,
		PPL::Grid &	gr,
		PPL::Pointset_Powerset< PPL::Grid > &	r
	)

On exit, the intersection of gr and congruence c is stored in gr, whereas a finite set of grids whose set-theoretic union contains the intersection of gr with the negation of c is added, as a set of new disjuncts, to the powerset r.

Definition at line 133 of file Pointset_Powerset.cc.

                                                             {
   using namespace PPL;
   const Coefficient& c_modulus = c.modulus();
   const Grid gr_copy(gr);
   gr.add_congruence(c);
   if (gr.is_empty()) {
     r.add_disjunct(gr_copy);
     return true;
   }
 
   const Congruence_System cgs = gr.congruences();
   const Congruence_System cgs_copy = gr_copy.congruences();
   // When c is an equality, not satisfied by Grid gr
   // then add gr to the set r. There is no finite
   // partition in this case.
   if (c_modulus == 0) {
     if (cgs.num_equalities() != cgs_copy.num_equalities()) {
       r.add_disjunct(gr_copy);
       return false;
     }
     return true;
   }
 
   // When c is a proper congruence but, in gr, this direction has
   // no congruence, then add gr to the set r. There is no finite
   // partition in this case.
   if (cgs.num_proper_congruences() != cgs_copy.num_proper_congruences()) {
     r.add_disjunct(gr_copy);
     return false;
   }
 
   // When  c is a proper congruence and gr also is discrete
   // in this direction, then there is a finite partition and that
   // is added to r.
   const Coefficient& c_inhomogeneous_term = c.inhomogeneous_term();
   Linear_Expression le(c.expression());
   le -= c_inhomogeneous_term;
   PPL_DIRTY_TEMP_COEFFICIENT(n);
   rem_assign(n, c_inhomogeneous_term, c_modulus);
   if (n < 0) {
     n += c_modulus;
   }
   PPL_DIRTY_TEMP_COEFFICIENT(i);
   for (i = c_modulus; i-- > 0; ) {
     if (i != n) {
       Grid gr_tmp(gr_copy);
       gr_tmp.add_congruence((le+i %= 0) / c_modulus);
       if (!gr_tmp.is_empty()) {
         r.add_disjunct(gr_tmp);
       }
     }
   }
   return true;
 }

template<typename PSET>

bool check_containment	(	const NNC_Polyhedron &	ph,
		const Pointset_Powerset< NNC_Polyhedron > &	ps
	)

                                                                     {
   if (ph.is_empty()) {
     return true;
   }
   Pointset_Powerset<NNC_Polyhedron> tmp(ph.space_dimension(), EMPTY);
   tmp.add_disjunct(ph);
   for (Pointset_Powerset<NNC_Polyhedron>::const_iterator
          i = ps.begin(), ps_end = ps.end(); i != ps_end; ++i) {
     const NNC_Polyhedron& pi = i->pointset();
     for (Pointset_Powerset<NNC_Polyhedron>::iterator
            j = tmp.begin(); j != tmp.end(); ) {
       const NNC_Polyhedron& pj = j->pointset();
       if (pi.contains(pj)) {
         j = tmp.drop_disjunct(j);
       }
       else {
         ++j;
       }
     }
     if (tmp.empty()) {
       return true;
     }
     else {
       Pointset_Powerset<NNC_Polyhedron> new_disjuncts(ph.space_dimension(),
                                                       EMPTY);
       for (Pointset_Powerset<NNC_Polyhedron>::iterator
              j = tmp.begin(); j != tmp.end(); ) {
         const NNC_Polyhedron& pj = j->pointset();
         if (pj.is_disjoint_from(pi)) {
           ++j;
         }
         else {
           const std::pair<NNC_Polyhedron, Pointset_Powerset<NNC_Polyhedron> >
             partition = linear_partition(pi, pj);
           new_disjuncts.upper_bound_assign(partition.second);
           j = tmp.drop_disjunct(j);
         }
       }
       tmp.upper_bound_assign(new_disjuncts);
     }
   }
   return false;
 }

template<typename PSET>

bool check_containment	(	const Grid &	ph,
		const Pointset_Powerset< Grid > &	ps
	)

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::add_disjunct(), Parma_Polyhedra_Library::Powerset< Parma_Polyhedra_Library::Determinate< PSET > >::begin(), Parma_Polyhedra_Library::Grid::contains(), Parma_Polyhedra_Library::EMPTY, Parma_Polyhedra_Library::Powerset< Parma_Polyhedra_Library::Determinate< PSET > >::end(), Parma_Polyhedra_Library::Grid::is_disjoint_from(), Parma_Polyhedra_Library::Grid::is_empty(), and Parma_Polyhedra_Library::Grid::space_dimension().

                                                           {
   if (ph.is_empty()) {
     return true;
   }
   Pointset_Powerset<Grid> tmp(ph.space_dimension(), EMPTY);
   tmp.add_disjunct(ph);
   for (Pointset_Powerset<Grid>::const_iterator
          i = ps.begin(), ps_end = ps.end(); i != ps_end; ++i) {
     const Grid& pi = i->pointset();
     for (Pointset_Powerset<Grid>::iterator
            j = tmp.begin(); j != tmp.end(); ) {
       const Grid& pj = j->pointset();
       if (pi.contains(pj)) {
         j = tmp.drop_disjunct(j);
       }
       else {
         ++j;
       }
     }
     if (tmp.empty()) {
       return true;
     }
     else {
       Pointset_Powerset<Grid> new_disjuncts(ph.space_dimension(),
                                                       EMPTY);
       for (Pointset_Powerset<Grid>::iterator
              j = tmp.begin(); j != tmp.end(); ) {
         const Grid& pj = j->pointset();
         if (pj.is_disjoint_from(pi)) {
           ++j;
         }
         else {
           bool finite_partition;
           const std::pair<Grid, Pointset_Powerset<Grid> >
             partition = approximate_partition(pi, pj, finite_partition);
 
           // If there is a finite partition, then we add the new
           // disjuncts to the temporary set of disjuncts and drop pj.
           // If there is no finite partition, then by the
           // specification of approximate_partition(), we can
           // ignore checking the remaining temporary disjuncts as they
           // will all have the same lines and equalities and therefore
           // also not have a finite partition with respect to pi.
           if (!finite_partition) {
             break;
           }
           new_disjuncts.upper_bound_assign(partition.second);
           j = tmp.drop_disjunct(j);
         }
       }
       tmp.upper_bound_assign(new_disjuncts);
     }
   }
   return false;
 }

template<typename PSET >

bool check_containment	(	const PSET &	ph,
		const Pointset_Powerset< PSET > &	ps
	)

                                                                      {
   // This code is only used when PSET is an abstraction of NNC_Polyhedron.
   const NNC_Polyhedron ph_nnc = NNC_Polyhedron(ph.constraints());
   const Pointset_Powerset<NNC_Polyhedron> ps_nnc(ps);
   return check_containment(ph_nnc, ps_nnc);
 }

bool check_containment	(	const C_Polyhedron &	ph,
		const Pointset_Powerset< C_Polyhedron > &	ps
	)

                                                              {
   return check_containment(NNC_Polyhedron(ph),
                            Pointset_Powerset<NNC_Polyhedron>(ps));
 }

template<typename PSET>

bool check_containment	(	const NNC_Polyhedron &	ph,
		const Pointset_Powerset< NNC_Polyhedron > &	ps
	)

template<typename PSET>

bool check_containment	(	const Grid &	ph,
		const Pointset_Powerset< Grid > &	ps
	)

template<typename PSET >

bool check_containment	(	const PSET &	ph,
		const Pointset_Powerset< PSET > &	ps
	)

Note: It is assumed that the template parameter PSET can be converted without precision loss into an NNC_Polyhedron; otherwise, an incorrect result might be obtained.

template<typename PSET >

std::pair< PSET, Pointset_Powerset< NNC_Polyhedron > > linear_partition	(	const PSET &	p,
		const PSET &	q
	)

Let p and q be two polyhedra. The function returns an object r of type std::pair<PSET, Pointset_Powerset<NNC_Polyhedron> > such that

r.first is the intersection of p and q;
r.second has the property that all its elements are pairwise disjoint and disjoint from p;
the set-theoretical union of r.first with all the elements of r.second gives q (i.e., r is the representation of a partition of q).

See this paper for more information about the implementation.

Referenced by Parma_Polyhedra_Library::Pointset_Powerset< PSET >::check_containment(), and Parma_Polyhedra_Library::Pointset_Powerset< PSET >::difference_assign().

template<typename PSET >

std::pair< PSET, Pointset_Powerset< NNC_Polyhedron > > linear_partition	(	const PSET &	p,
		const PSET &	q
	)

References Parma_Polyhedra_Library::Constraint_System::begin(), c, Parma_Polyhedra_Library::EMPTY, Parma_Polyhedra_Library::Constraint_System::end(), Parma_Polyhedra_Library::Constraint::expression(), Parma_Polyhedra_Library::Constraint::is_equality(), and Parma_Polyhedra_Library::Boundary_NS::le().

                                                {
   using Implementation::Pointset_Powersets::linear_partition_aux;
 
   Pointset_Powerset<NNC_Polyhedron> r(p.space_dimension(), EMPTY);
   PSET pset = q;
   const Constraint_System& p_constraints = p.constraints();
   for (Constraint_System::const_iterator i = p_constraints.begin(),
          p_constraints_end = p_constraints.end();
        i != p_constraints_end;
        ++i) {
     const Constraint& c = *i;
     if (c.is_equality()) {
       const Linear_Expression le(c.expression());
       linear_partition_aux(le <= 0, pset, r);
       linear_partition_aux(le >= 0, pset, r);
     }
     else {
       linear_partition_aux(c, pset, r);
     }
   }
   return std::make_pair(pset, r);
 }

template<typename PSET >

void linear_partition_aux	(	const Constraint &	c,
		PSET &	pset,
		Pointset_Powerset< NNC_Polyhedron > &	r
	)

On exit, the intersection of pset and constraint c is stored in pset, whereas the intersection of pset with the negation of c is added as a new disjunct of the powerset r.

Definition at line 1630 of file Pointset_Powerset_templates.hh.

References Parma_Polyhedra_Library::Polyhedron::add_constraint(), Parma_Polyhedra_Library::Pointset_Powerset< PSET >::add_disjunct(), Parma_Polyhedra_Library::Constraint::expression(), Parma_Polyhedra_Library::Polyhedron::is_empty(), Parma_Polyhedra_Library::Constraint::is_strict_inequality(), and Parma_Polyhedra_Library::Boundary_NS::le().

                                                            {
   const Linear_Expression le(c.expression());
   const Constraint& neg_c = c.is_strict_inequality() ? (le <= 0) : (le < 0);
   NNC_Polyhedron nnc_ph_pset(pset);
   nnc_ph_pset.add_constraint(neg_c);
   if (!nnc_ph_pset.is_empty()) {
     r.add_disjunct(nnc_ph_pset);
   }
   pset.add_constraint(c);
 }

template<typename PSET>

friend class Pointset_Powerset< NNC_Polyhedron >

friend

Definition at line 1308 of file Pointset_Powerset_defs.hh.

template<typename PSET >

void swap	(	Pointset_Powerset< PSET > &	x,
		Pointset_Powerset< PSET > &	y
	)

References Parma_Polyhedra_Library::Pointset_Powerset< PSET >::m_swap().

                                                              {
   x.m_swap(y);
 }

template<typename PSET >

void swap	(	Pointset_Powerset< PSET > &	x,
		Pointset_Powerset< PSET > &	y
	)

template<typename PSET >

Widening_Function< PSET > widen_fun_ref ( void(PSET::*)(const PSET &, unsigned *) wm )

                                                        {
   return Widening_Function<PSET>(wm);
 }

template<typename PSET , typename CSYS >

Limited_Widening_Function< PSET, CSYS > widen_fun_ref	(	void(PSET::)(const PSET &, const CSYS &, unsigned )	lwm,
		const CSYS &	cs
	)

                               {
   return Limited_Widening_Function<PSET, CSYS>(lwm, cs);
 }

template<typename PSET >

Widening_Function< PSET > widen_fun_ref ( void(PSET::*)(const PSET &, unsigned *) wm )

Parameters

wm	The widening method.

template<typename PSET , typename CSYS >

Limited_Widening_Function< PSET, CSYS > widen_fun_ref	(	void(PSET::)(const PSET &, const CSYS &, unsigned )	lwm,
		const CSYS &	cs
	)

Parameters

lwm	The limited widening method.
cs	The constraint system limiting the widening.

Member Data Documentation

template<typename PSET>

dimension_type Parma_Polyhedra_Library::Pointset_Powerset< PSET >::space_dim

private

The number of dimensions of the enclosing vector space.

Definition at line 1263 of file Pointset_Powerset_defs.hh.

The documentation for this class was generated from the following files:

Public Types

Public Member Functions

Static Public Member Functions

Private Types

Private Member Functions

Private Attributes

Friends

Related Functions

Additional Inherited Members

Detailed Description

template<typename PSET> class Parma_Polyhedra_Library::Pointset_Powerset< PSET >

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation

Friends And Related Function Documentation

Member Data Documentation

template<typename PSET>
class Parma_Polyhedra_Library::Pointset_Powerset< PSET >