Any PPL pointset. More...

#include <Any_Pointset_defs.hh>

Public Member Functions
	Any_Pointset ()
	Default constructor. More...

	Any_Pointset (const Any_Pointset &y)
	Ordinary copy constructor. More...

Member Functions that Do Not Modify the Pointset
virtual dimension_type	space_dimension () const =0
	Returns the dimension of the vector space enclosing `*this`. More...

virtual dimension_type	affine_dimension () const =0
	Returns , if `this` is empty; otherwise, returns the affine dimension of `this`. More...

virtual Constraint_System	constraints () const =0
	Returns a system of constraints that `*this` satisfies. More...

Poly_Con_Relation	relation_with (const Constraint &c) const
	Returns the relations holding between the pointset `*this` and the constraint `c`. More...

Poly_Gen_Relation	relation_with (const Generator &g) const
	Returns the relations holding between the pointset `*this` and the generator `g`. More...

virtual bool	is_empty () const =0
	Returns `true` if and only if `*this` is an empty pointset. More...

virtual bool	is_universe () const =0
	Returns `true` if and only if `*this` is a universe pointset. More...

virtual bool	is_topologically_closed () const =0
	Returns `true` if and only if `*this` is a topologically closed subset of the vector space. More...

virtual bool	is_discrete () const =0
	Returns `true` if and only if `*this` is discrete. More...

virtual bool	is_bounded () const =0
	Returns `true` if and only if `*this` is a bounded pointset. More...

virtual bool	contains_integer_point () const =0
	Returns `true` if and only if `*this` contains at least one integer point. More...

virtual bool	bounds_from_above (const Linear_Expression &expr) const =0
	Returns `true` if and only if `expr` is bounded from above in `*this`. More...

virtual bool	bounds_from_below (const Linear_Expression &expr) const =0
	Returns `true` if and only if `expr` is bounded from below in `*this`. More...

virtual bool	maximize (const Linear_Expression &expr, Coefficient &sup_n, Coefficient &sup_d, bool &maximum) const =0
	Returns `true` if and only if `this` is not empty and `expr` is bounded from above in `this`, in which case the supremum value is computed. More...

virtual bool	maximize (const Linear_Expression &expr, Coefficient &sup_n, Coefficient &sup_d, bool &maximum, Generator &point) const =0
	Returns `true` if and only if `this` is not empty and `expr` is bounded from above in `this`, in which case the supremum value and a point where `expr` reaches it are computed. More...

virtual bool	minimize (const Linear_Expression &expr, Coefficient &inf_n, Coefficient &inf_d, bool &minimum) const =0
	Returns `true` if and only if `this` is not empty and `expr` is bounded from below in `this`, in which case the infimum value is computed. More...

virtual bool	minimize (const Linear_Expression &expr, Coefficient &inf_n, Coefficient &inf_d, bool &minimum, Generator &point) const =0
	Returns `true` if and only if `this` is not empty and `expr` is bounded from below in `this`, in which case the infimum value and a point where `expr` reaches it are computed. More...

virtual bool	contains (const Any_Pointset &y) const =0
	Returns `true` if and only if `*this` contains `y`. More...

virtual bool	strictly_contains (const Any_Pointset &y) const =0
	Returns `true` if and only if `*this` strictly contains `y`. More...

virtual bool	is_disjoint_from (const Any_Pointset &y) const =0
	Returns `true` if and only if `*this` and `y` are disjoint. More...

virtual bool	OK () const =0
	Checks if all the invariants are satisfied. More...

Space Dimension Preserving Member Functions that May Modify the Any_Pointset
virtual void	add_constraint (const Constraint &c)=0
	Adds a copy of constraint `c` to the system of constraints of `*this` (without minimizing the result). More...

virtual void	add_constraints (const Constraint_System &cs)=0
	Adds a copy of the constraints in `cs` to the system of constraints of `*this` (without minimizing the result). More...

virtual void	unconstrain (Variable var)=0
	Computes the cylindrification of `this` with respect to space dimension `var`, assigning the result to `this`. More...

virtual void	unconstrain (const Variables_Set &vars)=0
	Computes the cylindrification of `this` with respect to the set of space dimensions `vars`, assigning the result to `this`. More...

virtual void	intersection_assign (const Any_Pointset &y)=0
	Assigns to `this` the intersection of `this` and `y`. The result is not guaranteed to be minimized. More...

virtual void	upper_bound_assign (const Any_Pointset &y)=0
	Assigns to `this` the smallest pointset, in the class of `this` and `y`, that contains both `*this` and `y`. More...

virtual void	difference_assign (const Any_Pointset &y)=0
	Assigns to `*this` the smallest pointset, in the class of `this` and `y`, that contains the set-theoretic difference of `this` and `y`. More...

virtual void	affine_image (Variable var, const Linear_Expression &expr, Coefficient_traits::const_reference denominator=Coefficient_one())=0
	Assigns to `this` the affine image of `this` under the function mapping variable `var` to the affine expression specified by `expr` and `denominator`. More...

virtual void	affine_preimage (Variable var, const Linear_Expression &expr, Coefficient_traits::const_reference denominator=Coefficient_one())=0
	Assigns to `this` the affine preimage of `this` under the function mapping variable `var` to the affine expression specified by `expr` and `denominator`. More...

virtual void	generalized_affine_image (Variable var, Relation_Symbol relsym, const Linear_Expression &expr, Coefficient_traits::const_reference denominator=Coefficient_one())=0
	Assigns to `this` the image of `this` with respect to the generalized affine relation $\mathrm{var}' \relsym \frac{\mathrm{expr}}{\mathrm{denominator}}$ , where $\mathord{\relsym}$ is the relation symbol encoded by `relsym`. More...

virtual void	generalized_affine_preimage (Variable var, Relation_Symbol relsym, const Linear_Expression &expr, Coefficient_traits::const_reference denominator=Coefficient_one())=0
	Assigns to `this` the preimage of `this` with respect to the generalized affine relation $\mathrm{var}' \relsym \frac{\mathrm{expr}}{\mathrm{denominator}}$ , where $\mathord{\relsym}$ is the relation symbol encoded by `relsym`. More...

virtual void	generalized_affine_image (const Linear_Expression &lhs, Relation_Symbol relsym, const Linear_Expression &rhs)=0
	Assigns to `this` the image of `this` with respect to the generalized affine relation $\mathrm{lhs}' \relsym \mathrm{rhs}$ , where $\mathord{\relsym}$ is the relation symbol encoded by `relsym`. More...

virtual void	generalized_affine_preimage (const Linear_Expression &lhs, Relation_Symbol relsym, const Linear_Expression &rhs)=0
	Assigns to `this` the preimage of `this` with respect to the generalized affine relation $\mathrm{lhs}' \relsym \mathrm{rhs}$ , where $\mathord{\relsym}$ is the relation symbol encoded by `relsym`. More...

virtual void	bounded_affine_image (Variable var, const Linear_Expression &lb_expr, const Linear_Expression &ub_expr, Coefficient_traits::const_reference denominator=Coefficient_one())=0
	Assigns to `this` the image of `this` with respect to the bounded affine relation $\frac{\mathrm{lb\_expr}}{\mathrm{denominator}} \leq \mathrm{var}' \leq \frac{\mathrm{ub\_expr}}{\mathrm{denominator}}$ . More...

virtual void	bounded_affine_preimage (Variable var, const Linear_Expression &lb_expr, const Linear_Expression &ub_expr, Coefficient_traits::const_reference denominator=Coefficient_one())=0
	Assigns to `this` the preimage of `this` with respect to the bounded affine relation $\frac{\mathrm{lb\_expr}}{\mathrm{denominator}} \leq \mathrm{var}' \leq \frac{\mathrm{ub\_expr}}{\mathrm{denominator}}$ . More...

virtual void	time_elapse_assign (const Any_Pointset &y)=0
	Assigns to `this` the result of computing the time-elapse between `this` and `y`. More...

void	topological_closure_assign ()
	Assigns to `*this` its topological closure. More...

Member Functions that May Modify the Dimension of the Vector Space
virtual void	add_space_dimensions_and_embed (dimension_type m)=0
	Adds `m` new space dimensions and embeds the old pointset in the new vector space. More...

virtual void	add_space_dimensions_and_project (dimension_type m)=0
	Adds `m` new space dimensions to the pointset and does not embed it in the new vector space. More...

virtual void	concatenate_assign (const Any_Pointset &y)=0
	Assigns to `this` the concatenation of `this` and `y`, taken in this order. More...

virtual void	remove_space_dimensions (const Variables_Set &vars)=0
	Removes all the specified dimensions from the vector space. More...

virtual void	remove_higher_space_dimensions (dimension_type new_dimension)=0
	Removes the higher dimensions of the vector space so that the resulting space will have dimension `new_dimension`. More...

void	expand_space_dimension (Variable var, dimension_type m)
	Creates `m` copies of the space dimension corresponding to `var`. More...

void	fold_space_dimensions (const Variables_Set &vars, Variable dest)
	Folds the space dimensions in `vars` into `dest`. More...

Miscellaneous Member Functions
virtual	~Any_Pointset ()
	Destructor. More...

void	m_swap (Any_Pointset &y)
	Swaps `this` with pointset `y`. (`this` and `y` can be dimension-incompatible.) More...

void	ascii_dump () const
	Writes to `std::cerr` an ASCII representation of `*this`. More...

void	ascii_dump (std::ostream &s) const
	Writes to `s` an ASCII representation of `*this`. More...

void	print () const
	Prints `*this` to `std::cerr` using `operator<<`. More...

bool	ascii_load (std::istream &s)
	Loads from `s` an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets `*this` accordingly. Returns `true` if successful, `false` otherwise. More...

virtual memory_size_type	total_memory_in_bytes () const =0
	Returns the total size in bytes of the memory occupied by `*this`. More...

virtual memory_size_type	external_memory_in_bytes () const =0
	Returns the size in bytes of the memory managed by `*this`. More...

virtual int32_t	hash_code () const =0
	Returns a 32-bit hash code for `*this`. More...

Related Functions
(Note that these are not member functions.)
std::ostream &	operator<< (std::ostream &s, const Any_Pointset &ph)
	Output operator. More...

void	swap (Any_Pointset &x, Any_Pointset &y)
	Swaps `x` with `y`. More...

bool	operator== (const Any_Pointset &x, const Any_Pointset &y)
	Returns `true` if and only if `x` and `y` are the same pointset. More...

bool	operator!= (const Any_Pointset &x, const Any_Pointset &y)
	Returns `true` if and only if `x` and `y` are different pointsets. More...

Detailed Description

Any PPL pointset.

Definition at line 82 of file Any_Pointset_defs.hh.

Constructor & Destructor Documentation

Parma_Polyhedra_Library::Any_Pointset::Any_Pointset ( )

inline

Default constructor.

Definition at line 30 of file Any_Pointset_inlines.hh.

30 {

31 }

Parma_Polyhedra_Library::Any_Pointset::Any_Pointset ( const Any_Pointset & y )

Ordinary copy constructor.

Parma_Polyhedra_Library::Any_Pointset::~Any_Pointset ( )

inlinevirtual

Destructor.

Definition at line 34 of file Any_Pointset_inlines.hh.

34 {

35 }

Member Function Documentation

virtual void Parma_Polyhedra_Library::Any_Pointset::add_constraint ( const Constraint & c )

pure virtual

Adds a copy of constraint c to the system of constraints of *this (without minimizing the result).

Exceptions

std::invalid_argument Thrown if *this and constraint c are topology-incompatible or dimension-incompatible.

virtual void Parma_Polyhedra_Library::Any_Pointset::add_constraints ( const Constraint_System & cs )

pure virtual

Adds a copy of the constraints in cs to the system of constraints of *this (without minimizing the result).

Parameters

cs	Contains the constraints that will be added to the system of constraints of `*this`.

Exceptions

std::invalid_argument Thrown if *this and cs are topology-incompatible or dimension-incompatible.

virtual void Parma_Polyhedra_Library::Any_Pointset::add_space_dimensions_and_embed ( dimension_type m )

pure virtual

Adds m new space dimensions and embeds the old pointset in the new vector space.

Parameters

m	The number of dimensions to add.

Exceptions

std::length_error Thrown if adding m new space dimensions would cause the vector space to exceed dimension max_space_dimension().

The new space dimensions will be those having the highest indexes in the new pointset, which is characterized by a system of constraints in which the variables running through the new dimensions are not constrained. For instance, when starting from the pointset 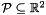$\cP \sseq \Rset^2$ and adding a third space dimension, the result will be the pointset

$\bigl\{\, (x, y, z)^\transpose \in \Rset^3 \bigm| (x, y)^\transpose \in \cP \,\bigr\}.$

virtual void Parma_Polyhedra_Library::Any_Pointset::add_space_dimensions_and_project ( dimension_type m )

pure virtual

Adds m new space dimensions to the pointset and does not embed it in the new vector space.

Parameters

m	The number of space dimensions to add.

Exceptions

std::length_error Thrown if adding m new space dimensions would cause the vector space to exceed dimension max_space_dimension().

The new space dimensions will be those having the highest indexes in the new pointset, which is characterized by a system of constraints in which the variables running through the new dimensions are all constrained to be equal to 0. For instance, when starting from the pointset 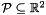$\cP \sseq \Rset^2$ and adding a third space dimension, the result will be the pointset

$\bigl\{\, (x, y, 0)^\transpose \in \Rset^3 \bigm| (x, y)^\transpose \in \cP \,\bigr\}.$

virtual dimension_type Parma_Polyhedra_Library::Any_Pointset::affine_dimension ( ) const

pure virtual

Returns $0$ , if *this is empty; otherwise, returns the affine dimension of *this.

virtual void Parma_Polyhedra_Library::Any_Pointset::affine_image	(	Variable	var,
		const Linear_Expression &	expr,
		Coefficient_traits::const_reference	denominator = `Coefficient_one()`
	)

pure virtual

Assigns to *this the affine image of *this under the function mapping variable var to the affine expression specified by expr and denominator.

Parameters

var	The variable to which the affine expression is assigned;
expr	The numerator of the affine expression;
denominator	The denominator of the affine expression (optional argument with default value 1).

Exceptions

std::invalid_argument Thrown if denominator is zero or if expr and *this are dimension-incompatible or if var is not a space dimension of *this.

When considering the generators of a pointset, the affine transformation

$\frac{\sum_{i=0}^{n-1} a_i x_i + b}{\mathrm{denominator}}$

is assigned to var where expr is 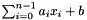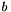$\sum_{i=0}^{n-1} a_i x_i + b$ ( $b$ is the inhomogeneous term).

If constraints are up-to-date, it uses the specialized function affine_preimage() (for the system of constraints) and inverse transformation to reach the same result. To obtain the inverse transformation we use the following observation.

Observation:

The affine transformation is invertible if the coefficient of var in this transformation (i.e.,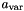 $a_\mathrm{var}$ ) is different from zero.
If the transformation is invertible, then we can write
$\mathrm{denominator} * {x'}_\mathrm{var} = \sum_{i = 0}^{n - 1} a_i x_i + b = a_\mathrm{var} x_\mathrm{var} + \sum_{i \neq var} a_i x_i + b,$
so that the inverse transformation is
$a_\mathrm{var} x_\mathrm{var} = \mathrm{denominator} * {x'}_\mathrm{var} - \sum_{i \neq j} a_i x_i - b.$

Then, if the transformation is invertible, all the entities that were up-to-date remain up-to-date. Otherwise only generators remain up-to-date.

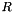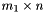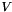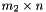In other words, if $R$ is a $m_1 \times n$ matrix representing the rays of the pointset, $V$ is a $m_2 \times n$ matrix representing the points of the pointset and

$P = \bigl\{\, \vect{x} = (x_0, \ldots, x_{n-1})^\mathrm{T} \bigm| \vect{x} = \vect{\lambda} R + \vect{\mu} V, \vect{\lambda} \in \Rset^{m_1}_+, \vect{\mu} \in \Rset^{m_2}_+, \sum_{i = 0}^{m_2 - 1} \mu_i = 1 \,\bigr\}$

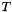and $T$ is the affine transformation to apply to 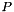$P$ , then the resulting pointset is

$P' = \bigl\{\, (x_0, \ldots, T(x_0, \ldots, x_{n-1}), \ldots, x_{n-1})^\mathrm{T} \bigm| (x_0, \ldots, x_{n-1})^\mathrm{T} \in P \,\bigr\}.$

Affine transformations are, for example:

translations
rotations
symmetries.

virtual void Parma_Polyhedra_Library::Any_Pointset::affine_preimage	(	Variable	var,
		const Linear_Expression &	expr,
		Coefficient_traits::const_reference	denominator = `Coefficient_one()`
	)

pure virtual

Assigns to *this the affine preimage of *this under the function mapping variable var to the affine expression specified by expr and denominator.

Parameters

var	The variable to which the affine expression is substituted;
expr	The numerator of the affine expression;
denominator	The denominator of the affine expression (optional argument with default value 1).

Exceptions

std::invalid_argument Thrown if denominator is zero or if expr and *this are dimension-incompatible or if var is not a space dimension of *this.

When considering constraints of a pointset, the affine transformation

$\frac{\sum_{i=0}^{n-1} a_i x_i + b}{denominator},$

is assigned to var where expr is 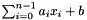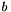$\sum_{i=0}^{n-1} a_i x_i + b$ ( $b$ is the inhomogeneous term).

If generators are up-to-date, then the specialized function affine_image() is used (for the system of generators) and inverse transformation to reach the same result. To obtain the inverse transformation, we use the following observation.

Observation:

The affine transformation is invertible if the coefficient of var in this transformation (i.e.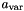 $a_\mathrm{var}$ ) is different from zero.
If the transformation is invertible, then we can write
$\mathrm{denominator} * {x'}_\mathrm{var} = \sum_{i = 0}^{n - 1} a_i x_i + b = a_\mathrm{var} x_\mathrm{var} + \sum_{i \neq \mathrm{var}} a_i x_i + b,$
, the inverse transformation is
$a_\mathrm{var} x_\mathrm{var} = \mathrm{denominator} * {x'}_\mathrm{var} - \sum_{i \neq j} a_i x_i - b.$
.

Then, if the transformation is invertible, all the entities that were up-to-date remain up-to-date. Otherwise only constraints remain up-to-date.

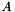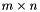In other words, if $A$ is a $m \times n$ matrix representing the constraints of the pointset, 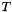$T$ is the affine transformation to apply to 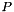$P$ and

$P = \bigl\{\, \vect{x} = (x_0, \ldots, x_{n-1})^\mathrm{T} \bigm| A\vect{x} \geq \vect{0} \,\bigr\}.$

The resulting pointset is

$P' = \bigl\{\, \vect{x} = (x_0, \ldots, x_{n-1}))^\mathrm{T} \bigm| A'\vect{x} \geq \vect{0} \,\bigr\},$

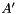where $A'$ is defined as follows:

${a'}_{ij} = \begin{cases} a_{ij} * \mathrm{denominator} + a_{i\mathrm{var}}*\mathrm{expr}[j] \quad \mathrm{for } j \neq \mathrm{var}; \\ \mathrm{expr}[\mathrm{var}] * a_{i\mathrm{var}}, \quad \text{for } j = \mathrm{var}. \end{cases}$

void Parma_Polyhedra_Library::Any_Pointset::ascii_dump ( ) const

Writes to std::cerr an ASCII representation of *this.

void Parma_Polyhedra_Library::Any_Pointset::ascii_dump ( std::ostream & s ) const

Writes to s an ASCII representation of *this.

bool Parma_Polyhedra_Library::Any_Pointset::ascii_load ( std::istream & s )

Loads from s an ASCII representation (as produced by ascii_dump(std::ostream&) const) and sets *this accordingly. Returns true if successful, false otherwise.

virtual void Parma_Polyhedra_Library::Any_Pointset::bounded_affine_image	(	Variable	var,
		const Linear_Expression &	lb_expr,
		const Linear_Expression &	ub_expr,
		Coefficient_traits::const_reference	denominator = `Coefficient_one()`
	)

pure virtual

Assigns to *this the image of *this with respect to the bounded affine relation $\frac{\mathrm{lb\_expr}}{\mathrm{denominator}} \leq \mathrm{var}' \leq \frac{\mathrm{ub\_expr}}{\mathrm{denominator}}$ .

Parameters

var	The variable updated by the affine relation;
lb_expr	The numerator of the lower bounding affine expression;
ub_expr	The numerator of the upper bounding affine expression;
denominator	The (common) denominator for the lower and upper bounding affine expressions (optional argument with default value 1).

Exceptions

std::invalid_argument Thrown if denominator is zero or if lb_expr (resp., ub_expr) and *this are dimension-incompatible or if var is not a space dimension of *this.

virtual void Parma_Polyhedra_Library::Any_Pointset::bounded_affine_preimage	(	Variable	var,
		const Linear_Expression &	lb_expr,
		const Linear_Expression &	ub_expr,
		Coefficient_traits::const_reference	denominator = `Coefficient_one()`
	)

pure virtual

Assigns to *this the preimage of *this with respect to the bounded affine relation $\frac{\mathrm{lb\_expr}}{\mathrm{denominator}} \leq \mathrm{var}' \leq \frac{\mathrm{ub\_expr}}{\mathrm{denominator}}$ .

Parameters

var	The variable updated by the affine relation;
lb_expr	The numerator of the lower bounding affine expression;
ub_expr	The numerator of the upper bounding affine expression;
denominator	The (common) denominator for the lower and upper bounding affine expressions (optional argument with default value 1).

Exceptions

std::invalid_argument Thrown if denominator is zero or if lb_expr (resp., ub_expr) and *this are dimension-incompatible or if var is not a space dimension of *this.

virtual bool Parma_Polyhedra_Library::Any_Pointset::bounds_from_above ( const Linear_Expression & expr ) const

pure virtual

Returns true if and only if expr is bounded from above in *this.

Exceptions

std::invalid_argument Thrown if expr and *this are dimension-incompatible.

virtual bool Parma_Polyhedra_Library::Any_Pointset::bounds_from_below ( const Linear_Expression & expr ) const

pure virtual

Returns true if and only if expr is bounded from below in *this.

Exceptions

std::invalid_argument Thrown if expr and *this are dimension-incompatible.

virtual void Parma_Polyhedra_Library::Any_Pointset::concatenate_assign ( const Any_Pointset & y )

pure virtual

Assigns to *this the concatenation of *this and y, taken in this order.

Exceptions

std::invalid_argument	Thrown if `*this` and `y` are topology-incompatible.
std::length_error	Thrown if the concatenation would cause the vector space to exceed dimension `max_space_dimension()`.

virtual Constraint_System Parma_Polyhedra_Library::Any_Pointset::constraints ( ) const

pure virtual

Returns a system of constraints that *this satisfies.

virtual bool Parma_Polyhedra_Library::Any_Pointset::contains ( const Any_Pointset & y ) const

pure virtual

Returns true if and only if *this contains y.

Exceptions

std::invalid_argument Thrown if *this and y are topology-incompatible or dimension-incompatible.

virtual bool Parma_Polyhedra_Library::Any_Pointset::contains_integer_point ( ) const

pure virtual

Returns true if and only if *this contains at least one integer point.

virtual void Parma_Polyhedra_Library::Any_Pointset::difference_assign ( const Any_Pointset & y )

pure virtual

Assigns to *this the smallest pointset, in the class of this and y, that contains the set-theoretic difference of this and y.

Exceptions

std::invalid_argument Thrown if *this and y are topology-incompatible or dimension-incompatible.

void Parma_Polyhedra_Library::Any_Pointset::expand_space_dimension	(	Variable	var,
		dimension_type	m
	)

Creates m copies of the space dimension corresponding to var.

Parameters

var	The variable corresponding to the space dimension to be replicated;
m	The number of replicas to be created.

Exceptions

std::invalid_argument	Thrown if `var` does not correspond to a dimension of the vector space.
std::length_error	Thrown if adding `m` new space dimensions would cause the vector space to exceed dimension `max_space_dimension()`.

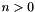If *this has space dimension $n$ , with $n > 0$ , and var has space dimension 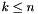$k \leq n$ , then the $k$ -th space dimension is expanded to m new space dimensions $n$ , $n+1$ , $\dots$ , $n+m-1$ .

virtual memory_size_type Parma_Polyhedra_Library::Any_Pointset::external_memory_in_bytes ( ) const

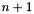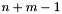pure virtual

Returns the size in bytes of the memory managed by *this.

void Parma_Polyhedra_Library::Any_Pointset::fold_space_dimensions	(	const Variables_Set &	vars,
		Variable	dest
	)

Folds the space dimensions in vars into dest.

Parameters

vars	The set of Variable objects corresponding to the space dimensions to be folded;
dest	The variable corresponding to the space dimension that is the destination of the folding operation.

Exceptions

std::invalid_argument Thrown if *this is dimension-incompatible with dest or with one of the Variable objects contained in vars. Also thrown if dest is contained in vars.

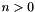If *this has space dimension $n$ , with $n > 0$ , dest has space dimension 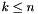$k \leq n$ , vars is a set of variables whose maximum space dimension is also less than or equal to $n$ , and dest is not a member of vars, then the space dimensions corresponding to variables in vars are folded into the $k$ -th space dimension.

virtual void Parma_Polyhedra_Library::Any_Pointset::generalized_affine_image	(	Variable	var,
		Relation_Symbol	relsym,
		const Linear_Expression &	expr,
		Coefficient_traits::const_reference	denominator = `Coefficient_one()`
	)

pure virtual

Assigns to *this the image of *this with respect to the generalized affine relation $\mathrm{var}' \relsym \frac{\mathrm{expr}}{\mathrm{denominator}}$ , where $\mathord{\relsym}$ is the relation symbol encoded by relsym.

Parameters

var	The left hand side variable of the generalized affine relation;
relsym	The relation symbol;
expr	The numerator of the right hand side affine expression;
denominator	The denominator of the right hand side affine expression (optional argument with default value 1).

Exceptions

std::invalid_argument Thrown if denominator is zero or if expr and *this are dimension-incompatible or if var is not a space dimension of *this or if *this is a Any_Pointset and relsym is a strict relation symbol.

virtual void Parma_Polyhedra_Library::Any_Pointset::generalized_affine_image	(	const Linear_Expression &	lhs,
		Relation_Symbol	relsym,
		const Linear_Expression &	rhs
	)

pure virtual

Assigns to *this the image of *this with respect to the generalized affine relation $\mathrm{lhs}' \relsym \mathrm{rhs}$ , where $\mathord{\relsym}$ is the relation symbol encoded by relsym.

Parameters

lhs	The left hand side affine expression;
relsym	The relation symbol;
rhs	The right hand side affine expression.

Exceptions

std::invalid_argument Thrown if *this is dimension-incompatible with lhs or rhs or if *this is a C_Any_Pointset and relsym is a strict relation symbol.

virtual void Parma_Polyhedra_Library::Any_Pointset::generalized_affine_preimage	(	Variable	var,
		Relation_Symbol	relsym,
		const Linear_Expression &	expr,
		Coefficient_traits::const_reference	denominator = `Coefficient_one()`
	)

pure virtual

Assigns to *this the preimage of *this with respect to the generalized affine relation $\mathrm{var}' \relsym \frac{\mathrm{expr}}{\mathrm{denominator}}$ , where $\mathord{\relsym}$ is the relation symbol encoded by relsym.

Parameters

var	The left hand side variable of the generalized affine relation;
relsym	The relation symbol;
expr	The numerator of the right hand side affine expression;
denominator	The denominator of the right hand side affine expression (optional argument with default value 1).

Exceptions

std::invalid_argument Thrown if denominator is zero or if expr and *this are dimension-incompatible or if var is not a space dimension of *this or if *this is a C_Any_Pointset and relsym is a strict relation symbol.

virtual void Parma_Polyhedra_Library::Any_Pointset::generalized_affine_preimage	(	const Linear_Expression &	lhs,
		Relation_Symbol	relsym,
		const Linear_Expression &	rhs
	)

pure virtual

Assigns to *this the preimage of *this with respect to the generalized affine relation $\mathrm{lhs}' \relsym \mathrm{rhs}$ , where $\mathord{\relsym}$ is the relation symbol encoded by relsym.

Parameters

lhs	The left hand side affine expression;
relsym	The relation symbol;
rhs	The right hand side affine expression.

Exceptions

std::invalid_argument Thrown if *this is dimension-incompatible with lhs or rhs or if *this is a C_Any_Pointset and relsym is a strict relation symbol.

virtual int32_t Parma_Polyhedra_Library::Any_Pointset::hash_code ( ) const

pure virtual

Returns a 32-bit hash code for *this.

If x and y are such that x == y, then x.hash_code() == y.hash_code().

virtual void Parma_Polyhedra_Library::Any_Pointset::intersection_assign ( const Any_Pointset & y )

pure virtual

Assigns to *this the intersection of *this and y. The result is not guaranteed to be minimized.

Exceptions

std::invalid_argument Thrown if *this and y are topology-incompatible or dimension-incompatible.

virtual bool Parma_Polyhedra_Library::Any_Pointset::is_bounded ( ) const

pure virtual

Returns true if and only if *this is a bounded pointset.

virtual bool Parma_Polyhedra_Library::Any_Pointset::is_discrete ( ) const

pure virtual

Returns true if and only if *this is discrete.

virtual bool Parma_Polyhedra_Library::Any_Pointset::is_disjoint_from ( const Any_Pointset & y ) const

pure virtual

Returns true if and only if *this and y are disjoint.

Exceptions

std::invalid_argument Thrown if x and y are topology-incompatible or dimension-incompatible.

virtual bool Parma_Polyhedra_Library::Any_Pointset::is_empty ( ) const

pure virtual

Returns true if and only if *this is an empty pointset.

virtual bool Parma_Polyhedra_Library::Any_Pointset::is_topologically_closed ( ) const

pure virtual

Returns true if and only if *this is a topologically closed subset of the vector space.

virtual bool Parma_Polyhedra_Library::Any_Pointset::is_universe ( ) const

pure virtual

Returns true if and only if *this is a universe pointset.

void Parma_Polyhedra_Library::Any_Pointset::m_swap ( Any_Pointset & y )

Swaps *this with pointset y. (*this and y can be dimension-incompatible.)

Exceptions

std::invalid_argument Thrown if x and y are topology-incompatible.

virtual bool Parma_Polyhedra_Library::Any_Pointset::maximize	(	const Linear_Expression &	expr,
		Coefficient &	sup_n,
		Coefficient &	sup_d,
		bool &	maximum
	)		const

pure virtual

Returns true if and only if *this is not empty and expr is bounded from above in *this, in which case the supremum value is computed.

Parameters

expr	The linear expression to be maximized subject to `*this`;
sup_n	The numerator of the supremum value;
sup_d	The denominator of the supremum value;
maximum	`true` if and only if the supremum is also the maximum value.

Exceptions

std::invalid_argument Thrown if expr and *this are dimension-incompatible.

If *this is empty or expr is not bounded from above, false is returned and sup_n, sup_d and maximum are left untouched.

virtual bool Parma_Polyhedra_Library::Any_Pointset::maximize	(	const Linear_Expression &	expr,
		Coefficient &	sup_n,
		Coefficient &	sup_d,
		bool &	maximum,
		Generator &	point
	)		const

pure virtual

Returns true if and only if *this is not empty and expr is bounded from above in *this, in which case the supremum value and a point where expr reaches it are computed.

Parameters

expr	The linear expression to be maximized subject to `*this`;
sup_n	The numerator of the supremum value;
sup_d	The denominator of the supremum value;
maximum	`true` if and only if the supremum is also the maximum value;
point	When maximization succeeds, will be assigned the point or closure point where `expr` reaches its supremum value.

Exceptions

std::invalid_argument Thrown if expr and *this are dimension-incompatible.

If *this is empty or expr is not bounded from above, false is returned and sup_n, sup_d, maximum and point are left untouched.

virtual bool Parma_Polyhedra_Library::Any_Pointset::minimize	(	const Linear_Expression &	expr,
		Coefficient &	inf_n,
		Coefficient &	inf_d,
		bool &	minimum
	)		const

pure virtual

Returns true if and only if *this is not empty and expr is bounded from below in *this, in which case the infimum value is computed.

Parameters

expr	The linear expression to be minimized subject to `*this`;
inf_n	The numerator of the infimum value;
inf_d	The denominator of the infimum value;
minimum	`true` if and only if the infimum is also the minimum value.

Exceptions

std::invalid_argument Thrown if expr and *this are dimension-incompatible.

If *this is empty or expr is not bounded from below, false is returned and inf_n, inf_d and minimum are left untouched.

virtual bool Parma_Polyhedra_Library::Any_Pointset::minimize	(	const Linear_Expression &	expr,
		Coefficient &	inf_n,
		Coefficient &	inf_d,
		bool &	minimum,
		Generator &	point
	)		const

pure virtual

Returns true if and only if *this is not empty and expr is bounded from below in *this, in which case the infimum value and a point where expr reaches it are computed.

Parameters

expr	The linear expression to be minimized subject to `*this`;
inf_n	The numerator of the infimum value;
inf_d	The denominator of the infimum value;
minimum	`true` if and only if the infimum is also the minimum value;
point	When minimization succeeds, will be assigned a point or closure point where `expr` reaches its infimum value.

Exceptions

std::invalid_argument Thrown if expr and *this are dimension-incompatible.

If *this is empty or expr is not bounded from below, false is returned and inf_n, inf_d, minimum and point are left untouched.

virtual bool Parma_Polyhedra_Library::Any_Pointset::OK ( ) const

pure virtual

Checks if all the invariants are satisfied.

void Parma_Polyhedra_Library::Any_Pointset::print ( ) const

Prints *this to std::cerr using operator<<.

Poly_Con_Relation Parma_Polyhedra_Library::Any_Pointset::relation_with ( const Constraint & c ) const

Returns the relations holding between the pointset *this and the constraint c.

Exceptions

std::invalid_argument Thrown if *this and constraint c are dimension-incompatible.

Poly_Gen_Relation Parma_Polyhedra_Library::Any_Pointset::relation_with ( const Generator & g ) const

Returns the relations holding between the pointset *this and the generator g.

Exceptions

std::invalid_argument Thrown if *this and generator g are dimension-incompatible.

virtual void Parma_Polyhedra_Library::Any_Pointset::remove_higher_space_dimensions ( dimension_type new_dimension )

pure virtual

Removes the higher dimensions of the vector space so that the resulting space will have dimension new_dimension.

Exceptions

std::invalid_argument Thrown if new_dimensions is greater than the space dimension of *this.

virtual void Parma_Polyhedra_Library::Any_Pointset::remove_space_dimensions ( const Variables_Set & vars )

pure virtual

Removes all the specified dimensions from the vector space.

Parameters

vars	The set of Variable objects corresponding to the space dimensions to be removed.

Exceptions

std::invalid_argument Thrown if *this is dimension-incompatible with one of the Variable objects contained in vars.

virtual dimension_type Parma_Polyhedra_Library::Any_Pointset::space_dimension ( ) const

pure virtual

Returns the dimension of the vector space enclosing *this.

virtual bool Parma_Polyhedra_Library::Any_Pointset::strictly_contains ( const Any_Pointset & y ) const

pure virtual

Returns true if and only if *this strictly contains y.

Exceptions

std::invalid_argument Thrown if *this and y are topology-incompatible or dimension-incompatible.

virtual void Parma_Polyhedra_Library::Any_Pointset::time_elapse_assign ( const Any_Pointset & y )

pure virtual

Assigns to *this the result of computing the time-elapse between *this and y.

Exceptions

std::invalid_argument Thrown if *this and y are topology-incompatible or dimension-incompatible.

void Parma_Polyhedra_Library::Any_Pointset::topological_closure_assign ( )

Assigns to *this its topological closure.

virtual memory_size_type Parma_Polyhedra_Library::Any_Pointset::total_memory_in_bytes ( ) const

pure virtual

Returns the total size in bytes of the memory occupied by *this.

virtual void Parma_Polyhedra_Library::Any_Pointset::unconstrain ( Variable var )

pure virtual

Computes the cylindrification of *this with respect to space dimension var, assigning the result to *this.

Parameters

var	The space dimension that will be unconstrained.

Exceptions

std::invalid_argument Thrown if var is not a space dimension of *this.

virtual void Parma_Polyhedra_Library::Any_Pointset::unconstrain ( const Variables_Set & vars )

pure virtual

Computes the cylindrification of *this with respect to the set of space dimensions vars, assigning the result to *this.

Parameters

vars	The set of space dimension that will be unconstrained.

Exceptions

std::invalid_argument Thrown if *this is dimension-incompatible with one of the Variable objects contained in vars.

virtual void Parma_Polyhedra_Library::Any_Pointset::upper_bound_assign ( const Any_Pointset & y )

pure virtual

Assigns to *this the smallest pointset, in the class of *this and y, that contains both *this and y.

Exceptions

std::invalid_argument Thrown if *this and y are topology-incompatible or dimension-incompatible.

Friends And Related Function Documentation

bool operator!=	(	const Any_Pointset &	x,
		const Any_Pointset &	y
	)

Note that x and y may be topology- and/or dimension-incompatible pointsets: in those cases, the value true is returned.

std::ostream & operator<<	(	std::ostream &	s,
		const Any_Pointset &	ph
	)

Writes a textual representation of ph on s: false is written if ph is an empty pointset; true is written if ph is a universe pointset; a minimized system of constraints and congruences ph is written otherwise, all constraints in one row separated by ", ".

bool operator==	(	const Any_Pointset &	x,
		const Any_Pointset &	y
	)

Note that x and y may be topology- and/or dimension-incompatible pointsets: in those cases, the value false is returned.

void swap	(	Any_Pointset &	x,
		Any_Pointset &	y
	)

The documentation for this class was generated from the following files:

Public Member Functions

Related Functions

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation

Friends And Related Function Documentation