#include <Floating_Point_Expression_defs.hh>

Inheritance diagram for Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >:

[legend]

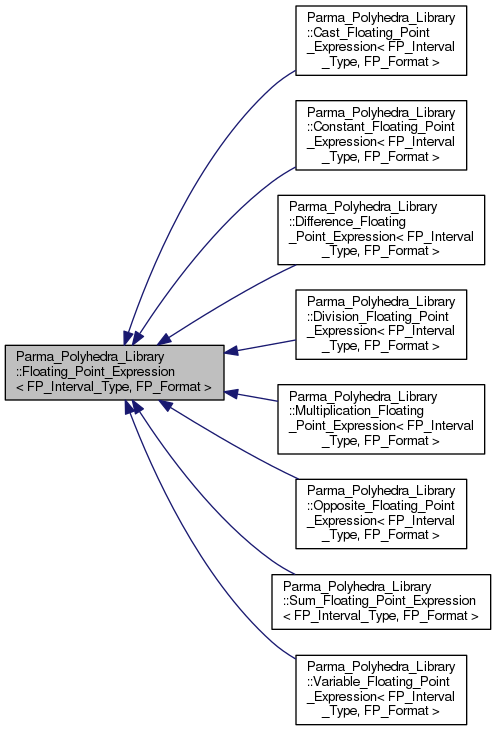
Public Types
typedef Linear_Form< FP_Interval_Type >	FP_Linear_Form
	Alias for a linear form with template argument `FP_Interval_Type`. More...

typedef Box< FP_Interval_Type >	FP_Interval_Abstract_Store
	Alias for a map that associates a variable index to an interval. More...

typedef std::map< dimension_type, FP_Linear_Form >	FP_Linear_Form_Abstract_Store
	Alias for a map that associates a variable index to a linear form. More...

typedef FP_Interval_Type::boundary_type	boundary_type
	The floating point format used by the analyzer. More...

typedef FP_Interval_Type::info_type	info_type
	The interval policy used by `FP_Interval_Type`. More...

Public Member Functions
virtual	~Floating_Point_Expression ()
	Destructor. More...

virtual bool	linearize (const FP_Interval_Abstract_Store &int_store, const FP_Linear_Form_Abstract_Store &lf_store, FP_Linear_Form &result) const =0
	Linearizes a floating point expression. More...

Static Public Member Functions
static bool	overflows (const FP_Linear_Form &lf)
	Verifies if a given linear form overflows. More...

static void	relative_error (const FP_Linear_Form &lf, FP_Linear_Form &result)
	Computes the relative error of a given linear form. More...

static void	intervalize (const FP_Linear_Form &lf, const FP_Interval_Abstract_Store &store, FP_Interval_Type &result)
	Makes `result` become an interval that overapproximates all the possible values of `lf` in the interval abstract store `store`. More...

Static Public Attributes
static FP_Interval_Type	absolute_error = compute_absolute_error()
	Absolute error. More...

Static Private Member Functions
static FP_Interval_Type	compute_absolute_error ()
	Computes the absolute error. More...

Detailed Description

template<typename FP_Interval_Type, typename FP_Format>
class Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >

\ A floating point expression on a given format.

This class represents a concrete floating point expression. This includes constants, floating point variables, binary and unary arithmetic operators.

Template type parameters

The class template type parameter FP_Interval_Type represents the type of the intervals used in the abstract domain. The interval bounds should have a floating point type.
The class template type parameter FP_Format represents the floating point format used in the concrete domain. This parameter must be a struct similar to the ones defined in file Float_defs.hh, even though it is sufficient to define the three fields BASE, MANTISSA_BITS and EXPONENT_BIAS.

Definition at line 55 of file Floating_Point_Expression_defs.hh.

Member Typedef Documentation

template<typename FP_Interval_Type, typename FP_Format>

typedef FP_Interval_Type::boundary_type Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >::boundary_type

The floating point format used by the analyzer.

Definition at line 81 of file Floating_Point_Expression_defs.hh.

template<typename FP_Interval_Type, typename FP_Format>

typedef Box<FP_Interval_Type> Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >::FP_Interval_Abstract_Store

Alias for a map that associates a variable index to an interval.

Alias for a Box storing lower and upper bounds for floating point variables.

The type a linear form abstract store associating each variable with an interval that correctly approximates its value.

Definition at line 70 of file Floating_Point_Expression_defs.hh.

template<typename FP_Interval_Type, typename FP_Format>

typedef Linear_Form<FP_Interval_Type> Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >::FP_Linear_Form

Alias for a linear form with template argument FP_Interval_Type.

Definition at line 60 of file Floating_Point_Expression_defs.hh.

template<typename FP_Interval_Type, typename FP_Format>

typedef std::map<dimension_type, FP_Linear_Form> Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >::FP_Linear_Form_Abstract_Store

Alias for a map that associates a variable index to a linear form.

The type a linear form abstract store associating each variable with a linear form that correctly approximates its value.

Definition at line 78 of file Floating_Point_Expression_defs.hh.

template<typename FP_Interval_Type, typename FP_Format>

typedef FP_Interval_Type::info_type Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >::info_type

The interval policy used by FP_Interval_Type.

Definition at line 84 of file Floating_Point_Expression_defs.hh.

Constructor & Destructor Documentation

template<typename FP_Interval_Type , typename FP_Format >

Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >::~Floating_Point_Expression ( )

inlinevirtual

Destructor.

Definition at line 35 of file Floating_Point_Expression_inlines.hh.

35 {}

Member Function Documentation

template<typename FP_Interval_Type , typename FP_Format >

FP_Interval_Type Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >::compute_absolute_error ( )

staticprivate

Computes the absolute error.

Static helper method that is used to compute the value of the public static field absolute_error.

Returns: The interval $[-\omega, \omega]$ corresponding to the value of absolute_error

Definition at line 95 of file Floating_Point_Expression_templates.hh.

References Parma_Polyhedra_Library::GREATER_OR_EQUAL, Parma_Polyhedra_Library::i_constraint(), and Parma_Polyhedra_Library::LESS_OR_EQUAL.

                          {
   typedef typename Floating_Point_Expression<FP_Interval_Type, FP_Format>
     ::boundary_type Boundary;
   boundary_type omega;
   omega = std::max(pow(static_cast<Boundary>(FP_Format::BASE),
                        static_cast<Boundary>(1 - FP_Format::EXPONENT_BIAS
                                              - FP_Format::MANTISSA_BITS)),
                    std::numeric_limits<Boundary>::denorm_min());
   FP_Interval_Type result;
   result.build(i_constraint(GREATER_OR_EQUAL, -omega),
                i_constraint(LESS_OR_EQUAL, omega));
   return result;
 }

template<typename FP_Interval_Type, typename FP_Format >

void Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >::intervalize	(	const FP_Linear_Form &	lf,
		const FP_Interval_Abstract_Store &	store,
		FP_Interval_Type &	result
	)

static

Makes result become an interval that overapproximates all the possible values of lf in the interval abstract store store.

Parameters

lf	The linear form to aproximate.
store	The abstract store.
result	The linear form that will be modified.

This method makes result become 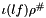$\iota(lf)\rho^{\#}$ , that is an interval defined as:

$\iota\left(i + \sum_{v \in \cV}i_{v}v\right)\rho^{\#} \defeq i \asifp \left(\bigoplus_{v \in \cV}{}^{\#}i_{v} \amifp \rho^{\#}(v)\right)$

Definition at line 76 of file Floating_Point_Expression_templates.hh.

References Parma_Polyhedra_Library::Linear_Form< C >::coefficient(), Parma_Polyhedra_Library::Box< ITV >::get_interval(), Parma_Polyhedra_Library::Linear_Form< C >::inhomogeneous_term(), Parma_Polyhedra_Library::Linear_Form< C >::space_dimension(), and Parma_Polyhedra_Library::Box< ITV >::space_dimension().

                                         {
   result = FP_Interval_Type(lf.inhomogeneous_term());
   dimension_type dimension = lf.space_dimension();
   assert(dimension <= store.space_dimension());
   for (dimension_type i = 0; i < dimension; ++i) {
     FP_Interval_Type current_addend = lf.coefficient(Variable(i));
     const FP_Interval_Type& curr_int = store.get_interval(Variable(i));
     current_addend *= curr_int;
     result += current_addend;
   }
 
   return;
 }

template<typename FP_Interval_Type, typename FP_Format>

virtual bool Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >::linearize	(	const FP_Interval_Abstract_Store &	int_store,
		const FP_Linear_Form_Abstract_Store &	lf_store,
		FP_Linear_Form &	result
	)		const

pure virtual

Linearizes a floating point expression.

Makes result become a linear form that correctly approximates the value of the floating point expression in the given composite abstract store.

Parameters

int_store	The interval abstract store.
lf_store	The linear form abstract store.
result	Becomes the linearized expression.

Returns: true if the linearization succeeded, false otherwise.

Formally, if *this represents the expression 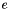$e$ , int_store represents the interval abstract store 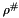$\rho^{\#}$ and lf_store represents the linear form abstract store 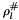$\rho^{\#}_l$ , then result will become 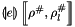$\linexprenv{e}{\rho^{\#}}{\rho^{\#}_l}$ if the linearization succeeds.

All variables occurring in the floating point expression MUST have an associated interval in int_store. If this precondition is not met, calling the method causes an undefined behavior.

template<typename FP_Interval_Type , typename FP_Format >

bool Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >::overflows ( const FP_Linear_Form & lf )

inlinestatic

Verifies if a given linear form overflows.

Parameters

lf	The linear form to verify.

Returns: Returns false if all coefficients in lf are bounded, true otherwise.

Definition at line 40 of file Floating_Point_Expression_inlines.hh.

References Parma_Polyhedra_Library::Linear_Form< C >::coefficient(), Parma_Polyhedra_Library::Linear_Form< C >::inhomogeneous_term(), and Parma_Polyhedra_Library::Linear_Form< C >::space_dimension().

                                     {
   if (!lf.inhomogeneous_term().is_bounded()) {
     return true;
   }
 
   dimension_type dimension = lf.space_dimension();
   for (dimension_type i = 0; i < dimension; ++i) {
     if (!lf.coefficient(Variable(i)).is_bounded()) {
       return true;
     }
   }
 
   return false;
 }

template<typename FP_Interval_Type , typename FP_Format >

void Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >::relative_error	(	const FP_Linear_Form &	lf,
		FP_Linear_Form &	result
	)

static

Computes the relative error of a given linear form.

Static helper method that is used by linearize to account for the relative errors on lf.

Parameters

lf	The linear form used to compute the relative error.
result	Becomes the linear form corresponding to a relative error committed on `lf`.

This method makes result become a linear form obtained by evaluating the function 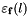$\varepsilon_{\mathbf{f}}(l)$ on the linear form lf. This function is defined such as:

$\varepsilon_{\mathbf{f}}\left([a, b]+\sum_{v \in \cV}[a_{v}, b_{v}]v\right) \defeq (\textrm{max}(|a|, |b|) \amifp [-\beta^{-\textrm{p}}, \beta^{-\textrm{p}}]) + \sum_{v \in \cV}(\textrm{max}(|a_{v}|,|b_{v}|) \amifp [-\beta^{-\textrm{p}}, \beta^{-\textrm{p}}])v$

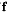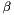where p is the fraction size in bits for the format $\mathbf{f}$ and $\beta$ the base.

Definition at line 36 of file Floating_Point_Expression_templates.hh.

References Parma_Polyhedra_Library::Linear_Form< C >::coefficient(), Parma_Polyhedra_Library::GREATER_OR_EQUAL, Parma_Polyhedra_Library::i_constraint(), Parma_Polyhedra_Library::Linear_Form< C >::inhomogeneous_term(), Parma_Polyhedra_Library::LESS_OR_EQUAL, and Parma_Polyhedra_Library::Linear_Form< C >::space_dimension().

                                                                  {
 
   FP_Interval_Type error_propagator;
   boundary_type lb = -pow(FP_Format::BASE,
   -static_cast<typename Floating_Point_Expression<FP_Interval_Type, FP_Format>
   ::boundary_type>(FP_Format::MANTISSA_BITS));
   error_propagator.build(i_constraint(GREATER_OR_EQUAL, lb),
                          i_constraint(LESS_OR_EQUAL, -lb));
 
   // Handle the inhomogeneous term.
   const FP_Interval_Type* current_term = &lf.inhomogeneous_term();
   assert(current_term->is_bounded());
 
   FP_Interval_Type
     current_multiplier(std::max(std::abs(current_term->lower()),
                                 std::abs(current_term->upper())));
   FP_Linear_Form current_result_term(current_multiplier);
   current_result_term *= error_propagator;
   result = FP_Linear_Form(current_result_term);
 
   // Handle the other terms.
   dimension_type dimension = lf.space_dimension();
   for (dimension_type i = 0; i < dimension; ++i) {
     current_term = &lf.coefficient(Variable(i));
     assert(current_term->is_bounded());
     current_multiplier
       = FP_Interval_Type(std::max(std::abs(current_term->lower()),
                                   std::abs(current_term->upper())));
     current_result_term = FP_Linear_Form(Variable(i));
     current_result_term *= current_multiplier;
     current_result_term *= error_propagator;
     result += current_result_term;
   }
 
   return;
 }

Member Data Documentation

template<typename FP_Interval_Type, typename FP_Format>

FP_Interval_Type Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >::absolute_error = compute_absolute_error()

static

Absolute error.

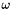Represents the interval $[-\omega, \omega]$ where $\omega$ is the smallest non-zero positive number in the less precise floating point format between the analyzer format and the analyzed format.

Definition at line 126 of file Floating_Point_Expression_defs.hh.

The documentation for this class was generated from the following files:

Public Types

Public Member Functions

Static Public Member Functions

Static Public Attributes

Static Private Member Functions

Detailed Description

template<typename FP_Interval_Type, typename FP_Format> class Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation

template<typename FP_Interval_Type, typename FP_Format>
class Parma_Polyhedra_Library::Floating_Point_Expression< FP_Interval_Type, FP_Format >